无轴轮缘推进器(Shaftless Rim-driven Thruster, SRDT)是近年来发展起来的一种新型推进技术,其借助导管内布局驱动电机,从而取消驱动长轴,达到减振降噪、增加紧凑性、比功率和机动性的目的,符合水下推进高集成发展趋势的需求[1-2]。然而,SRDT的集成化特点势必要求深入挖掘轮缘桨、电机及控制等各单元潜能,并确保相互之间的高度兼容,这使该种推进器的设计和研发难度大为增加。如SRDT电机定子是布局在狭小导管空间内的,由于电机转矩与其铁芯体积成正比,所以其转矩密度必须很高,致使过载余量有限;因SRDT无法配置位置传感器,存在无负载反馈的开环调控低速区间,此时负载动特性若出现偏差,控制难度大;作为辅推RDT需面临海浪、风力、海洋流速等自然条件引起的冲击变化,机动操纵频繁,要求SRDT具有高动态响应能力,以及电机具备长时过载能力等。为解决上述诸种问题,充分探明SRDT负载特性,特别是动态特性是非常必要的,其直接关乎推进系统的稳定性和可靠性,也影响推进系统的声隐身性,乃至对舰艇生存和高机动作战能力发挥都具有重要意义。
目前,关于舰船推进器负载动态特性研究大多还集中于传统推进器仿真和实验方面,如国外挪威科技大学、ABB、SIEMENS、ALSTON等研究机构都建有大型船舶电力推进实验室,都曾系统地对传统船舶电力推进仿真开展过研究。其中,挪威科技大学在船舶电力推进仿真系统领域有着丰富研究成果[3],尤其在模拟不同工况下螺旋桨的负载特性方面有重大突破[4]。国内中船712研究所、集美大学等相关单位也建有电力推进实验室,开展了负载动态特性的相关研究[5]。从国内外公开文献看,迄今还鲜有涉及无轴轮缘推进器动态特性仿真及试验的研究,对于轮缘推进器大多以稳态特性研究居多。如美国通用电船公司自20世纪90年代开始就对SRDT敞水性能开展了大量研究,指出轮缘推进器可比传统轴驱推进器高出5%~10%敞水效率[6]。目前国外已有一些SRDT产品开始步入应用,最大功率可达800 kW,用于千吨级舰船[7]。在国内,中船重工702研究所最早于20世纪90年代开始对SRDT进行研究,开发了有毂式20 kW级原理样机,系统地研究了导管、螺旋桨和间隙等边界因素对SRDT的性能影响[8]。陈政宏和李宗卫利[9]用PIV对SRDT试验分析,发现缘驱无毂螺旋桨可显著降低尾涡流损失。中船705研究所也曾从电机的角度研究过无轴推进特性[10]。这些从稳态角度关注SRDT特性的研究虽然可为设计提供初步参考,但SRDT作为一种有着高动态工况特点及过载带宽局限的推进器,关注其动态负载特性对其工程实用化设计更为重要。
鉴于无轴轮缘推进器负载动态特性的重要性,以及由于其独具的特殊构型,构建模拟实验负载难度大且成本高的现实,本文针对无轴轮缘推进器开展负载动态特性数值研究,为轮缘推进系统设计和优化提供参考依据,促进其机动推进性能提升,同时也可为轮缘推进的航行器操纵性奠定必要的动力学基础。
1 稳态特性数值验证无轴轮缘推进器作为一种新型推进器,迄今鲜有公开的水动力性能试验数据。为了研究轮缘推进器的负载动态特性,必须首先获取其稳态的敞水特性。
本文采用数值模拟方法获取其敞水性能。为确保所获取水动力特性的有效性和准确性,本文选取与轮缘推进具有相近结构的导管桨作为参考对比,所选轮缘推进器为所选导管桨的改型设计,以便利于对无轴化的针对性对比。本文选取具有试验数据的导管桨Ka4-7010+19A,对其进行无轴化简单推进器改型,对两者分别进行数值模拟,三维模型如图1所示。

|
图 1 导管螺旋桨和无轴轮缘推进器三维模型 Fig. 1 Three-dimensional model of ducted propeller and shaftless Rim-driven Thruster |
网格划分采用混合结构模式。对于转子域,采用结构化网格划分,以提高桨区流场的精度;对于静止域,采用非结构网格划分;对近壁面处进行边界层网格加密。以y+=3设定底层边界层高度,边界层总层数为6层,网格划分如图2所示。

|
图 2 计算域网格剖分 Fig. 2 Computational domain meshing |
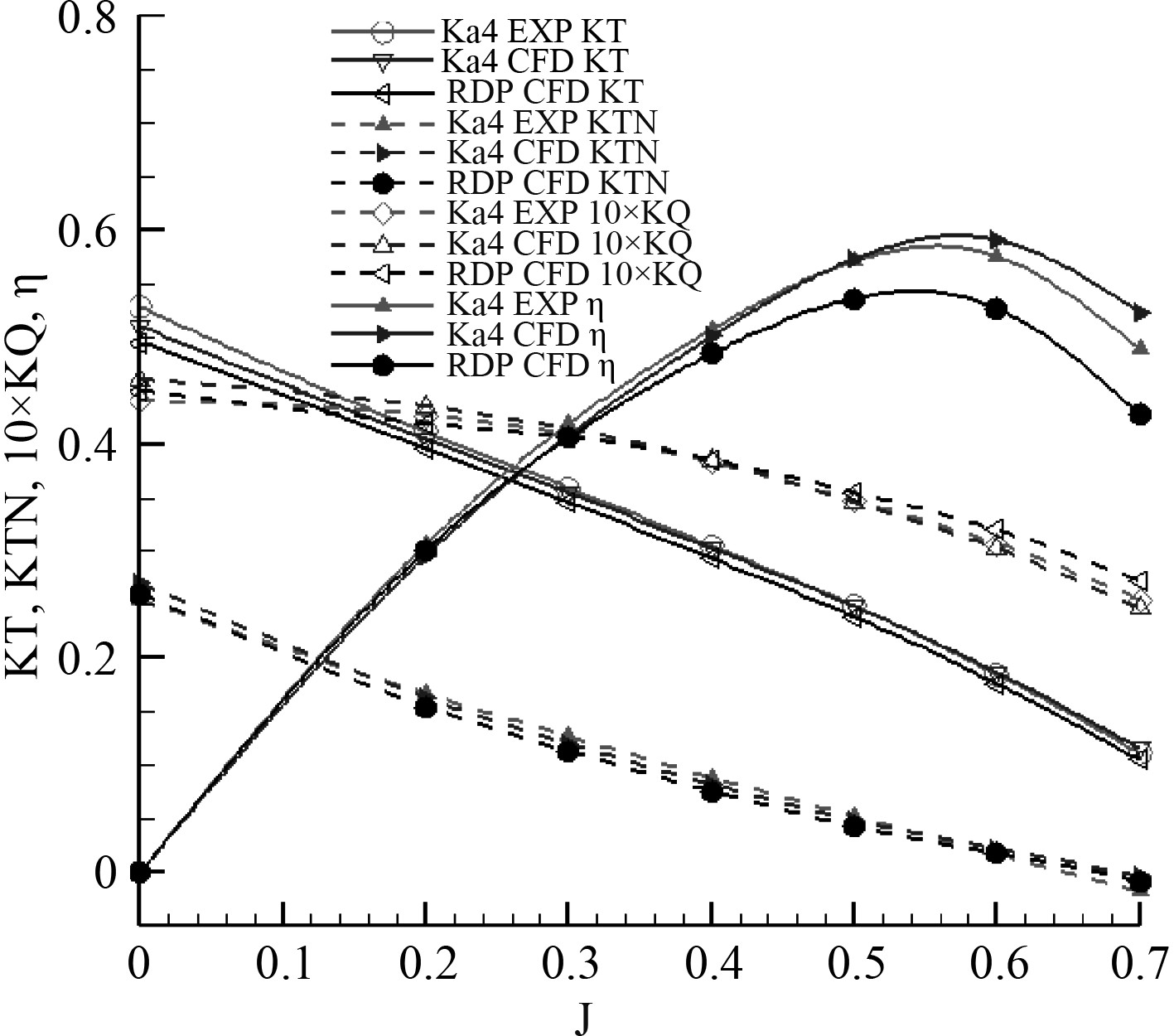
基于雷诺时均方法(RANS)离散求解流动不可压缩流体N-S方程,求解结果如图3所示。可以发现,Ka4-7010+19A的数值结果与试验吻合较好。误差范围4%以内,仿真方法的有效性获得了验证。SRDT与Ka4-7010+19A的性能比较相近,但也存在如下差异:SRDP的推力系数在全进速比范围内略低于导管桨;扭矩系数在低进速比下略低于导管桨,高进速比下略高于导管桨;效率在低进速比下接近导管桨,高进速比下明显低于导管桨。这主要是因为RDP没有轮毂端壁,且轮缘是随桨一起转动的,导致了轴向诱导速度比导管桨小,推力系数变小,效率也在高进速比时明显变小。本文CFD方法有效预示出了SRDP与导管桨的性能既相近又存在着差异,说明用其研究SRDP水动力学性能具有参考性。
|
图 3 SRDT与导管桨敞水特性曲线对比 Fig. 3 Comparison of open water characteristic curve between SRDT and ducted propeller |
对于航行器推进器,其进速比J、进程
| $J{\rm{ = }}\frac{{{h_p}}}{{{D_p}}} = \frac{{{V_p}}}{{n{D_p}}},$ | (1) |
航行器动态航行不同于其稳态航行,进速比J范围变化很大。比如当推进器从正航向倒航过渡过程中,当转速n经过0附近时,因惯性的存在,航速
| $ {J'}{\rm{ = }}\dfrac{{ {V_p}}}{{\sqrt {V_p^2 + {n^2}D_p^2} }} = \left\{ \begin{array}{l} 1,\begin{array}{*{20}{c}} {}&{n = 0,{V_p} > 0} , \end{array} \\ \dfrac{J}{{\sqrt {1 + {J^2}} }},\begin{array}{*{20}{c}} {}&{n > 0}, \end{array} \\ - \dfrac{{ J}}{{\sqrt {1 + {J^2}} }},\begin{array}{*{20}{c}} {}&{n < 0} , \end{array} \\ - 1,\begin{array}{*{20}{c}} {}&{n = 0,{V_p} > 0} , \end{array} \end{array} \right. $ | (2) |
| $ {J'}{\rm{ = }}\frac{{ {V_p}}}{{\sqrt {V_p^2 + {n^2}D_p^2} }} = \frac{{ {V_p}}}{{{D_p}|n|\sqrt {1 + V_p^2/{n^2}D_p^2} }} ,$ | (3) |
| $K_T' = \frac{T}{{\rho D_p^2\left( {V_p^2 + {n^2}D_p^2} \right)}},$ | (4) |
| $K_M' = \frac{M}{{\rho D_p^3\left( {V_p^2 + {n^2}D_p^2} \right)}}.$ | (5) |
式中:
将式(1)和式(2)分别代入式(4)和式(5)可获得T和扭矩M分别为:
| $T = \frac{{\rho D_p^2K_T'V_p^2}}{{J{'^2}}},$ | (6) |
| $M = \frac{{\rho D_p^3K_M'V_p^2}}{{J{'^2}}}{\text{。}}$ | (7) |
水下推进器一般处于航行器尾部,实际航行时对来流的抽吸作用会较裸航体额外增加一部分摩擦阻力和压差阻力,推进器只有多出一部分推力来抵消这一部分阻力,才能使有效推力与裸航体阻力值平衡,所以,工程设计中一般引入一推力减额系t,则推进器的有效推力表示为:
| ${T_{\rm{e}}}{\rm{ = }}T\left( {1{\rm{ - }}t} \right) = \left( {1{\rm{ - }}t} \right)\frac{{\rho D_p^2K_T'V_p^2}}{{J{'^2}}}{\text{,}}$ | (8) |
| $\left\{ \begin{array}{l} t = 0.33,\begin{array}{*{20}{c}} {}&{n < - {n_e}} \end{array} , \\ t = - 0.33n/{n_e},\begin{array}{*{20}{c}} {}&{ - {n_e} \leqslant n < {n_e}} \end{array} , \\ t = 0.33n/{n_e},\begin{array}{*{20}{c}} {}&{0 \leqslant n < {n_e}} \end{array} , \\ t = - 0.13,\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {}&{n \geqslant {n_e}} \end{array}} \end{array}{\text{。}} \end{array} \right.$ | (9) |
其中,
根据牛顿第二定律,航体-推进器系统的运动方程可表示为:
| $\left( {m + \Delta m} \right)\frac{{{\rm d}{V_s}}}{{{\rm d}t}} = {T_{\rm{e}}}{\rm{ - }}R{\text{。}}$ | (10) |
其中,
| $ {V}_{p}={V}_{s}(1-\omega),$ | (11) |
| $\omega {\rm{ = }}0.55{C_b} - 0.2,$ | (12) |
其中,
航行器所受到的阻力
| $R = ({C_f} + \Delta {C_f}) \cdot \frac{1}{2}\rho SV_s^2{\text{。}}$ | (13) |
其中,
| ${C_f} = \frac{{0.075}}{{{{(\lg {{Re}} - 2)}^2}}}{\text{,}}$ | (14) |
其中,Re为船舶航行的雷诺数。
推进器旋转运动动力学方程为:
| $\left( {I + \Delta I} \right)\frac{{60}}{\text{π} }\frac{{{\rm d}n}}{{{\rm d}t}} = {\rm{ }}{M_0}{\rm{ - }}M {\text{。}}$ | (15) |
其中:
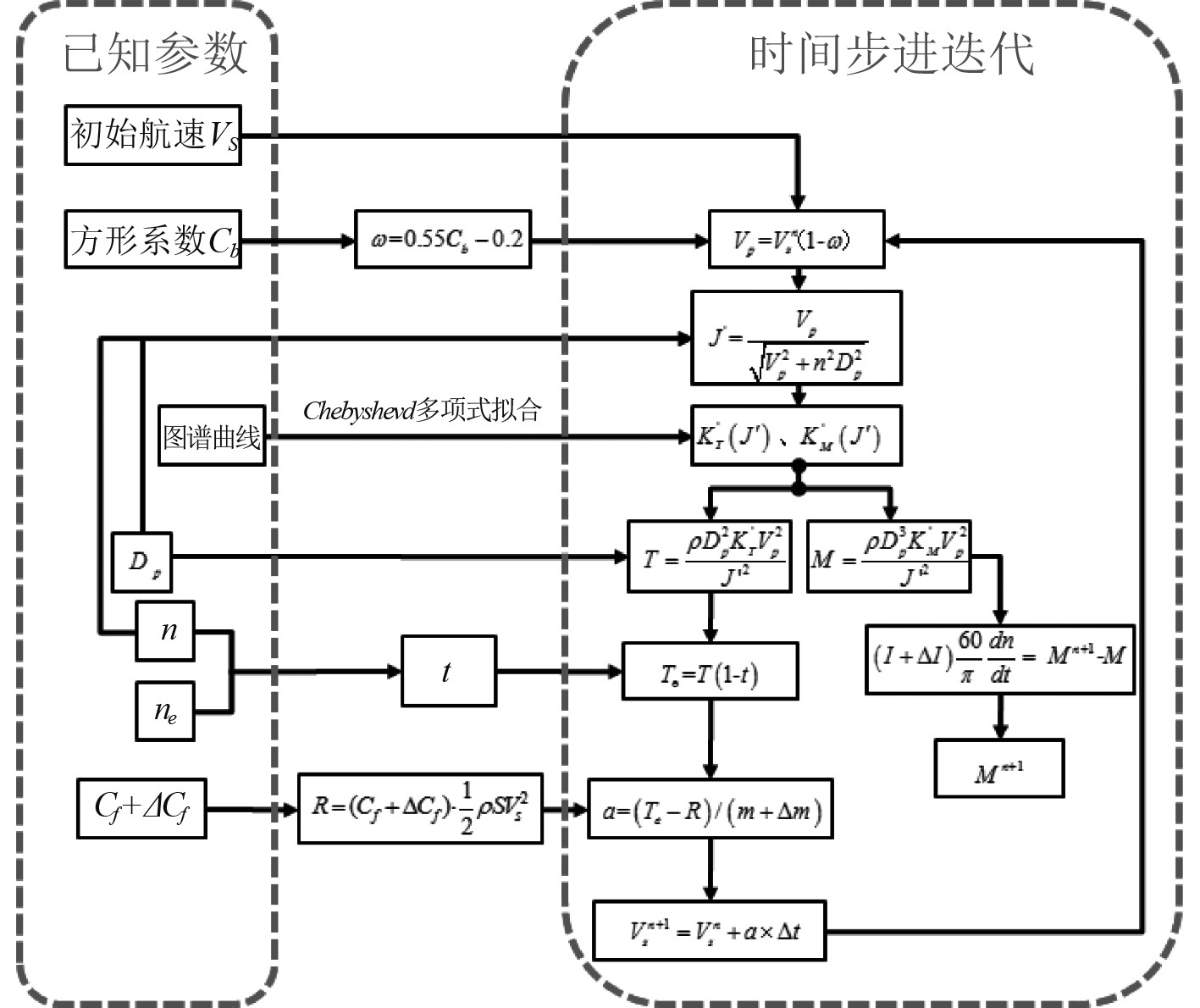
由船桨特性公式可以得到如图4所示的船桨数学模型。
|
图 4 船桨耦合数学模型图 Fig. 4 Ship-propeller coupling mathematical model diagram |
为获取无轴推进带来的动态特性差异,本文选取某一导管螺旋桨电推进船舶作为验证算例,并保持该导管推进器电机定转子重量、盘面直径、导管型线和螺距比等几何要素与无轴轮缘推进器一致,以便显著对比无轴与有轴之间动态特性。选定某电力推进导管桨船舶,该船最大航行速度15 kn,螺旋桨盘面直径0.8 m,船体总重量 100 t。以前文数值方法获取无轴轮缘推进器的敞水特性曲线,同样的初始航速条件下,分别进行典型的正车启动和停车2种工况下负载特性动态仿真,对比分析推进形式下特性曲线。表1给出了该船参数及实际航行记录的相关数据,以便于后续与仿真结果对比。
|
|
表 1 船舶参数及航行记录数据 Tab.1 Ship parameters and voyage record data |
1)直接启动
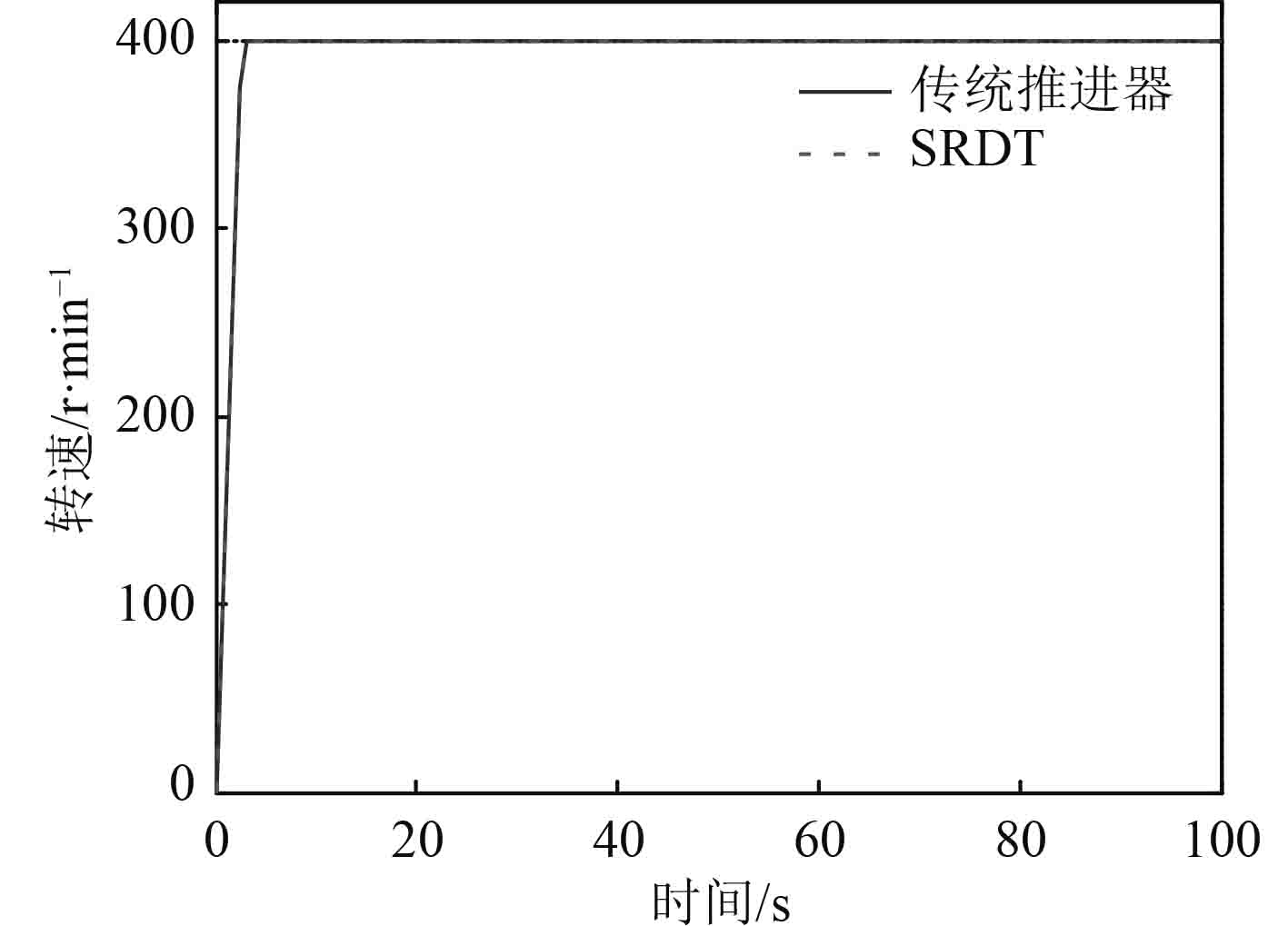
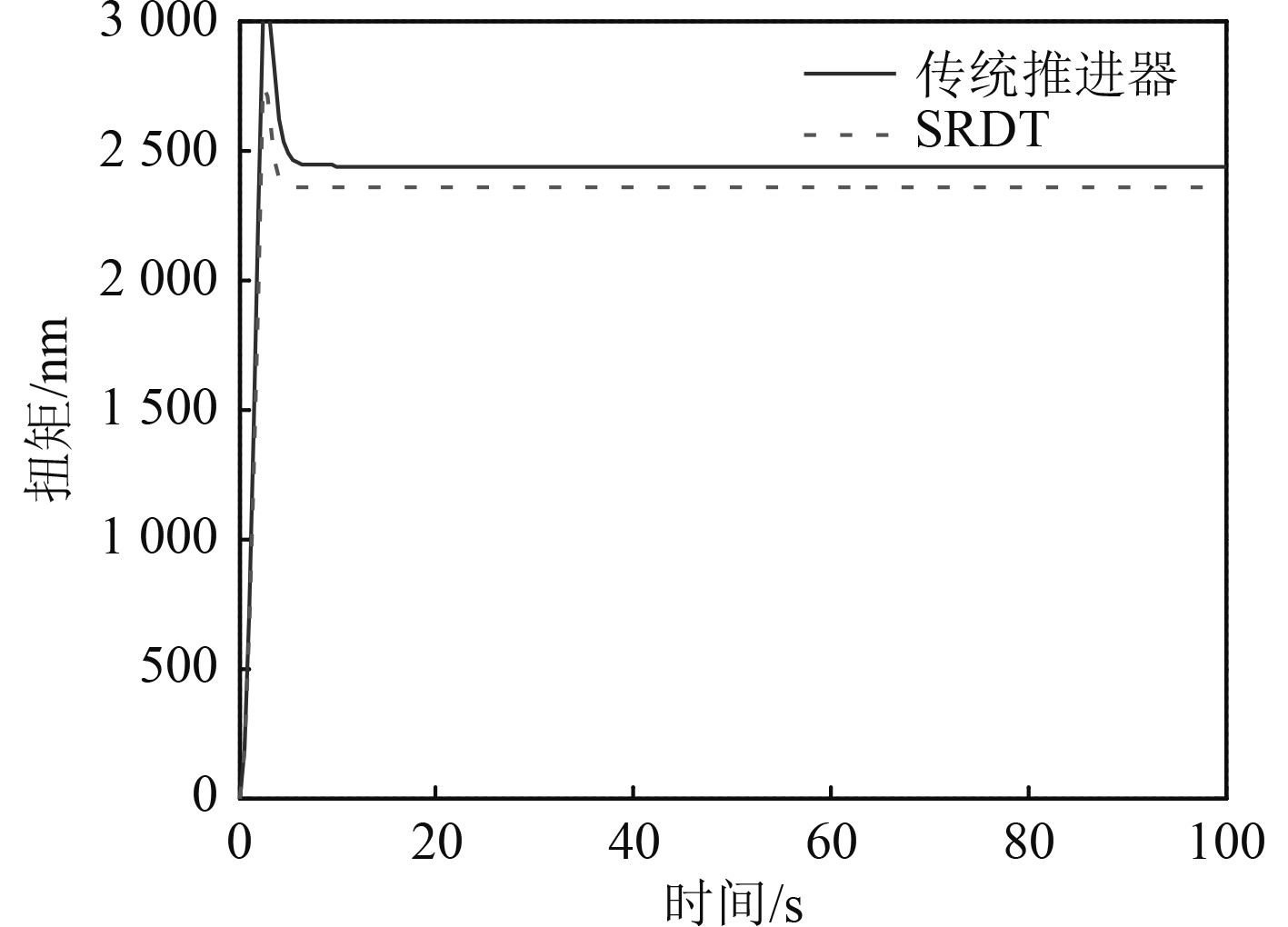
直接启动是为了最快达到目标转速,电机快速直接工作,推进器转速迅速升高,极短时间内即可达到目标转速。动态仿真的推进器转速n、航体航速Vs 以及推进器扭矩M变化情况如图5~图7所示。
|
图 5 桨速的响应过程 Fig. 5 Response process of propeller rotation speed |

|
图 6 船舶航速的响应过程 Fig. 6 The response process of ship sailing speed |
|
图 7 螺旋桨转矩响应过程 Fig. 7 Propeller torque response process |
由图5~图7可以看出,直接启动时,航速到达最大所需时间约为7.4 s,与该船航行记录的8 s比较接近,电机的峰值功率为126.6 kW,与航行记录的129 kW接近,表明本文仿真方法的有效性。仿真表明,电机转速被控制迅速达到最大转速400 r/min,无轴推进和传统桨的扭矩都是迅速接近峰值,两者扭矩趋势都是先增大后减小,最后逐渐平稳下来维持恒定值。两者提交的航速都很快随着转速达到最高值而达到最高航速15 kn。从中可以发现,2种推进存在显著差别。首先,峰值扭矩不同,无轴推进的峰值扭矩明显小于传统桨推进的扭矩,且达到平稳航行时,其扭矩也较传统推进小。其次,无轴推进的启动响应比传统推进快,大约提前了2 s。其主要原因是无轴轮缘推进器具有更小的启动力矩特性,以及更紧凑的结构所致。
直接启动过程仿真表明,急加速的起始阶段桨轴过载严重,这种状况对设备的损害较大。而采用无轴推进方式能在一定程度上减少这种伤害。
2)分级启动
分级启动一般可分为3个启动阶段,其目的是分级逐渐提高推进器转速到指定值。将推进器分别按125 r/min,250 r/min,400 r/min三级转速设定进行分级起动,转速n、船速Vs以及推进器扭矩M从启动到完全稳定的动态曲线如图8~图10所示。

|
图 8 桨速的响应过程 Fig. 8 Response process of propeller rotation speed |

|
图 9 船舶航速响应过程 Fig. 9 The response process of ship sailing speed |
|
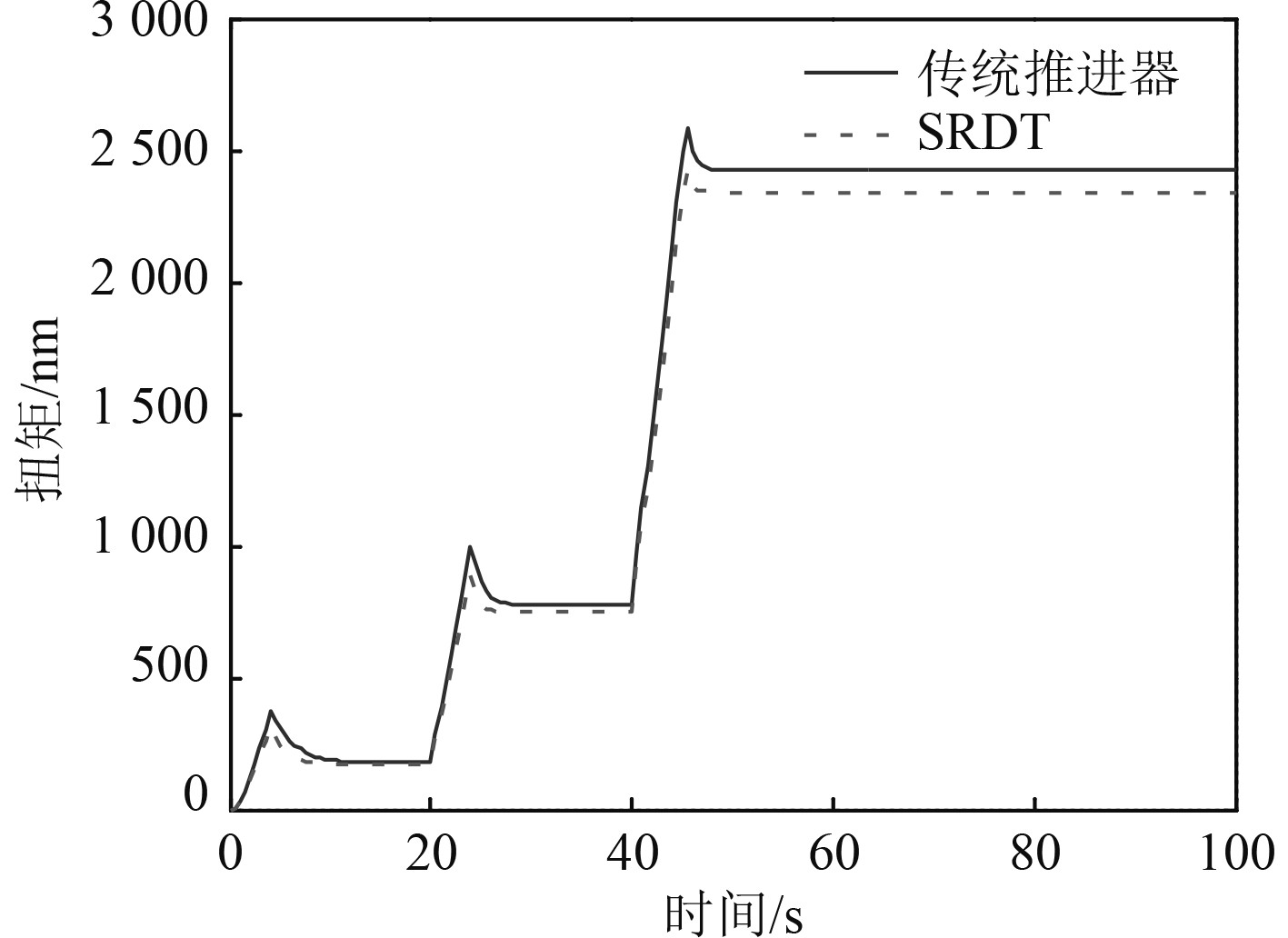
图 10 螺旋桨转矩响应过程 Fig. 10 Propeller torque response process |
分级启动仿真曲线可以发现,船舶一级加速后电机开始缓慢运行,推进器扭矩此时较低,船舶的航速缓缓提升。约5 s以后,船舶航速加速减缓并稳定在低速航行,2种推进器的转速几乎都能很快稳定在125 r/min,扭矩呈先增至一峰值后渐渐趋于稳定趋势。扭矩趋稳历时较长,约10 s的时间。扭矩达到约260 Nm。第20 s和40 s时分别开始第2次和第3次加速,2种推进器的转速和扭矩变化状态与第1次加速呈相同趋势,航行器航速也呈同样特点。最终,航行器航速达到15 kn,传统推进器的最大峰值扭矩达到了2.64 kNm,平稳后扭矩达到2.5 kNm,而轮缘推进器最大峰值扭矩为2.46 kNm,平稳后扭矩2.4 kNm,均比传统推进器小。
相比直接启动,无论是轮缘推进还是传统推进,分级启动最终的推进器扭矩峰值扭矩较小,分别约为直接启动扭矩的88%和83%。轮缘推进器比传统推进更容易在各级启动时先到达稳定航速,最终峰值扭矩也比传统推进的扭矩小。
3.2 正车启动后停车船舶经常会在正车稳定航行时进行停车操作,一般停车操作可以分2种方式:紧急停车和分级停车。与启动情况一样,本文分别对2种停车方式进行动态航行仿真,并对比无轴与传统推进的动态特性。
1)紧急停车
紧急停车是指在船舶航行过程中发生突遇情况时紧急制动,紧急停车过程中推进器的转速n、船速Vs和推进器扭矩M的动态仿真如图11~图13所示。
|
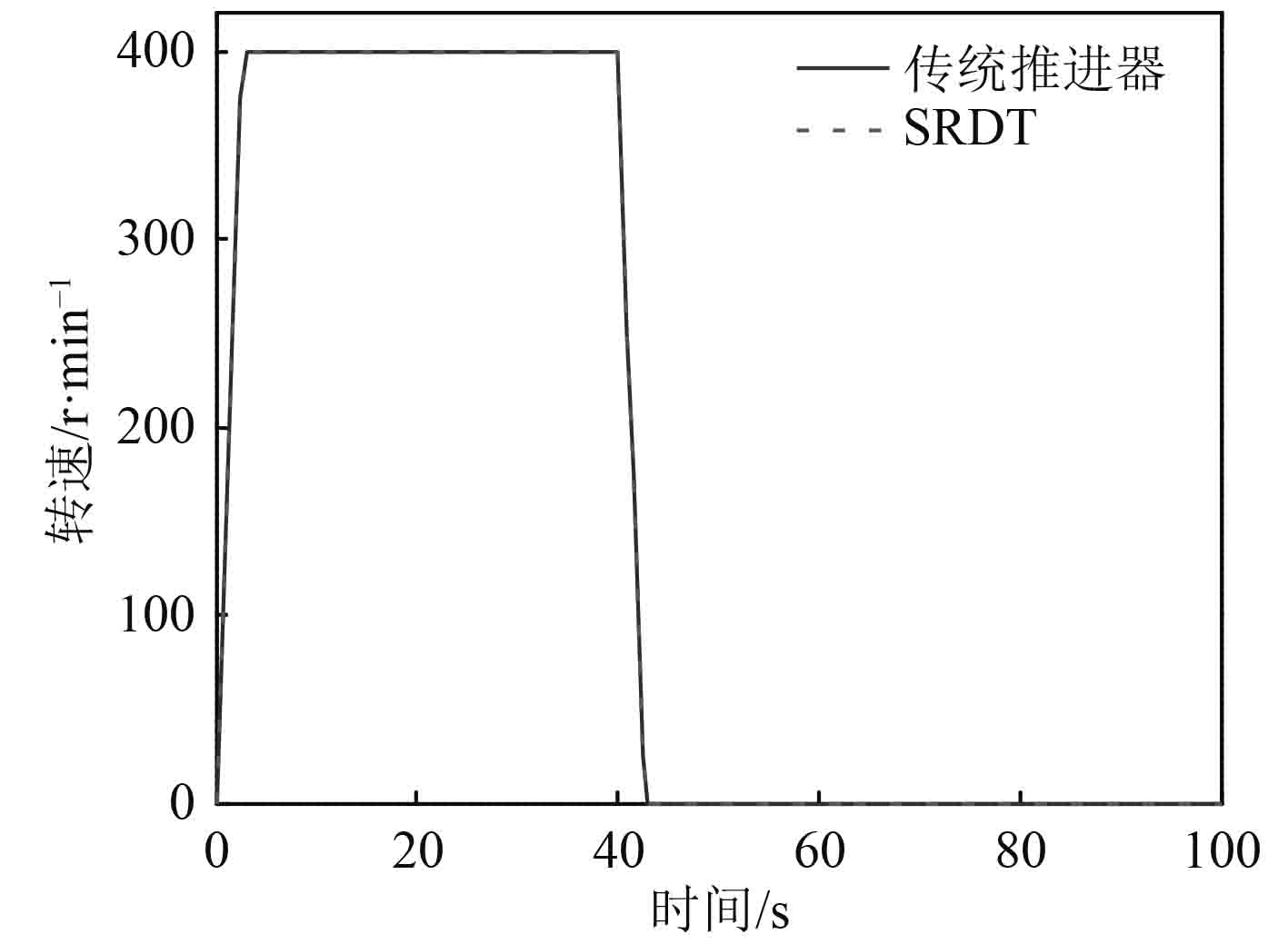
图 11 桨转速的响应过程 Fig. 11 Response process of propeller rotation speed |
|
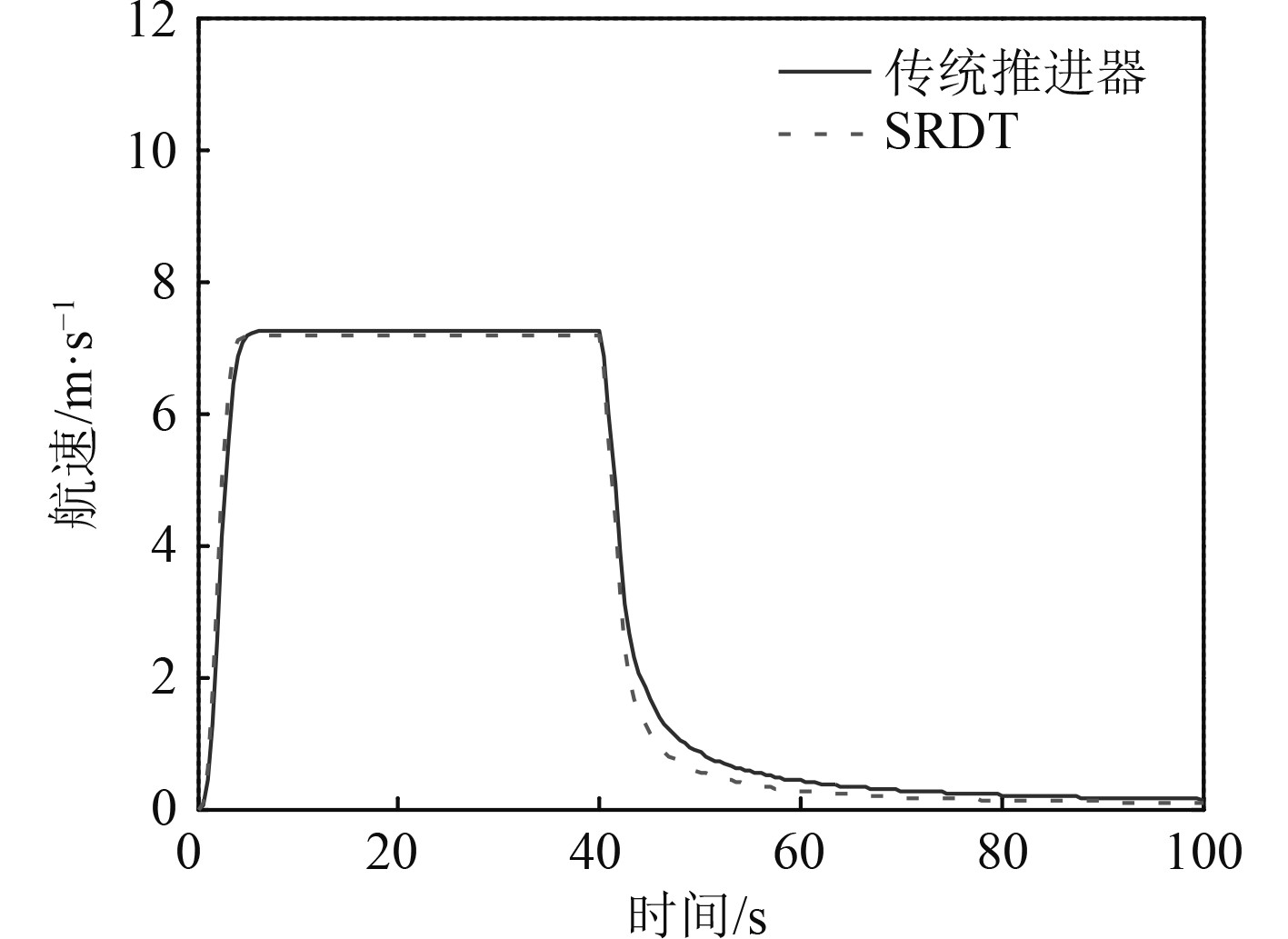
图 12 船舶航速响应过程 Fig. 12 The response process of ship sailing speed |
|
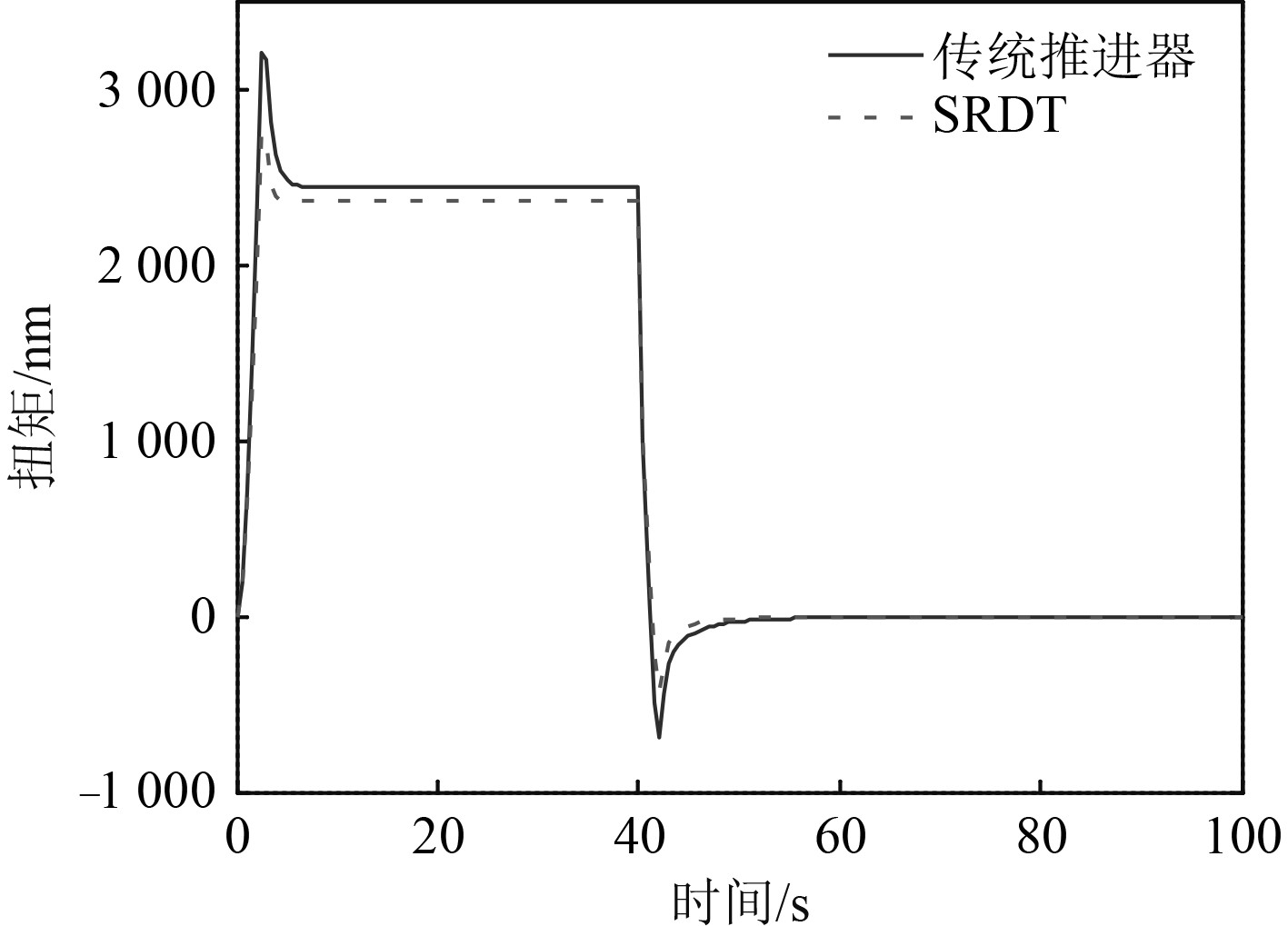
图 13 螺旋桨转矩响应过程 Fig. 13 Propeller torque response process |
从动态仿真图可以发现,当在40 s时使船舶从稳定航行状态下紧急制动,将推进器转速从400 r/min直接降到不转,2种推进形式的船舶航速都由15 kn迅速下降,其中,无轴推进船航速比有轴传统推进更快接近零航速。2种推进器的转矩都能从第40 s时的正向2.4 kNm 迅速变为反向,并经一反向峰值,约经历10 s后而逐渐减小趋于零扭矩。其中,无轴推进的扭矩反向峰值较小,达到了0.5 kNm,明显有轴推进反向扭矩值0.7 kNm小许多。
从紧急制动的仿真中可以看出,航速从最大减小接近0所需时间约为62 s,与该船航行记录的64 s比较接近,电机的反向峰值功率为33.8 kW,与航行记录的36 kW接近。说明本文仿真方法具有有效性。仿真表明,无论是有轴还是无轴推进,其转矩在短时间内突然由正值变为负值,并且变化幅度均超过了3 kNm,过载十分严重,此种模式将极大损害推进轴系和推进电机,易造成事故或增加维护成本。相比而言,无轴推进的过载稍小,因不存在细长轴系,其损害仅限于电机部分。但因电机为轮缘转子构型,尺寸半径大,其扭矩载荷较小,将损害大大降低,从这一点可以体现出无轴推进具有易于维护的优势。
2)分级停车
分级停车是指船舶从稳定的正向航行逐渐减速至静止的停车操纵,一般按两级减速进行。分级停车过程中推进器的转速n、船速Vs和推进器扭矩M的动态仿真如图14~图16所示。
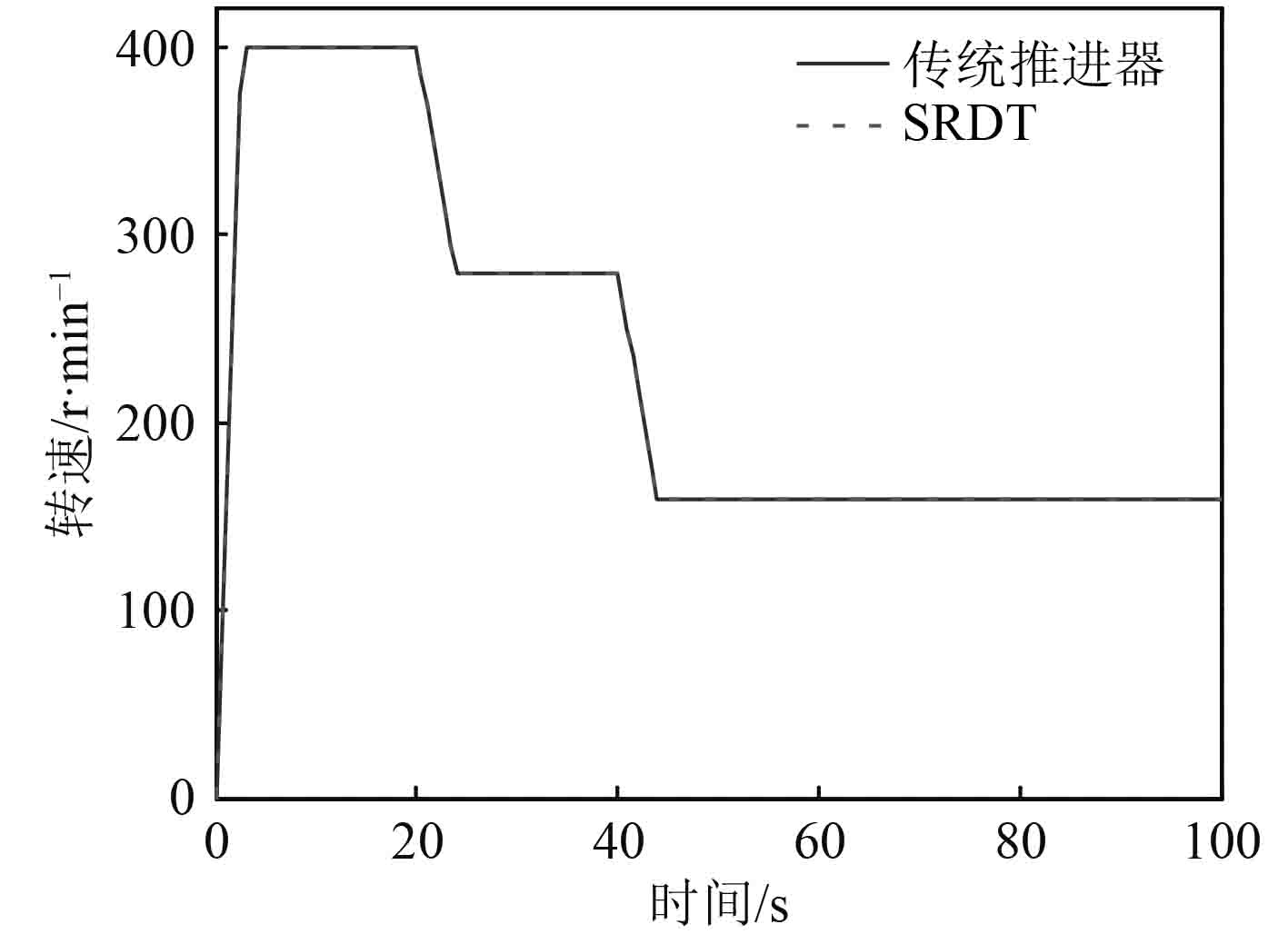
|
图 14 螺旋桨转速响应过程 Fig. 14 Response process of propeller rotation speed |
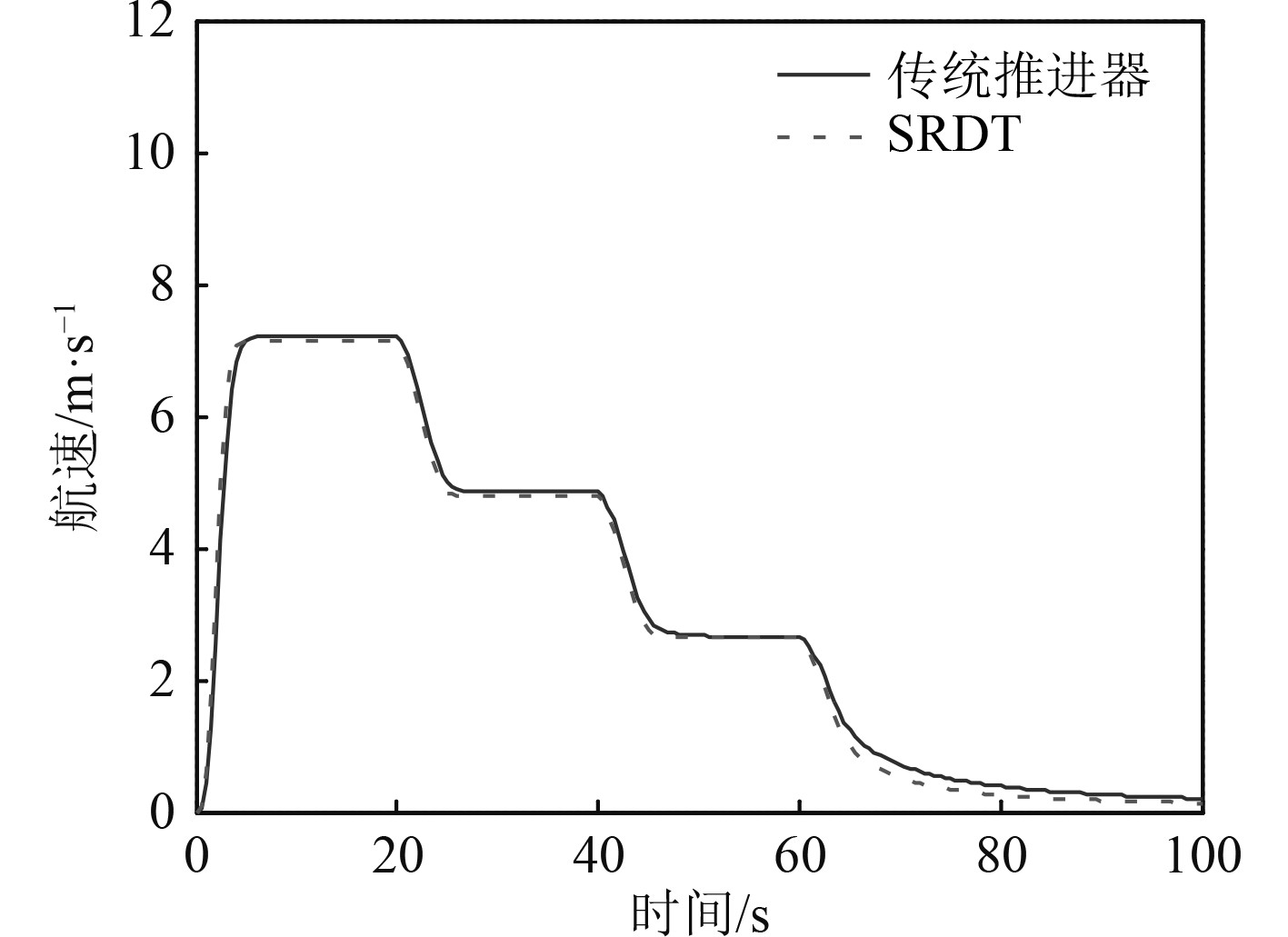
|
图 15 艇航速响应过程 Fig. 15 The response process of ship sailing speed |

|
图 16 螺旋桨转矩响应过程 Fig. 16 Propeller torque response process |
从分级停车动态仿真图可以发现,当在20 s时使船舶从稳定航行状态下进行第1次制动,将推进器转速从400 r/min降到280 r/min,2种推进形式的船舶航速都由15 kn相应下降至一航速后稳定航行,其中,无轴推进船航速比有轴传统推进稍快接近零航速。2种推进器的转矩都能从第20 s时的正向2.4 kNm 逐渐减小,并经一谷值,约经历5 s后而逐渐减小趋于某一正向扭矩值。其中,无轴推进的扭矩谷值较小。第2次减速,螺旋桨转速从280 r/min 缩减到160 r/min,航速与扭矩变化趋势与第一次减速基本类似。此后伴随船速的持续减小,螺旋桨转速在20 s内缩减到0,但是船舶自身重量必定会产生惯性,因此船速始终无法完全降至0。而螺旋桨的转矩在历经3次逐渐减小的过程后,最终完全降至0。
从分级制动的仿真可以看出,与紧急制动相比,无论是有轴还是无轴推进,其转矩变化都比较平缓减低,并未出现迅速减低为负扭矩的情形,过载都不严重,对推进系统的损害都不大。2种推进模型相比,无轴推进具有更小的过载,以及更快的航速响应能力。
4 结 语本文基于数值仿真方法对船舶无轴轮缘推进动态特性开展研究。借助CFD方法获取轮缘推进器敞水性能,并通过切比雪夫多项式拟合获得了无轴轮缘推进器四象限性能曲线。构建了船-桨耦合动态仿真数学模型以及仿真程序。通过某一实船为仿真算例,对比传统推进及实船航行记录数据,验证了研究的有效性。对比传统推进模式无轴轮缘推进器超载力矩更低、响应更快。
研究结果如下:
1)无轴轮缘推进器紧凑性好,质量轻,并且具有低进速比小扭矩系数的特点,使得其具有比传统电推进模式更快的响应能力。
2)轮缘推进器动态机动时具有更小的峰值扭矩,利于其在导管内进行集成。动态仿真的过载转矩可以作为轮缘电机设计参考,以便进行最优化的轮缘电机设计。
本文研究动态特性的数值仿真方法可以为船舶轮缘推进的操纵控制提供指导,使其可以根据需要进一步优化,提高负载响应速度,优化推进性能,增加航行器的机动性。
| [1] |
王汉刚. 美国核潜艇推进系统减振降噪技术发展分析[J]. 舰船科学技术, 2013, 35(7). DOI:10.3404/j.issn.1672-7649.2013.07.031 |
| [2] |
谈微中, 严新平, 刘正林, 等. 无轴轮缘推进系统的研究现状与展望[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39(3): 601-605. TAN Wei-zhong, YAN Xin-ping, LIU Zheng-lin, et al. Technology development and prospect of shaftless rim-driven propulsion system[J]. Journal of Wuhan University of Technology(Transportation Science& Engineering), 2015, 39(3): 601-605. |
| [3] |
DAMIR R. Integrated control of marine electrical power systems[D]: [Doctoral dissertation]. Norwegian University of Science and Technology, 2008.
|
| [4] |
VIND NOTLAND S. Control of marine propellers from normal to extreme conditions[D]: [Doctoral dissertation]. Norwegian University of Science and Technology, 2006.
|
| [5] |
罗耀华, 叶瑰的, 刘勇. 舰船全电力推进系统模拟研究[J]. 船舶工程, 2002(4): 59-61. DOI:10.3969/j.issn.1000-6982.2002.04.015 |
| [6] |
邱鹏, 郑高. 轮缘驱动推进器的研究与应用现状[J]. 广东造船(设计与研究版), 2019, 165(2): 28-30. |
| [7] |
曹庆明, 洪方文, 胡芳琳. 梢部驱动推进器的研究与进展[C]//第九届全国水动力学学术会议, 2009: 719–725. CAO Qing-ming, Hong Fang-wen, Hu Fang-ling. Research anddevelopment of rim-driven propulsors[C]//Proceedings of the Ninth National Symposium on hydrodynamics, 2009: 719–725. |
| [8] |
胡芳琳, 张志荣, 辛公正, 等. 梢部驱动推进器水动力性能CFD 预报[C]//全国水动力学学术会议暨两岸船舶与海洋工程水动力学研讨会, 2008, 817–824. HU Fang-lin, ZHANG Zhi-rong, XIN Gong-zheng, et al. CFD prediction of rim-driven thruster hydrodynamic performance[C]//Proceedings of the Eighth National Symposium on hydrodynamics, 2008, 817–824. |
| [9] |
李宗卫, 环驱式推进器之设计与流场特性[D]. 台湾, 国立成功大学, 1995.
|
| [10] |
钟宏伟, 韩雪, 刘亚兵. 无轴推进电机技术应用研究[J]. 舰船科学技术, 2015, 37(9): 1-6. ZHONG Hong-wei, HAN Xue, LIU Ya-bing. Shaftless propulsion motor technology application[J]. Ship Science and Technology, 2015, 37(9): 1-6. DOI:10.3404/j.issn.1672-7649.2015.09.001 |
 2021, Vol. 43
2021, Vol. 43
