2. 深海载人装备国家重点实验室,江苏 无锡 214082
2. State Key Laboratory of Deep-sea Manned Vehicles, Wuxi 214082, China
深海载人平台的总装台架作为框架结构的基础,承担平台总装过程中的结构载荷、设备载荷、人员载荷以及施工吊装等带来的其他载荷[1]。由于总装台架尺寸较大,重量较重,对其进行重量优化可以节约加工运输成本。本文以某深海载人平台总装台架为例,对其进行结构屈服强度校核。以重量为目标通过iSIGHT优化设计平台建立单目标优化模型,采用单目标优化中的自适应模拟退火算法(ASA)并以屈服强度作为约束,最终得出优化方案。
1 总装台架屈服强度计算总装台架由上下两部分组成。上层为3组尺寸相同的带有肋板的支撑结构,下层为由方管连接而成的“日”字型结构。上下2层通过焊接固定。模型采用板单元建立,单元尺寸0.2 m×0.2 m,如图1所示。
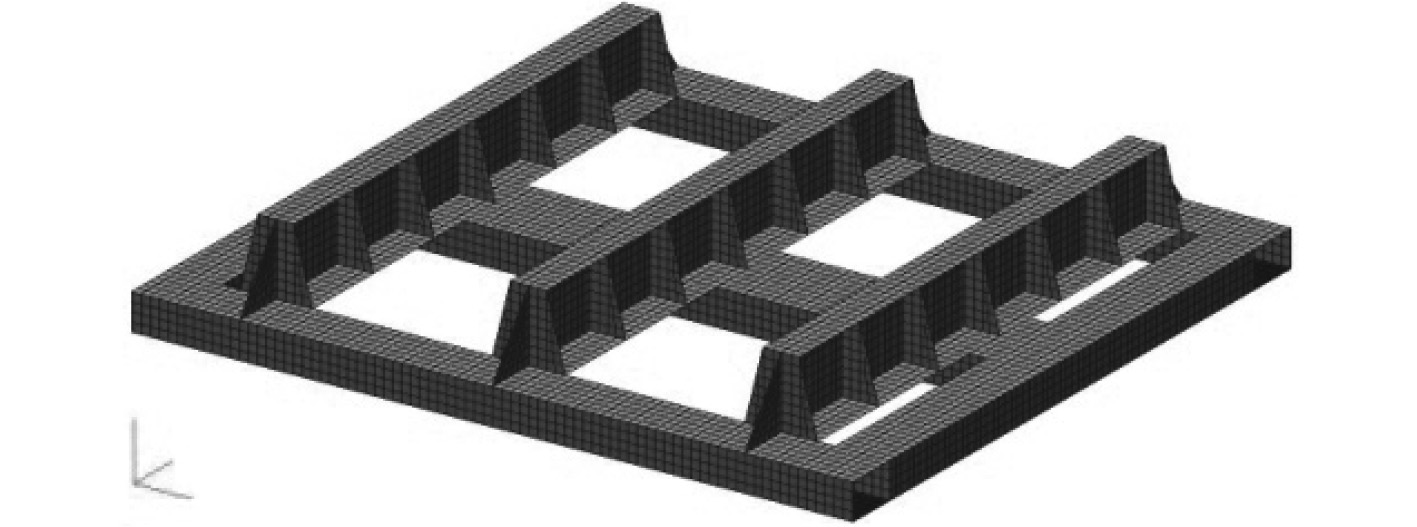
|
图 1 有限元模型 Fig. 1 Finite element model |
模型材料选用Q235-A钢,屈服强度
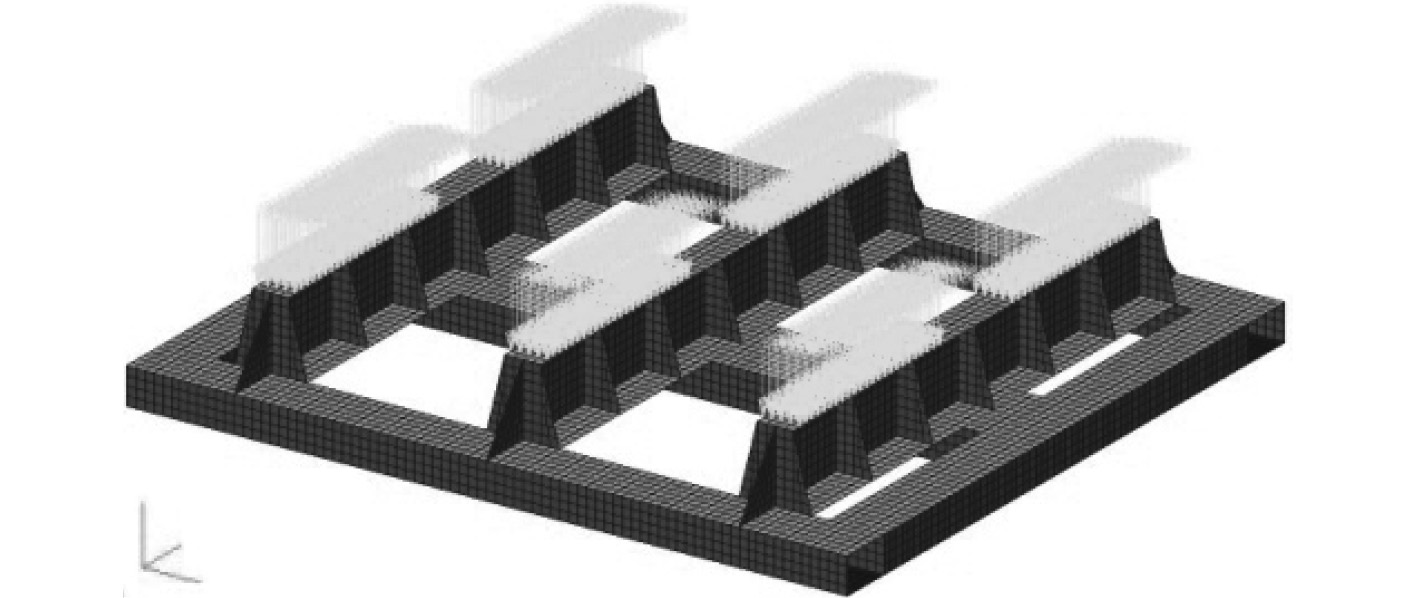
|
图 2 模型载荷施加 Fig. 2 Model load application |

|
图 3 模型约束定义 Fig. 3 Model constraint definition |
台架模型按照分组设置板厚,共分为4组。底部由方管组成的框架为一组,板厚10 mm,上层支撑结构的面板和腹板为一组,板厚20 mm,上层支撑结构肋板为一组,板厚10 mm,上层支撑结构和下层框架重叠部分为一组,板厚是二者的和,为30 mm。台架模型板厚分组设置情况如图4所示。
|
图 4 模型板厚设置 Fig. 4 Model plate thickness setting |
根据《潜水系统与潜水器入级与建造规范》中附录B的规定,结构相对与安全系数的许用应力值
| $[\sigma ] = {R_{eH}}/n{\text{。}}$ | (1) |
其中:

|
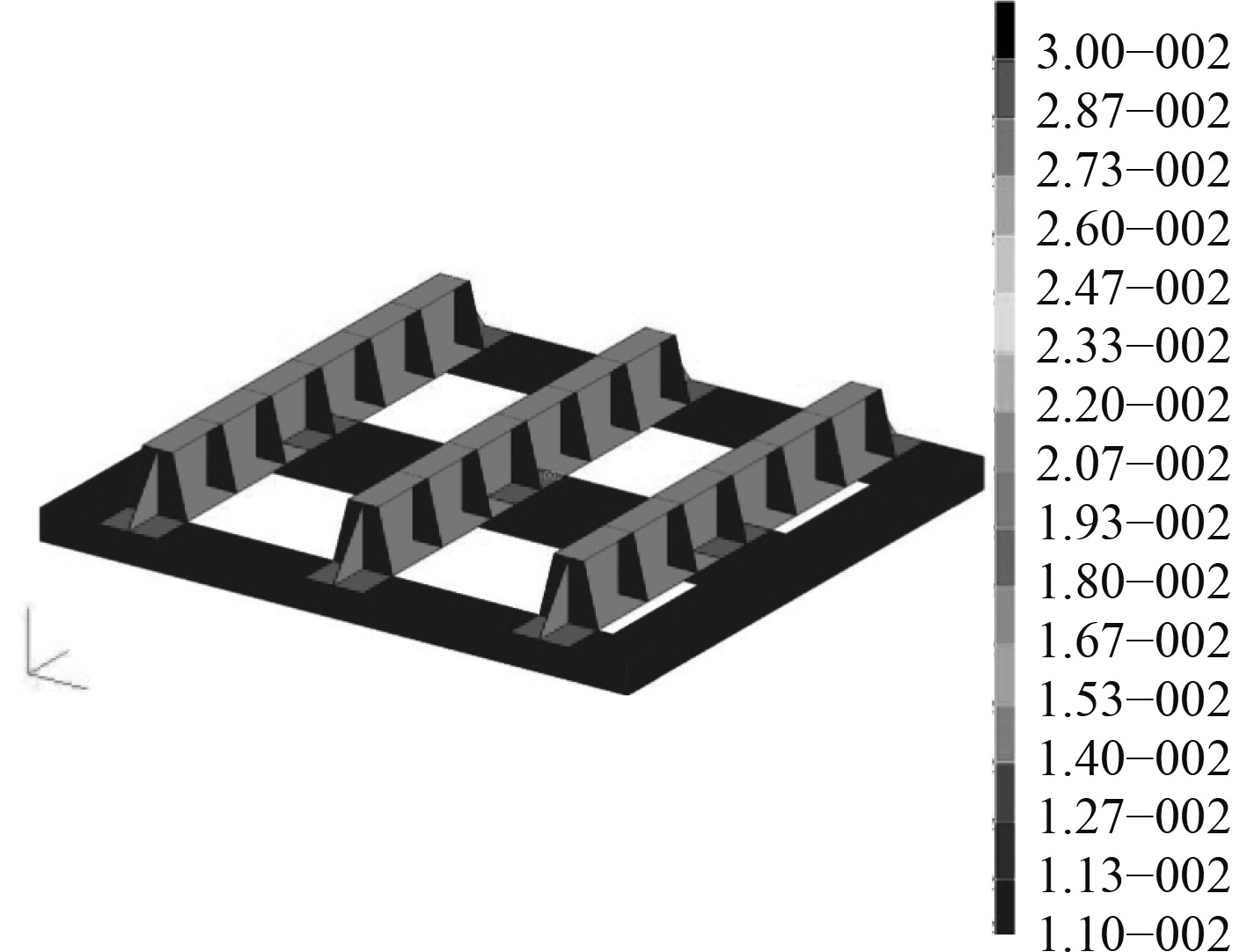
图 5 计算结果应力云图 Fig. 5 Stress nephogram of calculated results |
根据云图可知,最大应力发生在底部框架方管连接处,为137.14 MPa,其余部位应力值较小,相对于许用值而言仍有较大的强度裕度。考虑到此时结构重量较大,势必增加加工运输上的难度,同时也增加了建造预算,因此需要对台架结构进行满足屈服强度前提下的重量优化。
2 重量优化基于iSIGHT优化平台,对目标台架结构进行以重量为目标的单目标优化。单目标优化算法大体上分为3类:梯度优化法(Gradient Techniques)、直接搜索法(Direct Methods Techniques)、全局搜索法(Exploratory Techniques)。梯度法能在设计点周围进行快速的搜索,直接搜索法也能在设计点周围进行快速的搜索,并且搜索阶段采用大步长,具备比梯度优化法更大的搜索空间。然而以上2种方法容易受设计点初始位置影响,陷入局部最小解,无法对全局进行搜索。全局搜索法在全局整个空间内搜索最优解,不依赖于设计点初始位置,避免了陷入局部最优解的情况[2]。
2.1 优化算法选择优化算法的选择对最终优化结果具有决定性的影响[3]。根据刘峰的研究结果[4],对单目标优化算法的比较结果,全局搜索法中的自适应模拟退火算法(ASA)优化效果最好。因此本文采用全局搜索法中的自适应模拟退火算法(ASA)进行单目标优化。自适应模拟退火算法(ASA)是20世纪90年代初期,Lester Ingber根据传统模拟退火算法和模拟淬火过程提出的一种算法,该算法非常适用于算法简单的高度非线性优化问题,能够辨识不同位置的局部最优结果,具备以最小成本得到最优解的能力[5-8]。该方法通过模拟退火的过程,将优化问题与统计力学中的热平衡问题进行类比,对初始点开始进行的每一步都进行计算比较,计算得到的函数值只要下降即被接受,反复计算最终得到最优点[9]。此外,函数值的上升也有可能被接收,这样可以避免陷入局部最优解,这正是该算法相比梯度优化法的优势所在。函数值上升的点是否被接受,要依据温度函数Metropolis判据[10]。在温度函数不断降低过程中,考虑概率突跳特性在解空间中搜索目标函数的全局最优解,即能在局部最优解跳出并最终趋向全局最优解。
2.2 iSIGHT优化框架建立iSIGHT优化平台可以通过MSC.Patran模块或者Simcode组件进行集成优化[11]。Simcode组件具有不受MSC.Patran版本限制,操作更加清晰的特点,因此这里采用Simcode组件进行集成优化。Simcode组件的输入为已经录制好的.ses文件作为模板,命令为自行编制的.bat批处理文件。通过解析.ses文件中的板厚属性,将总装平台4组板厚分别定义为设计变量,分别为底部框架板厚t1,面板腹板板厚t2,肋板板厚t3,重叠部位板厚t4。考虑到实际加工建造过程中,重叠部位板厚可以独立于底部框架板厚和面板腹板板厚,因此在优化时将其作为一个独立的设计变量。.bat批处理文件在MSC.Patran中运行已经录制好的.ses文件,实现对修改板厚—屈服强度计算—结果输出的全过程。输出结果为.rpt文件和.f06文件。通过解析输出的.rpt文件和.f06文件中总装台架的重量和最大应力,并分别作为目标函数和约束值,最终完成优化框架的搭建。优化模型设置如下:
| $ \begin{aligned} &{\rm{Optimization}}\quad\quad{\rm{Min \{ MASS\} }}\\ &{\rm{s}}{\rm{.t}}{\rm{.}}\quad\quad\quad\quad\quad\quad\;{\rm{Max von Mises}} \leqslant[\sigma ]\\ &{\rm{DV}}\quad\quad\quad\quad\quad\quad\; {t_1} \in [5,30], \text m \text m\\ &\quad\quad\quad\quad\;\quad\quad\quad\;\;{t_2} \in [5,30], \text m \text m\\ &\quad\quad\quad\quad\;\quad\quad\quad\;\;{t_3} \in [5,30], \text m \text m\\ &\quad\quad\quad\quad\;\quad\quad\quad\;\;{t_4} \in [5,35], \text m \text m \end{aligned} $ | (2) |
变量增量为0.1 mm。
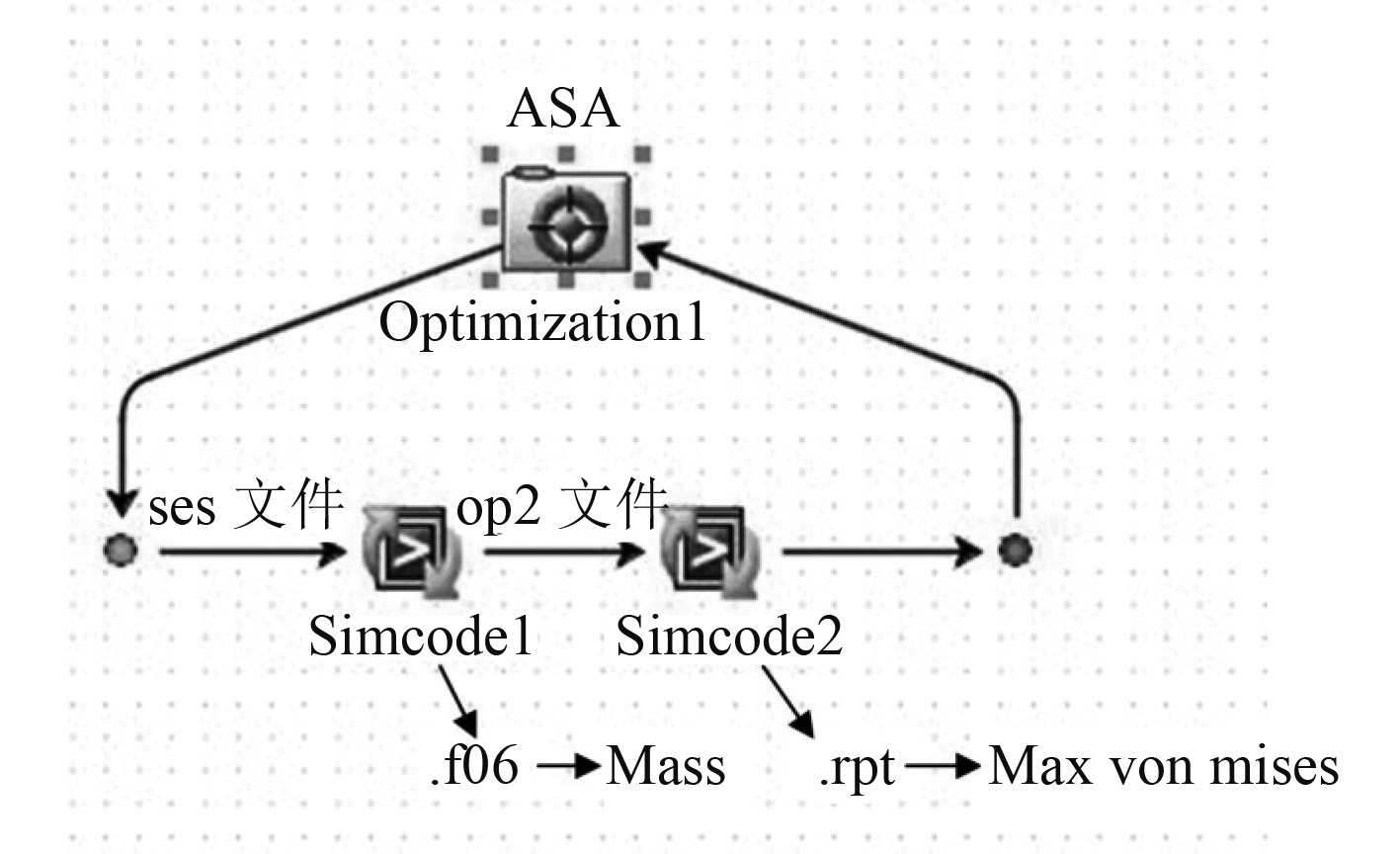
|
图 6 优化框架示意 Fig. 6 Schematic diagram of optimization framework |
需要注意的是,在搭建优化框架时,要检查输入输出文件的路径。例如.ses文件中,对.op2文件的输出与读取、.rpt文件的输出等,为了更灵活搭建优化框架,应尽量避免绝对路径的出现,以免造成优化结果不变的情况。
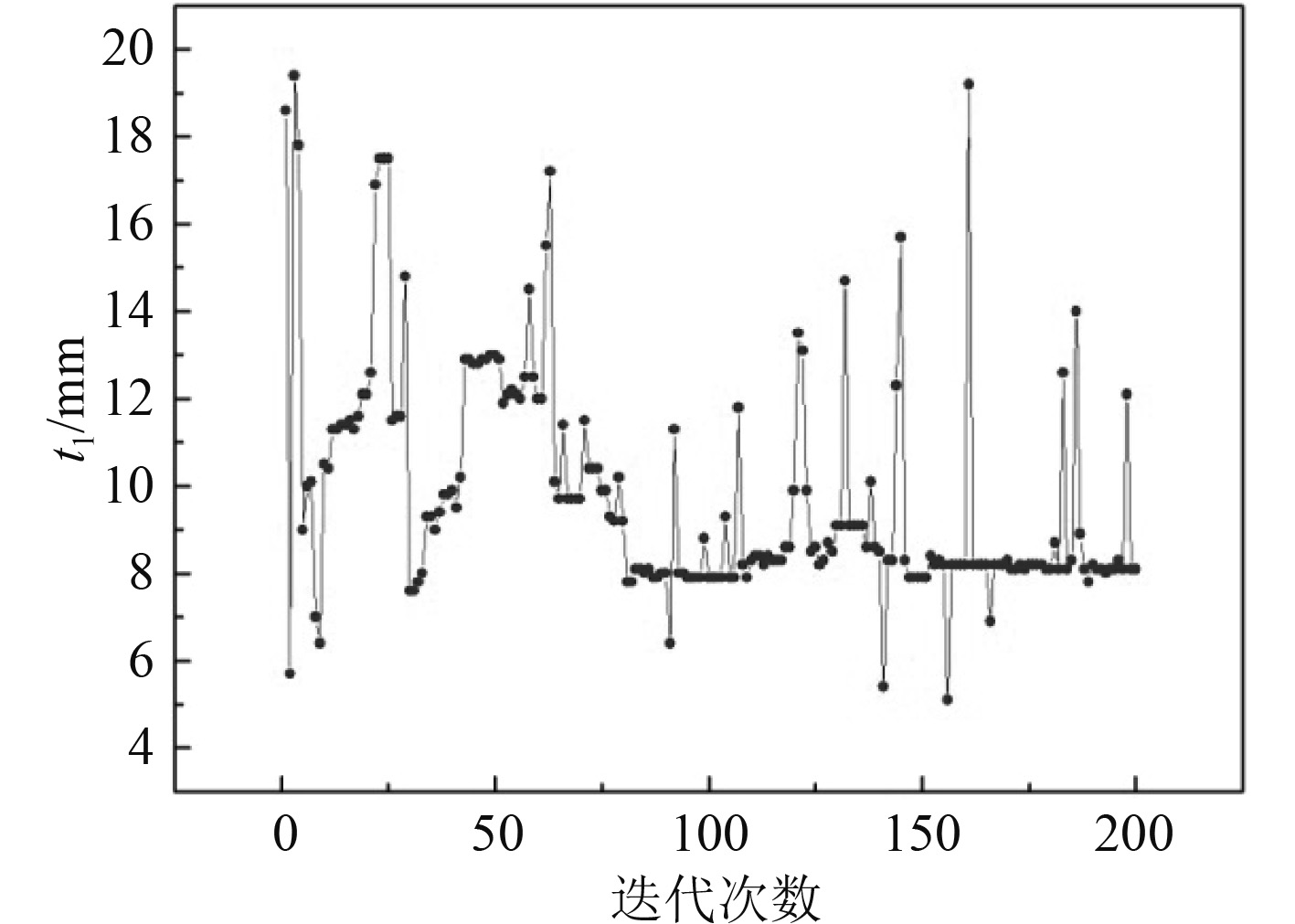
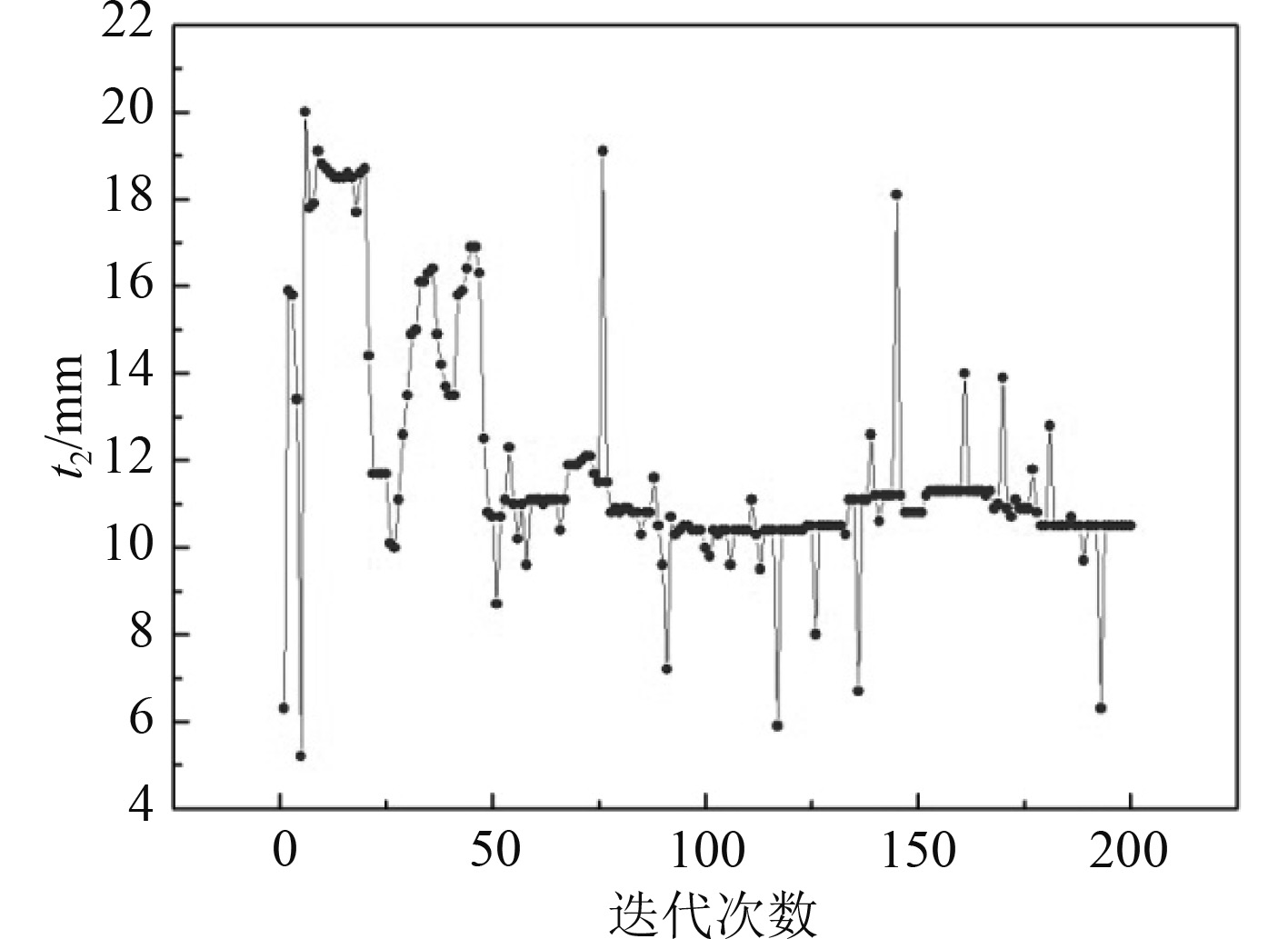
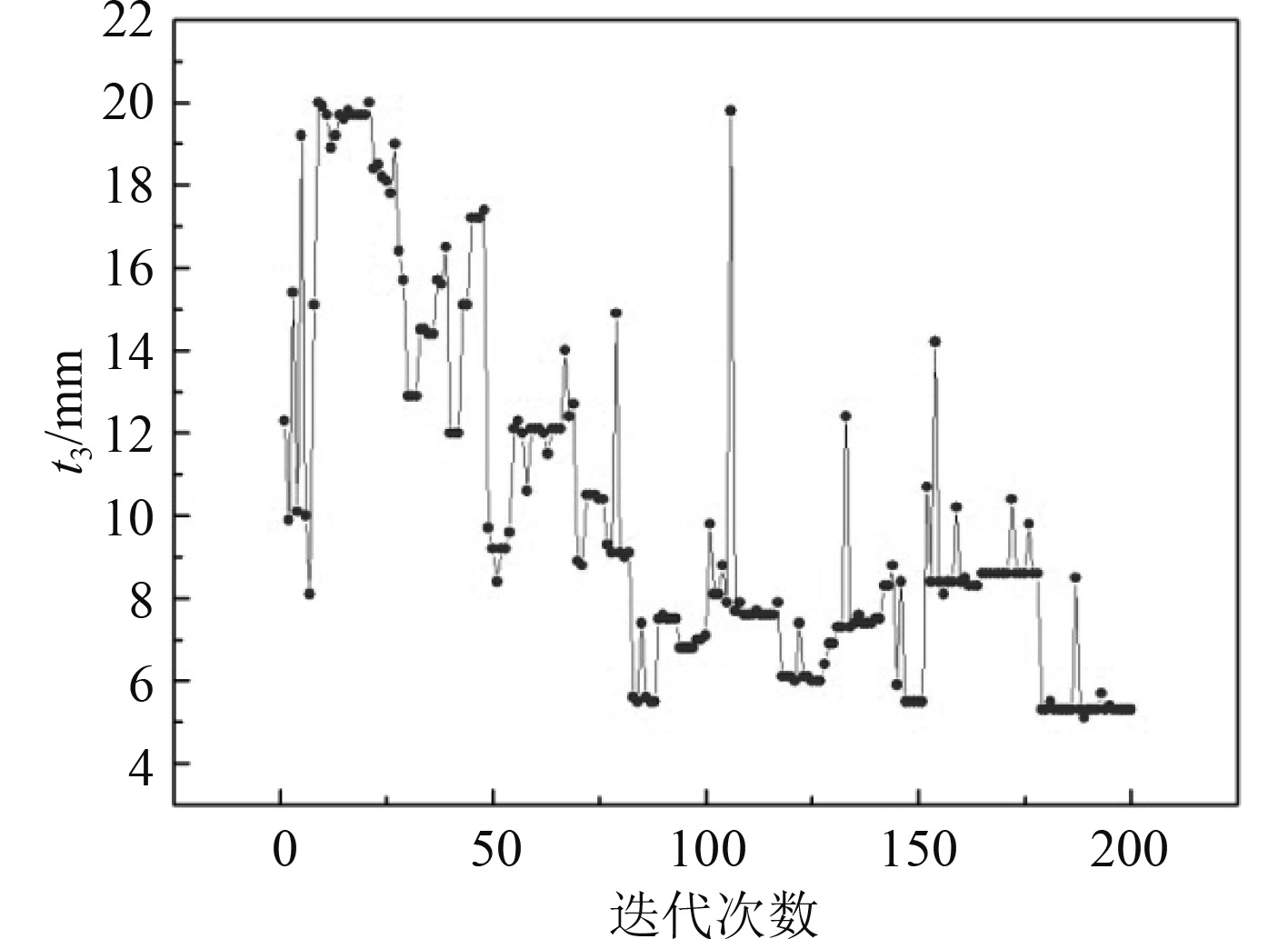
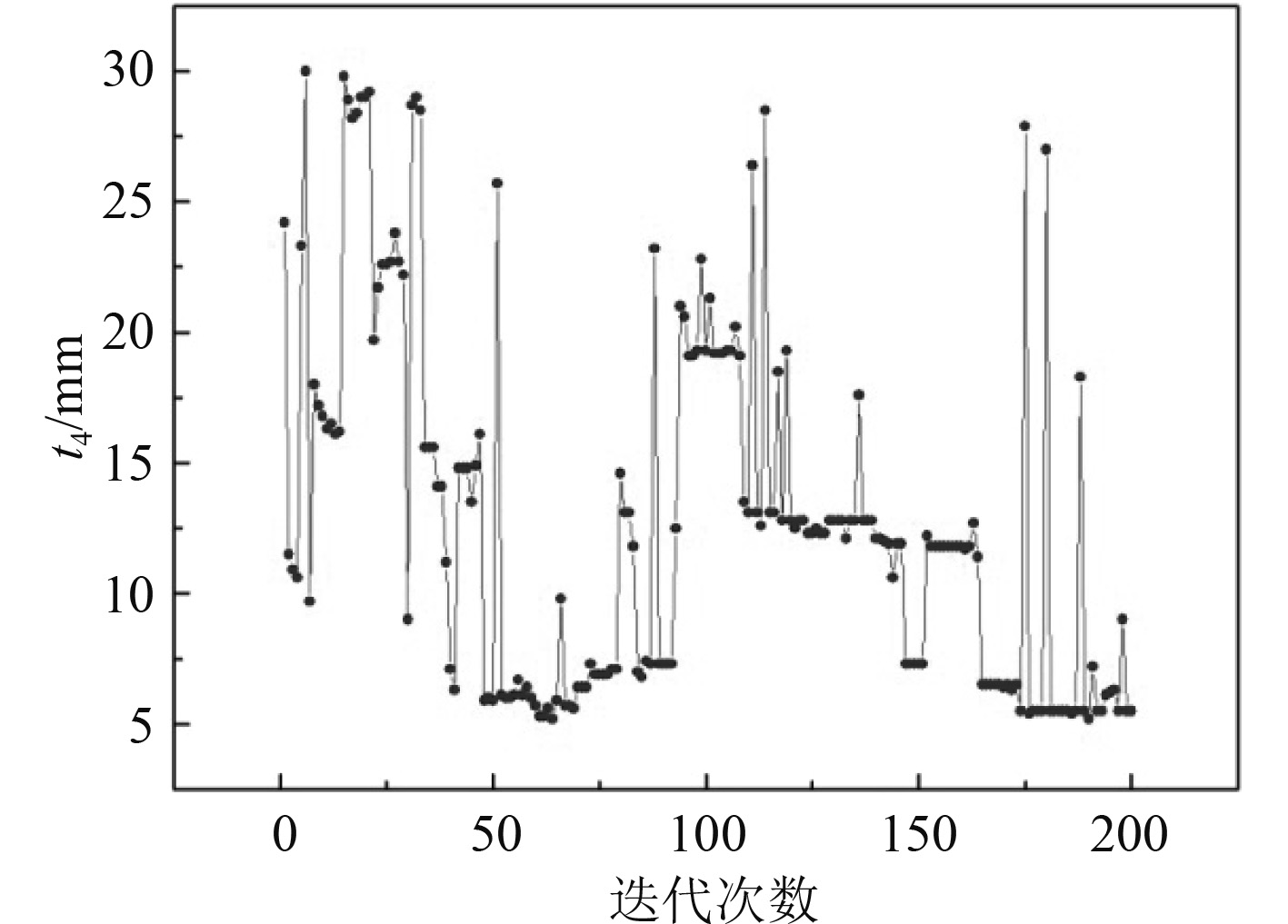
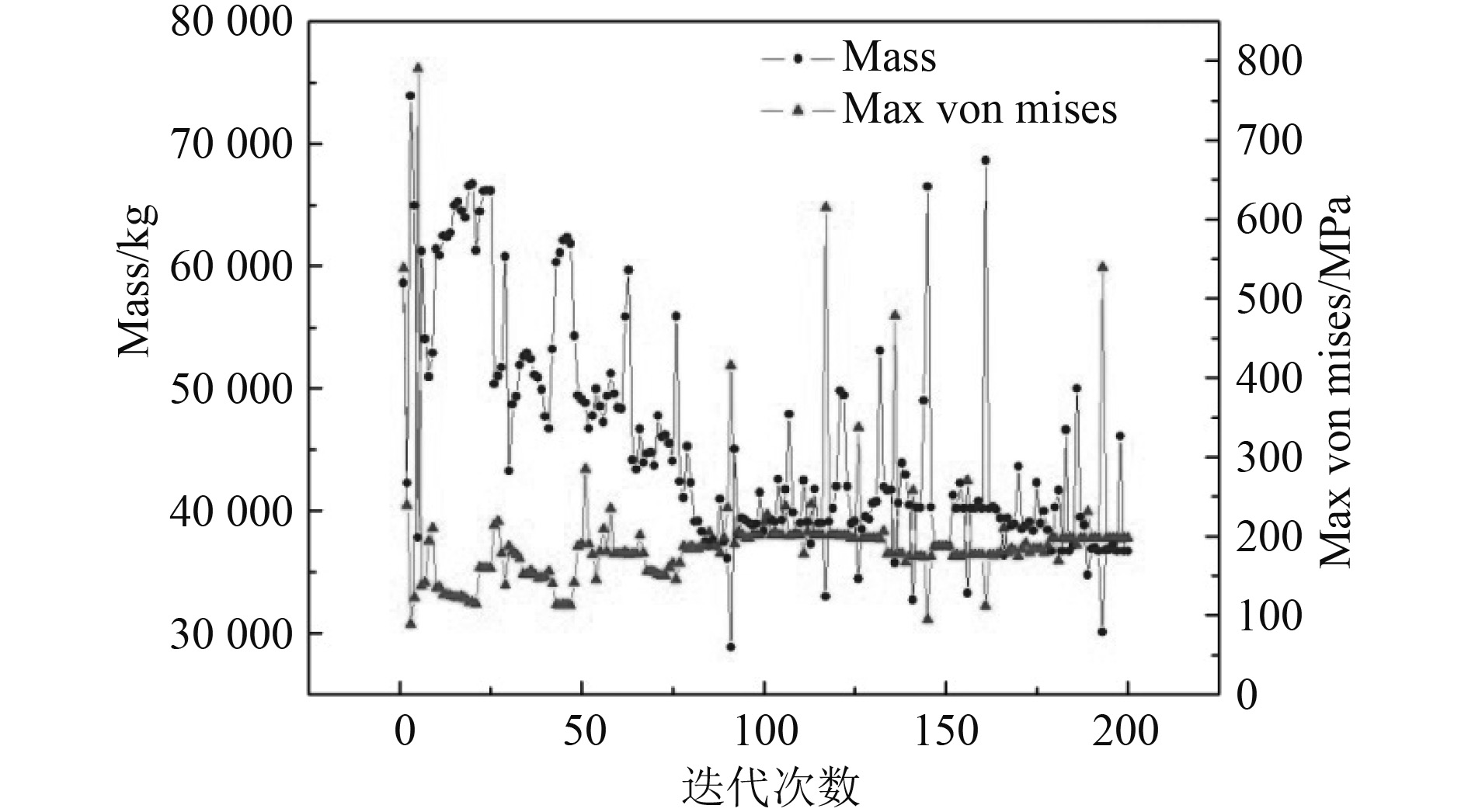
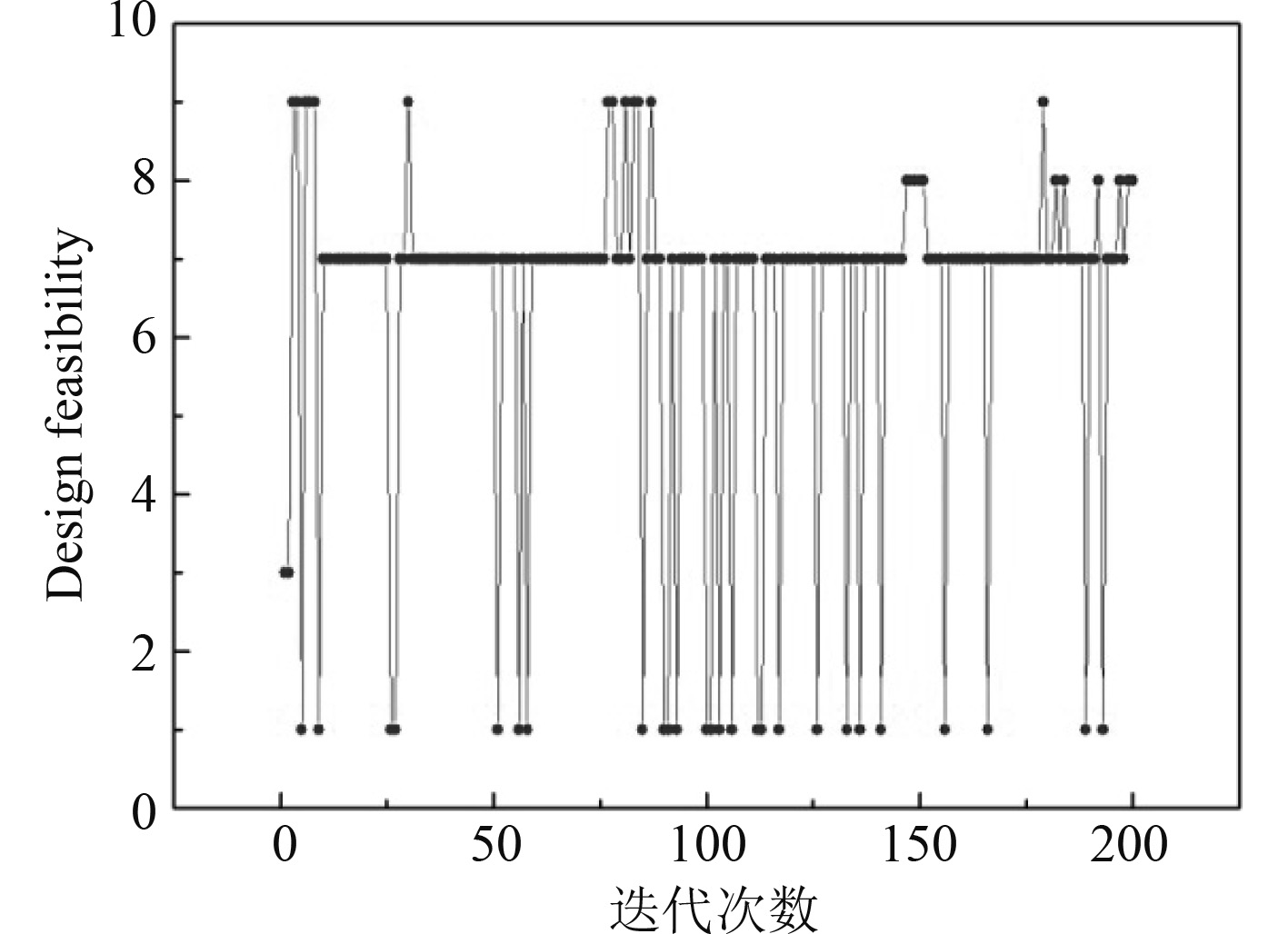
3 优化结果及分析经过200次迭代优化完毕,最优解点为第179次迭代结果。根据计算过程监控可知优化过程中设计变量、目标函数Mass, Max von Mises的变化过程以及设计可行性(Design feasibility)。相关参数随迭代变化过程如图8所示。
|
图 7 底部框架板厚t1随迭代次数变化 Fig. 7 Variation of t1 with number of iterations |
|
图 8 面板腹板板厚t2随迭代次数变化 Fig. 8 Variation of t2 with number of iterations |
|
图 9 肋板板厚t3随迭代次数变化 Fig. 9 Variation of t3 with number of iterations |
|
图 10 重叠部分板厚t4随迭代次数变化 Fig. 10 Variation of t4with number of iterations |
|
图 11 重量及最大应力随迭代次数变化 Fig. 11 Variation of weight and maximum stress with number of iterations |
|
图 12 设计可行性随迭代次数变化 Fig. 12 Variation of design feasibility with number of iterations |
由计算可知优化结果为底部框架板厚t1=8.1 mm,面板腹板板厚t2=10.5 mm,肋板板厚t3=5.3 mm,重叠部位板厚t4=5.5 mm,对应总装台架重量为36.71389 t,最大应力为197.661346 MPa,小于许用值满足设计要求。与原有方案相比,优化方案减重40.01%。
|
|
表 1 优化方案与初始方案板厚比较结果 Tab.1 Plate thickness comparison between the optimized scheme and the initial scheme |
提取优化方案与初始方案中,4组板厚对应的板单元最大应力,对应结果如表2所示。
|
|
表 2 优化方案与初始方案应力结果比较 Tab.2 Comparison of stress results between the optimization scheme and the initial scheme |
以优化方案中底部框架结构为例,其应力云图如图13所示。可知,最大应力仍然发生在方管连接位置,为183.1 MPa,接近许用值。方管中段部分应力范围在100 MPa以内,距离许用值仍有一段距离。因此如果将方管分为若干段,并赋予不同板厚,可以将重量进一步优化。同理,肋板、面板腹板、重叠部位板厚也可以细化成若干组。也就是说,本例中优化模型中的设计变量适当增加,可以得到重量更小的优化方案,这有待于下一步研究工作进行。

|
图 13 优化方案底部框架应力云图 Fig. 13 Stress nephogram of bottom frame in optimization scheme |
根据优化方案最大应力可知,优化方案是满足屈服强度前提下重量最优的方案。然而在许多其他结构设计中,结构的稳定性等同样应当作为约束条件。例如深海载人平台的框架、耐压壳体等结构,在优化时需要定义多个约束条件才能保证优化方案的可行性,此时可以采用NSGA-Ⅱ 优化算法对模型进行多目标优化,优化思路和具体过程与上述重量优化相似。因此在深海载人平台其他结构设计中,要根据结构的具体情况具体分析,最终形成可靠的优化方案。
4 结 语本文基于iSIGHT优化软件对某深海载人平台总装台架进行结构屈服强度校核和重量优化,得出如下结论:
1)该总装平台在设计载荷下满足结构屈服强度要求,存在较大的强度裕度;
2)采用自适应模拟退火算法(ASA)对目标台架进行重量优化,得到优化方案较初始方案减重40.1%,达到重量优化的目的。
针对总装台架的重量优化方法对深海载人平台结构设计具有一定参考价值。对于其他结构的优化设计思路与方法大同小异,需要注意的是要根据实际情况确定约束种类与个数,从而选择优化算法进行单目标/多目标优化,最终形成可靠的优化方案。
| [1] |
王东升, 曲文鑫, 刘帅, 等. 全海深载人潜水器总装台架屈服强度分析[J]. 内蒙古科技, 2019, 38(7): 109-111. WANG D S, QU W X, LIU S, etal. Yield strength analysis of the assembly bench for deep-sea manned submersibles[J]. Inner Mongolia Science and Technology Magazine, 2019, 38(7): 109-111. |
| [2] |
王江峰, 伍贻兆, 等. 进化算法与确定性算法在优化控制问题中的收敛性对比[J]. 计算力学学报, 2004, 21(3): 349-355. WANG J F, WU Y Z, etal. Comparison of convergence between evolutional algorithms and deterministic algorithms for optimal control problem[J]. Chinese Journal of Computational Mechanics, 2004, 21(3): 349-355. DOI:10.3969/j.issn.1007-4708.2004.03.015 |
| [3] |
王一伟, 钟星立, 杜特专. 翼型多目标气动优化设计方法[J]. 计算力学学报, 2007, 24(1): 98-102. WANG Y W, ZHONG X L, DU T Z. Multi-objective optimization of airfoils[J]. Chinese Journal of Computational Mechanics, 2007, 24(1): 98-102. DOI:10.3969/j.issn.1007-4708.2007.01.018 |
| [4] |
刘峰. 载人潜器总体设计优化方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2014. Liu F. Research on general design optimization method of human occupied vehicle[D]. Harbin: Harbin Engineering University, 2014. |
| [5] |
INGBER L. Adaptive simulated annealing(ASA): lessons learned[J]. Journal of Control and Cybernetics, 1996, 25(1): 33-54. |
| [6] |
CHEN S, LUK B L. Adaptive simulated annealing for optimization in signal processing applications[J]. Signal Processing, 1999, 79(1): 117-128. DOI:10.1016/S0165-1684(99)00084-5 |
| [7] |
SHIC Z, ZENG N, ZHANG M, ETAL. Adaptive simulated annealing algorithm for the fiberbragg grating distributed straining sensing[J]. Optics Communications, 2003, 226,(1-6): 167-173. DOI:10.1016/j.optcom.2003.08.032 |
| [8] |
JEONG IK, LEE J J. Adapted simulated annealing genetic algorithm for system identification[J]. Engineering Applications of Artificial Intelligence, 1996, 9(5): 523-532. DOI:10.1016/0952-1976(96)00049-8 |
| [9] |
张德富, 顾卫刚, 等. 一种解旅行商问题的并行模拟退火算法[J]. 计算机研究与发展, 1995, 32(2): l-4. ZHANG D F, GU W G, ETAL. A parallel simulated annealing algorithm for solving Travelling Salesman Problem (TSP)[J]. Computer Research and Development, 1995, 32(2): l-4. |
| [10] |
METROPOLIS N, ROSENBLUTH A W, ETAL. Equation of calculations by fast computing[J]. Journal of Chemical Physis, 1953, 21(4): 1087-1092. |
| [11] |
胡光兴, 王庆. 载人潜器非耐压结构多目标优化设计[J]. 舰船科学技术, 2016, 38(4): 99-104. HU guang-Xing, WANG Qing. Multi-objective optime design of the non-pressure hullin manned submersible[J]. Ship Science and Tecnology, 2016, 38(4): 99-104. DOI:10.3404/j.issn.1672-7619.2016.04.020 |
 2021, Vol. 43
2021, Vol. 43
