0 引　言

船舶在海上航行时，必然会承受船体自重、货重等各种各样的负荷，各种负荷形成的激励源就会引发船体产生不同程度的振动^[1]。近年来，随着VLCC和ULCC的出现，船舶自重、主机、螺旋桨等船用设备的重量随之增加，对船体以及船舶推进系统的刚度和强度提出了更高的要求^[2]。对于普通商船而言，由于制造成本等原因，轴系所用材料无法使用高强度合金，一般为钢制轴系。因此，要想提高支撑系统的耦合刚度来满足推进功率的需求，只能不断增大轴、轴承、法兰等部件的长度和直径，这样在增大系统刚度的同时，也会使支撑系统的耦合刚度呈现非线性的变化趋势，进而对轴系振动产生不良影响。

近年来，世界各国都在大力发展绿色船舶，进而建设海洋强国，而提高减振技术作为发展绿色船舶的重要标志，早已引起研究人员的关注，尤其是船舶动力系统的减振。王滨^[3]提出轴承在安装时由于安装工艺等原因会出现安装位置的偏移，轴承位置会对轴系振动形式及振动频率产生较大的影响。刘显军^[4]分析了轴系外力变化对支撑刚度的影响，结果表明轴系虽然一般认为是刚性体，但在分析振动时表面变形量是不可忽略的。Lgor Zverv^[5]首次提出预紧力会改变轴承的摩擦力矩，尤其对于大型船舶的高转速轴系，而摩擦力矩是轴系振动的重要影响因素之一。Panagopulos.E^[6]在之前经验公式的基础上，通过理论计算和实验验证，提出了新的轴系回旋振动计算公式，该公式表明，振动幅值与轴系的安装参数有着密切的关系，可以通过优化安装参数来减小振动幅值。

本文选取某集装箱推进轴系为研究模型，通过计算油膜刚度，得到转速、润滑油粘度和刚度的映射关系；根据经验公式计算轴承支撑系统的耦合刚度，并通过模态分析及谐响应分析得到不同的支撑系统耦合刚度对轴系回旋振动的影响结果。最后，给出了减小船舶轴系振动、优化轴系设计的结论。

1 轴承支撑系统耦合刚度计算

轴承支撑系统耦合刚度通常来自3个部分^[7]，第1部分为油膜刚度k₀，这也是油膜重要动力特性参数之一；第2部分为轴承刚度k_b；第3部分为船体刚度k_s。通过相关公式可以得到轴承支撑系统耦合刚度，为下一步分析刚度和轴系振动的关系奠定了基础。

1.1 油膜刚度分析 1.1.1 计算油膜刚度

轴承油膜刚度定义^[8]为：通过施加微小扰动，轴颈的平衡位置会产生扰动位移，同时油膜合力会增加，此时油膜合力的增量 $\Delta F$ 与扰动位移 $\Delta {\rm{s}}$ 的比值即为油膜刚度。为了方便研究，目前普遍认为只在水平方向和垂直方向存在扰动位移。假设沿2个方向的扰动位移分量分别为 $\Delta {\rm{x}}$ 和 $\Delta {\rm{y}}$ ，相应的油膜反力沿2个方向的变化为 $\Delta {F_x}$ 和 $\Delta {F_y}$ ，得到4个油膜刚度系数，分别为：

$\begin{aligned} &{K_{xx}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta {F_x}}}{{\Delta x}} \approx \frac{{\partial {F_x}}}{{\partial x}}{\text{，}}\\ &{K_{yx}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta {F_y}}}{{\Delta x}} \approx \frac{{\partial {F_y}}}{{\partial x}}{\text{，}}\\ &{K_{xy}} = \mathop {\lim }\limits_{\Delta y \to 0} \frac{{\Delta {F_x}}}{{\Delta y}} \approx \frac{{\partial {F_x}}}{{\partial y}}{\text{，}}\\ &{K_{yy}} = \mathop {\lim }\limits_{\Delta y \to 0} \frac{{\Delta {F_y}}}{{\Delta y}} \approx \frac{{\partial {F_y}}}{{\partial y}}{\text{。}} \end{aligned}$

(1)

本文通过对轴颈施加小扰动^[9]对近似求解油膜刚度。在刚度计算过程中，小扰动量的选择对于能否准确计算至关重要，通常认为小扰动量应介于1×10⁻¹⁰ mm和1×10⁻¹ mm之间。本文在计算过程中对轴颈施加的小扰动量为1×10⁻⁵ mm。以某集装箱船^[10]后尾轴承为计算模型，整段轴承长度1180 mm。为了保证计算的准确性，选取10个不同位置点分别计算油膜刚度，再将10个不同位置点油膜刚度的算术平均值作为整个轴承的油膜刚度，即 ${k_0} = \dfrac{{{k_1} + {k_2} + \cdots + {k_{10}}}}{{10}}$ ，求得轴承油膜刚度为 ${k_0} = 2.196 \times {10^8}\; \rm{N/m}$ 。

1.1.2 转速对刚度的影响

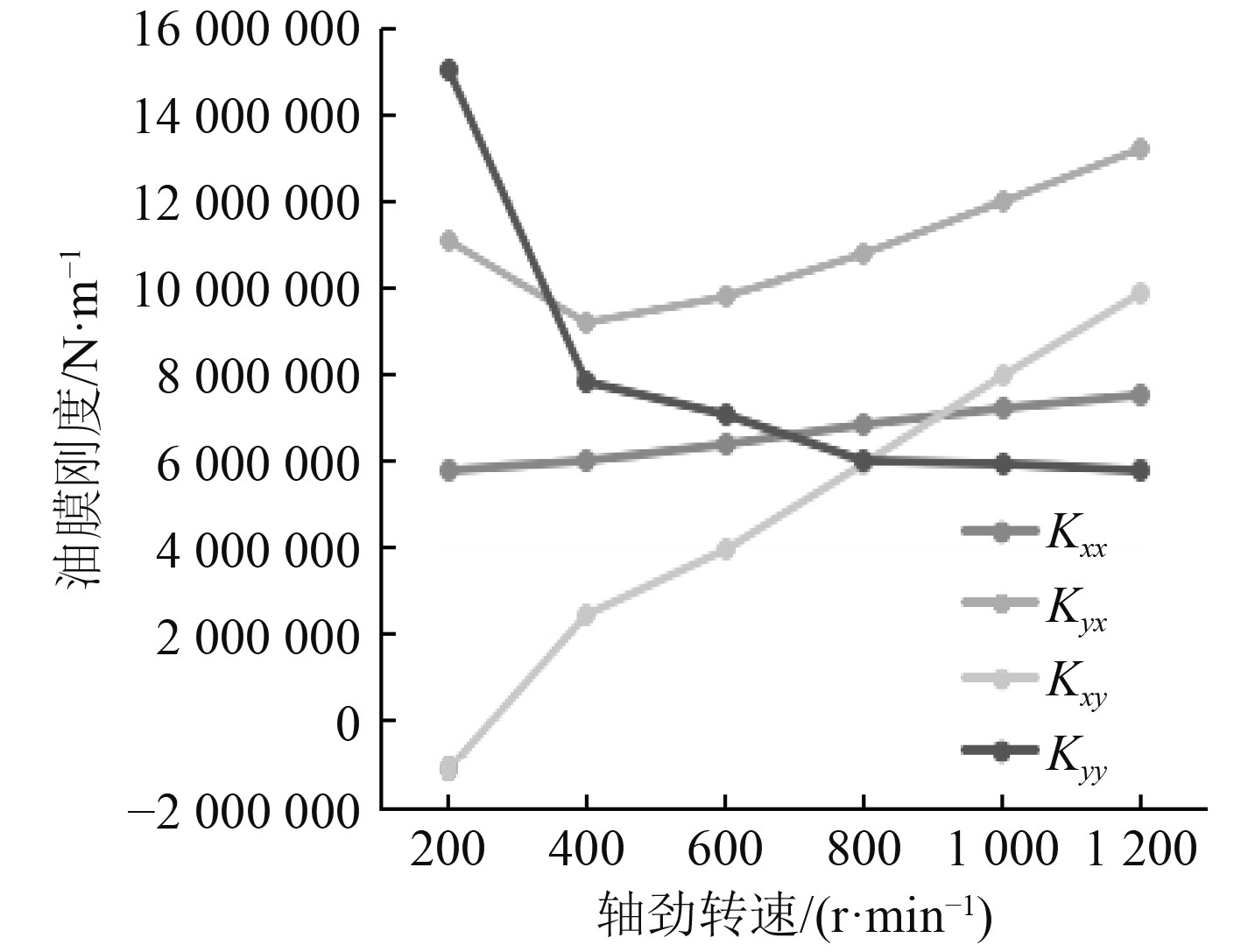
轴系转速是船舶运行工况重要参数之一，应根据运行工况随时做出调整，转速变化会影响轴承油膜的压力和厚度分布，同时影响油膜刚度和阻尼^[11]。提取文献[12]的轴承相关参数，分析转速在一定区间内变化（200～1200 r/min，间隔200 r/min）油膜刚度的变化情况，结果如图1所示。

对比图1和图2可知，本文计算结果和文献[12]计算结果基本一致，因此可以作为下文的分析依据。由计算结果可知，轴颈在低速运行时，4个刚度系数之间差异较大且变化速度明显，随着转速的提高，它们之间的差距有所减小且变化趋势趋于平稳。水平刚度 ${K_{xx}}$ 随转速增加变化趋势较为平缓。垂直刚度 ${K_{yy}}$ 随转速增加急剧下降，这是由于当轴承负荷不变时，转速增加会使惯性力增大，从而使平均油膜厚度变厚，垂直方向上施加相同的扰动位移时合力减小，因此垂直刚度 ${K_{yy}}$ 急剧下降。

1.1.3 粘度对刚度的影响

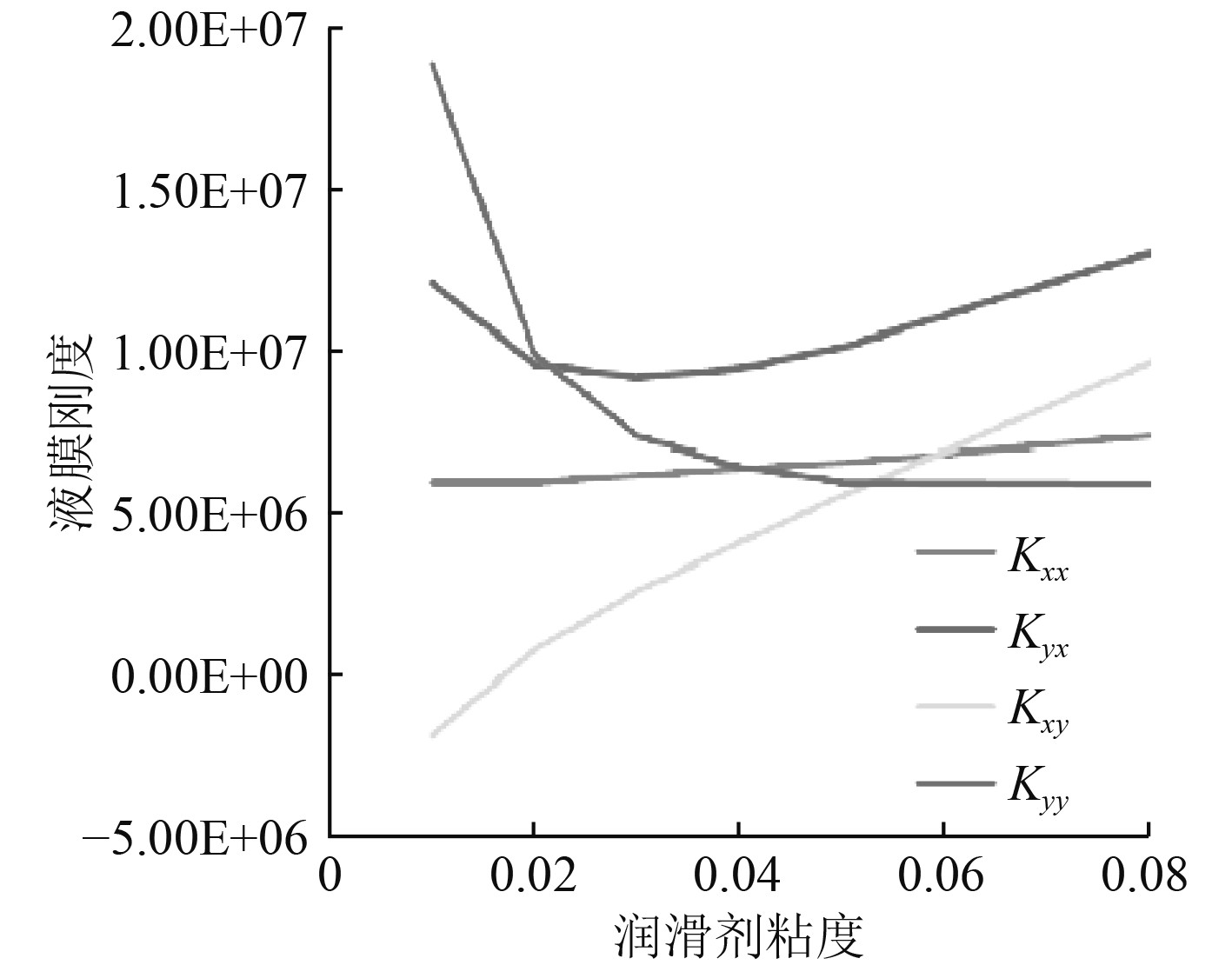
船舶推进轴系采用的不同润滑剂，因其分子结构不同，会表现出不同的物理性质和化学性质。此外，润滑剂相同时，温度、压力等外界工况的变化也会对粘度产生明显的影响^[13]。而润滑剂粘度是轴承刚度的重要影响因素之一。因此，分析粘度变化对油膜动力系数的影响对准确分析轴系的振动特性十分重要。提取文献[12]的轴承相关参数，采用单一变量的原则，分析润滑剂粘度分别为0.02，0.03，0.04，0.05，0.06，0.07，0.08 Pa·s时对油膜刚度的影响，结果如图3所示。

对比图3和图4可知，本文计算结果和文献[12]计算结果曲线趋势基本一致，计算数值误差在合理范围之内。随着粘度的增加，4个刚度系数的变化趋势全部趋于平稳。水平刚度 ${K_{xx}}$ 随粘度增加几乎线性增大，但总体来说增大趋势不明显。施加一定的外载荷，液膜厚度与粘度呈正相关，增加润滑剂粘度会减小液膜垂直方向上的平均承载力，因此垂直刚度 ${K_{yy}}$ 急剧下降。

1.2 计算轴承支撑系统耦合刚度

根据计算轴承支撑系统耦合刚度的经验公式，计算耦合刚度需要已知船体刚度、油膜和轴承的等效刚度。本文选用文献[14]的船体局部刚度1.224×10⁹ N/m $ \mathrm{作}\mathrm{为}{k}_{s} $ 进行计算。一般认为油膜刚度近似等于油膜和轴承等效刚度，因此使用1.1.1节中计算得到的油膜刚度 ${k_0}$ 近似代替油膜和轴承等效刚度 $ {k}_{{b}_{0}} $ ，将 ${k_s}$ 和 ${k_0}$ 代入式（2）进行轴承支撑系统耦合刚度的计算。

轴承支撑系统耦合刚度的经验公式为：

$\frac{1}{{{k_e}}} = \frac{1}{{{k_s}}} + \frac{1}{{{k_{{b_0}}}}}{\text。}$

(2)

式中： $ {k}_{e} $ 为支撑系统耦合刚度； $ {k}_{s} $ 为船体刚度； $ {k}_{{b}_{0}} $ 为油膜和轴承等效刚度。

计算求得轴承支撑系统耦合刚度为1.85×10⁸ N/m。

2 轴系振动分析

为研究轴承支撑系统耦合刚度对轴系振动的影响，减小分析误差，根据实际情况选取6个合适的耦合刚度值，分别计算刚度为4.625×10⁷，9.25×10⁷，1.85×10⁸，3.7×10⁸，7.4×10⁸，1.48×10⁹ N/m时轴系振动的前10阶固有频率，进而分析其振动响应。研究对象为某集装箱船^[15]推进轴系，该船轴系全长50 489 mm，轴系相关参数：轴径975 mm，尾轴长15 609 mm，1号中间轴长12 880 mm，2号和3号中间轴长11 000 mm。

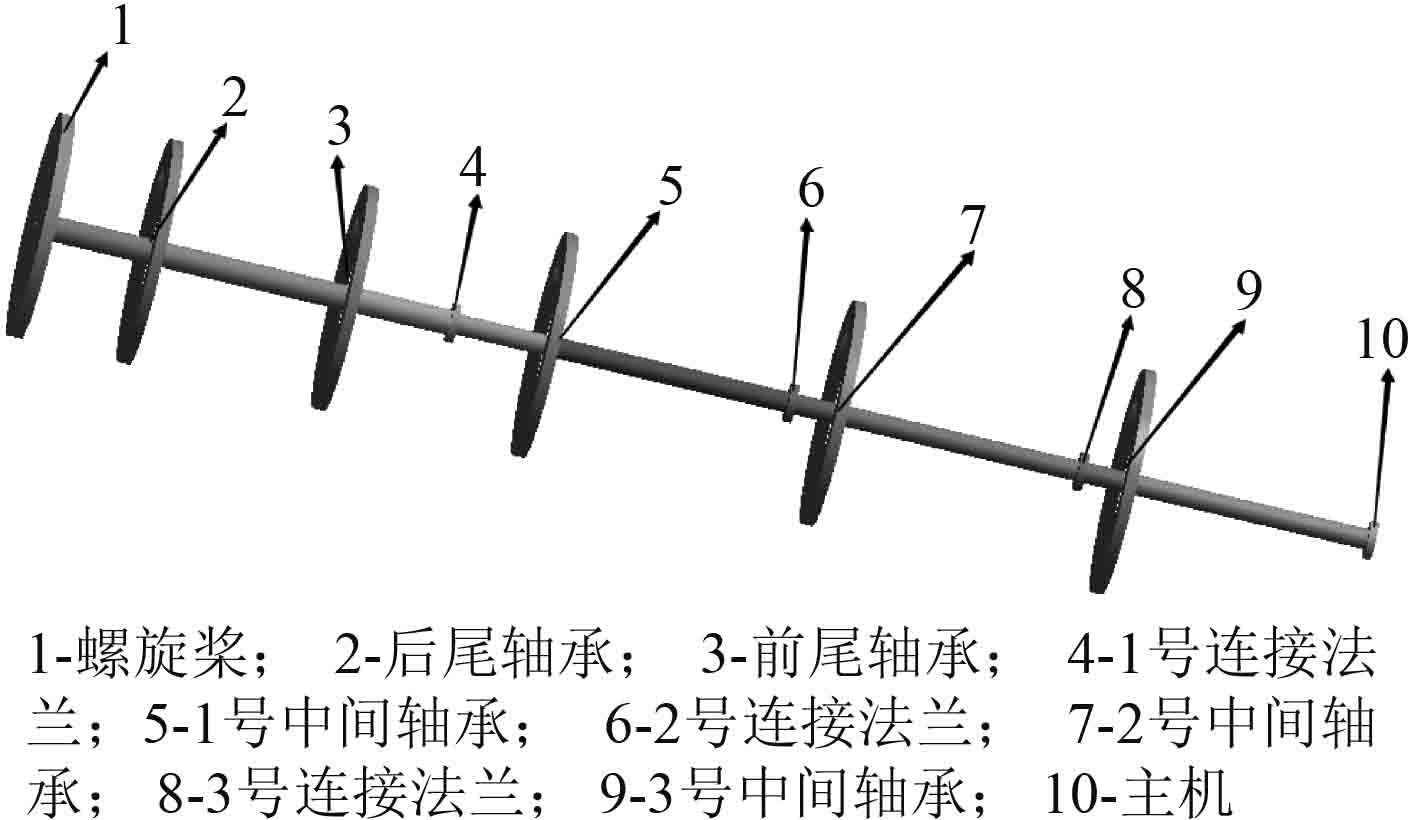
2.1 轴系有限元模型

本文构建的轴系模型每个节点具有6个自由度：UX，UY，UZ，ROTX，ROTY，ROTZ，轴系和螺旋桨的材料都定义为Structural Steel，轴承部分采用一维线性单元COMBINE 14模拟。根据计算需要COMBINE 14可以只沿轴向传递力或力矩，并约束其他方向的自由度。对COMBINE 14进行简化，使轴的两端分别连接结点和稳定端。螺旋桨和主机在建模过程中均简化为圆盘，假设材质、质量均匀，圆心位于各自的几何中心。其有限元模型如图5所示。

2.2 模态分析

在螺旋桨端对轴系施加一定的激励，对推进轴系进行考虑轴系自重的模态分析，依次改变尾轴耦合刚度，得到其前10阶固有频率，如表1所示。可知，该轴系在前10阶固有频率对应的振动形式单一，全部为回旋振动，并没有出现扭转振动、纵向振动或耦合振动形式。图6为刚度值为1.85×10⁸ N/m的第1，3，5，7阶振型图片。由表1及图6可知，因本文在计算中忽略了轴承交叉刚度和阻尼，因此回旋振动的模态在垂直和水平方向上相邻奇数阶和偶数阶的固有频率总是相等的（如1阶和2阶），且在振型图上也表现为只在水平和垂直2个方向上有振动，轴向并没有出现振动。耦合刚度值增大，固有频率随之增大，且高阶固有频率增加趋势更明显。

2.3 振动响应分析

振动响应分析从本质上来讲，就是当轴系发生强迫振动时，计算其动态响应，即计算轴系在不同刚度值下的动态响应。对各节点施加一定的螺旋桨激振力，振动频率介于0～15 Hz之间；从螺旋桨端至主机端分别选取3个节点（1号节点靠近螺旋桨端），以节点的垂向振动幅值为目标值进行谐响应分析。3个节点在不同刚度影响下振幅、频率的变化曲线如图7所示。

由图7可知，各节点在固有频率附近会产生一定程度的共振，但共振幅值各不相同。在省去一些振幅小的共振点后可见，节点1主要在1.35 Hz（1阶和2阶固有频率处）附近产生较大的共振幅值，且随着轴承耦合刚度的增大，共振幅值变化不是很明显，出现最大幅值时对应的刚度值为4.625×10⁷ N/m；节点2主要在1.35 Hz处产生较大的共振幅值。与节点1略有不同的是，刚度值为4.625×10⁷ N/m时，节点2还在5.3 Hz处产生1处较小的共振幅值，但这远小于1.35 Hz处的幅值，节点2在其余5种刚度值（除4.625×10⁷ N/m）下只在1.35 Hz处出现幅值，其余频率处都没有出现幅值；对于节点3，当轴承耦合刚度为4.625×10⁷ N/m时，主要在1.35 Hz和2.53 Hz附近产生较大的共振幅值，在6.97 Hz和14.59 Hz附近还产生2处较小的幅值；当耦合刚度为7.4×10⁸ N/m时，在2.61 Hz附近出现1处共振幅值，振幅约为0.72 mm。除这2种耦合刚度值以外，节点3几乎没有出现共振幅值。对节点1～节点3中最大幅值共振点的幅值进行比较分析，见表2。

由表2可知，当刚度一定时，3个节点出现最大共振幅值时对应的频率都相同，且都出现在各自刚度对应的1阶固有频率附近。在3个节点的最大共振幅值中，节点1的最大共振幅值明显高于其他两点，所以在考虑艉轴和中间轴连接处的轴承耦合刚度时，应主要以靠近螺旋桨端的振幅为目标值。由节点1的变化规律可知，当刚度值从4.625×10⁷ N/m变到9.25×10⁷ N/m时，振幅显著降低（下降1.9222 mm）；但当刚度值在其余5种刚度值之间变化时，振幅都变化不大，可见在一定范围之内，增加系统耦合刚度，各节点振动幅值会减小，尤其对于靠近螺旋桨端的节点，但超出一定区间继续增大刚度时，振幅不会一直持续减小，甚至会出现回升，且相关规则也对轴承耦合刚度有范围规定。因此，在选择轴承刚度时，不能一味地选取大刚度，应综合考虑各种因素。

3 结　语

油膜或者轴承等效刚度增大时，系统耦合刚度也会增大，同时增大了轴系的承载能力。本文通过对选用的推进轴系模型进行模态分析和振动响应分析，可以得到以下结论：

1）对于同一阶次的固有频率，增加支撑系统耦合刚度时，轴系振动的固有频率有所增加，且高阶固有频率的增加趋势更明显。

2）在一定刚度范围内，3个节点均在低刚度值时出现最大共振幅值，因此在耦合刚度较低时要特别注意对轴系振动的影响；对于同一节点而言，更容易在低阶固有频率（1～4阶）时产生较大的振动幅值，符合强迫振动的规律。

3）系统耦合刚度一定时，离激励源越近的地方共振幅值越大；对于同一节点而言，在一定范围内增加刚度可以使轴系工作频率有效避开共振频率，进而降低共振幅值，使幅值变化趋于稳定。