2. 中国科学院理化技术研究所,北京 100190
2. Technical Institute of Physics and Chemistry, CAS, Beijing 100190, China
固体浮力材料是现代深潜技术的重要组成部分之一,是深潜器设计装备的六大关键技术之一,也是海洋勘察及深海工程中最普遍应用的一种材料。这种材料主要是为深海装置提供浮力,以实现深海装置的悬浮定位,无动力上浮下潜,增大有效载荷,减少外型尺寸。它不仅广泛应用于深潜器,还在深水采油及采矿中如海底深水浮式生产系统、海底管线、钻井管道等领域得到广泛应用,对深海的勘探与开发具有非常重要的作用[1-4]。
固体浮力材料一般是由环氧树脂和空心玻璃微球经混合和热固化形成的复合材料,其中,环氧树脂作为基体,空心玻璃微球作为密度调节剂。空心玻璃微球具有密度低、强度高、流动性好、隔热、耐腐蚀等优点,是制备固体浮力材料的核心原材料,其主要成分是硼硅酸盐,其是一种微米级的球形粉体,粒径一般在10~120 μm,壁厚在0.5~2.0 μm,真密度一般在0.1~0.5 g/cm3。空心玻璃微球的密度和强度决定了固体浮力材料的密度和强度,因此,高性能空心玻璃微球是制备大深度固体浮力材料的关键一环[5-7]。空心玻璃微球的制备在国际上是一个技术难题,仅被少数国家掌握,高性能产品对我国禁售。目前,大规模工业化生产多品种型号空心玻璃微球的公司主要有美国3 M公司和PQ公司,所使用的方法分别为固相粉末法和液相雾化法。在国内,张敬杰等[8-9]通过自主研制的“软化学”法制备出了高性能空心玻璃微球,为制备大深度固体浮力材料奠定了基础。
1 体积弹性模量介绍及意义固体浮力材料在应用到深水装备之前,需要对其关键性能指标进行检验,以保证深水装备的安全使用。衡量固体浮力材料性能的关键指标包括密度、高压吸水率和体积弹性模量等。其中,密度和高压吸水率都可以通过现有的仪器测定,而体积弹性模量的检验则是一个技术难点。
固体浮力材料的体积弹性模量是衡量其在水下高压环境中体积变化的关键指标,浮力材料的体积变化直接影响其所能提供的净浮力[10]。该净浮力是深潜器在服役水深设计时所涉及的关键参数,直接影响到深水潜器、深水设备和深水平台的水下安全,尤其对载人深潜器来说,固体浮力材料的设计安装事关潜水员及随行科学家的人身安全,因此必须对固体浮力材料的体积弹性模量进行准确检验,以保证潜水器在服役水深具有足够的净浮力。目前,固体浮力材料的体积弹性模量的准确测量仍是一个难点,这主要是由于固体浮力材料在高水压下的体积形变量非常小,很难进行准确测量。同时,期望的是固体浮力材料的体积弹性模量尽可能小,这样浮力损失小,剩余浮力大,潜水器越安全,这对体积弹性模量的准确测量带来了更大的挑战。鉴于此,本文综述国内外固体浮力材料体积弹性模量的测试方法,为水下装备设计开发人员提供参考。
2 体积弹性模量测试方法固体浮力材料的体积弹性模量测量的主要难点是测量高水压下固体浮力材料的微小形变量。一般来说,固体浮力材料的体积弹性模量测试方法主要有:仿真计算法、超声测量法、高压原位测试法等。
2.1 仿真计算法仿真计算法是通过建立固体浮力材料的微观结构模型,包括空心玻璃微球和树脂基体,根据2种材料的物理性质和复合结构,基于有限元法对微观模型施加边界条件(温度、压强等)进行计算,得到体积弹性模量。
陈鹿等[11]针对固体浮力材料建立了体心立方单胞的微观力学模型,通过Ansys有限元软件,对不同玻璃微珠体积分数和不同玻璃微珠壁厚组合的浮力材料进行了力学分析,获得了玻璃微珠厚度、体积分数与有效弹性模量及浮力材料比重之间的关系图,为高性能全海深浮力材料的研制提供了理论依据。
Prabhakar等[12]采用解析和数值方法研究了空心微球填充复合材料的宏观弹性行为。在解析模型中,首先估计了复合材料的有效体模量,然后利用适合于单轴拉伸的固体谐波,确定了复合材料的有效泊松比。利用代表性单元的有限元分析,估算了材料的宏观性能。利用该解析模型,评价了单胞有限元法在估算复合泡沫材料有效弹性性能中的适用性。
MingYu等[13]提出一种基于微观结构的有限元模拟方法来预测空心球填充复合泡沫材料的弹性力学行为。采用内聚力单元模拟界面,建立了三维立方单元界面模型,以获取细观微观结构和应力应变场。采用均匀化方法计算了复合泡沫材料的有效弹性性能−杨氏模量和泊松比,为复合泡沫的设计和优化提供了有力的工具。
2.2 超声测量法固体材料中的超声波传播的速度与其弹性模量和密度直接相关。在固体材料的密度确定之后,通过测量超声波在固体材料中的传播速度,可以计算得到材料的弹性模量及泊松比。超声测量法是一种快速无损表征固体材料弹性模量的方法,已形成相应的国家标准(GB/T 38897-2020)。
固体浮力材料是一种固体复合泡沫,也属于固体材料。对于一定密度的复合泡沫,也可以利用超声的方法在测试声波在材料中的传播速度,进而计算得到材料的模量。
Phani 等[14]研究了超声波在24种不同复合泡沫的传输特性,对比了不同微球在不同体积填充比例(10%~60%)下的超声回波性能,进而根据复合泡沫的密度计算出弹性模量,如下式:
| $ \mathrm{E}=\frac{{V}_{L}^{2}\rho (1+\nu )(1-2\nu )}{1-\nu }\times \frac{0.733}{6.89\times {10}^{4}}\times 0.006\;89\;{\rm{MPa}} {\text。}$ | (1) |
其中:VL为纵波声速;ν为泊松比;ρ为密度。
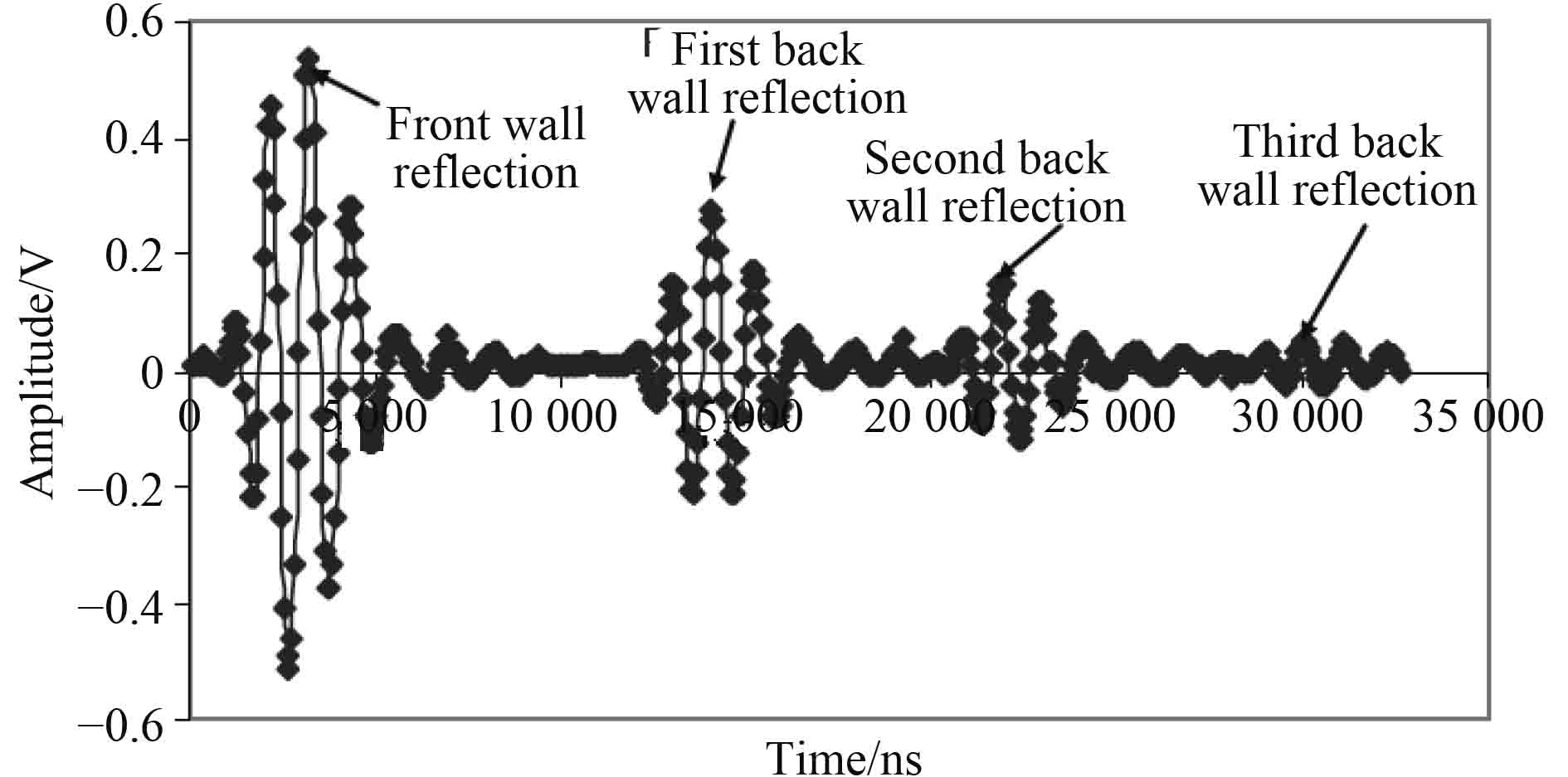
进一步研究发现超声波的衰减系数,声传播速度和弹性模量取决于微球的半径/壁厚比和体积分数。典型的复合泡沫超声回波-时间曲线如图1所示。
Pradeep等[15]在Phani的基础上,进一步研究了PE/微球复合材料的超声传播特性,提出了泊松比、剪切模量、体积模量和杨氏模量的计算方法,并对5种不同微球含量的复合泡沫进行了测试计算。研究发现,复合泡沫的体积模量随着微球含量先增加后减小,微球含量为14.8%时体积模量到达最大值5.43 GPa。计算公式如下式:
| $ \mathrm{\nu }=\left[\left(1-2{\left(\frac{{V}_{S}}{{V}_{L}}\right)}^{2}\right)\Biggr/\left(2-2{\left(\frac{{V}_{S}}{{V}_{L}}\right)}^{2}\right)\right] {\text,}$ | (2a) |
| $ {G}=\mathrm{\rho }{V}_{S}^{2}\times {10}^{-6} {\text,}$ | (2b) |
| $ {K}=\left(\mathrm{\rho }{V}_{L}^{2}-\frac{4}{3}{G}\right) {\text,}$ | (2c) |
| $ {E}=\frac{\left(\rho {V}_{L}^{2}\right)\left(1-2\nu \right)(1+\nu )}{(1-\nu )}\times {10}^{-6}{\text。} $ | (2d) |
其中:VS为横波声速;VL为纵波声速;ν为泊松比;G为剪切模量;K为体积模量;E为杨氏模量;ρ为密度。
另外,在4500 m载人潜水器“深海勇士”号浮力材料的研制过程中,中国科学院理化技术研究所联合中国科学院声学研究所通过声速法对固体浮力材料的弹性模量进行测定,根据声波在浮力材料内的传播速度和浮力材料的密度进行计算而得,测试方法如下:
1)测试中,用超声分析仪激励超声探头,使其发射超声波,并沿着被测试固体浮力材料样块传播,到底面反射被超声探头接收,根据接收的回波到时及样块厚度,计算声波在该样块中的声速。分别用纵波直探头和横波直探头测试,即可得到纵波声速和横波声速。
2)通过测量固体浮力材料样块的纵波声速(CL)和横波声速(CS),再结合其密度(ρ),模量(M)利用下式计算:
| $ {M}=\dfrac{\rho {C}_{S}^{2}\left(3{\left(\dfrac{{C}_{L}}{{C}_{S}}\right)}^{2}-4\right)}{{\left(\dfrac{{C}_{L}}{{C}_{S}}\right)}^{2}-1} {\text。}$ | (3) |
其中:M为弹性模量,GPa;
高压原位测试法是一种通过实验装置直接测量固体浮力材料样品的体积弹性模量的方法,其主要原理是测量固体浮力材料在一定压强下的体积变形量。实现该形变量的精确测量是难点。国际上的测试方法普遍参考美军标。近年来,随着我国对深海的高度关注,浮力材料的应用逐渐增加,其体积弹性模量测试也得到了相应发展。
国外Trelleborg Offshore公司、Emerson&Cuming公司等制造加工的固体浮力材料产品均符合美国军标MIL-S-24154A[16],该规范适用于为深海水下探索机器人及相关用途的水下装置提供浮力的硬质合成泡沫浮力材料。该军标用柱塞体积排量(排水量,位移)法测定复合泡沫浮力材料体积弹性模量,测试过程如下:
首先将一定体积的水和一块确定尺寸的长方体不锈钢块放入液压缸体中,通过柱塞加压至目标压强,其中,不锈钢块为基准样品,视为在压强下无形变。加压过程中,柱塞的位移和由此引起的水的体积变化被记录在仪表上。此部分水的体积变化为水在目标压强下的压缩量,记为
| $ {K}=-\frac{{\Delta V}_{s}}{{V}_{s}}=-\left(\frac{{\Delta V}_{c}-{\Delta V}_{w}}{{V}_{s}}\right){\text,}$ | (4) |
| $ {E}_{B}=\frac{-\Delta P}{{\Delta V}_{s}}\times {V}_{s}=\frac{\Delta P}{K} {\text。}$ | (5) |
其中:K为压缩比;
该方法通过柱塞加压测量液压缸体中分别装有不锈钢块和固体浮力材料时的水的体积变化,减去固体浮力材料的吸水体积,得到固体浮力材料的体积弹性模量。
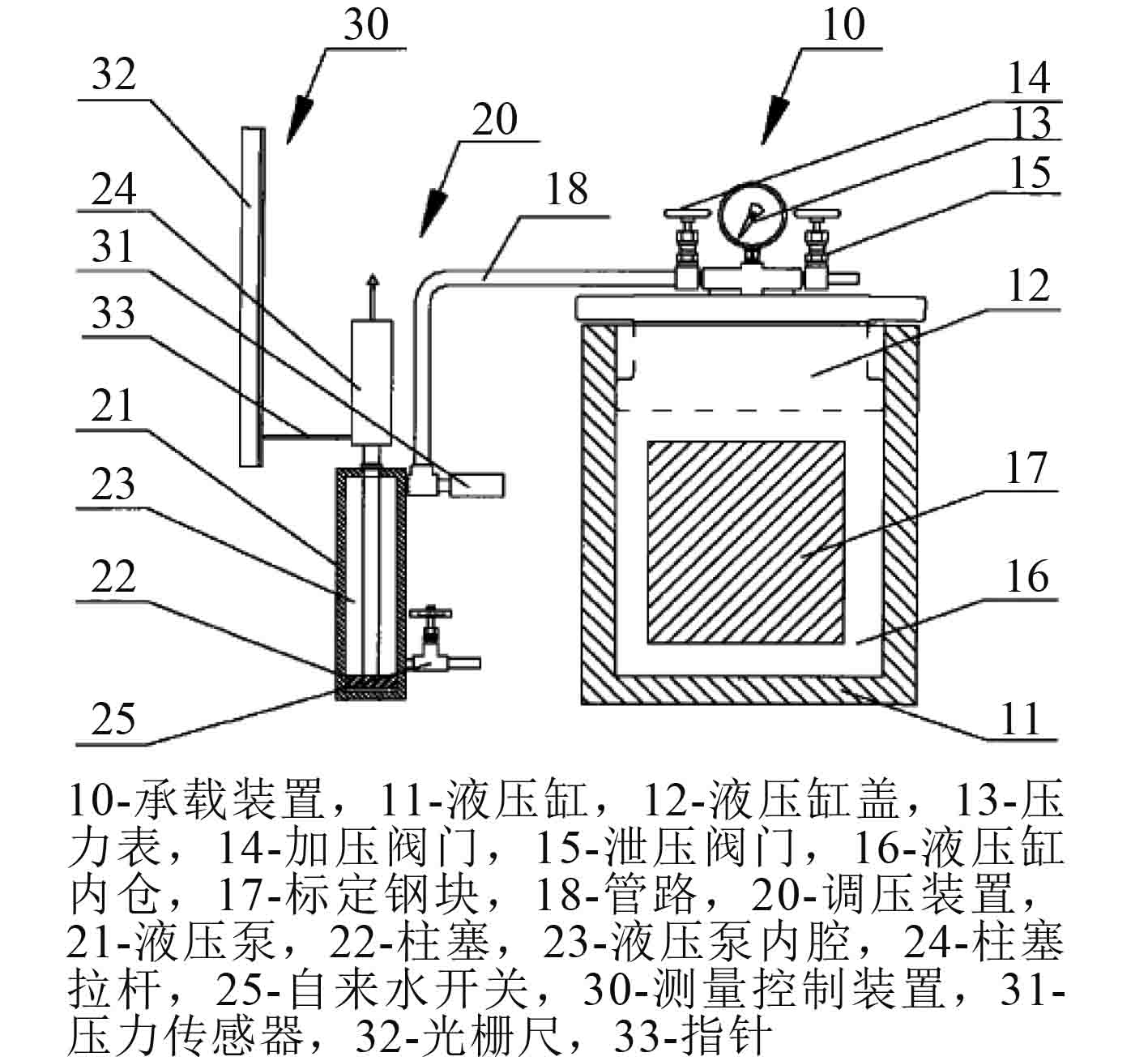
海洋化工研究院参考了美国军标MIL-S-24154A,制定了企业标准Q/HHY221-2005,并申请了申请号为200810158754.4的《固体浮力材料体积弹性模量测量装置及测试方法》发明专利[17],其测量装置示意图如图2所示。
|
图 2 固体浮力材料体积弹性模量测量装置的示意图 Fig. 2 Schematic diagram of measuring device for bulk modulus of elasticity of solid buoyancy materials |
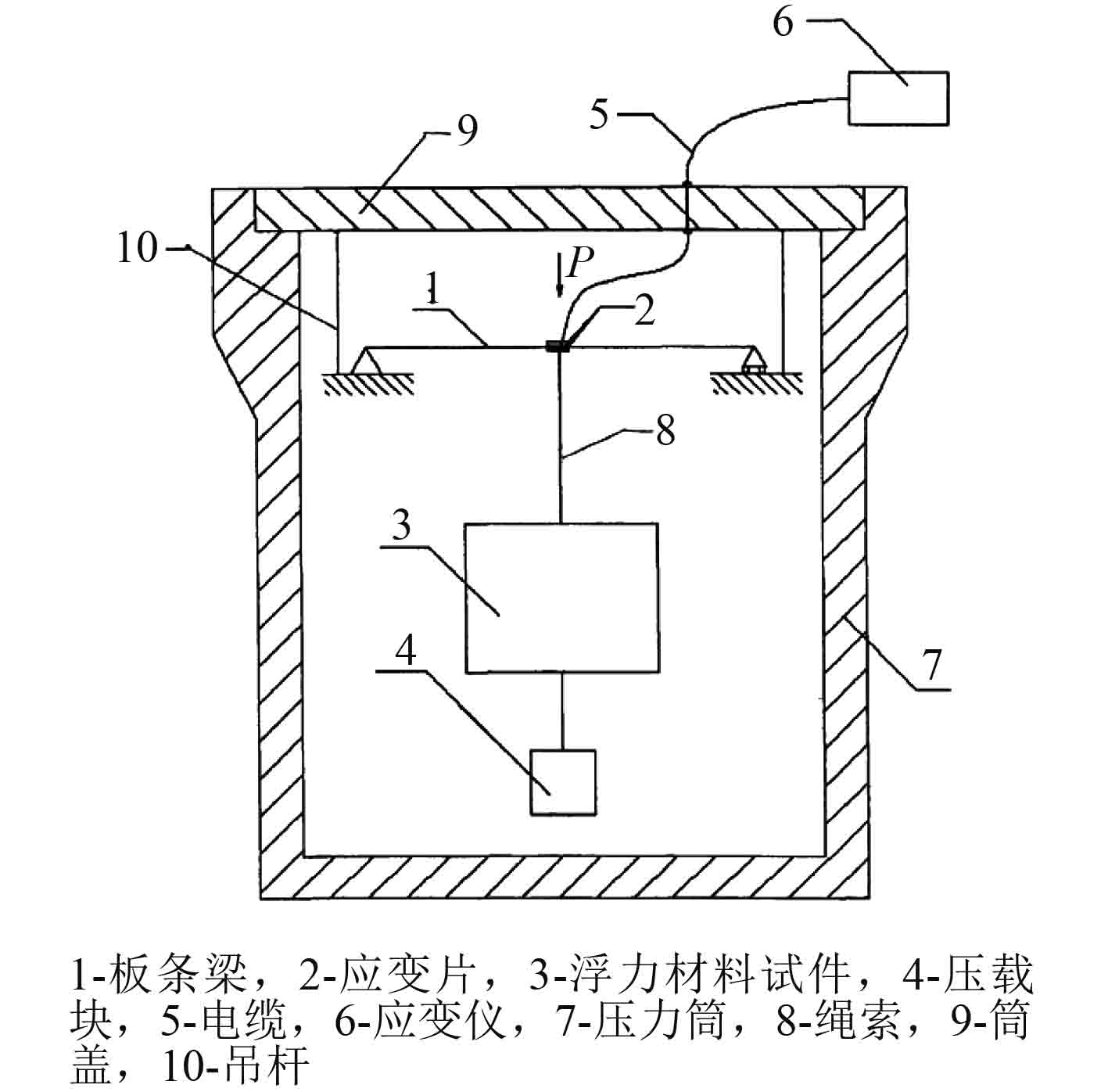
赵俊海等对固体浮力材料在高静水压力下的浮力损失进行了测量,并申请了申请号为200810022677.X的《高静水压力下浮力材料的浮力损失测试装置及方法》发明专利[18]。一般来说,固体浮力材料在高静水压力下的浮力损失由两部分构成,一部分是由固体浮力材料在高压下的体积收缩引起,即体积弹性模量;另一部分是由固体浮力材料在高压下的吸水引起。赵俊海等[19]将两部分综合考虑,研制了浮力材料的浮力损失测试装置,其示意图如图3所示。该方法用应变片测量吊装有浮力材料试件和压载块的板条梁从零到一定压强下的应变变化,换算为应力变化,通过公式计算确定浮力材料的浮力损失。具体方法是:
1)选取板条梁样品,测量其应力-应变曲线,得到板条梁的杨氏模量E;
2)标定板条梁,测定其应力-应变曲线的线性和重复性,择优取用;
3)将板条梁、吊杆、应变片、浮力材料和压载块按照图3所示组装,放入压力筒中,待稳定后,读取应变片的应变值,加压到目标压力,再次读取应变片的应变值;
4)根据上述测定的板条梁的应力-应变曲线,把板条梁的应变变化换算为应力变化;
5)根据板条梁跨中截面的弯矩和应力计算公式得到浮力材料的浮力损失。
该浮力损失测试装置和方法将固体浮力材料在高静水压力下的收缩引起浮力损失和吸水引起的浮力损失综合考虑,更贴近于浮力材料应用时产生的浮力。考虑到美国军标和海洋化工研究院的方法是将测试后的浮力材料取出称重,由于失去了静水压的作用,部分水会从浮力材料内部溢出和蒸发,使得浮力材料的吸水偏小,进而影响到浮力损失的测试精度。该方法在目标压力下综合考虑两部分引起的浮力损失,提高了浮力损失的测试精度。
|
图 3 高静水压力下浮力材料浮力损失测试装置示意图 Fig. 3 Schematic diagram of buoyancy loss test device for buoyancy materials under high hydrostatic pressure |
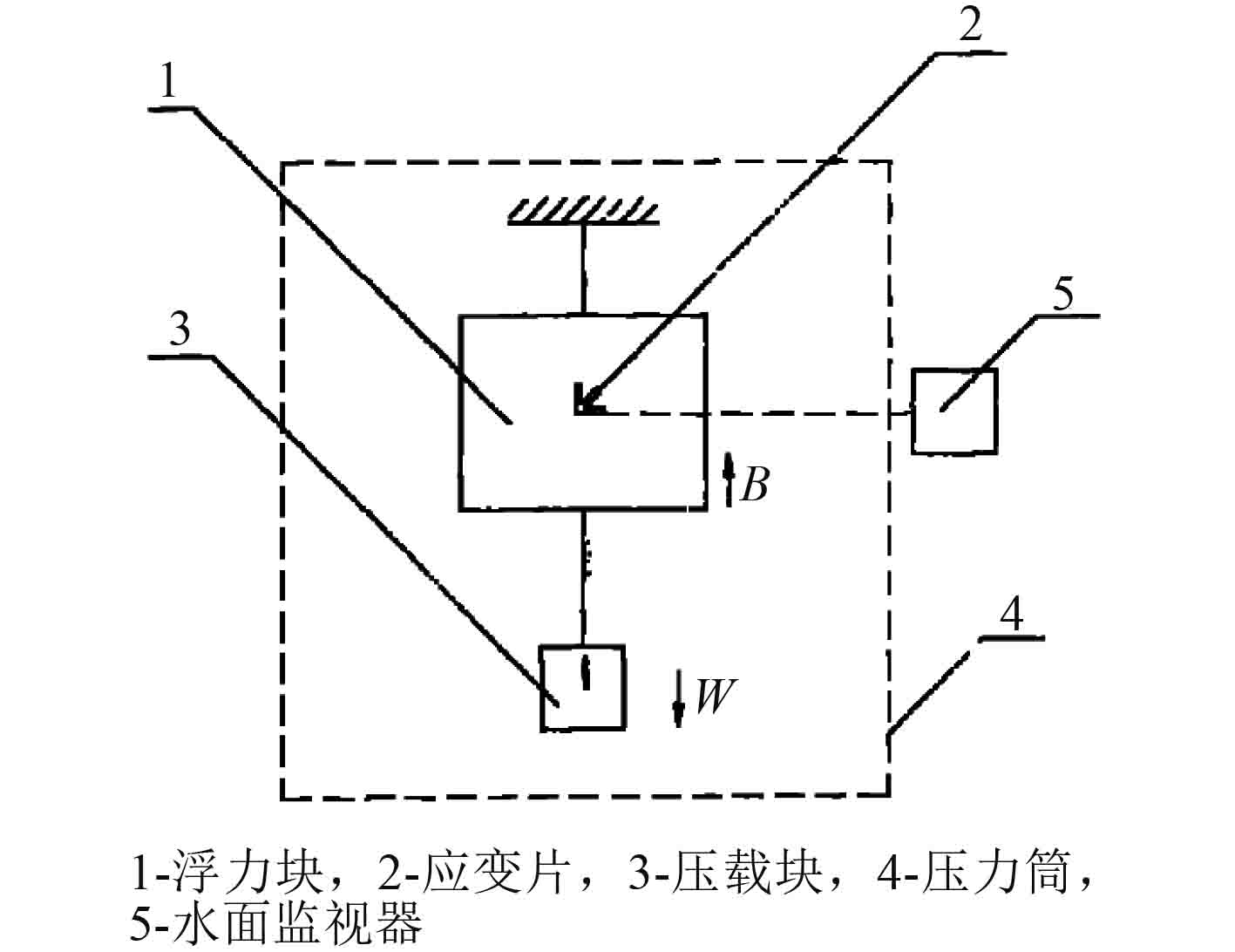
为了准确测量高静水压力下浮力材料的体积收缩率,马利斌等研制了测量装置和方法,并申请了申请号为201010559527.X的《高静水压力下浮力材料的体积收缩率测试方法》发明专利[20],测试装置示意图如图4所示。该方法通过浮力材料表面贴应变片的方法表征从零到一定压强下浮力材料的体积收缩率,根据应变片的应变值换算得到浮力材料的体积收缩率。具体方法是:
|
图 4 高静水压力下浮力材料的体积收缩率测试装置示意图 Fig. 4 Schematic diagram of measurement device for volume shrinkage of buoyancy material under high hydrostatic pressure |
1)根据浮力块的体积换算压载块的重量,将浮力块和压载块固定到试验工装上;
2)在浮力块表面不同位置贴应变片,并连接应变片与水面监视器之间的电路;
3)将上述工装放入压力筒中加压,通过水面监视器获取浮力块在不同压力条件下的应变值;
4)通过体积收缩率等于3倍应变值,换算得到浮力块在不同试验压力下的体积收缩率。
该方法可计算在目标压力下由于浮力材料的体积收缩所引起的浮力损失。
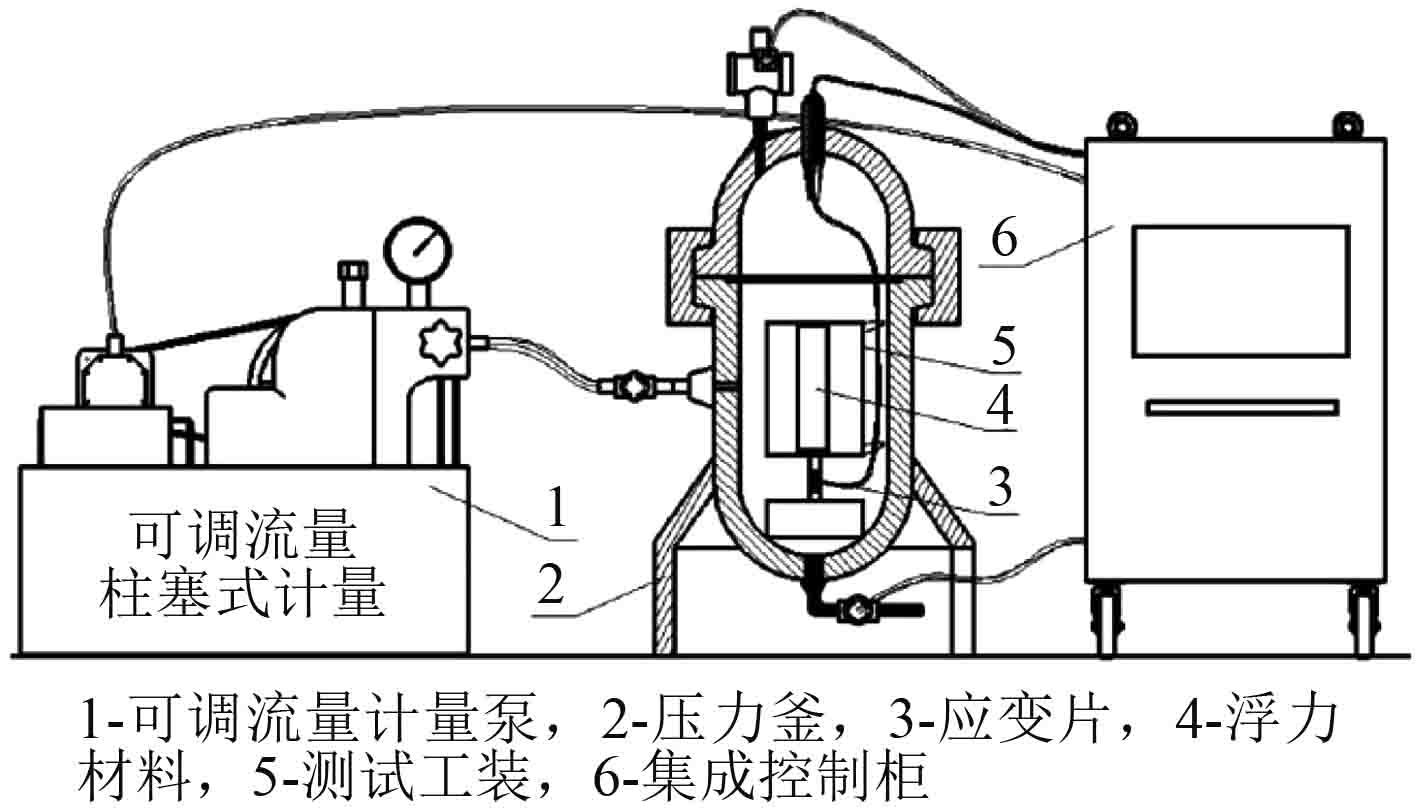
李东梁等[21]研究了浮力材料浮力损失的测试装置和方法,并申请了申请号为201811569359.5的《一种模拟深海环境下浮力材料浮力损失的测量方法》发明专利。该测试装置与上述浮力损失测试装置类似,有所不同的是该装置取消了板条梁的使用,将浮力材料和配重通过拉杆与框架连接,拉杆上安装应变片,可测量从零到目标压强下拉杆的应变变化,通过计算得到浮力材料的浮力损失,其测试装置如图5所示。该方法取消了板条梁的使用,使浮力损失的测量更加简便。
|
图 5 浮力损失测量装置示意图 Fig. 5 Schematic diagram of buoyancy loss measuring device |
张敬杰等通过自主研制的“软化学”法制备出高性能空心玻璃微球,又通过基体配方的调整优化,制备出了国产大深度固体浮力材料。目前已应用于“深海勇士”号和“奋斗者”号载人潜水器,以及一系列无人深潜器上。为了研究固体浮力材料在深海下的浮力损失及体积弹性模量,张敬杰团队的严开祺等研究了一系列装置和方法,并申请了专利。
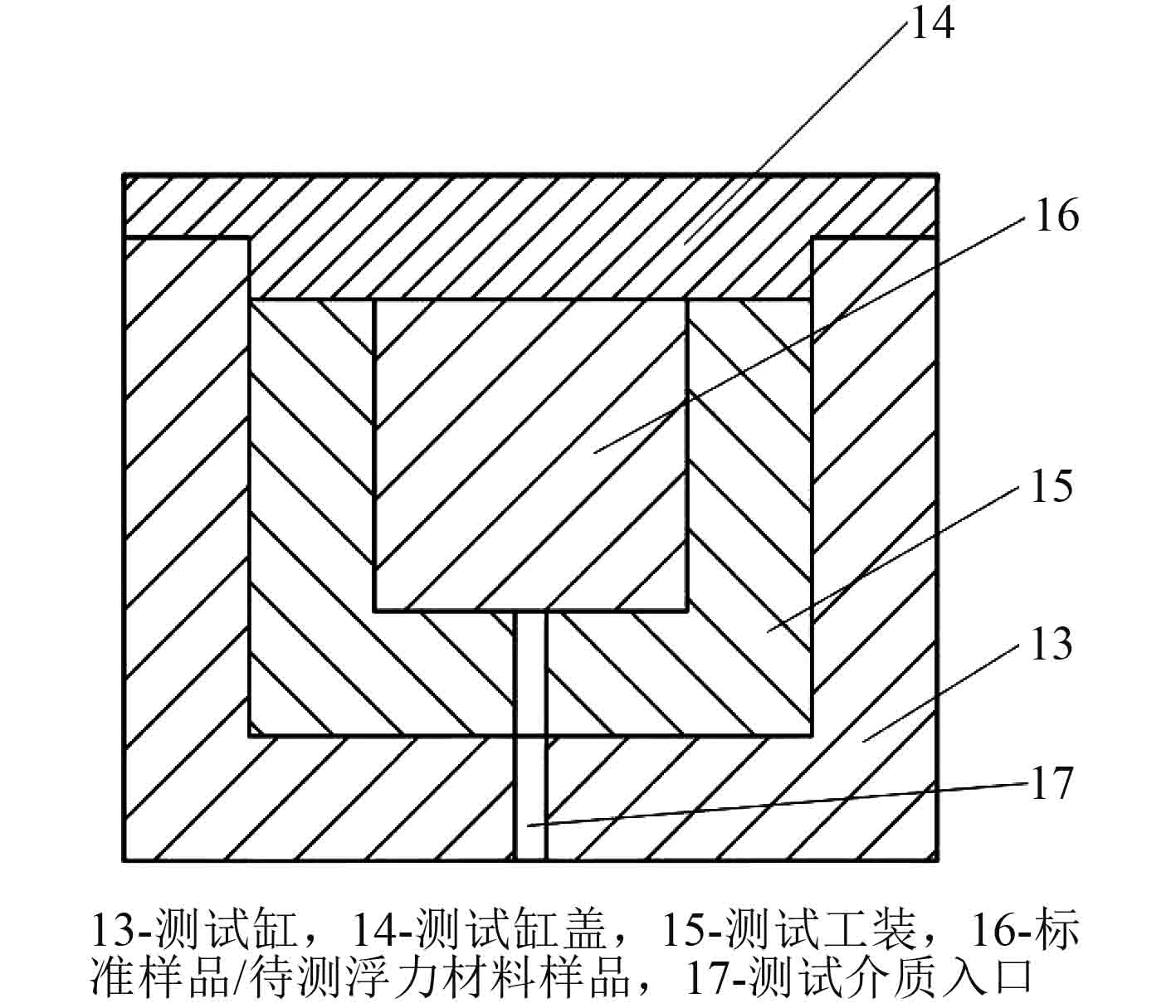
在固体浮力材料浮力损失的测试装置和方法上,严开祺等[22]研究的装置和方法与传统应变片法不同,通过测量测试仓内分别装有标定钢块和待测浮力材料样品时,在一定压强下压入测试仓内的水的体积差,得到质量差,通过简单计算得到固体浮力材料的浮力损失,包括由浮力材料的体积收缩和吸水共同引起的浮力损失。相比于应变片法,该方法的主要优势有:1)测试装置和方法简便易行,误差较小;测试过程中,没有线缆穿过测试仓,更利于高压下压强的稳定;3)该方法引入了测试工装,测试工装可占据测试仓内绝大部分空间,减少了测试流体的充入,使测试过程中水的压缩比带来的影响尽可能降低,测试结果更加准确。测试仓及测试仓内部测试工装和浮力材料样品的剖面示意图如图6所示。
|
图 6 测试仓的剖面示意图 Fig. 6 Section diagram of the test chamber |
为了精确测量固体浮力材料的体积弹性模量,严开祺等[23]进行了测试装置和方法的研究。在研究过程中发现,美国军标和海洋化工研究院的体积弹性模量测试方法没有考虑水的压缩比,这会为深海浮力材料体积弹性模量的测量带来较大的误差。严开祺等通过测量测试仓内分别装有标定钢块和待测浮力材料样品时,在一定压强下压入测试仓内的水的体积差,除以该压强下的水的压缩比,得到固体浮力材料在该压强下的真实收缩体积。该压缩比是通过测试仓内装有标定钢块时从零到一定压强下压入测试仓的水的体积计算得到的。该方法虽然能准确获得浮力材料的体积弹性模量,但是其只能测量目标压力下的体积弹性模量,测试点较为单一。由于固体浮力材料在不同压强下的吸水率不同,该方法是通过测量压前和压后的浮力材料的质量差计算吸水体积,再将吸水体积扣除得到体积弹性模量。
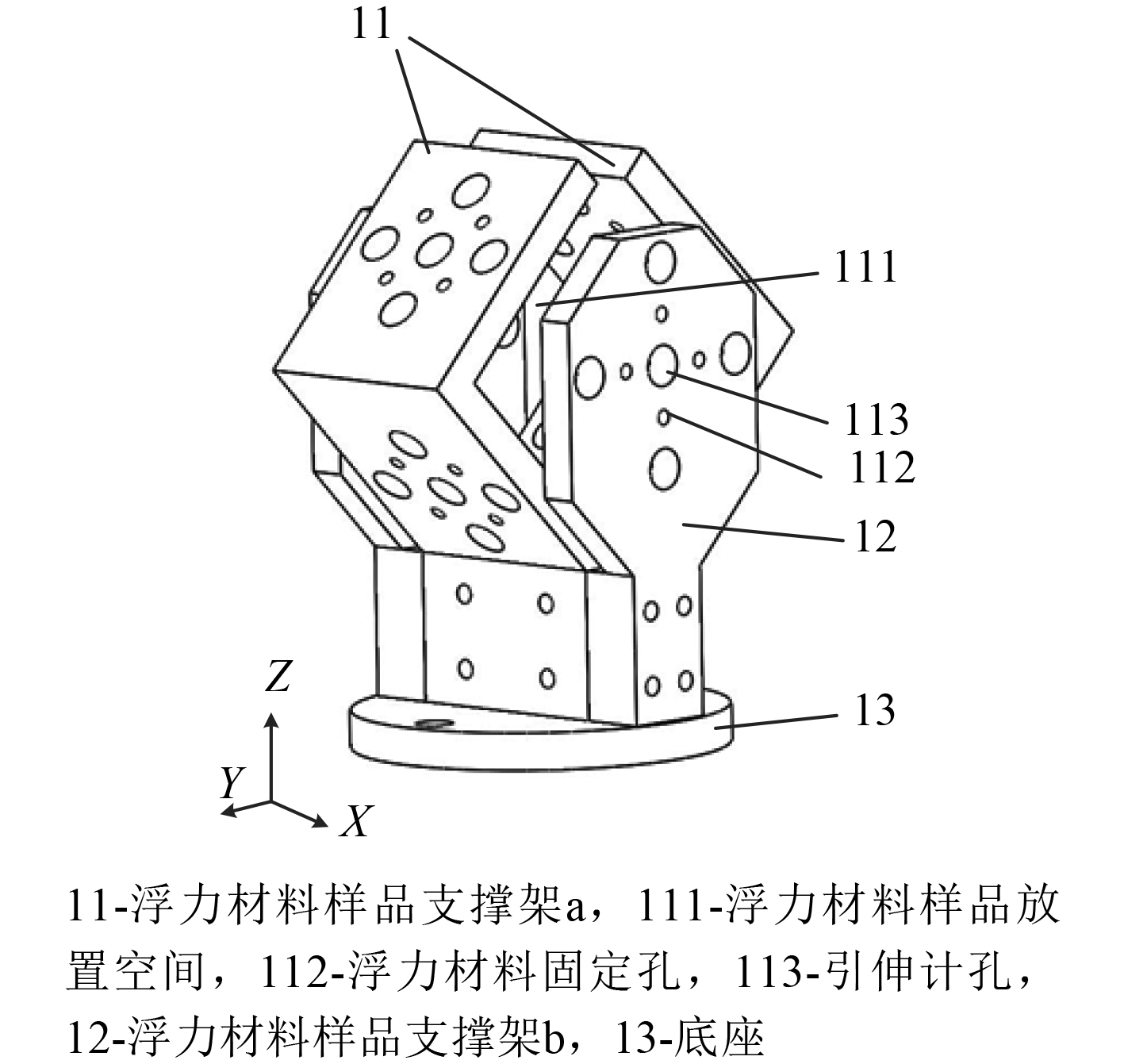
为了提高浮力材料体积弹性模量的测试效率,通过一次测量就可得到一系列压强下浮力材料的体积弹性模量,同时确保数据准确可靠,严开祺等[24]研究了固体浮力材料体积弹性模量的原位测量方法。该方法通过将高压引伸计成对布放在长方体或立方体形状的固体浮力材料表面,同轴上的2个引伸计为一对,通过零到目标压强一系列压强下的引伸计数据的采集,可得到浮力材料在零到目标压强下任一压强的体积收缩量,进而得到浮力材料的体积弹性模量。若要实现精确测量,可在2个平行面上多布放几对引伸计。此外,该方法还设置了专用的浮力材料样品夹具,其结构示意图如图7所示。该夹具不但有固定浮力材料的作用,还是引伸计的支架,使浮力材料的形变测量更加稳定、准确。该方法通过高压引伸计测量浮力材料的体积弹性模量,极大简化了操作,提高了测试效率,使我们对浮力材料在不同深度所造成的浮力损失实现了更加直观的把握。
|
图 7 引伸计法浮力材料体积弹性模量测试夹具 Fig. 7 Fixture for measuring bulk modulus of buoyancy material by extensometer method |
在固体浮力材料的性能检测中,其吸水率的测量也是重要指标。吸水率不但与水深有关,也与材料的性能有较大关系。通常测量浮力材料吸水率的方法是测量浮力材料压前和压后的质量差,计算得到吸水率。严开祺等[25]将上述压缩比法和引伸计法相结合,实现了零到目标压强一系列压强下固体浮力材料吸水率的实时测量。通过引伸计的原位测量值进行反算,得到吸水率的实时测量值。
张敬杰团队以固体浮力材料研究为基础,以实际应用需求为导向,配备了一系列固体浮力材料性能检测装置,包括固体浮力材料浮力损失测试装置、压缩比法体积弹性模量测试装置、引伸计法体积弹性模量测试装置、吸水率实时测量装置等。为固体浮力材料在不同因素引起的浮力损失进行定量描述,为高性能固体浮力材料的制备和潜水器净浮力及有效载荷的设计提供参考。
3 结 语近年来,随着我国对深海的高度关注,固体浮力材料的应用领域逐渐增加,应用深度也逐渐增加,其体积弹性模量检测也得到了快速发展。基于固体浮力材料体积弹性模量在实际应用中的重要性,本文对浮力材料体积弹性模量相关内容的装置和方法进行了综述,包括浮力损失、体积弹性模量和吸水率等,为水下装备设计开发人员提供参考和借鉴。
| [1] |
潘顺龙, 张敬杰, 宋广智. 深潜用空心玻璃微珠和固体浮力材料的研制及其研究现状[J]. 热带海洋学报, 2009, 28(4): 17-21. DOI:10.3969/j.issn.1009-5470.2009.04.004 |
| [2] |
王平, 严开祺, 潘顺龙, 等. 深水固体浮力材料研究进展[J]. 工程研究-跨学科视野中的工程, 2016, 8(2): 223-9. |
| [3] |
刘艳, 刘文智, 马春霞. 深水固体浮力材料的制备及性能研究[J]. 舰船科学技术, 2017, 39(3): 87-90. DOI:10.3404/j.issn.1672-7619.2017.03.018 |
| [4] |
熊利, 许晓武, 金星. 深海固体浮力材料的研制及性能探讨[J]. 矿冶工程, 2018, 38(5): 33-5. DOI:10.3969/j.issn.0253-6099.2018.05.008 |
| [5] |
严开祺. 空心玻璃微球力学性能研究方法及其应用探索[D]. 北京: 中国科学院大学, 2012.
|
| [6] |
严开祺, 谢虓, 张敬杰, 等. 高性能空心玻璃微球的力学特性研究[J]. 材料导报, 2011, 25(17): 116-21, 30. |
| [7] |
应枭. 固体浮力材料的力学性能研究[D]. 大连: 大连理工大学, 2019.
|
| [8] |
宋晓睿, 杨辉. 空心玻璃微球制备技术研究进展[J]. 硅酸盐学报, 2012, 40(3): 450-7. |
| [9] |
张敬杰, 宋广智, 崔燕菲, 等. 一种空心玻璃微球软化学制备方法和所制空心玻璃微球及其应用, CN201210056295.5.
|
| [10] |
朱忠华, 赵俊海, 胡震, 等. 高静水压力下浮力材料的浮力损失研究[C]// 2008年船舶水动力学学术会议暨中国船舶学术界进入ITTC30周年纪念会论文集, 杭州, 2008: 218-26.
|
| [11] |
陈鹿, 王芳, 崔维成, 等. 全海深载人潜水器用浮力材料的有效弹性模量特性研究[J]. 船舶力学, 2019, 23(12): 1486-99. |
| [12] |
MARUR P R. Numerical estimation of effective elastic moduli of syntactic foams[J]. Finite Elements in Analysis and Design, 2010, 46(11): 1001-7. DOI:10.1016/j.finel.2010.07.006 |
| [13] |
YU M, ZHU P, MA Y. Global sensitivity analysis for the elastic properties of hollow spheres filled syntactic foams using high dimensional model representation method[J]. Computational Materials Science, 2012, 61: 89-98. DOI:10.1016/j.commatsci.2012.04.005 |
| [14] |
MYLAVARAPU P, WOLDESENBET E. Characterization of syntactic foams — an ultrasonic approach[J]. Journal of Cellular Plastics - J CELL PLAST, 2008, 44: 203-22. DOI:10.1177/0021955X07087330 |
| [15] |
ROHATGI P, MATSUNAGA T, GUPTA N. Compressive and ultrasonic properties of polyester/fly ash composites[J]. Journal of Materials Science, 2009, 44: 1485-93. DOI:10.1007/s10853-008-3165-1 |
| [16] |
陈先, 周媛, 卢伟. 固体浮力材料[M]. 北京: 化学工业出版社, 2011.
|
| [17] |
陈先, 吴则华, 周媛, 等. 固体浮力材料体积弹性模量测量装置及测试方法, CN200810158754.4.[P].
|
| [18] |
赵俊海, 马利斌, 刘涛. 高静水压力下浮力材料的浮力损失测试装置及方法, CN200810022677. X.[P].
|
| [19] |
赵俊海, 马利斌, 刘涛. 浮力损失测试装置, CN200820040402.4.[P].
|
| [20] |
马利斌, 赵俊海, 侯德永. 高静水压力下浮力材料的体积收缩率测试方法, CN201010559527. X.[P].
|
| [21] |
李东梁, 高永宁, 周阁丽, 等. 一种模拟深海环境下浮力材料浮力损失的测量方法, CN201811569359.5.[P].
|
| [22] |
严开祺, 王平, 张敬杰, 廖斌. 一种固体浮力材料浮力损失测量装置, CN202020830000.5.[P].
|
| [23] |
严开祺, 王平, 张敬杰, 廖斌. 一种固体浮力材料体积弹性模量测量方法, CN202010421175.5.[P].
|
| [24] |
严开祺, 王平, 张敬杰, 廖斌. 一种弹性模量测量装置以及测量方法, CN202110254591.5.[P].
|
| [25] |
严开祺, 王平, 张敬杰, 廖斌. 一种吸水率测量装置以及测量方法, CN202110254585. X.[P].
|
 2021, Vol. 43
2021, Vol. 43