2. 海军装备部驻郑州地区军事代表室,河南 郑州 450015
2. Military Representative Office of Naval Equipment Department in Zhengzhou, Zhengzhou 450015, China
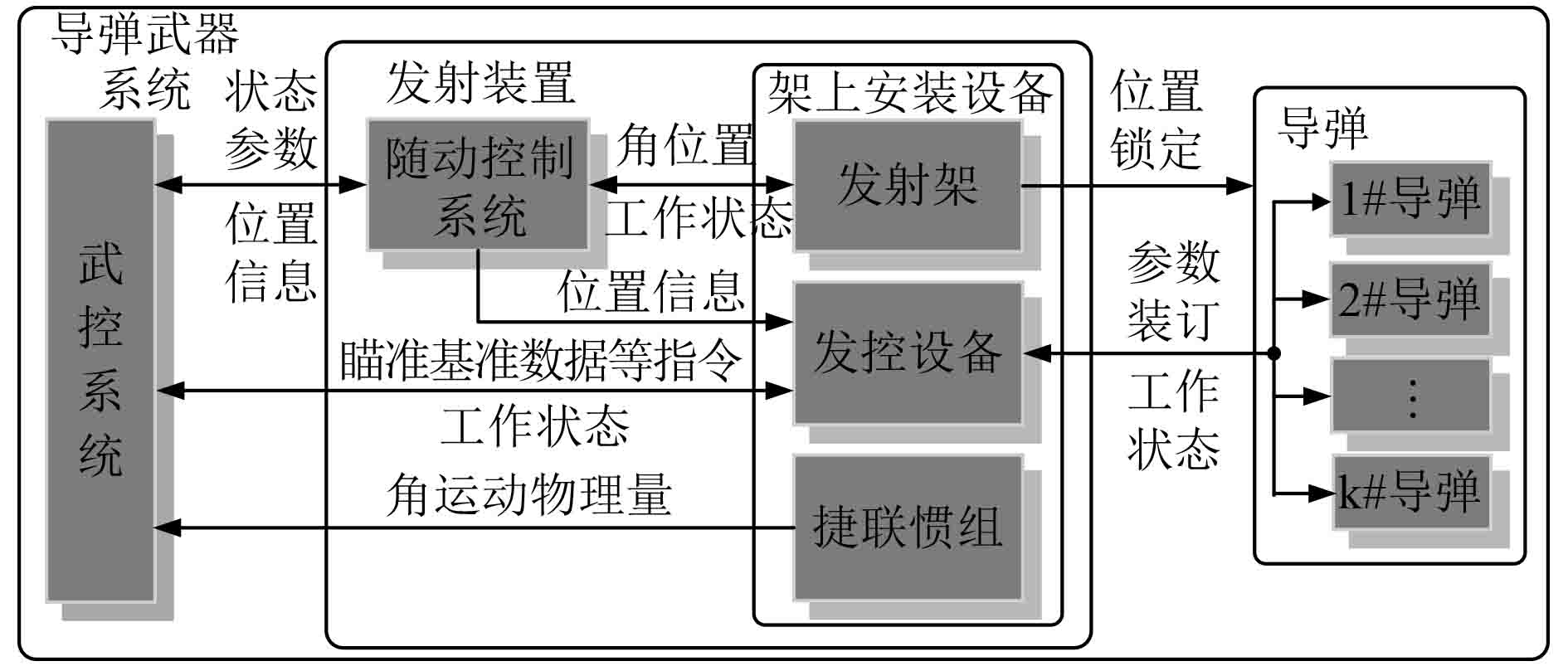
指向精度,作为导弹武器框架结构精度的重要指标之一,是指固连在框架上的单位矢量,经过发射装置转动一定角度后,实际指向与其应达到的指向之间的角度偏差[1]。偏差主要来源于基座安装误差、轴承跳动、定位和测量误差等。发射装置指向精度的优劣,直接影响导弹的初始发射精度,是导弹是否能够准确命中目标的关键因素之一[2]。在导弹点火时,如果发射装置提供的实际指向角度误差不能满足武器系统需求,则需要对发射装置指向精度进行修正和补偿。某舰载导弹武器系统采用将捷联惯性测量组合(简称捷联惯组,Strapdown Inertial Measurement Unit,SIMU)直接固连在发射装置俯仰架上,随俯仰架一起运动,捷联惯组内部的角速率陀螺仪和加速度仪,直接测量架上导弹的角运动物理量,将数据传递给武控系统,经武控系统融合发射装置位置信息后进行解算,通过发控设备为导弹装订基准数据参数,如图1所示。因此,如何准确地将发射瞄准的基准数据测得并赋予导弹武器系统,是某舰载导弹武器系统总体方案的关键技术之一。
|
图 1 某舰载导弹武器系统总体方案示意 Fig. 1 General scheme of a ship-based missile weapon system |
当捷联惯组在发射装置上安装后,理想情况下,捷联惯组的惯性组件敏感轴构成的坐标系应与发射装置俯仰架所在坐标系重合。但由于惯性组件安装定位和产品加工工艺限制,2个坐标系坐标轴不可避免地会存在一定的角度误差,造成发射装置的实际指向与捷联惯组测量值在偏航、滚转和俯仰3个方向上产生一定程度的偏差,直接影响导弹的发射精度。本文提出了一种针对捷联惯组在某舰载倾斜瞄准式发射装置上安装时产生的正交安装误差的标定方法,并通过合理的安装定位措施,减少了捷联惯组的正交安装误差,提高了发射装置上捷联惯组测量值与架上导弹实际指向的一致性。
1 误差描述捷联惯组安装误差一般有2种情况:一是由于惯性测量模块或加速度计的敏感轴按照相互正交的方式安装引起的偏角误差,称之为非正交安装误差;二是捷联惯组坐标系与发射装置载体坐标系不重合等引起的误差,称之为正交安装误差[3]。
非正交误差的存在将引起传感器测量信息之间的交叉耦合,在使用前必须通过标定实验确定出陀螺仪和加速度计等模块的各项误差系数,并在捷联惯组系统中进行补偿,通常在实验室转台上进行标定。其中,加速度计通过位置转台进行标定,光纤陀螺通过速率转台标定[4],误差标定方法较为成熟;捷联惯组的正交安装误差将引起载体实际指向角位置偏差,由于装载对象的结构复杂程度、安装方式的多样性以及测试场地的条件限制,使正交安装误差标定方法成为了一个难点。因此,本文主要针对捷联惯组在发射装置载体上安装引起的正交安装误差标定方法开展研究。
2 空间坐标系建立和定义如图2所示的方位-俯仰两轴式舰载发射装置中,捷联惯组与发射装置之间采用直接稳定方式[5]。捷联惯组安装在俯仰架后部,与发射装置的方位轴和俯仰轴同步转动,直接测量导弹在俯仰架上位置等数据。

|
图 2 各空间坐标系相对关系示意图 Fig. 2 Relative relationship diagram of spatial coordinate systems |
本文对捷联惯组和发射装置各部分运动关系的描述,涉及到空间坐标系变换的概念,主要有惯性坐标系、大地坐标系、基座坐标系、方位坐标系、俯仰坐标系和捷联惯组坐标系,所有坐标系自身三轴两两正交且符合笛卡儿坐标系规则[5]。下面结合图2对各空间坐标系的概念进行定义。
2.1 空间坐标系定义 2.1.1 惯性坐标系Oi—xiyizi的定义惯性坐标系原点Oi位于地心,xi轴与0°经线在赤道平面上投影重合并由地心向外;yi轴与东经90°经线在赤道平面上投影重合并由地心向外;zi轴与地轴重合指向北方。
2.1.2 大地坐标系Ot—xtytzt的定义大地坐标系原点Ot设定于发射装置重心位置垂直向下与大地的交点,xt轴代表当前位置的水平东方向;yt轴代表当前位置的水平北方向;zt轴代表与重力加速度相反的方向。
2.1.3 基座坐标系Ob—xbybzb的定义基座坐标系原点Ob位于发射装置基座的几何中心,xb轴沿发射装置基座的纵向指向基座前方,即发射装置的方位零点;yb轴沿发射装置基座的横向指向基座左侧;zb轴与发射装置基座平面垂直并指向上方。本文设定基座坐标系xb-yb平面与大地坐标系xt-yt平面平行。
2.1.4 方位坐标系Oa—xayaza的定义方位坐标系固连于方位轴,其原点Oa位于方位轴与基座上平面的交点,xa轴沿回转架的纵向指向回转架前方,即发射装置的方位指向;ya轴沿回转架的横向指向回转架左侧;za轴始终与方位轴重合指向上方。在方位轴处于零位时,xa轴、ya轴分别与基座坐标系中xb轴、yb轴平行;在方位轴旋转时,xa轴和ya轴随方位轴转动而转动,此时xa轴和xb轴(或ya轴和yb轴)之间的夹角α即为发射装置方位角。
2.1.5 俯仰坐标系Of—xfyfzf的定义俯仰坐标系固连于俯仰轴,其原点Of位于方位轴与俯仰轴的理论交点,xf轴沿俯仰架的纵向指向俯仰架前方,即发射装置的俯仰指向;yf轴始终与俯仰轴重合并指向俯仰架的左侧;zf轴与xf-yf平面垂直并指向上方。俯仰轴安装于回转架上,俯仰坐标系随俯仰轴、方位轴的转动而转动,因此,俯仰坐标系即为导弹所在坐标系。在俯仰轴处于零位时,xf轴、zf轴分别与方位坐标系中xa轴、za轴平行;在俯仰轴旋转时,xf轴和zf轴随俯仰轴转动而转动,此时xf轴和xa轴(或zf轴和za轴)之间的夹角β即为发射装置俯仰角。
2.1.6 捷联惯组坐标系Og—xgygzg的定义考虑到捷联惯组出厂时,已对非正交安装误差进行了标定,因此,本文设定捷联惯组坐标系原点Og位于捷联惯组各敏感轴的交点,捷联惯组坐标系的xg轴、yg轴和zg轴分别与捷联惯组内结构中对应的敏感轴重合。
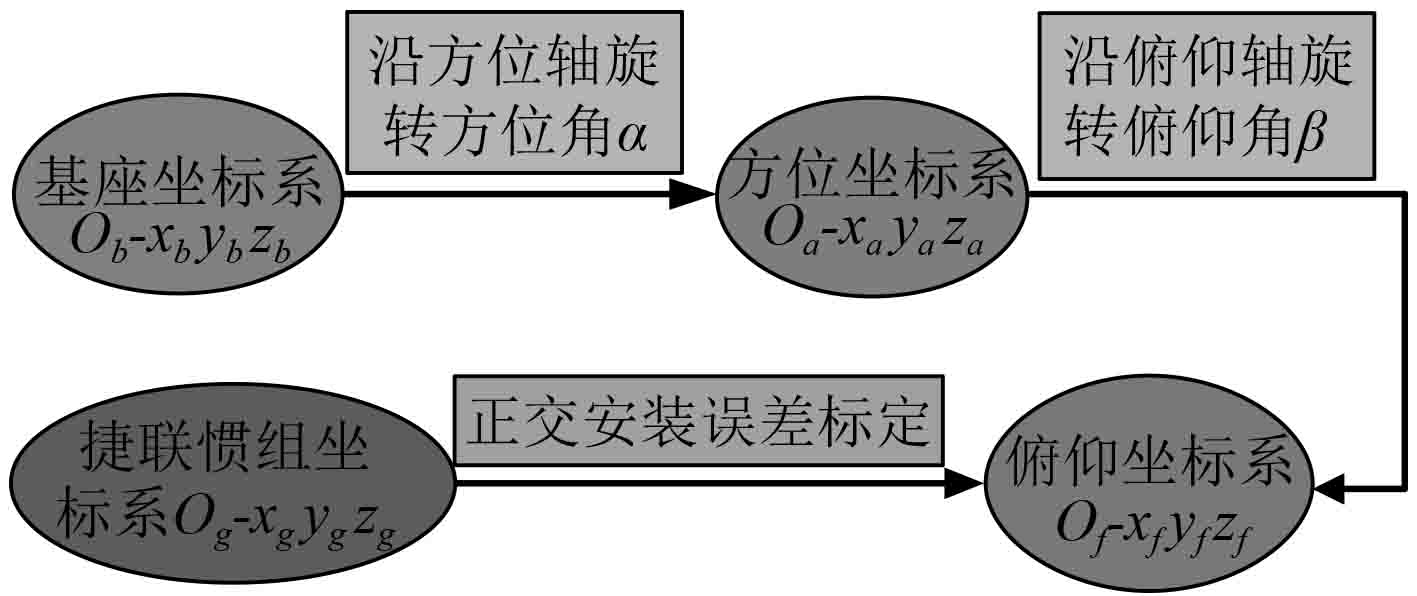
2.2 空间坐标系几何约束耦合关系当发射装置方位角为α、俯仰角为β时,基座坐标系、方位坐标系、俯仰坐标系和捷联惯组坐标系之间的几何约束耦合关系如图3所示。
|
图 3 空间坐标系几何约束耦合关系示意图 Fig. 3 Schematic diagram of geometric constraint coupling relationship in spatial coordinate system |
在发射装置实际工作过程中,各空间坐标系之间除了几何约束耦合关系外,还存在一定的轴系误差,影响导弹在架上的指向精度和初始数据装订。主要误差因素有:发射装置方位轴与基座法线的重合误差、俯仰轴与方位轴的正交误差、导弹轴线与俯仰轴的正交误差、捷联惯组坐标系与其内部敏感轴的非正交安装误差、捷联惯组坐标系和俯仰坐标系之间的正交安装误差等。前文中提到,发射装置和捷联惯组在各自产品出厂时,已对发射装置指向精度和捷联惯组的非正交安装误差进行了标定,因此,本文设定除捷联惯组坐标系和俯仰坐标系之间的正交安装误差外,不考虑其余坐标系误差的影响。
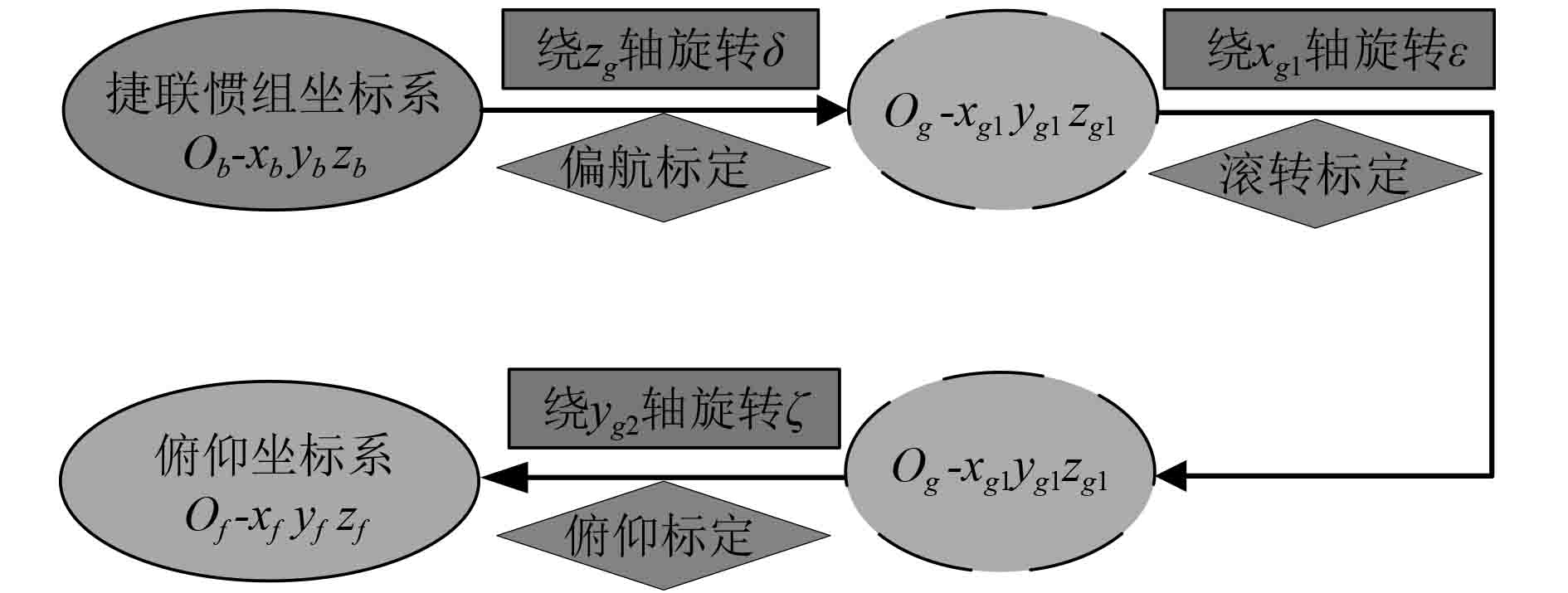
3.2 捷联惯组正交安装误差机理分析理想状态下,在捷联惯组与发射装置之间不存在正交安装误差时,捷联惯组坐标系的xg轴、yg轴、zg轴分别与架上导弹所在的俯仰坐标系中xf轴、yf轴、zf轴重合。但在实际工程应用中,由于定位方式和加工工艺等因素的影响,捷联惯组与发射装置之间产生的正交安装误差不可避免。此种情况下,xg轴和xf轴、yg轴和yf轴、zg轴和zf轴之间形成的夹角分别产生偏航误差δ、滚转误差ε和俯仰误差ζ。为保证捷联惯组数值能够尽可能代表架上导弹的运动矢量,提高导弹命中精度,必须对捷联惯组正交安装误差形成的偏航、滚转和俯仰误差进行标定。捷联惯组坐标系到俯仰坐标系的变换过程如图4所示。
|
图 4 捷联惯组坐标系到俯仰坐标系变换过程 Fig. 4 Transformation process from SIMU coordinate system to pitching coordinate system |
从图4可以看出,将发射装置上捷联惯组的正交安装误差量化后,从捷联惯组坐标系到俯仰坐标系的变换需要依次绕不同的坐标轴进行旋转,次数为3次,每次转动可以利用正交安装误差角度δ、ε、ζ来完成2个坐标系之间的转换,从而实现捷联惯组正交安装误差的标定。将这种坐标系转换写成姿态矩阵形式[6],可知:
| $\left[ \begin{gathered} {x_g} \\ {y_g} \\ {z_g} \\ \end{gathered} \right] = C_f^g \times \left[ \begin{gathered} {x_f} \\ {y_f} \\ {z_f} \\ \end{gathered} \right] = C_{g1}^g \times C_{g2}^{g1} \times C_f^{g2} \times \left[ \begin{gathered} {x_f} \\ {y_f} \\ {z_f} \\ \end{gathered} \right]{\text{。}}$ | (1) |
其中:
| $C_{g1}^g = \left[ {\begin{array}{*{20}{c}} {\cos \delta }&{ - \sin \delta }&0 \\ {\sin \delta }&{\cos \delta }&0 \\ 0&0&1 \end{array}} \right],$ | (2) |
| $C_{g2}^{g1} = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos \varepsilon }&{ - \sin \varepsilon } \\ 0&{\sin \varepsilon }&{\cos \varepsilon } \end{array}} \right],$ | (3) |
| $C_f^{g2} = \left[ {\begin{array}{*{20}{c}} {\cos \zeta }&0&{\sin \zeta } \\ 0&1&0 \\ { - \sin \zeta }&0&{\cos \zeta } \end{array}} \right],$ | (4) |
代入式(1),可得:
| $\begin{split} \left[ \begin{gathered} {x_g} \\ {y_g} \\ {z_g} \\ \end{gathered} \right] = &C_f^g \times \left[ \begin{gathered} {x_f} \\ {y_f} \\ {z_f} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \delta }&{ - \sin \delta }&0 \\ {\sin \delta }&{\cos \delta }&0 \\ 0&0&1 \end{array}} \right] \times \\ &\left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos \varepsilon }&{ - \sin \varepsilon } \\ 0&{\sin \varepsilon }&{\cos \varepsilon } \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {\cos \zeta }&0&{\sin \zeta } \\ 0&1&0 \\ { - \sin \zeta }&0&{\cos \zeta } \end{array}} \right] \times \\ &\left[ \begin{gathered} {x_f} \\ {y_f} \\ {z_f} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \delta \cos \zeta - \sin \delta \sin \varepsilon \sin \zeta }&{ - \sin \delta \cos \varepsilon } \\ {\sin \delta \cos \zeta + \cos \delta \sin \varepsilon \sin \zeta }&{\cos \delta \cos \varepsilon } \\ { - \cos \varepsilon \sin \zeta }&{\sin \varepsilon } \end{array}} \right. \\ & \left. {\begin{array}{*{20}{c}} {\cos \delta \sin \zeta + \sin \delta \sin \varepsilon \cos \zeta } \\ {\sin \delta \sin \zeta - \cos \delta \sin \varepsilon \cos \zeta } \\ {\cos \varepsilon \cos \zeta } \end{array}} \right] \times \left[ \begin{gathered} {x_f} \\ {y_f} \\ {z_f} \\ \end{gathered} \right] {\text{。}}\\[-30pt] \end{split} $ | (5) |
式中:
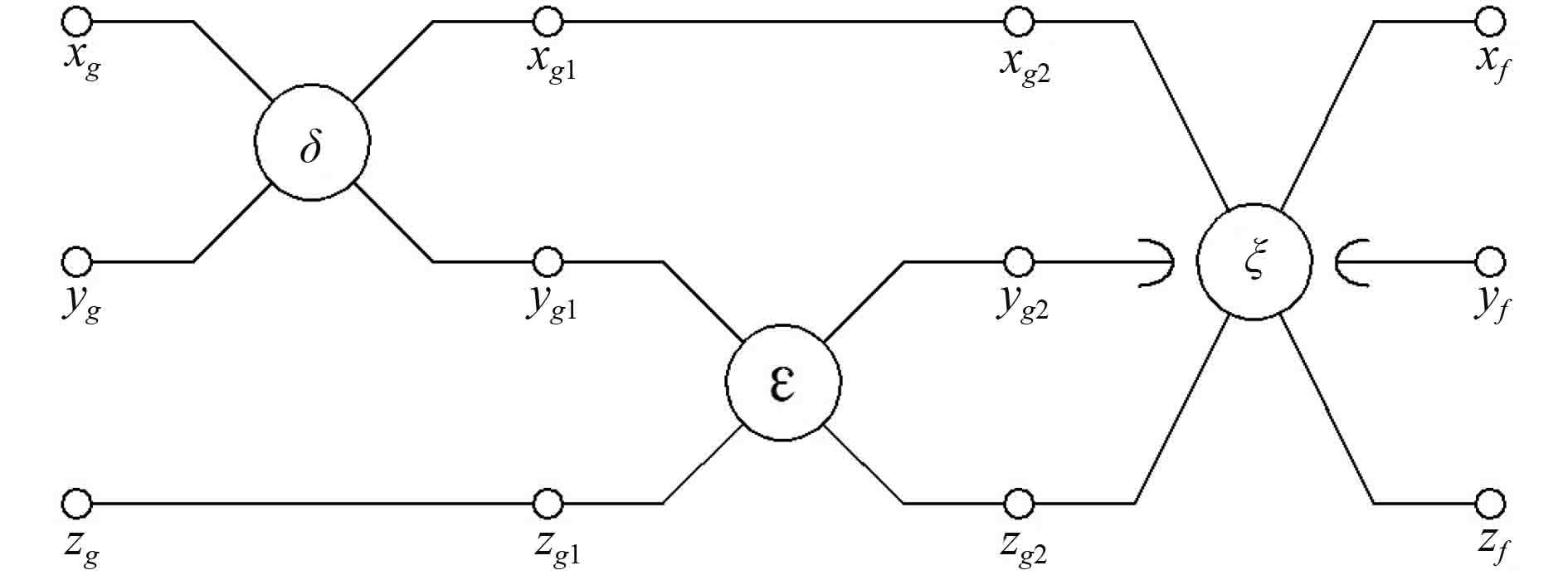
为了更加清晰、简洁地描述捷联惯组坐标系与俯仰坐标系之间旋转变换的过程,将二者关系采用图形化语言表示的PIOGRAM示意图[7]如图5所示。
|
图 5 捷联惯组坐标系到俯仰坐标系变换对应PIOGRAM图 Fig. 5 Transformation of PIOGRAM from SIMU coordinate system to pitching coordinate system |
本文针对某舰载发射装置捷联惯组正交安装误差,基于平行光管(Collimator)原理,采用“陀螺寻北仪[8]+多棱镜+瞄准线检查仪+电子差分水平仪”的综合方法,在有限距离地理条件下[9],对捷联惯组正交安装误差的全天候标定方法进行研究。
4.1 偏航误差δ标定方法为保证导弹武器系统在厂或船坞内全天候标定需求,本文提出一种在有限距离条件下,利用厂区或码头固定标校点,对捷联惯组在发射装置上安装后引起的偏航误差进行标定的方法。
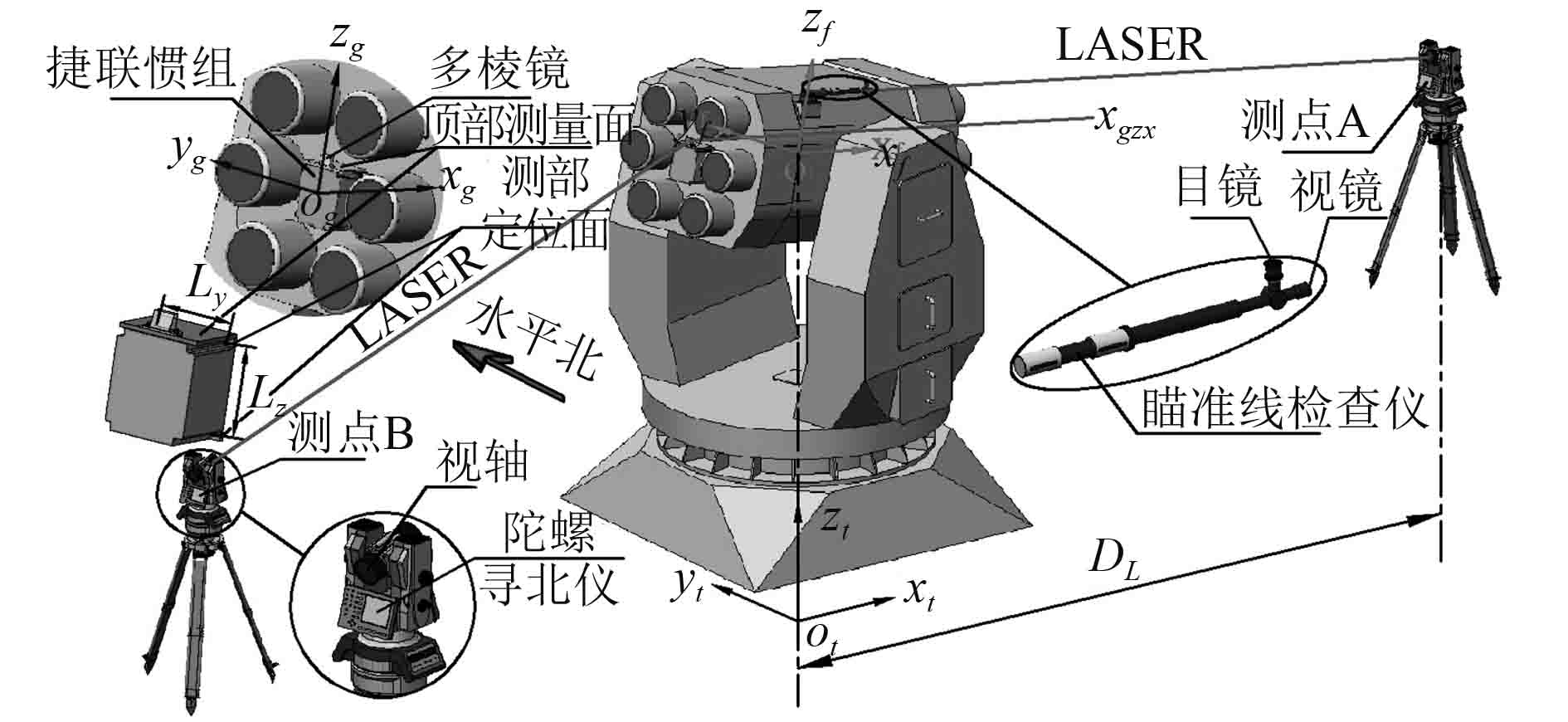
如图6所示,通过在发射装置俯仰架侧部基准平台上架设瞄准线检查仪,利用平行光管原理,实现与位于大地坐标系中的陀螺寻北仪在测点A处进行互瞄,使陀螺寻北仪视轴在测点A处发射的激光束(LASER)穿过瞄准线检查仪的视镜,与瞄准线检查仪的轴线重合。通过陀螺寻北仪在测点A惯性寻北后,可知瞄准线检查仪轴线(即导弹基准轴线zf)在大地坐标系xt-yt平面上的投影与水平北方向的夹角AFS。在发射装置产品出厂时,俯仰架侧部的瞄准线检查仪轴线与俯仰架上导弹基准轴线之间的平行度误差可通过“激光垂准仪+标准靶标”的方法进行标定[2];在捷联惯组顶部测量面上架设多棱镜,通过捷联惯组产品出厂前实验室标定,可将陀螺寻北仪视轴在测点B发射的激光束(LASER)折射后形成xgzx轴,使xgzx轴与捷联惯组xg轴平行。在测点A处的陀螺寻北仪与发射装置上瞄准线检查仪完成互瞄后,此时测点B处陀螺寻北仪的位置具有唯一性。
|
图 6 偏航误差标定方法示意图 Fig. 6 Diagram of yaw error calibration method |
为确保测量结果有效性的同时,提高标定效率,本文建议在发射装置方位角α=0°,即方位坐标系与基座坐标系重合时,通过位于大地坐标系中的陀螺寻北仪在测点B处惯性寻北后,从测点B处的陀螺寻北仪读取发射装置位于方位零位时,捷联惯组xg轴在大地坐标系xt-yt平面上的投影与水平北方向的基准夹角AGZ0,后续可改变陀螺寻北仪测点A的方位角α以及测点A处的陀螺寻北仪与基座坐标系原点的距离DL(DL可使用激光测距仪精确测量),通过多次测量排除偶然性,以便对数据进行科学、有效的分析。本文以图6所示舰载发射装置为例,其中0°
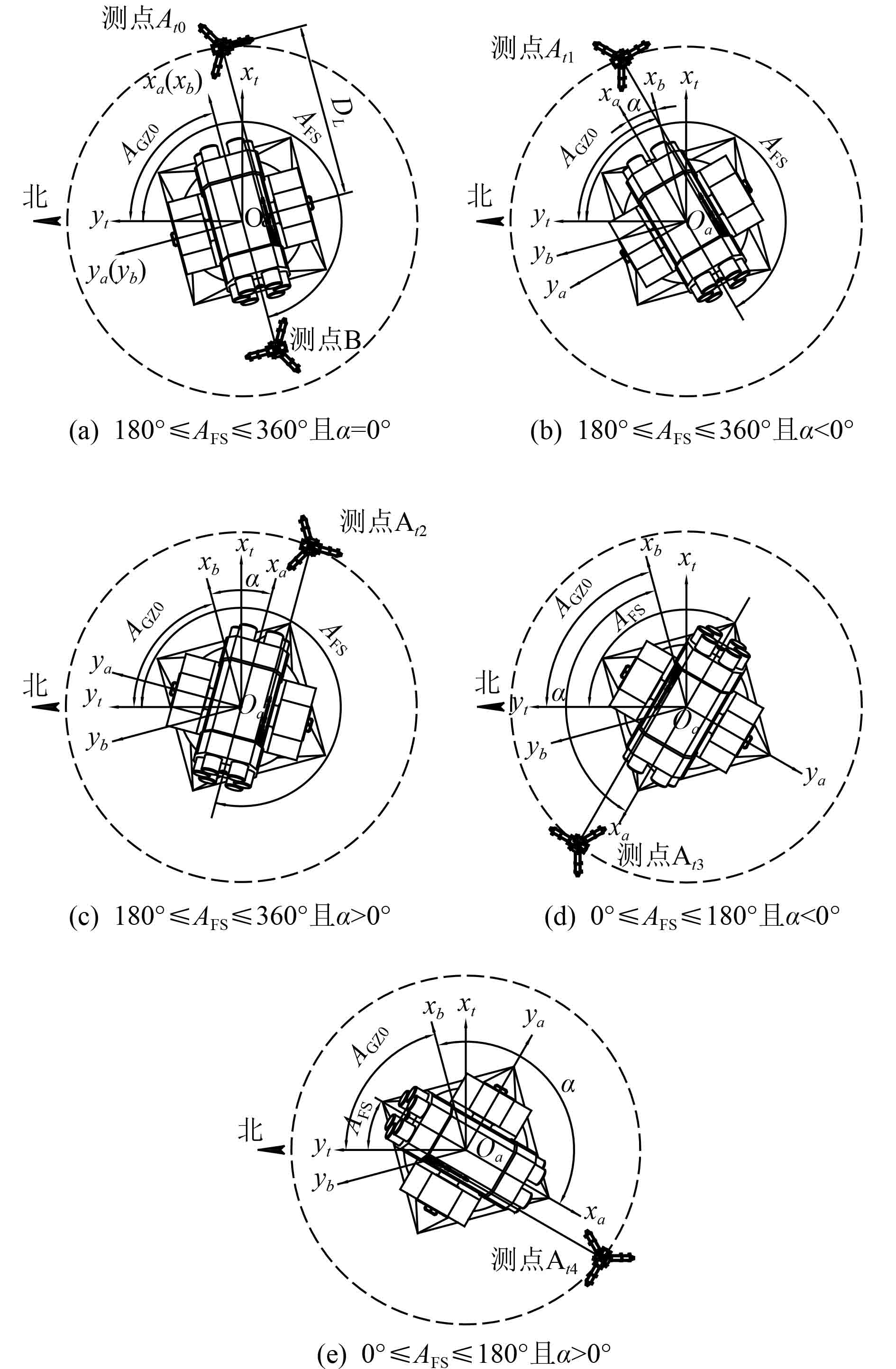
由图7可知,上述几种工作状态条件下,捷联惯组在发射装置上安装后产生的偏航误差δ为:
|
图 7 偏航误差标定的工作状态示意图 Fig. 7 Working state diagram of yaw error calibration |
| $ \delta =\left\{\!\!\!\!\begin{array}{l}{A}_{FS}-{A}_{GZ0}-180^\circ ,180^\circ \leqslant {A}_{FS}\leqslant 360^\circ {\text{且}}\alpha =0^\circ, \\ {A}_{FS}-{A}_{GZ0}-\alpha -180^\circ ,\; \left\{\!\!\!\!\begin{array}{l}180^\circ \!\leqslant\! {A}_{FS}\!\leqslant\! 360^\circ {\text{且}}\alpha \!<\! 0^\circ, \\ 180^\circ \!\leqslant\! {A}_{FS}\!\leqslant\! 360^\circ {\text{且}}\alpha \!>\! 0^\circ, \\ 0^\circ \!\leqslant\! {A}_{FS}\!\leqslant\! 180^\circ {\text{且}}\alpha \!<\!0^\circ, \end{array}\right.\\ {A}_{FS}-{A}_{GZ0}-\alpha +180^\circ ,0^\circ \leqslant {A}_{FS}\leqslant 180^\circ {\text{且}}\alpha >0^\circ{\text{。}} \end{array}\!\!\!\!\!\!\!\!\!\!\!\right.$ | (6) |
式中:AFS为导弹基准轴线在大地坐标系xt-yt平面上的投影与水平北方向的夹角,由测点A处的陀螺寻北仪读取;AGZ0为发射装置位于方位角α=0°时捷联惯组的xg轴在大地坐标系xt-yt平面上的投影与水平北方向的夹角,由测点B处的陀螺寻北仪读取;α为发射装置方位角且−180°
由于捷联惯组安装在发射装置俯仰架后部,安装面与俯仰架轴线xf的垂直度直接影响偏航误差的数值。若测量得到的偏航误差不满足系统要求时,可根据测量数值的方向和大小,可在捷联惯组yg轴方向左侧或右侧的安装支脚处,通过增加适量垫片或适当修锉等方式,进行偏航误差安装角度标定,将偏航误差控制在系统允许的误差范围之内。偏航误差调整量值Δδ为:
| ${\Delta _\delta } = {L_y} \times \sin \delta \text{。}$ | (7) |
式中:Δδ为偏航误差调整量值;Ly为捷联惯组沿yg轴方向安装支脚距离。
4.2 滚转误差ε标定方法鉴于俯仰架的空间约束条件,考虑到加工基准引出以及测量仪器尺寸限制等原因,在发射装置产品设计时,在回转架上设计了基准测量平台,并与加工基准严格保持一致,以此作为发射装置总装的测量和调整基线,主要用于方位坐标系与基座坐标系的水平度调整、俯仰坐标系与方位坐标系之间俯仰零位一致性和基准弹位滚转误差调整等。在发射装置总装时,利用导弹安装姿态测量工装将俯仰架基准弹位的滚转误差与回转架上基准测量平台进行比对安装调整,使得俯仰坐标系中基准弹位的滚转误差与方位坐标系中基准测量平台上的对应数据保持一致,实现俯仰坐标系中基准弹位滚转误差向方位坐标系的转换。
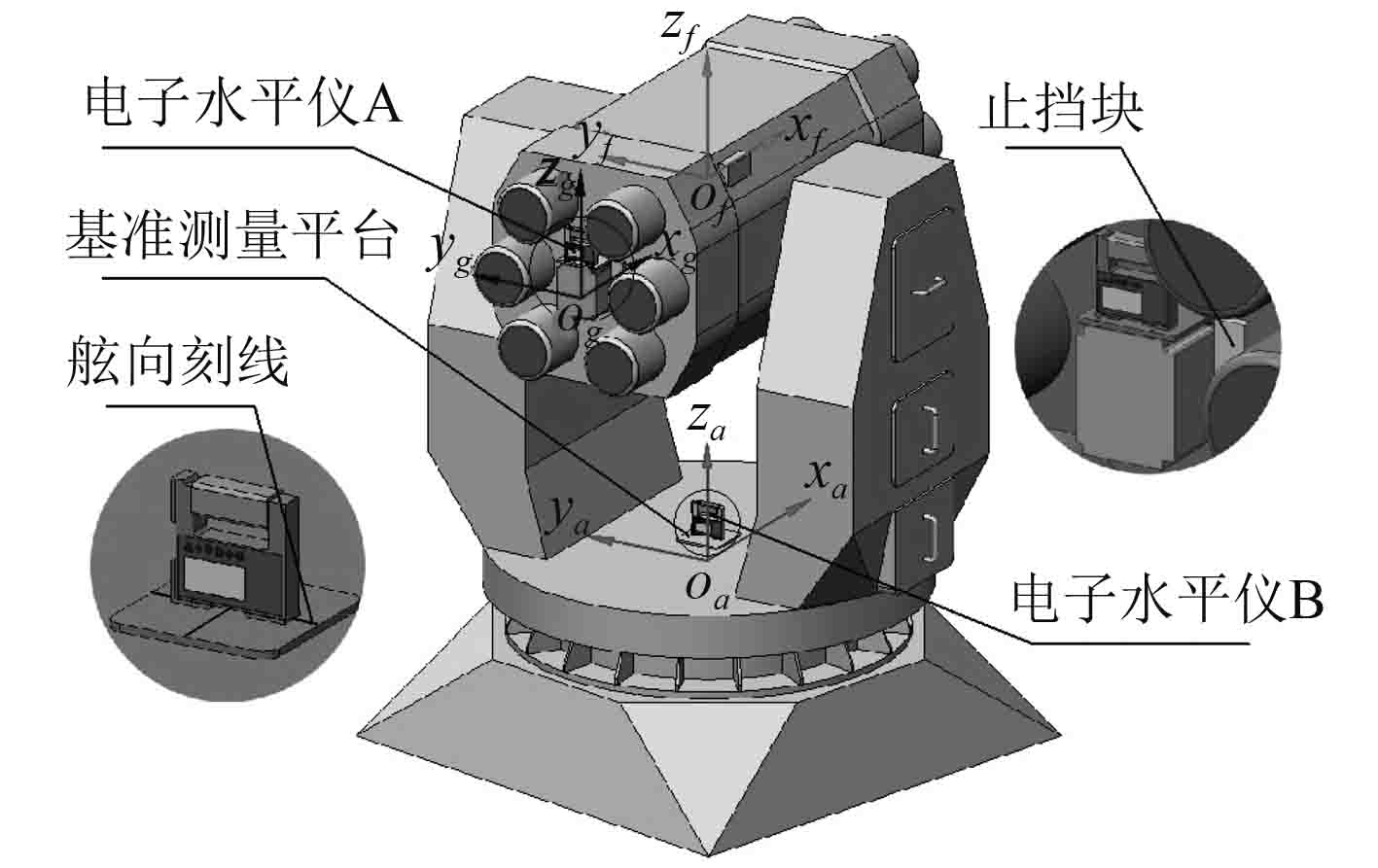
如图8所示,为保证捷联惯组架上安装时的初始定位精度,在俯仰架上捷联惯组预先安装位置处设计止挡块,通过产品出厂前标定,实现止挡块内侧定位面与俯仰坐标系中xf-zf平面平行。安装时捷联惯组侧部定位面与止挡块内侧定位面贴合,赋予捷联惯组在俯仰架上的初始定位精度。
|
图 8 滚转误差标定方法示意图 Fig. 8 Diagram of roll error calibration method |
考虑到实际标定环境条件下存在船坞内半坐墩情况[10],使发射装置在动基座平台上会出现微量的晃动。因此,为保证数据准确性,本文采用具备相对倾斜动态测量能力的电子差分水平仪的测量方法。电子差分水平仪由电子水平仪A、电子水平仪B以及1台差值比较显示器组成,通过分别动态测量捷联惯组顶部测量面沿捷联惯组坐标系yg轴方向和回转架基准测量平台沿方位坐标系ya轴方向(与图8所示舷向刻线平行)的水平度,实时地显示数据并进行差值比较,实现滚转误差的量化。另外,考虑到电子差分水平仪的使用方式和工作范围,测量前应将俯仰角β置于零位,即俯仰坐标系与方位坐标系重合,以提高测量数据的准确性和可信度。
通过上述方法,若测量得到的滚转误差不满足系统要求时,可采用与偏航误差类似的调整方法,根据测量数值的方向和大小,在捷联惯组zg轴方向上某一端的侧部定位面与俯仰架上止挡块内侧面之间,通过增加适量垫片或适当修锉等方式,进行滚转误差安装角度标定,进而将滚转误差控制在系统允许的误差范围之内。滚转误差调整量值Δε为:
| ${\Delta _\varepsilon } = {L_z} \times \sin \varepsilon $ | (8) |
式中:Δε为滚转误差调整量值;Lz为捷联惯组沿zg轴方向两端侧部定位面之间的距离。
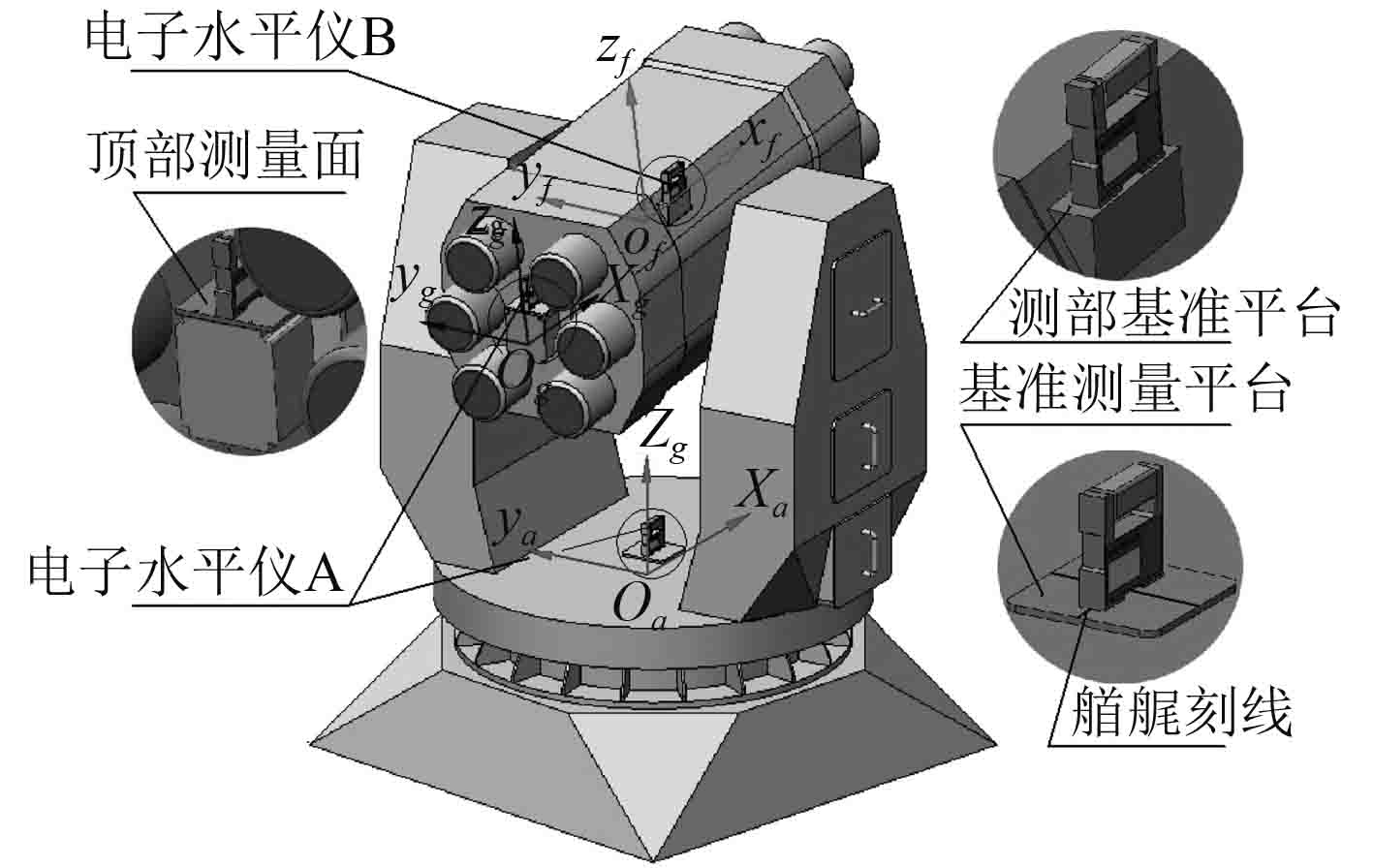
4.3 俯仰误差ζ标定方法在发射装置出厂前,在俯仰架侧部基准平台上沿俯仰坐标系xf轴方向以及回转架基准测量平台上沿方位坐标系xa轴方向(与图9所示艏艉刻线平行),分别架设电子水平仪,通过驱动俯仰架沿yf轴旋转,使得2个电子水平仪的读数相同,实现俯仰坐标系与方位坐标系重合,并以此时俯仰架的位置作为俯仰零位,保证捷联惯组安装后,捷联惯组坐标系、俯仰坐标系和方位坐标系之间的可靠变换。
|
图 9 俯仰误差标定方法示意图 Fig. 9 Diagram of pitching error calibration method |
俯仰误差的标定方法与前序章节中提出的滚转误差标定方法的原理基本相同。如图9所示,通过分别动态测量捷联惯组顶部测量面沿捷联惯组坐标系xg轴方向和俯仰架侧部基准平台沿俯仰坐标系xf轴方向的水平度,实时地进行差值比较并显示,实现俯仰误差的量化。
由于捷联惯组安装在发射装置俯仰架后部,安装面与俯仰坐标系zf轴的平行度直接影响俯仰误差的数值。因此,在偏航误差和滚转误差标定完成后,若测量得到的俯仰误差不满足系统要求时,可根据测量数值的方向和大小,在捷联惯组zg轴方向上侧或下侧的安装支脚处,通过增加适量垫片或适当修锉等方式,进行俯仰误差安装角度标定,将俯仰误差控制在系统允许的误差范围之内。俯仰误差调整量值Δζ为:
| ${\Delta _\zeta } = {L_z} \times \sin \zeta \text{。}$ | (9) |
式中:Δζ为俯仰误差调整量值。
4.4 正交安装误差统计方法为衡量捷联惯组正交安装误差的整体水平,本文采用均方根值(RMS)统计方法[2],将偏航误差、滚转误差和俯仰误差进行空间合成,得到捷联惯组正交安装误差θ为:
| $\theta = \sqrt {{\delta ^2} + {\varepsilon ^2} + {\zeta ^2}} \text{。}$ | (10) |
式中,θ为捷联惯组正交安装误差。
4.5 数据处理及分析 4.5.1 系统指标要求某舰载导弹武器系统对发射装置上的捷联惯组正交安装误差提出了技术要求,相关指标如表1所示。其中,偏航误差、滚转误差和俯仰误差不大于10',正交安装误差不大于15'。
|
|
表 1 正交安装误差指标要求 Tab.1 Index requirements of orthogonal installation error |
按照本文提出正交安装误差的标定方法,采用多位置、变距离测量手段,对发射装置捷联惯组正交安装误差进行标定,数据结果统计如表2~表5所示。
|
|
表 2 偏航误差数据处理结果 Tab.2 Data processing results of yaw error |
对表2~表5的数据结果进行分析可得:第一,在第1次测量偏航误差时,DL取值在20~50 m距离范围之间,使得表2中测得的偏航误差数据超差严重,伴随着测点A位置的变化,数值波动较大;同时随着距离逐渐增加,偏航误差的数值有明显的减少。经分析,出现此种现象的原因是陀螺寻北仪和瞄准线检查仪都是通过目视方式,将零位刻线置于瞄准点几何中心,距离越近,瞄准点几何尺寸越大,目视对准的误差越大。鉴于此,在第2次测量和标定后复测时,将DL取值范围增加至150 m以上,测得的偏航误差数值趋于稳定。另外,从第2次测量和标定后复测数据中可以看出,在方位角α分别位于正向和负向位置时,偏航误差出现一个约2'的固定差值,经分析,这是由于发射装置正反向运转时,由于传动链产生空回造成固有误差,后续可以通过合理制定发射装置关键部件的制造精度、优化结构设计以及减少误差源等措施降低固有误差的影响[2]。第二,由于捷联惯组在发射装置上安装时,采用了合理的侧面定位方式,其中,止挡块在发射装置上的定位方式与架上导弹相同,使得表3测得的滚转误差符合指标要求且数值较小,这也为后续产品设计提供了一种可行的设计方法。第三,鉴于某舰载发射装置采用俯仰正角发射,同时考虑到电子水平仪使用范围要求,因此表4中各测点选取的俯仰角β都为同向正值;测点1中电子水平仪B和A0测得的数据基本一致,说明发射装置在出厂时完成了发射装置高低零位一致性标定,实现了俯仰坐标系向方位坐标系的可靠转换,且符合度较高;另外,各测点电子水平仪B与相应俯仰角β的差值接近某一定值,从一定程度上体现了发射装置俯仰传动系统传动精度水平。因此,通过合理的误差标定方法和可靠的定位手段,使得表5中的捷联惯组正交安装误差满足了武器系统提出的指标要求。
|
|
表 3 滚转误差数据处理结果(β=0) Tab.3 Data processing results of roll error (β=0) |
|
|
表 4 俯仰误差数据处理结果(α=0) Tab.4 Data processing results of pitching error (α=0) |
|
|
表 5 正交安装误差数据统计结果 Tab.5 Statistical results of orthogonal installation error data |
本文针对某舰载发射装置上安装的捷联惯组设备,建立了空间坐标系的几何约束耦合关系模型,基于空间坐标系变换概念,阐述了捷联惯组正交安装误差的产生机理和误差标定原理;运用“陀螺寻北仪+电子差分水平仪等”组合标定方法,对捷联惯组在发射装置上安装产生的偏航误差、滚转误差和俯仰误差的标定方法以及正交安装误差的统计方法进行了研究和数据分析,为捷联惯组等高精设备在发射装置上的安装和标定提供了一种工程应用方法和思路;同时,对发射装置等载体的总体设计和结构优化方面也具有一定的参考价值。
| [1] |
汤其剑. 高精度多轴稳定平台指向误差的分析与研究[D]. 天津: 天津大学, 2014. TANG Qi-jian. Analysis and research of pointing error of high precision multi-axis stabilized plantform[D]. Tianjin: TIANJIN UNIVERSITY, 2014. |
| [2] |
王勇, 赵喜磊, 李翔宇. 舰载导弹发射筒指向精度研究[J]. 舰船科学技术, 2019, 41(4): 142-147. WANG Yong, ZHAO Xi-lei, LI Xiang-yu. Research on pointing accuracy of a ship-based missile launch canister[J]. SHIP SCIENCE AND TECHNOLOGY, 2019, 41(4): 142-147. DOI:10.3404/j.issn.1672-7649.2019.04.028 |
| [3] |
常路宾, 李安, 覃方君. 双轴转位式捷联惯导系统安装误差分析[J]. 计算机仿真, 2011, 28(3): 1-4, 10. CHANG Lu-bin, LI An, QIN Fang-jun. Analysis on installation error of dual-axis rotation-dwell strapdown inertial navigation system[J]. Computer Simulation, 2011, 28(3): 1-4, 10. DOI:10.3969/j.issn.1006-9348.2011.03.001 |
| [4] |
童树兵, 张志利, 周召发, 等. 一种基于双轴位置转台的IMU快速标定方法[J]. 压电与声光, 2016, 38(5): 815-818. TONG Shu-bing, ZHANG Zhi-li, ZHOU Zhao-fa, et al. A quick calibration method of imu based on two-axis turntable[J]. Piezoelectrics & Acoustooptics, 2016, 38(5): 815-818. DOI:10.11977/j.issn.1004-2474.2016.05.032 |
| [5] |
李雷雷. 光电稳定平台结构设计与陀螺安装误差测量补偿[D]. 西安: 西安电子科技大学, 2015. LI Lei-lei. Structure design of electro-optical stabilized platform and method of measurement and compensation of gyro installation error[D]. Xi'an: Xidian University, 2015. |
| [6] |
于莹莹. 单轴旋转式捷联惯导系统误差调制技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2013. YU Ying-ying. On error modulation for strapdown inertial navigation system with single-axis rotation[D]. Harbin: Harbin Engineering University, 2013. |
| [7] |
李岩, 范大鹏. 视轴稳定平台的装配误差机理分析与仿真[J]. 中国惯性技术学报, 2007, 15(1): 35-38. LI Yan, FAN Da-peng. Analysis and simulation on assembling-error mechanism for gyro-stabilization platform[J]. Journal of Chinese Inertial Technology, 2007, 15(1): 35-38. DOI:10.3969/j.issn.1005-6734.2007.01.010 |
| [8] |
薛海建, 郭晓松, 周召发. 寻北仪倾斜状态下转位误差分析[J]. 兵工自动化, 2012, 31(9): 50-53. XUE Hai-jian, GUO Xiao-song, ZHOU Zhao-fa. Transposition error analysis under north seeker incline state[J]. Ordnance Industry Automation, 2012, 31(9): 50-53. |
| [9] |
秦东兴. 舰炮机械零位的有限距离标校方法研究[J]. 舰船电子工程, 2015, 35(6): 105-108. QIN Dong-xing. Finite distance collating method of ship-borne gun mechanical zero mark[J]. Ship Electronic Engineering, 2015, 35(6): 105-108. |
| [10] |
顾颖闽, 郑剑波, 王嘉苏. 互瞄法在舰载武器系统电气零位标定中的应用[J]. 指挥控制与仿真, 2010, 32(3): 104-107. GU Ying-min, ZHENG Jian-bo, WANG Jia-su. Application of mutual aiming in the unifying of electrical zero of ship-borne weapon system[J]. Command Control & Simulation, 2010, 32(3): 104-107. DOI:10.3969/j.issn.1673-3819.2010.03.028 |
 2021, Vol. 43
2021, Vol. 43
