2. 河南省水下智能装备重点实验室,河南 郑州 450015
2. Henan Key Laboratory of Underwater Intelligent Equipment, Zhengzhou 450015, China
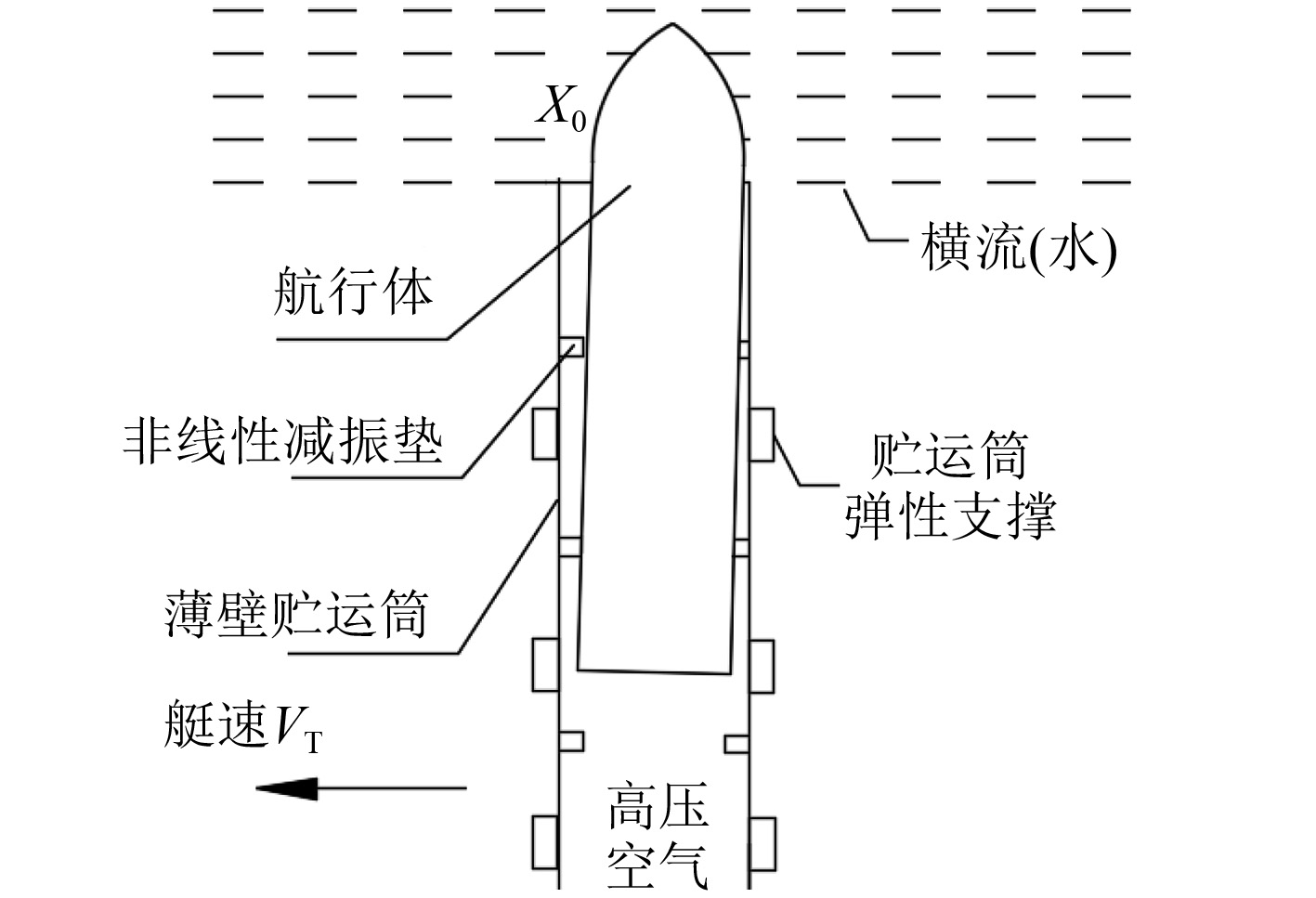
航行体水下发射出筒时,航行体在高压空气推力作用下沿贮运筒轴向运动,当航行体进入水中后,由受到流体动力的作用而倾斜,减振垫因航行体倾斜的作用力而压缩变形,并将力传递到贮运筒上。随着轻质、高容装要求的提高,水下航行体贮运筒变的非常轻薄,为了维持航行体水下发射时的出筒姿态,必须要控制发射过程薄壁贮运筒的变形。通过提高贮运筒弹性支撑(弹性支撑外侧粘贴在艇体上,内侧与贮运筒接触)的刚度可以减小贮运筒的变形,但为了确保贮运筒易于装填到艇上,同时确保系统具备更好的贮存隔振效果,贮运筒弹性支撑的刚度也不宜过大。
|
图 1 航行体水下发射示意图 Fig. 1 Schematic diagram of underwater launch of vehicle |
水下航行体发射过程的载荷环境十分复杂,涉及气-液-固耦合计算问题[1]。目前有采用商业有限元/有限体积计算软件进行流固耦合计算与自编程计算2种途径。但无论采用哪种方法,均要对模型进行大幅度的简化处理。马庆鹏[2]通过MPCCI数据交互软件耦合了流场求解软件Fluent和结构软件Abaqus求解器,实现了潜射导弹出筒过程流固耦合分析,但该模型将贮运筒简化为刚性壁面,也忽略了减振元件的建模。程载斌等[3]应用Ls-dyna显示程序提供的多物质耦合ALE网格模型,对潜射导弹出筒过程进行了三维数值模拟,但同样将导弹、贮运筒假定为刚体,也未考虑减振垫的非线性支撑特性。刘传龙等[4]建立了导弹发射非定常模型,其中流场求解由Fluent求解器完成,运动求解由UDF完成,从流场求解结果中获取弹体受力和力矩,边界运动由UDF控制,Fluent求解器完成。张红军等[5]利用Fluent软件,采用Simple方法实现了导弹水下垂直发射过程中导弹和减振垫横向动力学问题仿真研究,但模型中导弹、发射筒均简化为刚体。吕海波等[6]考虑了水弹性的影响,将水动力方程和结构动力学方程联合求解,对导弹出筒过程中的结构动响应问题进行了分析。Dawson[7]建立潜射导弹水下动力模型,研究了发射深度、初始俯仰角与出水俯仰角之间的关系。Burgdorf[8]探讨了2种不同构型导弹在水下发射过程中的姿态角变化。赵振军[9]将航行体简化为柔性梁模型,忽略发射筒的变形和运动,将其简化为固支边界条件,发射过程中的水动外力简化为沿弹长方向的分布力和头部的时变集中力。巩明[10]将发射筒设置为刚体,将导弹离散成有限段刚体,且相邻两刚体段间采用无质量Timoshenko梁连接。武龙龙[11]将发射筒做刚体处理,但建立航行体的弹性体模型,研究了航行体出筒弯矩载荷和姿态角与振垫数量的关系。
目前的研究一般将贮运筒(发射筒)假设为刚性,重点关注发射过程航行体的载荷环境,较少研究发射载荷对贮运筒的影响。随着轻质、高容装的发展,薄壁贮运筒设计时必须要考虑航行体发射对其结构变形的影响。虽然可以采用商业软件建立复杂的三维流固耦合计算模型,进而求解发射过程贮运筒的变形,但大型复杂非线性流固耦合计算单次耗时非常大,收敛性也往往存在问题,不能适应工程上多轮迭代计算进而论证了贮存筒弹性支撑布置位置、刚度、阻尼对贮运筒变形的影响。
本文采用了解耦的计算方法,即首先建立航行体水下发射出筒的刚体动力学微分方程,使用Matlab软件求解发射过程减振垫受力,然后将减振垫受力作为动载荷,施加到贮运筒动力学等效梁模型上,采用瞬态动力学的方法,实现发射过程贮运筒变形的快速求解,从而多工况论证弹性支撑在控制贮运筒变形的作用。
1 航行体水下发射出筒动力学计算模型航行体水下发射出筒过程中的流体动力包含了流体位置力、流体阻尼力、流体惯性力3部份流体动力,并且流体动力的大小与航行体出筒部分的高度
以航行体的质心为航行体坐标系oxy原点,建立航行体坐标系,其中ox轴沿航行体轴向指向航行体头部,oy轴与航速同平面。
在航行体坐标系中建立航行体发射过程的平面运动微分方程组:
| ${v_x} = {v_x}(t)\text{,}$ |
| $\left( {m + {\lambda _{22}}} \right)\frac{{{\rm d}{v_y}}}{{{\rm d}t}} + {\lambda _{26}}\frac{{{\rm d}{\omega _z}}}{{{\rm d}t}} + m{v_x}{\omega _z} = {Y_{L\alpha }} + {Y_{L\omega }} + {Y_S}\text{,}$ |
| $\left( {{J_z} + {\lambda _{66}}} \right)\frac{{{\rm d}{\omega _z}}}{{{\rm d}t}} + {\lambda _{26}}\frac{{{\rm d}{v_y}}}{{{\rm d}t}} = {M_{zL\alpha }} + {M_{zL\omega }} + {M_{zS}}\text{,}$ |
| $\frac{{{\rm d}\theta }}{{{\rm d}t}} = {\omega _z}\text{,}$ |
| $\frac{{{\rm d}{x_0}}}{{{\rm d}t}} = {v_x}\cos \theta - {v_y}\sin \theta \text{,}$ |
| $\frac{{{\rm d}{y_0}}}{{{\rm d}t}} = {v_x}\sin \theta + {v_y}\cos \theta \text{。}$ |
式中:
| ${M_{zS}} = \sum\limits_{i = 1}^N {{M_{zSi}}}{\text{。}} $ |
运动方程组为常微分方程组,可以利用4阶龙格库塔法求解,进而获得每一时刻的航行体运动学参数,通过编写Matlab程序可以求解以上微分方程组,获取发射过程减振垫的压缩量。利用获取的减振垫压缩量及其非线性刚度曲线可以求解贮运筒安装减振垫部位受力。
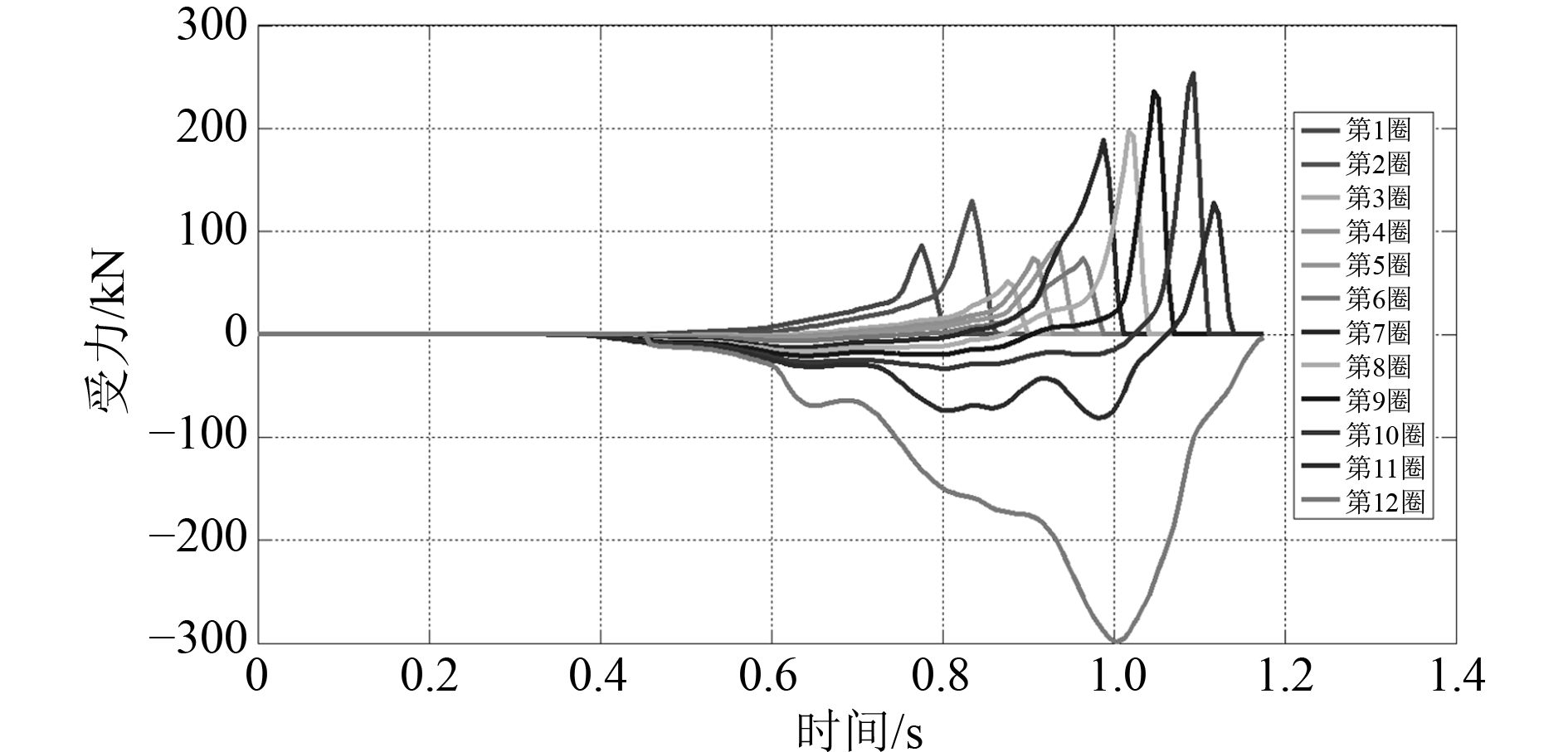
以3 kn艇速发射工况为例,求解方程组得到的贮运筒安装减振垫部位的受力如图2所示。
|
图 2 贮运筒安装减振垫部位受力 Fig. 2 The force on the part of storage tank where the damping pads are installed |
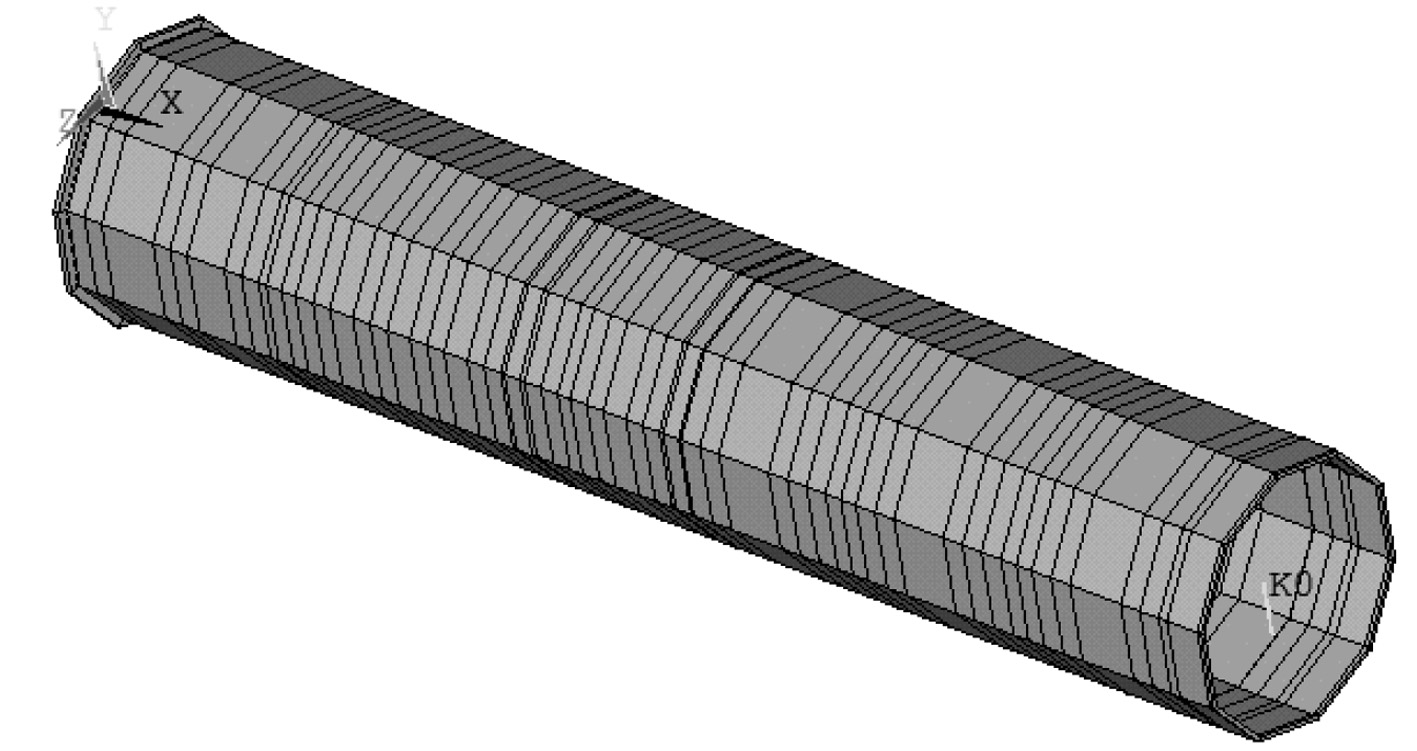
为了实现发射过程薄壁贮运筒变形的快速求解计算,根据薄壁贮运筒质量分布及刚度分布,使用缩聚梁建模方法,采用Ansys软件,建立贮运筒的beam188单元三维动力学等效梁模型,如图3所示。
|
图 3 贮运筒beam188梁单元模型(三维显示) Fig. 3 Beam188 model of the storage tank (three-dimensional display) |
弹性支撑采用线弹簧单元combin14单元模拟,通过实常数定义其刚度、阻尼特性。节点219,220,221的位置(横坐标)代表弹性支撑的布置位置,与贮运筒相应位置节点连接构成弹簧单元,模拟弹性支撑力学特性。贮运筒梁模型与弹性支撑弹簧单元模型如图4所示。

|
图 4 贮运筒梁模型与弹性支撑弹簧单元模型(二维显示) Fig. 4 Storage tank beam model and elastic support spring element model (two-dimensional display) |
对节点219,220,221施加固定约束,模拟艇体对弹性支撑的约束作用。贮运筒顶端与艇螺栓法兰连接,本文假设发射过程贮运筒与艇法兰连接部分没有位移,因而贮运筒梁模型顶端单元节点(节点编号89)设置固定约束。
本文的弹性支撑是以弹簧单元来模拟的,如果需要模拟不同刚度值的弹性支撑,只用直接改变弹簧单元的实常数即可。但若想要模拟弹性支撑的多种布置方案,则比较麻烦,这是由于若要在模型中调整弹性支撑(弹簧单元)的位置,则需要改变弹簧单元两端点的位置坐标,弹簧单元其中一个端点是贮运筒缩聚梁模型节点,其所在位置反映了贮运筒的质量分布、刚度分布,不能直接改变,也即缩聚模型中的弹性支撑位置是非参数化。弹性支撑位置非参数化对多工况论证计算极为不利,为实现快速的多工况论证计算,首先解决弹性支撑的位置参数化建模。
本文采用Ansys APDL语言编程实现弹性支撑位置参数化建模的方法如下:
1)构建3个数组,其中2个数组分别存储节点编号、节点横向坐标值,分别记为节点编号数组、节点位置数组,另外的一个数组存储定义航行体材料、截面特性实常数的编号。
2) 若要调整弹性支撑的布置位置方案,则改变节点位置数组相应元素值(表征弹性支撑位置的元素);
3)使用APDL语言编程冒泡法程序,对节点位置数组元素值进行从小到大排序,每调整一次排序,也相应的调整节点编号数组元素的排序;
4)根据排好的顺序,使用Beam188梁单元依次连接各节点,并根据单元所处区域(根据材料、截面特性数组),赋予单元相应的材料、截面属性。
完成以上步骤的APDL语言编程,即可在Ansys中实现弹性支撑位置的参数化建模。
完成贮运筒及弹性支撑动力学、参数化建模后,以本文第2节求得的减振垫受力作为冲击载荷,采用Ansys内置的瞬态完全法,即可计算求解发射冲击载荷下贮运筒的变形。
3 薄壁贮运筒变形多工况论证计算及变形控制分析根据工程实际,首先确定为贮运筒设计3圈弹性支撑,考虑通用性需求,要求3圈弹性支撑的刚度相同。
根据弹性支撑刚度设定值(0,4e6 N/m,8e6 N/m)、阻尼系数设定值(0,40000 Ns/m)、布置位置(A方案和B方案,见表1)及发射工况(母艇航速3 kn,4 kn)不同,设定了表2计算工况,研究弹性支撑对发射过程薄壁贮运筒变形的影响。
|
|
表 1 弹性支撑布置方案 Tab.1 Elastic support layout |
|
|
表 2 计算工况 Tab.2 Calculation conditions |
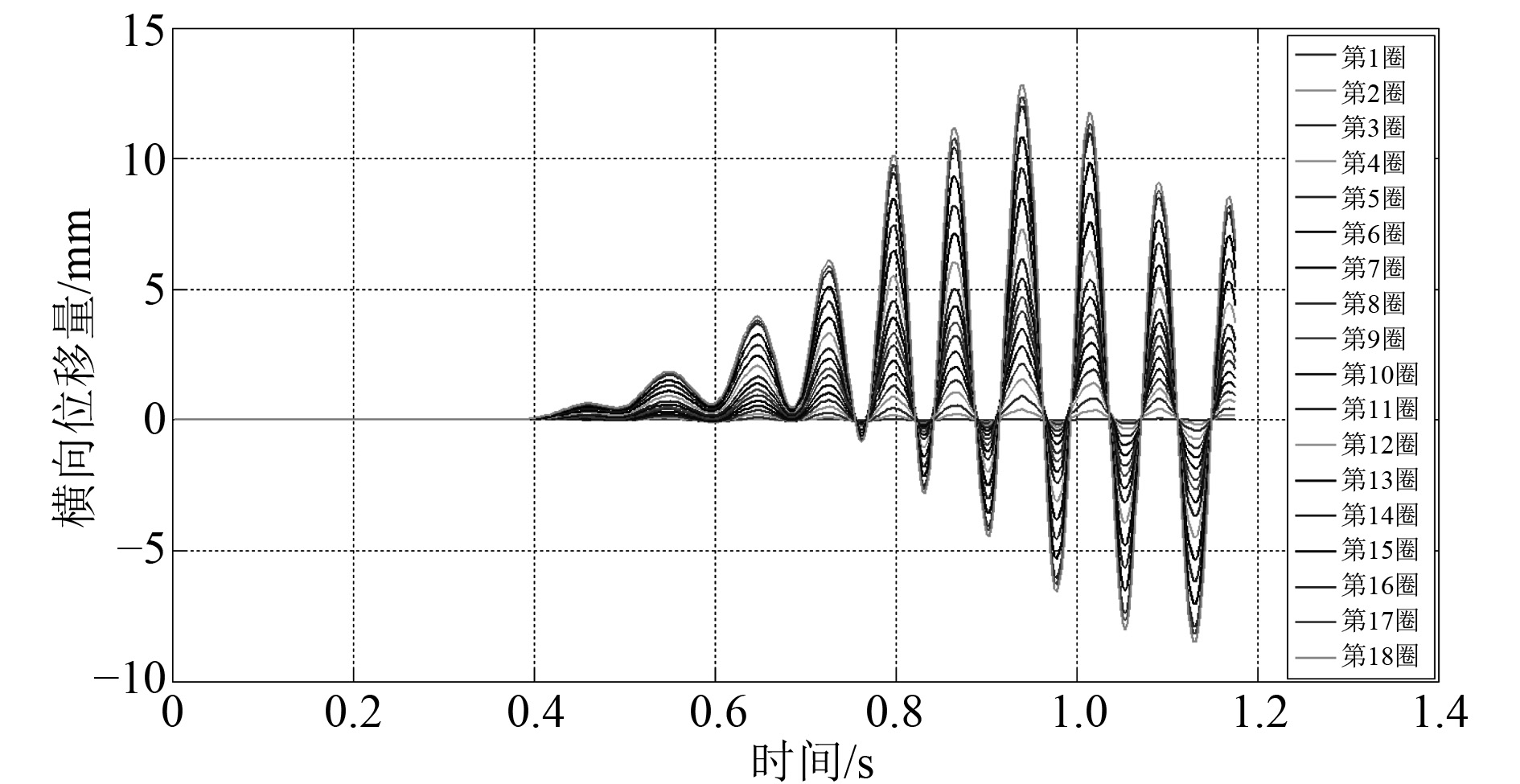
发射过程贮运筒受力变形越大,航行体的出筒姿态角越大,影响发射的安全性。若无弹性支撑,发射过程薄壁贮运筒典型部位(见表3)横向位移量计算结果见图5所示,薄壁贮运筒产生了较大振荡变形,其中筒底端变形最大,最大横移量接近13 mm,已严重影响航行体水下发射的姿态安全性。为进一步研究弹性支撑方案对航行体发射过程薄壁贮运筒变形响应的影响,将不同弹性支撑方案下薄壁贮运筒典型部位横向位移量计算结果统计为表3,进行对比分析。
|
|
表 3 发射过程贮运筒典型部位横向位移量统计 Tab.3 Statistics of lateral displacement of typical parts of storage tank |
|
图 5 贮运筒典型部位横向位移响应 Fig. 5 Transverse displacement response of typical parts of storage tank |
工况1(无弹性支撑)和工况2(有弹性支撑)对比见图6(a),表明由于弹性支撑的存在,贮运筒横向变形量大幅减少,说明薄壁贮运筒设计时考虑弹性支撑设计的必要性。
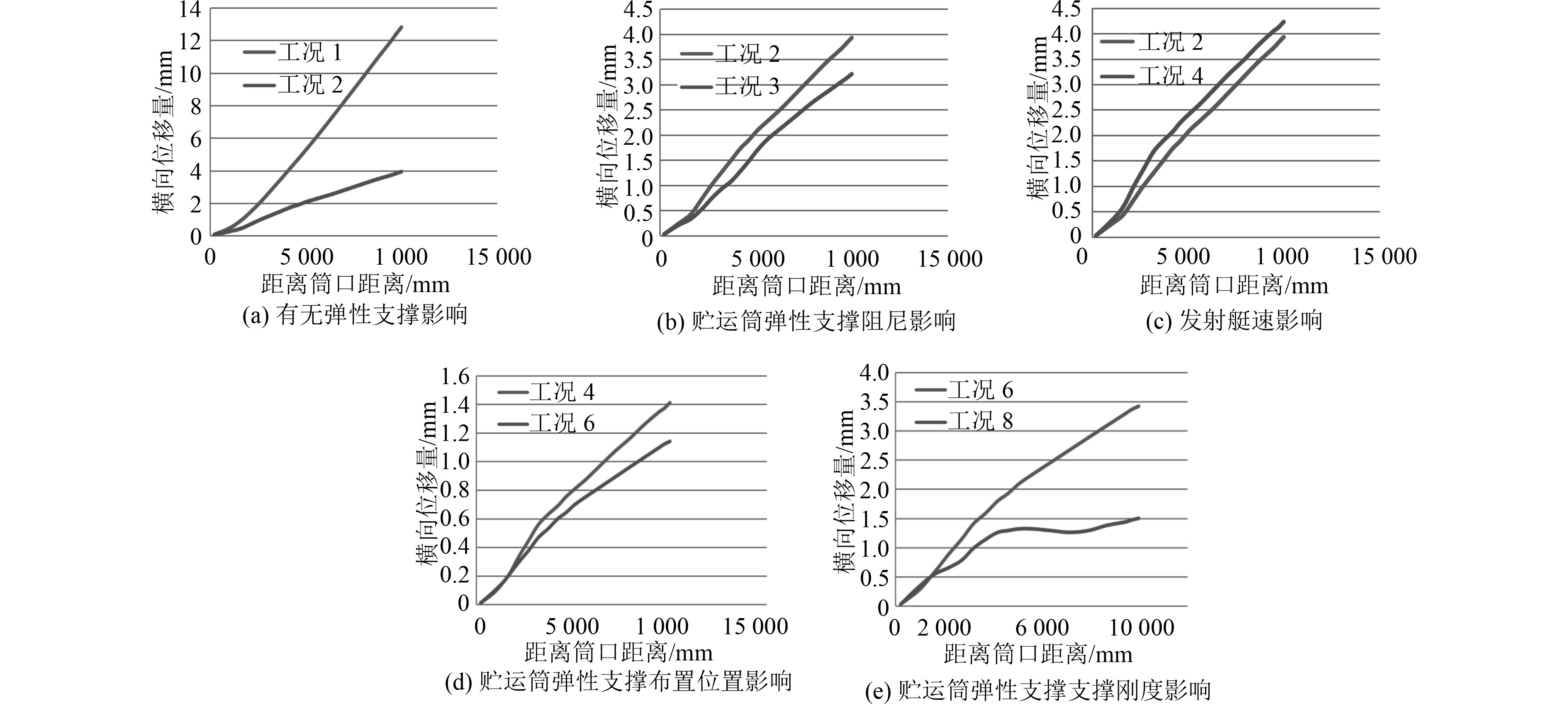
|
图 6 发射过程贮运筒变形影响因素对比分析 Fig. 6 Comparative analysis of factors affecting the deformation of the storage tank during the launch process |
工况2(无阻尼)和工况3(有阻尼)、工况4(无阻尼)和工况5(有阻尼)、工况6(无阻尼)和工况7(有阻尼)对比表明,选用高阻尼材料,可以有效控制贮运筒变形。工况2(艇速3kn)和工况4(艇速4 kn)对比见图6(c),表明发射时母艇的航速越高,贮运筒各部位的变形更大,这与实际情况相吻合。工况4(A方案)和工况6(B方案)见图6(d),表明B方案可以更好的控制贮运筒底端部位的变形,但控制贮运筒上半段变形的效果不明显。工况6(刚度4e6 N/m)和工况8(刚度8e6 N/m)对比见图6(e),表明增大弹性支撑的刚度,对控制贮运筒下半段的变形十分明显,但对控制贮运筒上半段变形的作用不太明显。
4 结 语水下发射过程涉及气-液-固耦合问题,采用大型复杂的模型无法实现工程上多工况论证计算的需求,本文通过解耦计算方法研究了弹性支撑方案对发射过程薄壁贮运筒变形的影响,得出以下结论:
1)航行体水下发射过程,若无筒间支撑的作用,薄壁贮运筒会存在较大的横向位移量,因而采用薄壁贮运筒必须要相应的考虑弹性支撑设计;
2)薄壁贮运筒的变形更多的是由于贮运筒受动态激振力引起的振动造成,由于贮运上端法兰连接,发射过程贮运筒下半段的横向位移较大,因而贮运筒弹性支撑应布置在贮运筒的下半段;
3)弹性支撑的阻尼系数对发射过程贮运筒的变形影响较大,弹性支撑应选用阻尼系数较大的粘弹性材料可以有效控制薄壁贮运筒的振荡变形;
4)薄壁贮运筒上的附属设备设计时也应考虑贮运筒振荡环境可能带来的设备共振破坏问题。
| [1] |
YUAN Chen, LIN Yu-wei. A 2.4-Gsample/s DVFS FFT processor for MIMO OFDM communication systems[J]. IEEE Journal of Circuits(S0018-9200)Solid-State, 2008, 43(5): 1260-1273. DOI:10.1109/JSSC.2008.920320 |
| [2] |
马庆鹏. 潜射航行体出筒过程载荷特性的数值模拟研究[D]. 哈尔滨: 哈尔滨工业大学, 2011.
|
| [3] |
程载斌, 刘玉标, 刘兆, 等. 导弹水下潜射过程的流体-固体耦合仿真[J]. 2018, 29(2).
|
| [4] |
刘传龙, 张宇文, 王亚东, 等. 考虑适配器弹性的潜射导弹出筒载荷特性研究[J]. 兵工学报, 2015, 36(2): 379-384. DOI:10.3969/j.issn.1000-1093.2015.02.027 |
| [5] |
张红军. 潜射导弹出筒过程的三维非定常数值模拟研究[J]. 水动力学研究与进展, 2010, 25(3).
|
| [6] |
吕海波, 权晓波, 尹云玉, 等. 考虑水弹性影响的水下航行体结构动响应研究[J]. 力学学报, 2010, 42(3): 350-356. DOI:10.6052/0459-1879-2010-3-2008-241 |
| [7] |
DAWSON J R. Hydrodynamic characteristics of missiles launched under water[J]. Technical Report Archive & Image Library, 1958. |
| [8] |
BURGDORF O. Hydrodynamics of unsteady underwater-launched missiles with trailing cavities and crossflow drag[R]. AIAA paper 87-1319, Jun. 1987.
|
| [9] |
赵振军, 王占莹, 武龙龙, 等. 弹性垫形式的水下弹性体发射动力学分析[J]. 船舶力学, 2017, 21(8): 976-982. DOI:10.3969/j.issn.1007-7294.2017.08.006 |
| [10] |
巩明, 王汉平, 杨鸣, 等. 模拟弹水下垂直发射载荷分析[J]. 弹箭与制导学报, 2015, 35(5): 41-49. |
| [11] |
武龙龙, 权晓波, 吕海波, 等. 航行体水下发射出筒的减振垫占空比研究[J], 导弹与航天运载技术, 2015, 377, 33−37.
|
 2021, Vol. 43
2021, Vol. 43
