水下地形辅助惯性导航主要是利用丰富的水下地形信息,通过匹配算法,将测量设备实时测得的地形水深数据与数字地图数据库中的高程进行相关匹配运算,估计出当前水下航行器的位置,以修正惯性导航误差[1-4]。因其可有效降低潜航器的导航定位误差,增强隐蔽性,提高生存能力,为水下高精度自主导航定位提供重要保证,因而受到各国的广泛研究[5-7]。
匹配算法是水下地形辅助导航的核心技术,目前地形匹配算法主要有基于地形轮廓相关匹配的TERCOM算法、基于扩展卡尔曼滤波的SITAN算法和基于直接概率准则的递推贝叶斯估计算法等。TERCOM算法属于相关批处理,有一定的延时性,无法进行实时匹配,但具有大范围搜索的优势,对初始位置偏差要求不高,而SITAN算法需要对地形作近似线性化处理,在这一过程中势必会产生误差[8-9]。基于直接概率准则的PMF算法可以有效处理非线性的状态估计问题。Meduna D等[10]利用不同性能的AUV进行了相关海试,验证了滤波算法能够克服测量设备精度对匹配结果的影响。刘洪等[11]对组合匹配算法的可行性进行了研究。王可东等[12]运用TERCOM算法对地形辅助导航匹配误差进行了研究。
目前对地形辅助导航匹配算法的改进研究相对较多[13-15],忽略了其他影响因素与匹配误差间的关系或者仅仅针对某一两个因素进行了分析,目的多数在于验证算法的可行性,而针对组合算法开展的多因素与匹配性能的关系研究较少且不全面,制约了匹配算法在地形辅助导航中的应用。本文根据某海域的真实水深数据,构建了水下数字地图模型,基于组合匹配算法,以导航性能为研究对象,综合分析多因素对匹配性能的影响,对匹配算法的应用性能进行剖析。
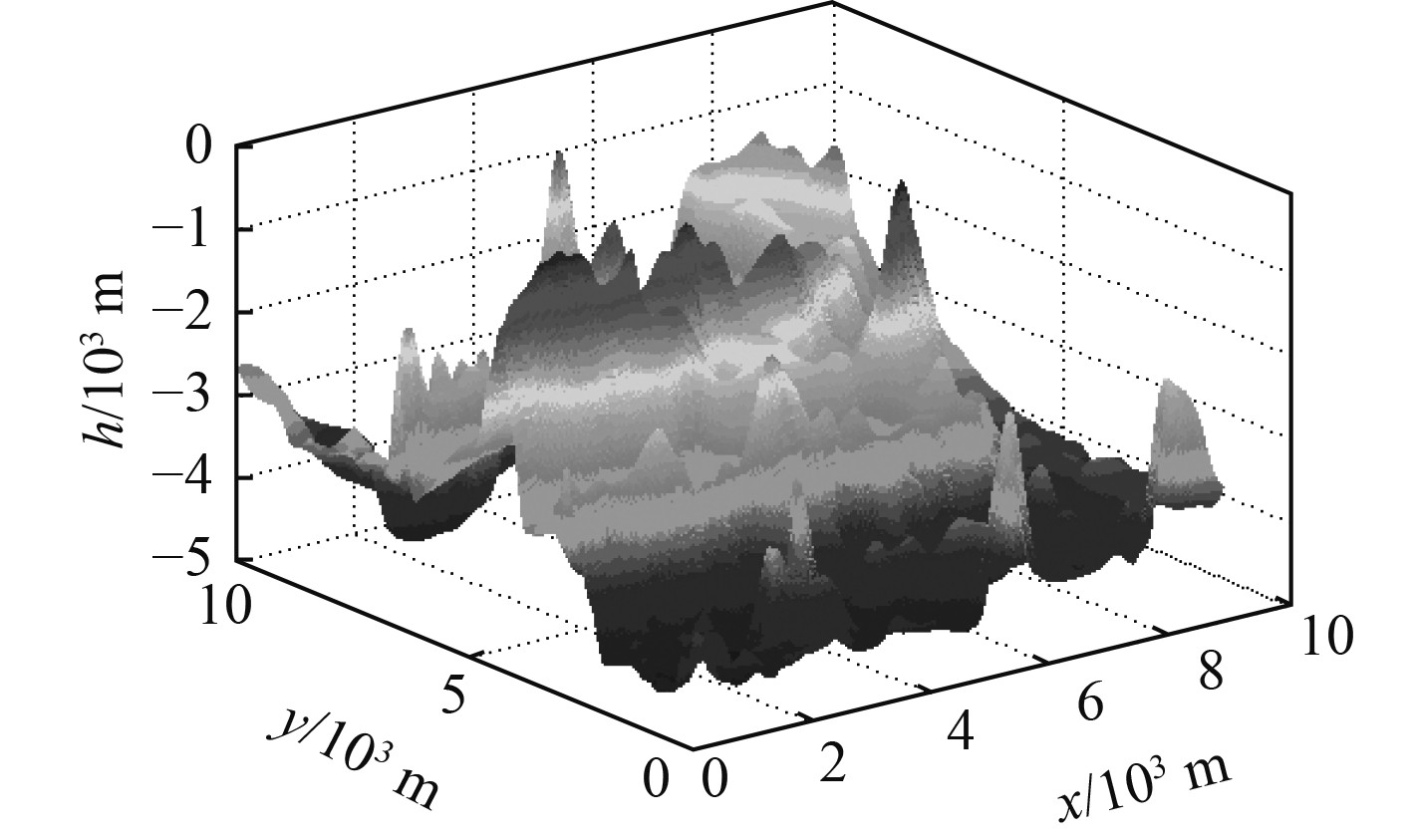
1 数字地图模型构建鉴于水下环境的复杂性,针对水下开展的地形辅助导航,通常选择数字高程模型(Digital Elevation Model,DEM)来表达水下地形信息。规则格网结构模型具有便于数据的存储、使用、管理、分析和计算等优点,因而被广泛采用。本文采用正方形规则格网结构模型(X和Y方向上的格网间距相等),将试验海域按照一定的格网尺寸划成二维格网结构。水下地形分布不均匀、非线性强,利用二维随机过程模拟生成地形不能真实地反映地形实际特征及分布情况。因此,本文选取我国某海域真实水深数据制备水下数字地图,水下三维地形图如图1所示。
|
图 1 水下地形DEM三维图 Fig. 1 Underwater topographic DEM 3D map |
受目前技术条件、工作量等各方面因素的制约,制备的水下数字地图分辨率较低,无法满足水下辅助导航需求,需要采用插值方法对原始数据进行相关预处理。鉴于双线性多项式插值法计算量较小,精度基本能够满足要求,本文基于双线性多项式插值法对水深数据进行插值处理,制备满足一定需求的地图分辨率。
2 匹配算法 2.1 PMF算法PMF算法将递推贝叶斯积分简化为在被简化离散了的搜索区域上的有限网格黎曼和。将后验概率密度用网格点集来进行逼近表示,各个网格点的权值表示状态变量在每个网格点的概率,解决了非线性模型的线性化近似所带来的一系列问题。
建立二维非线性模型:
| $\mathop {\delta x}\nolimits_{k + 1} = \mathop {\delta x}\nolimits_k + \mathop \upsilon \nolimits_k{\text{,}} $ | (1) |
| $\mathop z\nolimits_k = h(\mathop x\nolimits_k ) + \mathop \omega \nolimits_k {\text{。}}$ | (2) |
式(1)和式(2)分别为系统状态方程和观测方程,
用
| $\mathop {\overline \xi }\nolimits_{k + 1\left| k \right.}^j = \sum\limits_{i = 1}^N {p\left( {\mathop {\delta x}\nolimits_k^j \left| {\mathop {\delta x}\nolimits_k^i } \right.} \right)\mathop \xi \nolimits_k^i }{\text{,}} $ | (3) |
其中 i = 1,…N,j = 1,…N,将权值归一化:
| $\mathop \xi \nolimits_{k + 1\left| k \right.}^i = \tfrac{{\mathop {\overline \xi }\nolimits_{k + 1\left| k \right.}^i }}{{\displaystyle\sum\limits_{j = 1}^N {\mathop {\overline \xi }\nolimits_{k + 1\left| k \right.}^j } }}{\text{,}}$ | (4) |
测量更新:
| $\mathop {\overline \xi }\nolimits_{k + 1}^i = p(\mathop z\nolimits_{k + 1} \left| {\mathop {\delta x}\nolimits_k^i } \right.)\mathop \xi \nolimits_{k + 1\left| k \right.}^i{\text{,}} $ | (5) |
进一步归一化:
| $\mathop \xi \nolimits_{k + 1}^i = \tfrac{{\mathop {\overline \xi }\nolimits_{k + 1}^i }}{{\displaystyle\sum\limits_{j = 1}^N {\mathop {\overline \xi }\nolimits_{k + 1}^j } }}{\text{。}}$ | (6) |
根据权值求得逼近后验概率密度,算出定位估计误差,如此迭代重复计算,直至循环到既定次数结束。
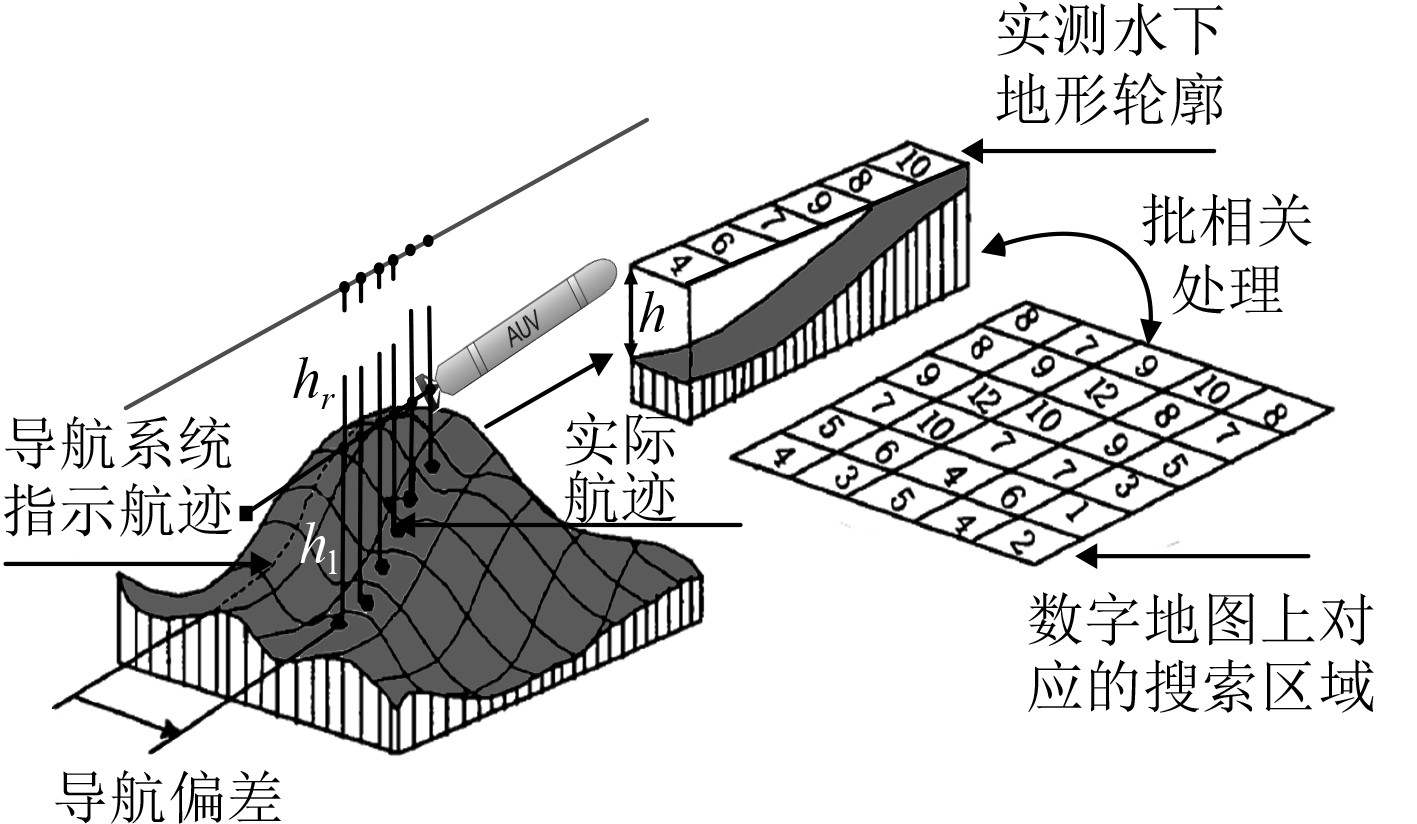
2.2 TERCOM算法TERCOM匹配算法实质上是对地形数字高程序列进行断续批相关处理以实现匹配定位,其基本原理如图2所示。
|
图 2 TERCOM算法原理图 Fig. 2 TERCOM algorithm schematic diagram |
当潜航器到达预定匹配区时,通过测量设备按一定采样间隔分别测得潜航器到海面和海底的距离
TERCOM算法常用的相关性计算方法主要有平均绝对差法(Mean Absolute Difference,MAD)、均方差法(Mean Square Difference,MSD)和互相关法(Cross Correlation,COR)三种:
| ${J_{MAD}}(x,y) = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {{h_r}(i) - {h_m}(i)} \right|}{\text{,}} $ | (7) |
| ${J_{MSD}}(x,y) = \frac{1}{N}{\sum\limits_{i = 1}^N {\left| {{h_r}(i) - {h_m}(i)} \right|} ^2}{\text{,}}$ | (8) |
| ${J_{COR}}(x,y) = \frac{1}{N}\sum\limits_{i = 1}^N {{h_r}(i){h_m}(i)} {\text{。}}$ | (9) |
式中:
最佳匹配剖面具有最大的
TERCOM算法在无偏转情况下,对初始定位精度要求不高,算法简单且计算量具有经典性、成熟性和简单实用性,计算量较小,可以大大缩短匹配计算时间,收敛速度快,但地形适应性较差,适合于初始阶段大范围搜索和粗匹配。PMF算法受初始位置偏差影响较大,计算量大,收敛速度慢,但地形适应性较好,适合于后期的精匹配。
基于2种算法的优缺点,扬长避短,将TERCOM算法用于粗匹配阶段,进行初始大范围全局搜索,找到离实际位置点较为接近的位置,将初始位置偏差降下来,并将其输出的匹配位置作为精匹配阶段PMF算法的初始位置偏差值,使初始位置偏差对PMF算法的影响降低,在提高匹配精度的同时缩短收敛时间,提高匹配效率,最大程度发挥算法的优势性能。
3 数值仿真分析选用某海域真实水深数据制备分辨率为20 m的水下数字地图,采用TERCOM+PMF组合匹配算法,对潜航器航速、测深误差、航向误差、速度误差、初始位置偏差、水下地形特征等诸多因素对导航性能的影响进行仿真分析。假设航行器以预设参数在既定水域沿X方向定速航行,航向0°,航路起始点为(1000 m,4200 m),每秒匹配一次,在进入匹配区时,对初始误差进行合理设定,导航系统在正东、正北方向的定位误差分别为
|
|
表 1 仿真参数设定 Tab.1 Settings of simulation parameters |
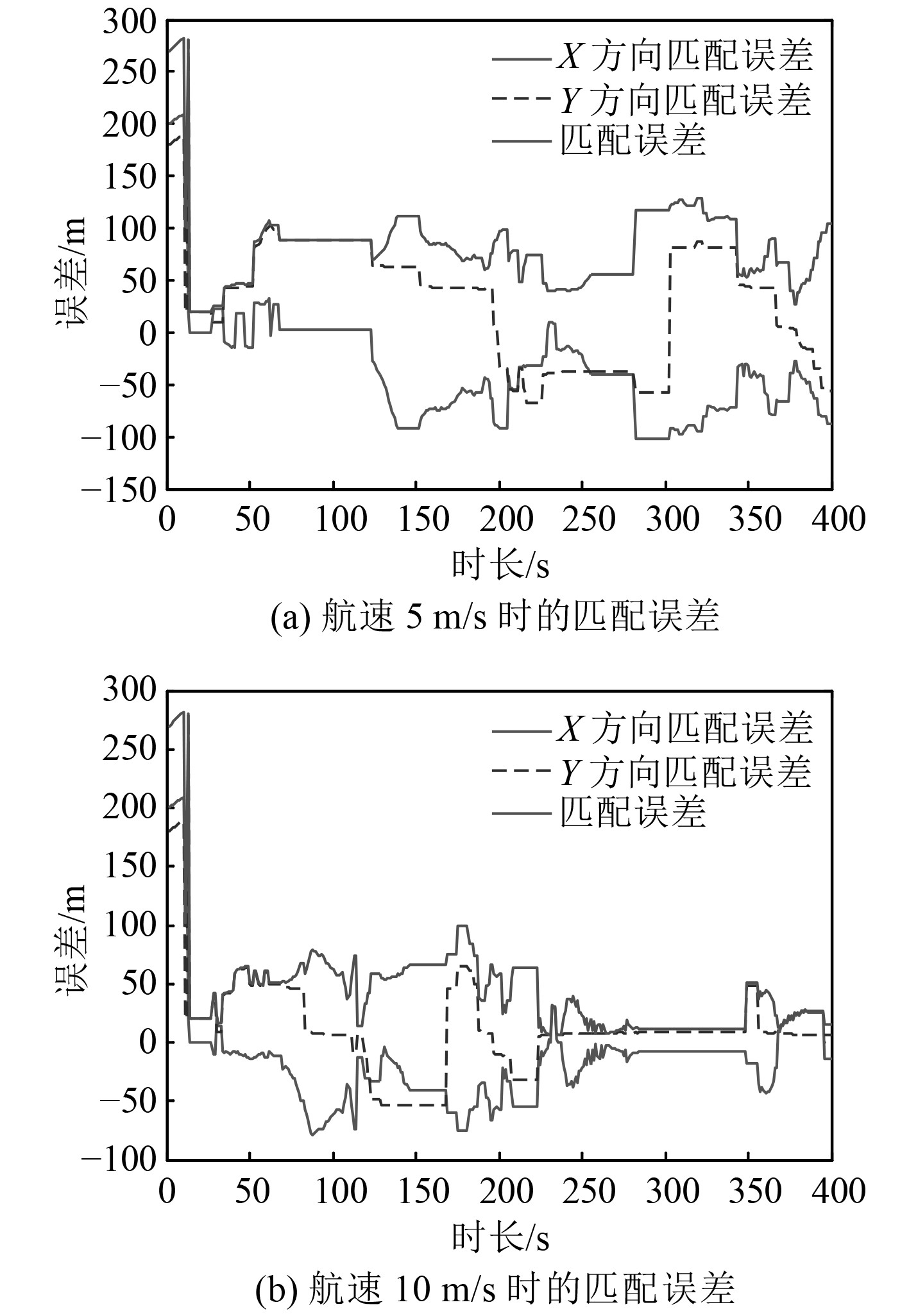
为了探究速度对匹配性能的影响,潜航器航速分别设定为0.5,1,2,4,8,10,12,15 m/s,航速为5 m/s和10 m/s时的匹配误差如图3所示,载体航速与匹配误差对应关系如表2所示。
|
图 3 对应航速下的匹配误差 Fig. 3 Matching error with corresponding speed |
|
|
表 2 载体不同航速与匹配误差对应关系 Tab.2 Relationship between vehicle speed and matching error |
由图3及表2分析知,匹配误差与载体航速密切相关,匹配误差随航速的适当增大而呈现减小且基本稳定的趋势,且收敛速度更快,匹配效率更高。其主要原因是航速过小,航经地形相似性较大,测深序列中冗余数据影响增大,易造成误匹配,影响匹配性能的发挥。随着航速的适当增大,加大各匹配点测深差异,降低了匹配过程中相似地形的干扰程度,使得获取的地形信息更加丰富有效,匹配误差得以有效抑制并渐趋平稳。因此,实际应用中应根据任务需要,结合地图分辨率及地形信息丰富程度合理地设定载体的航行速度。
3.2 测深误差对匹配性能的影响为了探究测深误差对匹配性能的影响,潜航器测深误差标准差分别设为1 m,4 m,10 m,15 m,20 m,30 m,40 m,80 m,测深误差为1 m和40 m时的匹配误差如图4所示,测深误差与匹配误差对应关系如表3所示。

|
图 4 不同测深误差下的匹配结果 Fig. 4 Matching results with different sounding error |
|
|
表 3 测深误差与匹配误差对应关系 Tab.3 Relationship between sounding error and matching error |
根据图4及表3的仿真结果分析可知,一定条件下,均方根误差和误差均值均随测深误差的增大而增大。组合算法整体抗误差性较强,但当测深误差大到一定程度时,匹配结果开始发散。这主要是因为算法实时测量匹配,每次匹配过程中测深误差都会影响测深序列与数字基准地图的精确匹配,因此应尽可能地提高测深精度,降低误匹配率。
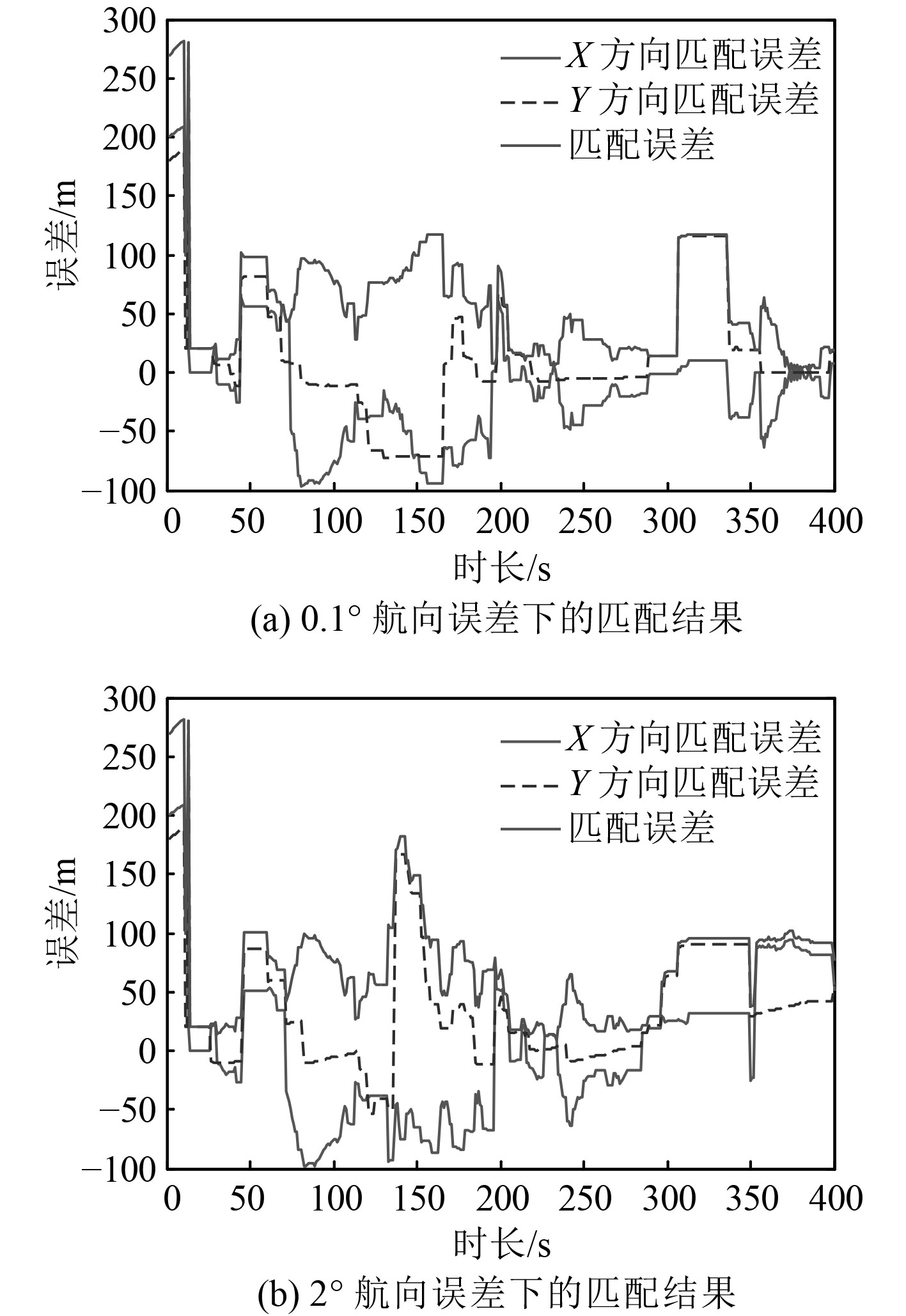
3.3 航向误差对匹配性能的影响为了探究航向误差对匹配性能的影响,潜航器航向误差标准差分别设为0.1°,1°,2°,4°,航向误差为0.1°和2°时的匹配误差如图5所示,航向误差与匹配误差对应关系如表4所示。
|
图 5 不同航向误差下的匹配结果 Fig. 5 Matching results with different heading error |
|
|
表 4 航向误差与匹配误差对应关系 Tab.4 Relationship between heading error and matching error |
从表4及图5可以看出,随着航向误差的增加,匹配误差随之增大,匹配性能变差,算法开始逐渐发散。这主要是因为航向误差关乎潜航器指示航迹偏离真实航迹的程度,潜航器惯导指示航迹与真实航迹间的物理间距随着航行时间的积累而变得越来越大,当航向误差超出算法容差范围时,以致航行到某一时刻时搜索区域无法覆盖真实位置,严重影响系统匹配性能。
3.4 航速误差对匹配性能的影响为了探究航速误差对匹配性能的影响,潜航器速度误差标准差分别设为0.1 m/s,0.5 m/s,1 m/s,2 m/s,2.5 m/s,航速误差为0.1 m/s,0.5 m/s,和1 m/s时的匹配误差如图6所示,航速误差与匹配误差对应关系如表5所示。
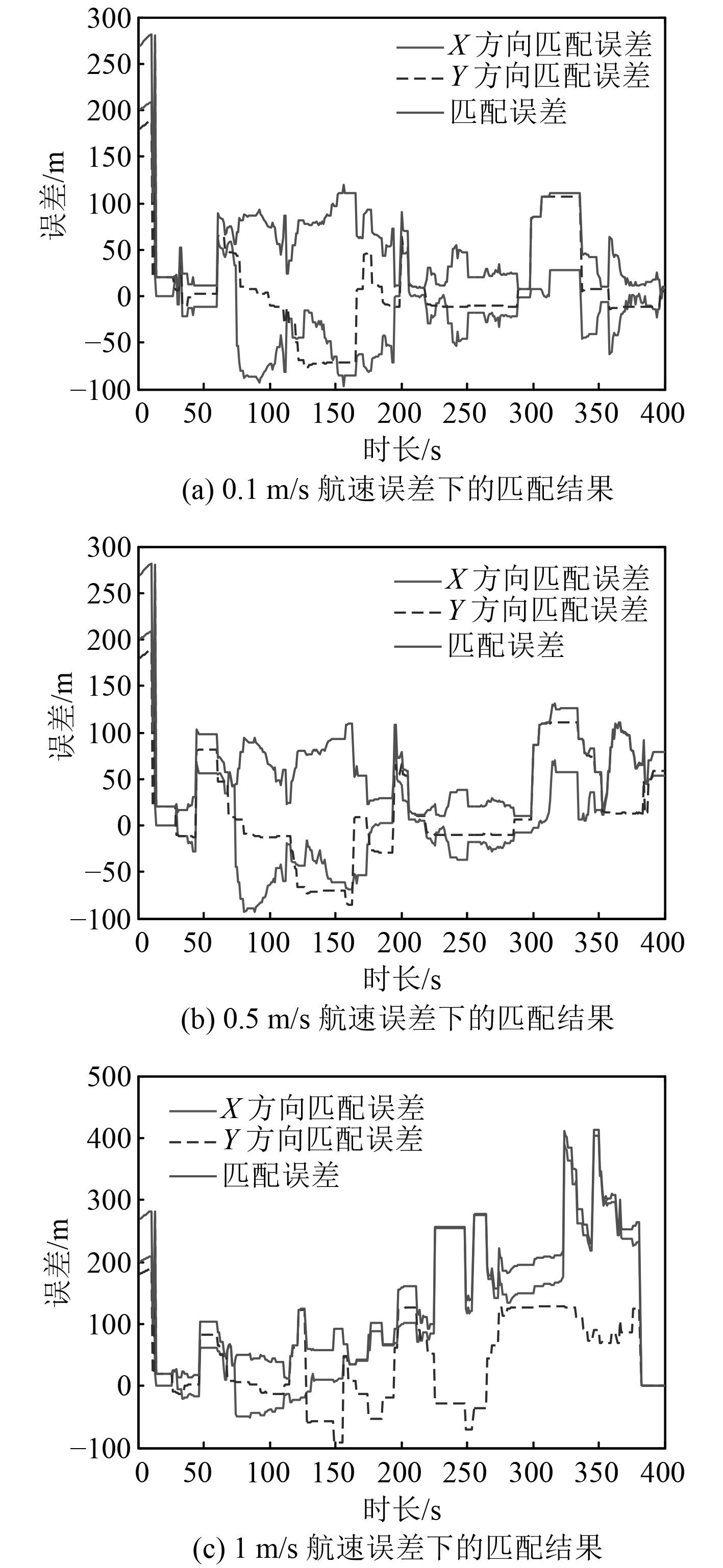
|
图 6 不同航速误差下的匹配结果 Fig. 6 Matching results with different velocity error |
|
|
表 5 航速误差与匹配误差对应关系 Tab.5 Relationship between velocity error and matching error |
从图6及表5可以看出,随着航速误差的增大,匹配误差随之增大,匹配性能变差,后期匹配结果逐渐发散,极不稳定。这主要是因为航速误差影响了潜航器指示航迹与真实航迹的间距,潜航器惯性导航指示航迹与真实航迹间的物理间距随着航行时间的积累而变得越来越大。匹配前期由于航行时间不长,算法逐渐收敛,当航行时间逐渐增大,累积误差超出算法容差范围时,以致航行到某一时刻时搜索区域无法覆盖真实位置,进而影响系统整体匹配性能,出现后期匹配不稳定的趋势。
3.5 初始位置偏差对匹配性能的影响为了探究初始位置偏差对匹配性能的影响,潜航器初始位置偏差分别设为(80 m,100 m),(100 m,180 m),(200 m,180 m),(300 m,280 m),(100 m,180 m),(200 m,180 m)偏差下匹配误差如图7所示,初始位置偏差与匹配误差对应关系如表6所示。
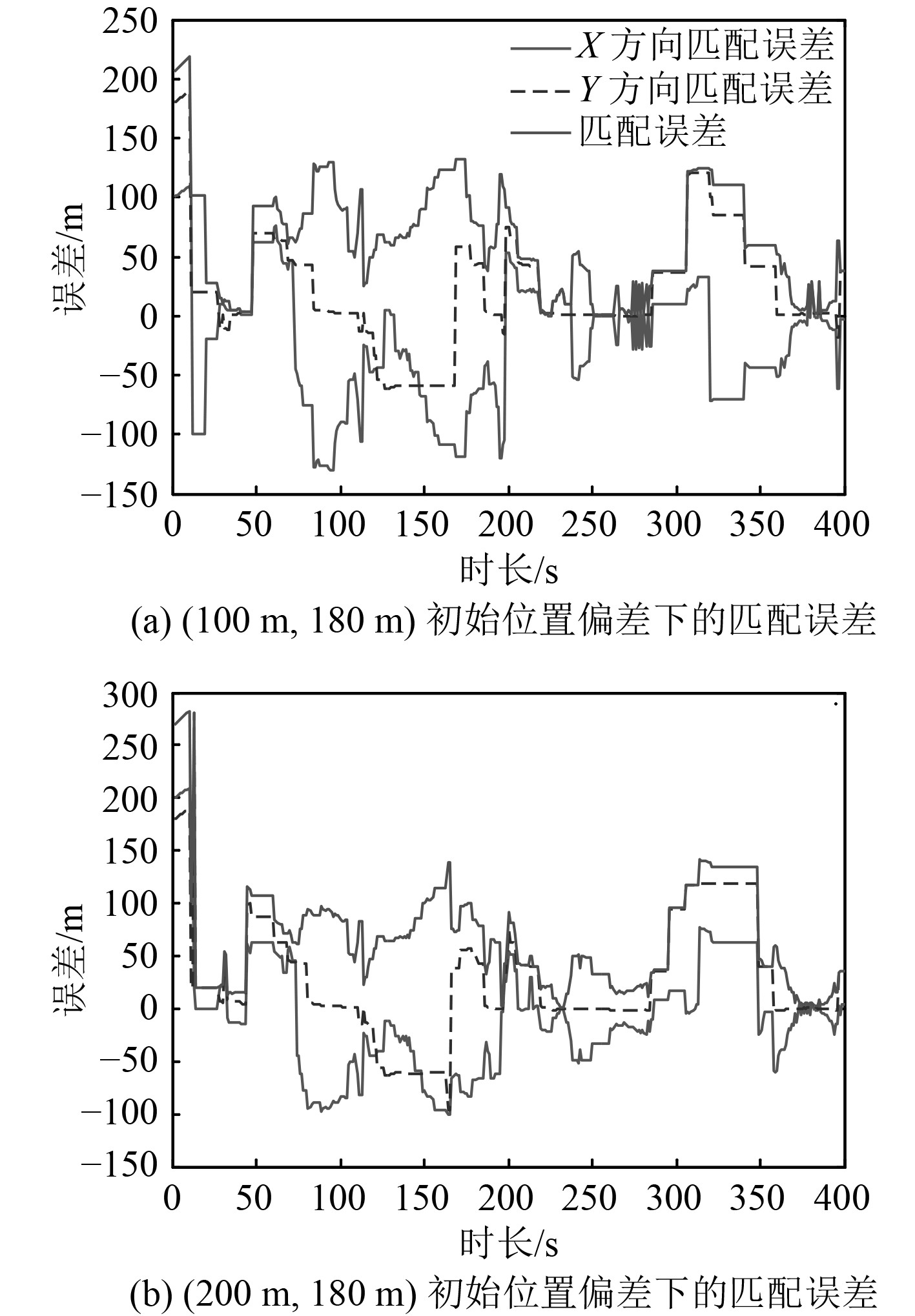
|
图 7 不同初始位置偏差下的匹配结果 Fig. 7 Matching results with different initial position error |
|
|
表 6 初始位置偏差与匹配误差对应关系 Tab.6 Relationship between initial position error and matching error |
由图7及表6可以看出,算法导航性能确受初始位置偏差影响,匹配误差随初始位置偏差的增大而变大,但组合算法在一定范围的初始偏差下,定位精度依然较高,最终使匹配结果渐趋平稳,说明组合算法具有较强的抗误差性。主要是因为PMF算法受初始位置偏差影响较大,组合算法中前期的TERCOM算法可将初始位置偏差进一步降低,为后期的PMF算法的发挥提供有利条件,使得组合算法下导航性能得以更好发挥。
3.6 地形特征对匹配性能的影响大起伏区地形起伏较大,水深序列差异明显,平坦区地形起伏不明显,地形信息丰富程度低于大起伏区,不同地形匹配区匹配效果不同。为了探究地形特征对匹配性能的影响,分别选取2种地形信息丰富程度不同的匹配区进行仿真分析,地形匹配航路及航路对应水下地形如图8和图9所示,匹配误差如图10所示。
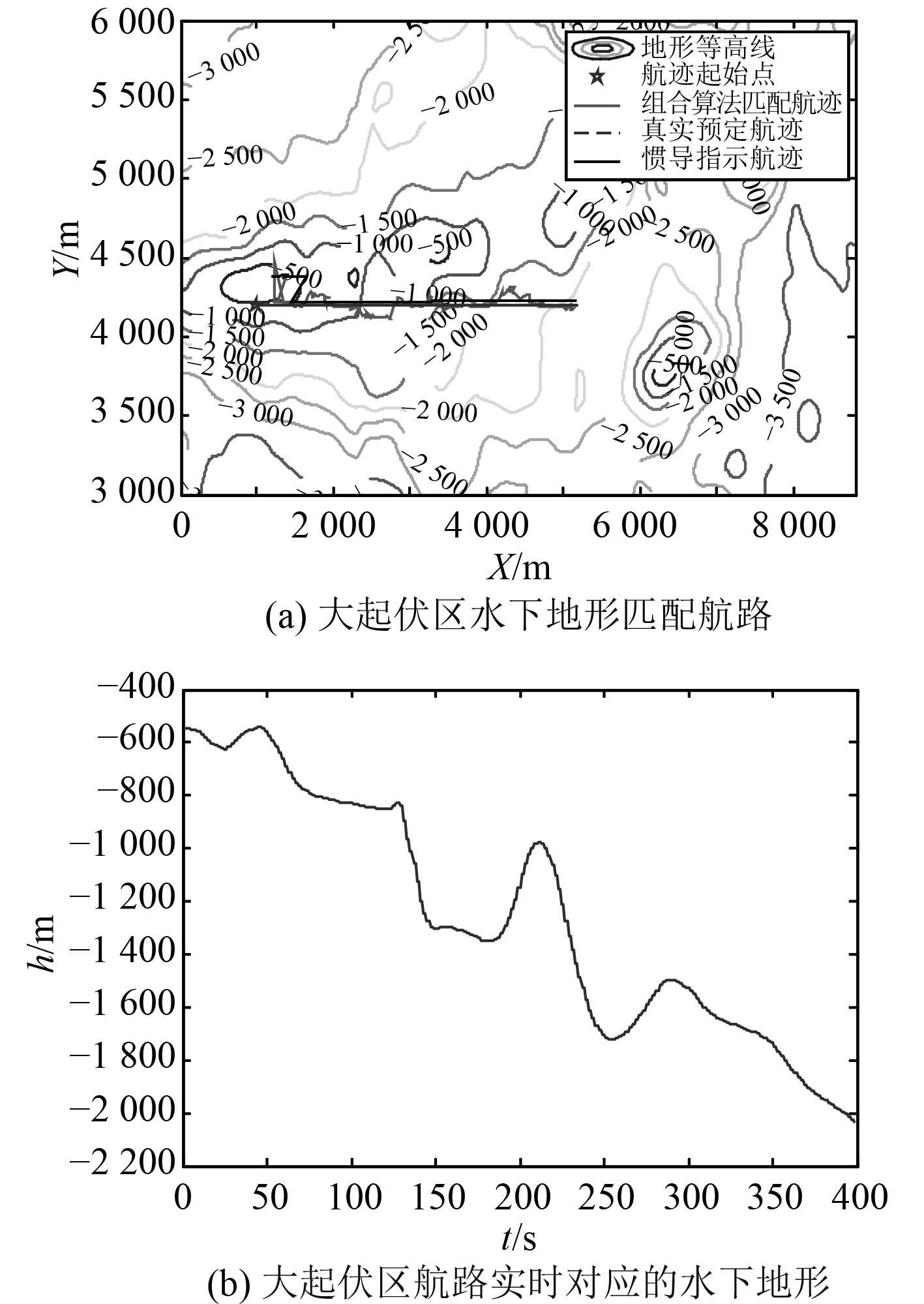
|
图 8 大起伏区匹配航路及对应水下地形 Fig. 8 Matching route and underwater topography in large fluctuation area |

|
图 9 平坦区匹配航路及对应水下地形 Fig. 9 Matching route and underwater topography in flat area |
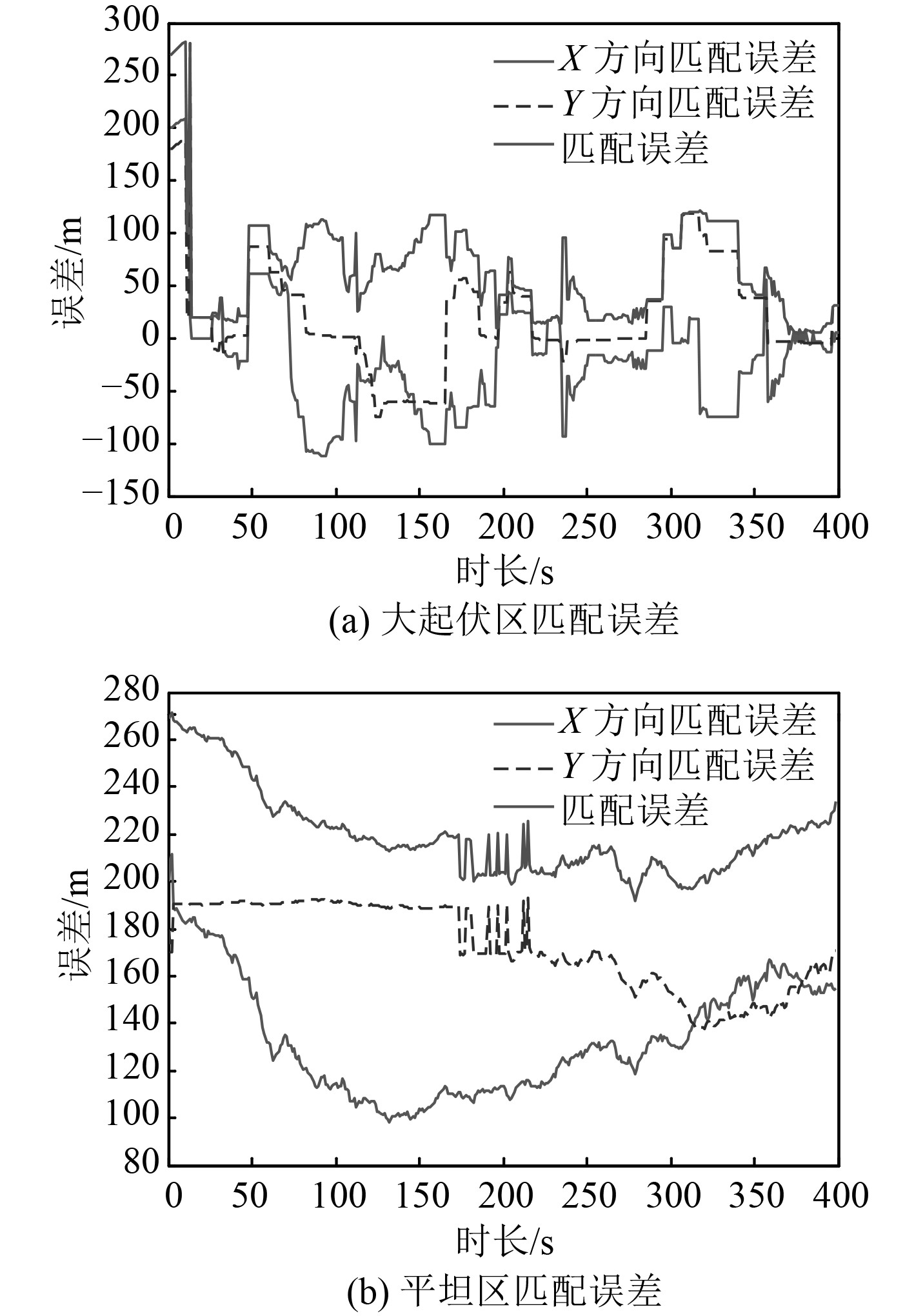
|
图 10 不同地形匹配误差 Fig. 10 Matching error of different areas |
由图8~图10可以看出,匹配算法性能的发挥与所选匹配区域的地形特征密切相关。在各自的地形匹配区中,大致在150~180 s时间段,潜航器各自航行到了地形较为平坦区,水深序列差异变小,匹配误差随之相应增大,导航效果较前期变差。纵观对比两种地形,平坦区地形信息不丰富或相对匮乏,地形起伏变化较小,匹配误差较大,导航性能较差;大起伏区地形信息丰富,地形起伏变化明显,匹配误差较小,收敛速度更快,导航效果较好,说明地形信息丰富区比匮乏区更适合导航,导航效果更好。
4 结 语本文基于TERCOM+PMF组合匹配算法针对提高辅助导航性能而开展的相关误差研究,相比以往研究较为全面、系统。通过仿真对比分析,全面细致讨论了潜航器航速、测深精度、航向误差、航速误差、初始位置偏差以及水下地形特征等多因素对导航性能的影响,对组合匹配算法的应用性能进行分析,得出了如下相关结论:TERCOM+PMF组合算法在地形辅助导航方面具有较好的抗误差性和适应性,在一定的误差范围内组合算法可以发挥较好的匹配性能,但随着误差的增大而超出算法承受能力时,导航性能就会变差;同等误差条件下,地形信息丰富的区域较平坦区更利于算法导航性能的发挥;可从提高测量设备精度及控制航行速度上解决速度、速度误差、测深误差等时空尺度因素对导航性能的影响,有效控制测量数据与基准数据的偏离度,减少误匹配;针对航向误差、初始位置偏差及地形特征等因素对导航性能的影响更多的是对系统整体性能提出了要求,在适当提高惯性导航系统性能的基础上,可通过合理设置匹配区数目及质量,使得潜航器导航误差得到及时修正。可以根据研究结果对应用参数和匹配地形进行综合衡量选取,既满足任务需求,又兼顾经济性,对相关因素进行取舍和资源分配,减小相关误差对匹配性能的影响,综合提高辅助导航性能。
| [1] |
KIM Y, PARK J, BANG H. Terrain-referenced navigation using an interferometric radar altimeter[J]. Navig. J. Inst. Navig., 2018, 65: 157-167. DOI:10.1002/navi.233 |
| [2] |
CLAUS B, BACHMAYER R. Terrain-aided navigation for an underwater glider[J]. J. Field Robot., 2015, 32: 935-951. DOI:10.1002/rob.21563 |
| [3] |
高永琪, 刘洪, 张毅. 测量误差对水下地形匹配性能的影响研究[J]. 箭弹与制导学报, 2014, 34(1): 180-183. |
| [4] |
邹炜, 孙玉臣. 水下地形匹配辅助导航技术研究[J]. 舰船电子工程, 2017, 37(8): 5-10. DOI:10.3969/j.issn.1672-9730.2017.08.002 |
| [5] |
WADHAMS P. The use of autonomous underwater vehicles to map the variability of under-ice topography[J]. Ocean Dynamics, 2012, 62(3): 439-447. DOI:10.1007/s10236-011-0509-1 |
| [6] |
张静远, 谌剑, 李恒, 等. 水下地形辅助导航技术的研究与应用进展[J]. 国防科技大学学报, 2015, 37(3): 128-135. DOI:10.11887/j.cn.201503021 |
| [7] |
RAMESH R, JYOTHI V B N, VEDACHALAM N, et al. Development and performance validation of a navigation system for an underwater vehicle[J]. J. Navig., 2016, 69: 1097-1113. DOI:10.1017/S0373463315001058 |
| [8] |
朱华勇, 沈林成, 常文森. 基于地形差分矩的TERCOM地图性能估计[J]. 国防科技大学学报, 2000, 22(4): 98-101. DOI:10.3969/j.issn.1001-2486.2000.04.023 |
| [9] |
YOO Y M, CHAN G P. Improvement of terrain referenced navigation using a point mass filter with grid adaptation[J]. Int J. Control Autom. Syst., 2015, 13(5): 1173-1181. DOI:10.1007/s12555-013-0410-4 |
| [10] |
MEDUNA D, ROCK S, MCEWEN R. AUV terrain relative navigation using coarse maps[C]//Proceedings of the 2009 Unmanned Untethered Submersible Technology Conference. University of New Hampshire, Durham, 2009: 1-11.
|
| [11] |
刘洪, 高永琪, 谌剑. 基于PMF和TERCOM组合算法的水下地形匹配技术[J]. 鱼雷技术, 2012, 20(6): 437-442. |
| [12] |
王可东, 杨勇. 地形辅助导航匹配误差研究[J]. 宇航学报, 2008, 29(6): 1809-1813. DOI:10.3873/j.issn.1000-1328.2008.06.024 |
| [13] |
ALLOTTA B, CAITI A, COSTANZI R, et al. A new AUV navigation system exploiting unscented Kalman filter[J]. Ocean Eng., 2016, 113: 121-132. DOI:10.1016/j.oceaneng.2015.12.058 |
| [14] |
KIM T, KIM J, BYUN S W. A comparison of nonlinear filter algorithms for terrain-referenced underwater navigation[J]. Int. J. Control Autom. Syst., 2018, 16: 2977-2989. DOI:10.1007/s12555-017-0504-5 |
| [15] |
NIEDFELDT P, BEARD R. Convergence and complexity analysis of recursive-RANSAC: A new multiple target tracking algorithm[J]. IEEE Trans. Autom. Control, 2016, 61: 456-461. |
 2021, Vol. 43
2021, Vol. 43

