目前人类在海洋中的活动大都集中在浅海,而水声信道由于具备良好的传播特性使其成为海洋研究的主要信息载体,浅海水声信道也成为人们研究的一个热点问题[1]。浅海水声信道具有衰减严重、多径效应和频散效应等特性,会引起传输信号幅度的起伏和相位的波动[2]。
目前,国内外许多学者针对浅海水声信道开展了研究工作,取得了一系列的成果。如文献[3]利用AR(p)模型对浅水时变多途信道模型进行修正;文献[4]在建立系统等效模型的基础上采用用多项式拟合法得到Rice衰落信道一定范围内的信噪比近似解;文献[5-6]采用BELLHOP模型对水下信道进行仿真,并研究了对目标声源的探测方法和阵列最佳布放方法与声线的关系;文献[7]应用Rice衰落模型对浅海水声信道进行研究;文献[8-10]对水声信道的传播特性进行了分析研究。
掌握高频水声信道的传播特性在军用和民用领域都有十分重要的实用价值,本文基于虚源法和Xiao模型建立高频水声信道模型,并对其统计特性和传播特性进行仿真分析。
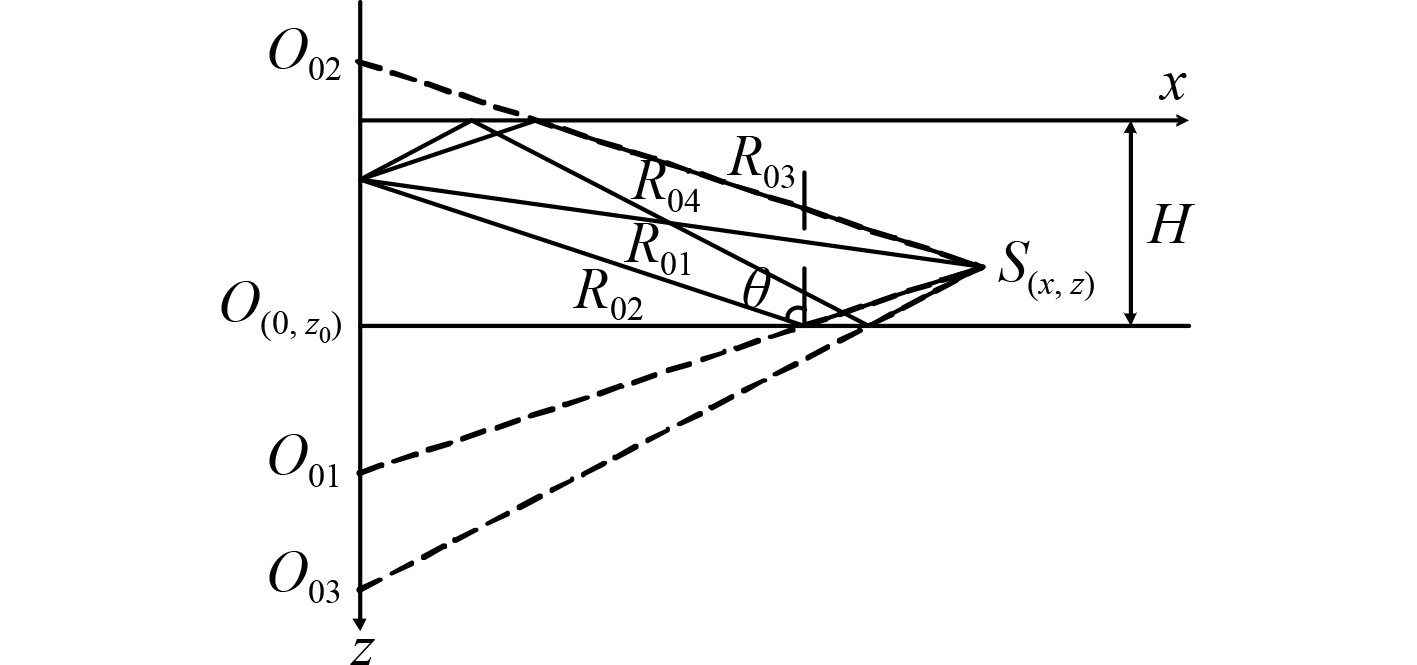
1 浅海高频水声信道模型 1.1 虚源法模型虚源法就是把每一根声线等效为一个对应的虚源所射出的到达接收点的直达声线,到达接收点的信号即为各虚源射出的直达声线的总和。虚源法的信号传播示意图如图1所示,假设海深为
|
图 1 虚源法信号传播示意图 Fig. 1 The signal propagation sketch map of image source method |
以平面波为例进行研究,根据线性叠加原理,归一化的接收信号声压可表示为:
| $p = \sum\limits_{n = 0}^\infty {\sum\limits_{i = 1}^4 {{C_{ni}}\exp (j{\varphi _{ni}})} }{\text{,}} $ | (1) |
其中各本征声线的衰减系数为:
| $\left\{ {\begin{array}{*{20}{c}} {{C_{n1}} = \dfrac{{V_1^nV_{2n1}^n}}{{{R_{n1}}}}}{\text{,}} \\ {{C_{n2}} = \dfrac{{V_1^nV_{2n2}^{n + 1}}}{{{R_{n2}}}}}{\text{,}} \\ {{C_{n3}} = \dfrac{{V_1^{n + 1}V_{2n3}^n}}{{{R_{n3}}}}}{\text{,}} \\ {{C_{n4}} = \dfrac{{V_1^{n + 1}V_{2n4}^{n + 1}}}{{{R_{n4}}}}} {\text{。}} \end{array}} \right.$ | (2) |
各本征声线相位为:
| ${\varphi _{ni}} = k{R_{ni}}{\text{,}}$ | (3) |
式中:
| $\left\{ \begin{gathered} {R_{n1}} = \sqrt {R_0^2 + {{(2nH + z - {z_0})}^2}} {\text{,}} \\ {R_{n2}} = \sqrt {R_0^2 + {{[2(n + 1)H - z - {z_0}]}^2}} {\text{,}} \\ {R_{n3}} = \sqrt {R_0^2 + {{(2nH + z + {z_0})}^2}} {\text{,}} \\ {R_{n4}} = \sqrt {R_0^2 + {{[2(n + 1)H - z + {z_0}]}^2}} {\text{。}} \\ \end{gathered} \right.$ | (4) |
式中:
海面反射系数
| ${V_1} = - \sqrt {\frac{{1 + 0.1{{({f_0}{\rm{ /}}{f_1})}^2}}}{{1 + {{({f_0}{\rm{ /}}{f_1})}^2}}}}{\text{,}} $ | (5) |
其中,
对于均匀海底,其反射系数
| ${V_{2ni}} = \frac{{a\cos {\theta _{ni}} - \sqrt {{b^2} - {{\sin }^2}{\theta _{ni}}} }}{{a\cos {\theta _{ni}} + \sqrt {{b^2} - {{\sin }^2}{\theta _{ni}}} }}{\text{。}}$ | (6) |
式中:
将发射器到接收器的几条不同信号传输路径称为本征路径。信号在本征路径上传输时,可看作一个稳定的主分量和许多随机的分散分量之和。其中主分量称为本征分量(本征声线),随机的分散分量称为多径分量。实验证明浅海水声信道传输近距离服从Rice模型,因此,每一条本征路径信道的传播特性可通过Rice衰落仿真体现。
1.2 Xiao模型Xiao模型是一种用正弦波叠加法实现的Rice信道仿真模型,其优越之处在于它对所有正弦波的路径增益、多普勒频移、初始相位均引入随机变量,尤其是引入随机直射分量,改善了统计特性,能真实反映实际信道的物理特性。其模型如下:
| $Z(t) = {Z_c}(t) + j{Z_s}(t){\text{,}}$ | (7) |
| $\begin{split} {Z_c}(t) = &\Biggr[\sqrt K \cos (2\text{π} {f_d}t\cos {\theta _0} + {\varphi _0}) + \\ &\frac{1}{{\sqrt N }}\sum\limits_{n = 1}^N {\cos (2\text{π} {f_d}t\cos {\alpha _n} + \varphi {}_n)} \Biggr]\Biggr/\sqrt {1 + K} {\text{,}} \end{split} $ | (8) |
| $\begin{split} {Z_s}(t) = &\Biggr[\sqrt K \sin (2\text{π} {f_d}t\cos {\theta _0} + {\varphi _0}) + \\ &\frac{1}{{\sqrt N }}\sum\limits_{n = 1}^N {\sin (2\text{π} {f_d}t\cos {\alpha _n} + \varphi {}_n)} \Biggr]\Biggr/\sqrt {1 + K}{\text{。}} \end{split} $ | (9) |
其中:
为体现浅海高频水声信道的传播特性,这里用本征声线来代替Xiao模型中的直射分量,并考虑信道的衰减作用,则接收信号可以表示为:
| $r(t) = \sum\limits_{m = 1}^M {{\zeta _m}(t)x(t - {\tau _m})}{\text{,}} $ | (10) |
其中:
| ${\zeta _m}(t) = {u_{cm}}(t) + j{u_{sm}}(t){\text{,}}$ | (11) |
| $\begin{split} {u_{cm}}(t) = &{C_m}\Biggr[\sqrt K \cos (2\text{π} {f_d}t\cos {\theta _m} + {\varphi _m}) +\\ &\frac{1}{{\sqrt N }}\sum\limits_{n = 1}^N {\cos (2\text{π} {f_d}t\cos {\alpha _n} + \varphi {}_n)} \Biggr]\Biggr/\sqrt {1 + K} {\text{,}} \end{split} $ | (12) |
| $\begin{split} {u_{sm}}(t) = &{C_m}\Biggr[\sqrt K \sin (2\text{π} {f_d}t\cos {\theta _m} + {\varphi _m}) + \\&\frac{1}{{\sqrt N }}\sum\limits_{n = 1}^N {\sin (2\text{π} {f_d}t\cos {\alpha _n} + \varphi {}_n)} \Biggr]\Biggr/\sqrt {1 + K}{\text{。}} \end{split} $ | (13) |
式中:
理想Rice衰落过程包络分布的概率密度函数为:
| $ P(r) = \frac{r}{{{\delta ^2}}}\exp \left( - \frac{{{r^2} + {u^2}}}{{2{\delta ^2}}}\right){I_0}\left(\frac{{ru}}{{{\delta ^2}}}\right){\text{,}} $ | (14) |
其中:
| $2{\delta ^2} = \frac{\varOmega }{{1 + K}}, {u^2} = \frac{{K\varOmega }}{{1 + K}}{\text{。}}$ | (15) |
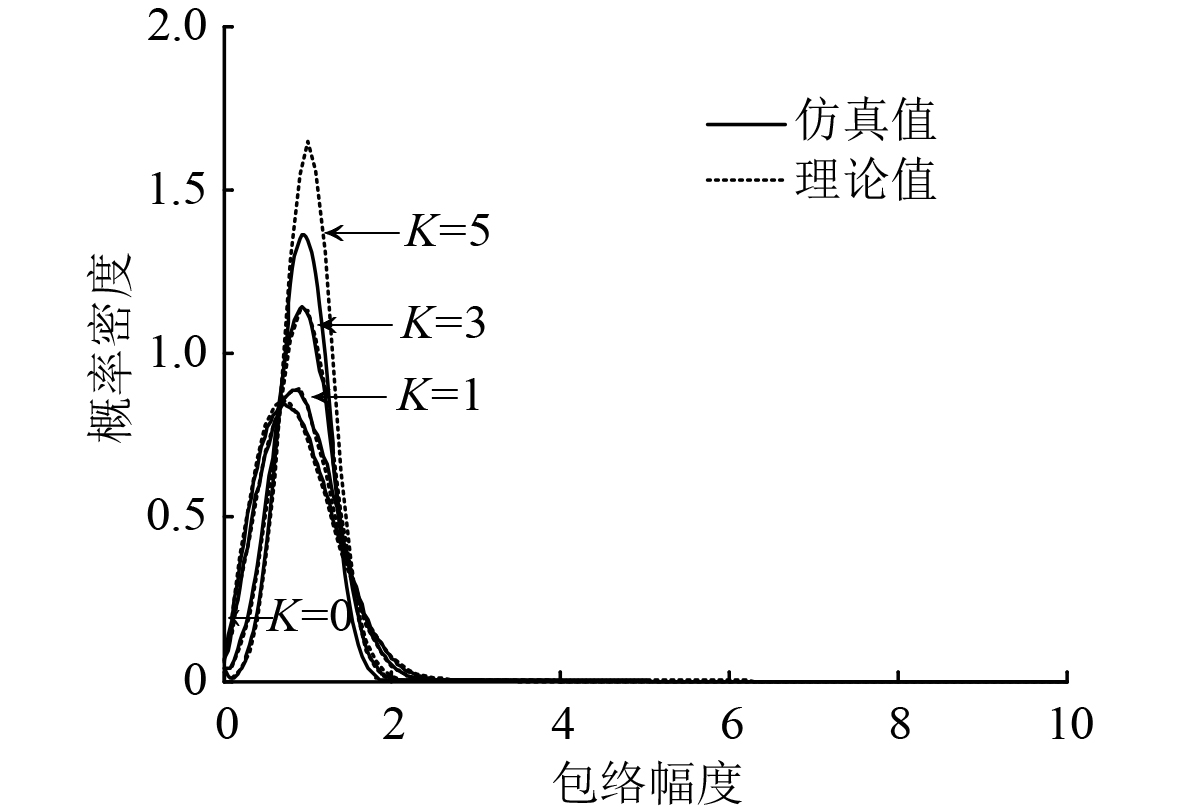
任选一条本征路径,分析Rice因子
|
图 2
|
对图2分析可知,当Rice因子
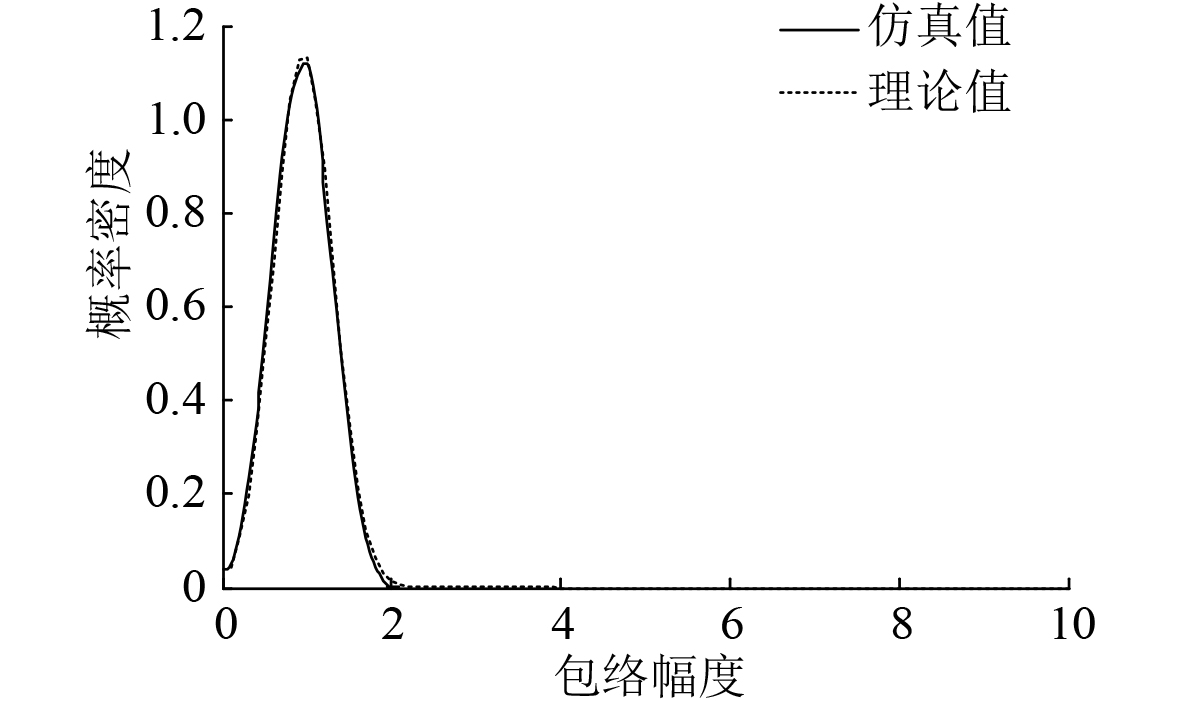
令
|
图 3
|
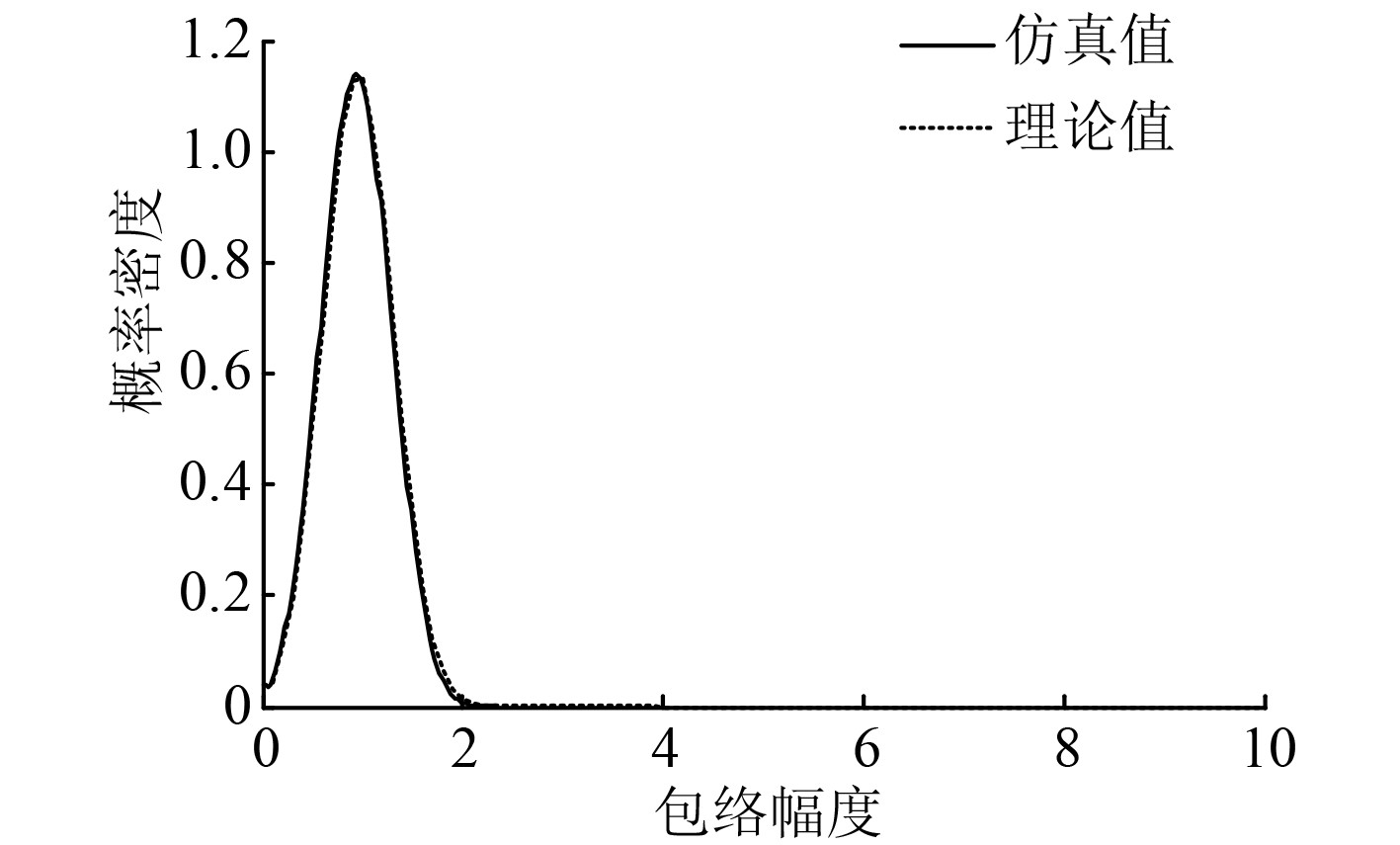
|
图 4
|
分析图3和图4可知,谐波函数个数
设发射器与接收器的水平距离
| $\begin{split} x(t) = &{A_0}[\cos (2\text{π} {f_0}t + {\theta _0})+ \\&\cos (2\text{π} {f_1}t + {\theta _0}) + \cos (2\text{π} {f_2}t + {\theta _0})]{\text{。}} \end{split} $ | (16) |
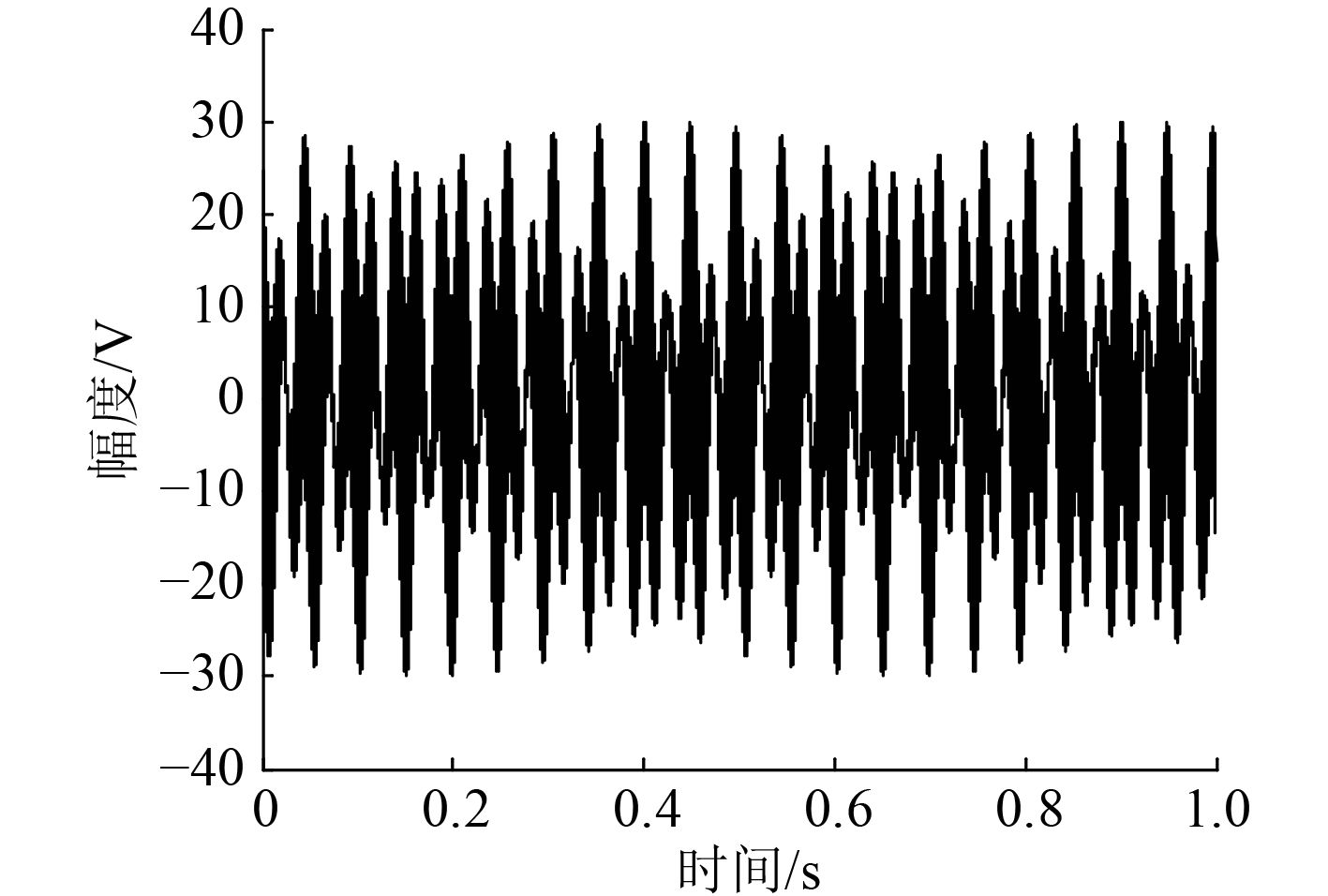
其中发射信号幅度
|
图 5 发射信号波形图 Fig. 5 The waveform image of transmitted signal |
在理论上,本征声线的数量是无穷多的,随着反射次数
接收信号的传播损失可由射线理论计算得到,即
| $TL = - 20\log \left| {\frac{p}{{{p_0}}}} \right|{\text{。}}$ | (17) |
其中
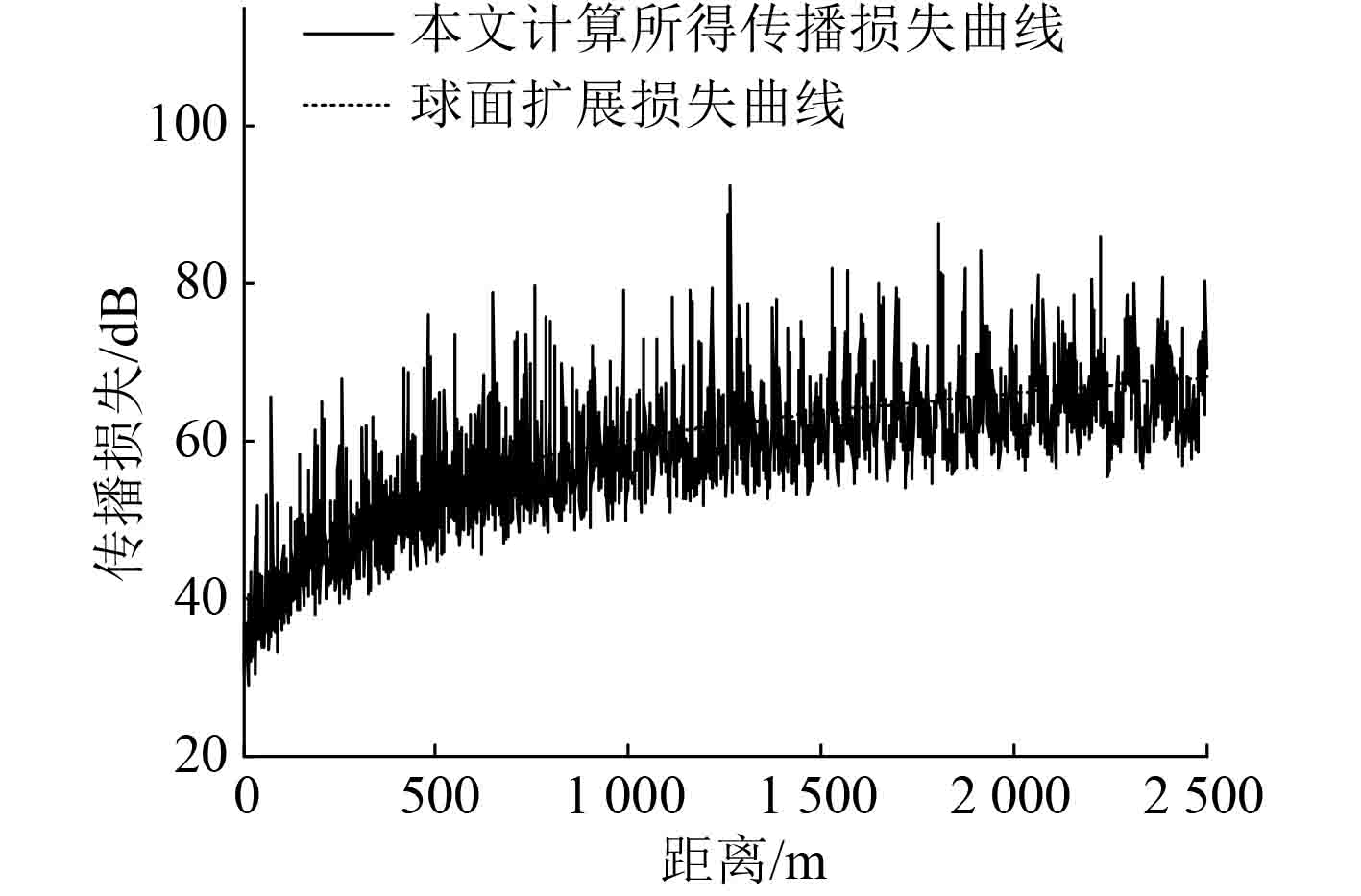
|
图 6 传播损失示意图 Fig. 6 The sketch map of transmission loss |
由图6分析可知,由本文方法计算所得传播损失曲线沿球面扩展损失曲线上下震荡,这是由于本文设定的仿真条件与球面扩展的传播条件相吻合。
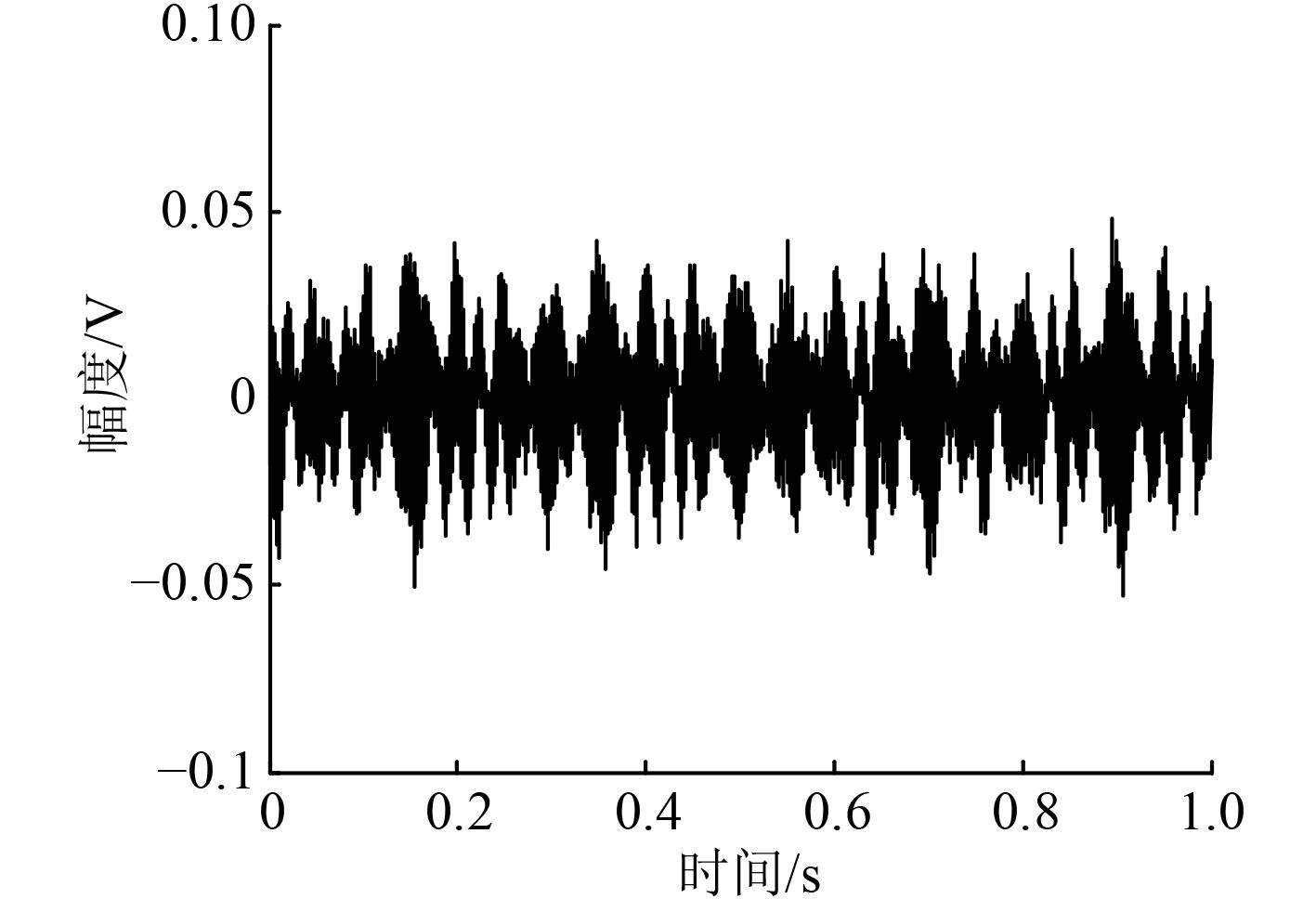
3.3 接收信号分析由式(10)进行仿真计算可得接收信号的波形如图7所示。
|
图 7 接收信号波形图 Fig. 7 The waveform image of received signal |
由图7可知,与发射信号相比,接收信号的波形明显发生变化,这是由于经过信道传播后,信号产生衰减、相移以及频散的结果。
此时,纳入计算的本征声线的数目为6,各本征声线与直达声线的幅度比值如表1所示。
|
|
表 1 各本征声线归一化幅度衰减值 Tab.1 The normalization amplitude loss value of each eigen acoustic ray |
对表1进行分析可知,从3号本征声线开始,其幅度就出现明显下降,经计算可知,海面反射系数
本文基于虚源法和Xiao模型建立高频水声信道模型,并分析其统计特性,当Rice因子
| [1] |
杨德坤, 雷波, 卢艳阳. 海洋声学典型声场模型的原理及应用[M]. 西安: 西北工业大学出版社, 2018.10-18.
|
| [2] |
陈韶华, 李世智, 陈川. 浅海多径时延估计的功率谱加权自相关方法[J]. 声学学报, 2017, 42(5): 543-550. |
| [3] |
尹艳玲, 乔钢, 刘凇佐, 张宇. 浅水时变多途信道特性分析与模型实验研究[J]. 声学学报, 2019, 44(1): . 96–105. |
| [4] |
陈萍, 熊蔚明. 一种可用于菜斯衰落信道的信噪比估计算法[J]. 东南大学学报(自然科学版), 2017, 47(2): . 209–214. |
| [5] |
李孟, 周荣艳. 基于BELLHOP模型的水下信道仿真方法研究[J]. 舰船电子工程, 2018, 38(8): . 166–169. |
| [6] |
GUL S. , ZAIDI S., KHAN R., et al. Underwater acoustic channel modeling using BELLHOP ray tracing method[C]. International Bhurban Conference on Applied Sciences & Technology, 2017: 665−670.
|
| [7] |
施建宇, 一种浅海水声信道的仿真方法[J]. 通信技术, 2019, 52(10). 2365–2369.
|
| [8] |
吴鹏, 周杰, 陈姜高路. SOC水声信道模型及其计算方法研究[J]. 计算机科学, 2018, 45(8): 94–99. |
| [9] |
李莉, 陈兆一, 杨丽娟. 水声传感器网络的水声信道建模与仿真[J]. 无线电通信技术, 2018, 44(2): 154–159. |
| [10] |
HEECHUN S., CHOMGUN C., WILLIAM H., et al.. Underwater sound channel in the northeastern East China Sea[J]. Ocean Engineering, 2018, .370-374. |
 2021, Vol. 43
2021, Vol. 43
