2. 江苏省镇江船厂(集团)有限公司,江苏 镇江 212002
2. Jiangsu Zhenjiang Shipyard (Group) Co., Ltd, Zhenjiang 212000, China
在船舶电网中,虽然都在使船舶的能源结构趋于多元化,但是考虑到成本问题,作为船舶能源供应的核心,船舶的柴油发电机组依然在船舶电站中占据主导地位。就目前的发展而言,船舶柴油发电机组的建模与相关仿真,是相关人员研究船舶电力系统的重要手段。通过仿真,可以更为深入了解柴油发电机的各种特性,如端电压、幅值、相位等。在船舶电网运行过程中,柴油发电机组的并联运行,是船舶运行中的主要运行模式,柴油发电机的并网过程影响着船舶电网运行的稳定性,也决定着船舶的柴油发电机能否顺利并网并实现稳定带载。利用仿真的方法,研究柴油发电机的启动以及并网过程,能够将复杂的数学模型以图形的方式表示出来,增强研究人员对于船舶柴油发电机特性的了解,而且还可以缩减研究成本与时间,更为主要的是,在实际操作中,如果操作不当,会不可避免地造成一些难以恢复的损坏与浪费。本文通过对柴油发电机启动过程的理解,利用Simulink中的相关模型,建立稳定的柴油发电机带载运行模型,并通过修改参数,观察柴油发电机起动过程中的转速等相关物理量的变化以及其端电压的建立过程。仿真表明,建立的模型能够较为准确的反映柴油发电机的启动过程和性能,建立的模型也可以作为柴油发电机并网的研究基础,在指导船舶电站电力开关等的选型,具有一定的参考意义。
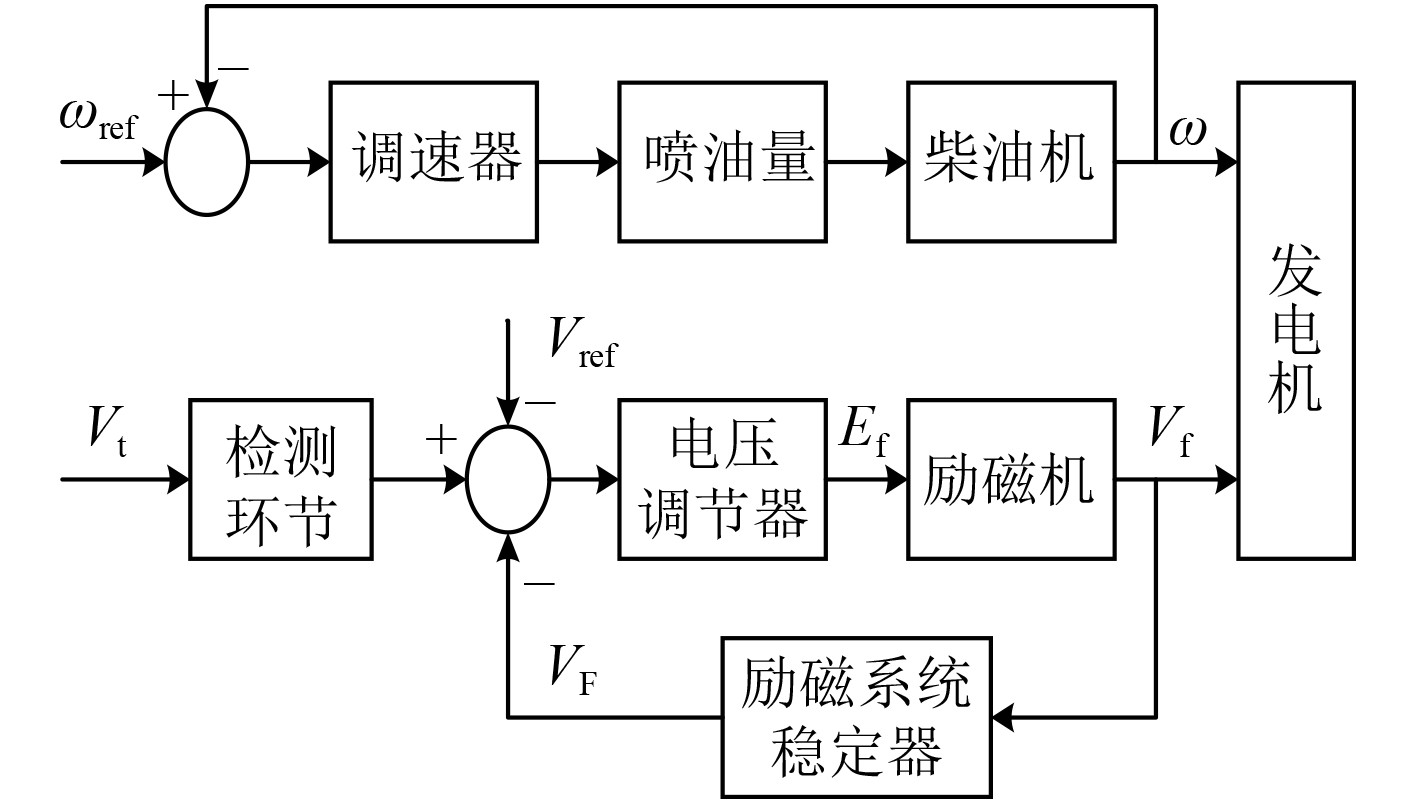
1 柴油发电机 1.1 柴油发电机的工作原理在船舶电网中,船舶的柴油发电机,可以看作是整个船舶电力系统的心脏,维持着船舶电网的有效运行。柴油发电机系统包括柴油机和发电机两部分,而柴油机和发电机最主要的部分分别为调速器和励磁调节器。调速器用于调节柴油机的转速;发电机转动发电后,为实现对其输出电压的控制,励磁调节器调节发电机的端电压。在目前的实船应用中,多采用四冲程的柴油机,通过调速器与励磁调节器的相互配合,柴油发电机系统就可以建立稳定的输出电压,实现稳定带载,具体的实现过程如图1所示。
|
图 1 柴油发电机原理 Fig. 1 Diesel generator principle |
船舶工况复杂,在其行驶的过程中,其电力负荷会经常性的发生变化,而柴油发电机所发出的电量就要做出相应的调整,柴油机的调速系统就起到这样的作用。柴油机的调速系统可以调节柴油机转速的频繁变动,使其转速稳定于某一固定值附近。
图1上半部分,为柴油机及其调速系统的工作原理。调速器包含转速传感器和PID控制器两部分,转速传感器采集转速信息,并经过计算,输出与转速成正比关系的电压信号。这一个过程,可以近似的看为一阶惯性环节,表达式为:
| $ {{G}}_{1}\left(s\right)=\frac{{U}_{f}\left(s\right)}{n\left(s\right)}=\frac{1}{1+{T}_{1}s} ,$ | (1) |
通过转速传感器,可以得到实际的转速信号,与输入的参考转速比较、做差,所得差值经过PID的调节作用,就可以调节柴油机的喷油量。PID的传递函数可以表示为:
| $ {G}_{2}\left(s\right)={K}_{p}\left[1+\frac{1}{{T}_{i}s}+{T}_{d}s\right], $ | (2) |
综合式(1)和式(2),可以得到柴油机调速系统的数学模型如下式:
| $ \begin{split} {G}\left(\mathrm{s}\right)=&{G}_{1}\left(\mathrm{s}\right){G}_{2}\left(\mathrm{s}\right) =\dfrac{1}{1+{T}_{1}s}\bullet {K}_{p}\left[1+\dfrac{1}{{T}_{i}s}+{T}_{d}s\right]=\\ &\dfrac{{K}_{1}\left(1+{T}_{2}s\right)\left(1+{T}_{3}s\right)}{s\left(1+{T}_{1}s\right)}{\text{。}}\end{split} $ | (3) |
柴油机的喷油量,由柴油机调速系统输出电压确定,根据PID调节器输出的电压信号,改变电磁铁的位移变化量,从而实现对于喷油量的控制。柴油机喷油量的运动增量方程可以表示为:
| $ m\frac{{{\rm{d}}}^{2}l}{{\rm{d}}{t}^{2}}+D\frac{{\rm{d}}l}{{\rm{d}}t}+{K}_{s}l={K}_{i}i-{K}_{l}l {\text{。}}$ | (4) |
式中:m为电磁铁质量;l为电磁体的位移变化量;D为阻尼系数;
对柴油机喷油量的运动增量方程进行拉普拉斯变换并整理后,可以得到如下传递函数:
| $ \begin{split}\mathrm{G}\left(\mathrm{s}\right)=&\dfrac{l\left(s\right)}{i\left(s\right)}=\dfrac{{K}_{i}}{m{s}^{2}+Ds+{K}_{s}+{K}_{l}} =\\ &\dfrac{{K}_{2}}{(1+{T}_{4}s)(1+{T}_{5}s)}{\text{。}}\end{split}$ | (5) |
柴油机的输出转矩
| $ \Delta {{T}}_{m}=K\Delta l, $ | (6) |
由于在柴油机的喷油到输出转矩变化间存在延迟,在设置延迟时间为
| $ \Delta{{T}}_{m}=K\Delta l{e}^{-{T}_{d}s} ,$ | (7) |
柴油发电机的传递函数可以表示为:
| $ \mathrm{G}\left(\mathrm{s}\right)=\frac{\Delta{{T}}_{m}}{\Delta l}=k{e}^{-{T}_{d}s} ,$ | (8) |
当
| $ {e}^{-{T}_{d}s}\approx \frac{1}{1+{T}_{d}s} {\text{。}}$ | (9) |
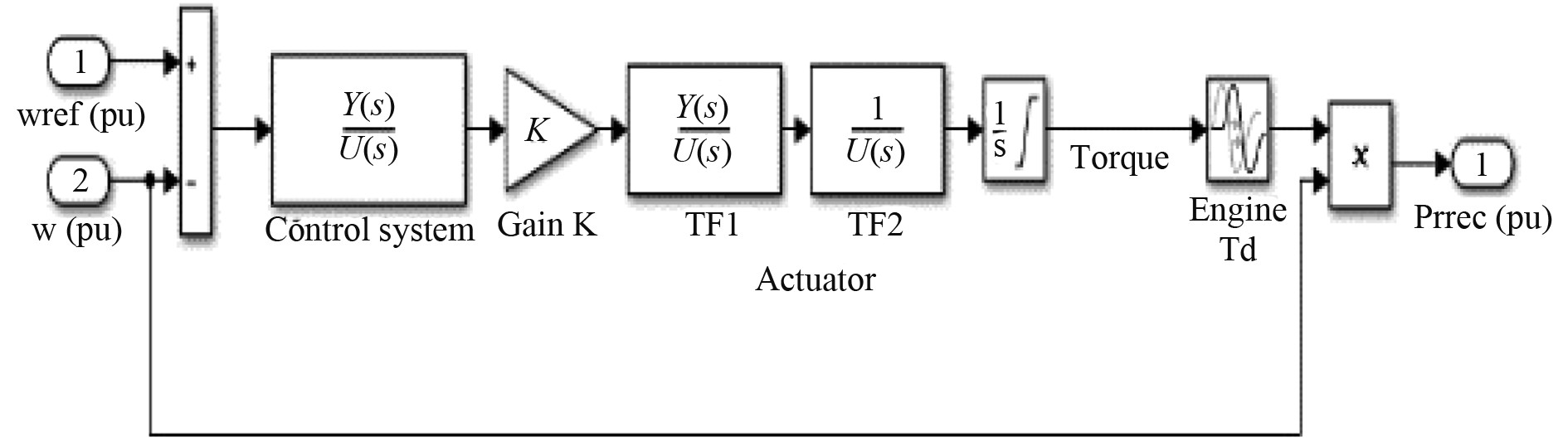
综合柴油机调速系统以及柴油机的数学模型并结合喷油量控制,可以得到如图2所示的柴油机及其调速系统的仿真模型。
|
图 2 柴油机及其调速系统仿真模型 Fig. 2 Simulation model of diesel generator and its speed regulation system |
同步发电机的励磁系统的工作原理如图1下半部分所示,主要由检测环节、电压调节器、励磁机与励磁稳定器四部分组成。
设检测环节检测到的发电机的端电压为
| $ {{G}}_{1}\left(s\right)=\frac{{k}_{r}}{{t}_{r}s+1} ,$ | (10) |
电压调节器的作用在于控制励磁机,通过放大、超前与滞后的补偿,
| $ {{G}}_{2}\left(s\right)=\frac{{k}_{a}\left({t}_{c}s+1\right)}{\left({t}_{a}s+1\right)\left({t}_{b}s+1\right)}, $ | (11) |
一般情况下,
| $ {{G}}_{2}\left(s\right)=\frac{{k}_{a}}{{t}_{a}s+1} {\text{。}}$ | (12) |
由于其励磁机为他励交流励磁机,其传递函数可以表示为:
| $ {{G}}_{3}\left(s\right)=\frac{1}{{t}_{e}s+{k}_{e}} ,$ | (13) |
励磁稳定器包含电压检测和积分2个环节,其传递函数可以表示为:
| $ {{G}}_{4}\left(s\right)=\frac{{k}_{fd}s}{{t}_{fd}s+1} {\text{。}}$ | (14) |
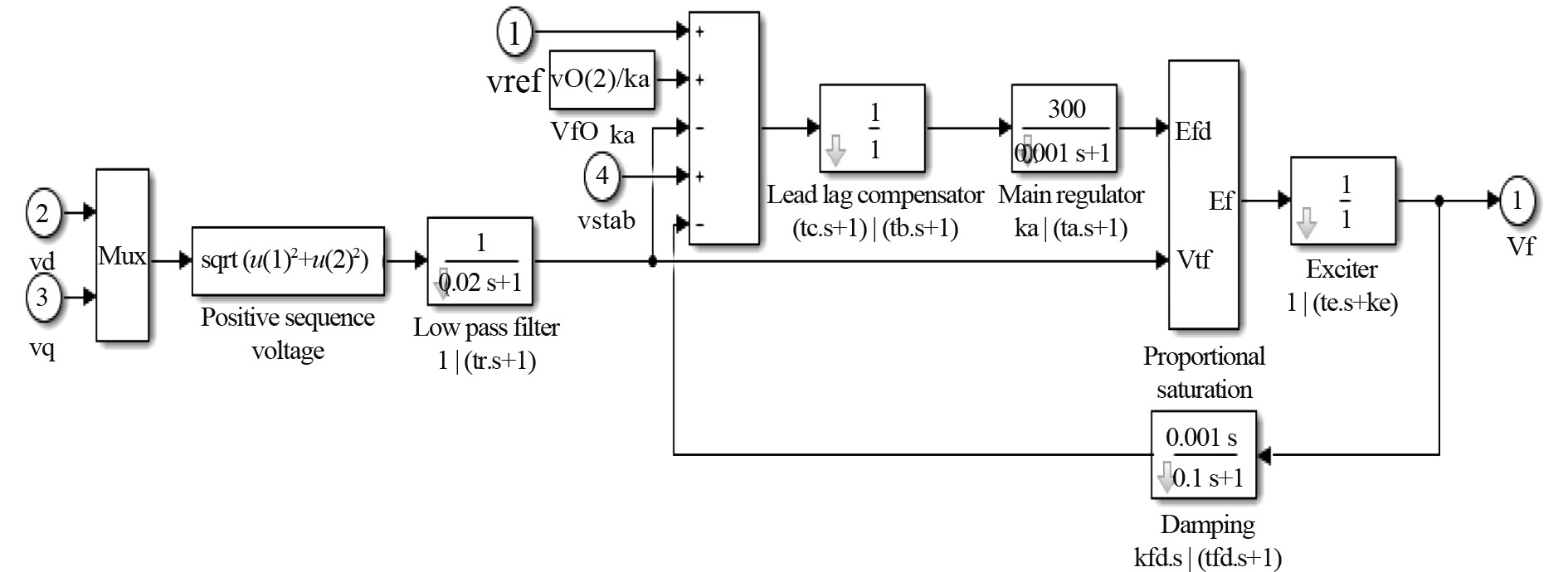
综合式(10)~式(14),并在考虑实际情况后,对电压调节器进行限幅后,其励磁系统仿真模型如图3所示。
|
图 3 同步发电机励磁系统仿真模型 Fig. 3 Simulation model of excitation system of synchronous generator |
在推导同步发电机方程时,除了理想化发电机的定子与转子,并对其磁链与电流正方向做出规定外,还常做出如下的假设:
发电机的3个定子绕组部分在结构上应完全相同并相差120°电角度,而且在气隙中,产生的磁动势呈正弦分布;转子部分磁路不饱和,并且结构与之完全对称。
1)通用电压方程
| $\begin{split} \left[\!\!\begin{array}{c}{u}_{d}\\ \begin{array}{c}{u}_{q}\\ \begin{array}{c}{u}_{0}\\ {u}_{f}\end{array}\\ 0\end{array}\\ 0\end{array}\!\!\right]=&\left[\!\!\begin{array}{cc}\begin{array}{ccc}r& 0& 0\\ 0& r& 0\\ 0& 0& r\end{array}& \begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\\ \begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}& \begin{array}{ccc}{r}_{f}& 0& 0\\ 0& {r}_{D}& 0\\ 0& 0& {r}_{Q}\end{array}\end{array}\!\!\right]\left[\!\!\begin{array}{c}-{i}_{d}\\ \begin{array}{c}-{i}_{q}\\ \begin{array}{c}-{i}_{0}\\ {i}_{f}\end{array}\\ {i}_{D}\end{array}\\ {i}_{Q}\end{array}\!\!\right]+\\ &\left[\begin{array}{c}-{\dot{\psi }}_{d}\\ \begin{array}{c}-{\dot{\psi }}_{q}\\ \begin{array}{c}-{\dot{\psi }}_{0}\\ {\dot{\psi }}_{f}\end{array}\\ {\dot{\psi }}_{D}\end{array}\\ {\dot{\psi }}_{Q}\end{array}\right]+\left[\begin{array}{c}-{\dot{\psi }}_{q}\\ \begin{array}{c}{\dot{\psi }}_{d}\\ \begin{array}{c}0\\ 0\end{array}\\ 0\end{array}\\ 0\end{array}\right] {\text{。}}\end{split}$ | (15) |
式中:
2)磁链方程
| $ \left[\!\!\!\!\begin{array}{c}\begin{array}{c}{\psi }_{d}\\ {\psi }_{q}\\ {\psi }_{0}\end{array}\\ \begin{array}{c}{\psi }_{f}\\ {\psi }_{D}\\ {\psi }_{Q}\end{array}\end{array}\!\!\!\!\right]=\left[\!\!\!\!\begin{array}{cc}\begin{array}{ccc}{x}_{d}& 0& 0\\ 0& {x}_{q}& 0\\ 0& 0& {x}_{0}\end{array}& \begin{array}{ccc}{x}_{ad}& {x}_{ad}& 0\\ 0& 0& {x}_{aq}\\ 0& 0& 0\end{array}\\ \begin{array}{ccc}{x}_{ad}& 0& 0\\ {x}_{ad}& 0& 0\\ 0& {x}_{aq}& 0\end{array}& \begin{array}{ccc}{x}_{f}& {x}_{ad}& 0\\ {x}_{ad}& {x}_{D}& 0\\ 0& 0& {x}_{Q}\end{array}\end{array}\!\!\!\!\right]\left[\!\!\!\!\!\!\begin{array}{c}-{i}_{d}\\ \begin{array}{c}-{i}_{q}\\ \begin{array}{c}-{i}_{0}\\ {i}_{f}\end{array}\\ {i}_{D}\end{array}\\ {i}_{Q}\end{array}\!\!\!\!\!\!\right] {\text{。}}$ | (16) |
式中:
3)转子运动方程
| $ {T}_{j}\frac{{\rm{d}}\omega }{{\rm{d}}t}={T}_{m}-{T}_{e} {\text{。}}$ | (17) |
式中:
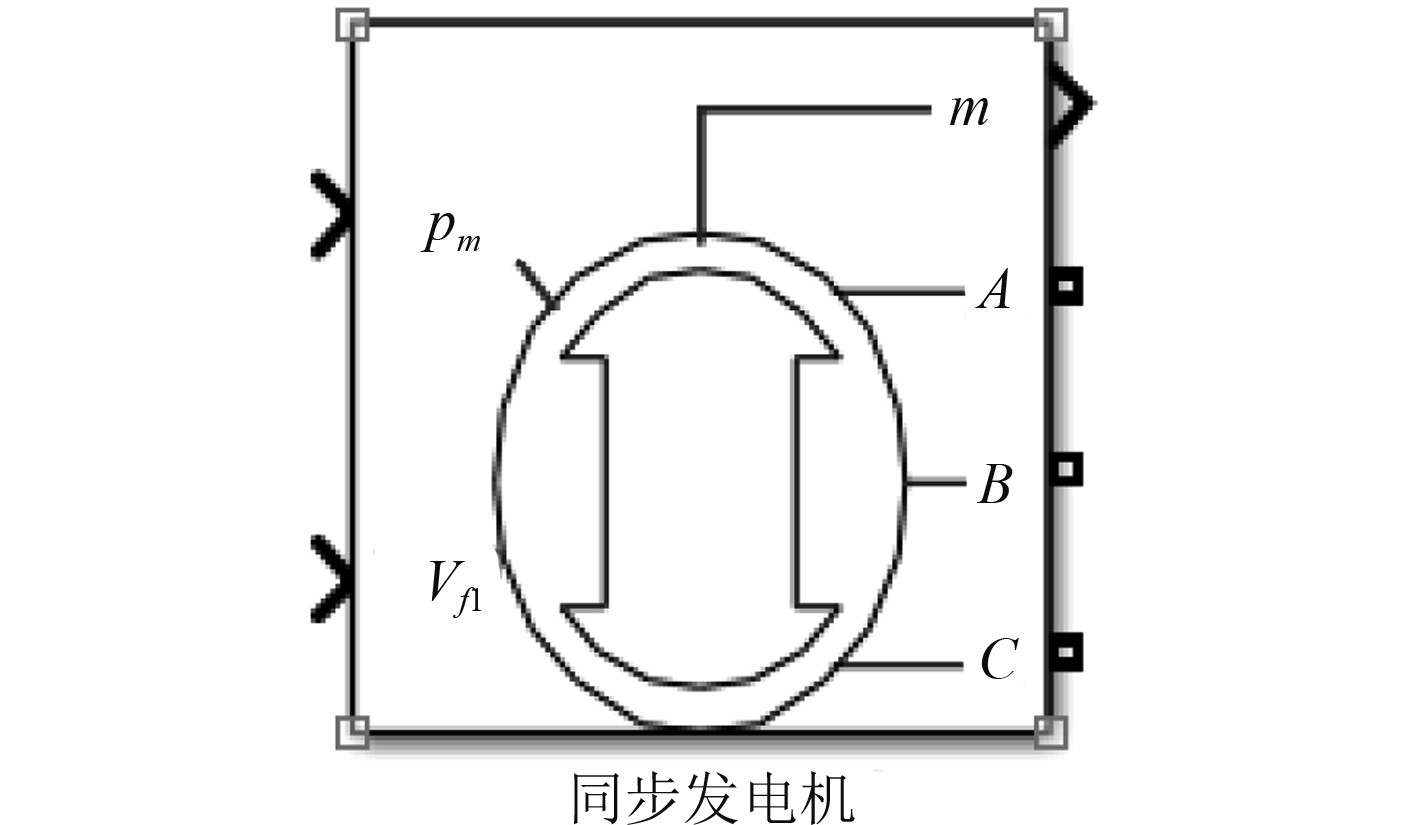
综合式(15)~式(17),即可得到发电机的总的数学模型,由于本次研究目的在于探究柴油发电机并车瞬间各物理量的情况,使用软件中自带的仿真模型即可,如图4所示。
|
图 4 同步发电机仿真模型 Fig. 4 Simulation model of synchronous generator |
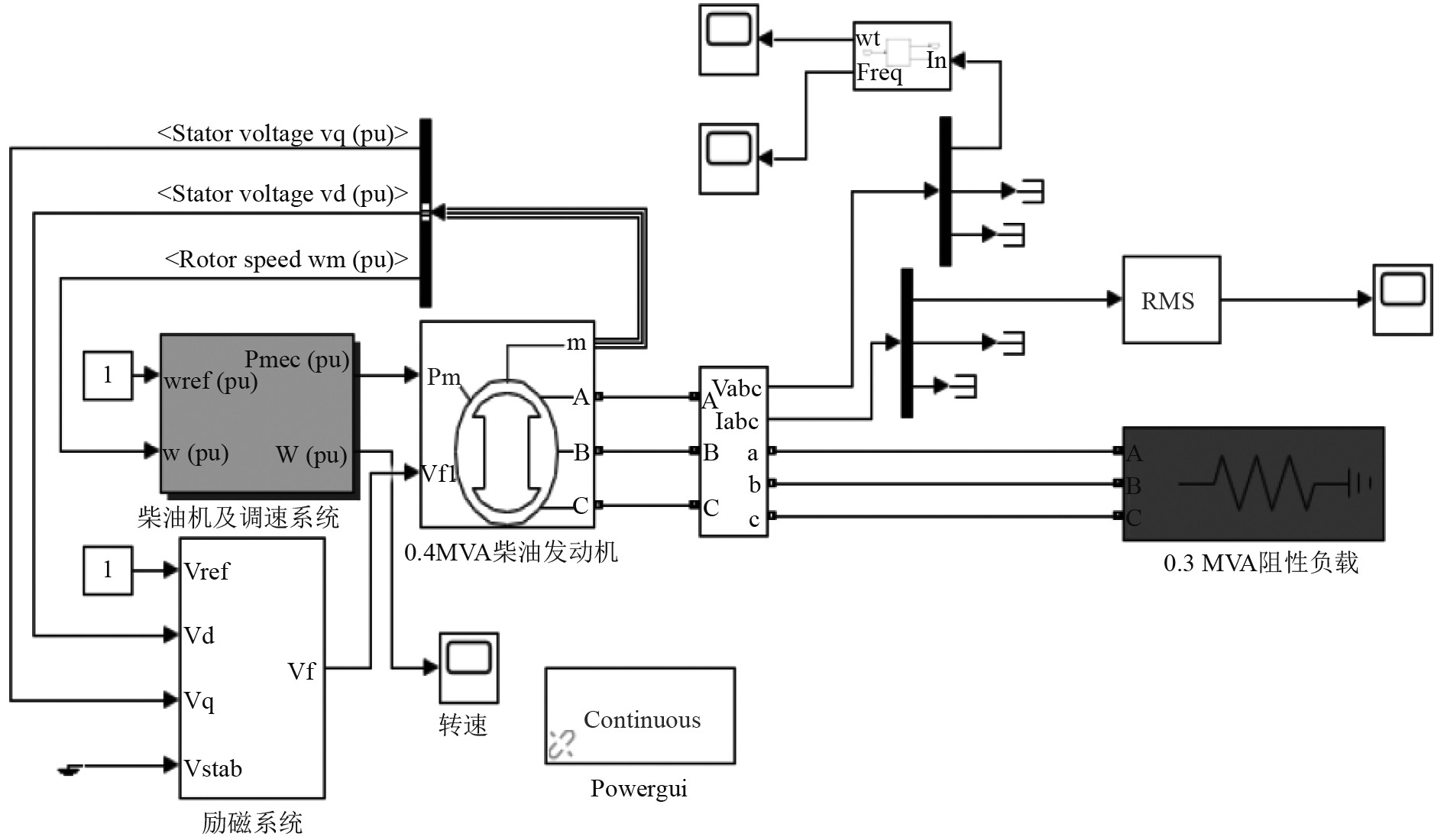
根据图2~图4的仿真模型,系统中,设置柴油发电机的容量为0.4 MW,额定频率定为60 Hz,额定线电压设置为480 V,并设置其负载属性为纯阻性负载,在Simulink中建立如图5所示的柴油发电机的仿真模型,点击运行,可以观察到如图6所示的柴油发电机端电压建立过程。
|
图 5 柴油发电机带载模型 Fig. 5 Diesel generator with load model |
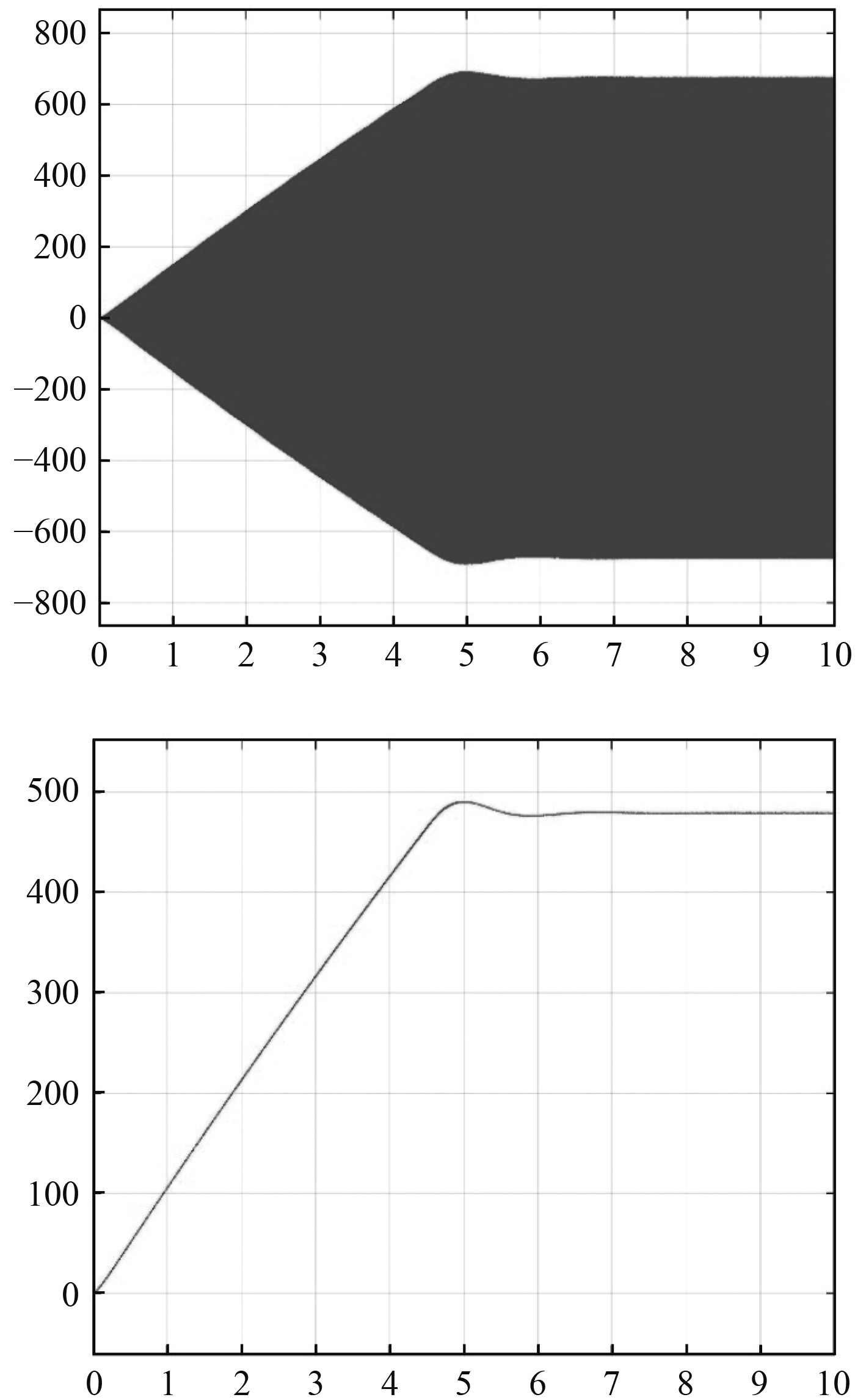
|
图 6 柴油发电机端电压建立过程 Fig. 6 Diesel generator terminal voltage establishment process |
在评估柴油发电机的性能与质量时,其启动性能常作为一个非常重要的指标。柴油发电机的启动过程,指的是利用启动装置使柴油机从静止开始转动,到柴油机通过压缩空气,燃烧机内柴油产生能量,使之达到稳定空载转速的过程。柴油机与发电机同轴连接,柴油机转动会带动发电机转子旋转,进而磁生电。所谓的柴油发电机端电压建立的过程,实际上就是柴油机从启动到稳定的过程。从图6可以看出,柴油发电机的端电压在5 s左右时达到最大值,并在6 s左右时,达到其稳定额定电压480 V。
图7为柴油发电机启动过程中转速和频率的变化过程。设定转速为1(标幺值),柴油发电机频率为60 Hz。可以看到,当柴油发电机启动后,由于柴油发电机带载运行,转速降低,频率升高,在4.5 s左右转速和频率均达到最低;接下来,为达到参考转速与频率并保持稳定,其调速系统调节转速,转速和频率开始上升,并在6 s左右上升至其转速最大值,此时调速系统继续对超调量进行调节,并使转速稳定于1(标幺值)、频率稳定于60 Hz,在7 s左右实现柴油机稳定运行,柴油发电机稳定输出电压,实现稳定带载运行。
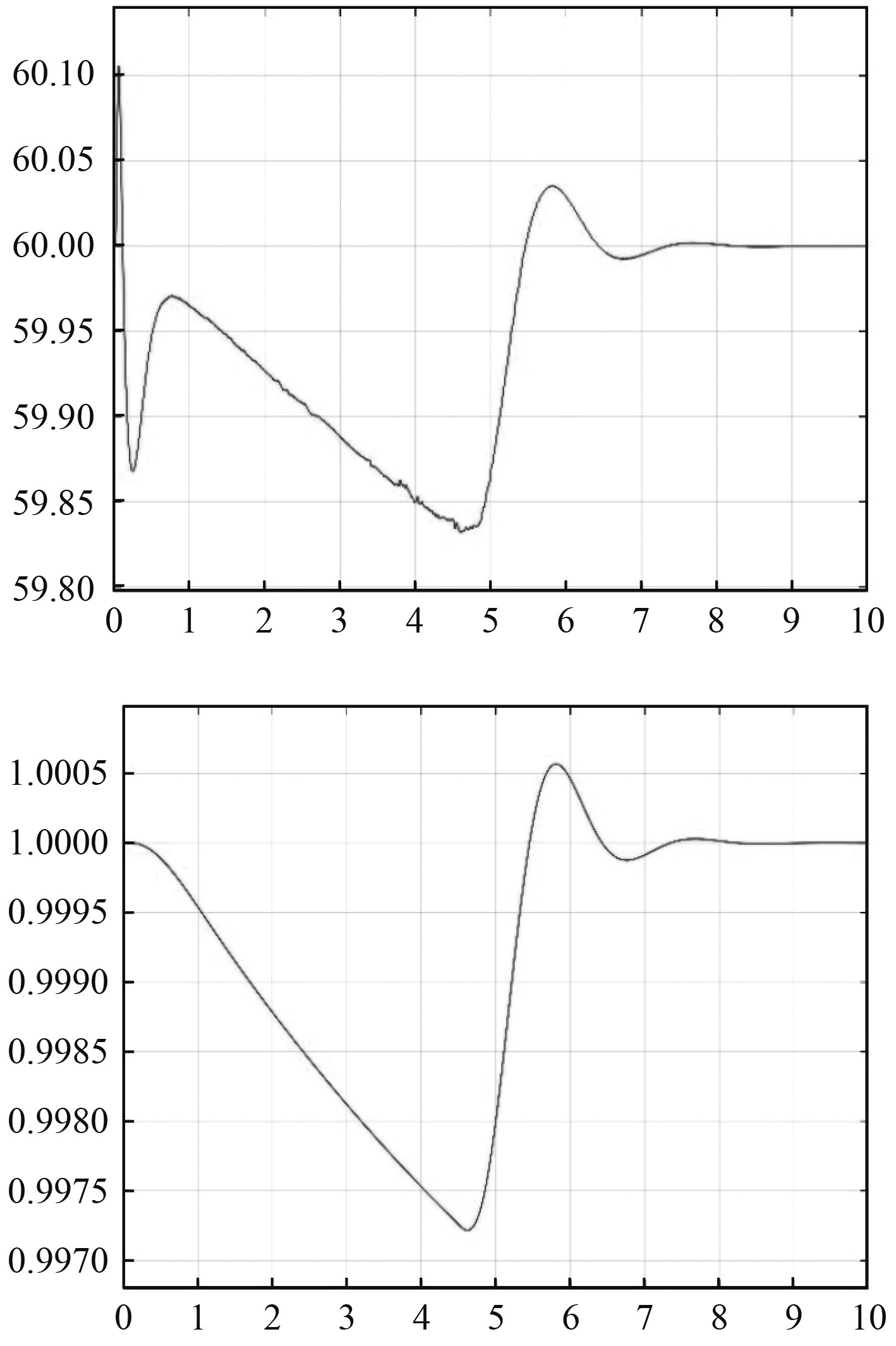
|
图 7 柴油发电机频率和转速变化过程 Fig. 7 Diesel generator frequency and speed variation process |
在船舶电站运行过程中,柴油发电机组的并联运行,常是船舶电网的主要运行模式,船舶柴油发电机组的并联运行的具体实现过程影响着船舶运行的稳定性。柴油发电机要实现并车过程,无论是相位幅值,还是频率与相序,都要相差不多或基本相等,图8为柴油发电机组并车的步骤。
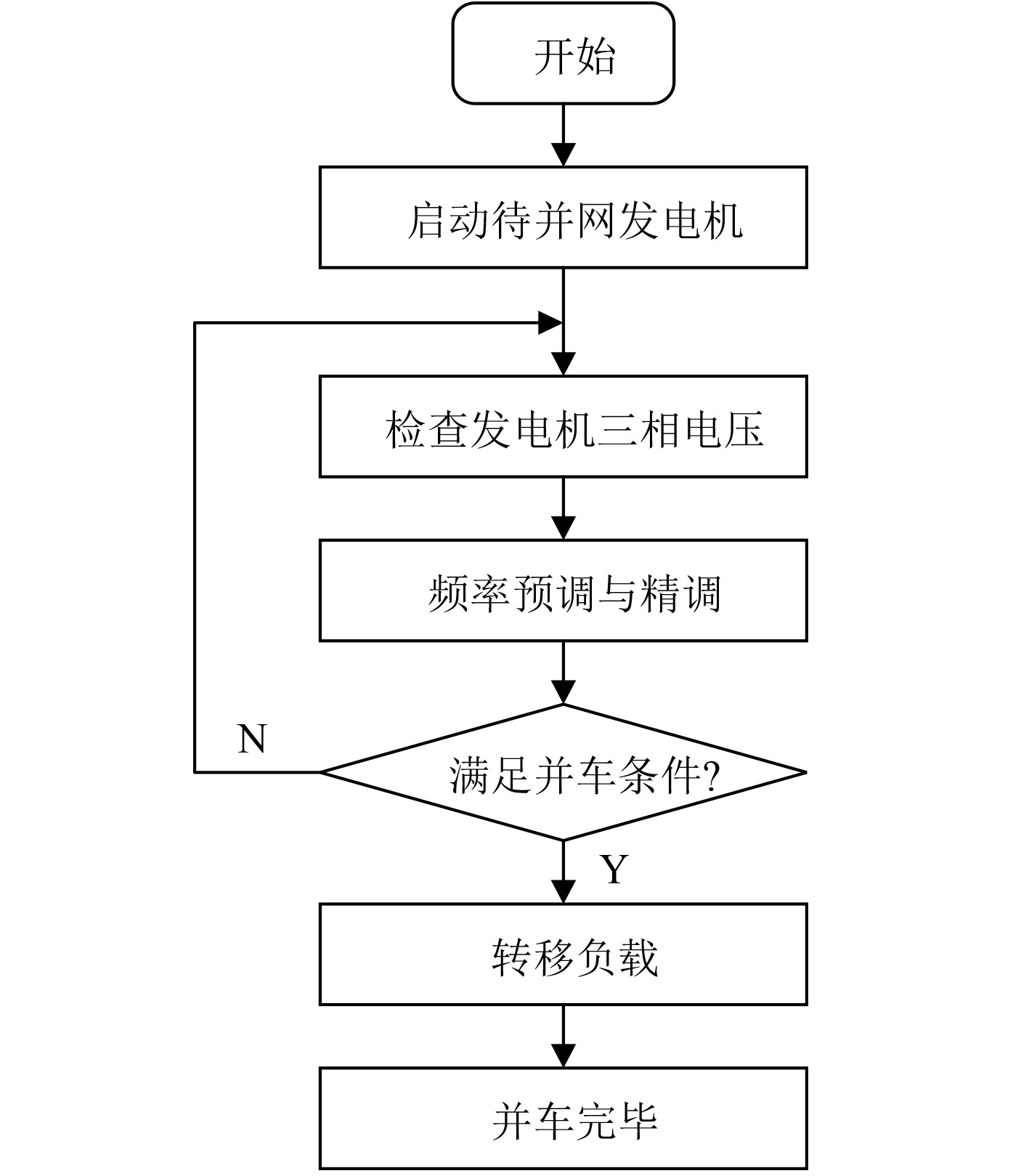
|
图 8 柴油发电机并车步骤 Fig. 8 Diesel generator and engine steps |
在柴油发电机并车时,按照图8所示步骤,就可以实现发电机的并网操作。而在现实生活中,由于人为动作或信息等各方面不可抗拒因素所造成的时间的延迟,并网操作常常不能够完全满足所有并车条件,如果在并车条件相差较大时,会对电网造成难以恢复的影响,如损毁电网中的保护设备、不能如期实现并网甚至是全船失电的危险。所以对于船舶柴油发电机并车的研究就显得十分有必要。
3 柴油发电机并车为了实现对于柴油发电机多相位差并网的分析与研究,需要建立能较为真实反映柴油发电机特性的仿真模型,这样才能实现对于柴油发电机并网特性的相关物理量分析。在模型中建立2台参数完全相同的柴油发电机,待并网柴油发电机的频率为60 Hz,频率偏差为0.2%,其余参数与在网发电机参数相同。设置并网相位差为20°~21°之间,并且采集并网相位差值与最大冲击电流值,可以得到如图9所示的仿真模型。
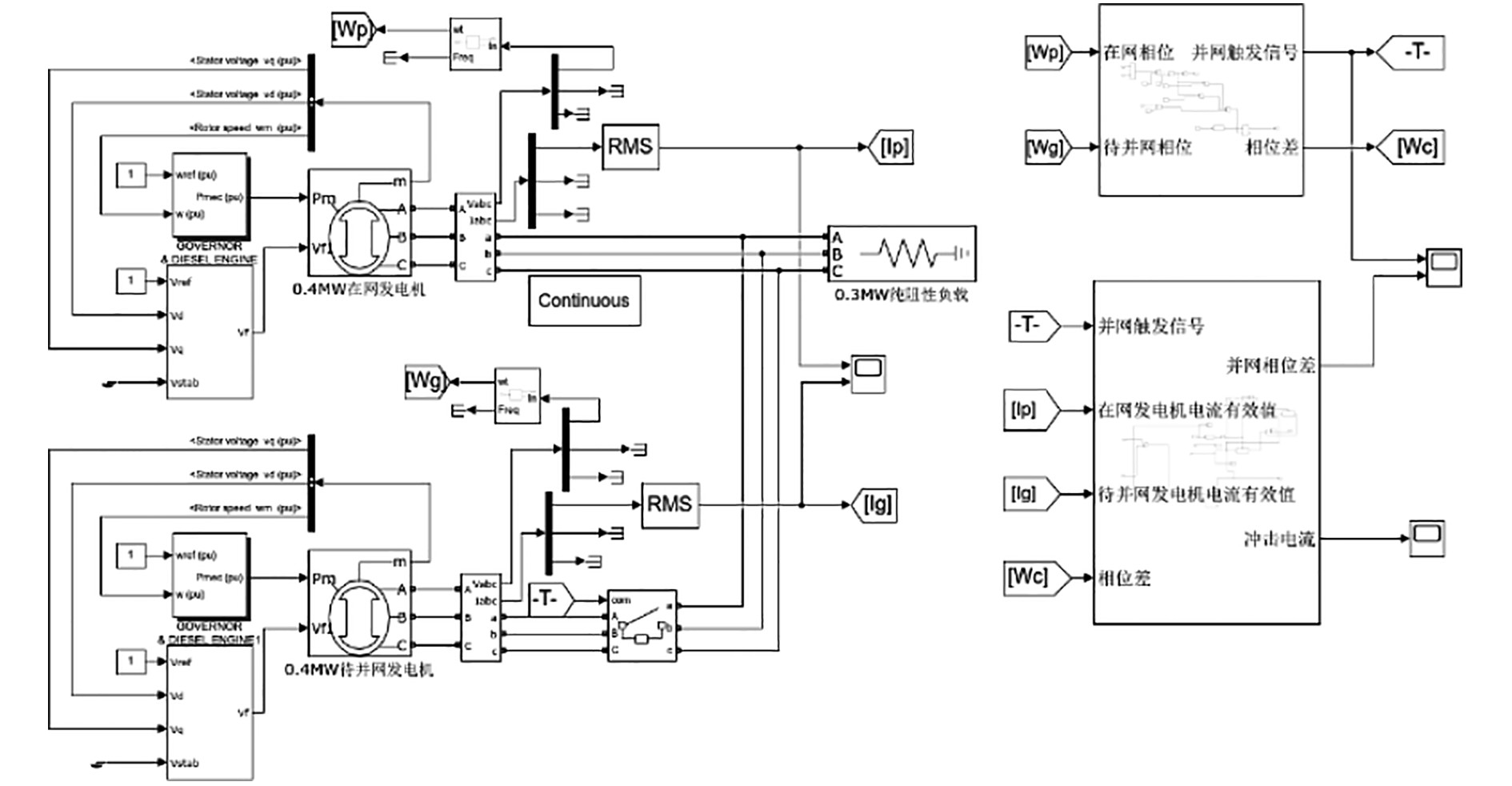
|
图 9 单相位差并网仿真模型 Fig. 9 Single phase differential grid-connection simulation model |
在仿真中,由于柴油发电机的启动需要时间,大概在7 s左右其频率才稳定于60 Hz,在网发电机实现稳定带载,所以设置并网时间大于等于7 s,设置仿真时长为20 s,在仿真中,提取电压、电流、频率等物理量信息,仿真结束后,得到仿真图形。
图10为柴油发电机的并网触发信号和并网前后相位差值图。在8.4 s左右时,检测到相位差值符合要求,并网控制模块发出并网信号,并网信号置1,三相断路器合闸并网,可以看到此时的合闸相位差值为21°。
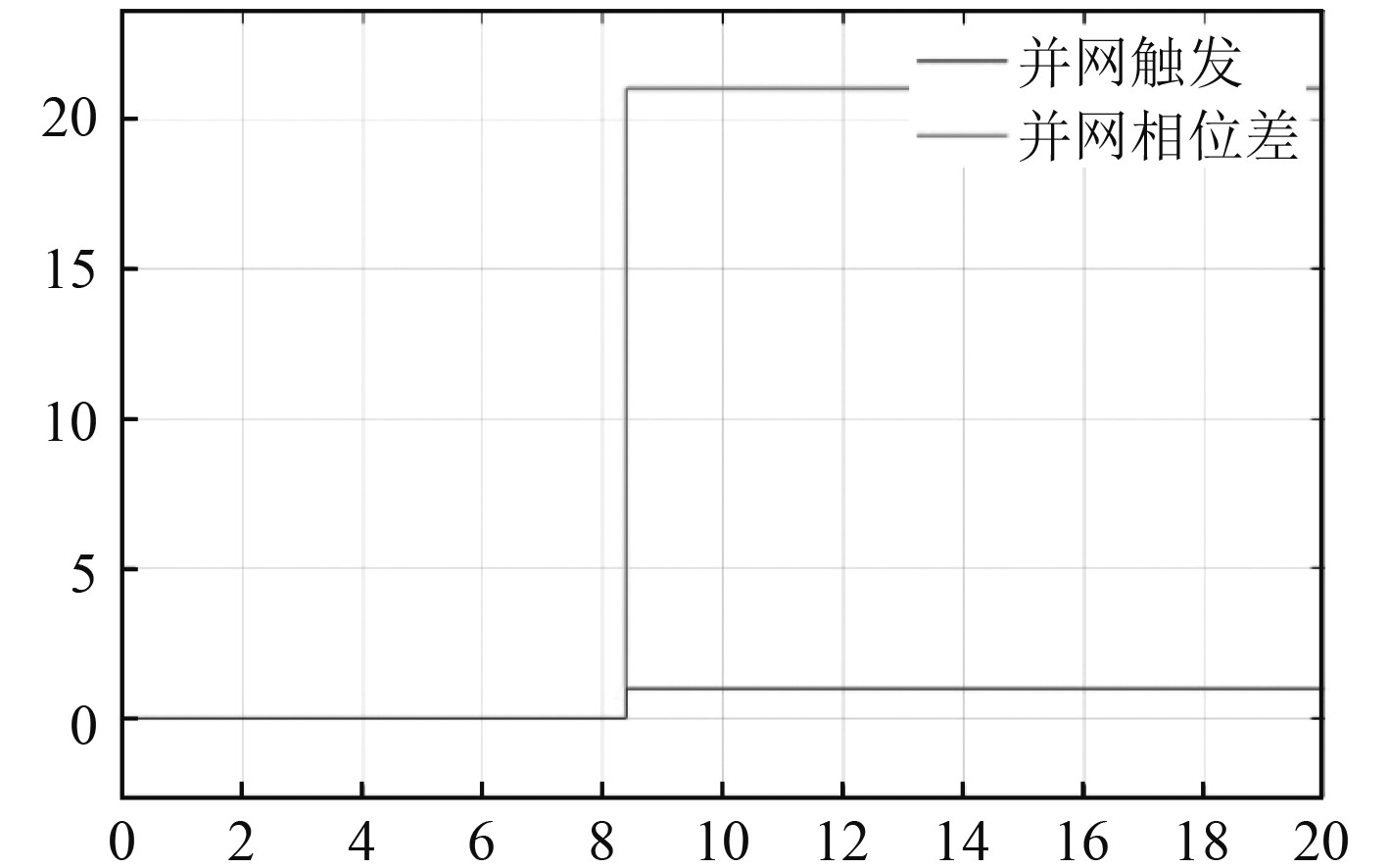
|
图 10 并网触发信号与并网相位差 Fig. 10 Grid-connected trigger signal and grid-connected phase difference |
图11和图12分别为在网与待并网发电机频率图和相位差值图。图11中,在8.4 s前,由于在网发电机与待并网发电机未实现并网,在网发电机频率由不稳定经过自身调节作用到达稳定;待并网发电机额定频率为60 Hz,频率偏差为0.2%,没有带任何负载,其频率经过调节稳定于60.3 Hz附近。图12中,在待并网发电机没有进行并网前,待并网发电机与在网发电机的相位差在
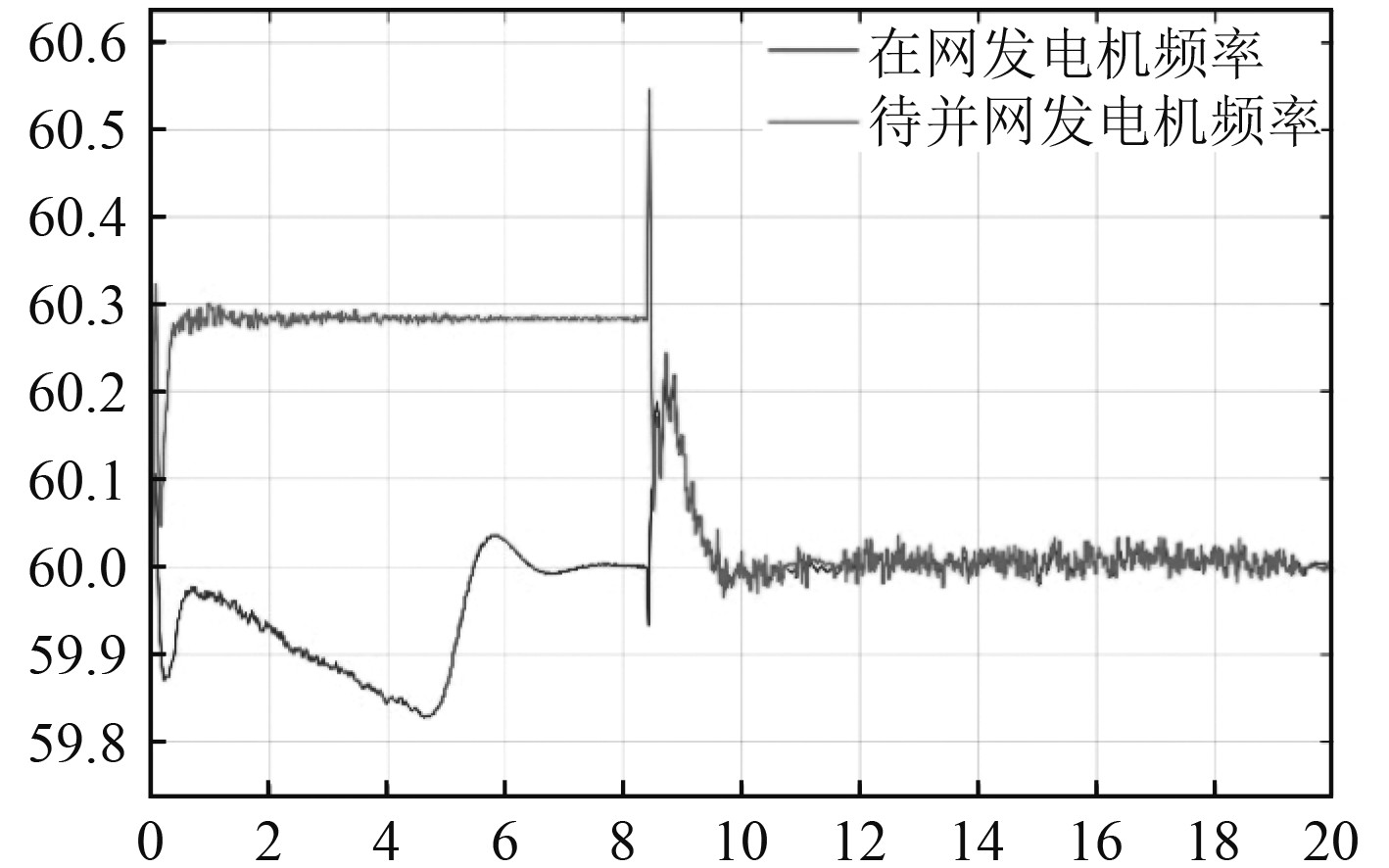
|
图 11 在网与待并网发电机频率 Fig. 11 On - grid and to - grid generator frequency |
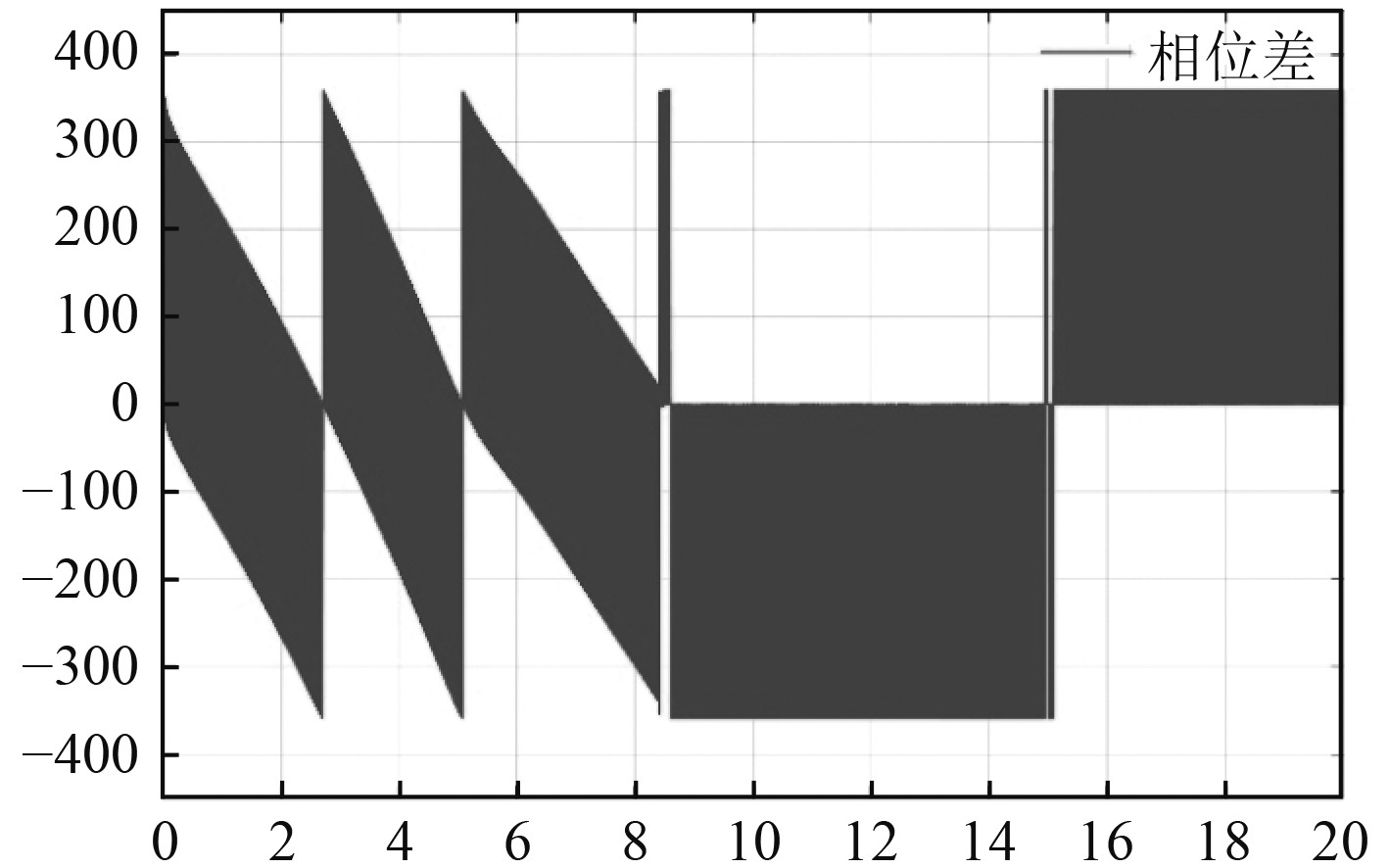
|
图 12 相位差 Fig. 12 Phase difference |
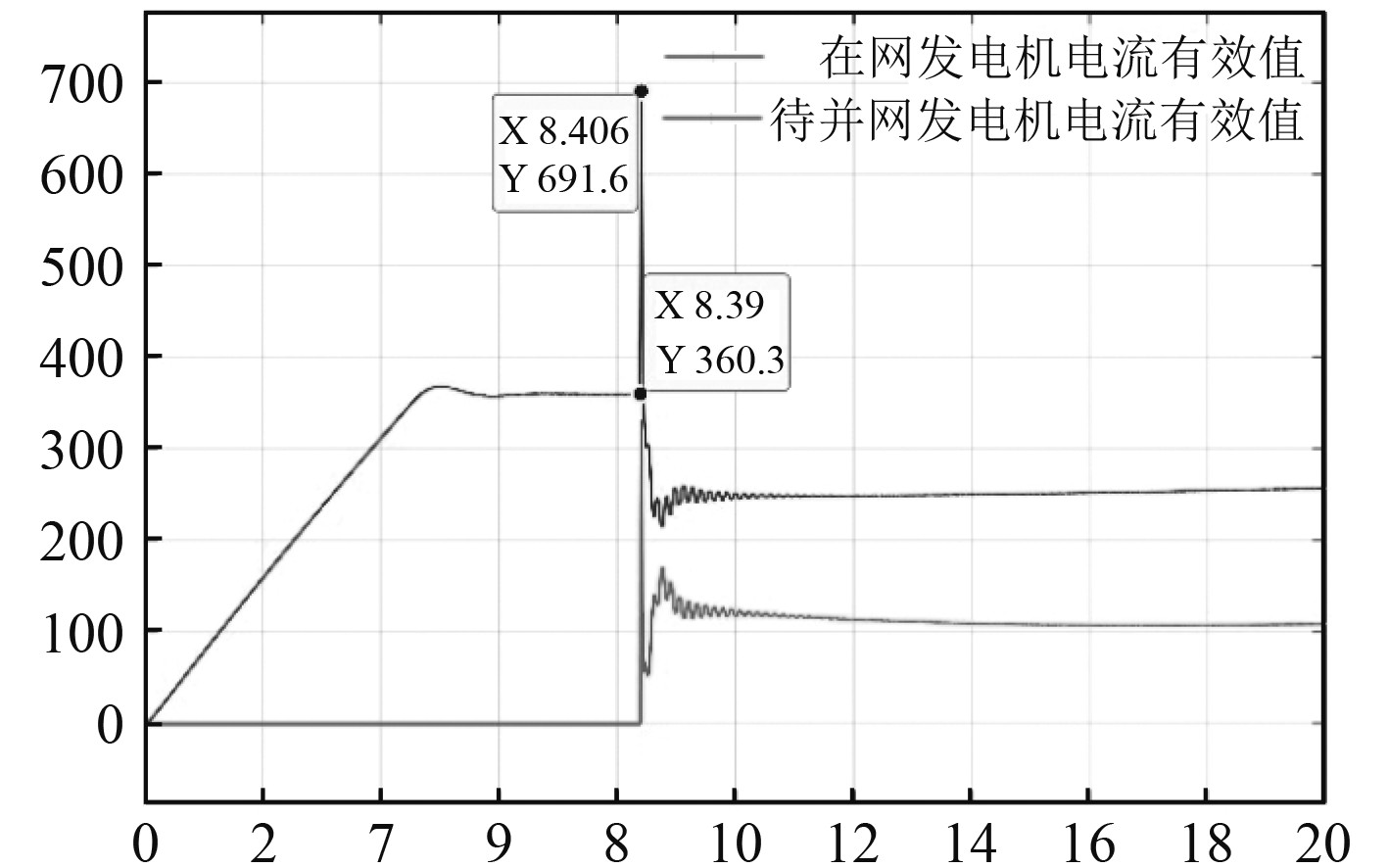
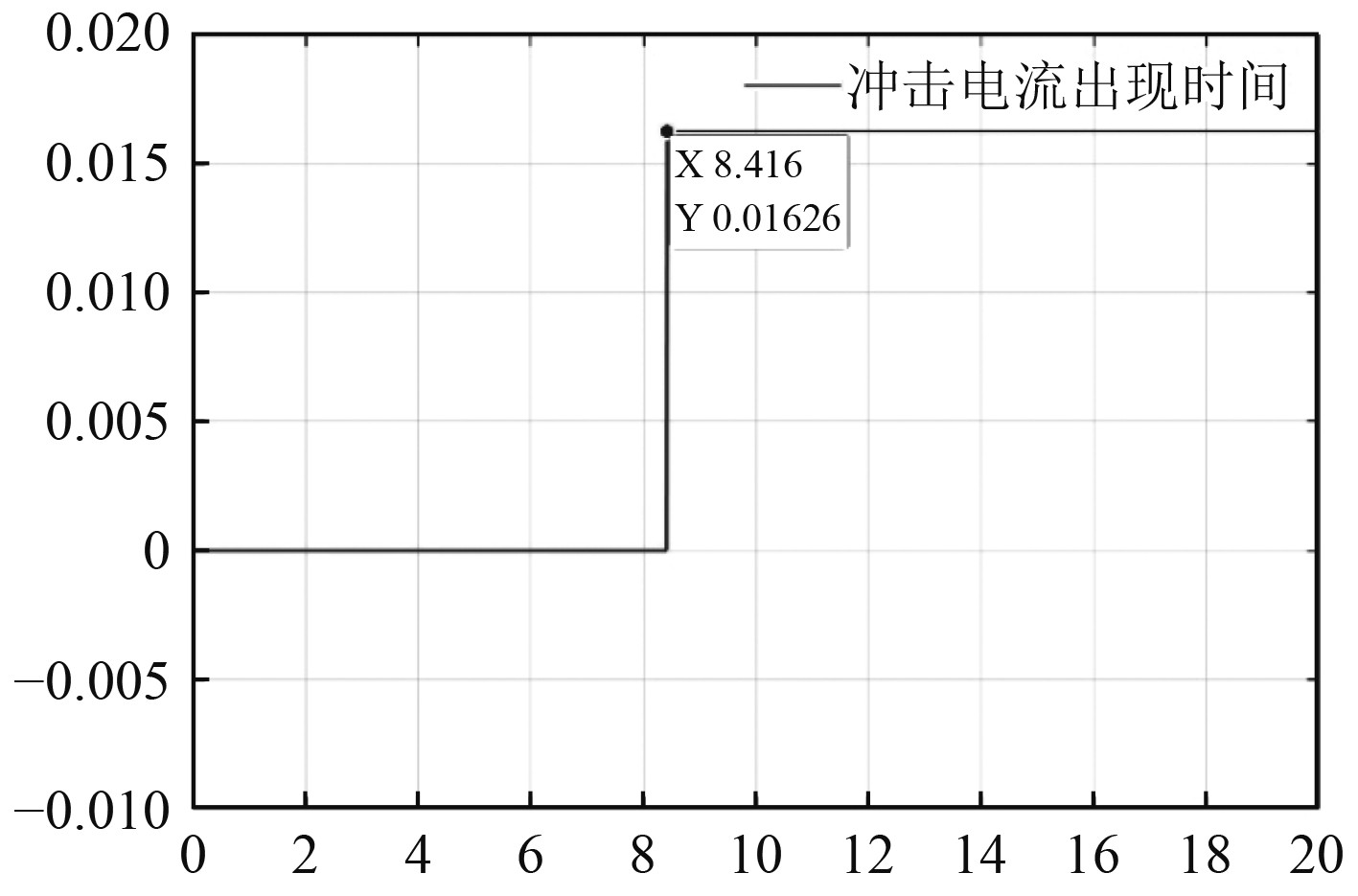
图13为在网与待并网发电机并网前后,其电流有效值的图,图14为待并网发电机合闸并网后冲击电流出现的时间图。在并网前,在网发电机处于经历端电压建立到稳定带载2个阶段。首先,由于在网发电机端电压未稳定,其电流值也缓慢上升,并大概在4.5 s后建立稳定端电压,实现稳定带载,其电流有效值也实现稳定;待并网发电机端电压与在网发电机的端电压相同,在4.5 s前均不稳定,由于待并网发电机未带任何负载,其电流值为0。并网后,待并网发电机与在网发电机电流急剧上升,从图13和图14可以看出,在0.01626 s时,电网电流达到最大值,本次冲击电流值为691.6 A,因此,在选择电力系统相关电力开关时,额定电流应小于最大冲击电流值,其延时保护开关动作时长也应略大于冲击电流出现的时长。在电流达到最大值后,待并网发电机实现并网操作,并与在网发电机共同带载。
|
图 13 在网与待并网发电机电流有效值 Fig. 13 The effective value of the generator current in the grid and to be connected |
|
图 14 合闸后冲击电流出现时间 Fig. 14 The occurrence time of shock current after closing |
经由以上分析,所建立的发电机并网实验模型能够较为准确描述发电机并网的操作过程,所建立的模型运行结果,符合发电机并网过程中的各个物理量的变化情况,能够真实反映发电机并网过程。所以在此模型基础上进一步完善,便可以继续探究其冲击电流值随并网相位差变化之间的规律,不仅可以在船舶电力系统设计中为相关电力开关的选型提供参考,指导船舶电站的设计,还可以在实船应用中,通过得到的函数规律以及根据船舶电力开关的实际参数,设定最大冲击电流,能够找到柴油发电机并联运行的最大并网相位差,以期在船舶电网运行过程中,减少柴油发电机并车对船舶电网的冲击,增强船舶运行的稳定性。
4 结 语在船舶电站的运行过程中,双机甚至是多机组并联运行,是船舶电站的必不可少的组成部分,一般也为船舶电站的主要运行模式。而整个船舶电站的容量大小,也基本取决于电站中可并联的柴油发电机组的数量。因此,柴油发电机并车过程能否顺利实现,就决定了船舶电站能否稳定运行。
本次研究所建立的柴油发电机并车的模型能够很好模拟实际柴油发电机并车的运行过程,并取得了与实际运行过程相符的结果。但是本文只对模型进行了单相位差并网的研究,为了进一步探究相位差与冲击电流之间的关系,还需要进一步完善模型,多次进行相关实验。
| [1] |
张文超. 大容量柴油发电机组多机=并车运行应用与设计研究[J]. 工程技术研究, 2019, 4(1): 187-189. |
| [2] |
王涌, 孙少帅. 柴油发电机机组并联应用[J]. 中国高新科技, 2018(13): 91-92. |
| [3] |
王文斌. 基于光柴储船舶微网功率分配策略研究[D]. 厦门: 集美大学, 2018.
|
| [4] |
CHUNHUA LI. Dynamic Modeling and Simulation of Parallel Operation of Ship Diesel Generators[A]. CRC Press/Balkema、南京理工大学、上海工程技术大学. Proceedings of the 2014 International Conference on Power and Energy(ICPE 2014)[C]// CRC Press/Balkema. 2014: 4.
|
| [5] |
李东辉. 船舶柴油发电机组的建模与运行仿真研究[D]. 大连: 大连海事大学, 2011.
|
| [6] |
张国强. 对柴油发电机并车的几点建议[J]. 教学与科技, 1982(1): 56-61. |
 2021, Vol. 43
2021, Vol. 43
