0 引　言

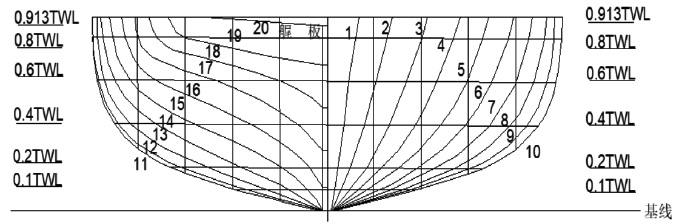
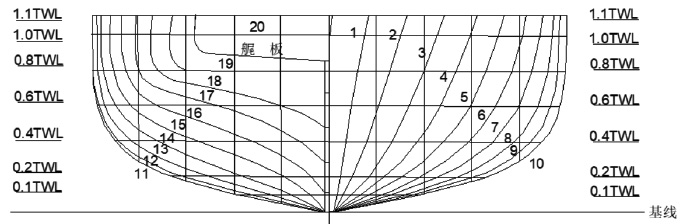
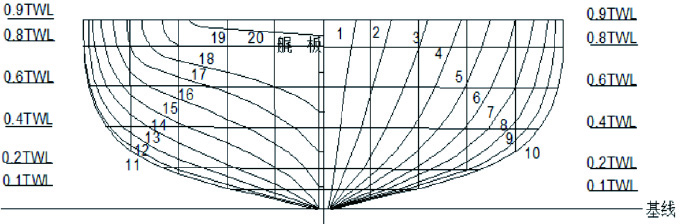
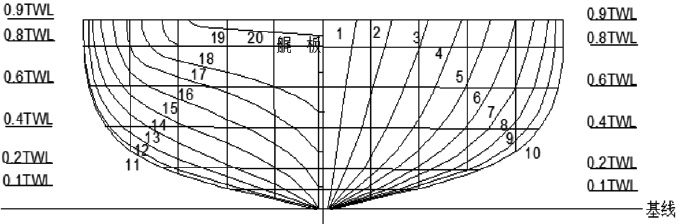
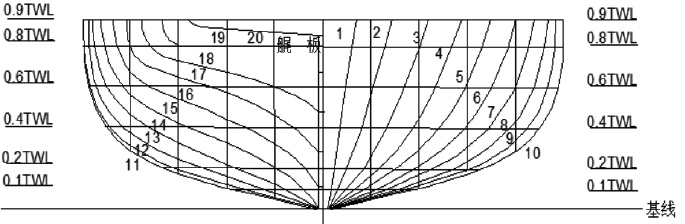
水面无人艇（USV）是无人系统中可自主完成任务的作业艇^[1]，与常规载人船相比，具备体积小、速度快、灵活机动性好等特点。此外，其搭载了自主作业系统，可在无人艇上安装雷达、水底探测声呐和机械作业系统等系列设备，能独立完成较为危险的任务。目前对水面无人艇的研究主要集中在各个功能模块设计（如能源、控制、避碰、跟踪等）、航行性能设计和无人艇协同技术^[2]研究等。Ashkan Makhsoos等^[3]对USV自带的光伏系统进行了优化设计。Andrzej Stateczny等^[4]研究了一种用于多任务的无人艇的通用自动控制和管理系统，对该系统进行了相关实艇的验证性试验。其中USV的航行性能设计分析对无人艇的综合作业能力有着不可忽视的作用。魏成柱等^[5]利用航模试验和CFD手段等研究了一种单体穿浪滑行无人艇艇型的水动力相关特性。刘曼^[6]针对一艘单体水面无人翼滑艇的性能（快速性、操纵性及耐波性）综合优化设计分析。罗富强等^[7]研究了一艘典型的高速水面无人艇在不同吃水和航行状态下的艇体阻力性能和相关的水动力运动特性。

目前对USV的性能综合优化设计分析主要集中在单体艇型，对于双体艇型的优化设计分析研究较少。王超等^[8]对一艘小水线面双体无人艇进行了参数化模型设计和快速性能得优化设计。对于普通双体无人艇的性能优化设计尚未见报道。而双体无人艇与单体无人艇相比，具有较宽敞的甲板面积有利于布置无人艇的相关设备或者铺设太阳能板以增强续航能力，同时相对较大的艇宽又保证了较好的稳性。且目前双体无人艇的主要作业区域为内河湖泊，因此可以忽略波浪的影响不考虑其耐波性。综合设计一艘性能优良的双体无人艇是一个较为复杂的问题，其综合性能与船型的主尺度和螺旋桨的各个参数以及电机的选型都密切相关。为了实现无人艇的综合性能最优，可以利用多学科优化的理念进行无人艇的综合性能设计^[9]，这样节省经济投入并可以缩短无人艇的设计周期且为后续双体无人艇的设计提供相关的参考。

本文选用1艘典型的不同吃水下的单体试验艇作为性能优化设计分析的基础，将艇型参数、螺旋桨参数和电机的转速和功率等参数作为双体无人艇的优化设计参数，综合双体无人艇的快速性和操纵性，对双体无人艇进行综合优化设计分析，并与常规双体船比较。首先在艇型参数上设置较宽的片体间距以保证较大的甲板面积和更大的艇型宽度，甲板上根据不同作战任务可布置相应的传感器和执行器或者铺展太阳能板以提高综合的续航能力^[10]。其次，双体无人艇的单个片体与普通的双体船的片体相比较为瘦长（长宽比约11∶1），可以保证更好的快速性。

1 综合优化数学模型 1.1 设计变量

本文选择了1艘典型不同吃水下的单体试验艇型（长宽比约11∶1）作为优化设计的基础艇型，其中单体试验艇型涉及到的船型参数：船长 $L$ 、船宽 $B$ 、方形系数 ${C_B}$ 、菱形系数 ${C_P}$ 、设计水线面系数 ${C_W}$ 、浮心纵向位置 ${L_{cp}}$ 等都是随着相对吃水 $T{\rm{/}}T_{wl}$ 而变化，其中 $T_{wl}$ 为标准吃水等于0.1054 m。

将上述参数用响应面拟合出关于 $T{\rm{/}}T_{wl}$ 的拟合公式作为优化设计的参数，如下式：

$\begin{split} L =& 3.144\;565\;711 - 0.403\;106\;365T/T_{wl} +\\ &0.447\;398\;89{\left( {T/T_{wl}} \right)^2} - 0.142\;684\;434{\left( {T/T_{wl}} \right)^3} , \end{split} $

(1)

$\begin{split} &B/T = 8.055\;178\;035 - 8.809\;533\;07T/T_{wl} + \\ &4.053\;7926\;17{\left( {T/TwlT_{wl}} \right)^2} - 0.644\;994\;856{\left( {T/T_{wl}} \right)^3}, \end{split} $

(2)

$\begin{split} Cb \!= &0.440\;050\;747 - 0.469\;490\;145T/T_{wl} + \\ &0.864\;235\;511{\left( {T/T_{wl}} \right)^2} \!-\! 0.338\;622\;296{\left( {T/T_{wl}} \right)^3} , \end{split} $

(3)

$\begin{split} Cp \!= & - 0.624\;919\;23 + 3.001\;109\;151T/T_{wl} - \\ &2.467\;768\;024{\left( {T/T_{wl}} \right)^2} \!+\! 0.700\;294\;893{\left( {T/T_{wl}} \right)^3} , \end{split} $

(4)

$\begin{split} Cw \!= &1.091\;440\;615 - 1.216\;513\;212T/T_{wl} + \\ &1.359\;367\;401{\left( {T/T_{wl}} \right)^2} \!-\! 0.478\;577\;909{\left( {T/T_{wl}}\right)^3} , \end{split} $

(5)

$\begin{split} & lcb =49.215\;598\;35 - 130.609\;468\;4T/T_{wl} +\\ & 112.156\;081\;5{\left( {T/T_{wl}} \right)^2} - 32.948\;487\;04{\left( {T/T_{wl}} \right)^3}\text{。} \end{split} $

(6)

本文的设计变量选择9个相关的参数，用一个向量X表示：

${{X}} = \{ T,{D_P},{A_{eo}},{P_{DP}},N,{V_S},k/D,d/D,C\} \text{。}$

其中：吃水d，螺旋桨参数（直径 ${K_T}$ 、盘面比 ${K_Q}$ 、螺距比 ${V_S}$ 、转速 $\operatorname{kn} $ ），设计航速 $\omega $ ，重心垂向位置与型深比k/D，吃水与型深比d/D，片体内间距C。相关的变量单位：d， ${K_T}$ ，C，m；N为r/min；V_S为kn；其余为无量纲单位。

1.2 目标函数

本文高速双体无人艇将衡量自身的快速性、操纵性作为子目标函数，以2个指数幂乘积的形式构造总目标函数：

$ f\left(x\right)={f}_{1}(x)^{\alpha 1}{f}_{2}(x)^{\alpha 2}{\text{。}} $

(7)

式中： ${f_1}\left( x \right)$ 为快速性目标函数； ${f_2}\left( x \right)$ 为操纵性目标函数； ${\alpha _1}$ 为快速性权重； ${\alpha _2}$ 为操纵性权重。需满足 $ {\alpha }_{1}\times $ $ {\alpha }_{2}=1，{\alpha }_{1}>0,{\alpha }_{2}>0$ ， ${f_1}\left( x \right)$ ， ${f_2}\left( x \right)$ 都大于1。当 ${f_1}\left( x \right)$ ， ${f_2}\left( x \right)$ 不满足大于1时对其进行适当调整使其大于1。

1）快速性的子目标函数

${f_1}\left( x \right) = \frac{{V_{\rm{s}}^3{\Delta ^{2/3}}}}{{{P_S}}} = \frac{{{V_{\rm{s}}}^{\rm{2}}{\Delta ^{2/3}}({\eta _0}{\eta _H}{\eta _R}{\eta _S})}}{{{R_t}*0.{\rm{6994}}*{{10}^{ - 3}}}}\text{。}$

(8)

其中 ${R_t}$ 分为 ${R_f}$ （摩擦阻力）和 ${R_r}$ （剩余阻力）。当片体中心相对距离和片体宽度之比大于2时，片体间的相互干扰较小。本文双体无人艇的相对中心距离与片体宽度之比约为2，所以可忽略片体间的互相干扰，将整个艇体受到的总阻力看成2个孤立片体受到的总阻力。

$ {R}_{t}={R}_{f}+{R}_{r}=0.5\rho {V}^{2}S({C}_{f}+{C}_{r}), $

(9)

摩擦阻力系数 ${C_f}$ 由桑海公式进行估算，当 $Re$ 在 ${10^6} \sim {10^9}$ 范围内:

${C_f} = \frac{{0.463\;1}}{{{{\left( {\lg {Re} } \right)}^{2.6}}}},$

(10)

式中， $Re $ 为雷诺数：

$Re = \frac{{\rho Vd}}{\upsilon }\text{。}$

(11)

剩余阻力系数 ${C_r}$ 根据 ${C_r}$ 图谱，得到以下拟合公式：

$\begin{split} C{\rm{r}} = &{\rm{ - 0}}{\rm{.000\;294\;696 - 0}}{\rm{.012\;108\;108}} \times F{\rm{r}} + {\rm{0}}{\rm{.078\;535\;171}} \times \\ & Dm{\rm{ - 0}}{\rm{.099\;484\;518}} \times F{\rm{r}} \times Dm + {\rm{0}}{\rm{.052\;851\;917}} \times \\ & F{\rm{r}}{{\rm{ }}^2}{\rm{ - 1}}{\rm{.319\;000\;495}} \times D{m^2}{\rm{ - 0}}{\rm{.102\;724\;362}} \times F{{\rm{r}}^3} + \\ & {\rm{11}}{\rm{.237\;831\;93}} \times D{m^3} + {\rm{0}}{\rm{.755\;080\;057}} \times F{{\rm{r}}^2} \times \\ & Dm{\rm{ - 1}}{\rm{.034\;831\;591}} \times D{m^2} \times F{\rm{r }}(0.28 > F{\rm{r}} > 0.2) , \\[-10pt] \end{split} $

(12)

$\begin{split} Cr =& - 0.007\;124\;378 + 0.099\;635\;29 \times Fr - 0.264\;138\;264 \times\\ &Dm + 1.243\;282\;073 \times Fr \times Dm - 0.393\;238\;162 \times\\ &F{r^2} + 1.994\;633\;037 \times D{m^2} + 1.192\;129\;892 \times F{r^3} + \\ &45.405\;209\;27 \times D{m^3} - 1.815\;249\;563 \times F{r^2} \times Dm -\\ & 1.062\;776\;263 \times D{m^2} \times Fr (0.34 > Fr > 0.28) , \\[-10pt] \end{split} $

(13)

$\begin{split} C{\rm{r}} =& {\rm{0}}{\rm{.049\;741\;513 - 0}}{\rm{.453\;878\;092}} \times F{\rm{r}} + {\rm{0}}{\rm{.700\;077\;477}} \times \\ &Dm{\rm{ - 3}}{\rm{.184\;247\;179}} \times F{\rm{r}} \times Dm + {\rm{1}}{\rm{.305\;854\;866}} \times\\ & F{{\rm{r}}^2}{\rm{ - 2}}{\rm{.521\;833\;116}} \times D{m^2}{\rm{ - 1}}{\rm{.215\;240\;053}} \times F{{\rm{r}}^3} + \\ & {\rm{4}}{\rm{.414\;980\;022}} \times D{m^3} + {\rm{4}}{\rm{.006\;419\;33}} \times F{{\rm{r}}^2} \times Dm{\rm{ }} +\\ & {\rm{5}}{\rm{.262\;115\;81}} \times D{m^2} \times F{\rm{r }}(0.42 > F{\rm{r > 0}}{\rm{.34)}} , \\[-10pt] \end{split} $

(14)

$\begin{split} C{\rm{r}} = &{\rm{ - 0}}{\rm{.045\;217\;449}} + {\rm{0}}{\rm{.299\;406\;841}} \times F{\rm{r - 0}}{\rm{.569\;693\;551}} \times \\ &Dm + {\rm{2}}{\rm{.327\;258\;809}} \times F{\rm{r}} \times Dm {\rm{ - 0}}{\rm{.651\;611\;436}} \times \\ &F{{\rm{r}}^2} + {\rm{1}}{\rm{.670\;189\;212}} \times D{m^2} + {\rm{0}}{\rm{.457\;723\;517}} \times F{{\rm{r}}^3} + \\ & {\rm{6}}{\rm{.868\;590\;52}} \times D{m^3} {\rm{ - 1}}{\rm{.903\;919\;5}} \times F{{\rm{r}}^2} \times Dm-\\ & {\rm{5.203\;128\;982}} \times D{m^2} \times F{\rm{r (0}}{\rm{.5 > }}F{\rm{r}} > 0.42{\rm{)}}, \\[-10pt] \end{split} $

(15)

$\begin{split} Cr =& - 0.042\;018\;205 + 0.211\;846\;112 \times Fr + 0.184\;825\;451 \times \\ &Dm + 0.160\;413\;531 \times Fr \times Dm - 0.380\;410\;099 \times\\ & F{r^2} - 2.624\;196\;952 \times D{m^2} + 0.230\;921\;484 \times F{r^3} +\\ & 19.471\;448\;06 \times D{m^3} - 0.283\;424\;627 \times F{r^2} \times Dm-\\ & 0.019\;949\;644 \times D{m^2} \times Fr\left( {0.6 > Fr > 0.5} \right), \\[-10pt] \end{split} $

(16)

$\begin{split} Cr =& 0.010\;587\;786 - 0.054\;000\;506 \times Fr + 0.132\;933\;056 \times \\ & Dm + 0.047\;247\;187 \times Fr \times Dm + 0.080\;870\;888 \times \\ & F{r^2} - 1.104\;646\;963 \times D{m^2} - 0.0413\;373\;6 \times F{r^3} +\\ & 15.824\;340\;89 \times D{m^3} - 0.016\;422\;749 \times F{r^2} \times Dm -\\ & 1.692\;590\;379 \times D{m^2} \times Fr \left( {0.7 > Fr > 0.{\rm{6}}} \right) {\text{。}}\\[-10pt] \end{split} $

(17)

湿表面积S由试验数据拟合得到：

$\begin{split} S =& 2.204\;226\;417 - 4.568\;614\;798T/T_{wl} + \\ &4.779\;776\;869{\left( {T/T_{wl}} \right)^2}- 1.449\;584\;583{\left( {T/T_{wl}} \right)^3} \text{。} \end{split} $

(18)

2）操纵性子目标函数

$C = {Y_v}{N_r} - {N_v}({Y_r} - m{u_1}){\text{。}}$

(19)

式中：C为稳定性衡准数，若 $C > 0$ 时，表示船艇具有直线稳定性， $C \leqslant 0$ ，则不具有直线稳定性。当 $C > 0$ ，式（19）可整理为^[11] $\dfrac{{{N_r}}}{{({Y_r} - m{u_1})}} - \dfrac{{{N_v}}}{{{Y_v}}} > 0$ ，无因次化后可得到

${f_2}(x) = \frac{{{N_r}^\prime }}{{({{Y'}_r} - m')}} - \frac{{{N_v}^\prime }}{{{Y_v}^\prime }},$

(20)

式中， ${Y'_v},{Y'_r},{N'_v},{N'_r}$ 为无因次速度流体动力导数， $m'$ 为无因次船体质量：

$m' = m/(0.5\rho {L^3}) = \rho {C_B}LBT/(0.5\rho {L^3}) = 2{C_B}\frac{B}{L}\frac{T}{L},$

(21)

其中的无因次系数 ${Y'_v},{Y'_r},{N'_v},{N'_r}$ 为由ClarkeD整理得到的回归公式^[11]：

$\left\{ \begin{array}{l} ({{Y'}_v}) = - \text{π} {(T/L)^2}(1 + 0.4{C_B}B/T) , \\ ({{Y'}_r}) = - \text{π} {(T/L)^2}( - 0.5 + 2.2B/L - 0.08B/T), \\ ({{N'}_v}) = - \text{π} {(T/L)^2}(0.5 + {\rm{2}}.4T/L) , \\ ({{N'}_r}) = - \text{π} {(T/L)^2}(0.25 + 0.039B/T - 0.56B/L)\text{。} \\ \end{array} \right.$

(22)

1.3 约束条件

1）等式约束

静水浮性约束

$ \Delta = 2\rho LBT{C_B}, $

(23)

推力和阻力平衡约束

$ {N_p}{K_T}\rho {N^2}D_P^4(1 - t) = {R_t}, $

(24)

转矩平衡约束

$ \frac{{{\eta _R}{\eta _s}{P_s}}}{{2\text{π} N}} = {K_Q}\rho {N^2}D_p^5\text{。} $

(25)

2）不等式约束

需满足螺旋桨空泡要求，按照Keller给出的公式：

$(1.3 + 0.3Z){T_e}/(({P_0} - {P_V})D_P^2) + K - ({A_E}/{A_0}) \leqslant 0,$

(26)

满足稳性规范要求，即正浮初稳性高需大于0.7 m：

$GM > 0.{\rm{7}}\text{。}$

(27)

2 优化方法及计算策略 2.1 优化方法

本文双体高速无人艇的综合优化数学模型为非线性、高耦合性，在设计变量的限定范围内可能存在着多个局部最优值。对于这类优化模型，常利用现代优化算法对其进行数值求解。

遗传算法^[12]作为一种现代优化算法，具有高效的概率搜索能力，且适用于许多数学模型较为复杂的实际应用之中。该算法利用适应度（Fitness）作为衡量染色体在进化过程中的能否取得繁衍下一代的机会或者保持自身染色体（精英保留策略^[13]）直接进入到下一代之中的可能性。

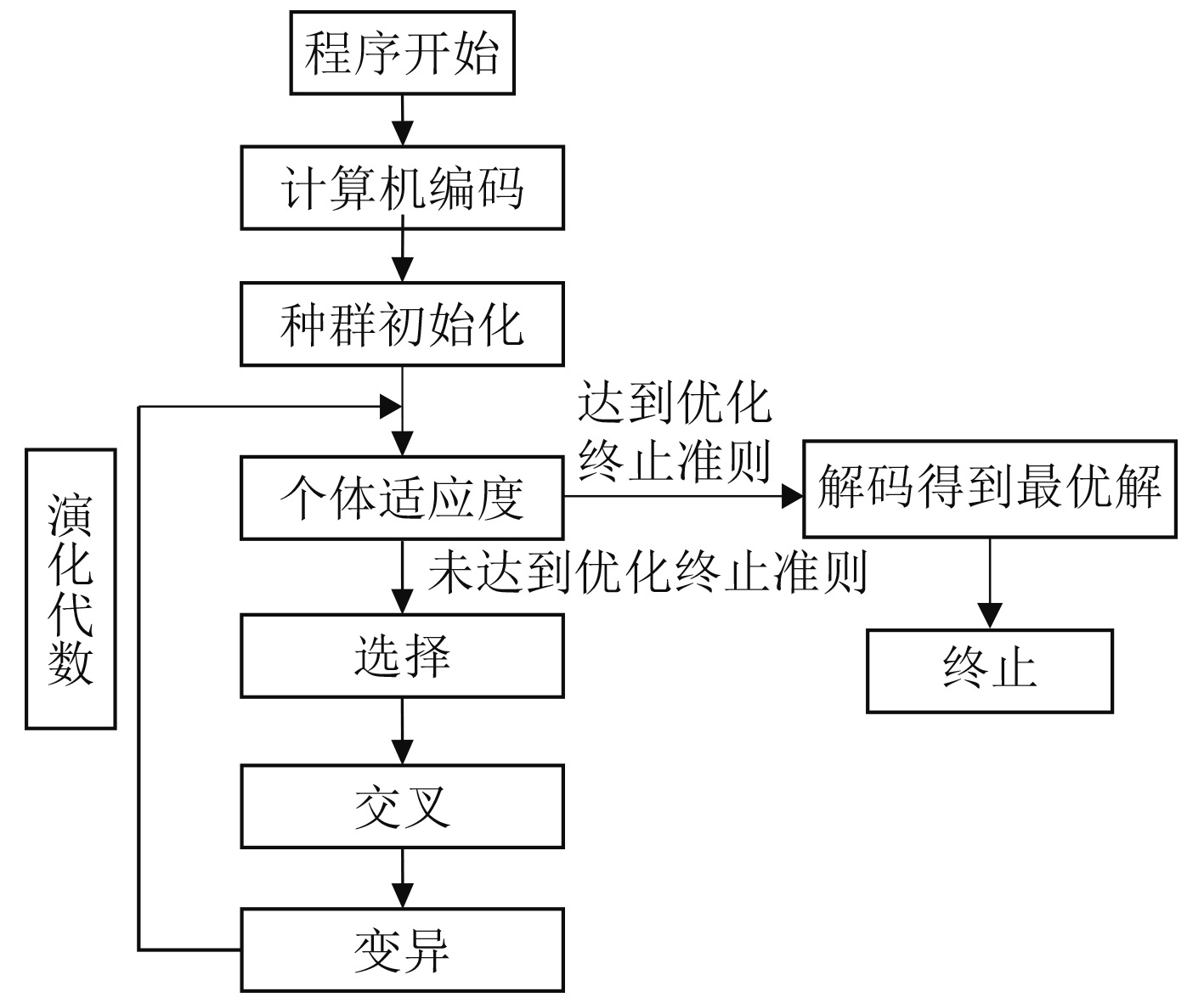
种群的进化过程中，两代之间的关系定义为父代和子代的关系，子代由父代选择（selection）、交叉（Crossover）、变异（Mutation）而产生。标准遗传算法计算流程如图1所示。

标准的遗传算法通常存在局部优化算法的早熟机制和算法对设定参数的敏感性，而且往往在后期的寻优搜索变得很低。因而有较多关于遗传算法的改进研究，这些研究主要涉及到个体参数编码、初始种群规模数、构造的适应度函数，遗传算子（选择、交叉和变异）改进、约束条件处理方式等。改进的措施主要针对以上要素进行改进和组合，目的是为了提高算法的收敛速度并且避免计算的最终结果陷入到局部最优解。

利用一种成长机制的改进遗传算法，其优化效果优于普通的轮盘机制遗传算法^[14]，其“成长”的本质在于：将下一代产生的种群中适应度排名处于尾端的个体淘汰，被淘汰的个体数量由父代的最好的几个个体的附近的领域随机产生。实现该改进策略，需要确定3个参数：

1）载波概率，父代的邻域范围与整个寻优的区域。

2）进化权重，下一代被淘汰的总数量与种群规模的比值。

3）遗传因子，选择父代中的精英（适应度函数较大）数量与种群规模的比值。

这种改进的方式类似于“精英保留策略”和“爆炸算子”^[13]。“精英保留策略”能够防止最优解在进化过程中受到破坏。“爆炸算子”是在最优解的局部进行搜寻，根据距离最优解值的靠近程度产生不同比例的搜寻数量，简单来说，距离最优解越近的搜寻到的数量越多。

使用成长机制的改进遗传算法可以使得群体的进化方向朝着最优化的方向更新变化，其本质是在进行了交叉变异之后，在新的种群中再次进行筛选（从父代中找到替代子代中的较差的解）。同时载波概率上可以选择载波概率随着进化代数的增加而逐渐减小，如0.001～0.01，这样的目的是为了解决最优解逐渐收敛。

采用这样的改进算法可能造成的不足是，最后的结果只局限在最优解的领域范围内而在一开始就被淘汰的适应度较小的个体中无法获取足够多的有用信息，陷入到局部最优值之中。为了解决这一改进带来的缺点，可以适当调高变异算子的概率而提高跳出局部最优值的概率。通常变异算子的取值范围在0.001～0.5之间^[15]，可以选择稍大的变异算子（本文选择0.01）来提高种群规模的多样性。

2.2 计算策略

惩罚函数的本质^[16]是将存在约束的优化问题利用函数的组合方式转换成无约束条件的优化问题，以降低问题寻优的难度。通过构造惩罚函数可以确保遗传群体中保留部分的非可行解并可以对其染色体中存在的有利于寻找全局最优解的信息加以利用，使得遗传的总群体构成更多样，从而扩大寻优空间的范围，提高搜索效率。

惩罚函数通过将建立的数学模型所有约束条件加以整合成惩罚函数 $P(X)$ ，适应度函数通常采用加法和乘法2种形式组合目标函数 $f(X)$ 和惩罚函数 $P(X)$ 。

加法形式的适应度函数的组合形式为F(X) = f(X) + P(X)；乘法形式的适应度函数的组合形式为F(X) = f(X) · P(X)。

比较上述2种构造形式，可以看出加法形式的构造需要考虑适应度函数出现负值的情况（在同样 $f(X)$ 大于0的情况下），所以在考虑复杂的约束情况下采用乘法形式构造适应度函数更合适。

${P_{}}(x)$ 由 ${P_e}(x)$ 和 ${P_{ue}}(x)$ 相乘得到，即 $F(X) = f(X) \cdot {P_e} $ $ (x) \cdot {P_{ue}}(x)$ 。

3 计算分析 3.1 设计变量的上下限

本文设计的双体无人艇排水量设为100 t，根据不同的航速区间，优化3种航速（低速、中速、高速）下的目标无人艇；根据单体试验艇的标准吃水为0.1054 m，选取试验艇标准吃水的0.9～1.1作为吃水的设计变量上下限；根据不同吃水下拟合出的排水量确定缩尺比，从而确定最终实际无人艇的设计吃水及其他与缩尺比相关的双体无人艇艇型参数。

拟合排水量公式如下：

$\begin{split}D_m =& {\rm{ - 0}}{\rm{.075\;373\;972}} + {\rm{0}}.222\;287\;0T/T_{wl} - \\ &{\rm{0.151\;741\;773}}{\left( {T/T_{wl}} \right)^{\rm{2}}} + {\rm{0}}{\rm{.049\;366\;914}}{\left( {T/T_{wl}} \right)^{\rm{3}}}{\text{。}}\end{split}$

(28)

其中：D_m为排水量，T_wl为标准吃水；T为设计吃水。

3.2 惩罚函数参数设置

等式约束的惩罚函数构造如下：

1）浮性约束的误差范围设为0.001，惩罚因子设为2；

2）推力约束的误差范围设为0.001，惩罚因子设为10；

3）转矩约束的误差范围设为0.001，惩罚因子设为10。

3.3 改进遗传算法内部参数设置

常规参数设置（种群规模400、遗传代数：1000～5000、交叉概率0.75、变异概率0.01），改进算法的特定设置（变载波概率为0.0001～0.01、进化权重0.5、遗传因子0.1）。

3.4 计算结果

1）设定不同子目标函数权重和不同的遗传代数，得到的低速双体无人艇优化结果如表1所示。

2）设定不同子目标函数权重和不同的遗传代数，得到的中速双体无人艇优化结果如表2所示。

3）设定不同子目标函数权重和不同的遗传代数，得到的高速双体无人艇优化结果如表3所示。

4 结　语

本文选择一艘典型单体船型（长宽比约11：1），根据船型参数之间的相互关系，拟合船长、船宽等船型系列参数关于相对吃水（T/T_wl）的关系式，根据剩余阻力曲线拟合了剩余阻力系数关于Fr（0.2-0.7）的相关关系。将拟合得到的参数和设定的10个独立的船型参数作为设计变量进行双体无人艇的优化设计分析。建立了双体无人艇综合性能（快速性和操纵性）优化数学模型，利用改进遗传算法和惩罚策略参与模型计算。

依据表1～表3的优化结果，可得到如下结论：

1）优化得到的九组结果在遗传代数为4000～5000代时结果开始收敛且达到最优解；

2）随着操纵性权重的增加（0.5～2），优化结果中设计吃水也随之增加，即不同权重下设计吃水对于优化结果最敏感；

3）快速性子目标函数在设定吃水较浅，趋近于最优解，而操纵性子目标函数则相反。具体表现为：吃水较浅时艇型更瘦长（B/L，T/L，Cb更小），快速性更好。而操纵性不仅与瘦长度相关，而且与艇体尾部的中纵剖面的投影面积大小相关（表现为T，L值越大越好）^[11]。本文的优化计算结果表明，在瘦长度变化不大时（B/L，T/L和Cb变化率），即适当提高吃水的深度，有助于提高操纵性。

因为双体无人艇的性能设计较为复杂且没有相关的设计参考，本文利用一艘单体艇的试验数据进行了一艘双体无人艇的性能综合优化分析。由于只考虑了2个性能，在今后的相关无人艇优化设计中可加入耐波性性能作为子目标函数。