2. 上海船舶研究设计院,上海 201203
2. Shanghai Ship Design and Research Institute, Shanghai 201203, China
在海洋资源的勘探和利用过程中,产生了多种海洋工程结构物,如海上风力发电设备、海洋石油钻井平台等。在这些海洋结构物的工程设计中,使用了大量的圆柱结构物,其中有些有多圆柱结构。在海流的作用下,多圆柱之间会产生相互的扰动,这种互扰效应可能会加剧结构的振动,从而造成结构的破坏,并且这种互扰效应会受到圆柱的数量、间距、排列方式等因素的影响。因此,有必要对圆柱之间的互扰效应展开研究。
针对多圆柱之间的互扰效应,许多学者展开了相关研究。李强 [1]、顾中明[2]等分析了圆柱群对流场的阻流特性以及水流结构如何改变。杨纪伟等[3]、杨枭枭等[4]、谢潇潇等[5]基于现有的研究成果,对双圆柱、三圆柱、四圆柱绕流受圆柱排列形式影响,流场结构和涡脱落状态的演变规律进行了归纳总结。在多圆柱绕流问题中,具有代表性的双圆柱绕流问题受到了广泛的关注。Sumner[6]对前人的研究进行了总结,将圆柱的布置分为并列、串联和交错3种情况,统一了研究者对间距比、间隙比等相对位置参数的定义。国内外学者对这3种双圆柱绕流的排列方式展开了大量的数值模拟研究,主要研究Re数、直径比、间距比等参数对双圆柱绕流的影响[7-12]。学者们对多圆柱的研究多集中在等直径的圆柱。针对不等直径圆柱之间的互扰效应,毕贞晓[13]以数值模拟的方法对不等直径并列双圆柱展开研究,分析了4种间距比下圆柱的受力特性,但缺乏对临界间距比的分析。刘洪超[14]以数值模拟的方法对不等直径串列双圆柱在不同间距比下进行研究,得到了涡脱落形态在小于临界间距比时呈单一涡脱落形态,在大于临界间距比时,呈现双旋涡脱落形态。但对于并列不等直径双圆柱的互扰效应以及临界间距比的相关方面的研究还不够充分。
本文基于CFD方法,在单圆柱绕流的基础上对不同间距比下的不等直径并列双圆柱绕流展开研究,探究小圆柱对大圆柱的影响,得到临界间距比。研究结果表明,在小于临界间距比时,存在一定的互扰效应,且互扰效应随间距比增大而减弱,在达到临界间距比之后,圆柱涡脱落稳定,几乎不存在互扰效应,接近单圆柱情况。
1 单圆柱绕流圆柱绕流的无量纲数包括斯特劳哈尔数
斯特劳哈尔数是等于当地惯性力与迁移惯性力之比,描述流场的非定常性和涡脱落频率的一个重要物理量。斯特哈尔数的定义如下:
| $S{\rm{t}} = \frac{{fvD}}{U}\text{。}$ | (1) |
式中:
雷诺数Re等于惯性力和粘性力之比,对于二维圆柱而言,其迎流面积是一条直线,长度等于直径。雷诺数的表达式如下:
| $Re = \frac{{\rho UD}}{\upsilon }\text{。}$ | (2) |
其中:
升力和阻力是表面压力在顺流向和横向的合力,单位长度的升力和阻力系数定义如下:
| $CD = \frac{{FD}}{{0.5\rho \mathop U\nolimits^2 D}},$ | (3) |
| $CL = \frac{{FL}}{{0.5\rho \mathop U\nolimits^2 D}}\text{。}$ | (4) |
建模过程主要按照几何建模、网格划分、设置物理参数、边界条件以及时间步等方面来进行。建模过程是以坐标原点为圆心,圆心距离上下边界分别为
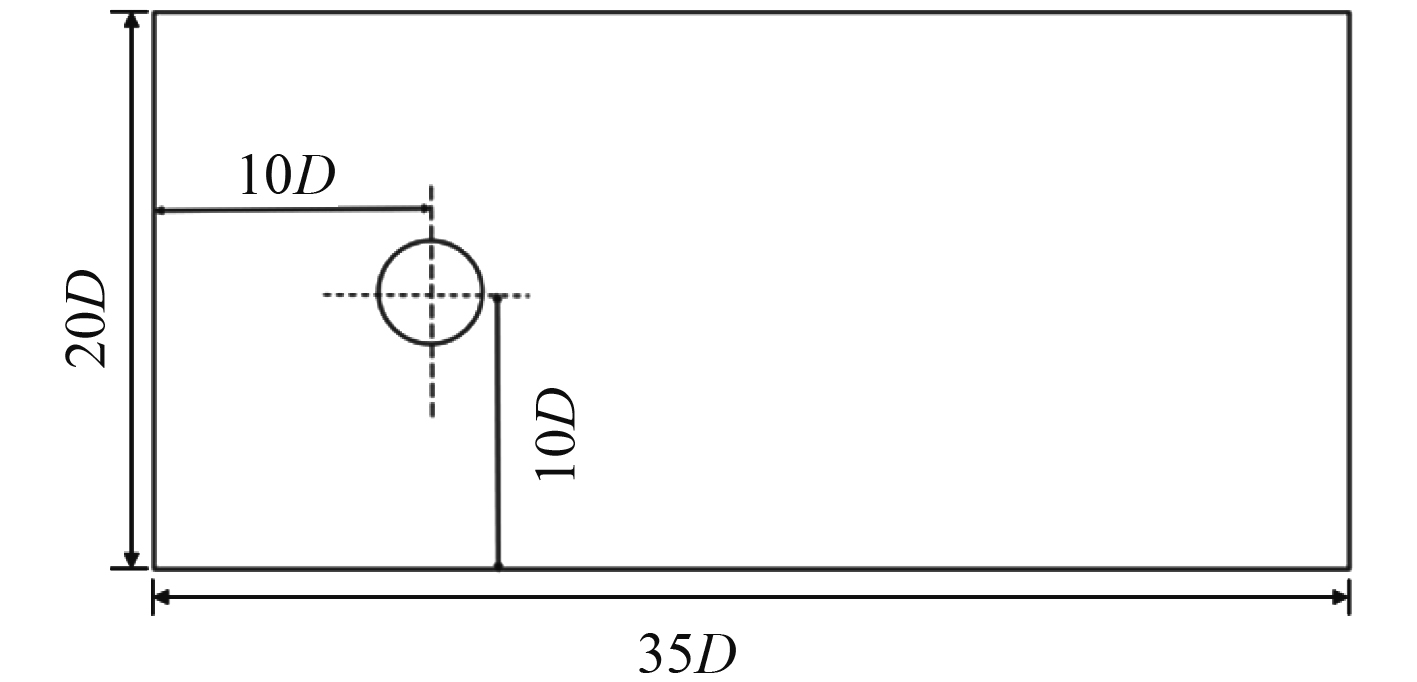
|
图 1 计算域尺寸图 Fig. 1 The size diagram of calculation domain |
网格划分过程中需要综合考虑计算精度和计算效率。按照6种网格节点数和时间步长的组合进行验证,计算参数和结果如表1所示。其中
|
|
表 1 Re = 3 900的圆柱绕流计算结果和参数 Tab.1 Calculation results and parameters of flow around a cylinder when Re = 3 900 |
当前的结果都在参考文献的范围之内[15],表明本文所建立的模型以及计算结果是有效的。在网格节点数为25275时,
雷诺数为3900的圆柱升阻力系数以及涡量图如图2所示。随着时间的推移,
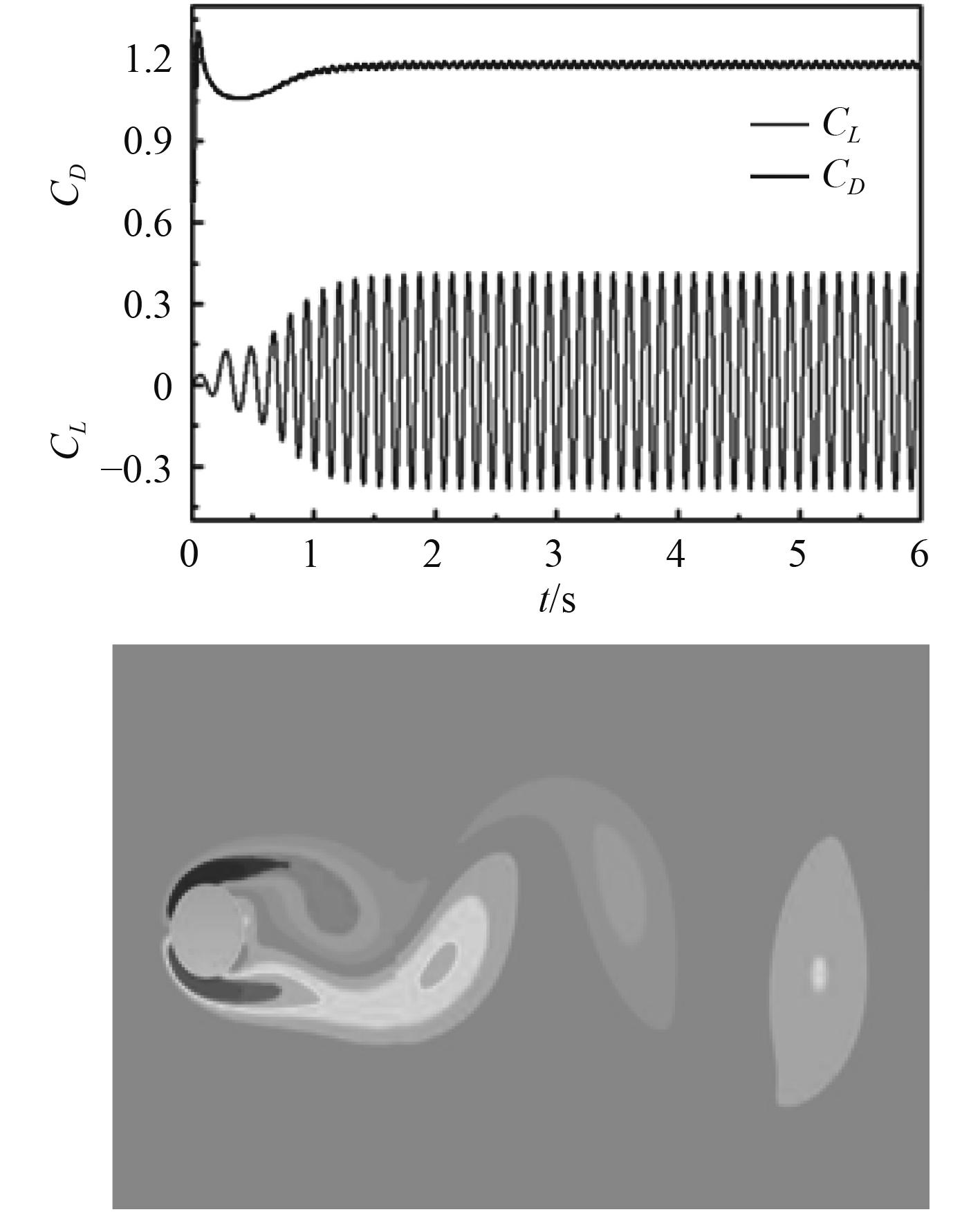
|
图 2
|
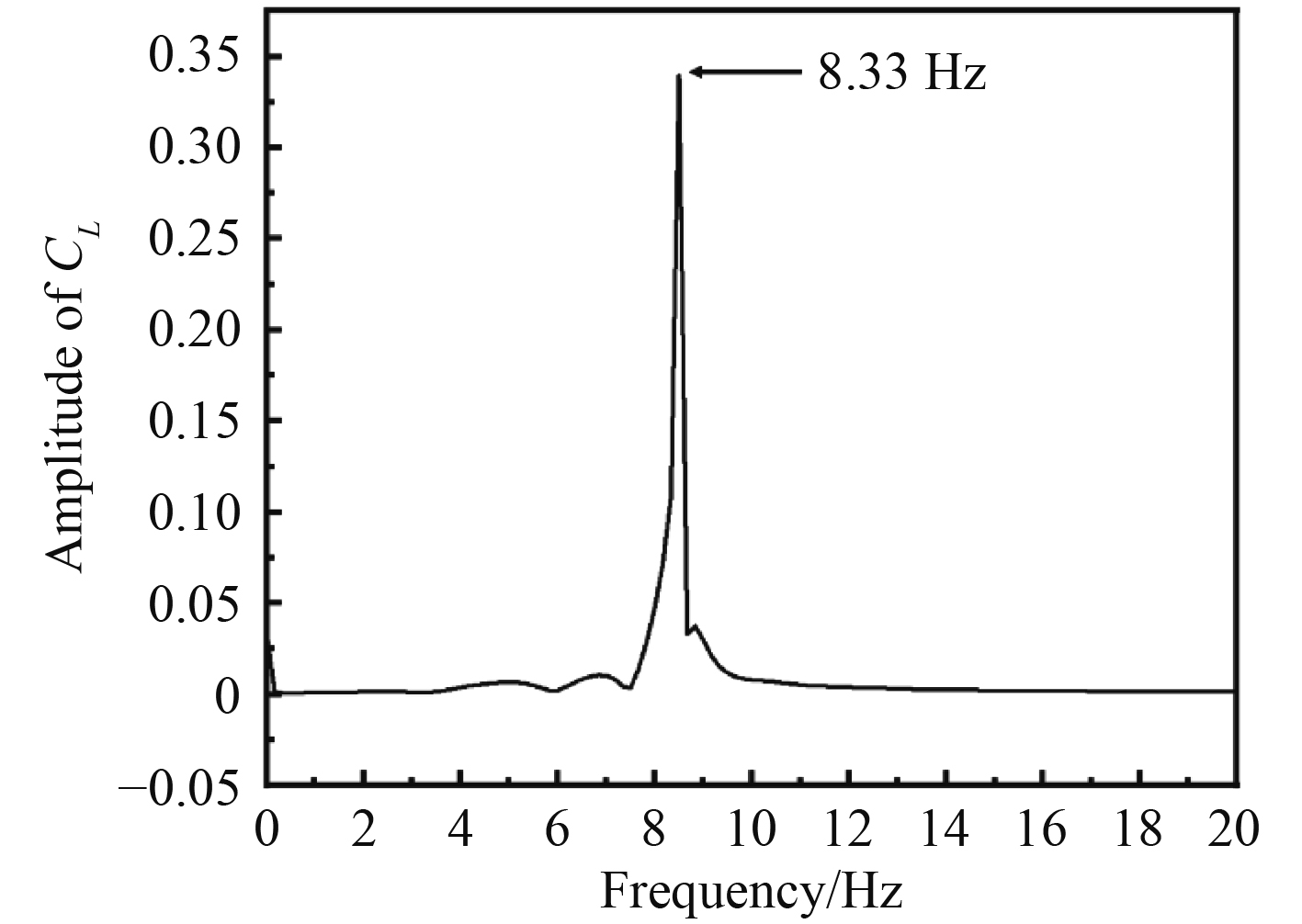
|
图 3 升力系数频谱图 Fig. 3 Frequency spectrum of lift coefficient |
在单圆柱绕流的基础上,对不等直径双圆柱绕流展开研究。主圆柱雷诺数为3900,与单圆柱一致。附属小圆柱的直径(d)与主圆柱直径(D)比为d/D=0.5,对7种间距比(T=1.2D,1.5D,1.8D,2.8D,3.0D,3.1D,3.5D)下的不等直径圆柱绕流进行分析。流体域网格划分方式、物理参数的设置与单圆柱绕流类似。
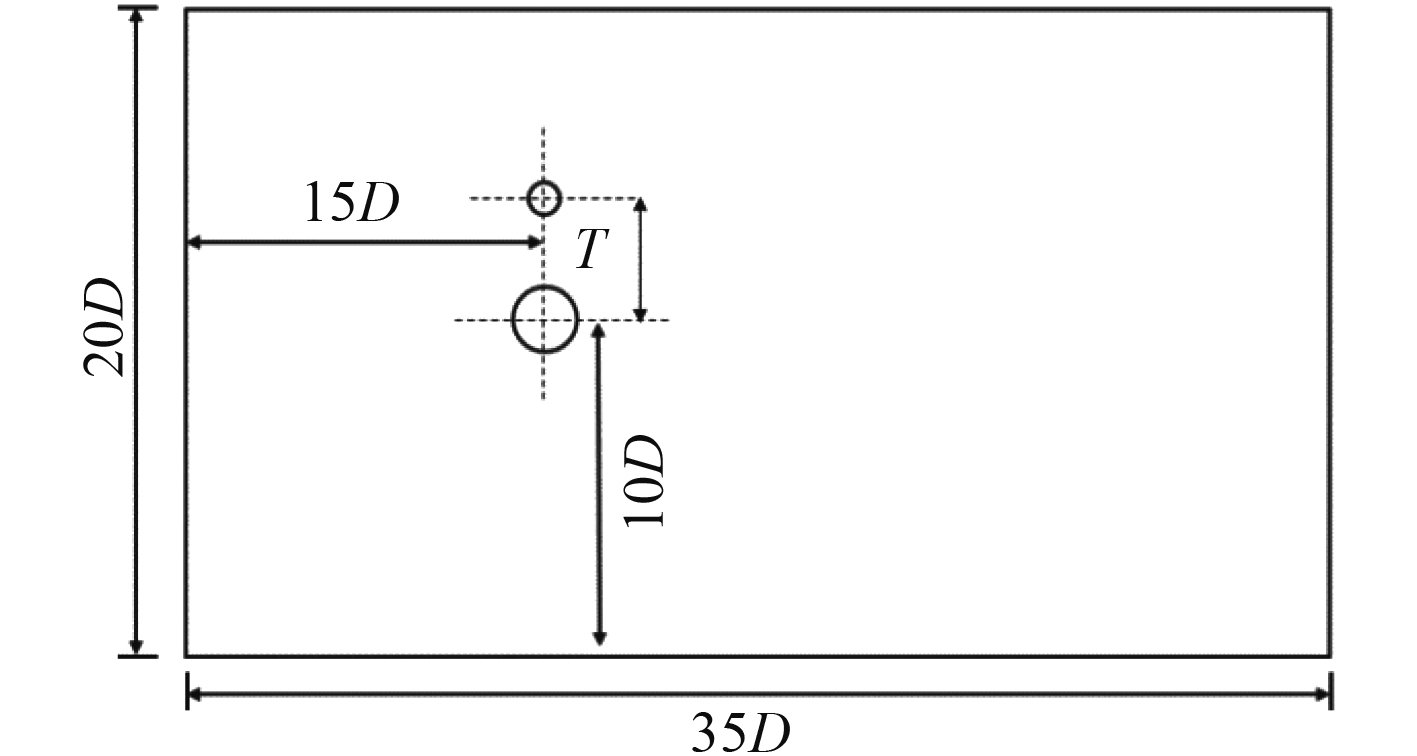
|
图 4 双圆柱计算域 Fig. 4 The calculation domain of two cylinders |
由图5和图6可知,当
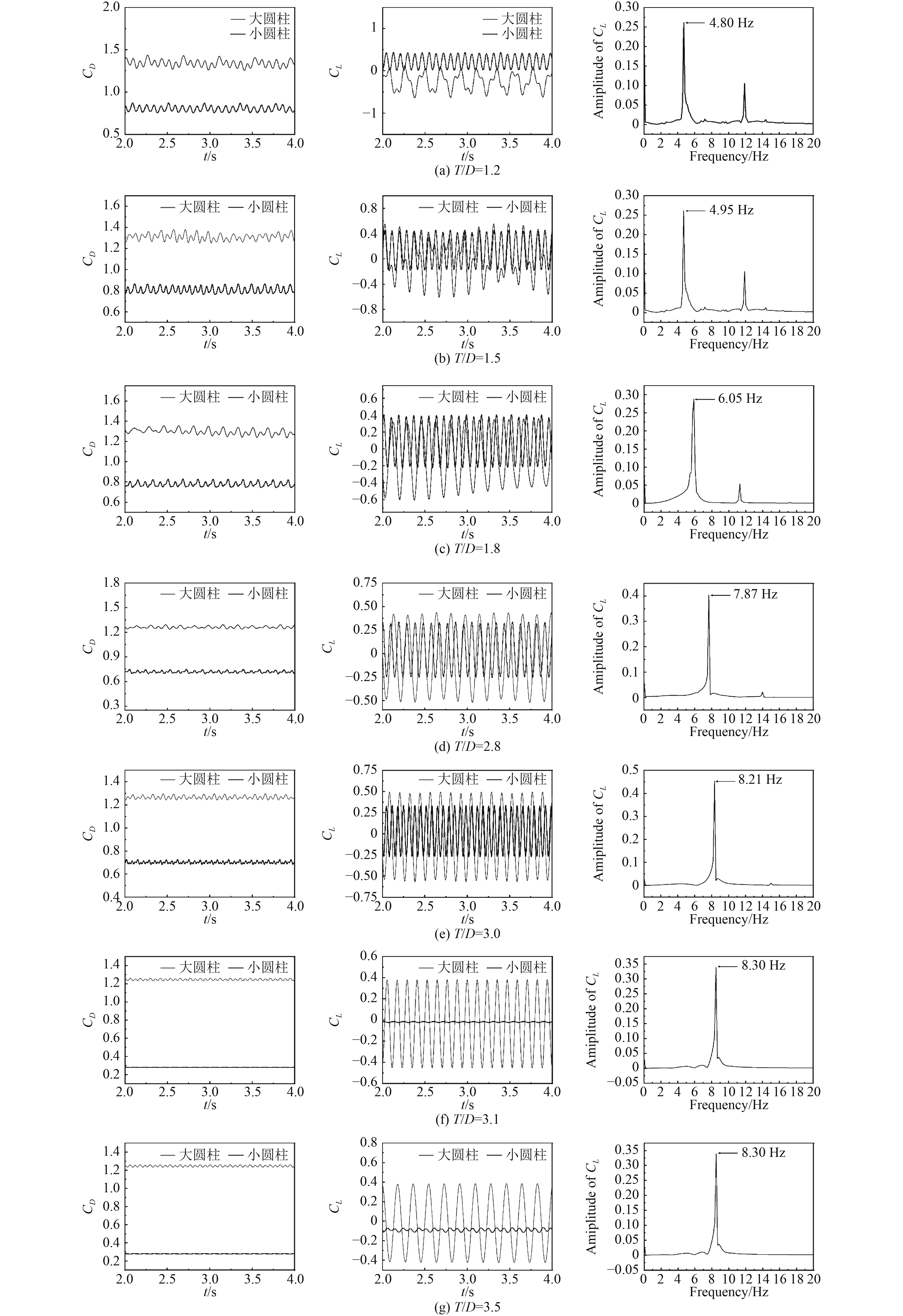
|
图 5 不同间距比下升力和阻力系数时间历程曲线 Fig. 5 Time history of lift and drag coefficients under different spacing ratios |
|
图 6
|
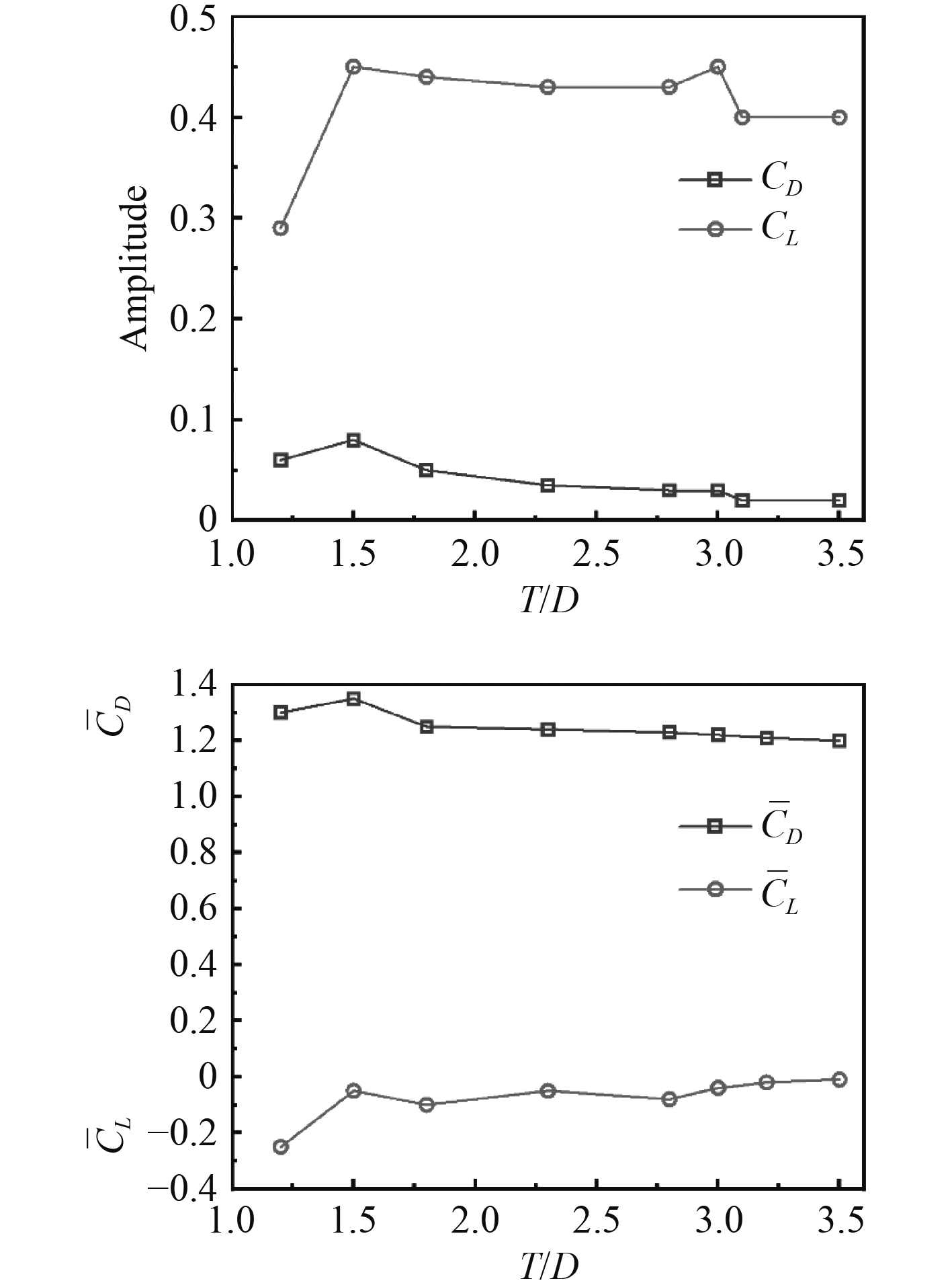
对不等直径双圆柱的水动力系数分析发现,当
从图7可以看出,在间距比
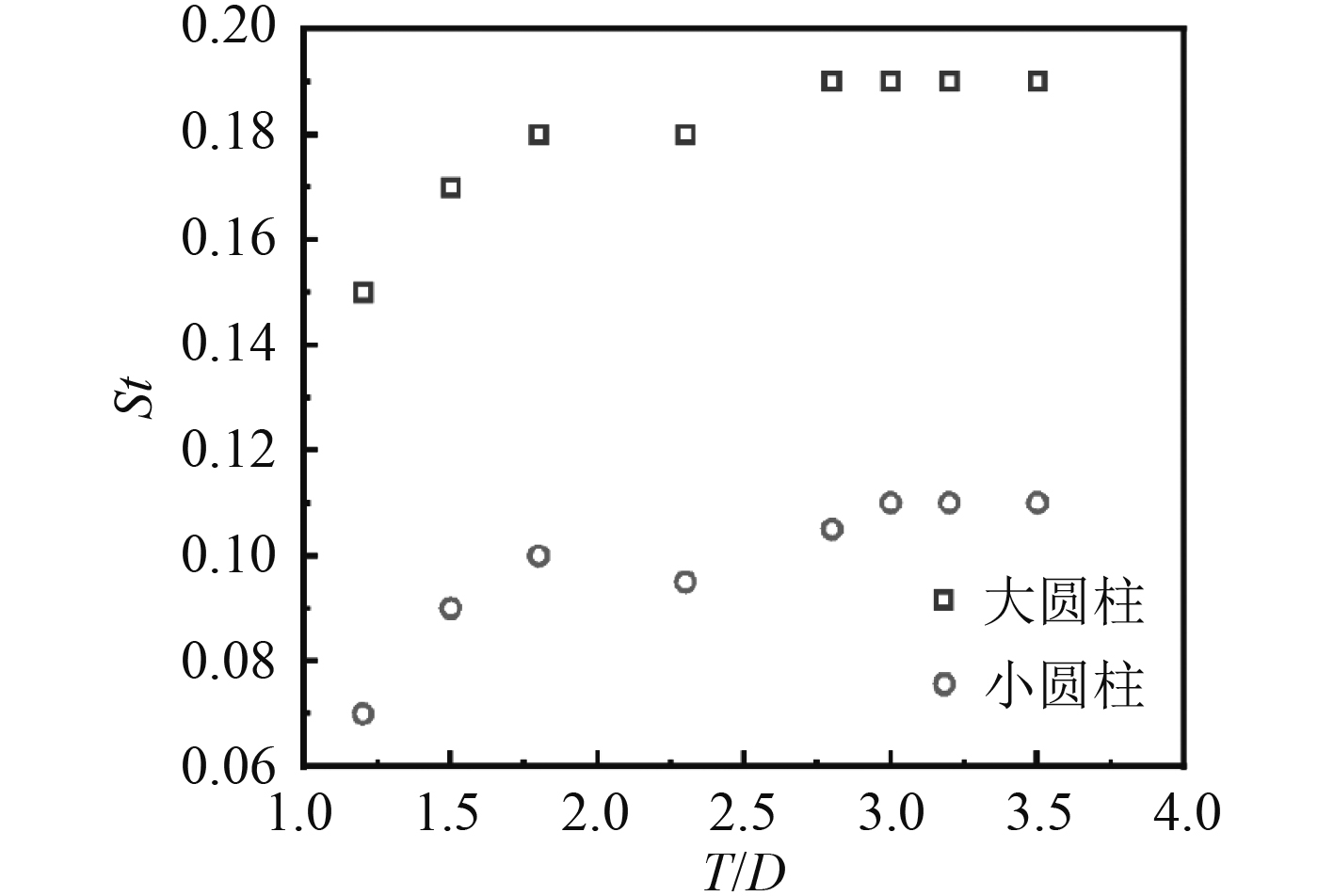
|
图 7
双圆柱斯特劳哈尔数
|
不同间距比下的涡量图如图8所示。当

|
图 8 不同间距比下涡量图 Fig. 8 Vorticity diagram under different spacing ratios |
本文主要采用CFD的方法,利用数值模拟软件Ansys/Fluent研究了二维并列双圆柱之间的互扰效应。
1)对雷诺数3900的单圆柱绕流进行分析,通过结果的比对验证了本文建立模型以及选择数值方法的有效性,并讨论了单圆柱的升阻力系数与尾流涡之间的相互关系。
2)对不等直径并列双圆柱进行研究,确定了
| [1] |
李强. 圆柱群绕流的实验及数值模拟研究[D]. 杭州: 浙江大学, 2014.
|
| [2] |
顾中明. 刚性圆柱群绕流及涡激振动实验研究[D]. 西安: 西安理工大学, 2018.
|
| [3] |
杨纪伟, 滕丽娟, 胥战海. 多圆柱绕流旋涡脱落和流场形态概论[J]. 人民长江, 2009, 40(3): 66-68+86. DOI:10.3969/j.issn.1001-4179.2009.03.025 |
| [4] |
杨枭枭, 及春宁, 陈威霖, 等. 三角形排列圆柱绕流尾流模式及其流体力特性[J]. A辑, 2019, 34(1): 69-76. |
| [5] |
谢潇潇, 及春宁, John Williams. 低雷诺数下不同顶角三棱柱体绕流受力和尾涡脱落机制[J]. 水电能源科学, 2018, 36(6): 73-76. |
| [6] |
SUMMER D. Two circular cylinders in cross-flow: a review[J]. Journal of Fluids and Structures, 2010, 26(6): 849. DOI:10.1016/j.jfluidstructs.2010.07.001 |
| [7] |
BEARMAN P W. Circular cylinder wakes and vortex-induced vibrations[J]. Journal of Fluids Structure, 2001, 27(5-6): 648-658. |
| [8] |
ZARAVKOVICH M M. Flow induced oscillations of two interfering circular cylinders[J]. Journal of Sound Vibration, 1985, 101(4): 511-521. DOI:10.1016/S0022-460X(85)80068-7 |
| [9] |
CHEN S. A review of flow-induced vibration of two circular cylinders in crossflow[J]. Journal of pressure vessel technology, 1986, 108(4): 382-393. DOI:10.1115/1.3264802 |
| [10] |
何长江, 段忠东. 二维圆柱涡激振动的数值模拟[J]. 海洋工程, 2018, 26(1): 57-63. |
| [11] |
刘爽. 低雷诺数下并列圆柱涡激振动的数值模拟及其机理研究[D]. 天津: 天津大学, 2014. LIU Shuang. Numerical simulation and mechanism study of vortex-induced vibration of parallel cylinders at low Reynold number[D]. Tianjin: Tianjin University, 2014. |
| [12] |
秦伟, 康庄, 孙丽萍, 等. 并列双圆柱涡激振动的经验性模型研究[J]. 海洋工程, 2012, 31(2): 11-18. |
| [13] |
毕贞晓. 不等直径并列双圆柱绕流的受力分析和湍流特性研究[D]. 上海: 上海应用技术学院, 2015.
|
| [14] |
刘洪超. 不等直径串列双圆柱体绕流的数值研究[D]. 青岛: 中国海洋大学, 2012.
|
| [15] |
何鸿涛. 圆柱绕流及其控制的数值模拟研究[D]. 北京: 北京交通大学, 2009.
|
 2021, Vol. 43
2021, Vol. 43
