在现代船舶中,方尾由于具有增加虚长度、减小阻力、增大排水体积等优点,无论是在单体船舶还是高速三体船舶上都已经得到了广泛的应用。尤其对于高速三体船,由于大多采用了喷水推进,相比与传统螺旋桨推进在高速段拥有更好的推进效率,并且利于尾部的布置,也使得方尾的尺寸相对于螺旋桨推进船型更大,在阻力与航态预报中的重要性也更大。因此,在三体船型设计中,能够准确、快速地对方尾船型的兴波阻力、总阻力以及航行姿态进行预报,在方尾船型的设计和优化过程中具有十分重要的作用。
船舶兴波阻力及航态的预报方法经过多年发展,主要可分为基于势流方法和粘流方法。随着21世纪以来计算机计算效率大幅提高,粘流方法有了显著发展。但是,粘流方法网格划分和计算机要求较高。Sherbaz研究表明,与表面压力和力矩相比,粘性力对航态影响较小,大多在10%以内[16]。在势流理论的范围内,对于方尾船型的计算所运用的方法主要有Michell积分法、Havelock源法,Dawson方法和Rapid方法。改进后的Michell积分虽然可以用于方尾船型的计算,但是无法对航态及近场兴波进行模拟;Havelock源法运用于高速方尾船舶计算,计算精度较低;而全非线性方法,在方尾船型计算时,自由面迭代容易产生发散。计算近场兴波的线性兴波理论由Dawson[5]于1977年提出,将速度势分解为叠模速度势和扰动速度势,并对自由面条件进行展开,采用迎风差分格式来实现兴波的从前向后传播;陈京普、Tarafdera等[4,8-10]改进了近场兴波方法,采用贴水线自由面网格提高了计算精度及稳定性,使得方法应用更加广泛,并运用于约束模的兴波模拟。Peng等[15]改进自由面船尾后的计算网格,减少了肥大船型尾部流场紊乱及不稳定的问题。由于非线性方法避免了升高面元及自由面迭代等问题,也被广泛应用于兴波计算及船型优化等领域[8-15]。
本文基于势流理论,针对具有实用价值的大方尾三体船,运用改进后Dawson方法和Rankine源,建立三维的兴波阻力及航行姿态的预报方法。针对方尾船型的自身特点,对自由面条件求解的数值计算方法进行了一定的改进,采用自然迭代形成的方尾后尾流区域,避免了虚长度估算所带来的误差。由于直接对物体表面进行压力积分,本方法运用与多体船舶计算时,可以直接反映出片体间的相互作用,同时也可以更为直观地得到船舶周围近场的兴波情况,利于船型优化工作。本文运用该方法分别对单体、三体方尾船型进行理论预报,并将预报结果与实验结果进行对比分析,对方法的优缺点进行了具体的研究。
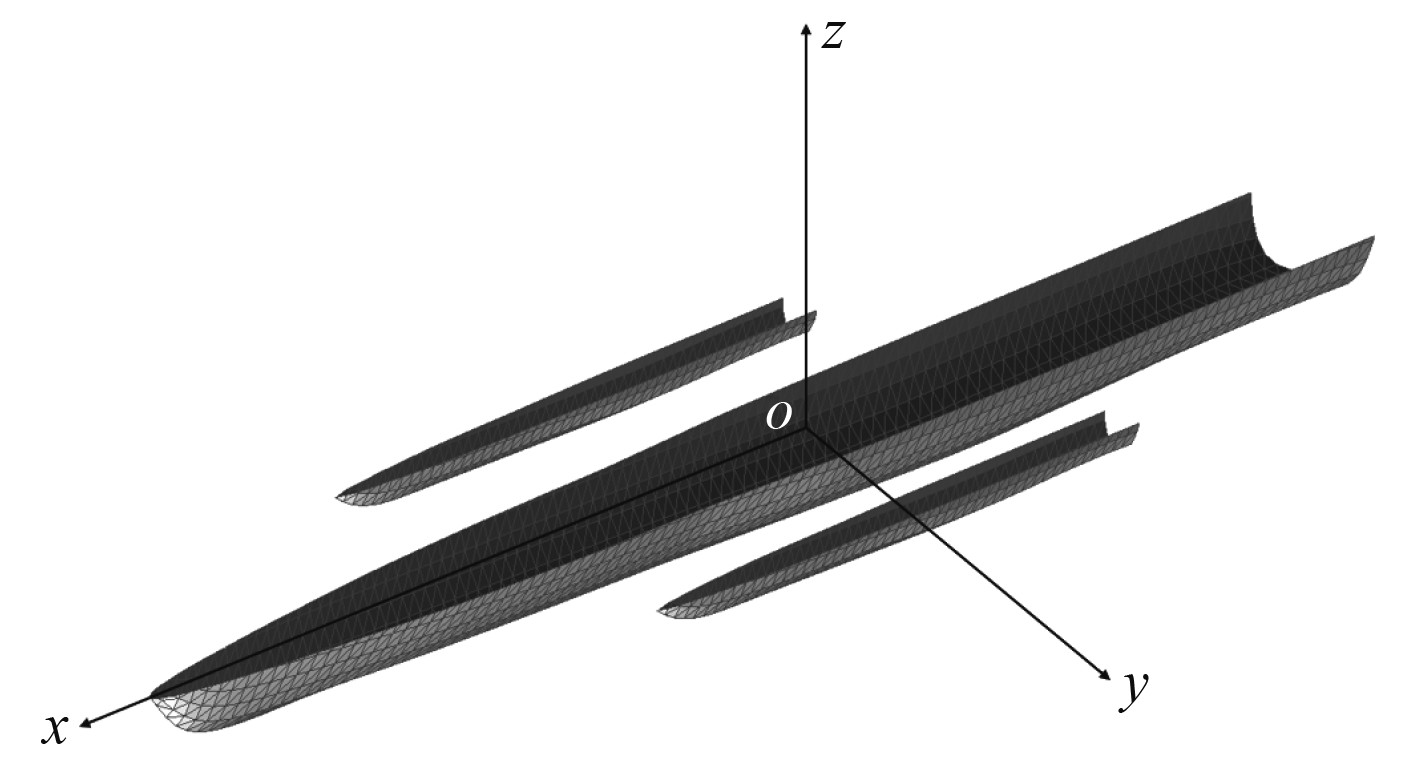
1 数学模型 1.1 基本模型采用随船坐标系,坐标系如图1所示。坐标系原点o位于船舶中心,z轴垂直向上,x轴由船首指向船尾,y轴指向右舷为正,xy平面与静水面重合。
|
图 1 坐标系 Fig. 1 Coordinate system |
假设流体理想,流动定常,无限水深,船舶兴波为微幅波。流场速度势
| $\psi = \phi + \varphi \text{,} $ | (1) |
| $\phi = Ux + \bar \phi\text{,} $ | (2) |
由于重叠模速度势中包含了来流速度势,因此假设,
| $\zeta = \xi + \eta\text{,}\qquad \xi > > \eta \text{,}$ |
流场中有
| ${\nabla ^2}(\phi + \varphi ) = 0\text{,}$ | (3) |
物面上满足
| $\nabla (\phi + \varphi ) \cdot n = 0\text{,}$ | (4) |
其中
速度势
| ${\varPhi _x}{\zeta _x} + {\varPhi _y}{\zeta _y} - {\varPhi _z} = 0\text{,} \;\;\;\;z = \zeta \text{,}$ | (5) |
| $g\zeta + \frac{1}{2}(\nabla \varPhi \cdot \nabla \varPhi - {U^2}) = 0\text{,}\;\;\;\;z = \zeta \text{,}$ | (6) |
由式(6)和式(7)可得在
| $\frac{1}{2}{\psi _x}{(\nabla \psi \cdot \nabla \psi )_x} + \frac{1}{2}{\psi _y}{(\nabla \psi \cdot \nabla \psi )_y} + g{\psi _z} = 0\text{。}$ | (7) |
速度势满足无穷远处趋于零的远方辐射条件。
1.2 自由面边界条件考虑到
| ${\phi _z} = 0\text{,}\;\;\;\;z = 0\text{。}$ | (8) |
将式(8)在
| $\begin{split} \frac{1}{2}{\phi _x}{(\phi _x^2 + \phi _y^2)_x} +& \frac{1}{2}{\phi _y}{(\phi _x^2 + \phi _y^2)_y} + {\phi _x}{({\phi _x}{\varphi _x} + {\phi _y}{\varphi _y})_x} + \\ &{\phi _y}{({\phi _x}{\varphi _x} + {\phi _y}{\varphi _y})_y} + \frac{1}{2}{\varphi _x}{(\phi _x^2 + \phi _y^2)_x} + \\ &\frac{1}{2}{\varphi _y}{(\phi _x^2 + \phi _y^2)_y} + g{\varphi _z} = 0{(z = 0)} \text{。} \\ \\[-10pt] \end{split} $ | (9) |
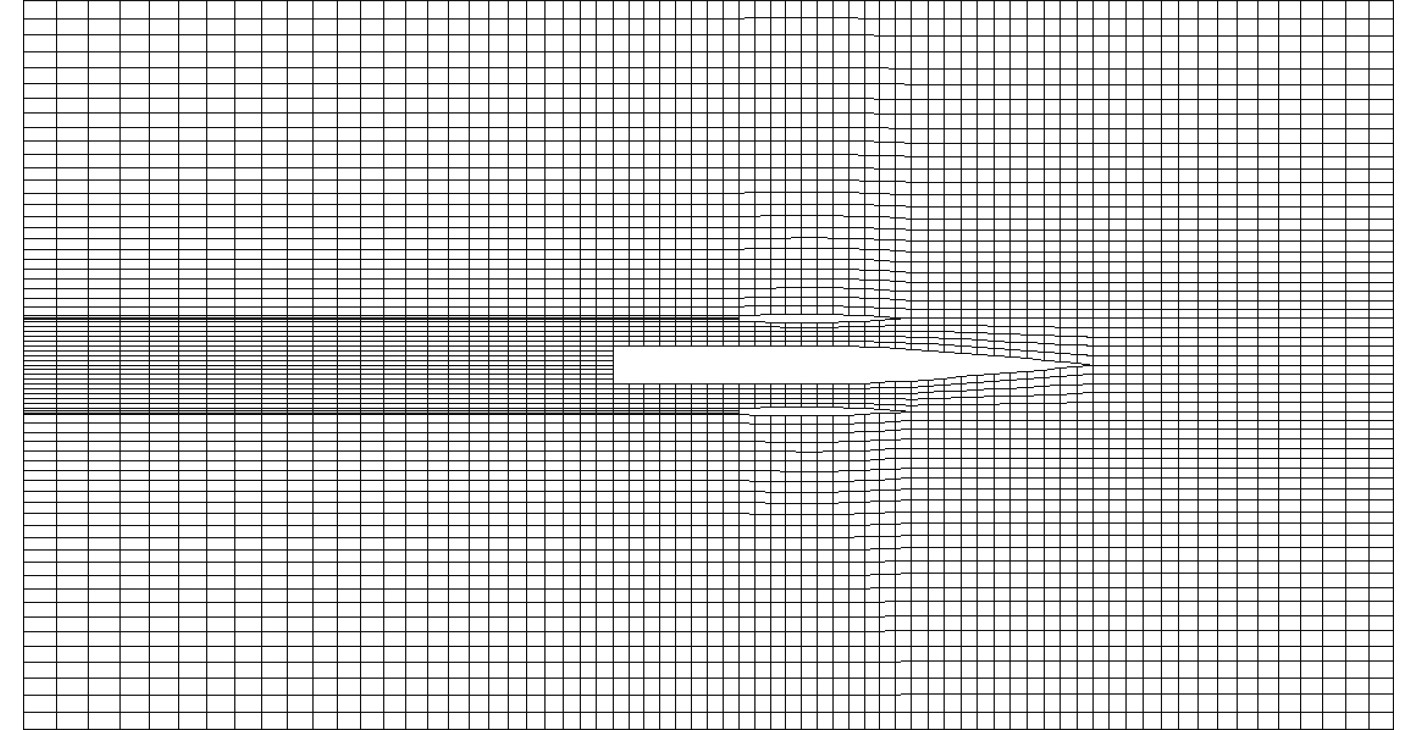
计船体网格数为Nb,自由面网格数Nf。在船体网格离散时以四边形网格为主,船体首部倾斜处采用三角形网格进行处理。自由面采用贴面网格,方尾后网格单独生成,并进行一定程度的加密。船体处网格长度保持不变,前后以rx的比例递增,方尾处网格宽度不变,ry的比例递增。不同的航速所产生的波长不同,即λ=2πFn2Lwl ,选择不同的初始网格大小,以得到更加精确的自由面波形以及计算结果。某单体方尾船型自由面网格示意图如图2所示。
|
图 2 自由面网格 Fig. 2 Free surface mesh |
离散单元布置源汇后,物面控制点
| ${\phi _p} = - Ux + \iint\limits_{{S_B}} {{{({\sigma _{B0}})}_q}\frac{1}{{{r_{pq}}}}{\rm d}{S_q}}\text{。}$ | (10) |
其中:Sb为物面;σB0为物面控制点处源强;rpq为任意源点q到控制点p的距离。
对式(12)离散,考虑物面条件条件可得:
| $\begin{split}\nabla {\phi _p} =& - U - 2\text{π} {({\sigma _{B0}})_p} +\\ &\sum\limits_{\begin{smallmatrix} q=1 \\ q\ne p \end{smallmatrix}}^{{{N}_{B}}}{\left( {{\sigma }_{B1}} \right)}\iint\limits_{{{S}_{B}}} {\frac{\partial }{{\partial {n_p}}}\left(\frac{1}{{{r_{pq}}}}\right)} {\rm d}{S_q} = 0\text{,}\end{split}$ | (11) |
扰动速度势表示为:
| $\begin{split}\nabla {\varphi _p} =& 2\text{π} {({\sigma _{B1}})_p} + \sum\limits_{\begin{smallmatrix} q=1 \\ q\ne p \end{smallmatrix}}^{{{N}_{B}}}{\left( {{\sigma }_{B1}} \right)} \iint\limits_{{{S}_{B}}} {\frac{\partial }{{\partial {n_p}}}\left(\frac{1}{{{r_{pq}}}}\right)} {\rm d}{S_q} +\\ &\sum\limits_{\begin{smallmatrix} q=1 \\ q\ne p \end{smallmatrix}}^{{{N}_{F}}}{\left( {{\sigma }_{F}} \right)} \iint\limits_{{{S}_{B}}} {\frac{\partial }{{\partial {n_p}}}\left(\frac{1}{{{r_{pq}}}}\right)} {\rm d}{S_q} = 0\text{。}\end{split}$ | (12) |
为了保证自由液面不发生震荡以得到更加光顺、贴合实际的自由面波形,进而使计算结果更加精确,在计算时对自由面单元的控制点进行升高,升高高度与波长和各个单元各自的长度成一定比例。同时,为了更好满足远方辐射条件,使得向前差分不受单元对控制中心切向诱导速度为零对数值计算造成的影响,将控制点统一前移一定距离,移动距离为单元长度的0.1倍。
2.2 方尾后自由面条件处理及静水力计算由于航速较低的情况下,方尾并未完全出水,因此采用理论计算方法进行数值模拟时,必须对方尾在低速时未出水部分所受到的静水力进行估算。通过经验公式,对方尾船型在不同航速下方尾中心及两侧的吃水情况进行估算,并对方尾网格重新加密划分,积分得到方尾所受到的静水力,进而提高阻力计算的精度,具体公式如下:
| ${F_t} = V/\sqrt {g{D_t}}\text{,} $ |
| ${R_{NT}} = \sqrt {VD_t^3} /\nu\text{,} $ |
| ${\eta _{dry}} = {C_1}F_t^{{C_2}}{({B_t}/{D_t})^{{C_3}}}R_{NT}^{{C_4}}\text{。}$ |
其中:ηdry为方尾中心与两侧未浸水长度系数;Bt,Dt为方尾的宽度与吃水;Ft为方尾傅汝德数;RNT为方尾雷诺数。参照文献数据对系数C1,C2,C3,C4进行取值,求得方尾中心与两侧的吃水后,对方位进行静水力修正。
2.3 兴波阻力及航态计算船体表面控制点压力系数为:
| ${C_{{p_i}}} = \frac{{(1/2)\rho ({U^2} - \nabla {\psi _i}\nabla {\psi _i}) - \rho g{z_i}}}{{(1/2)\rho {U^2}}}\text{。}$ |
其中,Zi为控制点到静水面间距离。
船体受到的兴波阻力Rw、兴波阻力系数Cw、升力Fz和纵倾力矩Ny表示为:
| ${R_w} = \sum\limits_{i = 1}^{{N_B}} {\frac{1}{2}\rho {U^2}{C_{{p_i}}}{n_{{x_i}}}{S_i} - {R_{{h_x}}}}\text{,} $ |
| ${C_w} = \frac{{{R_w}}}{{(1/2)\rho {U^2}{S_w}}}\text{,}$ |
| ${F_z} = \sum\limits_{i = 1}^{{N_B}} {\frac{1}{2}\rho {U^2}{C_{{p_i}}}{n_{{z_i}}}{S_i} - {R_{{h_z}}}} \text{,}$ |
| ${N_y} = \sum\limits_{i = 1}^{{N_B}} {\frac{1}{2}\rho {U^2}{C_{{p_i}}}\left[ {({z_i} - {z_g}){n_{{x_i}}} - ({x_i} - {x_g}){n_{{z_i}}}} \right]{S_i} - {N_{{h_y}}}} \text{。}$ |
其中:Si表示船体的湿表面积;xi,zi为控制点坐标;xg,zg为船舶的重心坐标;nxi,nzi为单元法线x,z方向分量;Rhx,Rhx,Nhy为傅汝德数Fn=0时由于船体表面的网格离散划分使船体受到的静水阻力、升力、力矩修正值。
给定时间步长Δt,可以得到船舶下一时刻的吃水St+Δt以及纵倾值Tt+Δt为:
| ${S_{t + \Delta t}} = {S_t} + \frac{{{F_z}}}{m}\Delta t\text{,}$ |
| ${T_{t + \Delta t}} = {T_t} + \frac{{{N_y}}}{m}\Delta t\text{。}$ |
仅对船体水线以下近水面处局部网格进行实时划分,而大部分网格始终保持不变,这样既减小了网格重新离散带来的误差,也节省了计算时间。通过反复迭代直到满足收敛条件(Fz<ε,Ny<ε)即可得到考虑船体姿态变化影响的兴波阻力,进行船体姿态预报。
3 算例及结果分析 3.1 数值计算及验证以具有较大方尾的某三体船为例,对该船型的兴波阻力、航行姿态以及方尾吃水进行理论预报并与相应的试验结果对比。在总阻力计算时,参照文献[12]取粘压阻力系数为0.1。
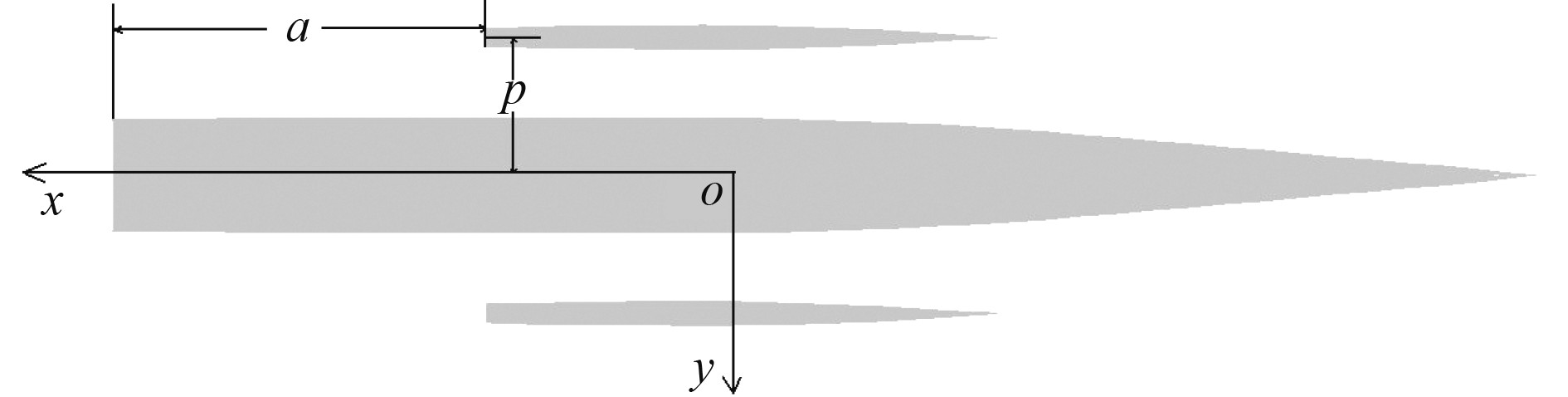
计算过程中,片体间距L,B,D为主体水线长、水线宽和吃水,B/L=0.08,D/L=0.04;L1,B1,D1为侧体水线长、水线宽和吃水,B1/L1=0.05,D1/L1=0.05。BT,DT分别为主体方尾水线宽和吃水,Bt/Dt=3.65;Bt1,Dt1分别为侧体方尾水线宽和吃水,Bt1/Dt1=3.55。在计算过程中,保持片体与主体尾部平齐,即a/L=0.0,片体间距p/L=0.1,三体船片布局示意图如图3所示。
|
图 3 三体船片体布局示意图 Fig. 3 Layout diagram of trimaran hull |
主体纵向网格60个,垂向网格10个;侧体纵向网格30个,垂向网格5个。自由表面网格采用随船长傅汝德数变化而变化,单个波长保持25个网格,船首、尾及横向网格保持1.05的扩张比例,动态保证计算域船首往前1L,船尾往后1.5L,横向1L。船体网格如图4所示,在Fn =0.3时自由面网格如图5所示。

|
图 4 船体表面网格示意图 Fig. 4 Schematic diagram of hull surface grid |

|
图 5 自由面网格示意图 (Fn = 0.3) Fig. 5 Schematic diagram of free surface grid (Fn = 0.3) |
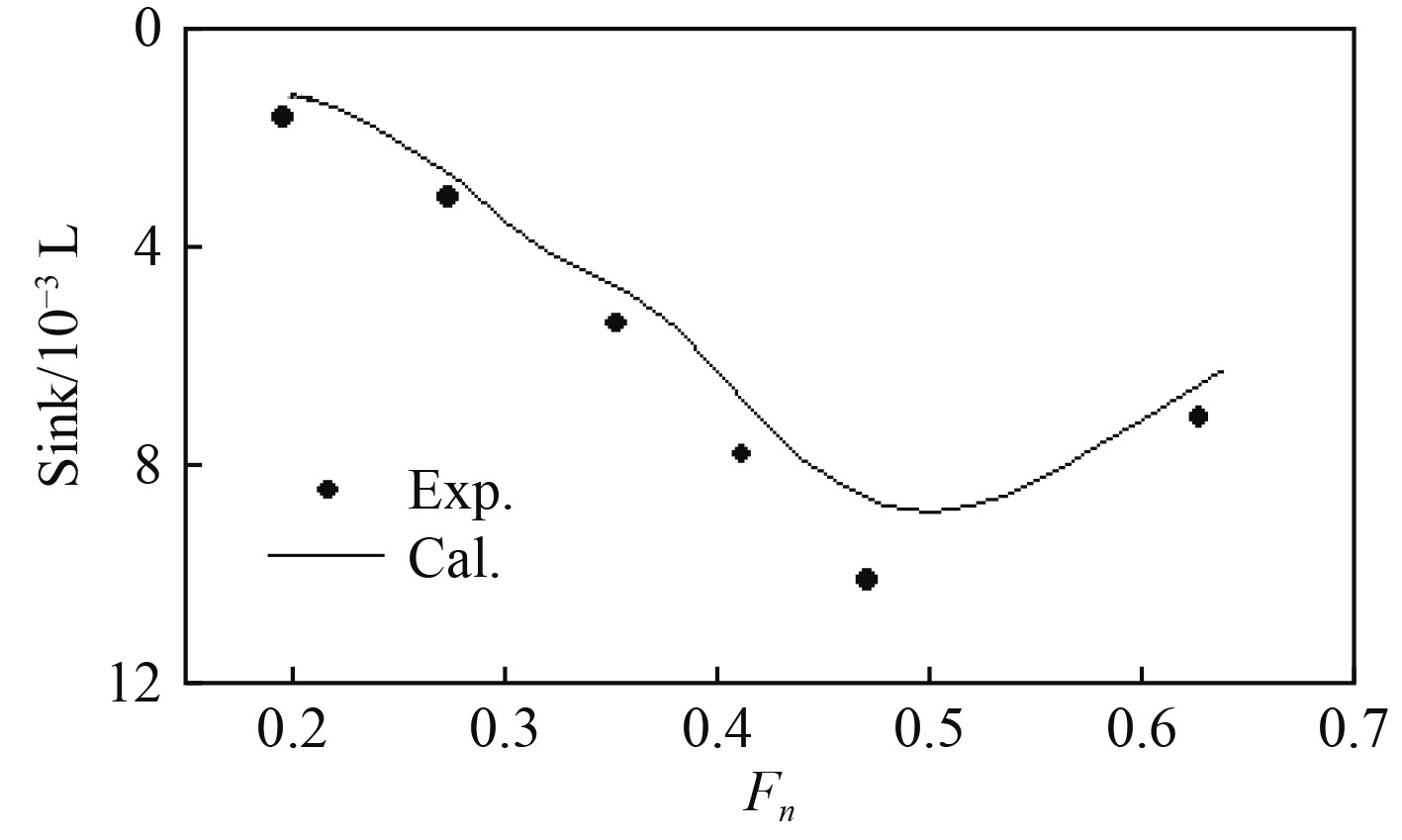
将该船型兴波阻力计算结果与试验结果进行对比,升沉、纵倾、阻力计算结果如图6~图8所示。
|
图 6 升沉计算结果与试验值对比 Fig. 6 Comparison of heave calculation results and test values |
|
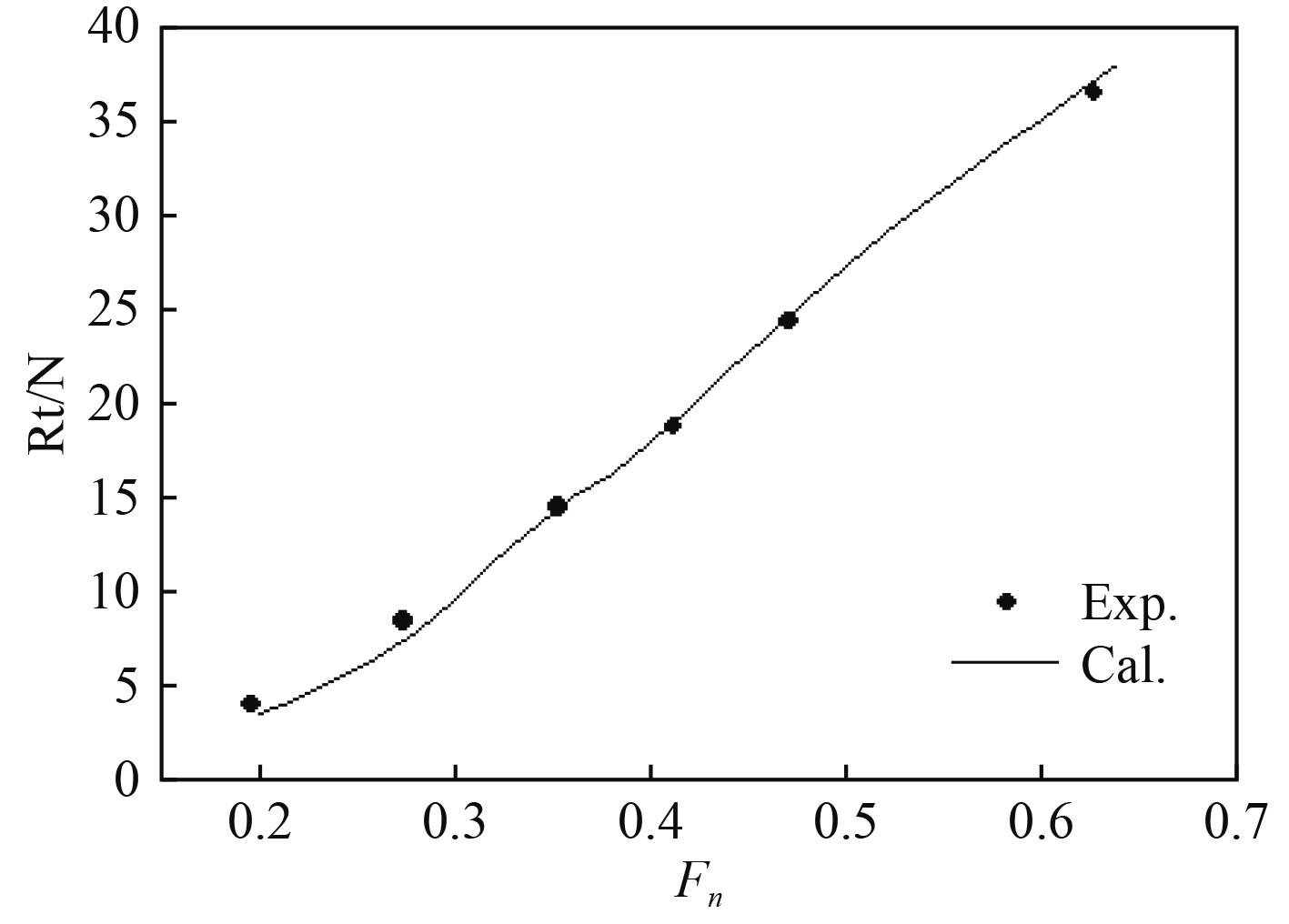
图 8 总阻力计算结果与试验值对比 Fig. 8 Comparison of total resistance calculation result and test value |
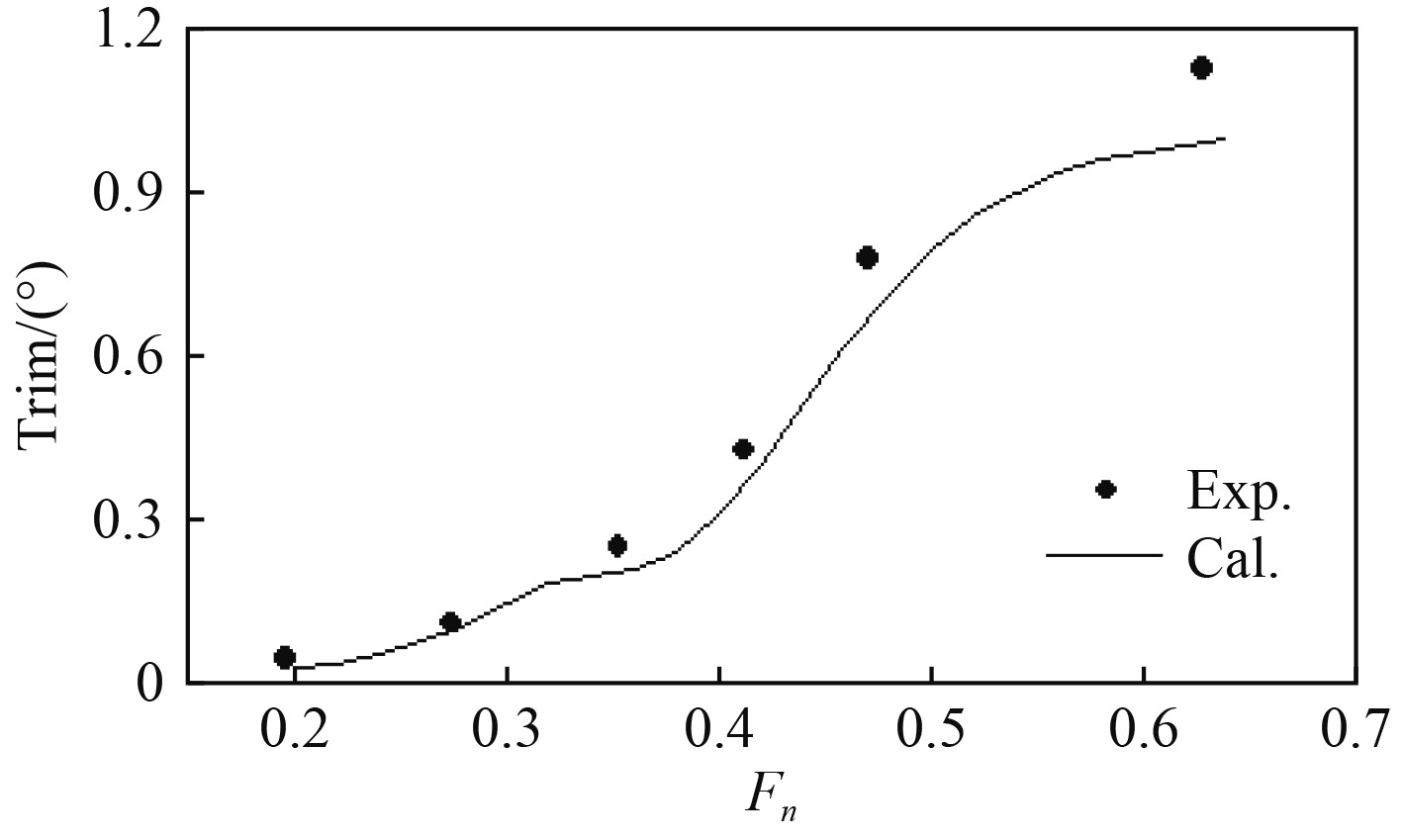
从图6和图7可以看出,理论方法对于方尾三体船舶航行姿态的模拟有着较高的精度,变化趋势与试验值基本一致,幅值也较为接近,但是都略小于试验结果,这可能是由于忽略了边界层粘性切向力的影响。文献[13]也认为随着航速的增大,粘性作用对于航行姿态的模拟存在10%左右的影响。由图8可以看出,理论计算方法引入了方尾处理后,对于傅汝德数小于0.35的方尾未完全出水的模拟具有一定精度。而随着航速增大,在傅汝德数大于0.35方尾完全出水后,计算精度也相对更高,误差可以控制在2%以内。
|
图 7 纵倾计算结果与试验值对比 Fig. 7 Comparison of trim calculation results and test values |
在三体船型设计与优化过程中,如何对不同片体布局方案的阻力及航行姿态进行快速而准确的预报起着十分关键的作用。为了验证本文方法在片体布局优化过程中的计算精度,对上述三体船型进行片体间距和纵向位置的变化,并将计算结果与试验结果进行对比分析。计算工况如表1所示。
|
|
表 1 片体布局方案 Tab.1 Different layout options |
方案1计算结果与上述对比结果相同,将方案2、方案3计算结果与试验值对比,结果如图9~图11所示。
|
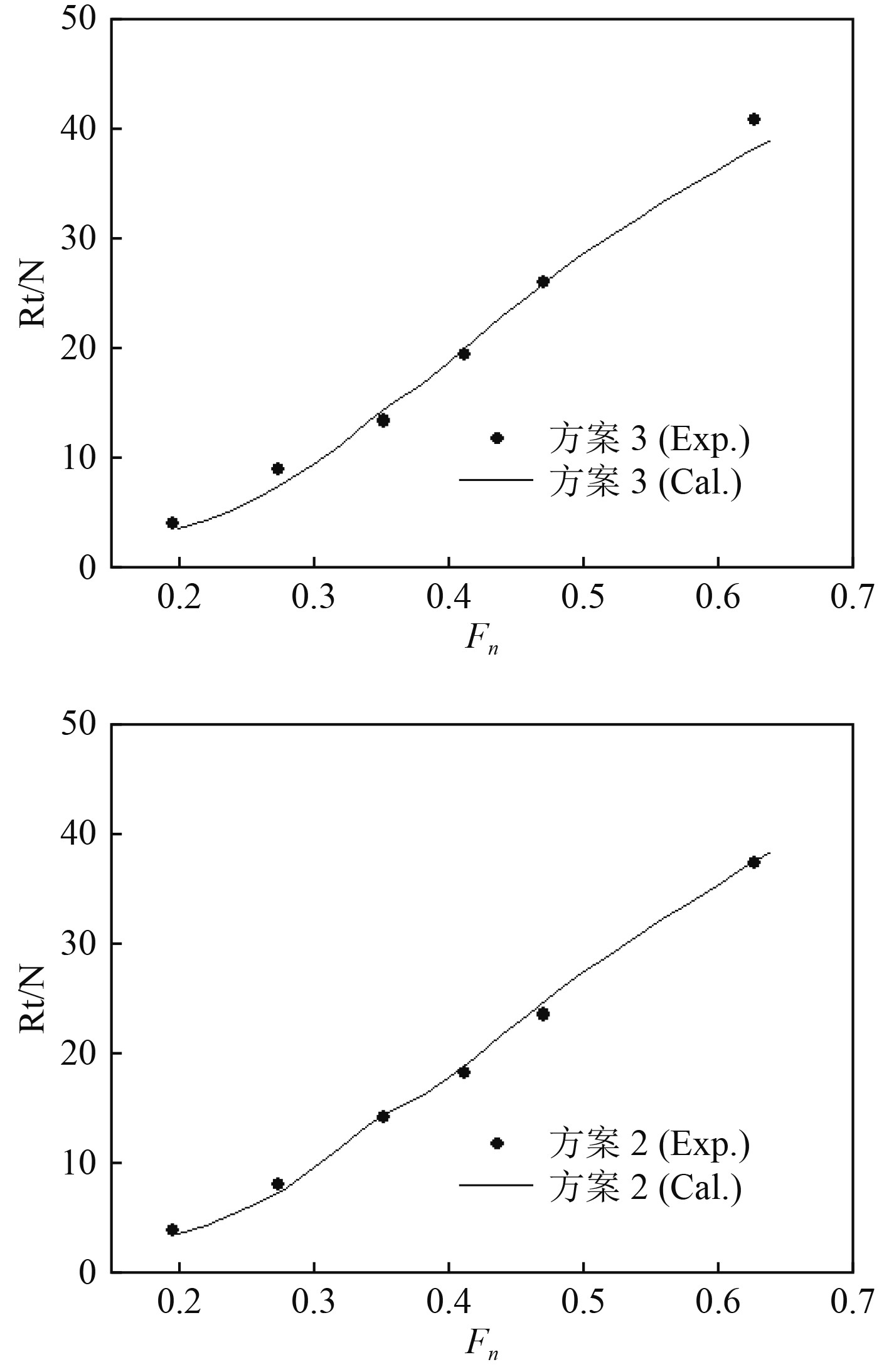
图 9 阻力计算结果与试验值对比 Fig. 9 Comparison of resistance calculation results and test values |
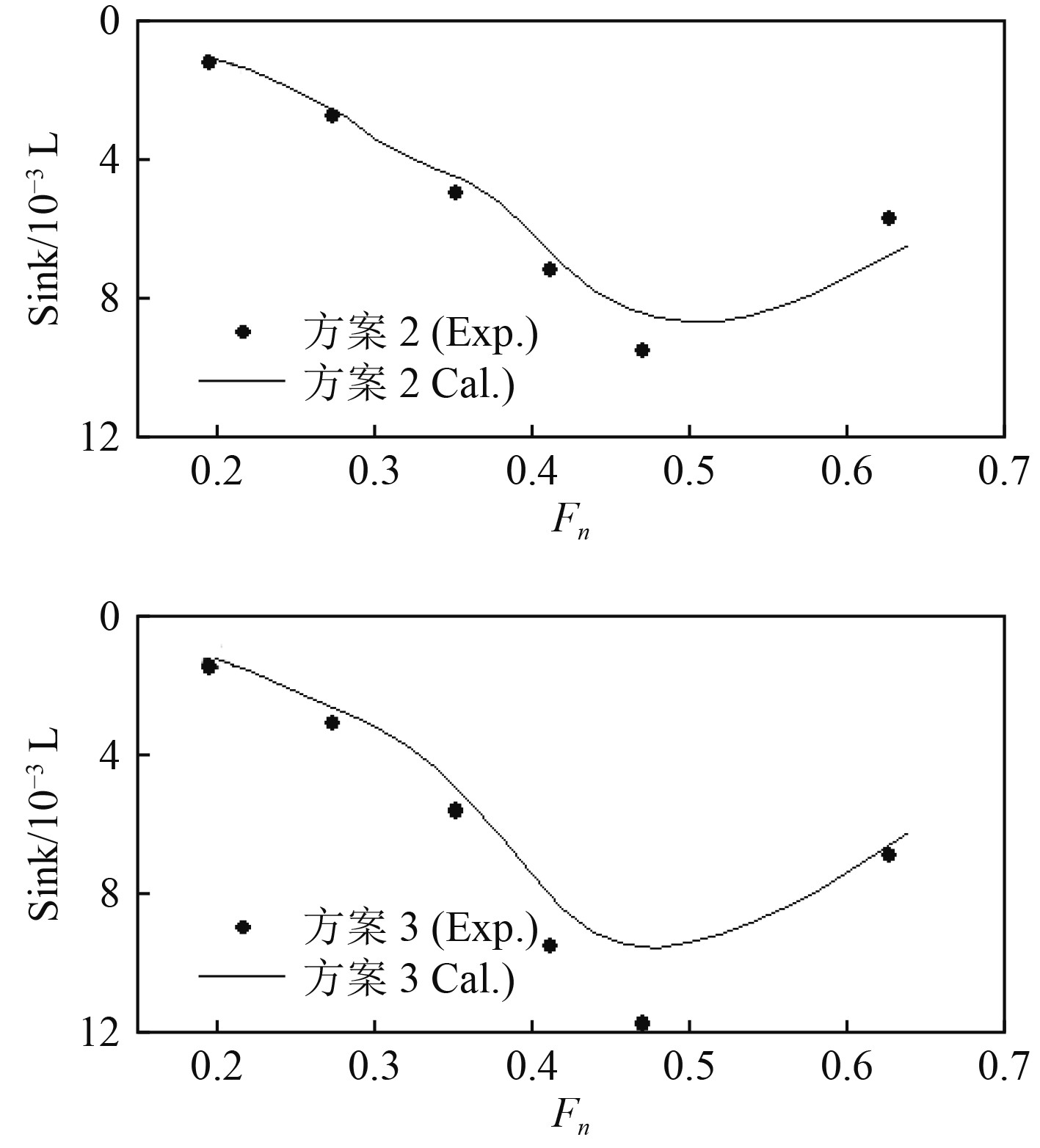
由图9可以看出,加入方尾假设后的理论方法计算所得的总阻力在低速段(Fn<0.35)与试验值相符良好,而在方尾完全出水的较高傅汝德数阶段与试验值接近,最大误差发生在傅汝德数0.63左右,约为6%,这主要是由于傅汝德数高于0.6后将产生一定的喷溅及破波会对阻力造成影响。
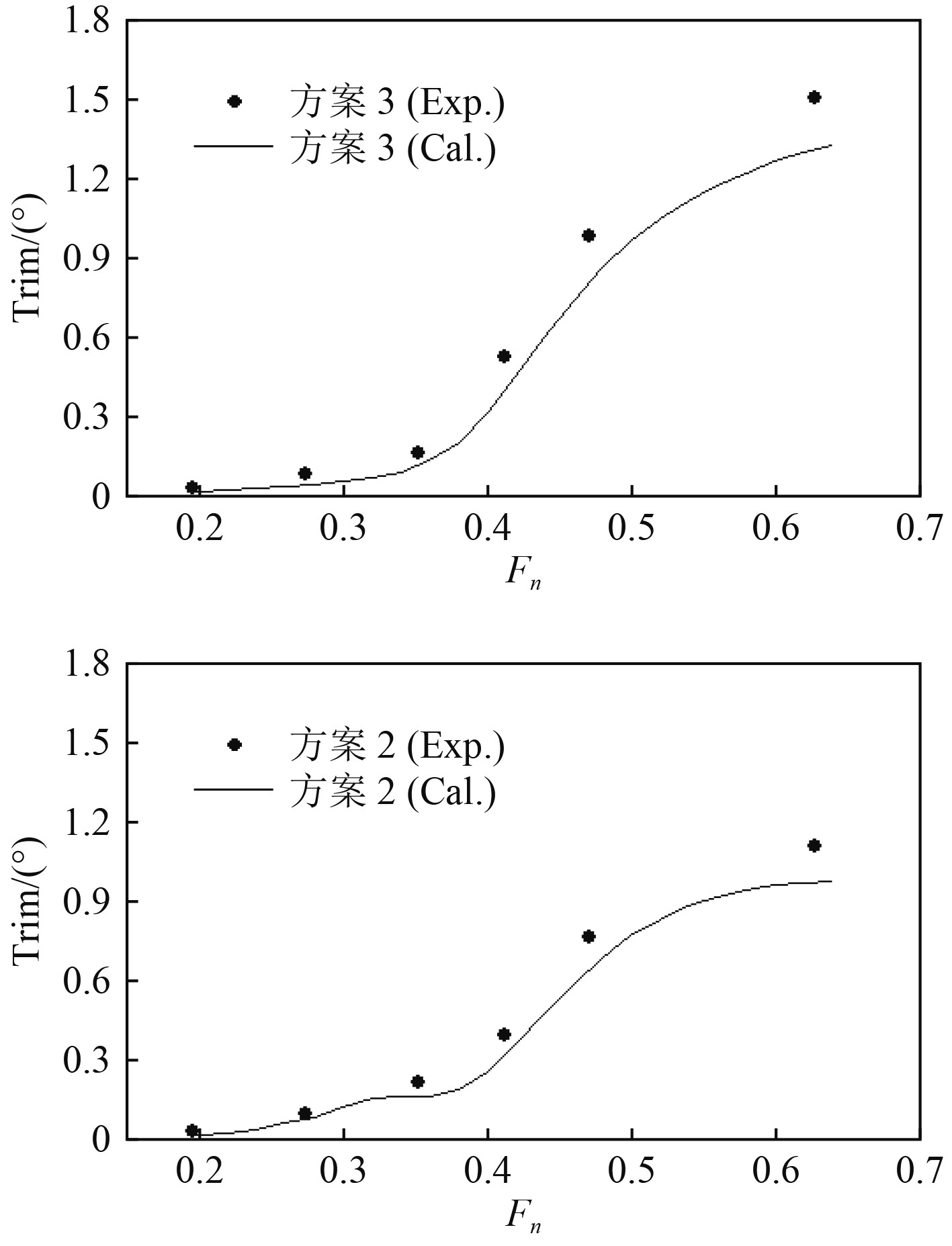
由图10和图11的纵倾、升沉结果可以看出,理论方法对于不同片体布局下航行姿态的预报结果与试验值在大小和趋势上相符良好,同样由于忽略了粘性的影响,计算结果都略小于试验值。图11的升沉结果在傅汝德数0.48左右的峰值处,理论计算结果与试验结果误差最大,在其余航速范围内误差相对较小,这可能时由于在该该航速下片体与主体间兴波干扰较强对于升沉产生较大的影响。从图10和图11不同片体布局结果的对比可以看出,片体的前移使得纵倾值、升沉值总体是增大的,纵倾值的上升趋势和峰值位置也发生了一定的变化,而理论与试验结果所反映出来的趋势变化时相同的,因此证明理论方法可以很好反映出片体布局变化所造成的深沉和纵倾结果的趋势变化。
|
图 10 纵倾计算结果与试验值对比 Fig. 10 Comparison of trim calculation results and test values |
|
图 11 升沉计算结果与试验值对比 Fig. 11 Comparison of heave calculation results and test values |
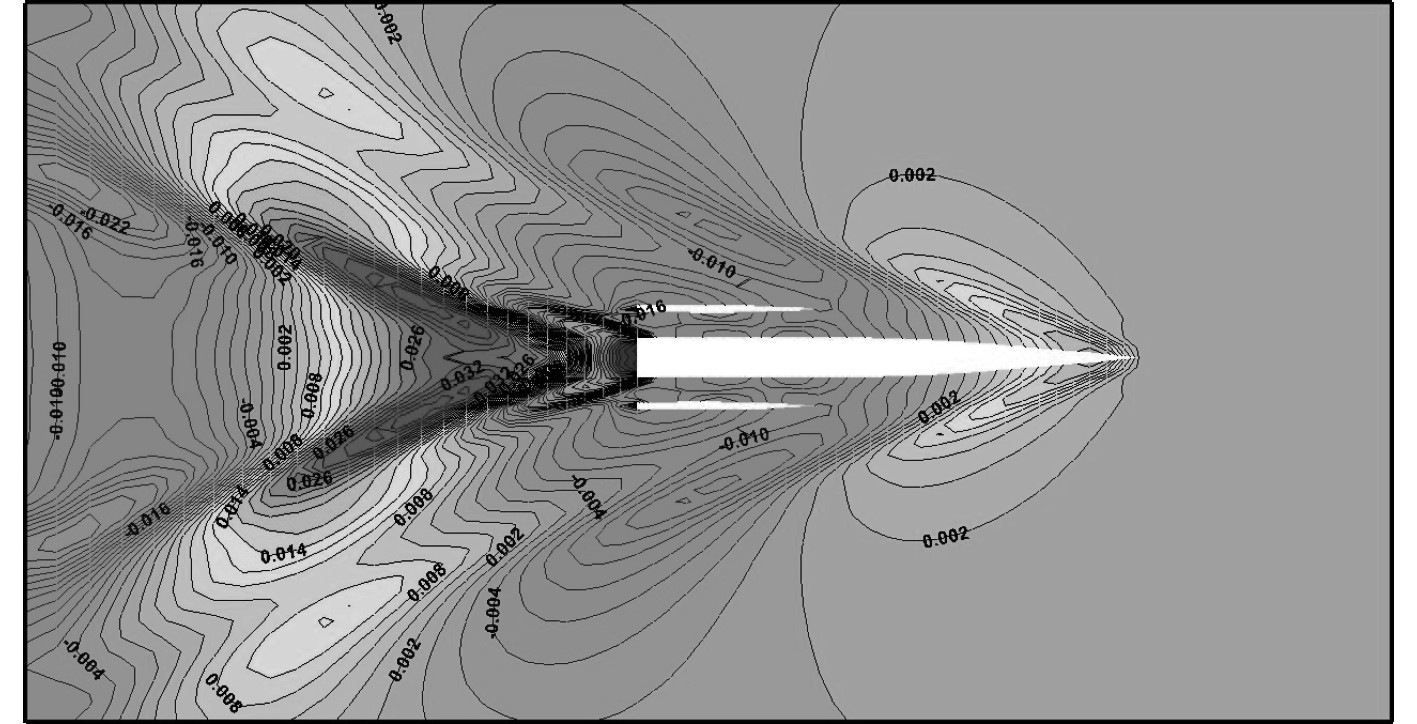
图12~图15为傅汝德数0.46时,不同片体布局下的近场兴波云图。
|
图 12 方案1波形云图 (Fn=0.46) Fig. 12 Scheme 1 waveform nephogram (Fn=0.46) |

|
图 13 方案2波形云图 (Fn=0.46) Fig. 13 Scheme 2 waveform nephogram (Fn=0.46) |
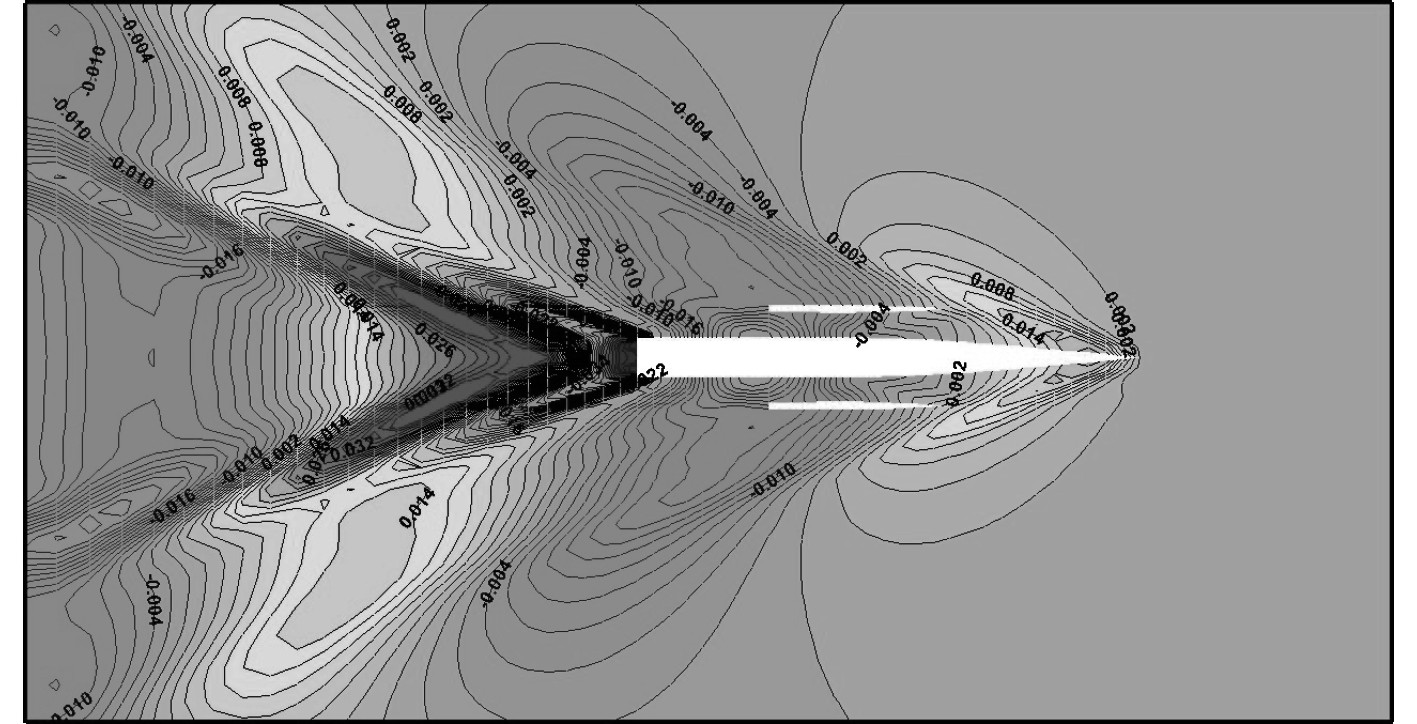
|
图 14 方案3波形云图 (Fn=0.46) Fig. 14 Scheme 3 waveform nephogram (Fn=0.46) |
由图12~图15可以看出,与方案1、方案2相比,当侧体位于船中时兴舶高度有着明显的增大,而随着侧体宽度增加,方案4所产生的兴波又相对方案3有所增加,这与理论计算结果和试验结果是完全相符的。由方案1与方案2的波形对比可以看出,理论方法很好捕捉到了由于片体横向位置变化所造成的波形变化,图13尾部横向散波数相对于图12有明显的增加,这对于片体布局设计阶段是十分有意义的。同时,理论方法中对于差分条件、控制点处理等数值方法,可以得到光顺的兴波波形并很好满足远方辐射条件。由于不再使用传统的方尾虚长度模拟,通过方尾后自由面条件的处理使得方尾后气穴、兴波波形可以自然形成,更加贴近实际情况。

|
图 15 方案4波形云图 (Fn=0.46) Fig. 15 Scheme 4 waveform nephogram (Fn=0.46) |
本文基于近场兴波理论,探讨具有较大方尾的三体船型的阻力及航态预报方法,给出三体船近场兴波及阻力、航态计算的算法、网格划分等数值处理方法。通过与试验值对比,验证了本方法的计算精度;通过对不同侧体布局船型的算例进行数值模拟,探讨和分析了本方法对不同布局三体船型的普适性。可以得出以下结论:
1)本方法对方尾后自由面条件的处理,可以增加理论方法在较小傅汝德数方尾未完全出水情况下对于方尾三体船型阻力及航态数值模拟的精度;
2)理论方法在较大傅汝德数范围内,对于不同片体布局的方尾三体船型的阻力及航态预报有较高的计算精度,理论预报结果与试验结果整体相符良好;
3)理论方法计算所得的三体船型周围流场及近场兴波很好反映出了片体布局变化对于兴波造成的变化,这对于三体船型设计阶段具有实际意义;
4)由于片体布局变化对于粘压阻力也产生一定的影响,因此在后续工作中需要将这一变化代入总阻力预报中,进而提升计算精度。
| [1] |
邹早建, 罗青山, 史一鸣. 小水线面双体船阻力预报研究[J]. 中国造船, 2005, 168(1): 14-21. DOI:10.3969/j.issn.1000-4882.2005.01.003 |
| [2] |
羊少刚, 李干洛, 余灵. 高速双体船兴波阻力的数值计算[J]. 自然科学版本, 1995, 23(10): 16-25. |
| [3] |
黄鼎良. 小水线面双体船性能原理[M]. 北京: 国防工业出版社, 1993.
|
| [4] |
陈京普, 朱德祥, 何术龙. 双体船/三体船兴波阻力数值预报方法研究[J]. 船舶力学, 2006, 10(2): 23-29. DOI:10.3969/j.issn.1007-7294.2006.02.004 |
| [5] |
DAWSON C W. A Practical Computer Method for Solving Ship-Wave Problems[C]. Second International Conference on Numerical Ship Hydrodynamics, 1977: 30-38.
|
| [6] |
RAVEN H. C., 1994. Nonlinear ship wave calculations using the rapid method[C]// In: Sixth International Conference on Numerical Ship Hydrodynamics, Iowa City.
|
| [7] |
RAVEN H. C., 1996. A solution method for the nonlinear ship wave resistance problem[D]. Delft, Netherlands: Delft University of Technology.
|
| [8] |
TARAFDER M S, SUZUKI K. Numerical calculation of free-surface potential flow around a ship using the modified Rankine source panel method[J]. Ocean Engineering, 2008, 35(5): 536-544. |
| [9] |
TARAFDER S M, SUZUKI K. Wave-Making Resistance of a Catamaran Hull in Shallow Water Using a Potential-Based Panel Method[J]. Journal of Ship Research, 2008, 52(1): 16-29. DOI:10.5957/jsr.2008.52.1.16 |
| [10] |
龚家烨, 李云波, 马庆位. 自由面条件ΦZZ项对非对称双体船阻力及航态预报影响[J]. 中国造船, 60(1): 103−114.
|
| [11] |
贺五洲, 程明道, 俞汉祥. 方艉舰船及加装尾板的兴波阻力计算[J]. 中国造船, 1998(2): 13. |
| [12] |
刘应中. 船舶兴波阻力理论[M]. 北京: 国防工业出版社, 2003: 81−91.
|
| [13] |
王中, 卢晓平, 王玮. 考虑升沉和纵倾的方尾船非线性兴波阻力计算[J]. 水动力学研究与进展, 2010(3): 150-156. |
| [14] |
周广利. 三体船型阻力预报、优化与系列性试验分析研究[D]. 哈尔滨工程大学, 2010.
|
| [15] |
PENG H, SHAOYU N, QIU Wei. Wave pattern and resistance prediction for ships of full form[J]. Ocean Engineering, 2014, 87(5): 162-173. |
| [16] |
SHERBAZ S. Ship Trim Optimization for Reducing Resistance by CFD Simulations[D]. Harbin, China, Harbin Engineering University, 2014.
|
 2021, Vol. 43
2021, Vol. 43
