0 引　言

螺旋桨激励是舰船水下噪声辐射的主要激励源^[1]。针对舰艇推进轴系的一般结构形式计算螺旋桨轴承力，仿真计算螺旋桨敞水特性，模拟螺旋桨激振力敞水环境中的变化规律。

轴系振动过程中，螺旋桨纵向激励的传递效率远高于横向激励的传递效率,轴系对螺旋桨纵向非定常激励的放大作用明显^[2]。因此通过建立桨轴耦合系统纵向振动动力学模型，求解轴系受纵向激励作用的振动响应和振动功率流。

将计算获得螺旋桨轴承力的脉动成分输入耦合系统，分析轴系在螺旋桨激励下的纵向振动响应和功率流传递、耦合效应和影响因素。相比已有研究，本文将螺旋桨激励特性和桨—轴—艇耦合振动结合起来进行分析，更加符合实际工况。

1 螺旋桨轴承力的计算

流体运动过程中满足质量守恒定理和动量守恒定律^[3]。使用Pro/E软件进行螺旋桨建模，用CFD方法仿真螺旋桨敞水动力性能，用MRF模型模拟稳态下的螺旋桨水动力性能。采用滑移网格模型提取螺旋桨定常轴承力随时间变化的曲线，Fourier变换获取螺旋桨激振力随频率变化的曲线。

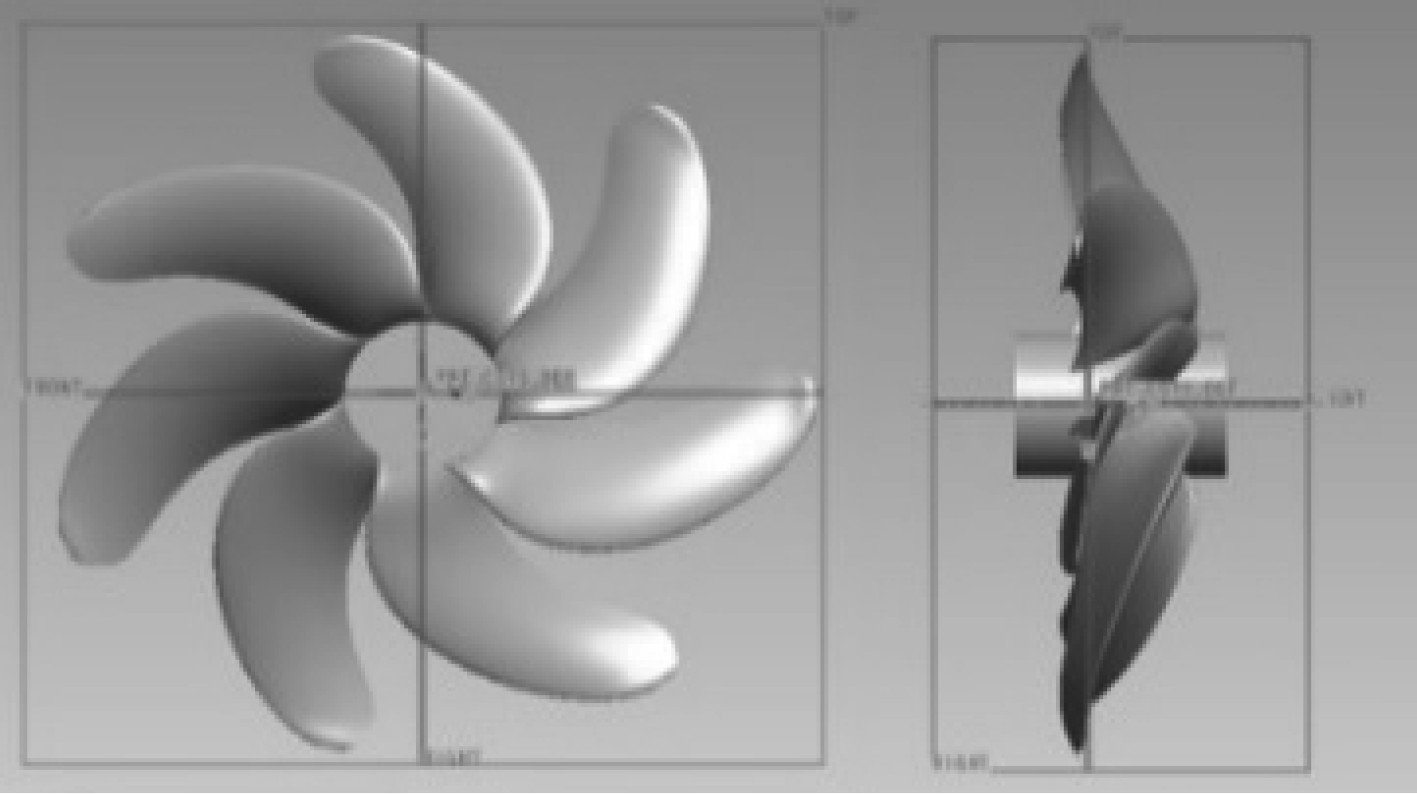
1.1 螺旋桨敞水特性计算

目标螺旋桨为7叶桨，直径3.10 m，螺距比0.753，伸展面积5.56 m²，直角坐标系如图1所示，来流方向为x轴负方向。

采用ICEM划分2个计算域，一是随桨转动的转动域，二是较大的静止域。转动域直径为1.2D，坐标原点至入口距离1D，至出口距离0.68D，网格质量为0.2，网格总数290万；静止域直径为6D，坐标原点至入口和出口距离分别为3D和6.9D。采用结构网格划分，网格质量为0.67，网格总数21万。

设置完毕后开始仿真计算。螺旋桨转速n=140 r/min，由 $ J=\dfrac{{V}_{s}}{nD} $ 可得相应进速系数下的平均来流速度 $ {V}_{s} $ 。

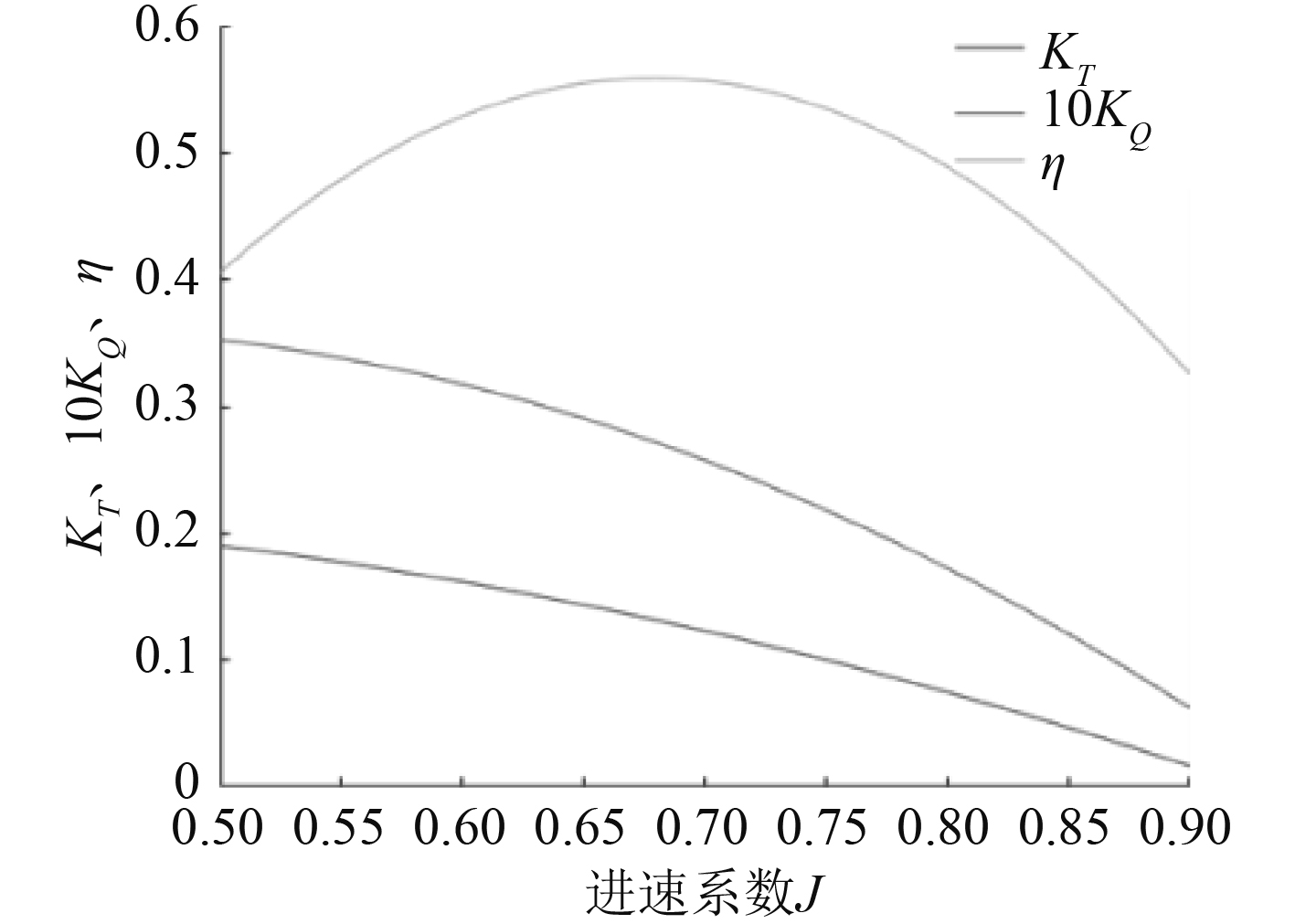
为将计算结果适用于其他转速，则需定义螺旋桨效率 $ \eta =\dfrac{J{K}_{T}}{2\text{π} {K}_{Q}} $ ，其中K_Q为功率系数,且 $ {K}_{Q}=\dfrac{Q}{\rho {n}^{2}{D}^{5}} $ ;K_T为推力系数，且 $ {K}_{T}=\dfrac{T}{\rho {n}^{2}{D}^{4}} $ 。选取第1800次迭代值作为稳定解，将数据点用多项式拟合后得到敞水特性曲线，如图2所示。 $ {K}_{T} $ 和扭矩系数随着J升高而降低，推进效率在J=0.7附近出现最值，仿真结果收敛。

1.2 螺旋桨轴承激振力的敞水计算

敞水环境下，桨叶转动过程中会形成复杂的流场，并使得螺旋桨推力和转矩呈现脉动。基于稳态计算，将区域运动模型变为滑移网格模型，其余设置不变，采样频率1×10³ Hz，步长0.001 s。监测发现，各轴承纵向力的脉动周期约为轴承力频率的7倍，与叶频一致。轴承力频率脉动的最大幅值也在叶频处，且在2倍叶频和3倍叶频处也有明显的脉动幅值，符合螺旋桨激振力的相关理论。

2 桨轴耦合系统纵向振动建模与解析

建立桨轴耦合系统纵向振动的力学模型，运用子结构导纳法求解运动微分方程，推导能量传递、能量分布等振动特性的计算方法。

2.1 系统纵振的建模与解析

假设各弹性支承件均为理想的线性弹性元件，螺旋桨质量集中于一点，如图3所示。

1）螺旋桨

螺旋桨的纵向激励包括螺旋桨推力的交变分量 $ {\tilde {F}}_{x} $ 和各轴承之间轴承力的交变分量 $ {\tilde {F}}_{L} $ 。设螺旋桨质量m_p，振动阻尼系数C_S， $ {\tilde {u}}_{p}\mathrm{为} $ 振动位移，正方向如图所示，则

$ {m}_{p}{\ddot{\tilde {u}}}_{p}=-{\tilde {F}}_{x}-{\tilde {F}}_{L}-{C}_{S}{\dot{\tilde {u}}}_{p}\text{。} $

(1)

2）传动轴

设轴密度为 $ {\ \rho }_{2} $ ，横截面积为S₂，杨氏弹性模量E₂，则有：

$ {\rho }_{2}{S}_{2}{\ddot{\tilde {u}}}_{2}\left({x}_{2,}t\right)-{E}_{2}{S}_{2}{\ddot{\tilde {u}}}_{2,xx}\left({x}_{2,}t\right)=0 \text{。}$

(2)

3）传动轴两端的端点处边界条件

$ {\tilde{u}}_{2}\left(0,t\right)={u}_{\rm{P}}，{\tilde{u}}_{2}\left({L}_{2},t\right)={\tilde{u}}_{\rm{LL}}\text{，}$

(3)

$ {S}_{2}{\tilde {U}}_{2,x}\left(0,\mathrm{t}\right)={\tilde {F}}_{P1},{E}_{2}{S}_{2}{\tilde {u}}_{2,\mathrm{x}}\left(L2,t\right)={\tilde {F}}_{A}\text{。} $

(4)

其中， $ {\tilde {u}}_{LL} $ 为传动轴远桨端纵向振动位移。

4）推力轴承

假设轴承润滑膜为周向均匀的线性弹性元件，则

${\tilde F_{\rm{F}}} = {k_{\rm{F}}}{\delta _u} = {\tilde F_{{\rm{FH}}}} = {k_F}\left( {{{\tilde u}_{{\rm{LR}}}} - {{\tilde u}_{{\rm{LL}}}}} \right)\text{。}$

(5)

式中：K_A为润滑膜刚度； $ {\delta }_{u} $ 为润滑膜纵向振动的厚度变化量； $ {\tilde {F}}_{FH} $ 润滑膜传至轴承座的激振力； $ {\tilde {u}}_{LR} $ 为推力轴承座的振动位移。

对上述微分方程组进行Fourier变换，其中式（2）有通解

${U_{\rm{2}}}\left( {{x_2},\omega } \right) = {{\rm{C}}_{\rm{1}}} \cdot \exp \left( { - {\rm{j}}{\lambda _{{\rm{L2}}}}{x_2}} \right) + {C_2} \cdot \exp \left( {{\rm{j}}{\lambda _{{\rm{L2}}}}{x_2}} \right)\text{，}$

(6)

再对Fourier变换后的方程组求解可得C₁和C₂表达式为：

$\left\{\begin{split}{C}_{1}\!=&[{\left({k}_{HH}\!-\!j{E}_{2}{S}_{2}{\lambda }_{L2}\right)\mathrm{exp}\left(j2{\lambda }_{L2}{L}_{2}\right)}]/[\left({Z}_{PL}{\!+\!jE}_{2}{S}_{2}{\lambda }_{L2}\right)\times\\ &\left({k}_{HH}-j{E}_{2}{S}_{2}{\lambda }_{L2}\right)\mathrm{exp}\left(j2{\lambda }_{L2}{L}_{2}\right)-\left({Z}_{PL}{-jE}_{2}{S}_{2}{\lambda }_{L2}\right)\times\\ &\left({k}_{HH}+j{E}_{2}{S}_{2}{\lambda }_{L2}\right)]{\tilde {F}}_{F}\text{，}\\ {C}_{2}\!=&[{{k}_{HH}+j{E}_{2}{S}_{2}{\lambda }_{L2}}]/[\left({Z}_{PL}{-jE}_{2}{S}_{2}{\lambda }_{L2}\right)\times\\ &\left({k}_{HH}+j{E}_{2}{S}_{2}{\lambda }_{L2}\right)-\left({Z}_{PL}{+jE}_{2}{S}_{2}{\lambda }_{L2}\right)\times\\ &\left({k}_{HH}-j{E}_{2}{S}_{2}{\lambda }_{L2}\right)\mathrm{exp}\left(j2{\lambda }_{L2}{L}_{2}\right)]\widetilde {{\tilde {F}}_{F}}\text{。}\end{split}\right.$

(7)

式中： $ {Z}_{PL}={\omega }^{2}{m}_{p}-j\omega {C}_{Px} $ 。当 $ {\tilde {F}}_{F}=0 $ 时，能使C₁和C₂表达式的分母部分为零的 $ \omega $ 解均为轴系纵向振动的固有频率。

2.2 功率流及振动能量密度的计算

轴系纵振的能量耗散途径主要有2个：一是通过推进轴系以激振力的方式传递给船体，二是在流场中以噪声的形式向外辐射。

螺旋桨轴向激励 $ {\tilde {F}}_{x}\mathrm{输}\mathrm{入} $ 的振动功率流

$ {P}_{FX}=\frac{\omega }{2\text{π} }{\int }_{0}^{2\pi /\omega }Re\left\{{\tilde {F}}_{x}\right\}\bullet Re\left\{{\dot{\tilde {u}}}_{p}\right\}{\rm d}t \text{，}$

(8)

振动阻尼耗散平均功率

$ {P}_{cpx}=\frac{\omega }{2\text{π} }{\int }_{0}^{2\text{π} /\omega }Re\left\{{c}_{pk}{\dot{\tilde {u}}}_{p}\right\}\bullet Re\left\{{\dot{\tilde {u}}}_{p}\right\}{\rm d}t\text{，} $

(9)

桨轴连接面的功率流传递

$ {P}_{FL}=\frac{\omega }{2\text{π} }{\int }_{0}^{2\text{π} /\omega }Re\left\{{\left(ES\right)}_{2}{\tilde {u}}_{2,x}\left(0,t\right)\right\}\bullet Re\left\{-{\dot{\tilde {u}}}_{2}\left(0,t\right)\right\}{\rm d}t \text{，}$

(10)

推力轴承向轴承座及船体的功率流

$ {P}_{FX}=\frac{\omega }{2\text{π} }{\int }_{0}^{2\text{π} /\omega }Re\left\{-{\tilde {F}}_{FH}\left(t\right)\right\}\bullet Re\left\{{\dot{\tilde {u}}}_{LR}\right\}{\rm d}t \text{。}$

(11)

3 桨轴耦合纵向振动功率流传递特性

基于Matlab建模计算轴系纵向振动功率流。推进系统相关基础参数参照文献[4]中关于某型船推进系统的基础参数。输入前文计算得出的螺旋桨轴承激振力数据，分别观察系统在单位激励和计算所得激励的作用下产生的振动响应，计算并分析螺旋桨激励在耦合系统中的功率流传递特性和能量耗散过程。

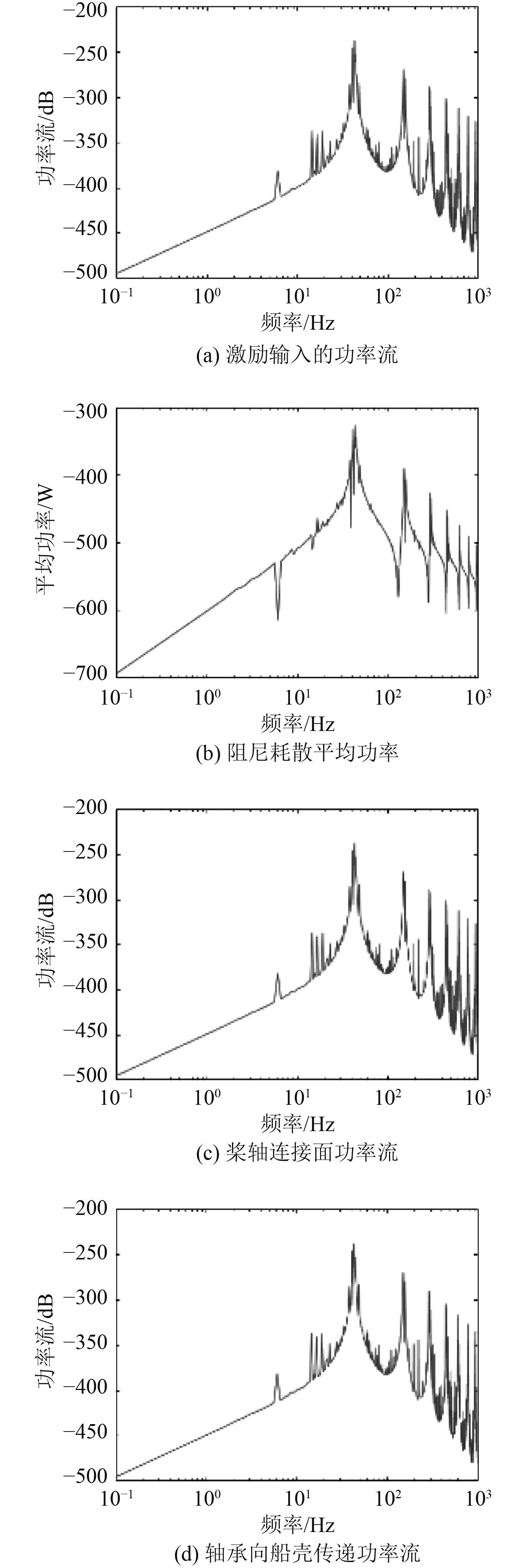
将单位激振推力输入桨轴耦合系统得到频谱组如图4所示。

图中各图较明显的共振峰表达了轴的模态特性。由于轴承纵向刚度很大，因此轴壳之间的耦合作用效果也较强。

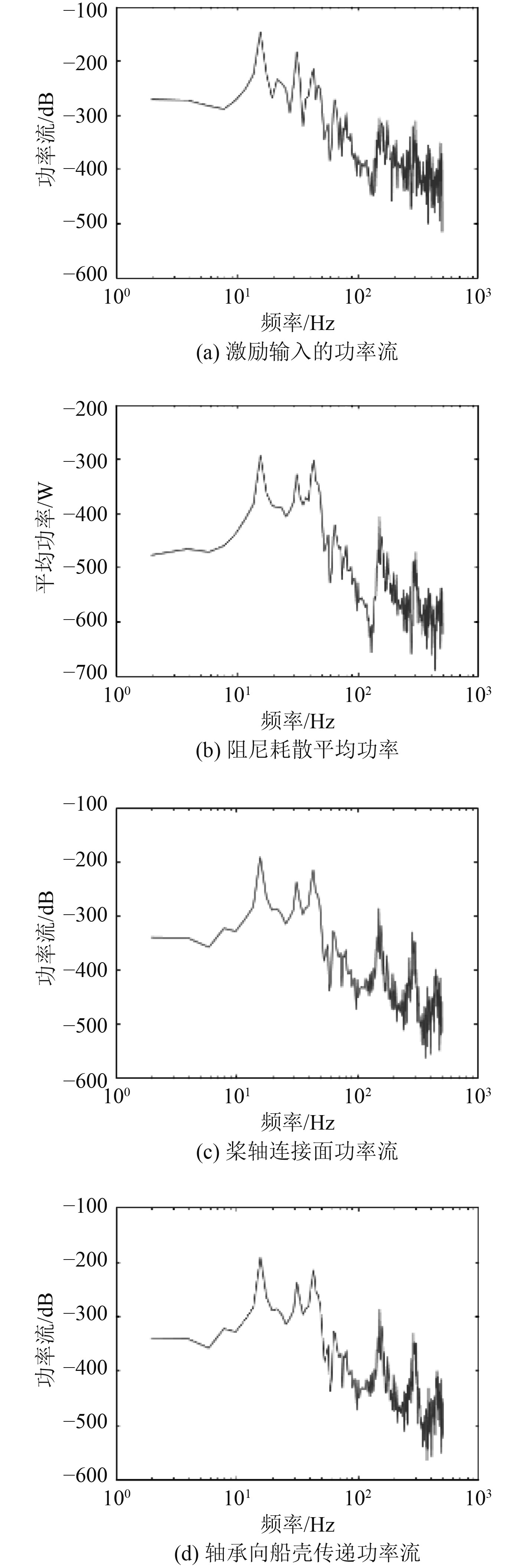
将计算所得激励作为激励源输入系统得到图5。

2组频域图的相同之处：在第1段主峰（54～58 Hz）前的频域，各功率流和能量值均与频率成正比，越过第1段主峰后曲线的表现形式改为震荡下行；当激振力频率接近系统固有频率时产生共振现象；频率越高曲线振动的模态就越密集。

不同之处：比较2组图中的(a)和(c)，单位激励输入的功率流几乎全部经过桨轴连接面传递至传动轴。而在本文计算所得螺旋桨激励下，螺旋桨受流体的激功率远高于通过桨轴连接面至传动轴的部分。

纵向振动的功率流始终以较高的效率传递给船体，这也证明了前文中关于纵向振动在能量传递上处于主导地位的引述。

4 结　语

通过以上研究分析得出如下结论：

1）桨轴耦合系统纵向振动中的各传递功率流随着激振力频率升高呈逐渐降低、震荡下行的趋势；

2）激振力频率与系统固有频率相近会引发共振现象；

3）推力轴承的纵向传递路径相对简单，刚度很大，轴与船体结构在轴向方向的联结精确且可靠，因此振动耦合作用较强。螺旋桨激振力频率越高时，各功率流模态的密集型就越强；

4）纵向激励输入的功率流以较高的效率最终传递给船体，纵向振动能量传递是能量传递整体的主体部分；

5）在螺旋桨激励输入系统前，流体阻尼等因素就已经损耗掉部分振动功率流，损耗比例与激振力频率成正比。

关于螺旋桨激励下桨轴艇系统纵向振动响应机理的分析，有助于更加深入的研究螺旋桨激励与船体结构振动的必然联系，为舰船减振降噪工程提供部分理论参考。