2. 喷水推进技术重点实验室,上海 200011
2. Science and Technology of Water Jet Propulsion Laboratory, Shanghai 200011, China
舵是船舶的转向构件,对于螺旋桨推进的船舶一般采用平面舵,而喷水推进船则采用箱型舵和球形舵。球形舵是国内外中小型喷水推进装置采用较多的一种方向舵,外形如图1所示。球形舵尺寸小、重量轻、舵效较好,但是对其水动力性能缺乏系统研究,在以往的设计中对操舵力和操舵扭矩预报多基于经验公式,准确性有待验证。另外,球形舵的设计参数较多,不同参数下球形舵的操舵力和操舵扭矩不同,本文对球形舵的水动力性能进行研究,并通过改变收缩角度以研究收缩角对其水动力性能的影响,这对球形舵的工程设计具有重要的指导意义。

|
图 1 球形舵 Fig. 1 The spherical rudder |
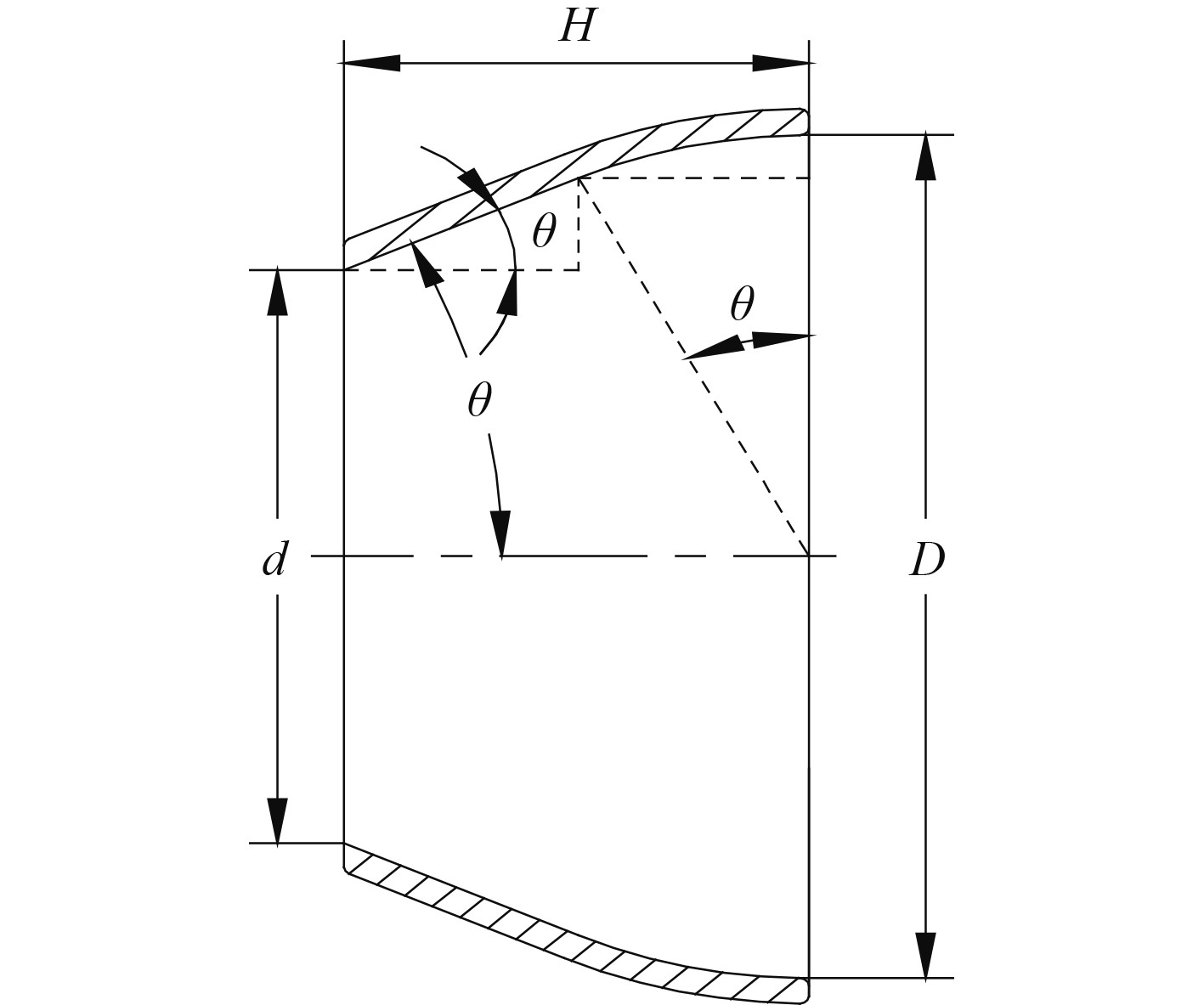
球形舵是中小型喷水推进装置操舵倒航机构的组成部件,球形舵的特征尺寸如图2所示。
|
图 2 球形舵的特征尺寸图 Fig. 2 The feature dimensions of spherical rudder |
图中,D为球形舵的入口端直径,d为球形舵的出口端直径,θ为球形舵的收缩角,H为球形舵的长度。在以上的尺寸中,D和d为由喷水推进装置喷口Dj的大小决定的,是球形舵设计中的固定量;H为球形舵的长度,根据图3的辅助虚线可得出其表达式为
|
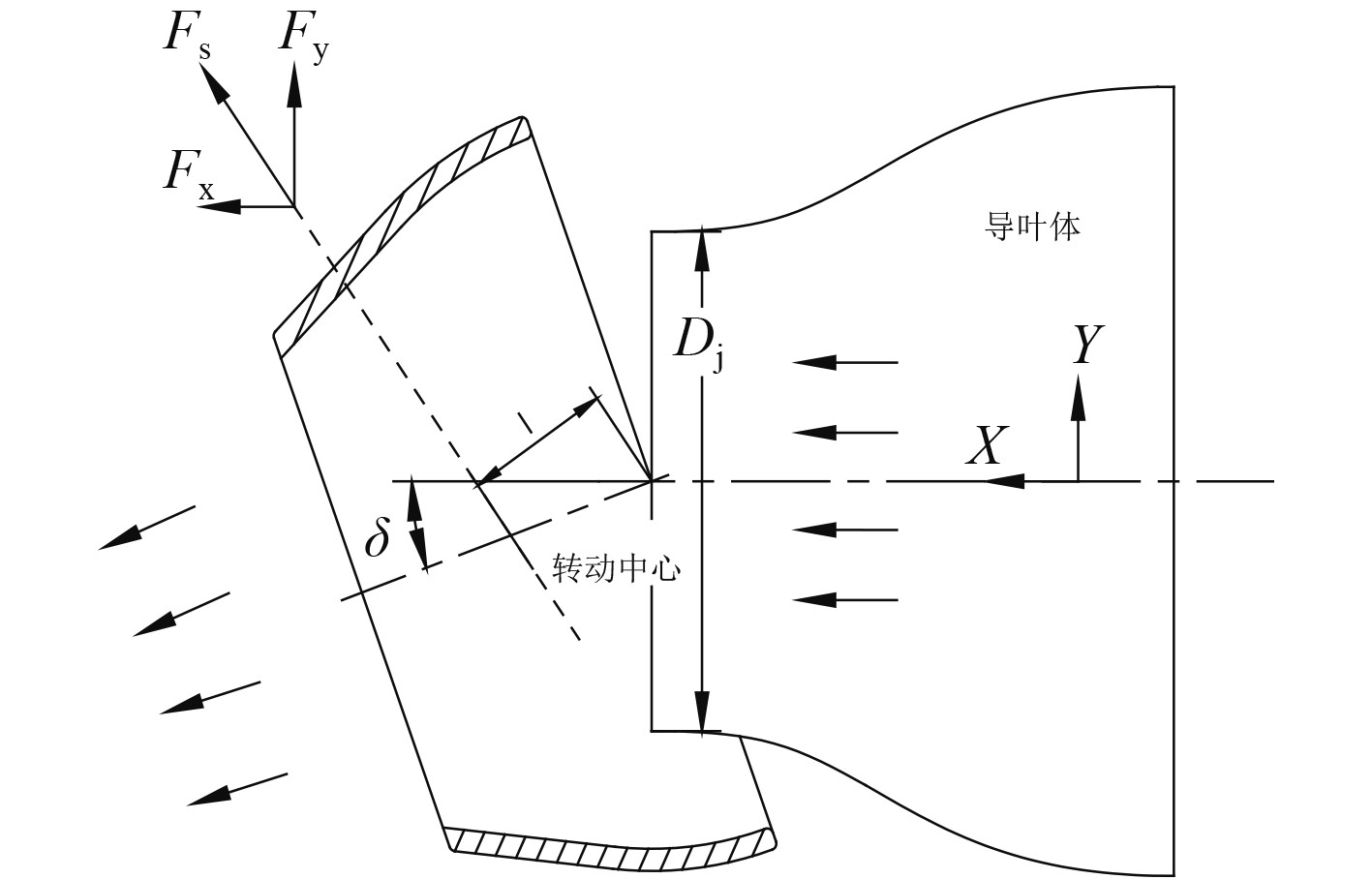
图 3 球形舵的操舵力示意图 Fig. 3 The steering force of spherical rudder |
球形舵在操舵液压缸的驱动下发生偏转,引起喷水推进泵喷出的高速水流发生偏转,根据作用力和反作用力,水流对船体产生围绕其重心的力矩,该力矩引起船体转向。
球形舵偏转舵角δ,导叶体喷出的高速水流冲击在球形舵上,对球形舵产生操舵力FS,FS产生转船力矩为:
| $M = {F_S} \times L \text{,}$ | (1) |
式中:L为舵力FS到船舶重心G的距离。
FS可以分解为沿船宽方向的侧向作用力Fy和沿船长方向的纵向作用力Fx,Fy是产生船舶转向力矩的作用力,Fx是导致船舶航速降低的作用力,是阻力。就舵的水动力性能而言,希望Fy越大越好,Fx越小越好。
在操舵倒航机构的设计中,不仅要设计方向舵的形式,还需提供驱动方向舵偏转的操舵扭矩MS,为操舵液压缸的设计提供输入条件。
| ${M_S} = {F_S} \times l \text{。}$ | (2) |
式中:l为操舵力FS到方向舵转动中心的距离。
对舵力FS的分力Fy,Fx和MS进行水动力性能研究。
2 数值计算 2.1 计算模型和计算区域在球形舵的水动力研究中,设计了3个不同的收缩角,分别是24°,26°和28°。数值模拟计算中确定喷水推进器的喷口Dj为0.2 m,出口流量Q为0.32 m3/s,球形舵的偏转角度δ设定为5°,10°,15°,20°,25°,30°,35°共21个计算工况,计算区域如图4所示。

|
图 4 计算域模型 Fig. 4 Computational domain model |
由于球形舵结构形状不规则,采用适应性更强的非结构化网格。对局部曲率变化比较大的区域采用网格加密处理,网格数量在225万左右。
2.3 边界条件及求解方法外部边界为压力出口,喷口为速度入流条件,近壁区为标准壁面函数,球形舵进口监测面为内部面,球形舵及喷口为固壁面。采用RNG k-ε湍流模型和PISO算法,湍动能、湍动能耗散率及动量方程中的对流项采用二阶迎风格式,扩散项采用中心差分格式。
3 计算结果分析 3.1 侧向作用力Fy分析以进入方向舵的水流作为研究对象,应用牛顿第二定律和动量定理,如果不考虑损失,侧向作用力理想值等于球形舵侧向动量变化量和偏折角的正弦:
| ${F_{yt}} = \rho Q{V_j}\sin \delta \text{。} $ | (3) |
式中:ρ为水的密度;Q为进入球形舵内的流量;Vj为进入方向舵内水流的速度;δ为舵角。
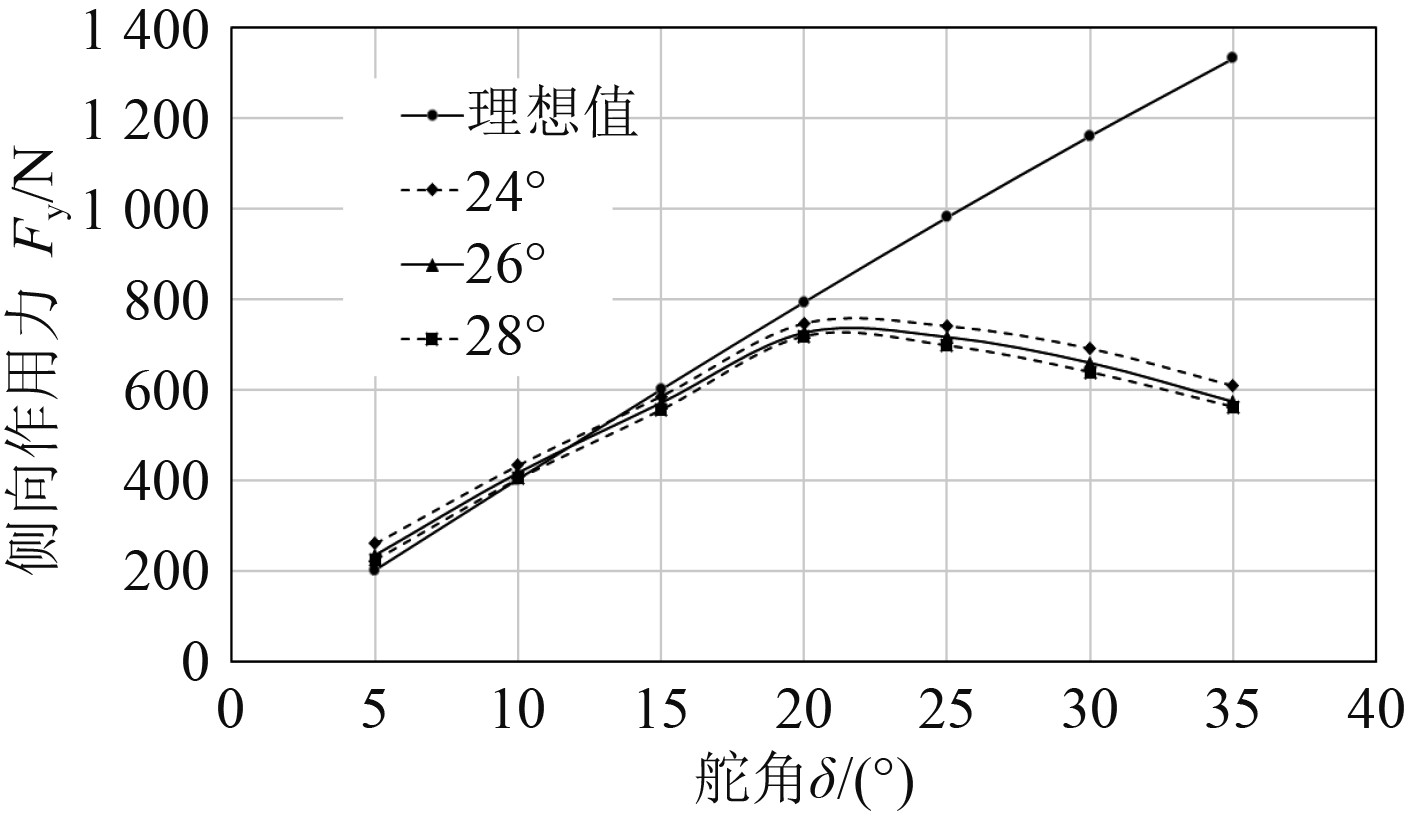
侧向作用力计算值与理想值随舵角变化如表1所示,绘制曲线后如图5所示。可以看出侧向作用力理想值Fyt和侧向作用力Fy计算值随着操舵角δ的增加而增加,但Fy计算值并不会一直增大,而是在23°左右达到最大值,随后继续下降,在操舵角超过30°后,计算值仅为理想值的一半。收缩角度的变化对侧向作用力产生了一定的影响,收缩角度越小侧向作用力越大。
|
|
表 1 侧向作用力计算结果 Tab.1 Yawing force calculation results |
|
图 5 侧向作用力Fy对比图 Fig. 5 Comparison diagram of yawing force |
纵向作用力Fx是引起船体速度降低的作用力。根据牛顿第二定律和动量定理,纵向作用力Fxt理想值为:
| ${F_{xt}} = \rho Q{V_j}(1 - \cos \delta )\text{。}$ | (4) |
式中:ρ为水的密度;Q为进入球形舵内的流量;Vj为进入方向舵内水流的速度;δ为舵角。
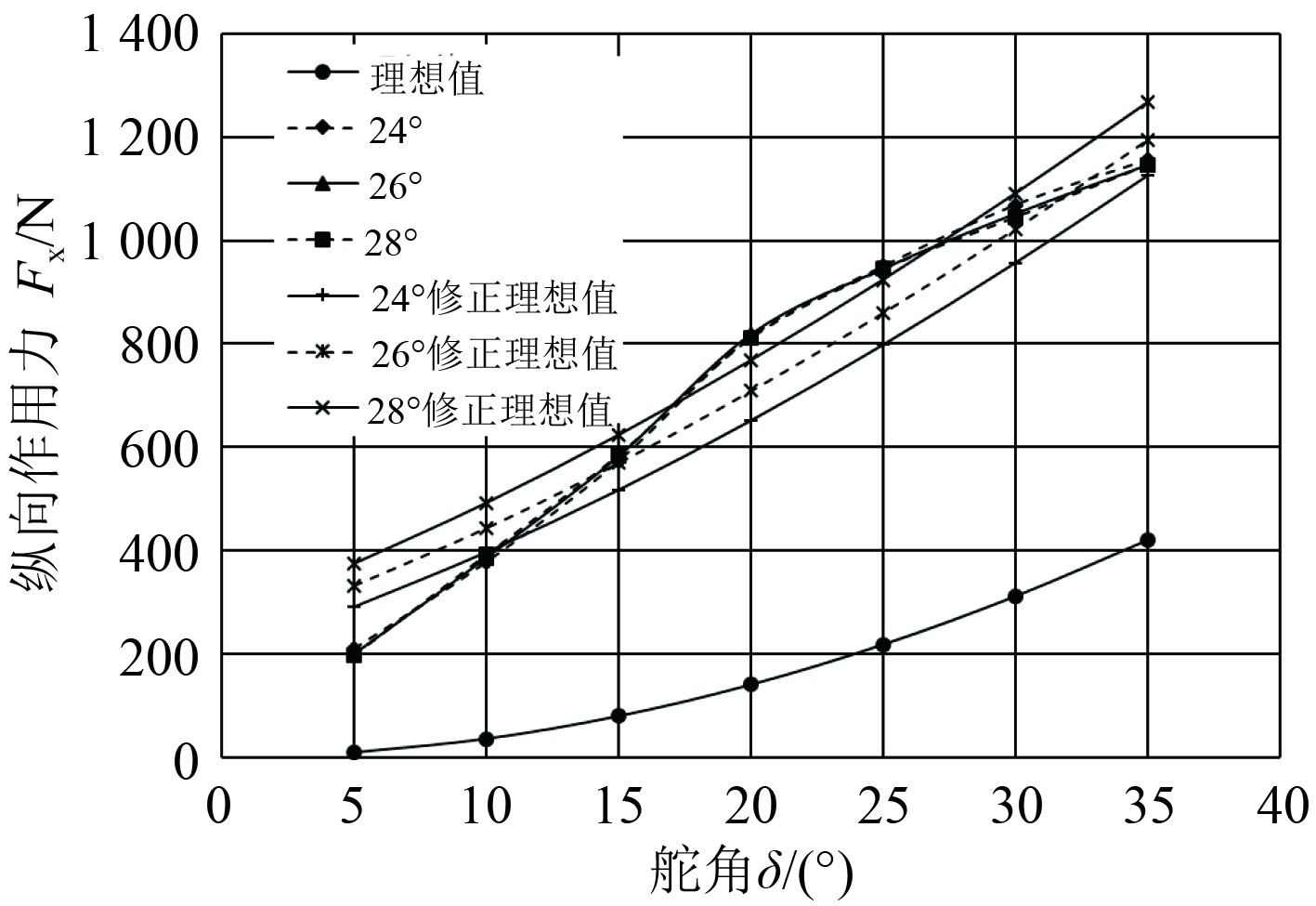
纵向作用力计算值和理想值如表2所示,绘制成曲线如图6所示。可以看出数值计算出的结果较理想值大,且偏差超过100%。对出现此现象的原因进行分析,结合图2,认为Fx理想值公式是以进入方向舵内的水流为控制体进行分析的,而实际状况是高速水流冲击在方向舵的内侧板上,内侧板偏转的角度为θ+δ,Fxt理想值的表达式应该修正成:
| ${F_{xt}} = \rho Q{V_j}(1 - \cos (\theta + \delta )) \text{。}$ | (5) |
将修正过的纵向作用力也绘制在图6中,可以看出修正过的理想值和计算值较为接近。从图6还可以看出纵向作用力对收缩角的敏感性较低,收缩角度变化,纵向作用力变化不大。
|
|
表 2 纵向作用力计算值 Tab.2 Longitudinal force calculation results |
|
图 6 纵向作用力对比图 Fig. 6 Comparison diagram of longitudinal force |
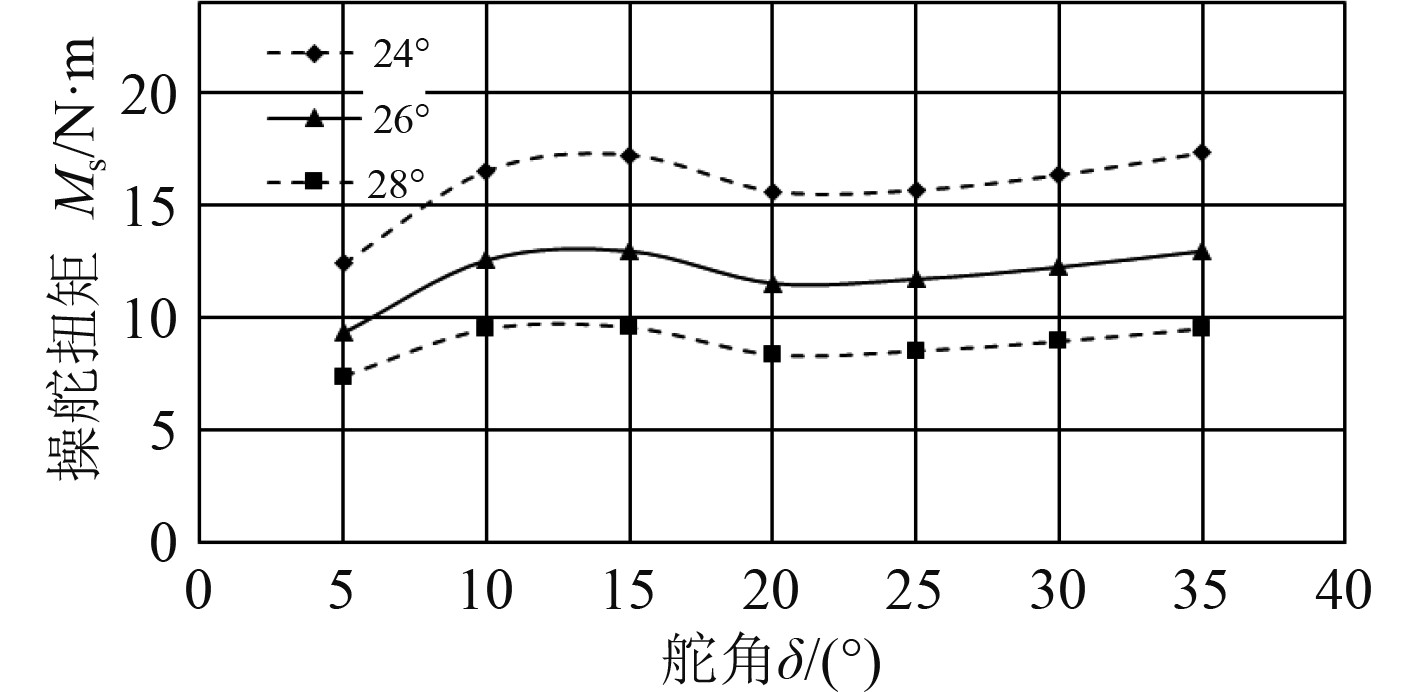
操舵扭矩的确定是球形舵设计的重要组成部分,其是操舵液压缸的设计输入,本次借助数值模拟计算手段,计算的操舵扭矩数值如表3所示,绘制成曲线如图7所示。
|
|
表 3 操舵扭矩MS计算值 Tab.3 The torque of steering calculation results |
|
图 7 操舵扭矩的计算值对比图 Fig. 7 Comparison diagram of the torque of steering force |
从上述计算结果可看出操舵扭矩并不随着舵角的增加而不断增大,而是先随着舵角增加而增大,在操舵角15°左右达到最大值,随后继续下降,在操舵角23°左右达到最小值,然后随着舵角增加而增大,增速较缓。由此可知在预报操舵扭矩时不应仅计算最大设计舵角工况的力矩,而应该对整个操舵角度范围内的典型舵角进行计算,求出操舵扭矩的最大值指导操舵液压缸的设计。不同收缩角度的操舵扭矩相差较为明显,收缩角越大,操舵扭矩越小。由式(2)可知,操舵力矩偏差较大的原因是操舵力到舵转轴中心的距离相差较大,据此可得出距离对收缩角度较敏感。
4 结 语本文借助数值模拟手段计算了球形舵的水动力性能,得出结论如下:
1)球形舵的最大舵角建议设计在23°左右,侧向作用力在舵角23°达到最大值。
2)侧向作用力的大小和收缩角存在负相关,收缩角越大,侧向作用力越小,但减小较慢;而纵向作用力和收缩角关系不大。在实际工程设计中,在布置空间有限的条件下,可以适当增大收缩角以减小球形舵的纵向长度。
3)操舵扭矩的确定需借助数值模拟手段确定,因为操舵扭矩和操舵角并不是线性关系,其最大值可能出现在操满舵的过程中。
4)操舵扭矩随着球形舵收缩角度的增加下降明显,在工程设计中,在保证侧向作用力的条件下,增加球形舵的收缩角度,可明显降低操舵液压缸的重量。
| [1] |
ZHAI Zhihong, LIU Xueqin, WANG Jun, et al. Numerical simulations of the steering device in waterjet propulsion and analyses of steering forces[C]. Proceedings of the 13th International Conference on Hydrodynamics. Songdo, Korea, 2018.
|
| [2] |
LI Guibin, WANG Lixiang, WANG Jun. Research of forces on the steering and reversing gear[C]. The Second International Workshop on Waterjet Propulsion, Shanghai, China, 2017, 44-51.
|
| [3] |
JOHN ALLISON, CHARLES DAI. Steering and Reversing Gear for Very Large Waterjets[C]. International Symposium on Waterjet Propulsion Latest Developments. London. UK. 1994.
|
| [4] |
M S CHISLETT, MSC ECLECTICS, AXEL MΦLGAARD. Waterjet Steering and Stopping force[C]. The International Conference on Waterjet Propulsion Latest Developments. Amsterdam. Sweden. 1998.
|
| [5] |
AARTOJÄRVI R, HEDER Dr. M, UNDBERG J L, etc. Implementation of results of CFD analysis to the design of a new waterjet steering and reversing unit[J]. The Royal Institution of Naval Architects, 2004. |
| [6] |
蔡佑林, 夏立明, 刘建国. 喷水推进混流泵流道主参数确定方法与验证[J]. 船舶, 2014(2): 58-61. CAI You-lin, XIA Li-ming, LIU Jian-guo. Determination and verification of major parameters of flow channel for water-jet mixed-flow pumps[J]. SHIP& BOATS, 2014(2): 58-61. DOI:10.3969/j.issn.1001-9855.2014.02.011 |
| [7] |
汲国瑞, 蔡佑林, 李宁, 尹晓辉, 俞瑜. 喷水推进进口流道倾斜角对其效率影响分析[J]. 舰船科学技术, 2016(3): 55-58. JI Guo-rui, CAI You-lin, LI Ning, YIN Xiao-hui, YU yu. Analysis about affect of inclination angle on the efficiency of the waterjet propulsion inlet duct[J]. Ship Science and Technology, 2016(3): 55-58. DOI:10.3404/j.issn.1672-7619.2016.03.012 |
| [8] |
王福军. 计算流体动力学分析——流体动软件原理与应用[M]. 北京: 清华大学出版社, 2004.
|
 2021, Vol. 43
2021, Vol. 43
