现代潜艇的升降舵一般分为首升降舵和尾升降舵2种。由于首升降舵布置在靠近潜艇的首部,距离重心的距离比尾升降舵要小的多,因此现代潜艇上的传统操舵方式是首升降舵控制深度,尾升降舵控制纵倾。操首升降舵时,舵力的作用与舵力矩的作用方向相同,首升降舵的舵力也是促使潜艇运动速度改变方向的作用力之一。因此,操首升降舵时没有反向位移,刚开始转舵就能够迅速改变潜艇垂速方向。在潜艇低速航行时,尤其当航速处于尾舵逆速附近时,操纵首舵显得更加有效。首升降舵的舵力和力矩作用方向相同的特点,还用来克服部分二阶波浪吸力,以保持艇的潜望镜深度。目前潜艇的首升降舵布置分为首端首舵和围壳舵2种形式。不同形式的首升降舵布置对潜艇的垂直面操纵性能的影响是不一样的。围壳舵适于保持深度和无纵倾或以甚小纵倾来变深,而首端首舵可以提供较大的纵倾力矩。英国潜艇专家R.Burcher曾经评论[1]:“即便迄今,潜艇设计师们在设置首升降舵在潜艇上的位置方面仍存在着许多的争论和广泛的意见分歧。”可以说,首升降舵的设置是肯定也是必须的,但其布置确有多样的见解。
本文以模型潜艇为研究对象,仿真分析不同布置方式下单位舵角的操舵响应和梯形操舵响应,计算升速率、逆速和平衡舵角,并对2种首升降舵布置方式条件下的潜艇垂直面操纵性能进行了模糊综合评判。
1 首升降舵的布置方式首升降舵布置分为围壳舵和首端首舵2种形式。首端首舵一般布置在潜艇艇体首部靠下的位置,其布置方式如图1所示。首端首舵的特点是力臂较长,因此相同的舵面积产生的水动力矩较大。一般来说,首端首舵都是可折叠或伸缩的,在潜艇水上航行时为减少航行阻力首端首舵处于收回状态。另外,为了降低潜艇在垂直面内可能产生摆动现象的几率,并考虑到高速时首升降舵的操纵效率较低,在潜艇水下高速航行时,首端首舵在必要的情况下也需要收回[2]。由于首端首舵及其伸缩装置需要占用潜艇首部的空间资源,因此首端首舵的舵面积相对较小,其提供的舵力也相对不大。

|
图 1 首端首舵布置方式 Fig. 1 Head bow rudder layout |
围壳舵是指布置在潜艇指挥室围壳上的首升降舵,其布置方式如图2所示。由于没有布局空间的限制,围壳舵的舵面积要比首端首舵大的多,一般围壳舵舵面积比首端首舵大90%~120%,但是其舵力的作用点受限于指挥室围壳的位置,距离重心较近,因此围壳舵可提供较大的升力和较小的纵倾力矩,适于保持深度和无纵倾或以甚小纵倾来变深。从使用上看,围壳舵减免了繁琐的收舵机构,减小了备潜过程中首舵收放机构产生故障的概率,并减轻了艇员的相关操作。另外,潜艇水下高速航行时,围壳舵的布置方式也避免了因操舵干扰艇首声呐工作的情况。但是在冰区航行时上浮过程中可能会损坏围壳舵舵叶,因此限制了围壳舵潜艇在北极冰层下的作战活动[3]。

|
图 2 围壳舵布置方式 Fig. 2 Enclosure bow rudder layout |
采用计算机仿真技术分析首升降舵布置方式对潜艇操纵性能影响,首先要建立潜艇操纵运动方程。由于首升降舵主要用来改变和保持潜艇垂直面内的深度和纵倾角而不涉及水平面的航向变化,因此采用垂直面操纵运动非线性方程[4-5](忽略水平面的影响)来描述操纵升降舵后的潜艇的运动状态,即
| $\begin{split} & m(\dot u + wq) = \\ &\quad\frac{1}{2}\rho {L^4}\left( {{{X}_{qq}^{'}}{q^2}} \right) + \frac{1}{2}\rho {L^3}\left( {{{X}_{\dot u}^{'}}\dot u + {{X}_{wq}^{'}}wq} \right) +\\ &\quad \frac{1}{2}\rho {L^3}\left( {{{X}_{uu}^{'}}{u^2} + {{X}_{ww}^{'}}{w^2}} \right) + \frac{1}{2}\rho {L^2}{u^2}\left( {{{X}_{{\delta _s}{\delta _s}}^{'}}\delta _s^2 + {{X}_{{\delta _b}\delta b}^{'}}\delta _b^2} \right)+ \\ &\quad \frac{1}{2}\rho {L^2}\left( {{a_T}{u^2} + {b_T}u{u_c} + {c_T}u_c^2} \right)\text{,} \\[-15pt] \end{split} $ | (1) |
| $\begin{split} & m(\dot w - uq)= \\ & \quad\frac{1}{2}\rho {L^4}\left( {{{Z}_{\dot q}^{'}}\dot q + {{Z}_{q\left| q \right|}^{'}}q\left| q \right|} \right)+ \\ & \quad\frac{1}{2}\rho {L^3}\left( {{{Z}_{\dot w}^{'}}\dot w + {{Z}_{q}^{'}}uq + {{Z}_{w\left| q \right|}^{'}}w\left| q \right|} \right) +\\ &\quad \frac{1}{2}\rho {L^2}\left( {{{Z}_0^{'}}{u^2} + {{Z}_w^{'}}uw + {{Z'}_{\left| w \right|}}u\left| w \right| + {{Z}_{w\left| w \right|}^{'}}w\left| w \right|} \right)+ \\ &\quad \frac{1}{2}\rho {L^2}\left( {{{Z}_{ww}^{'}}{w^2} + {{Z}_{{\delta _b}}^{'}}{u^2}{\delta _b} + {{Z}_{{\delta _s}}^{'}}{u^2}{\delta _s}} \right) \text{,} \end{split} $ | (2) |
| $\begin{split} &{I_{{\rm{yy}}}}\dot q =\\ & \quad\frac{1}{2}\rho {L^5}\left[ {{{M}_{\dot q}^{'}}\dot q + {{M}_{q\left| q \right|}^{'}}q\left| q \right|} \right]+ \\ & \quad\frac{1}{2}\rho {L^4}\left[ {{{M}_{\dot w}^{'}}\dot w + {{M}_{q}^{'}}uq + {{M}_{\left| w \right|q}^{'}}\left| w \right|q} \right] +\\ & \quad\frac{1}{2}\rho {L^3}\left[ {{{M}_{0}^{'}}{u^2} + {{M}_{w}^{'}}uw + {{M}_{w\left| w \right|}^{'}}w\left| w \right|} \right] +\\ & \quad\frac{1}{2}\rho {L^3}\left[ {{{M}_{\left| w \right|}^{'}}u\left| w \right| + {{M}_{ww}^{'}}{w^2} + {{M}_{{\delta _b}}^{'}}{u^2}{\delta _b} + {{M}_{{\delta _s}}^{'}}{u^2}{\delta _s}} \right] \text{,} \\[-8pt] \end{split} $ | (3) |
| $\dot \theta = q\text{,}$ | (4) |
| $\dot \zeta = - u\sin \theta + w\cos \theta \text{。} $ | (5) |
式中:u为纵向速度;w为垂向速度;θ为纵倾角;q为纵倾角速度;uc为潜艇指令航速;m为潜艇质量;L为艇长;Iyy为纵向转动惯量;h为纵稳性高,δb为首升降舵角;δs为尾升降舵角;
需要强调的是,式(1)~式(3)中带下标的为潜艇水动力系数,本文中模型潜艇的水动力系数均是由平面运动机构测得的模型试验结果。
2.2 首升降舵舵力(矩)系数的确定潜艇垂直面操纵运动方程中的诸水动力系数中与首升降舵直接相关的水动力是
在保持模型潜艇其他所有参数不变和首端首舵操纵面形状不变的条件下,将首升降舵舵面积扩大一倍并移至指挥室围壳上(围壳舵舵力中心点距离潜艇重心减小至6.8 m),重新利用平面运动机构测得与首升降舵相关的水动力系数为:
基于垂直面操纵运动数学模型,以模型潜艇为研究对象,采用C#语言编写潜艇操纵运动仿真软件[6-7]。通过仿真实验进一步分析首升降舵不同布置方式下的潜艇运动特性。
3.1 单位舵角下的操舵响应图3为初始航速8 kn,初始深度30 m,首升降舵布局方式分别为首端首舵和围壳舵操单位舵角时潜艇的自由运动曲线。

|
图 3 不同布局方式下的操单位舵角潜艇运动参数 Fig. 3 Motion parameters of submarine operating unit rudder Angle under different layouts |
可以看出:
1)处于无纵倾等速直线定深运动状态的潜艇操纵首升降舵单位舵角后潜艇最终趋向定常直线潜浮运动。对首端首舵来说,操单位舵角后潜艇最终将以首倾1°左右做首倾下潜运动;而对于围壳舵来说,操单位舵角后潜艇最终做无纵倾(纵倾角仅有不到0.2°,近似于无纵倾)下潜运动。
2)首端首舵操单位舵角300 s后,深度从30 m下潜至50.85 m;而围壳舵操单位舵角300 s后,深度从30下潜至36.69 m。首端首舵的变深能力优于围壳舵。
3)由于围壳舵的舵力作用点距离潜艇重心很近,因此围壳舵适于操纵潜艇做无纵倾变深运动。而单独操纵首端首舵很难做到无纵倾变深。对于首升降舵是首端首舵的潜艇来说,如果希望潜艇做无纵倾变深运动,必须首、尾升降舵配合操纵控制。
3.2 梯形操舵响应处于定深航行状态下的潜艇,如果操纵潜艇转换至新的航行深度,有多种操舵模式均可以实现,但是在研究潜艇垂直面运动的机动性时,通常将这种变深的操舵模式简化为某种确定的操舵规律,其中最为典型的就是梯形操舵。所谓梯形操舵,是指潜艇在做无纵倾定深直航中仅操纵升降舵舵角(依从线性规律)δ0,潜艇形成一定的纵倾角变深,当到达规定的纵倾角和深度后再回舵,使升降舵逐渐回到最开始的舵角,纵倾角逐渐归零而艇进入另一个深度作无纵倾直航[4]。梯形操舵的数学表达式可写成:
| $ \delta(t)=\left\{\begin{array}{ll} \dot{\delta}t \text{,} & t \leqslant t_{1} \text{,}\\ \delta_{0} \text{,} & t_{1} \leqslant t \leqslant t_{2}\text{,} \\ \delta_{0}-\delta\left(t-t_{2}\right) \text{,} & t_{2} \leqslant t \leqslant t_{3}\text{。} \end{array}\right. $ | (6) |
其中:
图4和图5分别为首升降舵的布置方式分别为首端首舵和围壳舵时梯形操舵方式下潜艇的深度和纵倾响应曲线。其中梯形操舵的规律为潜艇初始航速8 kn,初始深度30 m,仿真开始后,操首升降舵下潜舵20°,30 s开始回舵至初始舵角。
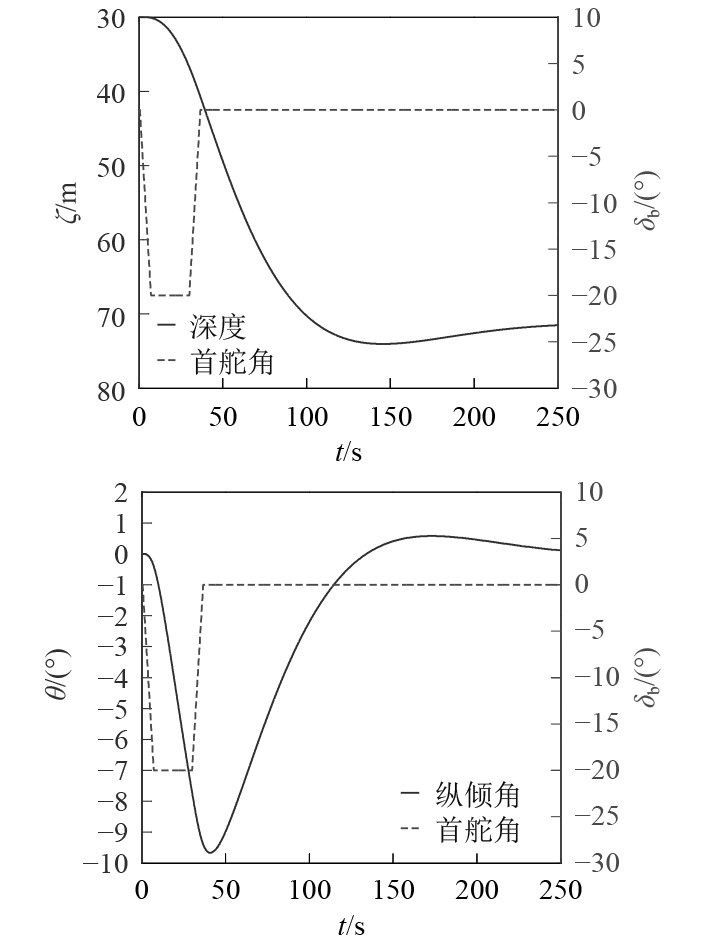
|
图 4 首端首舵梯形操舵深度和纵倾角响应曲线 Fig. 4 Trapezoidal steering depth and inclination response curve (Head bow rudder) |
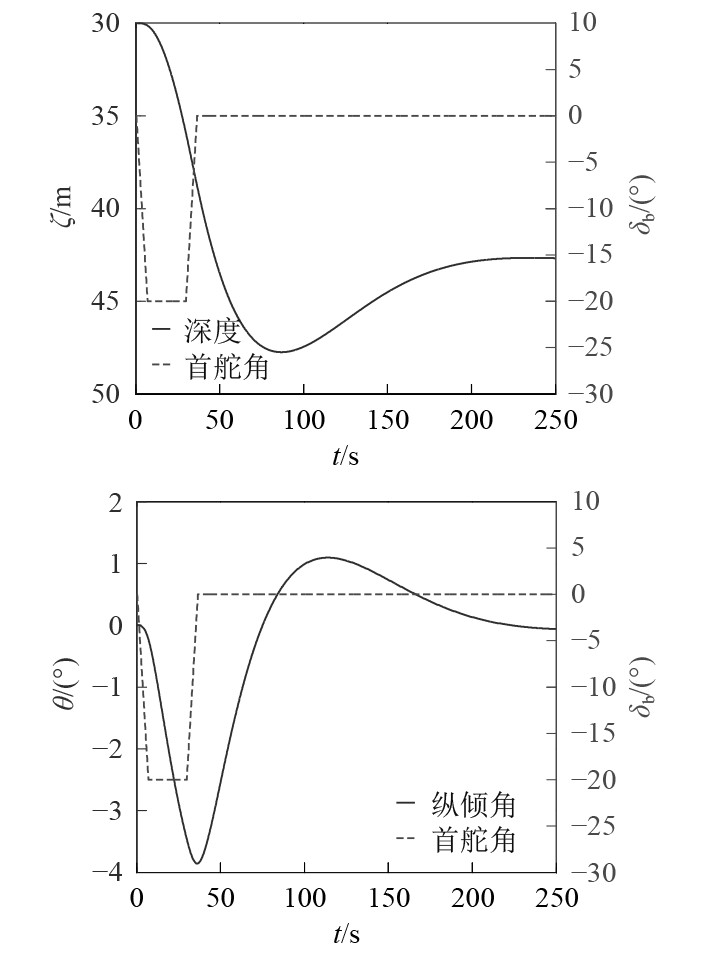
|
图 5 围壳舵梯形操舵深度和纵倾角响应曲线 Fig. 5 Trapezoidal steering depth and inclination response curve (Enclosure bow rudder) |
表1为不同布局条件下首升降舵梯形操舵下的运动响应参数。潜艇对梯形操舵的运动响应的主要特征参数包括:
ζmax和θmax为梯形操舵过程中潜艇能够到达的最大深度和最大纵倾角的值。
ζs和θs为梯形操舵结束后的稳定深度和稳定纵倾角的值。
ζe和θe为梯形操舵过程中,首舵舵角到达执行舵角并持续一段时间后开始回舵时刻的深度和纵倾角的值。
ζov和θov为反向操舵后,纵倾角、深度继续增大的幅度,即
| $\left\{ \begin{aligned} \zeta {}_{ov} = {\zeta _{\max }} - {\zeta _e}\text{,} \\ {\theta _{ov}} = {\theta _{\max }} - {\theta _e}\text{。} \\ \end{aligned} \right.$ | (7) |
|
|
表 1 梯形操舵运动响应特征参数 Tab.1 Trapezoidal steering motion response characteristic parameters |
1)在相同的梯形操舵规律下,首端首舵的最大深度和稳定深度分别达到了74.04 m和71.47 m,远远大于围壳舵的47.74 m和42.68 m。
2)2种布局方式下的执行深度分别为36.73 m和35.92 m,二者差异并不大。但首端首舵的执行纵倾角为首倾7.71°,围壳舵的执行纵倾角仅为首倾3.61°。就执行纵倾角这一特征参数来说,首端首舵是围壳舵的两倍左右。正是由于执行纵倾角的巨大差异,才导致二者的超越深度的差别巨大(首端首舵40.77 m,围壳舵11.82 m)。
3)虽然首端首舵的舵面积只有围壳舵的1/2,但由于首端首舵可以布置在靠近艇首处,因此首端首舵的纵倾响应比围壳舵要快。首端首舵的垂直面机动性要优于围壳舵。
3.3 升速率与逆速经良好潜水均衡后的潜艇,假设处于无纵倾等速直线定深运动状态(α0=θ0=χ0=0),以此初始状态作为基准运动,再操纵首升降舵单位,潜艇最终趋向定常直线潜浮运动,潜浮运动的垂速就是该航速下的升速率。升速率
潜艇在首升降舵作用下的运动平衡方程式可以由潜艇垂直面线性操纵运动方程[2]简化为如下形式:
| $\left\{ \begin{aligned} &{{Z}_{w}^{'}}w + {{Z}_{{\delta _b}}^{'}}{\delta _b} = 0 \text{,}\\ &{{M}_{w}^{'}}w + {{M}_{\theta}^{'} }\theta + {{M}_{{\delta _b}}^{'}}{\delta _b} = 0 \text{。} \\ \end{aligned} \right.$ | (8) |
由于w'=α,并给定操舵角δb,则可求得:
| $\alpha = - \frac{{Z'{}_{{\delta _b}}}}{{{{Z}_{w}^{'}}}}{\delta _b}\text{,}$ | (9) |
| $\theta = - \frac{1}{{{M_\theta }}}\left( - \frac{{M'{}_w}}{{{{Z}_{w}^{'}}}} + \frac{{{{M}_{{\delta _b}}^{'}}}}{{{{Z}_{{\delta _b}}^{'}}}}\right){Z_{{\delta _b}}^{'}}{\delta _b}\text{。}$ | (10) |
由于:
| ${V_\zeta } = - V\sin \chi \approx - V\chi = - V(\theta - \alpha )\text{,}$ | (11) |
将式(9)和式(10)代入式(11),经过化简可整理得出升速率的表达式为:
| $V_\zeta ^ \circ = \frac{{{V^3}}}{{57.3m'gh}}\left(\frac{{{{M}_{w}^{'}}}}{{{{Z}_{w}^{'}}}} - \frac{{{{M}_{{\delta _b}}^{'}}}}{{{{Z}_{{\delta _b}}^{'}}}} + \frac{{{{M}_\theta }^{'}}}{{{{Z}_{w}^{'}}}}\right){Z_{{\delta _b}}^{'}}\text{。}$ | (12) |
将模型潜艇的相关参数和水动力系数代入式(12),可以计算得出在8 kn航速下,首端首舵的升速率为0.07 m/s,围壳舵的升速率为0.02 m/s,显然从升速率这项能反应潜艇垂直面潜浮机动性的指标来看,首端首舵是优于围壳舵的。
等速定深直航中的潜艇,操纵升降舵无法改变潜浮角(或垂速)时对应的航速称为“逆速”[2],记作Vr。对于首升降舵来说Vrb表示式可按其定义求得,即令式(12)等于零,不难解得:
| ${V_{rb}} = \sqrt {\frac{{m'gh{{Z}_{{\delta _b}}^{'}}}}{{{{Z}_{{\delta _b}}^{'}}{{M}_{w}^{'}} - {{Z}_{w}^{'}}{{M}_{{\delta _b}}^{'}}}}} \text{。}$ | (13) |
将模型潜艇的相关参数和水动力系数代入式(13),可以看出,无论是围壳舵还是首端首舵,逆速表达式中的根号内的值均小于零,也就是说,布局方式无论是首端首舵还是围壳舵,其首升降舵均不存在逆速。对模型潜艇来说,首端首舵布局和围壳舵布局均能满足首升降舵无逆速的设计要求。
3.4 平衡舵角静均衡好的潜艇,由于潜艇艇体上下不对称存在零升力Z0和零升力矩M0,所以当增速后以一定航速航行时,必须同时操纵首、尾升降舵,方能保持无纵倾等速直线定深运动。此时的平衡方程可由潜艇垂直面线性操纵运动方程简化得到:
| $\left\{ \begin{aligned} &{{Z}_{0}^{'}} + {{Z}_{{\delta _s}}^{'}}{\delta _s} + {{Z}_{{\delta _b}}^{'}}{\delta _b} = 0 \text{,} \\ &{{M}_{0}^{'}} + {{M}_{{\delta _s}}^{'}}{\delta _s} + {{M}_{{\delta _b}}^{'}}{\delta _b} = 0 \text{。} \\ \end{aligned} \right.$ | (14) |
由此可解出首、尾升降舵应操的平衡舵角的表达式为:
| ${\delta _s} = \frac{{ - {{M}_{0}^{'}}{{Z}_{{\delta _b}}^{'}} + {{M}_{{\delta _b}}^{'}}{{Z}_{0}^{'}}}}{{{{M}_{{\delta _s}}^{'}}{{Z}_{{\delta _b}}^{'}} - {{M}_{{\delta _b}}^{'}}{{Z}_{{\delta _s}}^{'}}}}\text{,}$ | (15) |
| ${\delta _b} = \frac{{ - {{M}_{0}^{'}}{{Z}_{{\delta _s}}^{'}} + {{M}_{{\delta _s}}^{'}}{{Z}_{0}^{'}}}}{{{{M}_{{\delta _s}}^{'}}{{Z}_{{\delta _b}}^{'}} - {{M}_{{\delta _b}}^{'}}{{Z}_{{\delta _s}}^{'}}}}\text{。}$ | (16) |
将模型潜艇相关水动力系数代入式(15)和式(16),可以解得首升降舵布置方式为首端首舵的平衡舵角为δs=1.24°,δb=2.55°;布置方式为围壳舵的平衡舵角为δs=0.37°,δb=−2.22°。
平衡舵角对于潜艇垂直面操纵来说是个不利因素,平衡舵角的产生意味着要占用及其宝贵的舵角资源来平衡潜艇的零升力和零升力矩。可以看出,首升降舵布局方式为围壳舵时,无论是首舵还是尾舵,其平衡舵角均小于首端首舵的布局方式。
不难看出,就平衡舵角这一操纵指标来说,围壳舵的布局方式优于首端首舵。
4 垂直面操纵性能综合评判升降舵对潜艇操纵性能的影响,是由诸多因素组成的。通过仿真计算可以看出,对有些性能指标,首端首舵是优于围壳舵的,例如升速率;有些性能指标围壳舵时优于首端首舵的,例如平衡舵角;有些性能指标,二者是类似的,例如逆速。因此需要选择一种合适的综合评判法对首端首舵和围壳舵的操纵性能进行综合评判[8]。应用模糊综合评判,可以使首升降舵的不同布局方式的操纵性优劣的评判成为可能。
4.1 模糊综合评判基本公式以潜艇操纵性作为评判集论域,论域内因素集u为潜艇垂直面内操纵运动的各个操纵参数:
| $u = \{ {u_1},{u_2},{u_3},{u_4},{u_5}\} \text{。}$ |
其中:u1为升速率;u2为逆速;u3为平衡舵角,取首、尾升降舵平衡舵角绝对值的和。u4为纵倾响应,表示操1°舵角100 s后的纵倾变化。
权函数用来表示操纵参数的重要与次要程度,综合垂直面内各操纵参数的权函数为:
| $P = \{ 1.5,1.0,1.5,1.25\} \text{,} $ |
综合评判的基本公式包括:
1)模糊综合评判
| $ {\mathop B\limits _{\sim}} = {\mathop A\limits _{\sim}} \circ {\mathop R\limits _{\sim}} \text{。} $ | (17) |
式中:
2)综合评判值
| $ {\mathop C\limits _{\sim}} = {\mathop B\limits _{\sim}} \circ {Q^{ \rm T}} \text{。} $ | (18) |
式中:
式(17)和式(18)中的运算算符集“
| ${b_j} = \min ({a_1} \cdot {r_{1j}} + {a_2} \cdot {r_{2j}} + \cdots + {a_n} \cdot {r_{nj}},1)\text{。}$ | (19) |
所谓“全参数计入型”评判是指评判过程考虑了所有参数的影响。通常的
模糊集的运算,是通过隶属函数来实现的。对于各操纵参数的隶属函数,采用岭形分布的评判方法,经过归一化处理后,分别按下面公式确定:
1)“升速率”隶属函数
| $\mu {{\mathop A\limits _{\sim}} _1} = \left\{ \begin{gathered} 1\text{,}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{} \end{array}}&{}&{} \end{array}}&{\left| {{u_1}} \right| \geqslant 0.5} \text{,} \end{array} \\ 1 - \frac{{25}}{8}{(0.5 - \left| {{u_1}} \right|)^2}\text{,}\begin{array}{*{20}{c}} {}&{0.5 > \left| {{u_1}} \right| \geqslant 0.1} \text{,} \end{array} \\ \frac{{1\;000}}{5}{(0.05 - \left| {{u_1}} \right|)^2}\text{,}\begin{array}{*{20}{c}} {}&{0.1 > \left| {{u_1}} \right| \geqslant 0.05} \text{,} \end{array} \\ 0\text{,}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{}&{}&{} \end{array}}&{0.05 > \left| {{u_1}} \right|} \text{。} \end{array} \\ \end{gathered} \right.$ | (20) |
2)“逆速”隶属函数
| $ \mu {{\mathop A\limits _{\sim}}}_{2}=\left\{\begin{array}{l}1\text{,}\begin{array}{cc}& {\text{无逆速}}\text{,}\end{array}\\ 0\text{,}\begin{array}{cc}& {\text{有逆速}}\text{。}\end{array}\end{array}\right.$ | (21) |
3)“平衡舵角”隶属函数
| $\mu {{\mathop A\limits _{\sim}} _3} = \left\{ \begin{gathered} 1\text{,}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{} \end{array}}&{}&{} \end{array}}&{\left| {{u_3}} \right| \geqslant 1} \text{,} \end{array} \\ 1 - \frac{{50}}{{81}}{(0.5 - \left| {{u_3}} \right|)^2}\text{,}\begin{array}{*{20}{c}} {}&{1 > \left| {{u_3}} \right| \geqslant 0.1} \text{,} \end{array} \\ \frac{{5\;000}}{{81}}{(\left| {{u_3}} \right|{\rm{ - }}0.01)^2}\text{,}\begin{array}{*{20}{c}} {}&{0.1 > \left| {{u_3}} \right| \geqslant 0.01} \text{,} \end{array} \\ 0\text{,}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{}&{}&{} \end{array}}&{0.01 > \left| {{u_3}} \right|} \text{。} \end{array} \\ \end{gathered} \right.$ | (22) |
4)“纵倾响应”隶属函数
| $\mu {{\mathop A\limits _{\sim}}_4} = \left\{ \begin{gathered} 1\text{,}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{} \end{array}}&{}&{} \end{array}}&{\left| {{u_4}} \right| \geqslant 1} \text{,} \end{array} \\ 1 - \frac{{50}}{{81}}{(0.5 - \left| {{u_4}} \right|)^2}\text{,}\begin{array}{*{20}{c}} {}&{1 > \left| {{u_4}} \right| \geqslant 0.1} \text{,} \end{array} \\ \frac{{5\;000}}{{81}}{(\left| {{u_4}} \right|{\rm{ - }}0.01)^2}\text{,}\begin{array}{*{20}{c}} {}&{0.1 > \left| {{u_4}} \right| \geqslant 0.01} \text{,} \end{array} \\ 0\text{,}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{}&{}&{} \end{array}}&{0.01 > \left| {{u_4}} \right|} \text{。} \end{array} \\ \end{gathered} \right.$ | (23) |
以模型潜艇航速为8 kn时为例,首升降舵的布局方式为首端首舵时的操纵参数为u1=0.063,u2=1,u3=0.27,u4=0.83;布局方式为围壳舵时的操纵参数为u1=0.024,u2=1,u3=0.79,u4=0.36。
利用式(20)~式(22)计算出隶属函数后,将μA各项乘以相应的权函数值,依照式(18)和式(19),最终得出首端首舵的综合评判值为4.267,围壳舵的综合评判值为3.983。综合评判的结果是在中速(8 kn)条件下,首端首舵的操纵性优于围壳舵。
在低速(4 kn)和高速(18 kn)条件下以同样的方法对2种首升降舵布局方式的操纵性能进行模糊综合评判,结果仍是首端首舵操纵性优于围壳舵。需要特别指出的是在进行模糊综合评判时,各参数之间的权重会直接影响到最后的评判结果,如何根据实际需要和经验合理进行分配以及确定模糊关系方程是下一步要解决的问题。
5 结 语通过对首升降舵2种布置方式条件下的仿真计算,进而进行了操纵性能的模糊综合评判,在首端首舵的舵面积只有围壳舵一半的前提下,首端首舵的操纵性能仍然优于围壳舵。况且由于首端首舵的垂向布局是低于围壳舵的,对于首升降舵布局方式为首端首舵的潜艇,在潜艇自水面状态转入水下状态时,一般深度超过2~3 m就可以操纵首升降舵进行变深机动;而对于首端首舵为围壳舵的潜艇,当潜水深度超过7~8 m时,其围壳舵才能没入水中参与垂直面操纵。这也是首端首舵优于围壳舵的特点之一。本文仅是针对2种布置方式对潜艇操纵性能的影响进行分析,实际上具体采用哪种布置方式,除了操纵性能之外还有许多其他客观因素需要考虑。虽然首端首舵的操纵性能优于围壳舵,但目前之所以有相当数量型号的潜艇选用围壳舵的原因主要是首端首舵要占用潜艇首部宝贵的空间资源,并且由于潜艇在水面航行和离靠码头时首端首舵需要收回,因此还需要加装相应的首升降舵收舵机构,客观上增加了发生故障的概率。同时首端首舵的机械噪声和水流噪声对于艇首声呐器材的正常工作也有一定的影响。
| [1] |
Buzcher, R. RYDILL L. Concepts in submarine design. cambridge ocean technology series[M]. Cambridge University Press. 1994.
|
| [2] |
施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 1995.
|
| [3] |
马运义, 许建. 现代潜艇设计理论与技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 2019.
|
| [4] |
徐亦凡. 潜艇操纵原理与方法[M]. 北京: 兵器工业出版社, 2002.
|
| [5] |
李麓, 李维嘉. 潜艇水下六自由度运动仿真数学模型[J]. 计算机仿真, 2001, 18(5): 33-38. DOI:10.3969/j.issn.1006-9348.2001.05.010 |
| [6] |
Jon Skeet. 深入理解C#[M]. 北京: 人民邮电出版社, 2014.
|
| [7] |
Mark Michaelis. C#7.0本质论[M]. 北京: 机械工业出版社, 2019.
|
| [8] |
孙元泉, 马运义, 邓志纯. 潜艇和深潜器的现代操纵理论与应用[M]. 北京: 国防工业出版社, 2001.
|
 2021, Vol. 43
2021, Vol. 43
