复合材料在结构工程中的应用日益广泛,复合材料的损伤与失效问题也受到人们的关注。针对复合材料损伤失效的研究,Chang等[1]建立了一种可以表征破坏类型、剩余极限强度等的逐渐破坏模型,通过应力分析完成了对含应力集中层合板的失效分析,为后续相关研究提供了一定基础。Puck等[2]通过引入新的纤维间断裂准则,使得断裂分析较以往更符合实际,并可以初步区分出不同的断裂模式。通过断裂力学、损伤力学等方法,学者们总结提出了复合材料失效准则,有效地区分了纤维失效与基体失效,但是在复合材料的破坏分析中,许多学者只对一种破坏模型的结果进行分析比较,如单层失效等。之后,复合材料损伤失效的评估方法进一步发展。Camanho等[3]开始考虑层间效应,将一个基于位移的单相关损伤参数应用于退化法则中追踪层间的失效状态,并建立双悬臂梁、端部切口屈曲与混合模式弯曲试件,预测结果与试验结果吻合较好。Adrian等[4]对复合材料叶片加筋结构的损伤、扩展与破坏行为进行了试验与数值研究,采用铺层失效退化模型和全局-局部方法对板的屈曲进行预测分析。目前,针对复合材料在船海领域相关应用的研究仍处于起步阶段,对船用复合材料层合板结构的研究较少涉及到层间、层内各自的损伤失效及相互耦合作用,同样也缺乏对目视不可见损伤、层间脱粘及子层屈曲失稳等复合材料特有力学行为的研究。
本文针对船用复合材料层合板的结构损伤失效进行研究,采用精细化分析模型,考虑层内与层间损伤,比较层合板在拉压载荷和横向载荷下的结构响应与渐进失效过程。
1 渐进失效理论介绍 1.1 层合板失效评估理论层合板的失效过程复杂,呈现逐渐劣化的特点。开始受外载作用后,复合材料结构中薄弱局部首先产生损伤,应力重新分配,但在宏观上结构没有显著的变化。随着外载的持续作用,局部损伤累积叠加,层合板结构承载能力与性能逐渐降低,最终结构完全失去承载能力并发生破坏。渐进失效分析法考虑了层合板的各类局部损伤方式以及材料性能退化[5],可以准确模拟损伤的破坏机理及层内层间的耦合作用,从而能更好地预测结构损伤扩展及极限强度等。
1.2 复合材料层内材料失效准则综合考虑计算精度及损失模式的多样性,选择Hashin失效准则作为层内材料的失效判据,分拉伸失效及压缩失效两类,每类根据纤维损伤及基体损伤进一步细分。
1)拉伸失效
纤维损伤(
| ${\left( {\frac{{{\sigma _{11}}}}{{{X_T}}}} \right)^2} + \alpha {\left( {\frac{{{\tau _{12}}}}{{{S_L}}}} \right)^2} = 1\text{,}$ | (1) |
基体损伤(
| ${\left( {\frac{{{\sigma _{22}}}}{{{Y_T}}}} \right)^2} + {\left( {\frac{{{\tau _{12}}}}{{{S_L}}}} \right)^2} = 1\text{。}$ | (2) |
2)压缩失效
纤维损伤(
| ${\left( {\frac{{{\sigma _{11}}}}{{{X_C}}}} \right)^2}{\rm{ = }}1\text{,}$ | (3) |
基体损伤(
| ${\left( {\frac{{{\sigma _{22}}}}{{2{S_T}}}} \right)^2} + \left[ {{{\left( {\frac{{{Y_C}}}{{2{S_T}}}} \right)}^2} - 1} \right]\frac{{{\sigma _{22}}}}{{{Y_C}}} + {\left( {\frac{{{\tau _{12}}}}{{{S_L}}}} \right)^2} = 1\text{。}$ | (4) |
式中:
采用二次应力失效准则[6]作为分层损伤的初始准则,即
| ${\left( {\frac{{{\sigma _3}}}{N}} \right)^2} + {\left( {\frac{{{\tau _1}}}{S}} \right)^2} + {\left( {\frac{{{\tau _2}}}{T}} \right)^2}{\rm{ = }}1\text{。}$ | (5) |
式中:
损伤起始后,分层损伤产生扩展,又因实际中破坏模式并不单一,多种模式共同作用,因此损伤演化采用混合模式的开裂准则,即Benzeggagh-Kenane能量释放率准则[7],判别式如下:
| ${G_{IC}} + \left( {{G_{IIC}} - {G_{IC}}} \right){\left( {\frac{{{G_{shear}}}}{{{G_T}}}} \right)^\eta } = {G_{TC}}\text{。}$ | (6) |
式中:
选取文献[8]中国产先进复合材料工型加筋板结构试验结果进行数值模型验证,于筋条-蒙皮处二次粘合层采用内聚力单元,考虑层内与层间损伤,对加筋板进行轴压屈曲计算并与试验结果对比,验证本文基于渐进失效理论及内聚力单元模拟层间接触的合理性。
复合材料加筋板试验模型如图1所示。所用材料主要为BA9916-II/HF10A-3K高温固化环氧碳纤维单向板,单层厚度0.125mm;筋条部分铺层材料为BA9916-II/HFW220TA,单层厚度0.23mm。加筋板的各区域铺层方式及其选用材料如表1所示,具体材料参数见表1、表2和表3,内聚层刚度可取为基体刚度或单向板横向刚度[9],层间刚度设置为
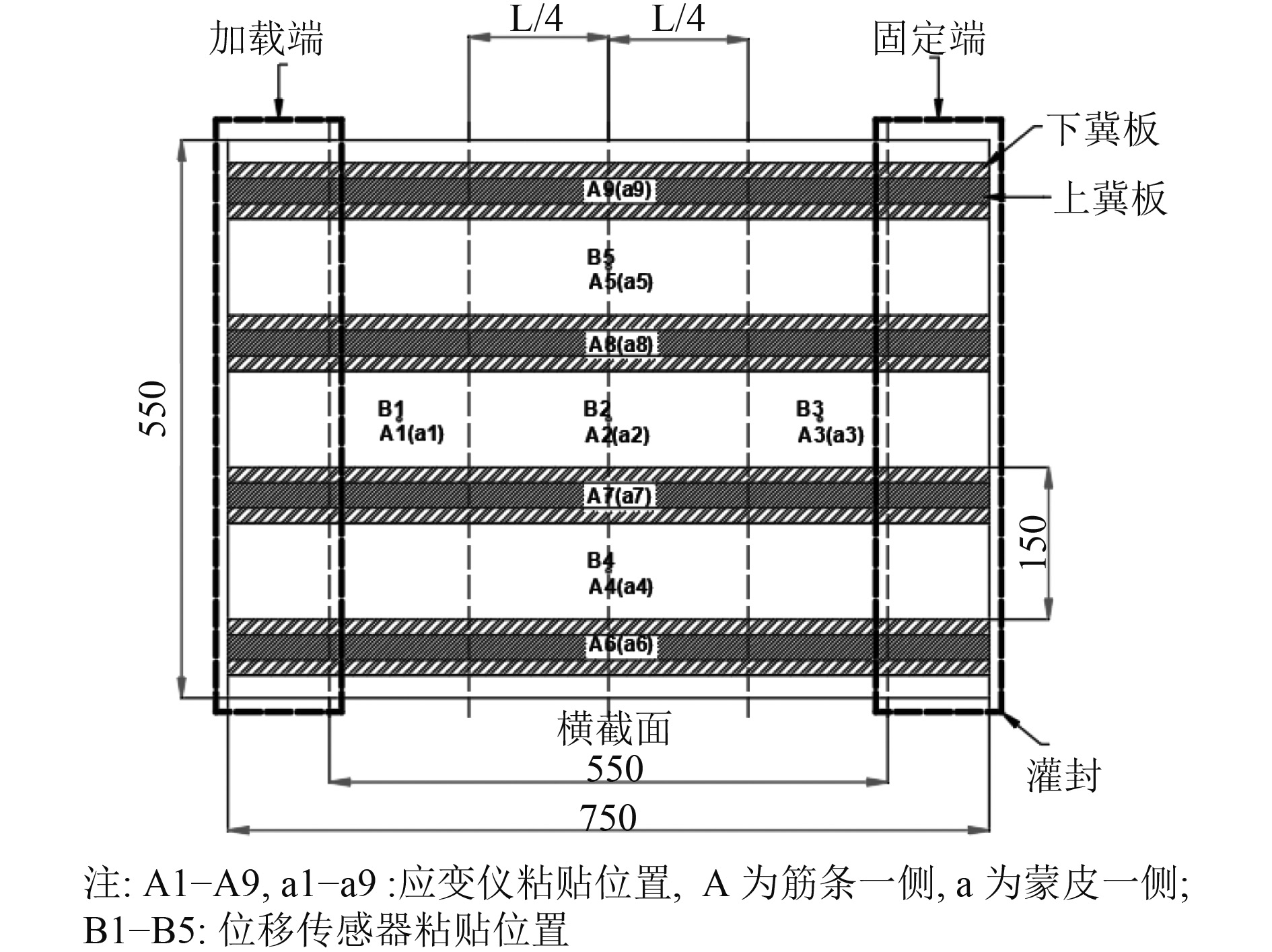
|
图 1 复合材料加筋板几何尺寸及边界条件 Fig. 1 Geometrical dimension and boundary condition of stiffened composite plate |
|
|
表 1 复合材料加筋板的铺层方式及选用材料 Tab.1 Layer design and material selection of stiffened composite plate |
|
|
表 2 复合材料层合板材料性能参数 Tab.2 Material parameters of composite laminate |
|
|
表 3 复合材料层内断裂韧性参数(kJ·m−2) Tab.3 Fracture toughness of composite material |
依照试验中应变仪与位移传感器的布置方式,输出有限元模型中相同位置应变与位移曲线,图2为本文模型预测结果与试验结果的对比情况。表5为本文模型预测的屈曲载荷与结构极限强度与试验结果的对比情况。由此可以看出,在误差允许范围内,本文模型预测的结构屈曲响应及极限强度值与文献试验结果吻合良好,证明本文所用内聚力单元方法与渐进失效分析方法均具有合理性。
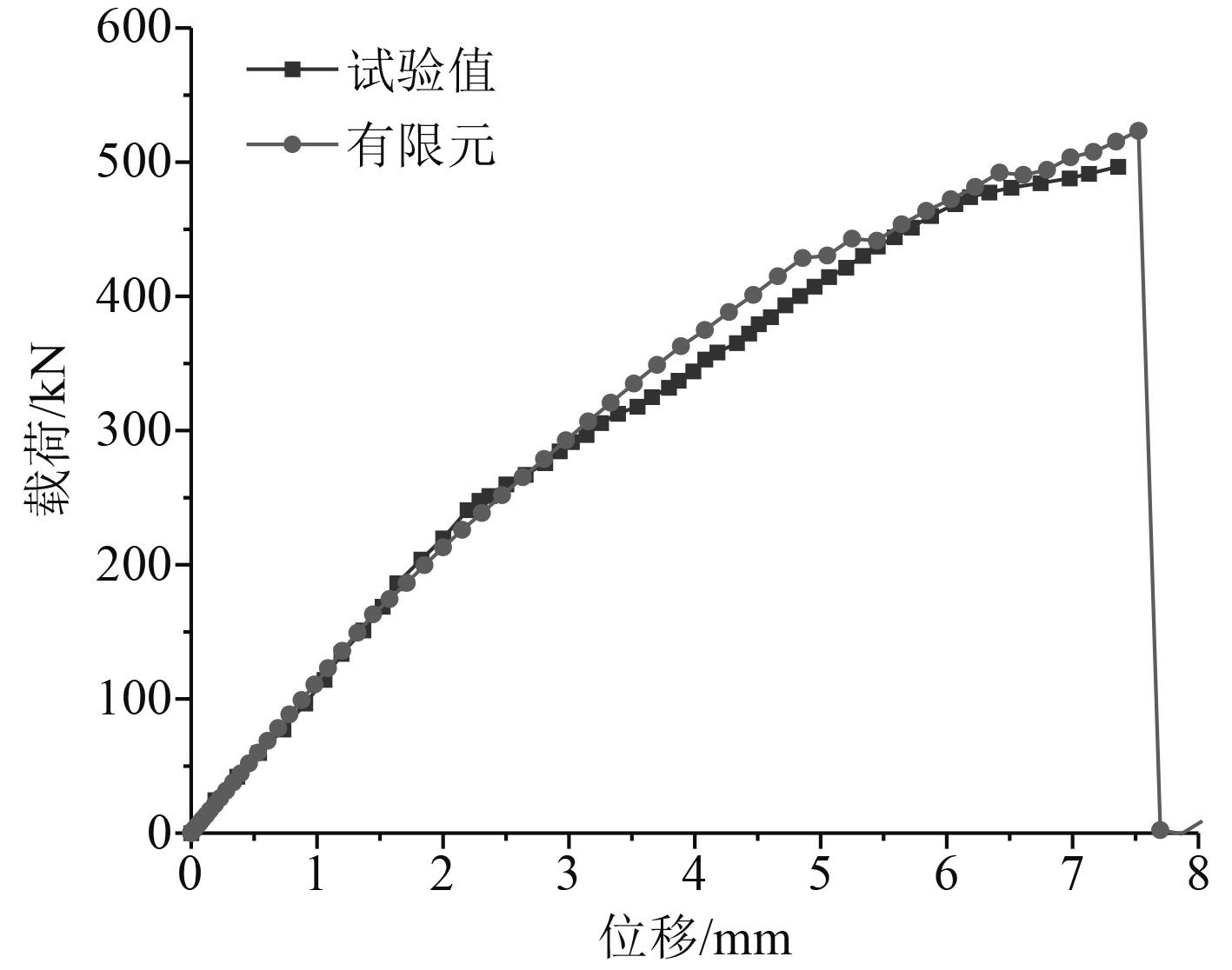
|
图 2 载荷-位移曲线 Fig. 2 Load-displacement curve |
|
|
表 5 复合材料加筋板试验及数值结果 Tab.5 Test and numerical results of stiffened composite plate |
利用Abaqus软件建立复合材料层合板的三维实体有限元模型,采用SC8R体单元模拟层内单向板,采用COH3D8内聚力单元模拟层合板中具体的层间界面胶层。层合板材料性能参数、层内断裂韧性参数、层间界面参数参考上节模拟对象,分别见表2~表4,内聚层刚度设置为
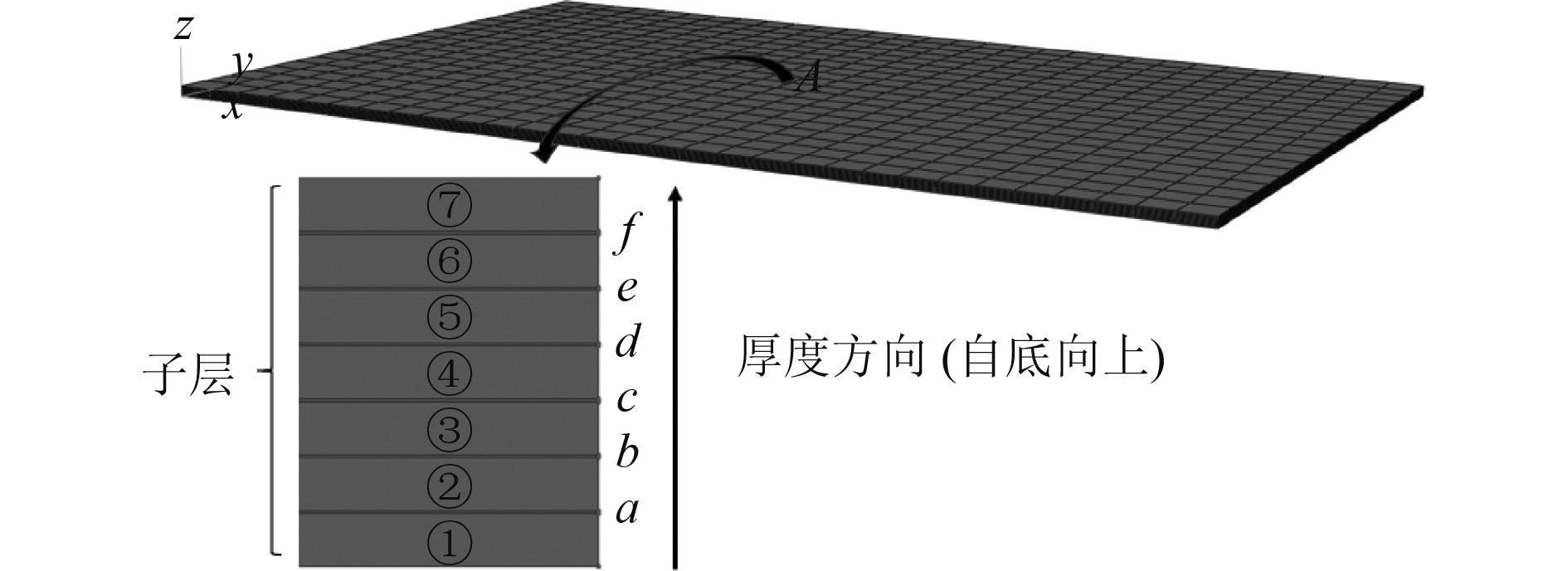
|
图 3 复合材料层合板有限元模型 Fig. 3 Finite element model of composite laminate |
|
|
表 4 复合材料层间界面参数 Tab.4 Interlaminar interface parameters of composite material |
对复合材料层合板进行拉伸极限强度计算,图4为拉伸载荷-位移曲线图,其中最高点即为拉伸极限强度87.181kN,实体模型在达到极限承载力后,载荷突降后结构仍能继续承载一段时间,之后随着位移载荷的继续增加才最终完全断裂。这是因为当拉伸载荷达到层合板的极限承载力后,层合板部分子层板失效断裂破坏,但层内部分纤维仍具有承载能力,故载荷-位移曲线会有二次突降的现象。
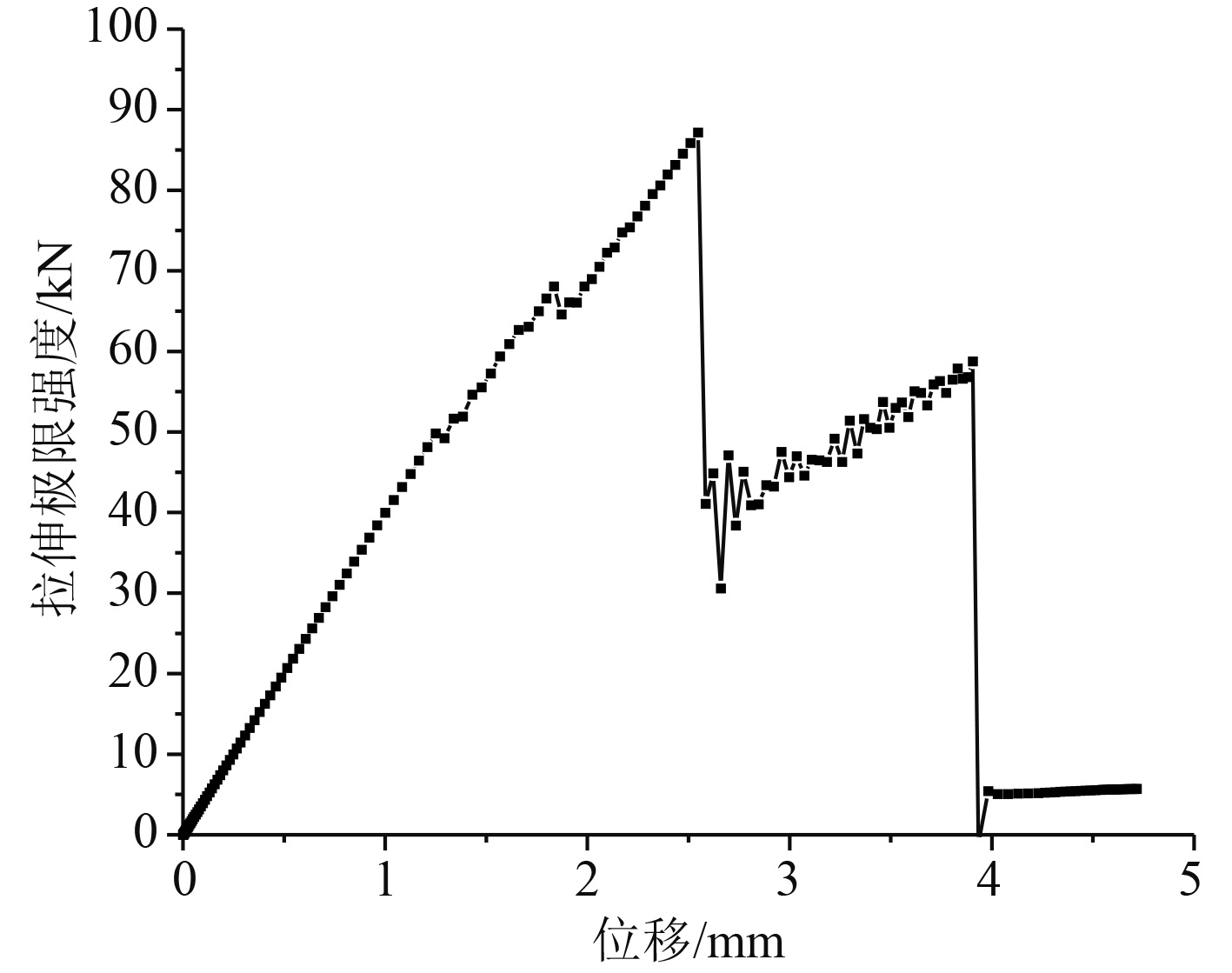
|
图 4 载荷-位移曲线 Fig. 4 Load-displacement curve |
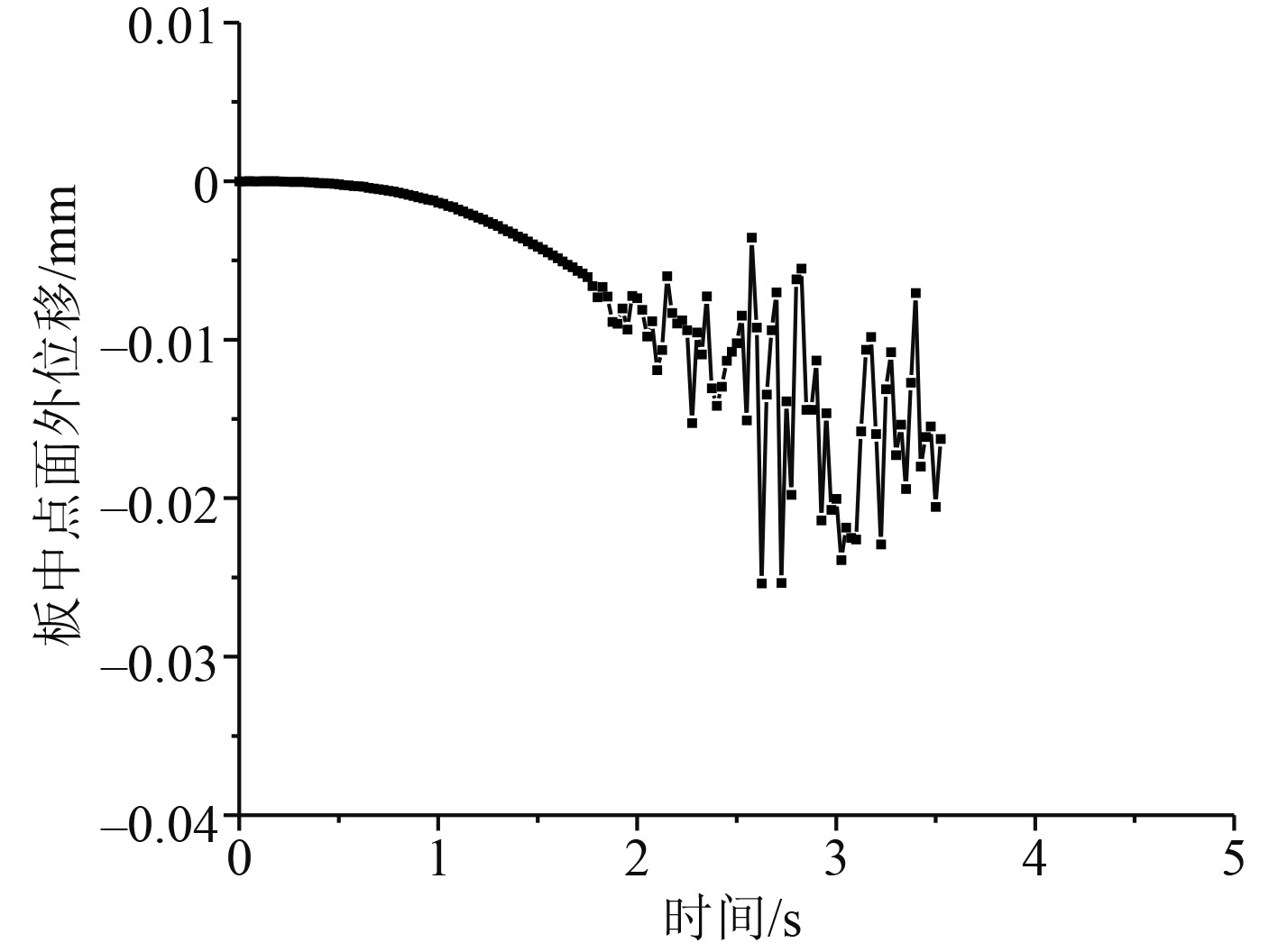
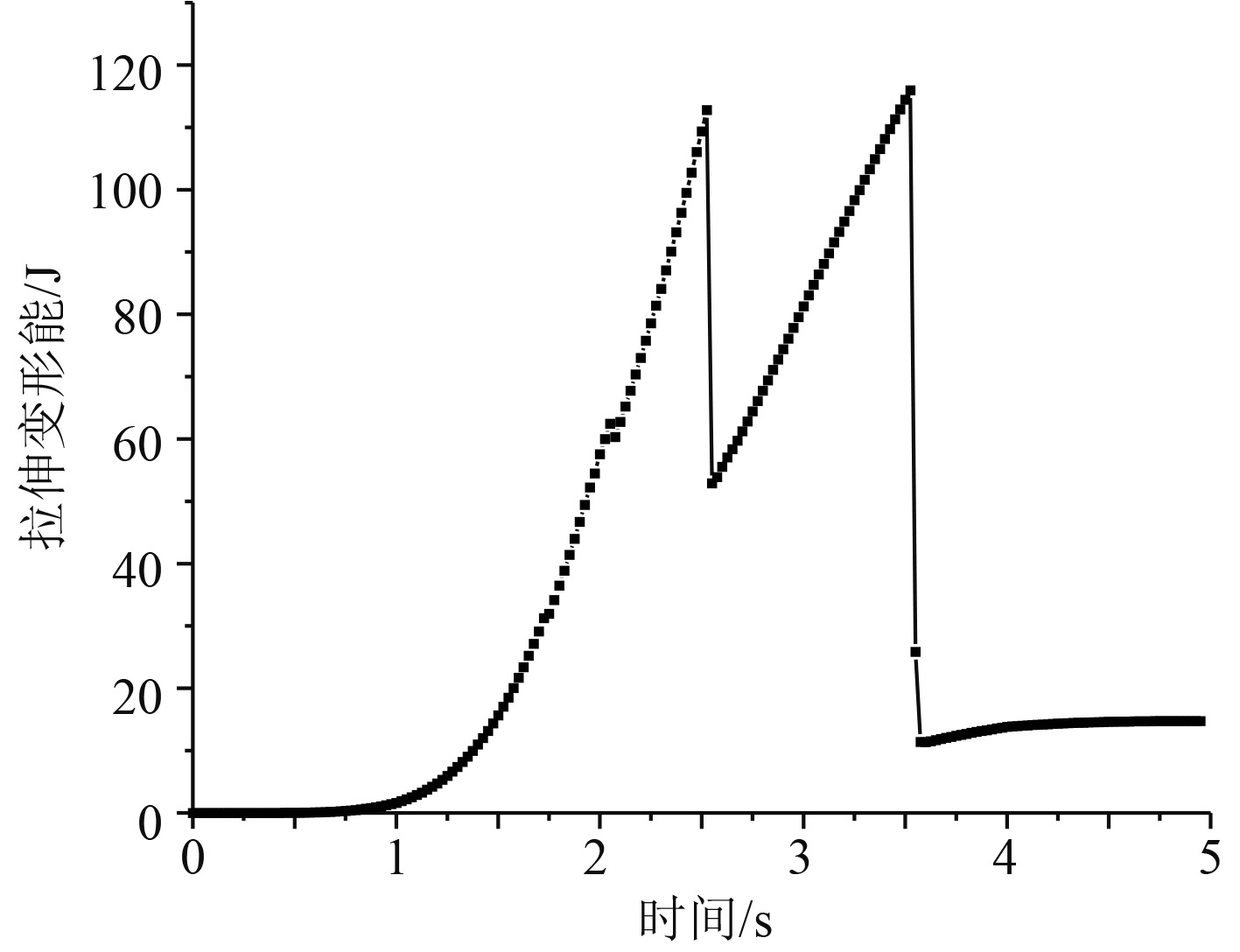
图5和图6分别为板中点面外位移及系统变形能时历。与金属材料在拉伸中会产生弹塑性变形继而颈缩相类似,层合板整体在拉伸时同样会有延展现象,板表层中心点在拉伸中产生z轴的负向位移,即说明层合板产生屈服延展,致使形变应力增加,直至层合板断裂。此外,加载至2.5~4 s左右时,板中点面外位移产生动荡,这2个时刻,层合板分别达到了极限承载力和二次断裂,层合板子层中相继失效断裂,结构积蓄的变形能下降转化为机械能释放,从而体现为面外位移的震荡[10]。
|
图 5 板中点面外位移时历曲线 Fig. 5 Out-of-plane displacement time history at plane center |
|
图 6 变形能时历曲线 Fig. 6 Deformation energy time history |
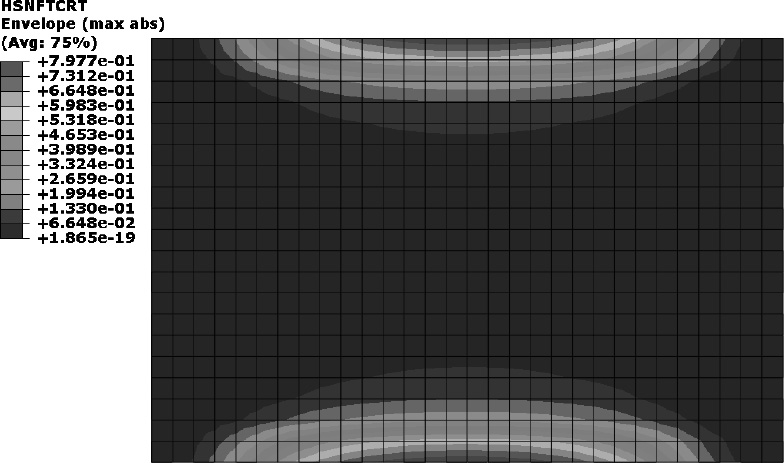
选取3个刚度跃变时刻即极限载荷步2.525 s,2.05 s和完全破坏步3.525 s,提取这些加载步的纤维损伤、基体损伤形态图,列入表6,部分载荷步视具体损伤情形给出最具代表的子层损伤图并在表中给出注释。在拉伸载荷持续作用下,产生的损伤以纤维基体拉伸损伤为主。因为基体抗拉强度较弱仅为87.1 MPa,且90°单向板在受载的长边轴向上强度也最弱,因此可以看出在2.05 s时②⑥两个90°子层就已产生了大面积失效。另外,0°子层具有最强的轴向刚度,因此在受拉时中心0°层也产生了较大范围的损伤,到极限载荷步时,0°层产生了大量纤维拉伸失效而断裂,诱使层合板直接失效破坏,此时层合板各子层基体也已基本开裂失效。到3.525 s时,则又因为其他子层被拉断,层合板整体才完全失去承载能力。
|
|
表 6 拉伸载荷下层合板损伤状态变化 Tab.6 Damage variation of laminate with tensile load |
表7为拉伸过程中内聚力层的损伤扩展变化,考虑到对称性铺层方式,表中只给出a,b,c层结果用以说明。拉伸前期,0°层承受了主要的轴向拉力,层内损伤还未影响到层间胶层,所以各层内聚力未产生明显的损伤;但当层合板达到极限承载能力时,中心0°层的失效断裂,应力波通过其相邻胶层重新传递给其余子层,因此此时c,b内聚胶层就产生了失效带;再到二次断裂时,结构已大部分失效,各层内聚胶层也产生了大面积失效分层。
|
|
表 7 拉伸载荷下内聚力层损伤状态变化 Tab.7 Damage variation of cohesive layer with tensile load |
在拉伸载荷下,层合板中具备较强抗拉能力的纤维起主要承力作用,主要承载层失效断裂后结构也随之达到极限承载能力而破坏;层合板基体与胶层在拉伸时也承担了部分载荷并能传递应力,但由于强度较低也较容易产生开裂破坏,并加剧纤维损伤。因此拉伸下层合板失效过程复杂,是多种损伤失效模式共同作用相互影响的结果。
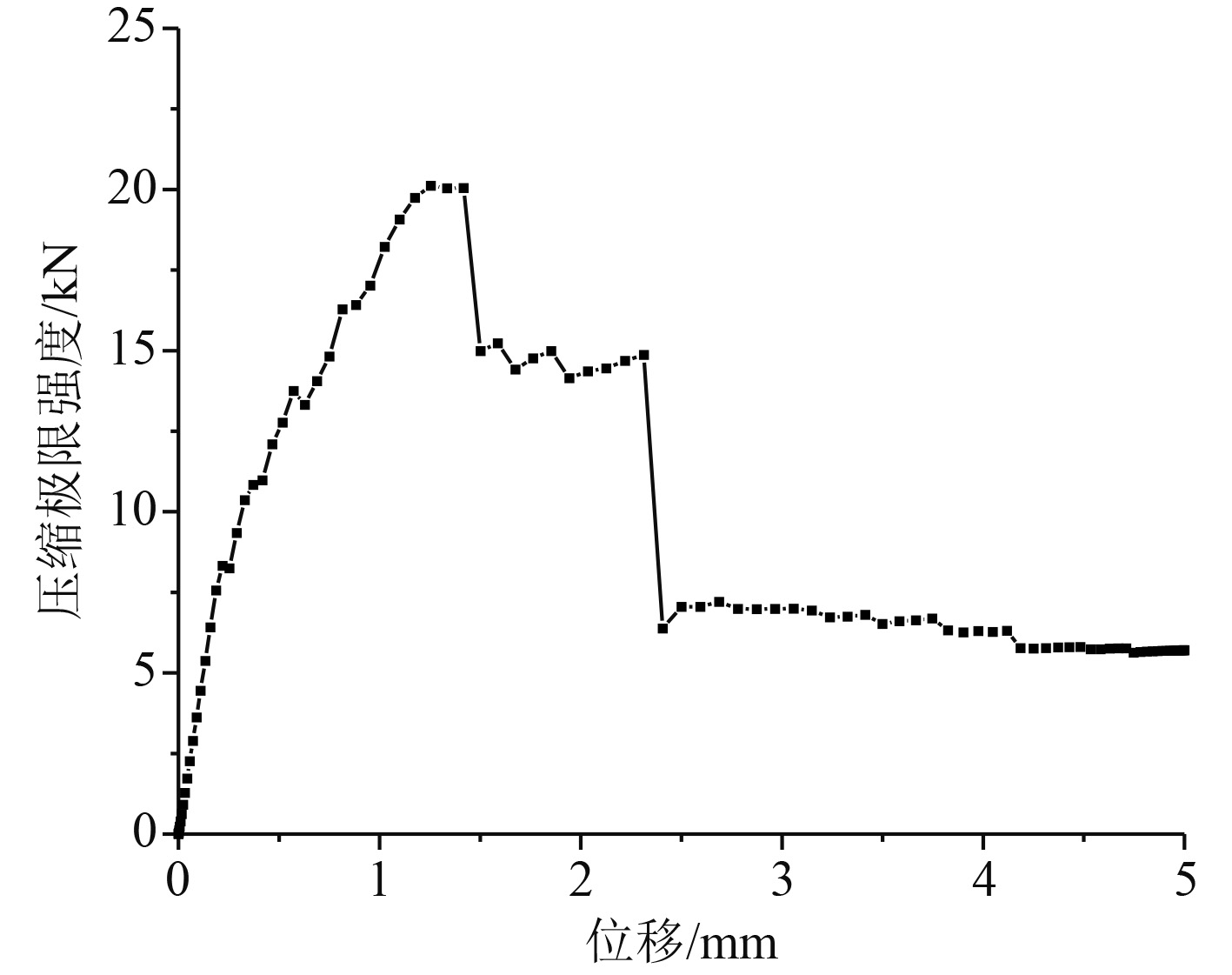
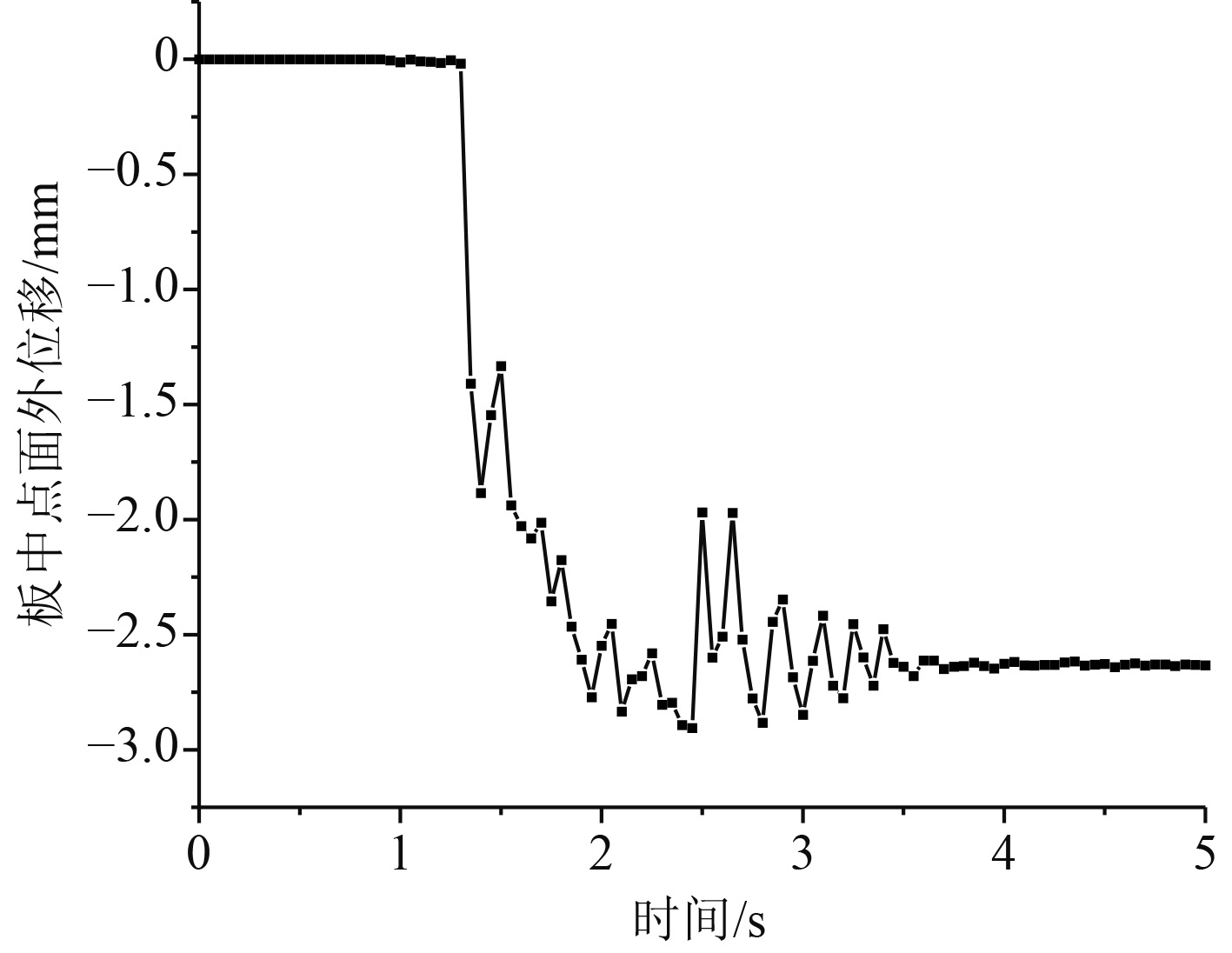
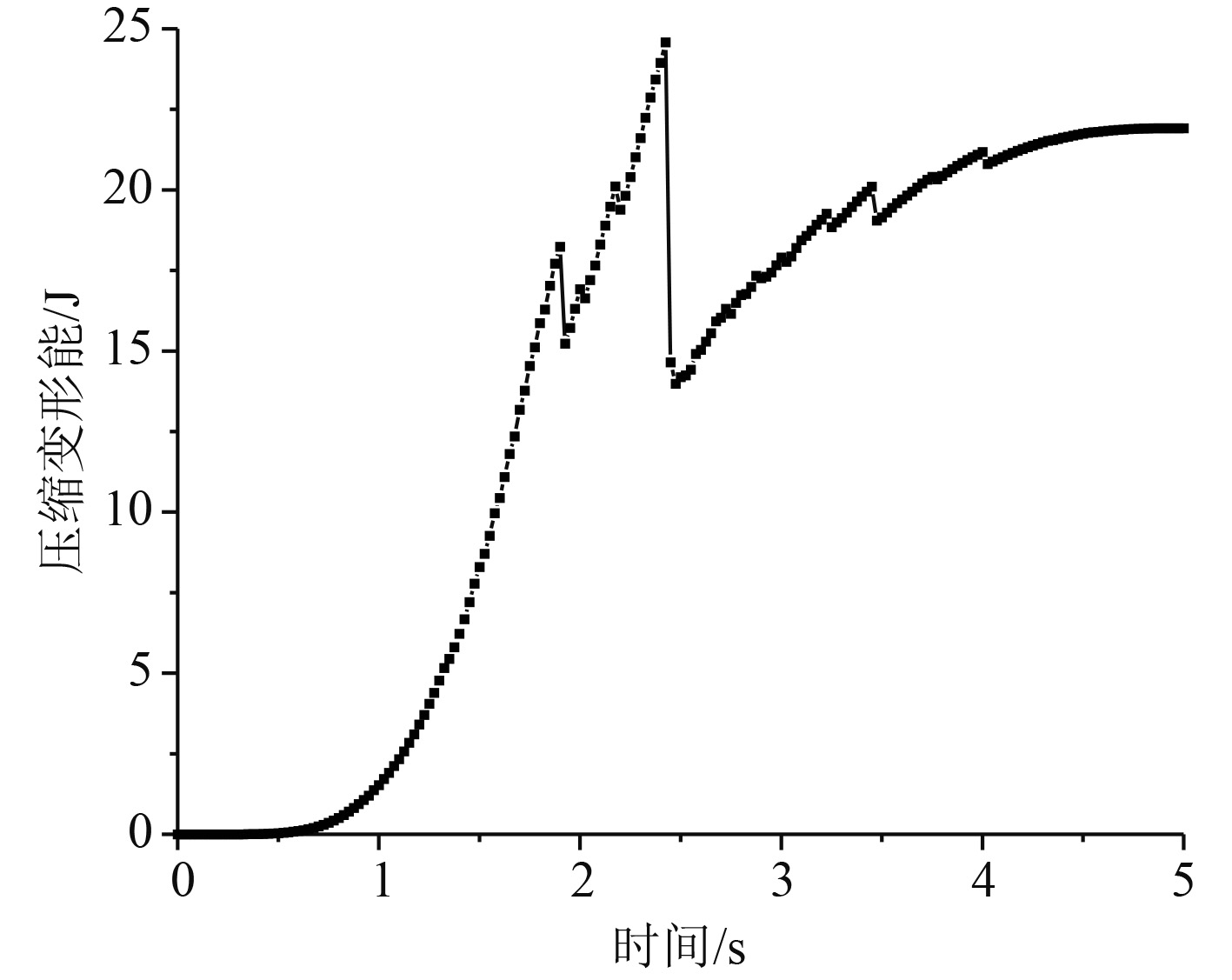
3.3 压缩载荷下层板损伤研究图7为压缩工况的载荷-位移曲线,同样具有二次突降趋势,其压缩极限承载力为20.047 kN。但与拉伸工况不同,在一段线性上升后,曲线就出现转折点并随后出现微弱的抖动段,这是因为层合板发生了局部失稳。如图8所示,加载至1.3 s左右时,伴随着层合板的局部失稳,板中心点的面外位移不再趋近零而急速增大,说明此时层合板快速屈曲,结构刚度降低,直至压溃破坏。因层合板发生局部屈曲,变形能转化为机械能释放,出现图9所示变形能曲线的首次骤降,结构的体系能量下降,随后结构发生整体屈曲,变形能再次骤降且幅度更大。尽管层合板已压溃破坏,但因板四周刚固且仍有单元未失效,因此继续加载时结构变形能仍在缓慢积累增长。
|
图 7 载荷-位移曲线 Fig. 7 Load-displacement curve |
|
图 8 板中点面外位移时历曲线 Fig. 8 Out-of-plane displacement time history at plane center |
|
图 9 变形能时历曲线 Fig. 9 Deformation energy time history |
参照3.2节,同样提取较关键的3个刚度突变载荷步的损伤,如表8所示。
|
|
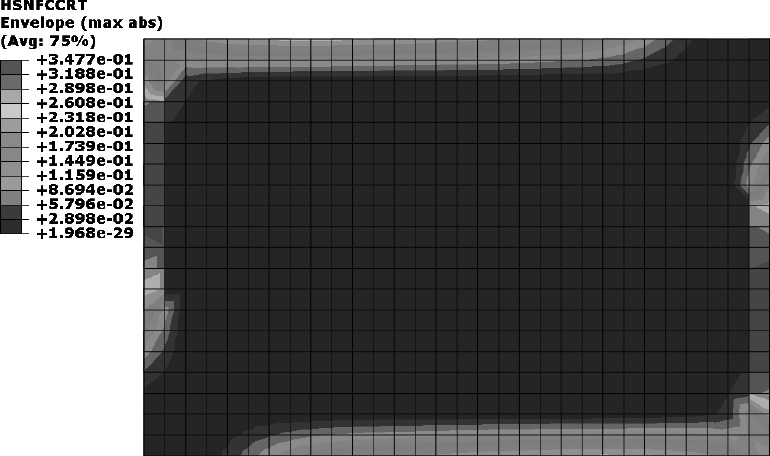
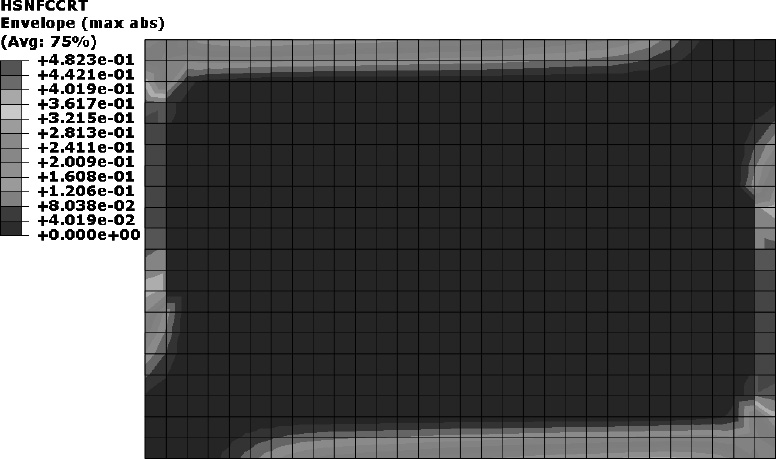
表 8 压缩载荷下层合板损伤状态变化 Tab.8 Damage variation of laminate with compressive load |
与拉伸情况相同,压缩载荷下层合板中起主要承力作用仍为纵向抗压能力较强的0°子层,1.3 s层合板已经发生了局部屈曲失稳,而刚固边界抵抗了板的屈曲变形,因此沿长边边界区域形成了一片纤维压缩损伤带,板中心区域无边界约束,因此在正弦半波的上拱区域基体受拉产生损伤。加载到1.9 s时,因为屈曲变形的加剧,原来的损伤区域扩大并演变为失效区,所以层合板到达极限承载步并发生整体屈曲破坏。之后的二次承载直至2.4 s时再次完全失去承载力,此时各子层失效区域进一步扩散,并集中于边界、屈曲半波节点线与波腹等应力较大区域。
如表9所示,在加载前期直至发生局部失稳,内聚胶层都未发生明显损伤,原因是层内纤维与基体已承受了主要压应力。到1.9s极限载荷步时,内聚力胶层在屈曲波边界波腹位置产生一块损伤区,破坏后期也仅限在损伤区发生失效。
|
|
表 9 压缩载荷下内聚力层损伤状态变化 Tab.9 Damage variation of cohesive layer with compressive load |
层合板在压缩载荷下仍为纤维起主要承力作用,纤维压缩失效后会引起层合板刚度的大幅下降。同时铺层损伤大多从应力集中处开始扩散,并由于层板受压时会发生屈曲,屈曲半波的存在使得上拱波腹与波节处容易发生基体损伤,从而进一步诱导纤维断裂及结构失效。
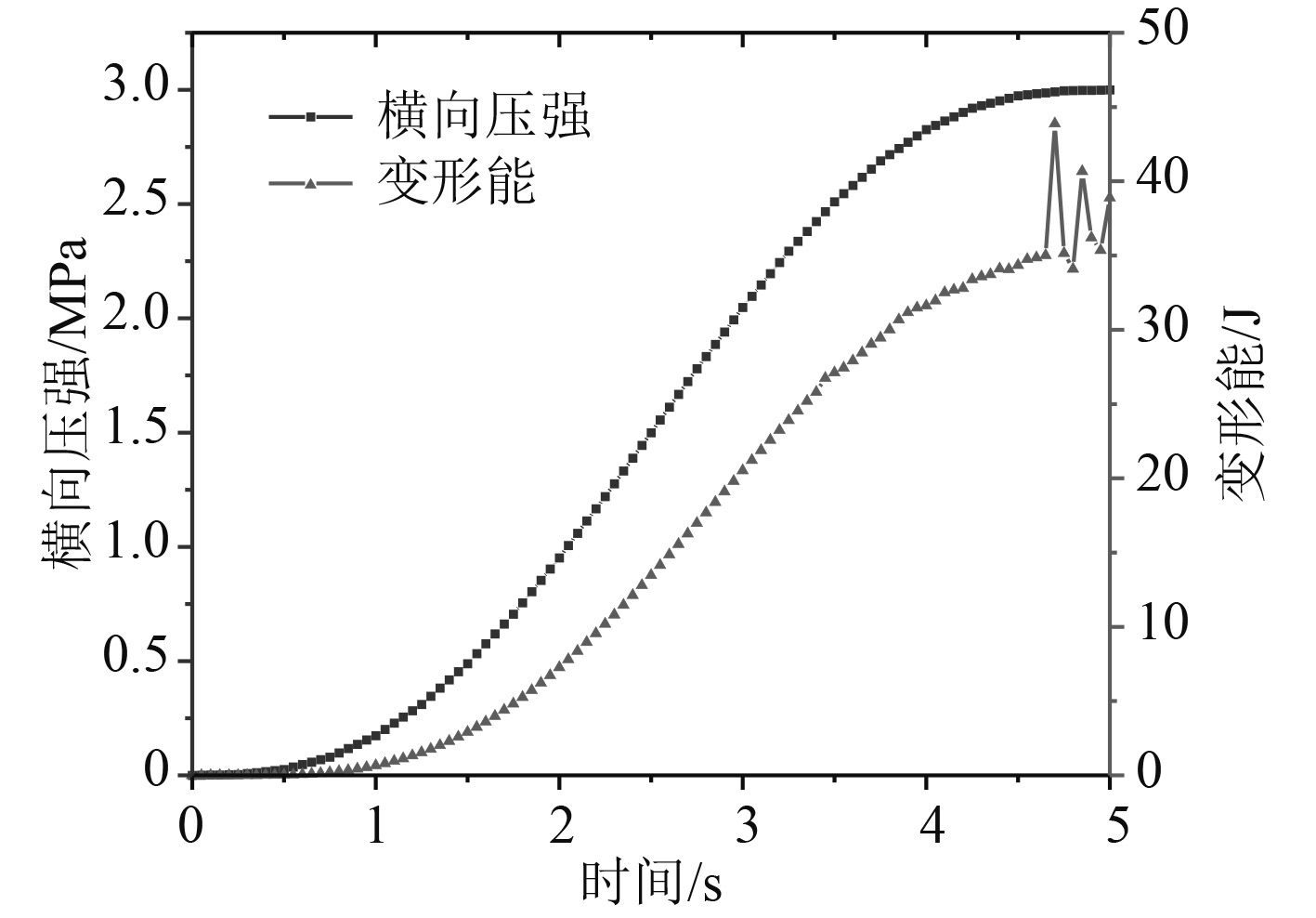
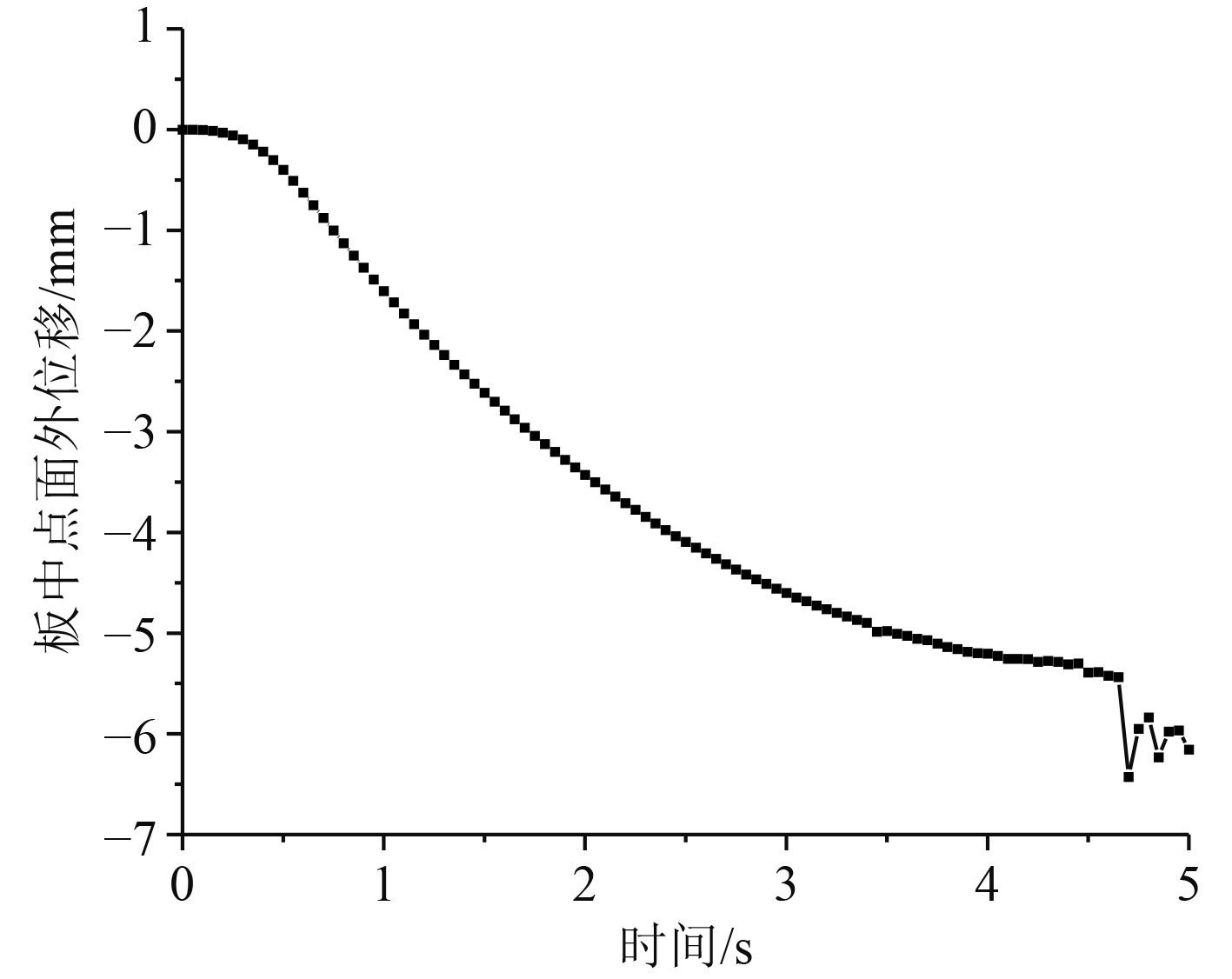
3.4 横向载荷下层板损伤研究除面内拉压载荷外,船用复合材料层合板还经常受到面外横向弯曲作用。按照平滑步加载方式,对四周刚固的层合板施加均布载,即由0逐级准静态地加载至3 MPa。绘制横向压强载荷与结构变形能的时历曲线与板中点面外位移时历曲线,如图10和图11所示。加载到4.65 s时结构变形能产生了大幅变化,且板中点面外位移也沿z轴负向产生了突增,说明此时层合板已无法承受横向压强而突然破坏,此时横向载荷值2.988 MPa即为层合板的横向载荷极限强度。
|
图 10 横向压强与变形能时历曲线 Fig. 10 Time histories of transverse pressure and deformation energy |
|
图 11 横向载荷下板中点面外位移时历曲线 Fig. 11 Out-of-plane displacement time history at plane center with transverse laod |
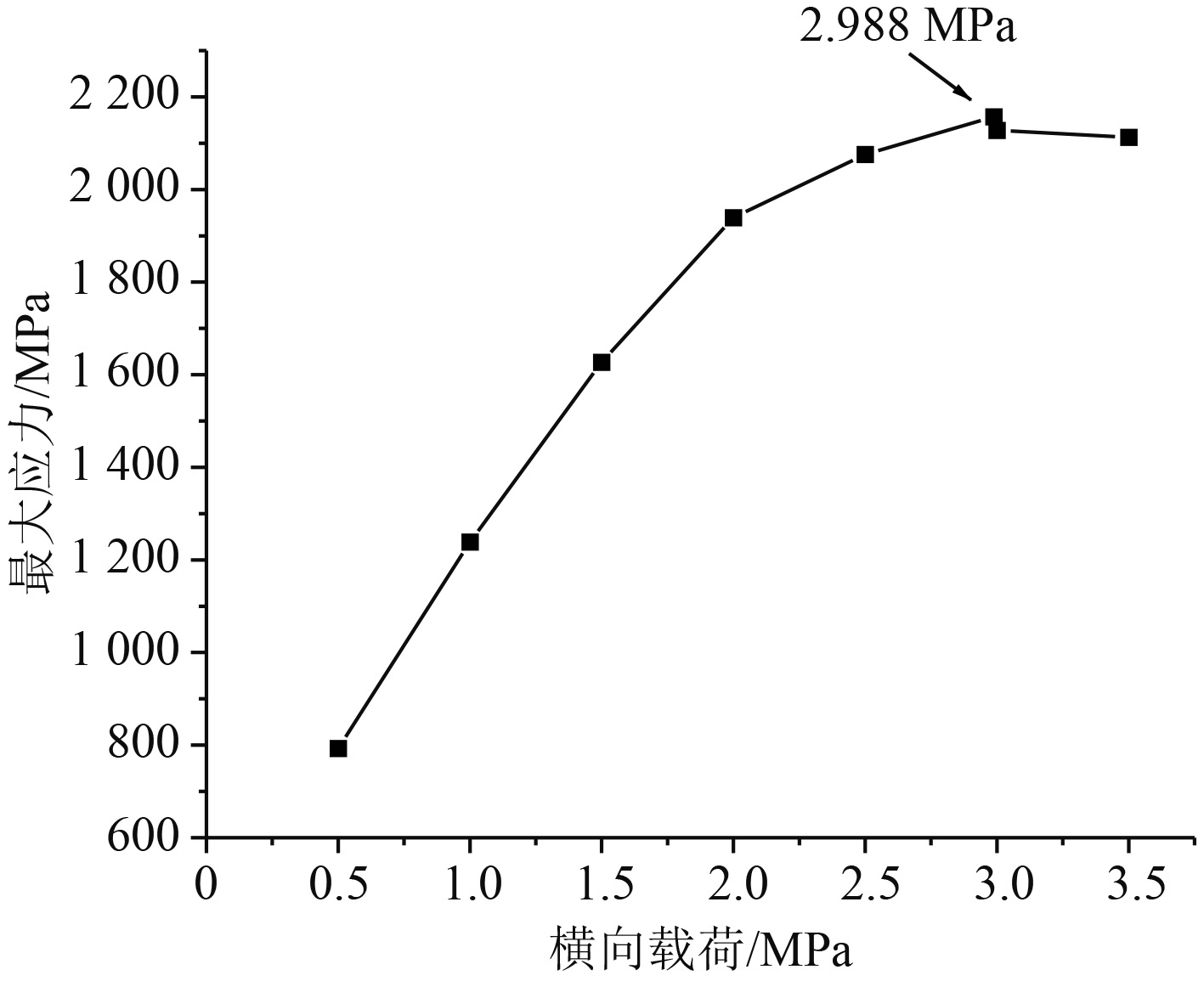
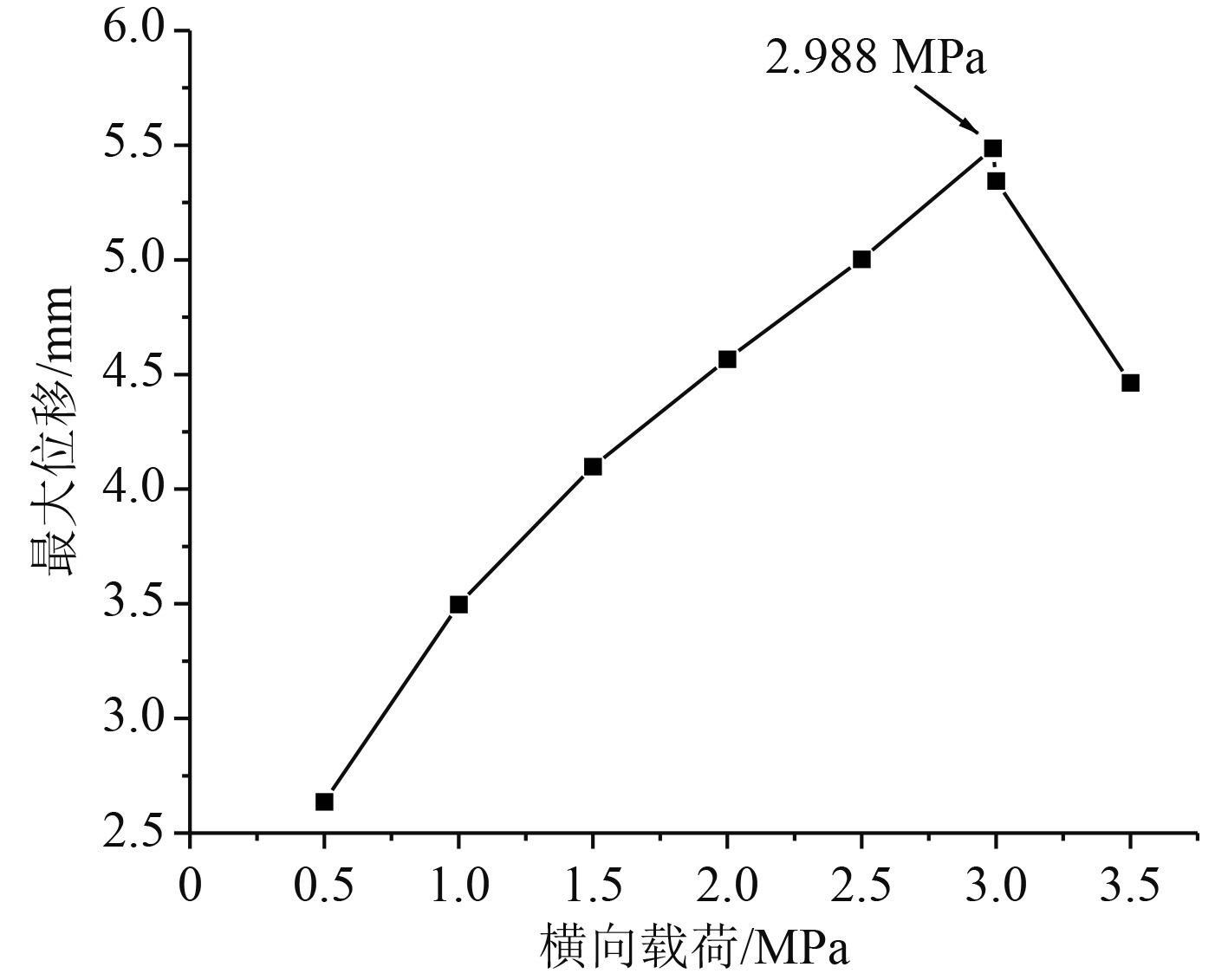
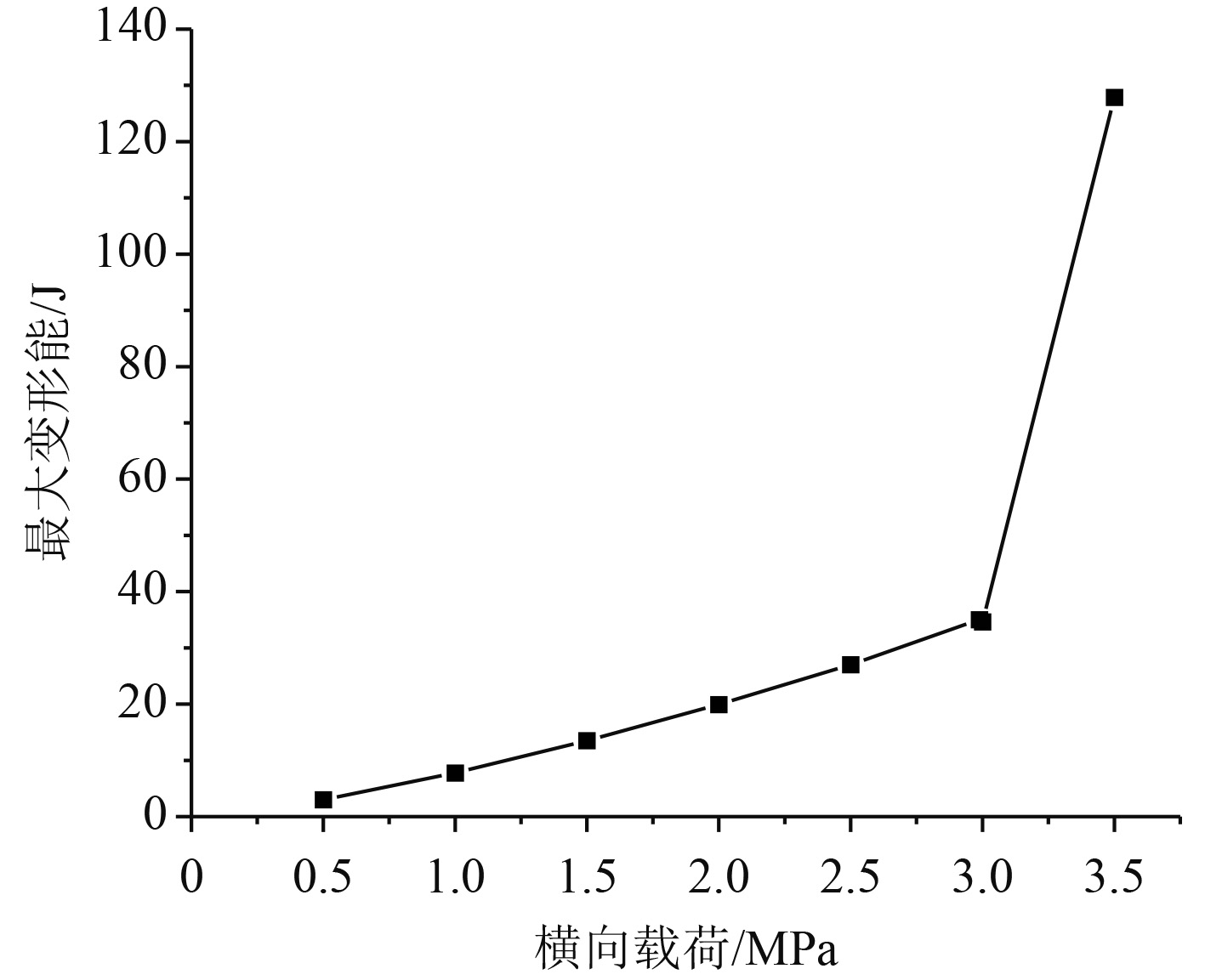
为探讨横向载荷下层板的结构响应特性与损伤形式,从0~3.5 MPa中选取8组不同横向均布载荷值进行计算分析,经计算得到每个工况的应力分布,整理各个工况中层合板的最大应力、最大位移及最大变形能,如图12~图14所示。
|
图 12 最大应力曲线 Fig. 12 Maximum stress |
|
图 13 最大位移曲线 Fig. 13 Maximum displacement |
|
图 14 最大变形能曲线 Fig. 14 Maximum deformation energy |
随着施加压强逐渐增大,结构最大应力线性增大后增速放缓,至极限载荷时达到峰值,破坏后期应力逐渐下降。在横向载荷小于2.988 MPa时,结构中最大位移随着载荷增加而线性增大,结构变形能随加载而积蓄;但载荷达到极限值后,层合板破坏,原本具有结构最大位移的板中点单元失效,故最大位移在后期反而降低,而当层合板破坏后,最大变形能爆发式增长,原因是破坏后层合板弯曲程度严重,积蓄了较大的应变能,同时结构动能并没有上升,因此结构体系能量增大。
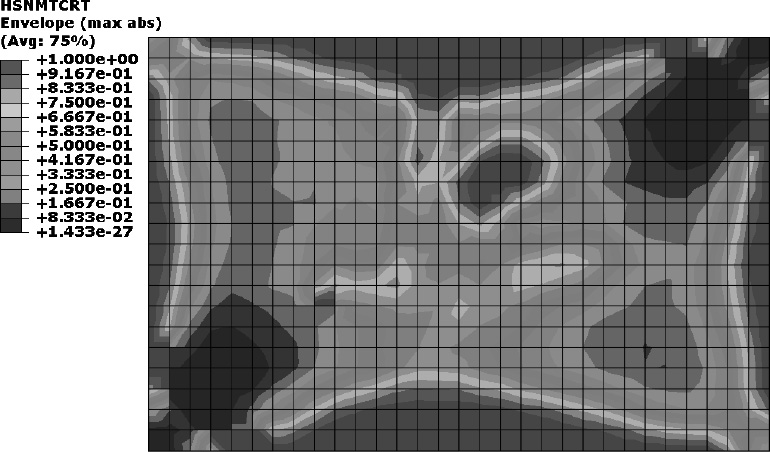
选取2 MPa与2.988 MPa两个工况的层合板损伤状态进行研究,如表10和图15所示。不同大小横向载荷作用下,层合板在损伤状态上具有较相似的分布。大载荷下损伤值会在较小载荷损伤状态基础上增大,并在单元失效后沿着易产生纤维断裂与基体开裂的方向扩展。2 MPa横向载荷下,层合板中已产生明显失效,这解释了图12中2 MPa时最大应力曲线产生转折的原因,即结构中应力较大,接近材料标定强度,许多单元临近失效,载荷增大,应力上升空间有限,故曲线变缓。
|
|
表 10 横向载荷下层合板损伤状态变化 Tab.10 Damage variation of laminate with transverse load |
|
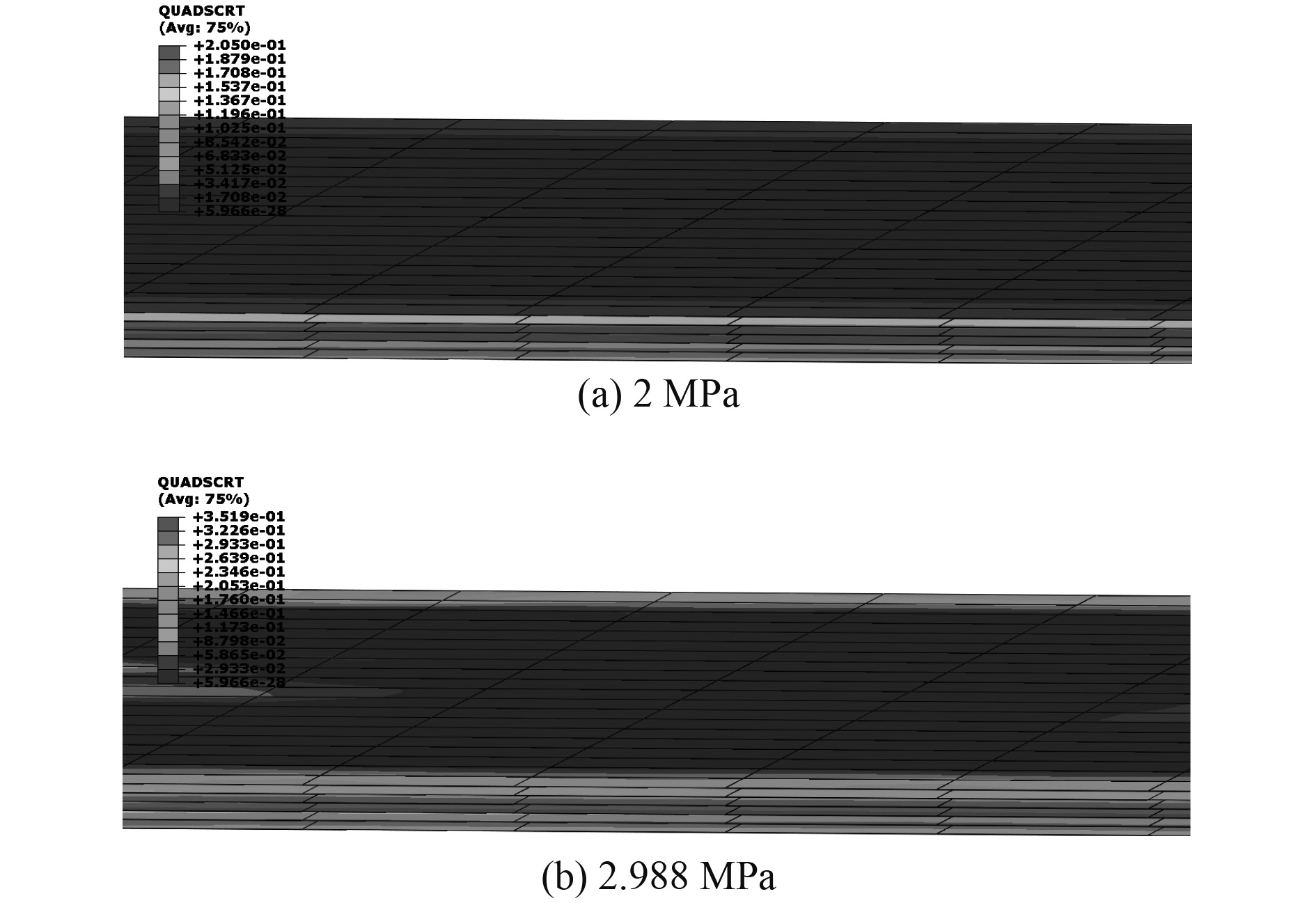
图 15 内聚力层损伤状态 Fig. 15 Damage situation of cohesive layer |
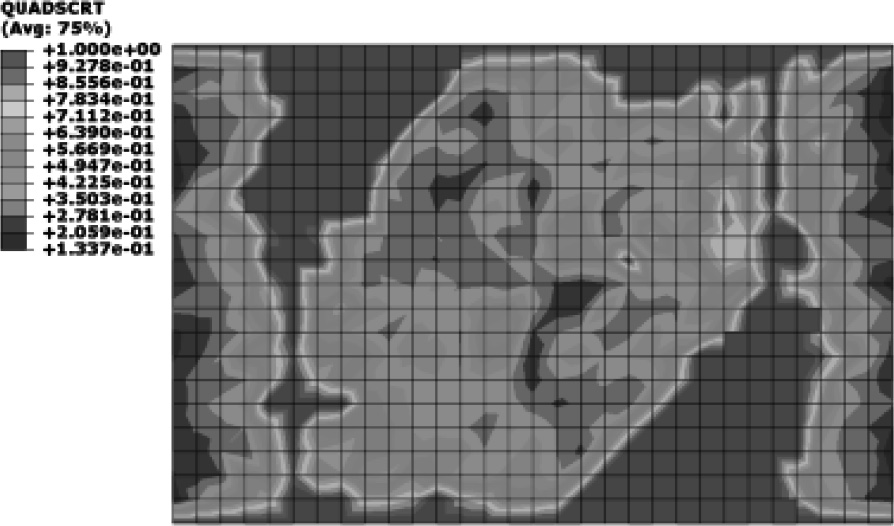
观察内聚力层的损伤状态,结果如图15所示。2 MPa工况的初始损伤Quadscrt最大值为0.205,2.988 MPa工况则为0.352,都位于层板边界长边中间子层区域,且STATUS值为1(0代表单元完全失效,1代表仍可承载),说明层间界面胶层在横向极限载荷作用下未发生破坏,单元最大失效35.2%。在横向载荷作用下,层合板层间胶层从起始到结构破坏,主要承受面外压缩及面内拉压应力,而内聚力单元基于牵引-分离响应描述[11],其面外的正牵引强度较弱,即胶层单元在受面外拉力(正牵引力)时更易失效,故在横向载荷作用下层间胶层未发生破坏而仅产生了损伤。横向载荷作用下层合板具有复杂的损伤失效模式,层内纤维基体失效与层间胶层失效会相互影响,同时各子层间损伤结果差异较大。
4 结 语本文采用实体单元和内聚力模拟出复合材料层合板三维实体精细化模型,采用Hashin失效准则作为层内损伤判据,采用二次应力准则与BK失效准则作为层间损伤判据,对不同载荷形式下层合板结构响应与渐进损伤失效行为进行研究,结果表明:
1)通过与试验结果对比验证可知,本文所用三维实体数值模型与渐进失效判据可有效模拟预测复合材料层合板受载情况下层间与层内渐进损伤过程,相较采用层合板单元的常规分析模型,本文方法所反映出的结构损伤破坏行为更为全面细致。
2)层合板受拉伸载荷时,0°层等主要纵向承载层断裂后直接诱导层合板的失效破坏。层合板受压缩载荷时,因为结构的屈曲失稳,层合板以纤维压缩损伤以及屈曲半波的波腹、波节处的基体损伤为主。层合板胶层在层间起到传递应力以及承担部分载荷的作用,其损伤失效会加剧纤维损伤。
3)层合板在横向载荷作用下,以加载面的纤维/基体拉伸失效为主,其中基体失效是最早发生且范围最大的失效模式,局部失效后易在纤维断裂与基体开裂的方向产生失效带,加载面与背载面之间的损伤差异明显。
| [1] |
CHANG FK, CHANG KY. A progressive damage model for laminated composites containing stress concentrations[J]. Composite Materials, 1987(21): 834-855. |
| [2] |
PUCK A, SCHÜRMANN H. Failure analysis of FRP laminates by means of physically based phenomenological models[J]. Composite Science Technology, 1998(58): 45-67. |
| [3] |
CAMANHO PP, DÁVILA CG. Mixed-mode decohesion finite elements for the simulation of delamination in composite materials[S]. NASA/TM-2002-211737, VA, USA: NASA Langley Research Center, 2002.
|
| [4] |
ADRIAN C. ORIFICI, Iñigo Ortiz de Zarate Alberdi, Rodney S. Thomson, et al. Compression and post-buckling damage growth and collapse analysis of flat composite stiffened panels[J]. Composites Science and Technology, 2008, 68(15): 3150-3160. |
| [5] |
SLEIGHT, D. W. Progressive failure analysis methodology for composite laminated structural[R]. NASA/TP-1999-209107, 1999.
|
| [6] |
ABAQUS Inc. Abaqus Analysis User’s Manual[M]. Providence, RI, USA: Dassault Systemes Simulia Corp., 2010.
|
| [7] |
BENZEGGAGH M L, KENANE M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus[J]. Composites Science & Technology, 1996, 56(4): 439-449. |
| [8] |
张浩宇, 何宇廷, 冯宇, 等. 先进复合材料薄壁加筋板轴压屈曲特性及后屈曲承载性能[J]. 航空材料学报, 2016, 36(4): 58-66. |
| [9] |
朱炜垚, 许希武. T300/QY8911层合板低速冲击试验及有限元模拟[J]. 材料科学与工程学报, 2013, 31(1): 68-73, 77. |
| [10] |
解江, 张雪晗, 苏璇, 等. 铺层顺序对复合材料薄壁圆管轴向压溃吸能特性的影响研究[J]. 工程力学, 2018, 35(6): 240-248. |
| [11] |
Analysis of Composite Materials with Abaqus. Abaqus Analysis User’s Manual.
|
 2021, Vol. 43
2021, Vol. 43