目前,舱门结构大量应用在舰载设备中,如舰船通道的启闭、某型发射装置舱口盖的启闭等,是船舶上的重要组成部分之一[1]。大多数的舱门采用电机或机械挡块的结构形式进行舱门开关状态的控制,如采用电机旋转实现舱门的启闭并通过电机的自锁实现舱门的锁定;或手动开启舱门并通过机械挡块进行限位锁定舱门角度,关闭舱门时需进行手动解锁后才能关闭舱门。目前的舱门结构在日常使用和维护中主要存在以下问题:1)电机结构主要存在成本高,结构占用空间大,维保成本高;2)机械挡块结构主要存在舱门开启角度恒定,无法在多种角度下锁定舱门,舱门解锁较为不便。针对以上问题,本文以舱门为研究对象,设计开发一种自锁式舱门[2-5]。
1 结构设计利用棘轮机构自锁原理实现舱门多角度开启和锁定功能,通过自锁解锁机构实现棘轮机构解锁即实现舱门关闭功能。
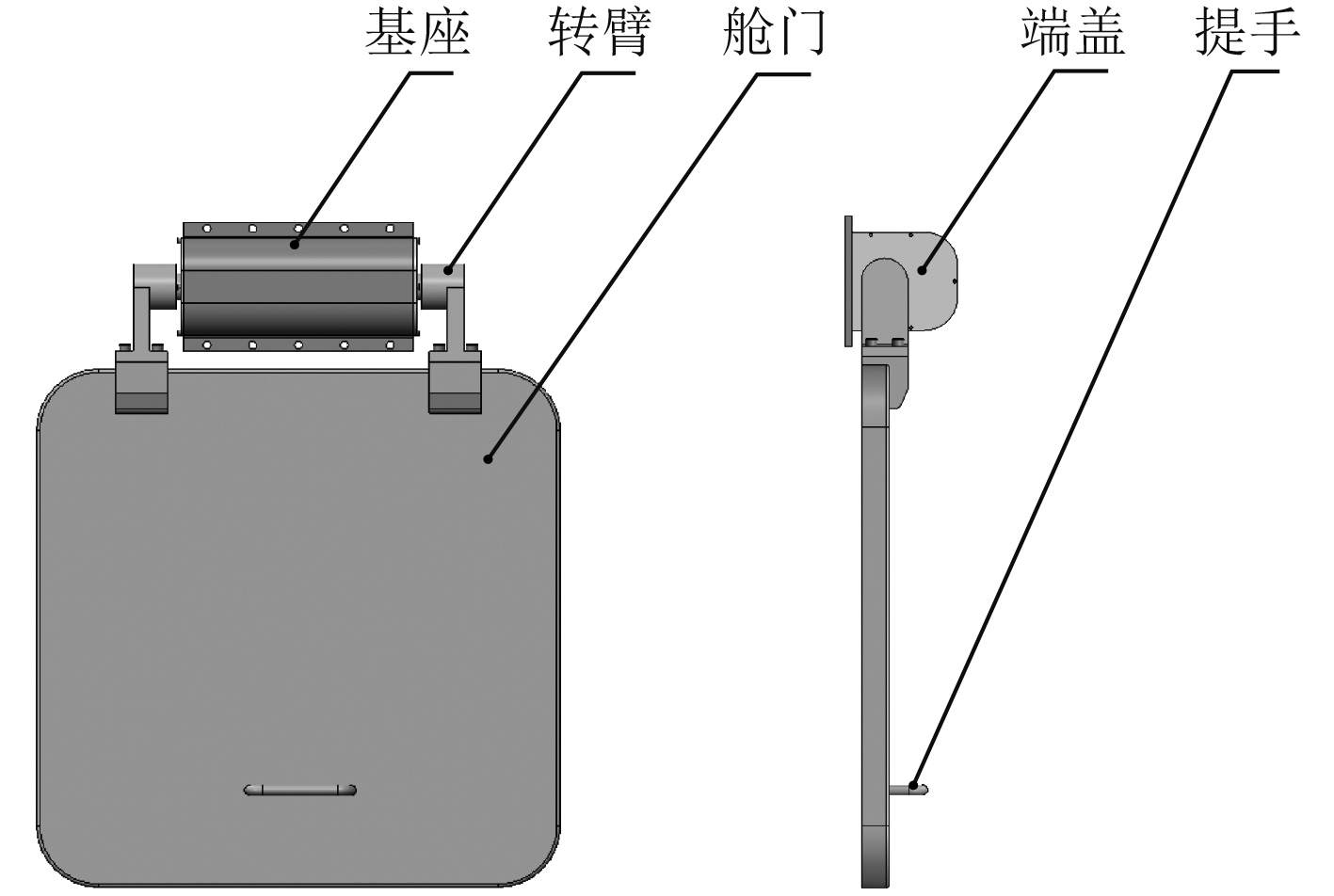
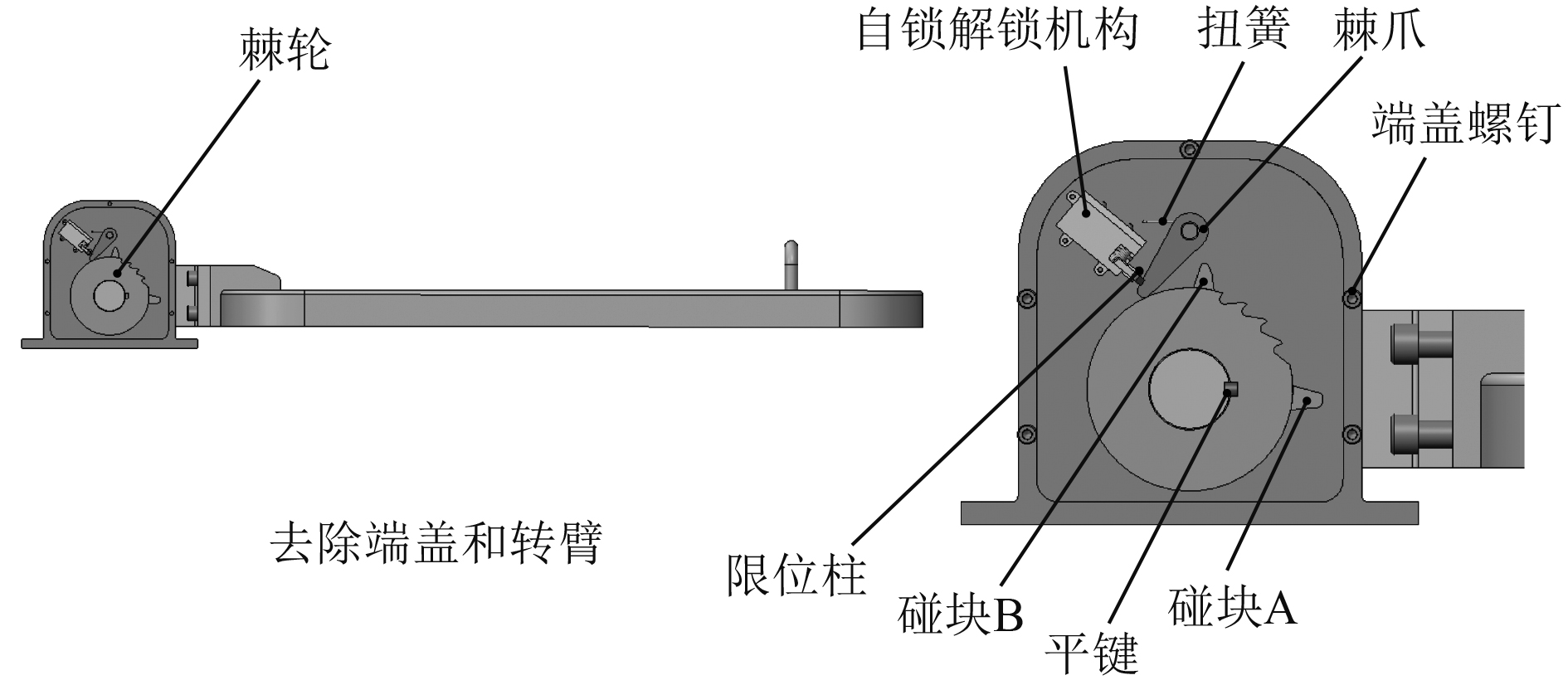
1.1 整体结构如图1和图2所示,该舱门主要由基座、转臂、舱门、端盖、提手、棘轮、自锁解锁机构、扭簧、棘爪、端盖螺钉、限位柱、碰块A、平键和碰块B等组成。基座为舱门提供旋转中心和固定机体,转臂与舱门通过连接螺栓安装在基座上,舱门上设计有提手用于舱门的启闭。棘轮安装在转臂上并通过平键传递扭矩从而实现转臂旋转带动棘轮转动,扭簧用于实现棘爪的复位功能。基座内壁安装有自锁解锁结构并通过碰块A和碰块B实现自锁解锁结构对棘爪的锁定和释放功能,从而实现舱门启闭时的自锁和解锁的功能。
|
图 1 舱门总体结构组成图 Fig. 1 Overall structural composition of cabin door |
|
图 2 舱门内部结构组成图 Fig. 2 Interior structural composition of cabin door |
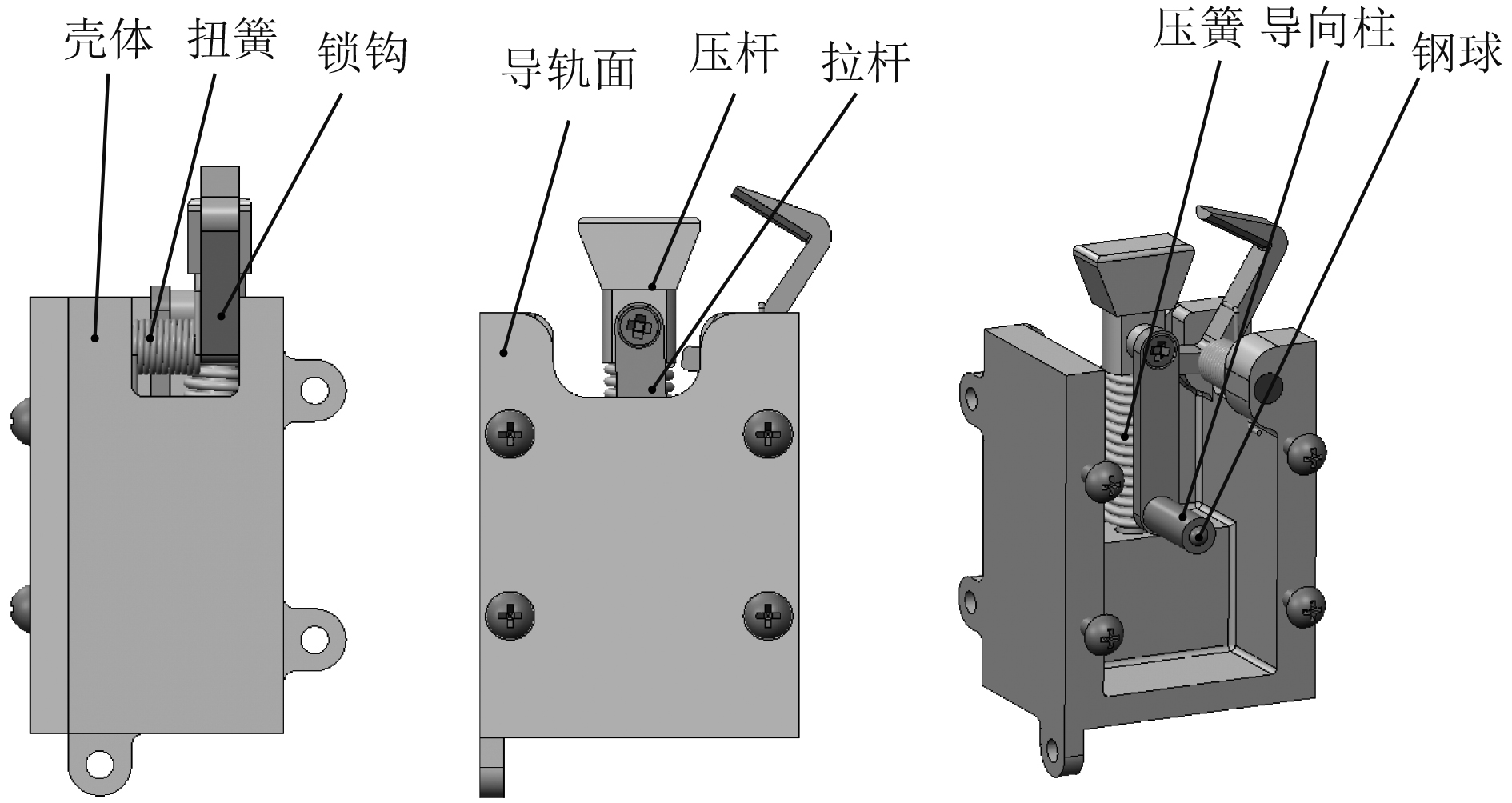
自锁解锁机构用于实现对棘爪的锁定和释放功能,从而实现舱门启闭时的自锁和解锁功能,其主要由壳体、扭簧、锁钩、导轨面、压杆、拉杆、压簧、导向柱和钢球等组成。其中,壳体为自锁解锁机构提供安装接口;导轨面安装在壳体上,其内表面设计有阶梯差和凹槽,分别为导向柱的移动提供路径约束和锁定点;导向柱内的钢球利于减少导向柱与导轨面之间的摩擦力并实现限位功能;压簧和扭簧用于实现压杆和锁钩的复位功能。
|
图 3 自锁解锁机构组成图 Fig. 3 Composition diagram of self-locking and unlocking mechanism |
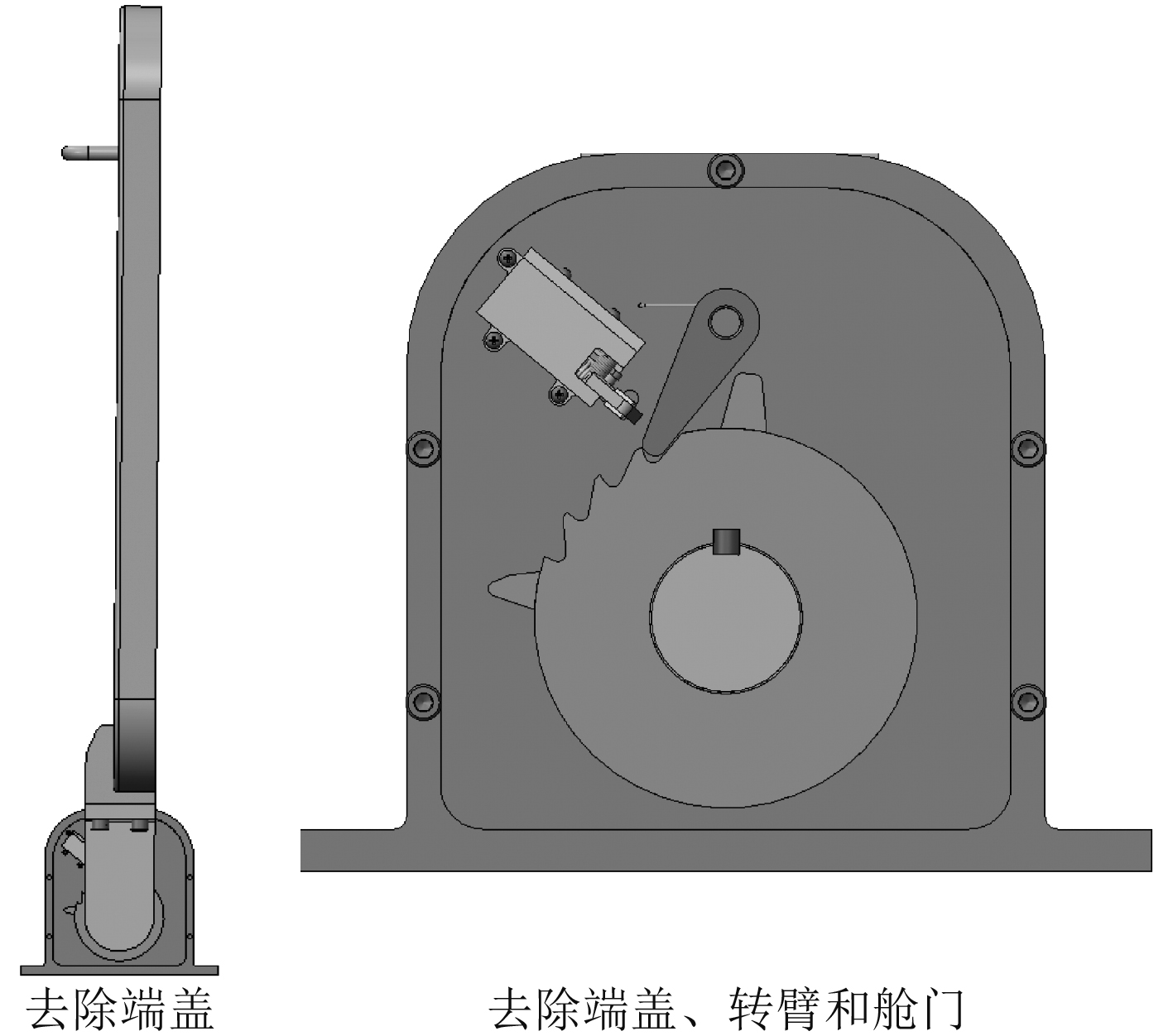
将舱门沿旋转轴逆时针转动开启,舱门上的转臂棘轮转动,舱门开启至一定角度时(约45°),棘轮机构中棘爪在扭簧的作用下与棘轮上的轮齿配合,实现舱门顺时针旋转锁定功能(即舱门只能顺时针开启,不能逆时针关闭)。同时,棘轮上设计有多个轮齿,可实现舱门多角度开启和顺时针旋转锁定功能。图4为舱门开启的最大角度约90°时的状态示意图。
|
图 4 舱门开启锁定状态 Fig. 4 Cabin door open lock status |
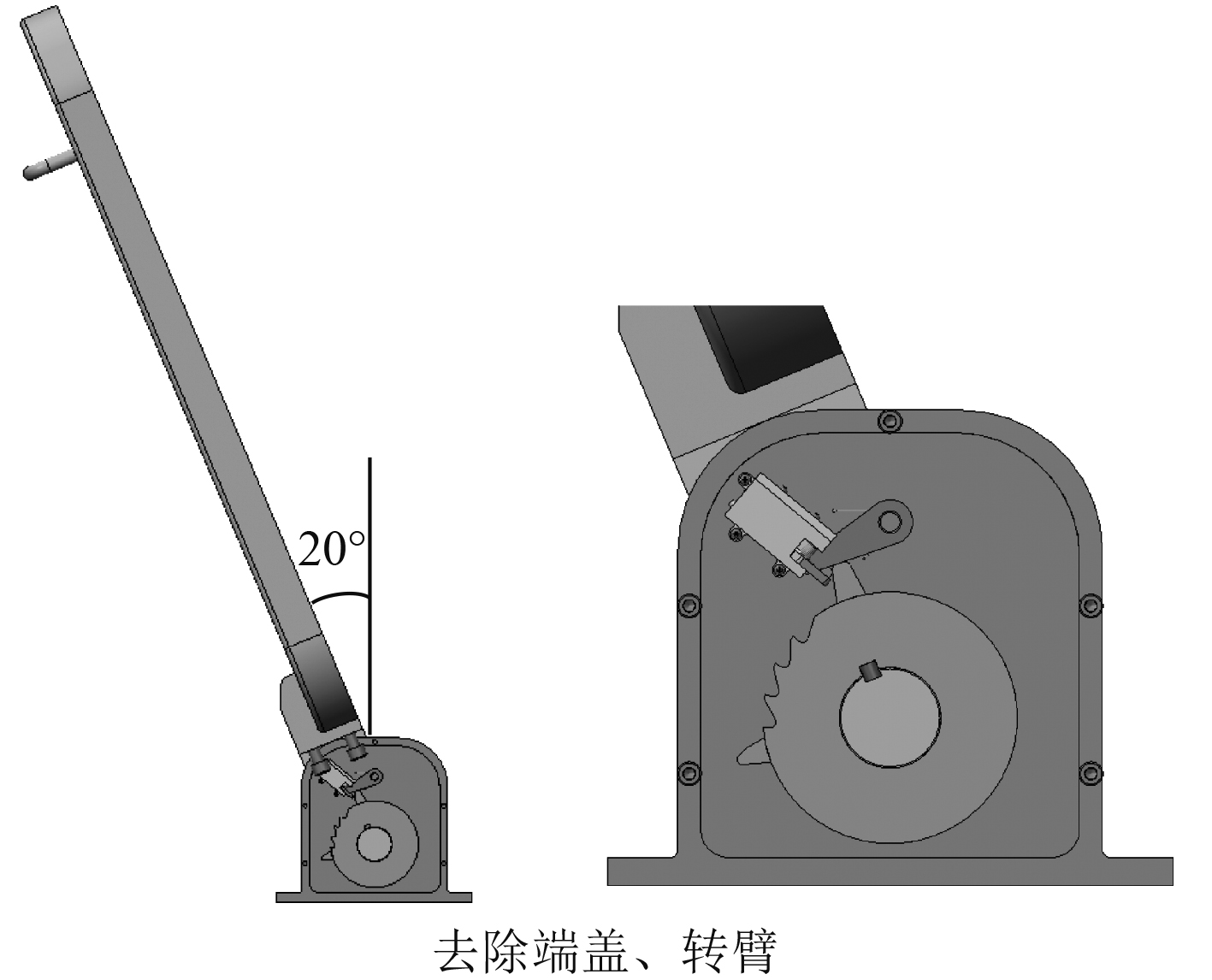
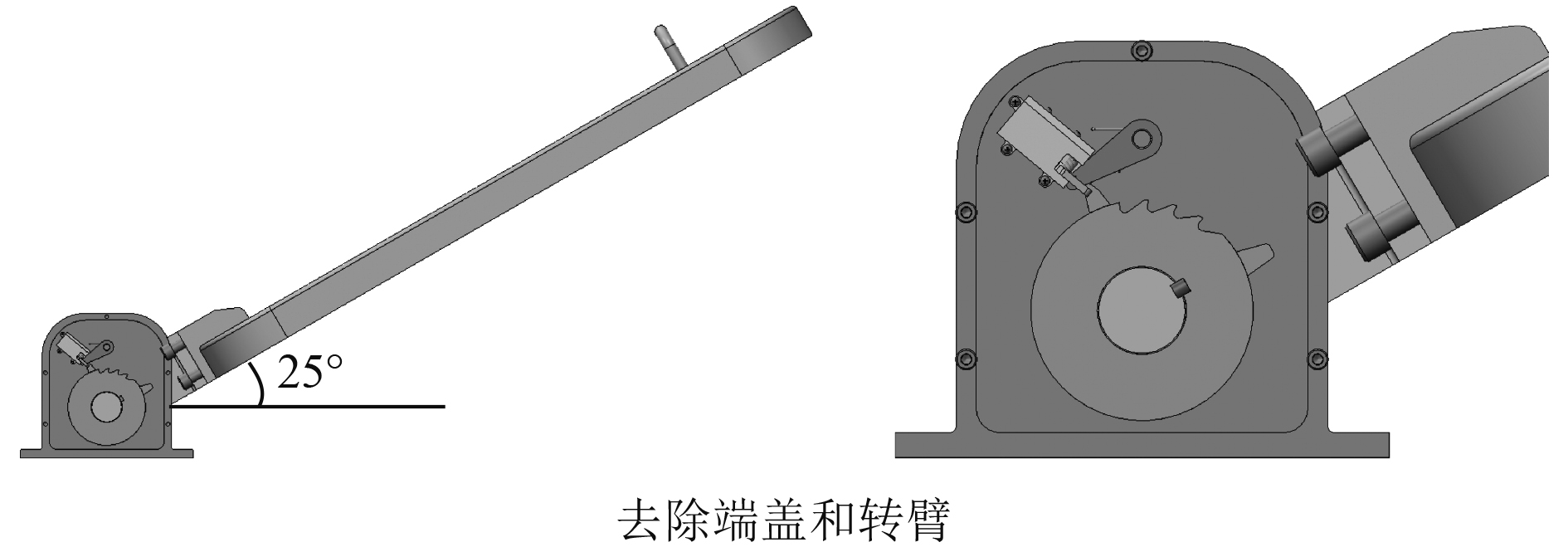
当需要关闭舱门时,首先将舱门逆时针旋转约20°,棘轮上的碰块A碰触棘爪旋转并推动自锁解锁机构中的压杆下移,压杆带动锁钩转动并将棘爪限位,此时棘爪与棘轮上的轮齿脱离,棘轮可自由转动,即舱门处于解锁状态(见图5),可进行旋转关闭操作。舱门关闭至一定角度时(约25°),碰块B碰触棘爪旋转并推动自锁解锁机构中的压杆复位并解锁(见图6),棘爪在扭簧的作用下复位,在再次开启舱门时仍可实现舱门的自锁功能。
|
图 5 舱门解锁状态 Fig. 5 Cabin door unlocked |
|
图 6 舱门复位 Fig. 6 Cabin door reset |
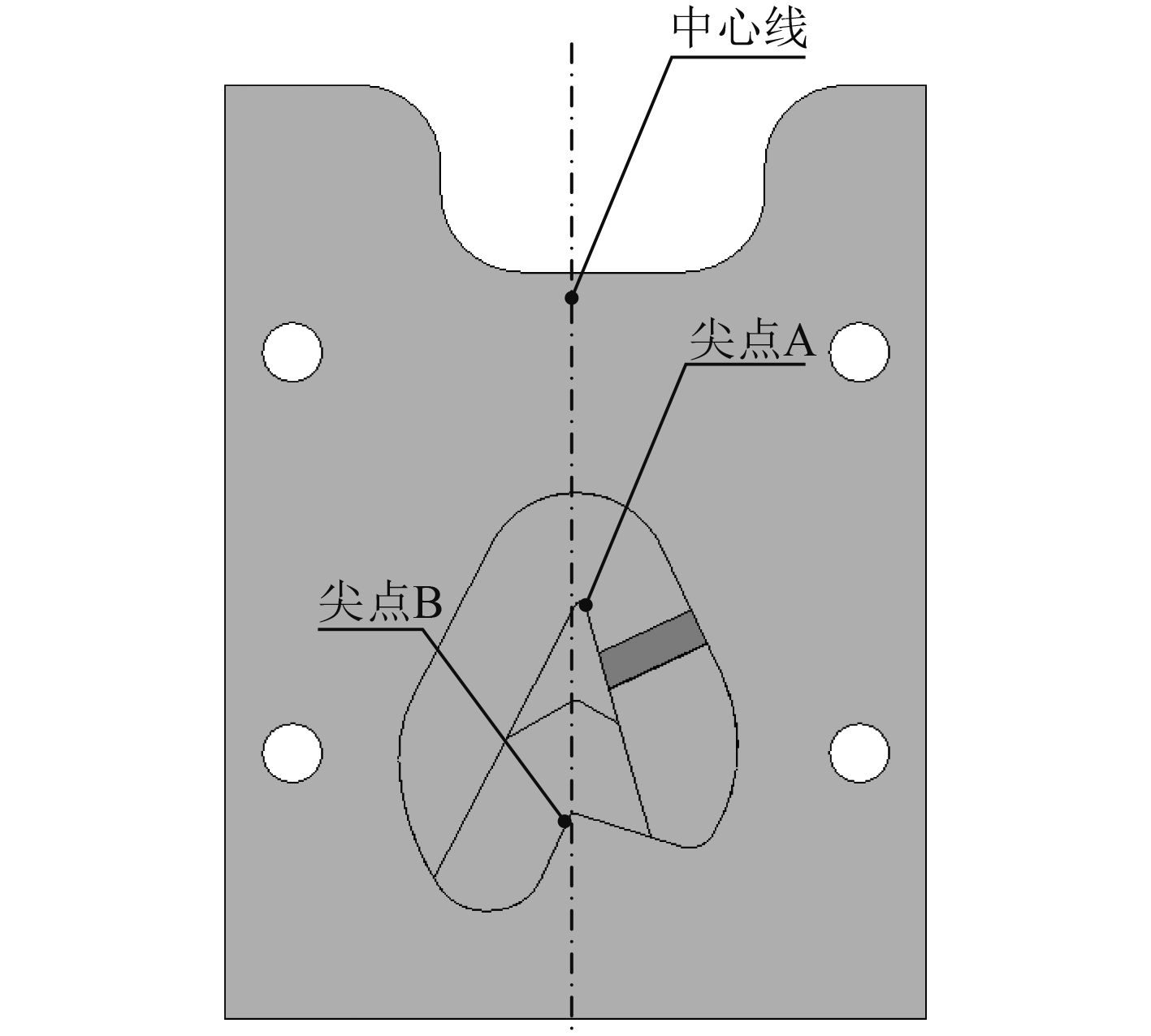
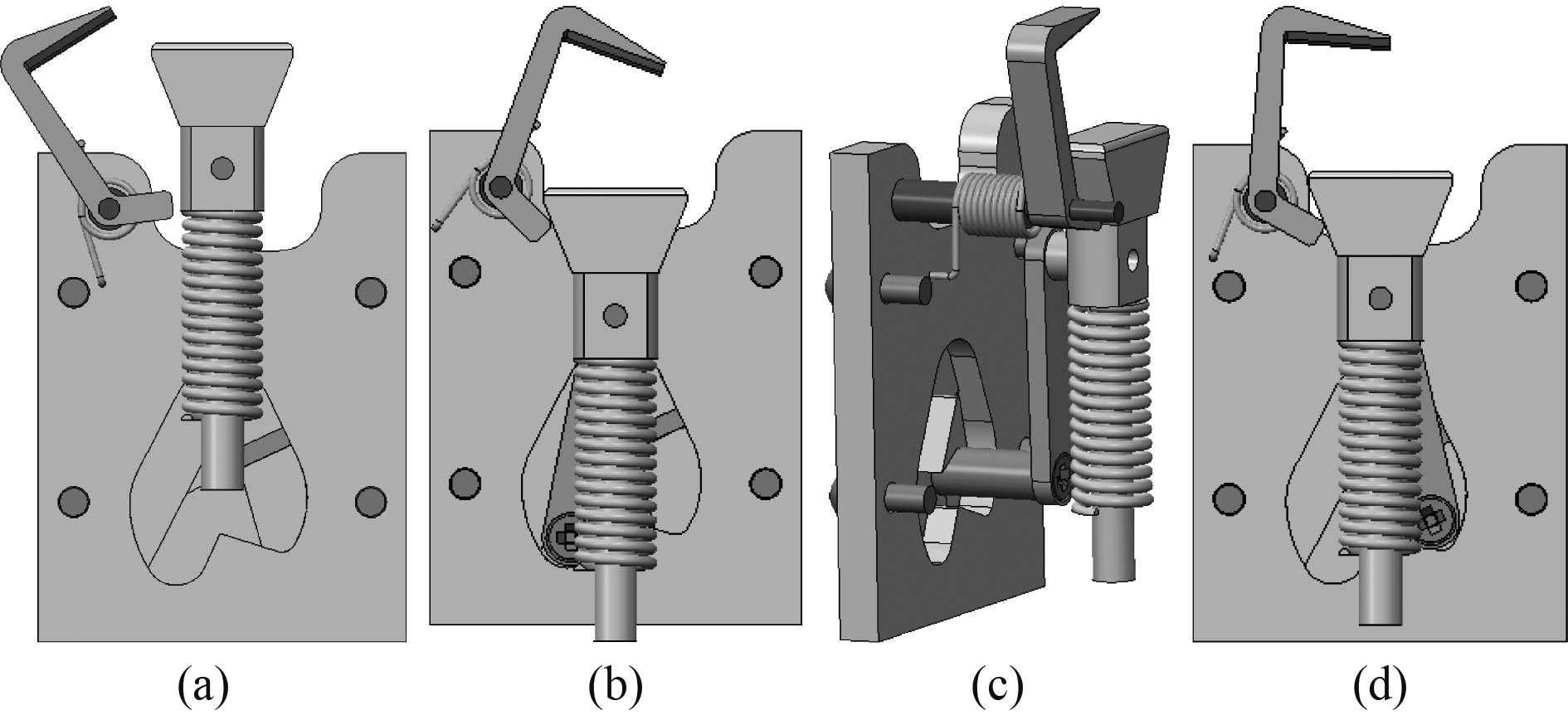
在关闭舱门时,先将舱门逆时针旋转约20°(见图5)至棘轮上的碰块A碰触限位柱(此时舱门到达最大开启角度),棘轮上的碰块A推动自锁解锁机构中的压杆,压杆带动拉杆在导向柱和钢球的导向下沿着导轨面上尖点A位置的左侧移动(见图7),压杆由初始状态(图8(a)所示位置)移动至如图8(b)所示位置,压杆同时带动锁钩旋转。然后将舱门关闭,舱门带动棘轮顺时针转动,棘爪在扭簧作用下复位,压杆在压簧作用下复位并带动拉杆向上移动,导轨面内设置有阶梯差,并在导向柱内装有压簧和钢球。压杆在导向柱和钢球的作用下沿着导轨面移动至图8(c)所示位置,实现压杆位置锁定并固定锁钩旋转角度,此时锁钩将棘爪锁定,棘爪与棘轮上的轮齿脱离,棘轮可自由转动,舱门解锁并可顺时针关闭。
|
图 7 导轨面结构图 Fig. 7 Structural drawing of guide surface |
|
图 8 自锁解锁机构工作原理图 Fig. 8 Working principle diagram of self-locking and unlocking mechanism |
当舱门旋转至约25°时(见图6),棘轮上的碰块B推动自锁解锁机构中的压杆,压杆带动拉杆在导向柱和钢球的导向下沿着导轨面上尖点B右侧(见图7)移动至图8(d)所示位置,自锁解锁机构中的压杆解锁,在舱门关闭的同时,压杆在压簧作用下复位并带动拉杆向上移动至初始状态(图8(a)所示位置),锁钩在扭簧的作用下复位至初始状态(图8(a)所示位置),棘爪在扭簧作用下复位至初始状态。
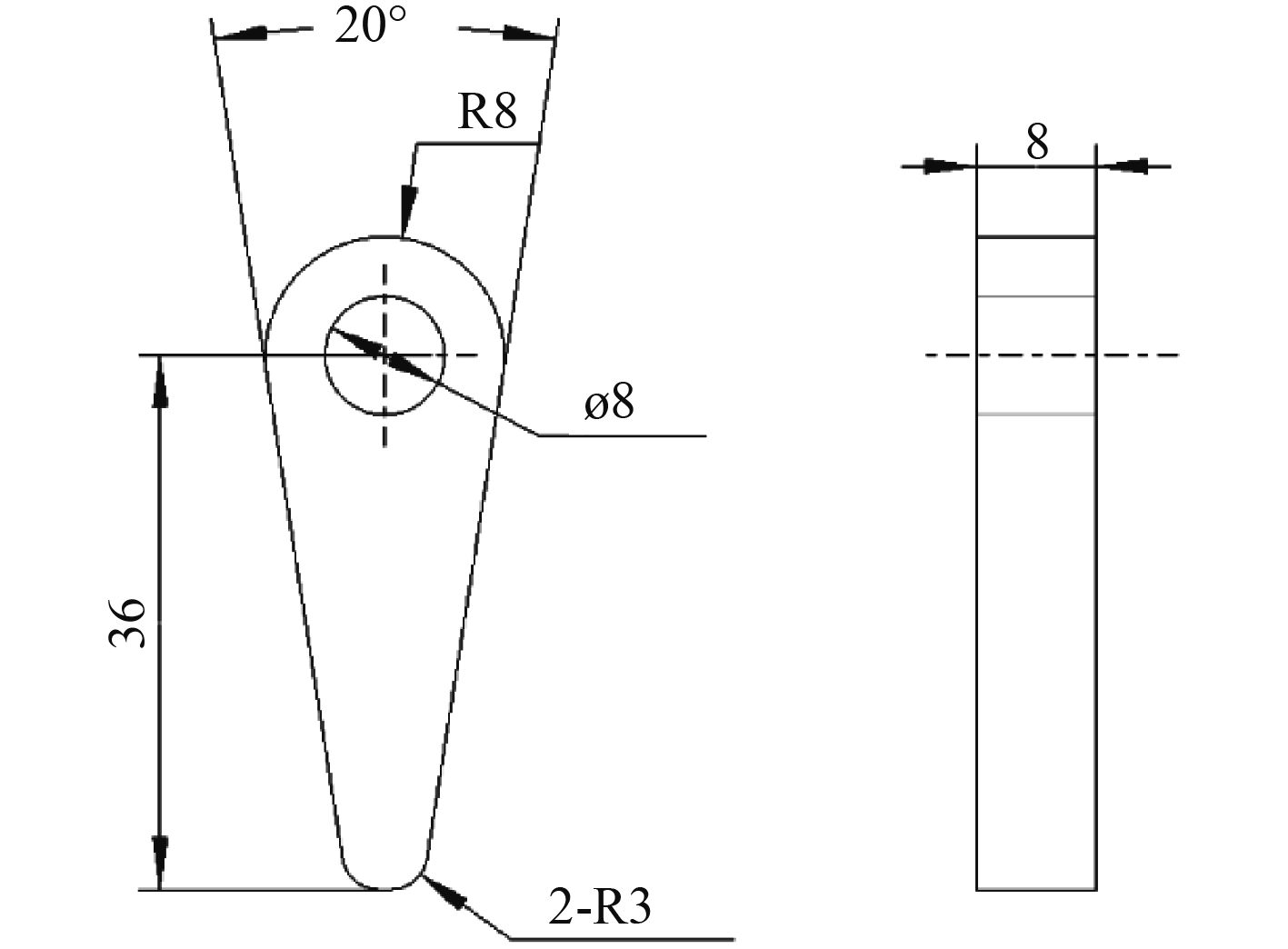
3 关重件强度校核在本自锁式舱门机构中,棘爪为舱门实现自锁和解锁功能的关重件,因此,本文对该零件进行强度和刚度分析。棘爪的材料选用Q235低碳钢,屈服强度235 MPa,抗拉强度370 MPa,抗剪强度141 MPa[6],结构尺寸如图9所示。
|
图 9 棘爪结构尺寸图 Fig. 9 Structure size drawing of pawl |
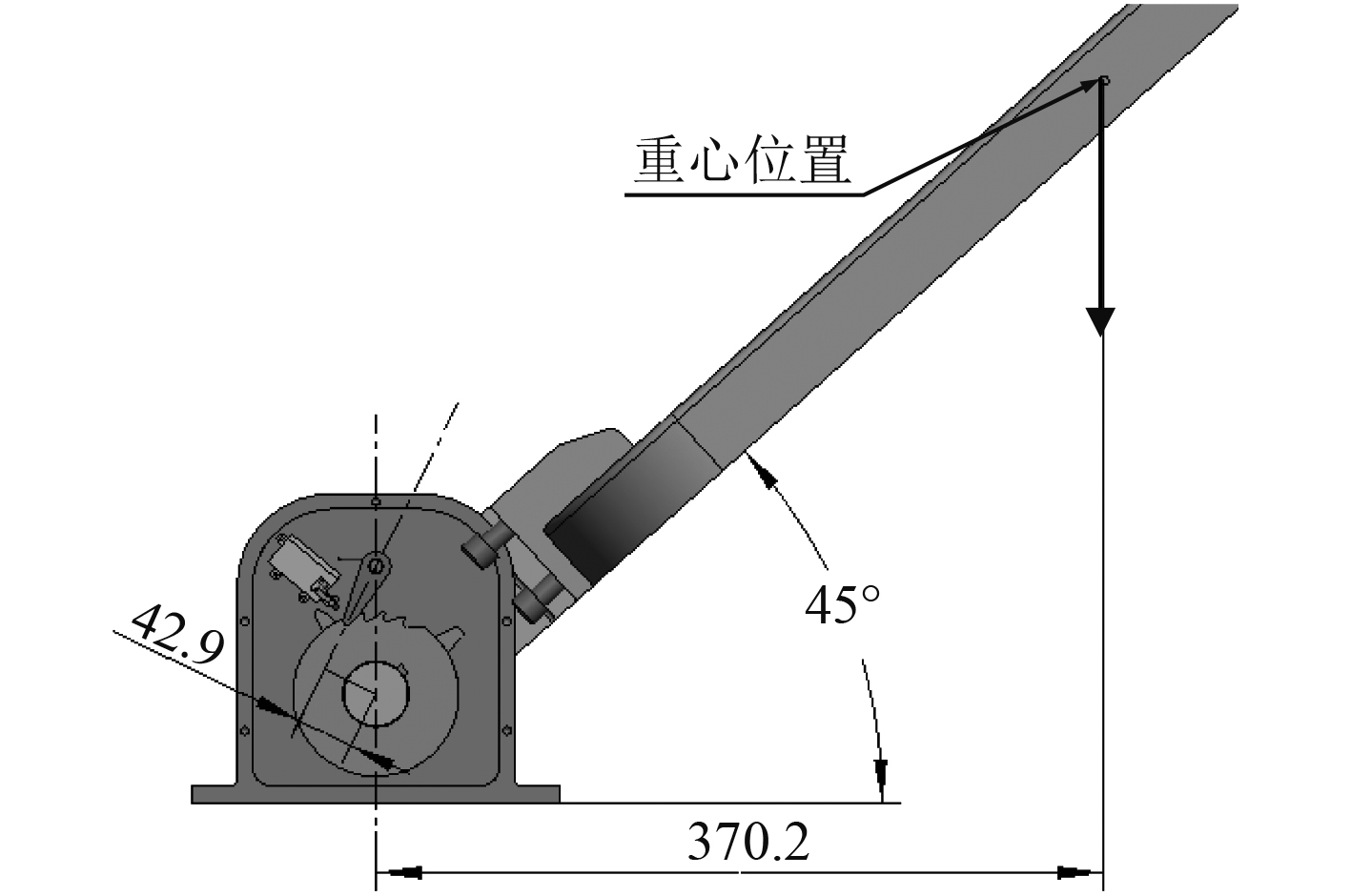
在本舱门结构中,棘爪的主要功能是实现舱门自锁。舱门在一定角度开启并锁定时,以舱门重心位置为力作用点,竖直向下为力的方向,舱门重心位置至舱门旋转轴的垂直距离L为力臂,在舱门重力F作用下产生舱门转动的力矩M。为实现舱门自锁功能,棘爪限制舱门转动并承载旋转力矩,舱门受力情况如图10所示。
|
图 10 舱门受力分析图 Fig. 10 Force analysis diagram of cabin door |
采用Creo三维软件进行三维建模,并对该方案中的零部件添加材料属性进行重量测量,测量结果如表1所示。
|
|
表 1 主要零部件重量 Tab.1 Weight of major components |
力矩计算公式为:
| $M = F \times L\text{。}$ | (1) |
式中:M为力矩;F为力;L为力臂。
在舱门开启至45°时,舱门重力产生的力矩最大,即棘爪受到的作用力最大,因此以该状态进行受力校核计算。根据表1的计算结果舱门组件的总重量为95.858 kg,为便于计算将其圆整为96 kg。通过三维实体模型测量,舱门重心位置至舱门旋转轴的垂直距离为370.2 mm,因此舱门重力产生的最大力矩为:
| ${M_{{\rm{max}}}} = F \times {L_{\rm{1}}} = {\rm{960}} \times {\rm{0}}{\rm{.37}} = {\rm{355}}{\rm{.2\;N}} \cdot {\rm{m}}$ |
式中:F为舱门重力;
同样,根据《材料力学》中力矩计算公式(式(1))可推导出棘爪受到的最大力
| ${F_{\max }} = {M_{\max }}/{L_2} = 355.2/0.043 = 8260.47{\rm N}\text{。}$ |
式中:
根据《材料力学》可知,其抗压结构强度可用式(2)进行计算和校核[7]。
| $\sigma = \frac{{{{kF}}}}{{{A}}} < \left[ \sigma \right],$ | (2) |
式中:k为安全因数;F为棘爪承受载荷;A为棘爪截面面积;
棘爪最小截面面积通过Creo三维建模软件对三维实体模型进行测量,最小截面面积为为52.1 mm2。
则:
| $\sigma = \frac{{2 \times {\rm{8}}260.47}}{{{\rm{52}}{\rm{.1}}}} = 317.1\;{\rm{MPa}} < \left[ \sigma \right] = 370\;{\rm{MPa}}\text{。}$ |
经对棘爪进行理论计算强度校核,在安全系数为2的情况下,最大应力为317.1 MPa,小于许用应力370 MPa,可满足设计使用要求。
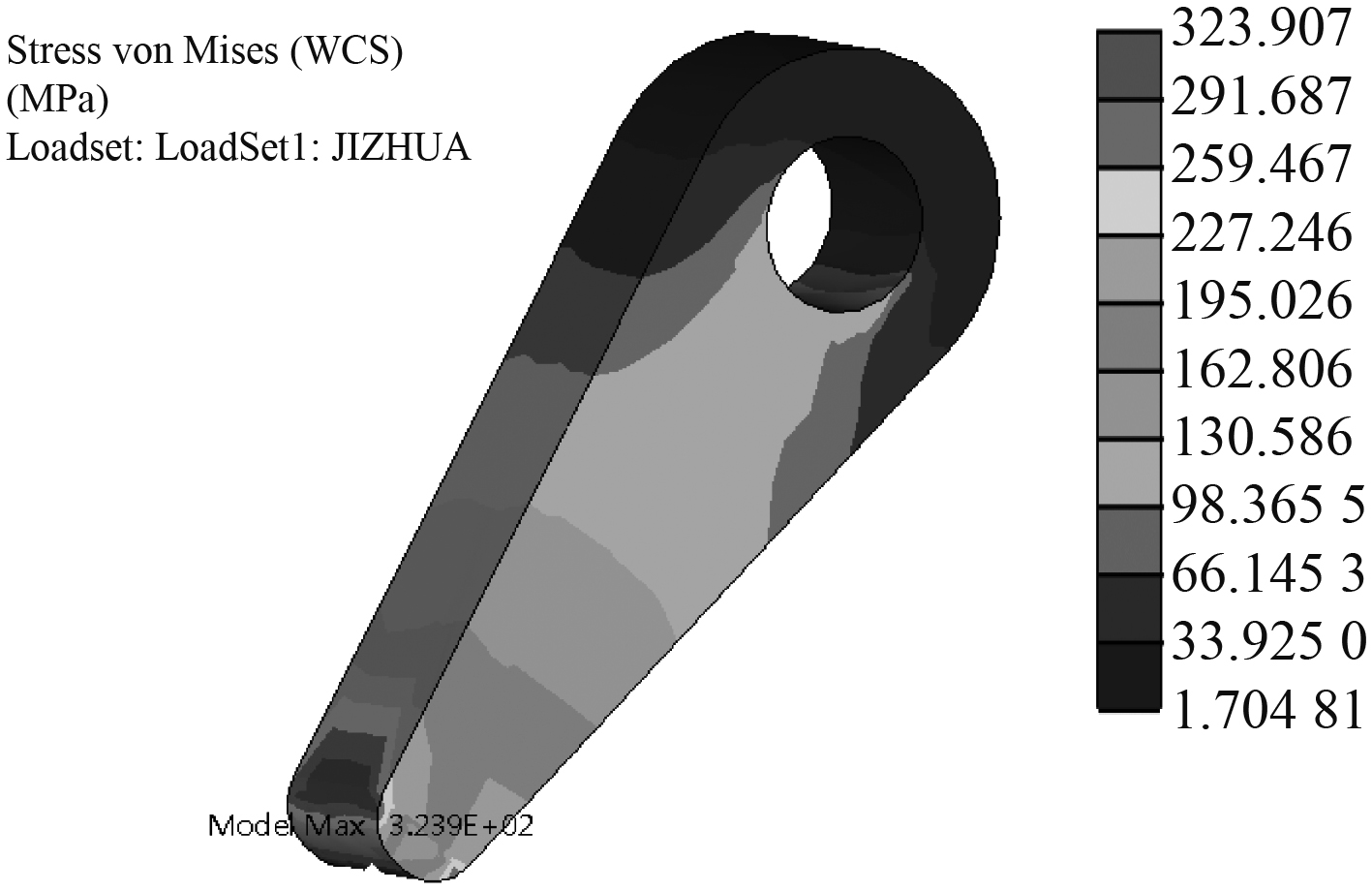
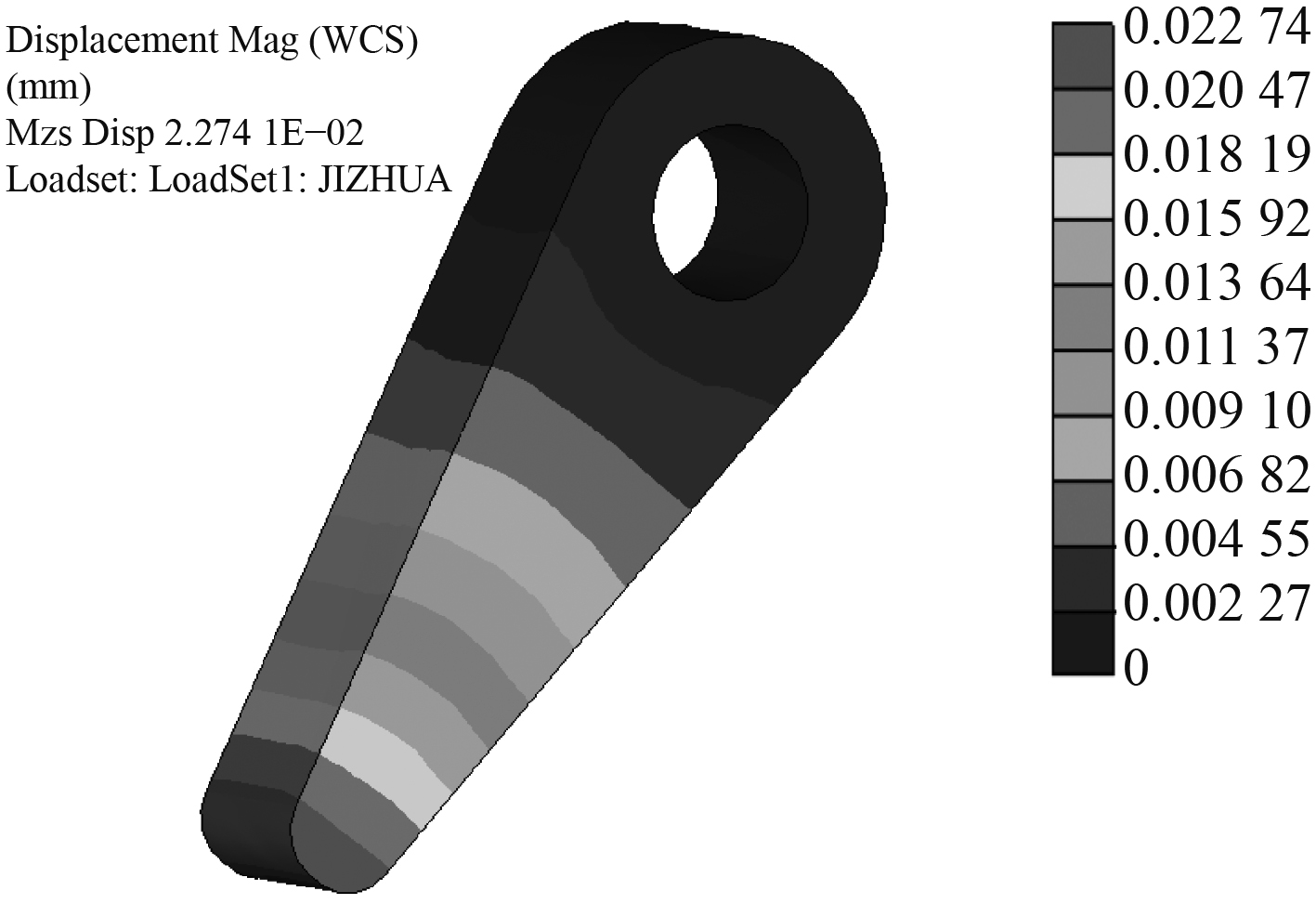
3.2 有限元分析为验证理论计算的正确性,普遍采用有限元方法进行校核[8]。本文采用Creo Simulate对棘爪进行有限元仿真分析。通过对棘爪分别添加材料、约束和载荷,得到有限元模型[9](具体过程不再一一赘述),最后对棘爪的有限元模型进行静态分析,得到相对应的应力和应变情况,结果如图11和图12所示。
|
图 11 棘爪应力图 Fig. 11 Pawl stress diagram |
|
图 12 棘爪应变图 Fig. 12 Pawl strain diagram |
通过仿真分析,棘爪的最大应力为323.9 MPa,小于屈服强度370 MPa,且变形量较小,在规定工况下不会发生结构性破坏,满足设计使用要求。
3.3 对比分析分别使用理论计算和Creo Simulate仿真分析的方法对通用棘爪进行强度和刚度计算校核,分析结果表明,仿真结果与理论计算基本一致,棘爪的强度和刚度能够满足工作的要求。
4 结 语本文以舱门为研究对象,设计开发了一种自锁式舱门,该舱门通过棘轮和棘爪结构实现舱门开启后的锁定,采用自锁解锁机构和碰块将棘爪限位自锁实现舱门关闭时的解锁,同时使用自锁解锁机构和碰块将棘爪复位解锁实现舱门自锁结构的复位,并对其结构原理和受力情况进行分析研究,通过理论计算对关键零部件进行强度校核,完成了舱门的结构设计。利用Creo三维软件进行三维实体建模,并使用Creo Simulate对关键零部件进行强度刚度仿真分析,仿真结果验证了理论计算的正确性。通过理论计算和仿真分析验证了所设计的自锁式舱门的可行性,能够满足舱门多角度开启和自锁解锁的工作要求。
| [1] |
刘炳楠, 孙先波, 等. 船舶舱口盖的分类及修理[J]. 中国修船, 2006, 19(2): 19-21. DOI:10.3969/j.issn.1001-8328.2006.02.008 |
| [2] |
刘建伟, 耿楷真. 空间RSSR机构在舰船舱门设计中的应用[J]. 舰船科学技术, 2019, 41(6): 143-146. LIU Jianwei, GENG Kaizhen. Application of mechanism RSSR in the ship cabin design based on the method of Genetic Algorithm[J]. Ship Science and Technology, 2019, 41(6): 143-146. DOI:10.3404/j.issn.1672-7649.2019.06.030 |
| [3] |
刘永亮, 任克亮. 平面四杆机构在舰载垂直发射装置舱口盖系统中的应用分析[J]. 装备环境工程, 2019, 16(5): 13-17. |
| [4] |
吴四川, 赵云清. 船舶舱盖的修理[J]. 中国修船, 2002(5): 12-13. DOI:10.3969/j.issn.1001-8328.2002.05.006 |
| [5] |
陈苏秧. 基于腐蚀影响的折叠式舱口盖结构优化设计[J]. 舰船科学技术, 2018, 40(9A): 208-210. |
| [6] |
GB/T700-2006, 碳素结构钢[S].
|
| [7] |
范钦珊, 殷雅俊, 唐靖林. 材料力学[M]. 北京: 清华大学出版社, 2004: 112−113.
|
| [8] |
徐双喜, 张浩, 等. 舱口盖强度计算方法[J]. 船舶工程, 2018, 40(6): 12-16. |
| [9] |
齐从谦, 李文静. Creo3.0三维创新设计与高效仿真[M]. 北京: 中国电力出版社, 2017: 220−225.
|
 2021, Vol. 43
2021, Vol. 43
