舰载外露设备通常遭受着比较恶劣的环境和复杂的载荷作用,如风载荷、惯性载荷、冰雪载荷、温差载荷,以及冲击、振动载荷等,考虑到设备的实际使用条件和特点,风载荷、惯性载荷和振动载荷是强度计算中的主要考虑因素[1]。在复杂的外载作用下,为保证设备的正常使用和安全性,设备结构需要具有足够的刚强度,同时受舰船空间尺寸和吨位的限制,对设备的尺寸及重量都有严格控制要求,因此设计时需要充分利用材料的力学性能,在结构上进行优化设计。在技术实现上,随着CAD /CAE 技术的发展,有限元分析及优化技术被广泛运用在结构设计领域,通过有限元分析能够预先对产品的合理性进行可视化评价,为设计人员提供理论参考和优化策略,是一种实用的设计方法和优化手段。
本文以某型舰载搜索雷达稳定平台的部分设计指标及环境条件为依据,对稳定平台基座的受力情况进行分析,并利用有限元技术对基座进行结构力学仿真和优化设计,使其满足一定的减重要求以及复杂载荷条件下的强度要求。
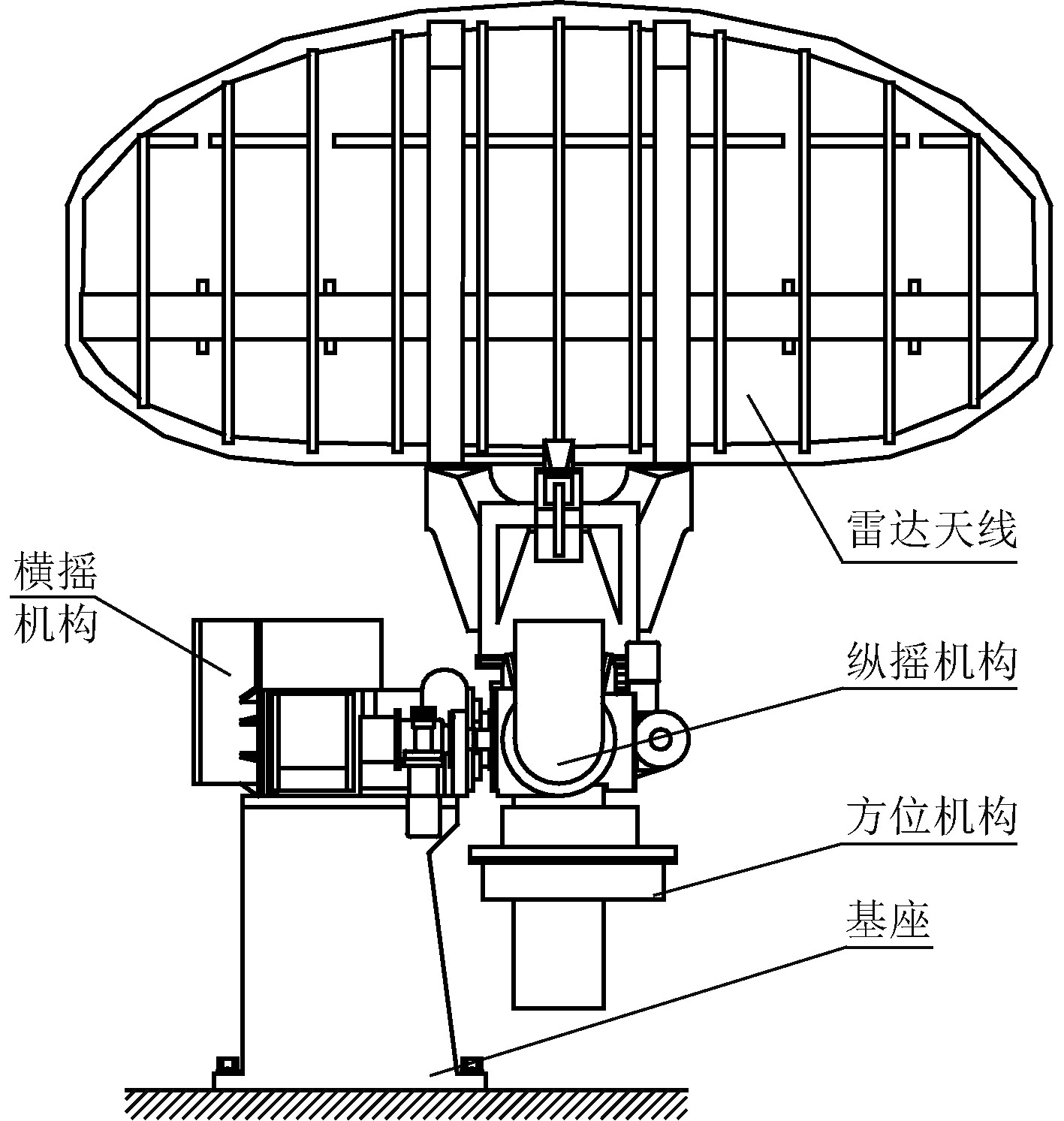
1 基座载荷计算某舰载雷达设备安装在舰船桅杆上,主要包括雷达天线、稳定平台和基座3部分。稳定平台分为横摇机构,纵摇机构和方位机构3部分,其中横摇机构安装在基座上,纵摇机构安装在横摇机构旋转轴轴端,方位机构安装在纵摇旋转轴轴端,并且方位转轴与雷达天线连接为一体,如图1所示。设备工作时,通过横摇、纵摇和方位3个轴向的联动,保证雷达天线在船摇工况下始终保持在水平面上360°扫描搜索。此时基座承受的载荷主要包括稳定平台和天线在船摇时的惯性载荷(重力、摇摆力和垂荡力)、风载荷以及振动载荷。
|
图 1 雷达设备组成 Fig. 1 Composition of radar equipment |
舰船在特定海况的海浪冲击下,会产生摇摆和垂荡运动,使得设备承受一定的惯性载荷,一般的船体的纵摇、横摇和垂荡运动符合正弦运动规律,而其中纵摇、横摇载荷为主要影响因素,垂荡载荷为次要影响因素。舰载雷达设备跟随船体运动时,可根据正弦运动规律计算出设备的载荷[2-3]。
船体横摇、纵摇和垂荡运动时摇摆角位移和垂荡位移为:
| $\phi = {\phi _p}{\rm{sin}}{\omega _1}t\text{,}$ |
| $h = {h_m}\sin {\omega _2}t\text{,}$ |
其中:
| $\omega = 2\text{π} f = \frac{{2\text{π} }}{T}\text{。}$ |
式中:φ p为摇摆振幅,(°);hm为垂荡振幅,m;f为摇摆或垂荡频率,Hz;T为摇摆或垂荡周期,s。
| ${\text {摇摆角加速度}}\varepsilon = \dfrac{{{{\rm d}^2}\phi }}{{{\rm d}{t^2}}} = - {\phi _p}{\omega _1}^2\sin {\omega _1}t \text{,}$ |
| ${\text {垂荡加速度}}a = \dfrac{{{{\rm d}^2}h}}{{{\rm d}{t^2}}} = - {h_m}{\omega _2}^2\sin {\omega _2}t\text{。}$ |
已知技术条件为:满足6级海况使用条件,雷达设备重量m=240 kg,距离吃水线架高H=15 m,横摇最大摇摆角R=45°,摇摆周期T1=8~12 s;纵摇最大摇摆角P=15°,摇摆周期T2=4~8 s;船体垂荡运动与海况和结构有关,参考某类似船体6级海况下试验数据可知,静止状态船体的垂荡幅值大于航行时的垂荡幅值,0kn时最大垂荡幅值为3.39 m,6级海况海浪有义波高和周期为6 m和9 s [4]。根据峰值角速度和峰值角加速度计算公式,当取摇摆角φ p为最大值,摇摆周期T为最小值时可计算出最大加速度值:
| ${_{{\rm{max}}}} = {\rm{ - }}{\phi _{{\rm{max}}}}{({\rm{2}}\text{π} {\rm{/}}{T_{{\rm{min}}}})^{\rm{2}}}\text{,}$ |
| $ {a}_{\mathrm{max}}={\rm-}{h}_{{m}}(2\text{π} {\rm{/}}{T}_{\mathrm{min}}{)}^{2}\text{,}$ |
代入数值计算可得纵摇、横摇和垂荡时设备的惯性加速度为:
| ${\epsilon }_{\rm{R-max}}={\phi }_{\rm{R}}(2\text{π} /{T}_{\rm{1min}}{)}^{2} \approx 28({\rm{^\circ }}/{\rm s}^2)\text{,}$ |
| ${\epsilon }_{\rm{P-max}}={\phi }_{P}(2\text{π} /{T}_{\rm{2min}}{)}^{2} \approx 37({\rm{^\circ }}/{\rm s}^2)\text{,}$ |
| ${a}_{\mathrm{max}}={h}_{}(2\text{π} /{T}_{3}{)}^{2} + g \approx 11.5({\rm m}/{{\rm s}^{2}})\text{。}$ |
船摇状态下横摇机构、纵摇机构和方位机构共同作用在雷达基座上的最大惯性载荷如表1所示。
|
|
表 1 基座承受的惯性负载 Tab.1 Inertial load on the base |
雷达设备的3部分中,稳定平台和基座的迎风面和结构相对圆滑规则,与天线部分相比迎风面积较小,因此一般的风载计算时常将天线部分以外的其他部分的风载忽略,在基座设计计算时适当增加安全裕量。
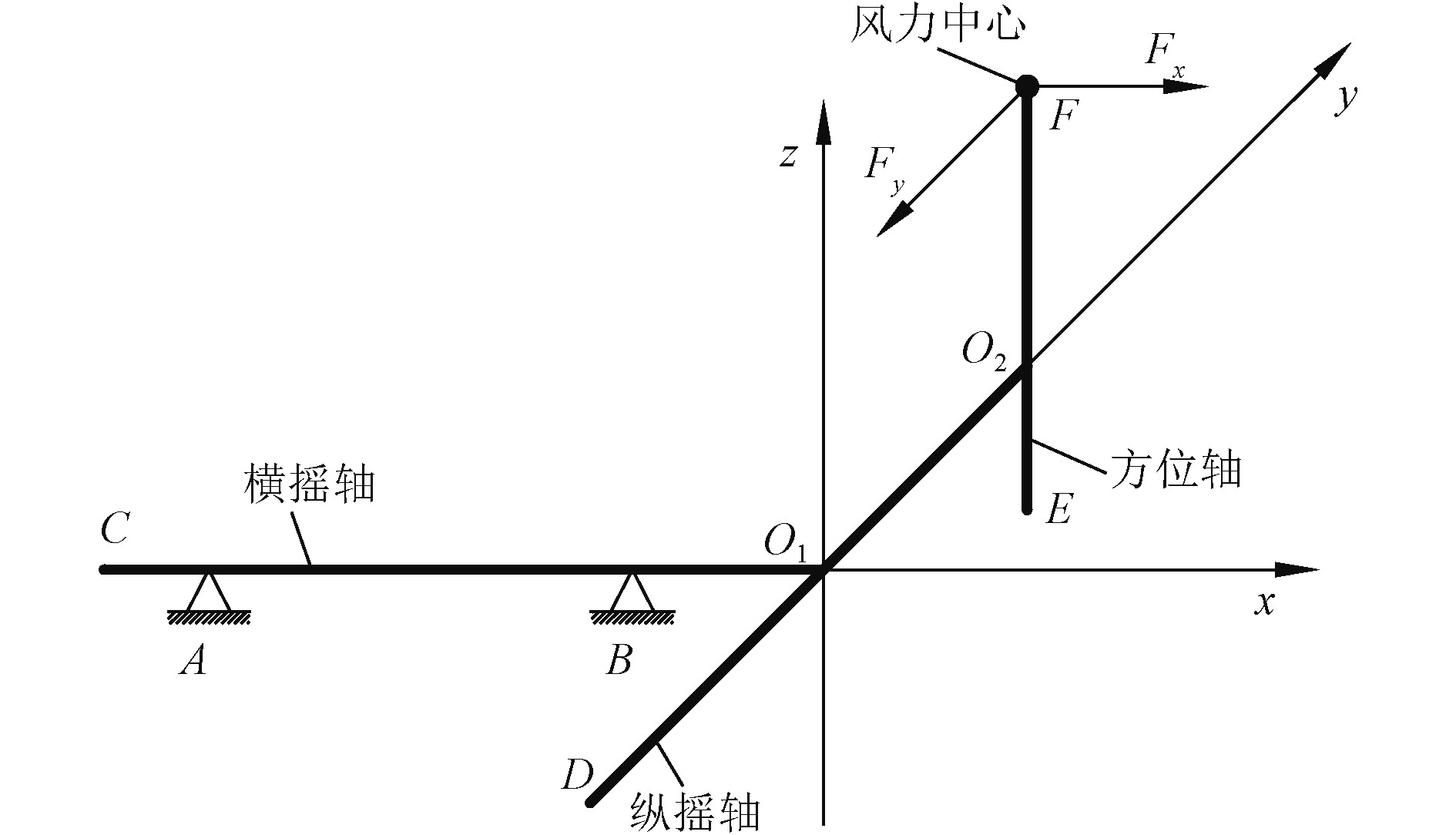
为方便受力分析,将稳定平台各部分机构简化为轴线,如图2所示。设F点为雷达天线的风力中心,风阻力为Fx,Fy;O′点为纵摇轴的轴端连接点,O点为横摇轴的端端连接点和坐标原点。方位机构和天线部分简化为方位轴(轴EF),纵摇机构部分简化为纵摇轴(轴DO’),横摇机构部分简化为横摇轴(轴CO),基座部分简化为固连点A和B两点。
|
图 2 稳定平台机构简化和受力图 Fig. 2 Simplification and force diagram of stable platform mechanism |
极限条件下各部分机构处于锁定状态,纵摇机构、横摇机构及方位机构的连接点O和O′视为刚性连接,三部视为一体,天线部分的风阻力经过传递最终作用在基座上。经计算,天线风载荷对基座的作用力如表2所示。
|
|
表 2 基座负载数值 Tab.2 Load value of base |
舰船在特定海况下行进时,舰载雷达设备会同时作用惯性载荷和风载荷,当2种负载方向一致叠加时,基座总负载最大,具体数值取整如表3所示,方向如图3所示。
|
|
表 3 基座综合负载 Tab.3 Comprehensive load of base |
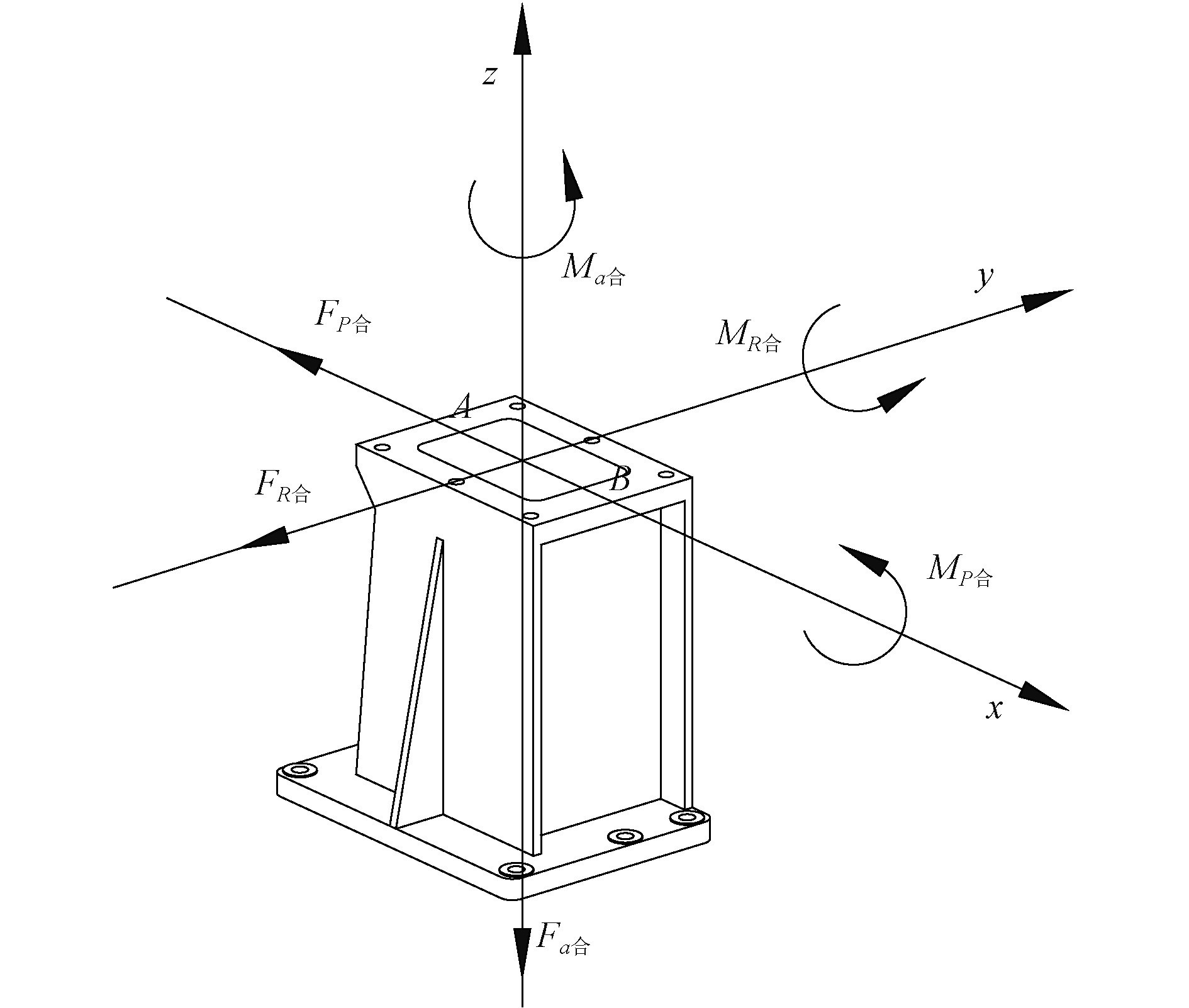
|
图 3 基座综合负载 Fig. 3 Comprehensive load of base |
舰船设备不仅承受惯性载荷和风载荷作用,同时还受到舰船上的随机振动载荷作用,如船体晃动、发动机螺旋桨运转、其他设备运转和船体结构局部共振等,随机作用在各个方向,通过稳定平台基座向上传递给稳定平台,加速度功率谱密度值及振动频率如图4所示。但是考虑到设备在运输、安装和使用等各环节的综合振动环境,GJB150.16A-2009规定的安装在舰船上的设备在实验室环境试验时综合振动试验量值如表4所示[5]。利用有限元仿真时将此过程作为载荷谱响应分析过程,在设备上加载振动载荷频谱,计算设备的最大响应值,检验基座的强度。
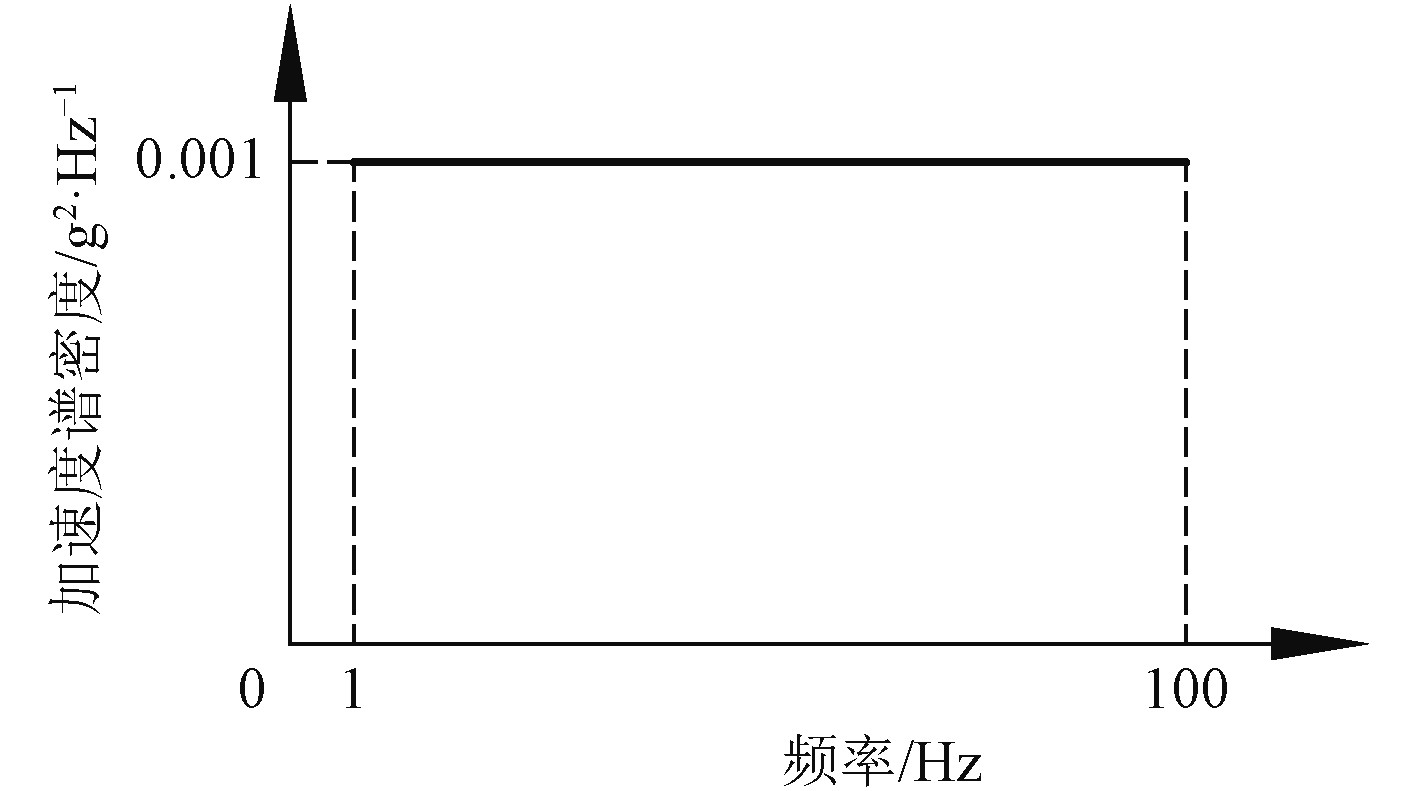
|
图 4 舰船随机振动功率谱密度值 Fig. 4 Power spectral density value of ship random vibration |
|
|
表 4 实验室环境试验振动载荷频谱 Tab.4 Vibration load spectrum of laboratory environmental tests |
基座在进行有限元分析时,为减小计算量,加快计算速度,将几何体的部分细节特征进行简化或者在模型上忽略,如小螺纹孔,小圆角和凸台等,对计算结果不会产生较大影响[3,6]。模型网格划分时采用Ansys Workbench自动生成的细化网格和单元,类型为三维10节点四面体固体结构单元。
2.2 基座有限元分析基座的载荷根据基座综合负载的大小和方向施加在上安装表面,下安装表面设置为固定约束。经计算基座的综合变形结果如图5所示,由图看出基座上表面的变形量最大,产生约0.1 mm的位移,变形相对较小,表明基座刚度较好;图6为基座的应力图,最大应力31 MPa,远小于基座材料铸造铝合金的强度值,满足强度要求,安全裕量较大。
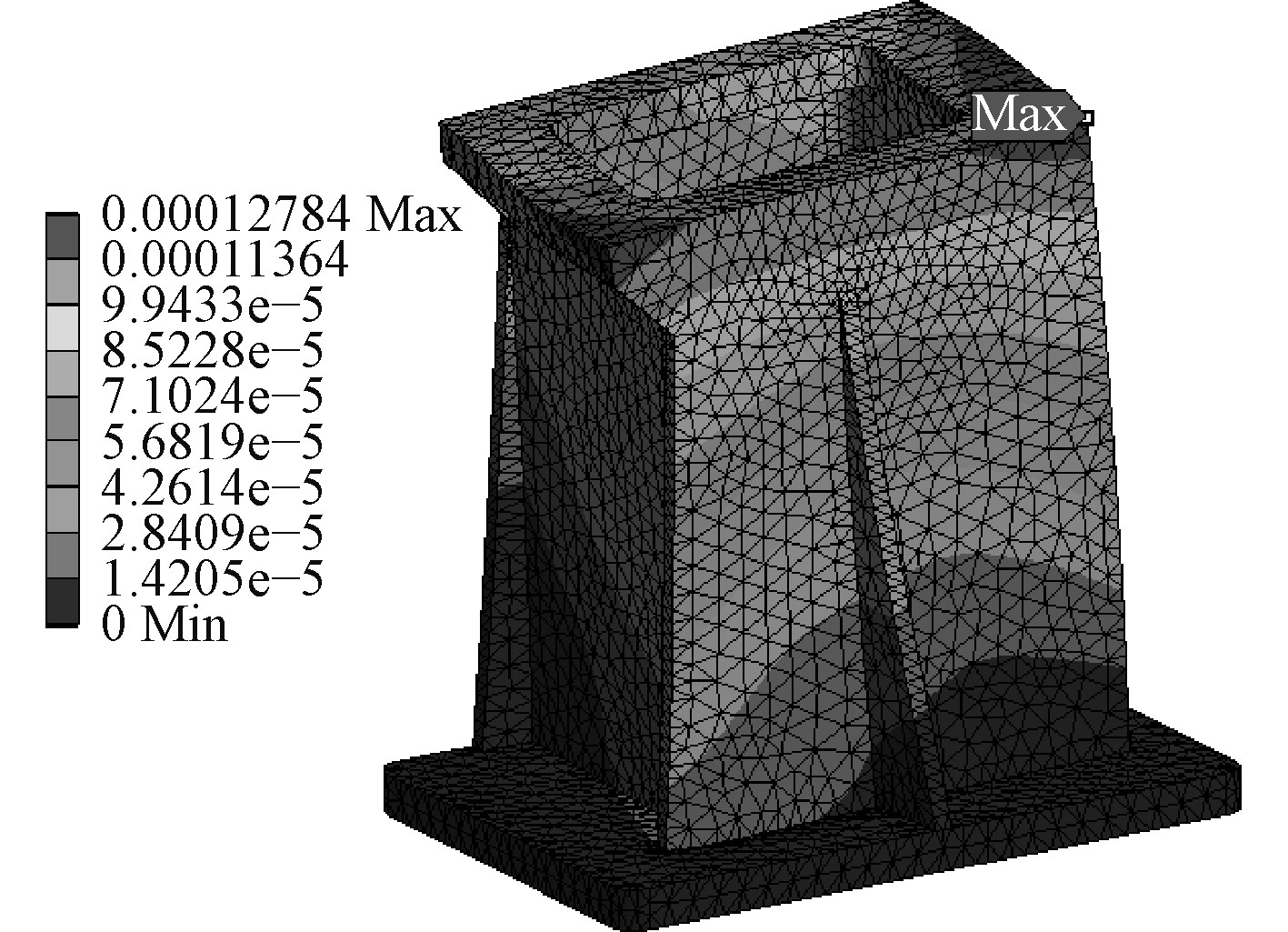
|
图 5 基座变形图 Fig. 5 Deformation diagram of base |
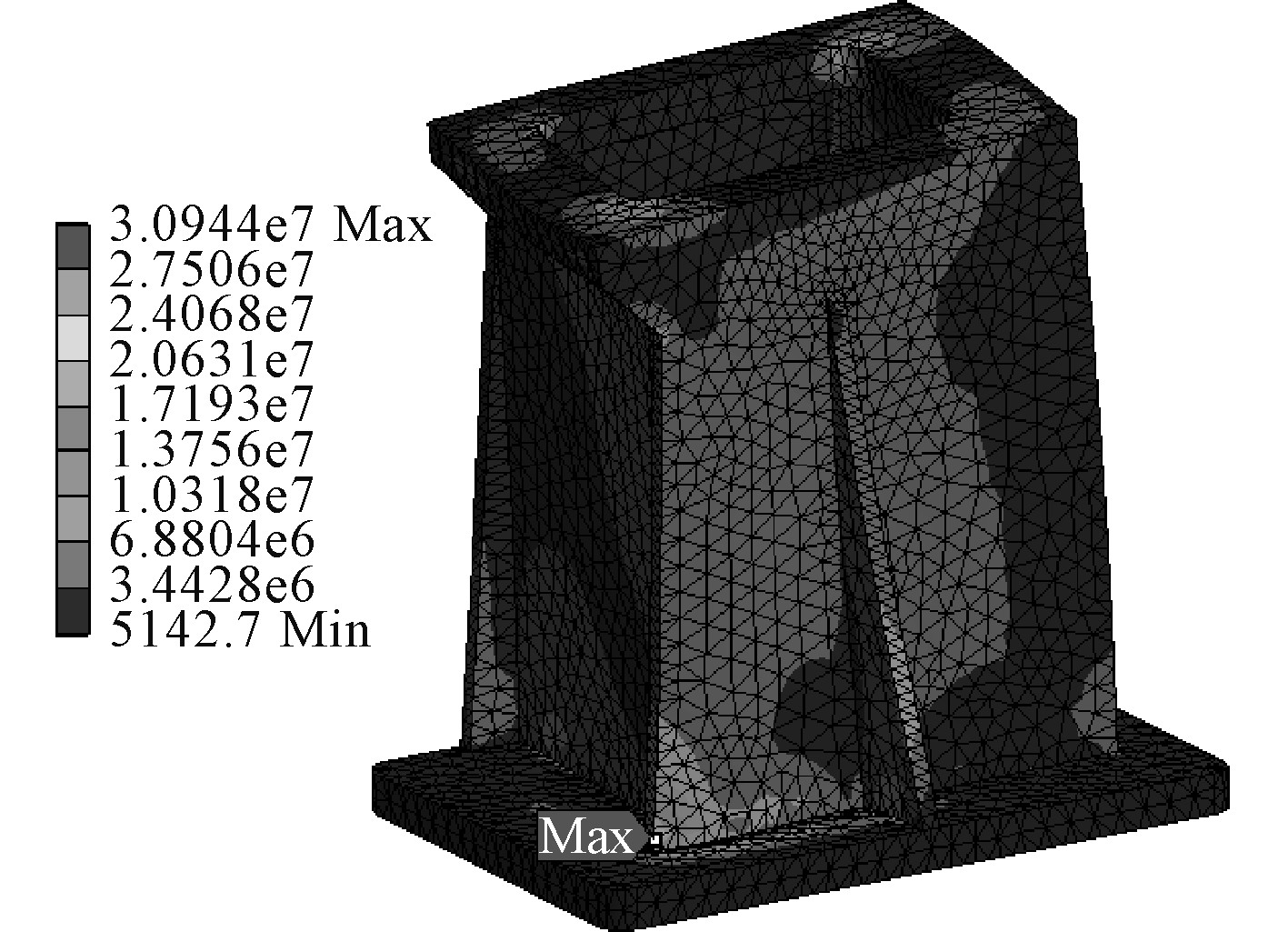
|
图 6 基座应力图 Fig. 6 Stress diagram of the base |
结构优化技术是在给定负载情况、约束条件和性能指标,在给定区域内对材料分布进行优化设计的设计方法,结构优化方法大致分为4个类型:拓扑优化(Topology Optimization)、形貌优化(Topography Optimization)、尺寸优化(Size Optimization)和形状优化(Shape Optimization),特点如表5所示[7-8]。
|
|
表 5 优化方法的特点及应用 Tab.5 Features and applications of optimization methods |
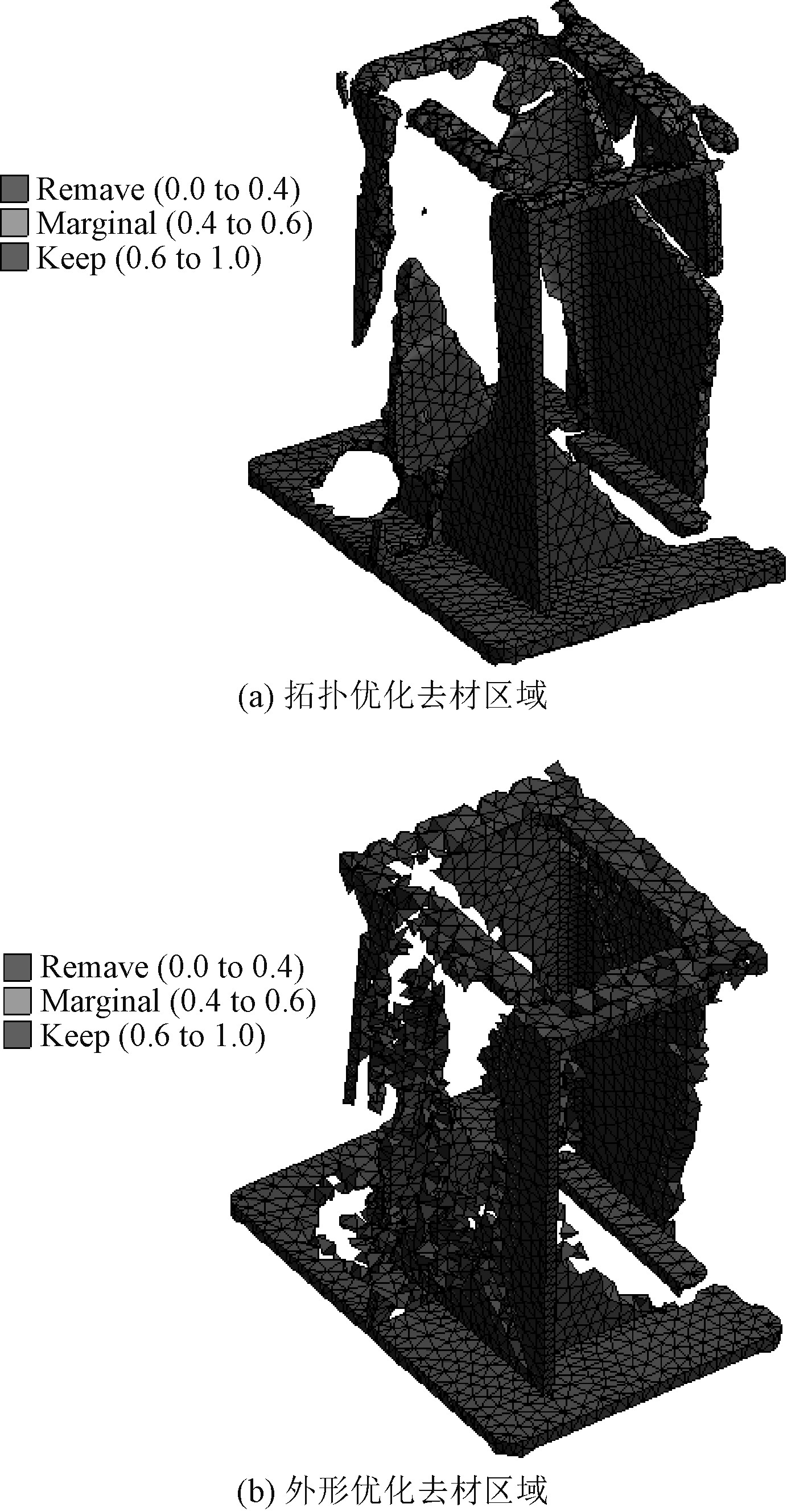
在Workbench中通过对基座模型的加载及优化计算,模型上的单元被划分为3部分:去除部分,保留部分,临界部分。去除部分应力较小,没有在空间主传力路径上,在结构上为冗余部分;保留部分为主要受力的部分,位于空间主传力路径上,应力较大,必须保留,否则会影响基座的强度;临界部分介于两者之间,去除或保留对结果影响不大。
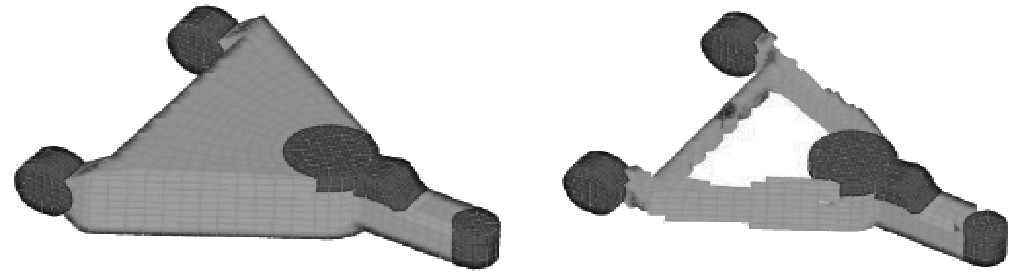
拓扑优化处理和外形优化处理后的基座去材区域如图7所示,2种优化结果和整体优化趋势相似,在基座的上、下安装面,加强筋及4个侧面均可以去除部分材料,说明安装面、加强筋及侧壁面部分尺寸较厚,这部分结构功能作用较小,可进行减材优化。
|
图 7 基座去材区域 Fig. 7 Removal area of base |
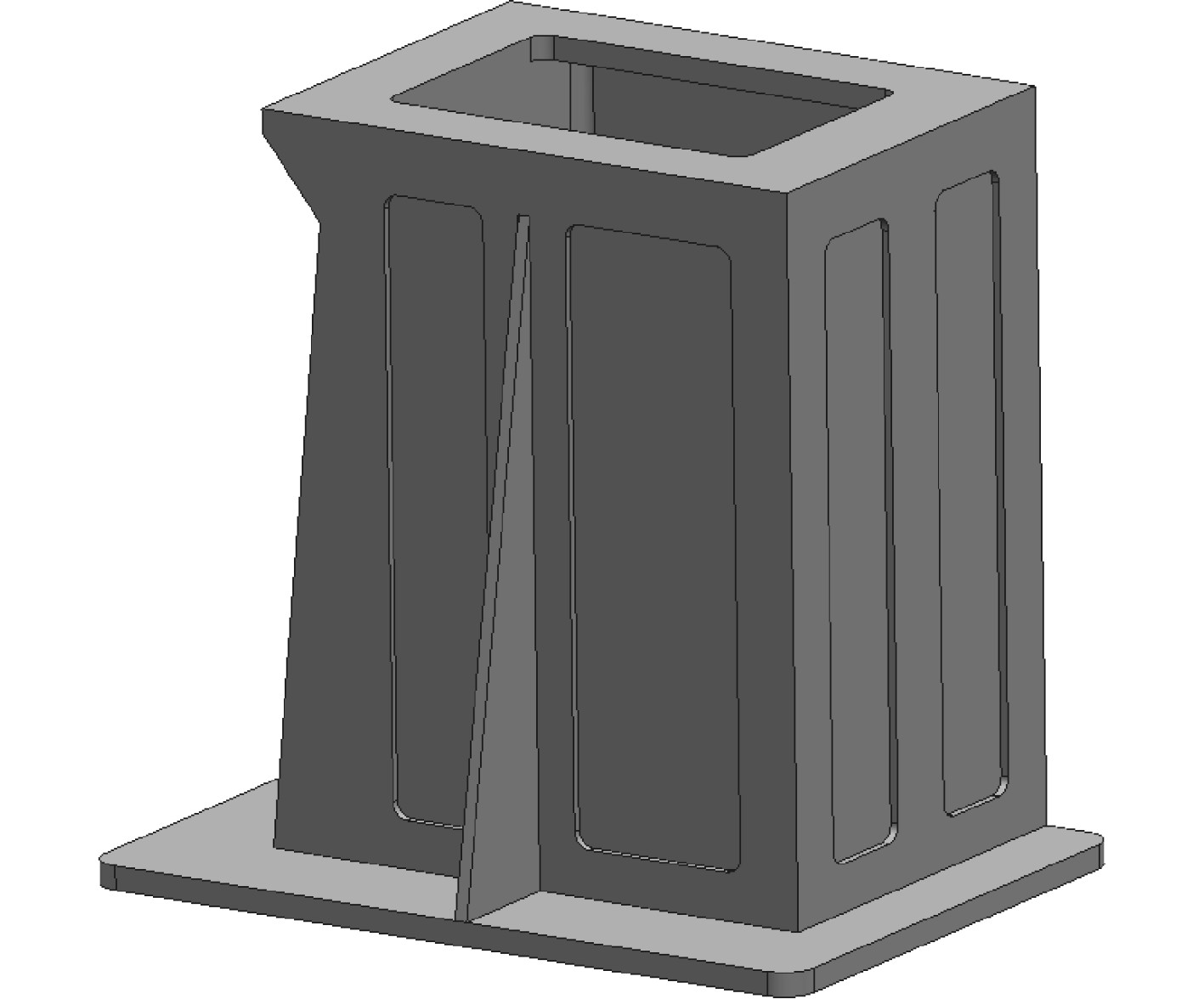
根据上述分析,综合基座的外形结构和受力情况,通过结构优化和逆向构造,初步优化结果如图8所示,将上下安装面的厚度由30 mm减小为15 mm,紧固位置局部加强,侧壁及加强筋厚度由13 mm减小为8 mm,去掉多余的加强筋,且在侧壁上增加减重孔,优化后基座重量减少15 kg。
|
图 8 基座优化模型 Fig. 8 Base optimization model |
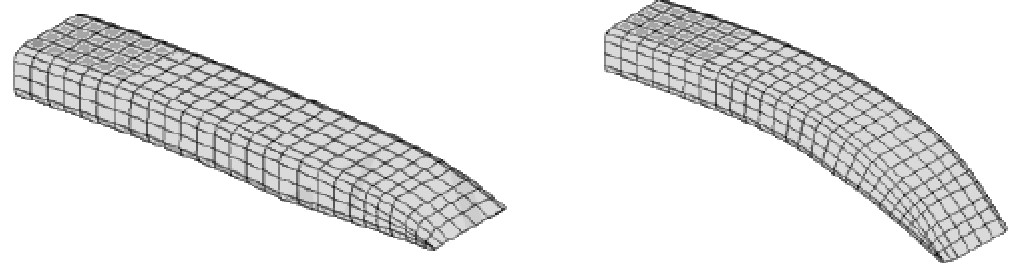
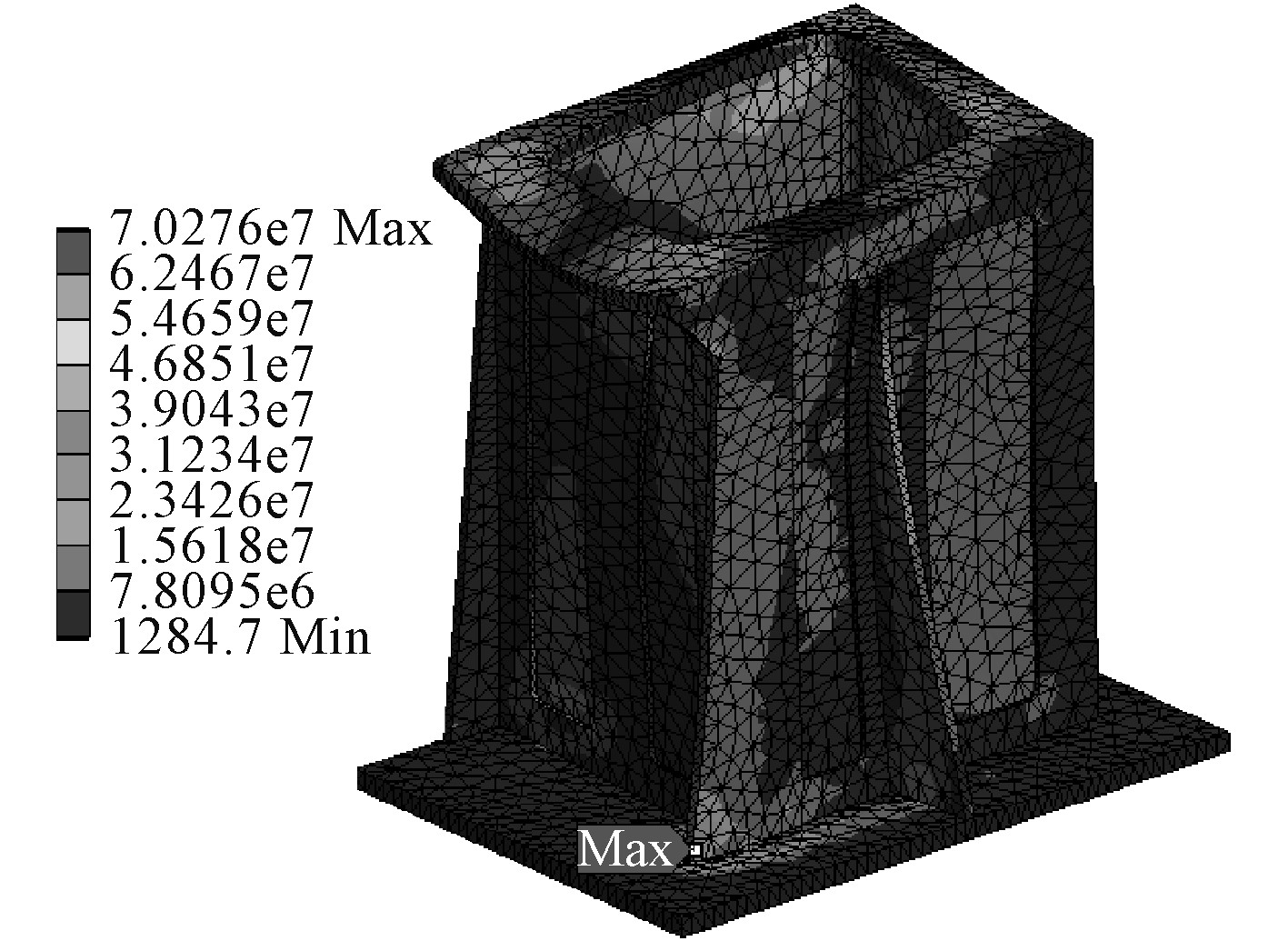
在优化后的基座上施加与原基座相同的负载进行有限元分析,分析结果如图9和图10所示,最大变形量和最大应力约为0.3mm和70.3MPa,基座变形量增加约3倍,应力增加约2.3倍。分析结果表明基座变形和应力增加,刚度略微降低,但仍然满足要求。

|
图 9 优化后的基座变形图 Fig. 9 Deformation diagram of the optimized base |
|
图 10 优化后的基座应力图 Fig. 10 Stress diagram of the optimized base |
对优化后的基座进行振动分析时,整个设备的质量分布对基座的振动响应影响较大,因此需要根据实际设备的质量分布情况,对模型进行等质量简化,如图11所示,主要简化为基座,横摇机构,纵摇机构,方位机构和天线5部分。
|
图 11 简化模型 Fig. 11 Simplified model |
模型网格划分时采用Ansys Workbench 自动生成的细化网格和结构单元。基座下表面设置为固定约束,振动载荷通过固定约束的下表面传递给基座及其他机构。
2.4.2.2 模态分析进行振动分析时,首先要计算结构的振阶和固有频率,在模态的基础上进行分析,计算载荷谱下的最大响应。根据振动要求,2种情况下的振动频段为0~60 Hz和0~100 Hz,因此需对0~100 Hz频段内的模态进行计算。经计算,设备的振阶和对应的频率见表6。
|
|
表 6 设备的振阶和频率 Tab.6 Vibration order and frequency of the equipment |
按照图4的随机振动试验量值分析时,分别在设备的X,Y和Z方向施加随机振动功率谱载荷,分析计算完成后,提取基座部分的计算结果,测量基座最大应力,进行强度校核,基座分析结果如表7和图12所示,数值为结果量的3σ值。
|
|
表 7 基座各方向的应力值 Tab.7 Maximum stress values in all directions of the base |

|
图 12 基座随机振动应力分布 Fig. 12 Random vibration stress distribution of base |
可以看出,在不同加载方向和测量方向组合中,随机振动加载在X,Y和Z方向时,分别在6阶频率70.964 Hz和2阶频率25.581 Hz处基座的响应最大,此时基座最大应力值约为24.9MPa,21.2 MPa和10.9 MPa。
按照表4的实验室环境试验振动试验量值分析时,分别在设备的X、Y和Z方向施加振动载荷谱,分析计算完成后,提取基座部分的计算结果,进行强度校核。通过计算分析,基座的结构响应结果如表8所示,由表中可看出在Z方向上施加给定的载荷频谱时,基座的总体响应最大,最大应力为86.3 MPa,位置见图13。
|
|
表 8 基座各方向最大应力值 Tab.8 Maximum stress values in all directions of the base |

|
图 13 基座最大应力位置 Fig. 13 Position of maximum stress on base |
由上述分析对比可知,在舰船随机振动试验量值载荷条件下,基座的最大应力为24.9 MPa,而在实验室环境试验振动试验量值载荷条件下,基座的最大应力为86.3 MPa,说明实验室环境试验振动试验量值比舰船随机振动试验量值更加严苛,设备承受的振动载荷更大。
2.4.3 分析结果基座材料为铸造铝合金ZL101A-T6的抗拉强度值为275 MPa,最大载荷远小于基座材料铸造铝合金的抗拉强度值,满足振动强度要求,但考虑到铸造件不可避免的存在部分内部缺陷,安全系数一般适当增大,保证设备安全,通过计算基座静强度安全系数为3.9,振动条件下的强度安全系数约为3.1,在合理范围内。
3 结 语本文对某舰载雷达基座在极端环境下的船摇、风载和振动载荷作用下的受力情况进行了分析计算,并运用有限元分析技术对基座上的受力情况进行了分析,通过结构优化技术对基座结构进行了减重优化,并对雷达基座的静强度和振动强度进行了有限元分析和校核。通过上述分析,得出的结论有:
1)原基座满足刚强度要求,但是具有较大设计冗余;
2)基座的拓扑优化和外形优化结果和减材趋势相似,通过减重设计后,基座质量减少15kg;
3)优化后的基座满足船摇、风载及振动强度要求。
| [1] |
刘长海. 舰载雷达天线稳定转台系统的结构 载荷分析与计算[J]. 雷达与对抗, 2009(1): 63-66. |
| [2] |
龚振邦, 陈守春. 伺服机械传动装置[M], 北京: 国防工业出版社, 1979.
|
| [3] |
沈春元, 郁圣杰. 舰载雷达稳定转台系统受力计算和有限元分析[J]. 雷达与对抗, 2011, 31(2): 67-71. |
| [4] |
高峰. 基于拖曳和自航模试验的小水线面双体船水动力性能研究[J]. 哈尔滨工程大学报, 2008, 11(29): 1154-1159. |
| [5] |
GJB 150.16A -2009, 军用装备实验室环境试验方法第16部分: 振动试验[S]. GJB 150.16A -2009, Environmental test methods for military equipment laboratories - Part 16: vibration test[S]. |
| [6] |
陈伟. 舰载雷达天线稳定转台系统动态特性的有限元分析[J]. 雷达与对抗, 2007(4): 56-60. CHEN Wei. The finite element analysis of dynamic features of antenna stabilizing platform of ship-borne radars[J]. Radar & ECM, 2007(4): 56-60. |
| [7] |
庄绪法, 翁俊. 一种机载雷达新型结构设计 模式的研究与应用[J]. 电子机械工程, 2018, 34(6): 6-8. |
| [8] |
马洪泰. 高精度空间目标探测雷达天线座结 构设计与分析[D].哈尔滨: 哈尔滨工业大学, 2014. MA Hong-tai. Design and analysis of antenna pedestal structure of high precision space Target detection radar[D]. Harbin: Harbin Institute of Technology, 2014. |
 2021, Vol. 43
2021, Vol. 43