舰船惯导水平姿态精度直接影响了舰船导弹武器系统的使用。当受到强干扰、损伤以及特殊气候环境的影响时,将难以实时获得准确外界参考导航校准信息对惯导系统进行校正或精度评估,极大影响舰船战斗力的发挥。针对舰船惯导水平姿态误差实时动态自主评估愈发重要,同时也是需要解决的关键性难点问题之一。
在海上动态条件下,受到海况、舰船运动等因素的影响,舰船姿态不断变化,舰船高精度水平姿态信息主要由高精度旋转惯导系统提供,对长时间无校正连续工作的惯导系统,受到各种误差因素的影响,其水平姿态精度不断降低,由于惯导系统自身水平姿态精度相对较高,难以在动态情况下找到合适的仪器对惯导系统水平姿态精度进行评估[1]。
目前,针对舰船惯导系统水平姿态误差主要在实验室或坞内等静态条件下进行评估 [1-3],或通过卫星组合导航比对、天文导航、差分GPS姿态测量比对等方式进行动态评估[1,4-6],而对于长时间海上航行的舰船而言,当无法适时获取星体测量、卫星导航及其他导航校准信息时,上述提出的方法均无法采用。在无外界参考信息条件下,如何解决舰船惯导水平姿态误差动态自主评估方面,目前没有查到相关研究资料。
本文针对舰船旋转惯导水平姿态误差动态评估问题,提出利用惯导自身信息实现水平姿态误差评估的新方法。利用舰船稳速直航状态下的实际加速度值近似为零的特点,分别分析惯导等效加速度信息和惯导速度误差与水平姿态角误差之间的关系,建立惯导水平姿态误差自主评估模型,在不依赖外部导航信息条件下,实现惯导水平姿态误差进行动态自主评估与补偿,有效提高惯导系统的水平姿态精度,具有重要的实际应用价值。
1 惯导水平姿态误差自主评估模型以当地地理坐标系为导航坐标系,惯导解算的舰船相对地球的运动加速度在导航坐标系中的投影
| ${{\dot{\tilde{{\mathit{\boldsymbol{v}}}}}}}_e^n={{\mathit{\boldsymbol{ \tilde f}}}}_{in}^n - (2{\tilde{\mathit{\boldsymbol{\omega }}}}_{ie}^n + {\tilde{\mathit{\boldsymbol{\omega }}}}_{en}^n) \times {\tilde{\mathit{\boldsymbol{v}}}}_e^n + {{\tilde{\mathit{\boldsymbol{g}}}}^n}\text{。}$ | (1) |
式中:
| ${{\dot{\tilde{{\mathit{\boldsymbol{v}}}}}}}_e^n ={{\mathit{\boldsymbol{ \dot v}}}}_e^n{\rm{ + }}\delta {{\mathit{\boldsymbol{\dot v}}}}\text{,}$ | (2) |
式中:
由于
| $\begin{split} \delta {{\mathit{\boldsymbol{\dot v}}}} =& \left[ {{{\mathit{\boldsymbol{f}}}}_{in}^n \times } \right]{\phi _{nb}} - \left( {2{{\mathit{\boldsymbol{\omega}}}}_{ie}^n + {{\mathit{\boldsymbol{\omega}}}}_{en}^n} \right) \times \delta {{\mathit{\boldsymbol{v}}}} - \\ &\left( {2\delta {{\mathit{\boldsymbol{\omega}}}}_{ie}^n + \delta {{\mathit{\boldsymbol{\omega}}}}_{en}^n} \right) \times {{\mathit{\boldsymbol{v}}}}_e^n + {{\mathit{\boldsymbol{C}}}}_b^n{{\mathit{\boldsymbol{C}}}}_r^b\delta {{\mathit{\boldsymbol{f}}}}_{ir}^r\text{。} \end{split} $ | (3) |
式中:
载体实际比力表达式如下式:
| ${{\mathit{\boldsymbol{f}}}}_{in}^n ={{\mathit{\boldsymbol{\dot v}}}}_e^n + (2{{\mathit{\boldsymbol{\omega}}}}_{ie}^n + {{\mathit{\boldsymbol{\omega}}}}_{en}^n) \times {{\mathit{\boldsymbol{v}}}}_e^n - {{\mathit{\boldsymbol{g}}}^n}\text{,}$ | (4) |
上式写成分列式为:
| $\left\{ \begin{gathered} {f_E} = {{\dot v}_E} - \left( {2{\omega _{ie}}\sin \phi + \frac{{{v_E}\tan \phi }}{R}} \right){v_N} \text{,} \\ {f_N} = {{\dot v}_N} + \left( {2{\omega _{ie}}\sin \phi + \frac{{{v_E}\tan \phi }}{R}} \right){v_E} \text{,} \\ {f_U} = {{\dot v}_U} + \left( {2{\omega _{ie}}\cos \phi + \frac{{{v_E}}}{R}} \right){v_E} + \frac{{v_N^2}}{R} - g \text{,} \\ \end{gathered} \right.$ | (5) |
将式(5)代入式(3),不考虑垂向速度及其误差以及垂向高度误差,写成分量形式,如下式:
| $\left\{ \begin{gathered} \delta {{\dot v}_E} = \left( {g - {k_{{\phi _N}g}}} \right){\phi _N} + {k_{E1}} + {k_{E2}} + {k_{E3}}{\rm{ + }}{k_{E4}} + {\nabla _E} \text{,} \\ \delta {{\dot v}_N} = \left( { - g + {k_{{\phi _E}g}}} \right){\phi _E} + {k_{N1}} + {k_{N2}} + {k_{N3}} + {\nabla _N} \text{。} \end{gathered} \right.$ | (6) |
其中:
对于海上航行的舰船而言,其运动速度相对较低,惯导速度误差、纬度误差、方位角误差以及加速度计东向和北向零位误差相对较小,引起的东向和北向加速度误差分量为相对小量,为简化分析,式(6)可简化为:
| $\left\{ \begin{gathered} \delta {{\dot v}_E} = g{\phi _N} \text{,} \\ \delta {{\dot v}_N} = - g{\phi _E} \text{,} \\ \end{gathered} \right.$ | (7) |
根据式(7),等效东向和北向加速度误差主要由惯导北向水平误差角和东向水平误差角引起。
根据式(2),当舰船处于稳速直航状态时,舰船实际加速度
| ${{\dot{\tilde{{\mathit{\boldsymbol{v}}}}}}}_e^n \approx \delta {{\mathit{\boldsymbol{\dot v}}}}\text{。}$ | (8) |
当舰船处于稳速直航状态时,惯导等效东向和北向加速度约等于惯导等效东向和北向加速度误差。因此,当舰船处于静止或匀速航行状态时,
利用等效东向和北向加速度误差可对惯导水平姿态角误差进行估计,如下式:
| $\left\{ \begin{aligned} {{\phi }_{N}}=\delta {{{\dot{v}}}_{E}}/g \text{,} \\ {{\phi }_{E}}=-\delta {{{\dot{v}}}_{N}}/g \text{。} \end{aligned} \right.$ | (9) |
在舰船海上航行条件下,若实现对惯导水平姿态角误差进行动态估计,需要获取惯导等效东向和北向加速度误差。
综合以上分析过程可知,当舰船处于稳速直航状态时,舰船实际等效东向和北向加速度信息约为0。由于加速度计零偏、标度因素误差、安装误差、姿态角误差和重力误差等引起的误差分量以及由于补偿由地球自转和舰船在地球表面运动引起的加速度不完全等因素的影响,惯导输出等效东向和北向加速度信息不为0,且等效东向加速度将与惯导北向水平角实际误差振荡保持一致,等效北向加速度将与惯导东向水平角实际误差振荡保持一致。此时,惯导等效东向和北向加速度误差主要由于惯导水平姿态角误差引起的,根据这一特点,提出了利用惯导自身加速度信息实现惯导水平姿态误差估计的新方法,可实现海上动态条件下舰船惯导水平姿态误差的实时动态自主估计,而不需要天文导航、卫星导航等外界定位手段。
2 惯导水平姿态误差与速度误差之间关系分析由于惯导等效加速度误差直接决定惯导输出的速度精度,在舰船稳速直航状态下,受到各种误差因素的影响,惯导输出的速度信息中存在较大的周期性振荡误差特点,因此在式(9)的基础上,可进一步分析惯导水平姿态误差与速度误差之间的关系,为实现利用惯导速度误差对水平姿态误差进行评估奠定基础。
受到各种误差因素的影响,舰船惯导速度误差主要呈现受傅科周期振荡调制的舒拉周期振荡特点,且误差均值近似为零。为简化分析,以舰船惯导东向速度误差为例,不考虑傅科周期振荡调制影响,则舰船惯导东向速度误差表达式可表示为:
| $\delta {v_E} = k\sin ({\omega _s}t{\rm{ + }}{\phi _{s0}})\text{。}$ | (10) |
式中:
对式(10)两边求微分得:
| $\delta {\dot v_E} = k{\omega _s}\cos ({\omega _s}t{\rm{ + }}{\phi _{s0}})\text{,}$ | (11) |
根据式(9)和式(11)得
| ${\phi _N} = \frac{{k{\omega _s}}}{g}\cos ({\omega _s}t{\rm{ + }}{\phi _{s0}})\text{,}$ | (12) |
根据式(10)和式(12),在任意一段舒拉周期时间内,存在如下关系式:
| $\left| {{\phi _{N{\rm{ - }}\max }}} \right| = \frac{{{\omega _s}}}{g}\left| {\delta {v_{E - \max }}} \right|\text{。}$ | (13) |
式中,
在海上动态条件下,由于很难找到比惯导姿态精度更高的参考基准,难以对惯导水平姿态误差进行估计,本文采用计算仿真实验方法,验证提出惯导水平姿态自主评估方法的可行性。如通过仿真,可获得惯导实际输出的等效东向和北向加速度、水平姿态角误差、速度误差等信息,分析等效水平加速度信息、水平速度误差与水平姿态角误差之间的关系等。
结合某型激光陀螺惯导系统公开文献中给出的激光陀螺和加速度计的主要技术参数以及安装误差、标度因数误差、初始误差、旋转方案等参数,设置仿真条件如下[9-10]:3个激光陀螺的常值漂移为
|
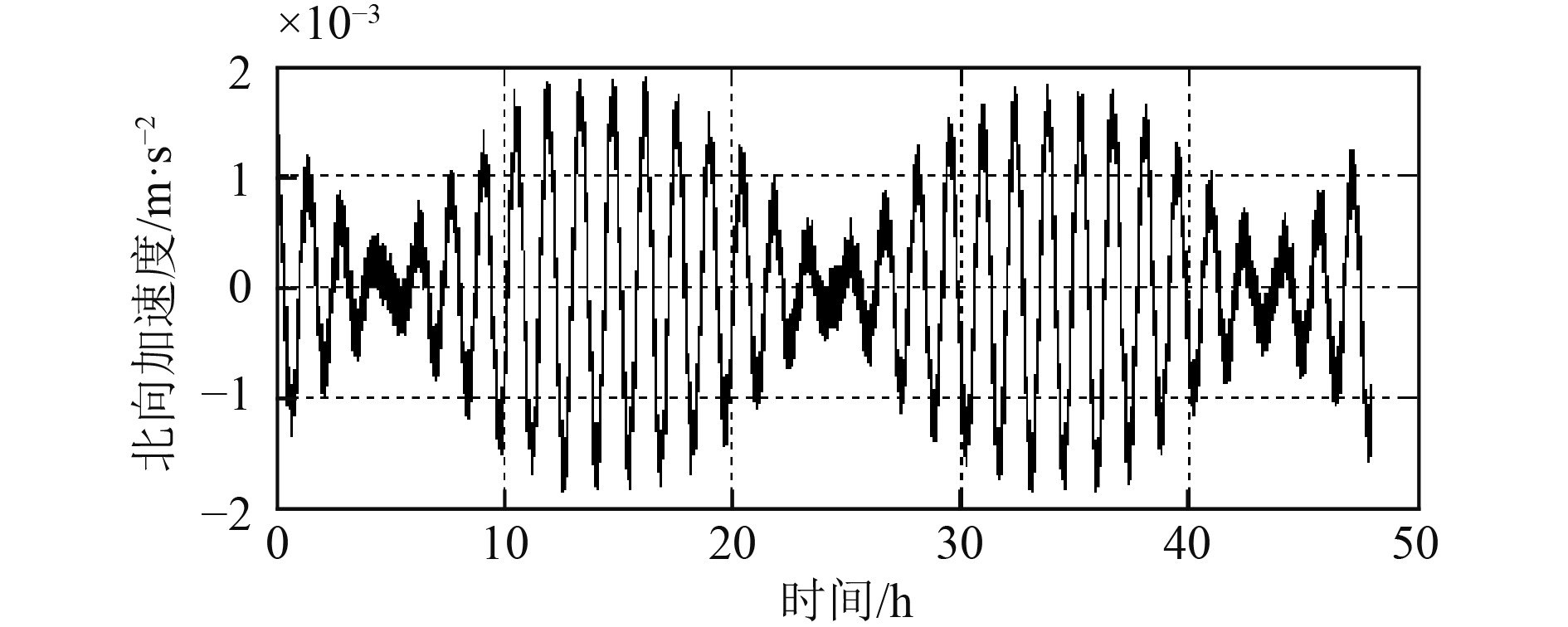
图 1 惯导等效北向加速度 Fig. 1 Equivalent northward acceleration of INS |
|
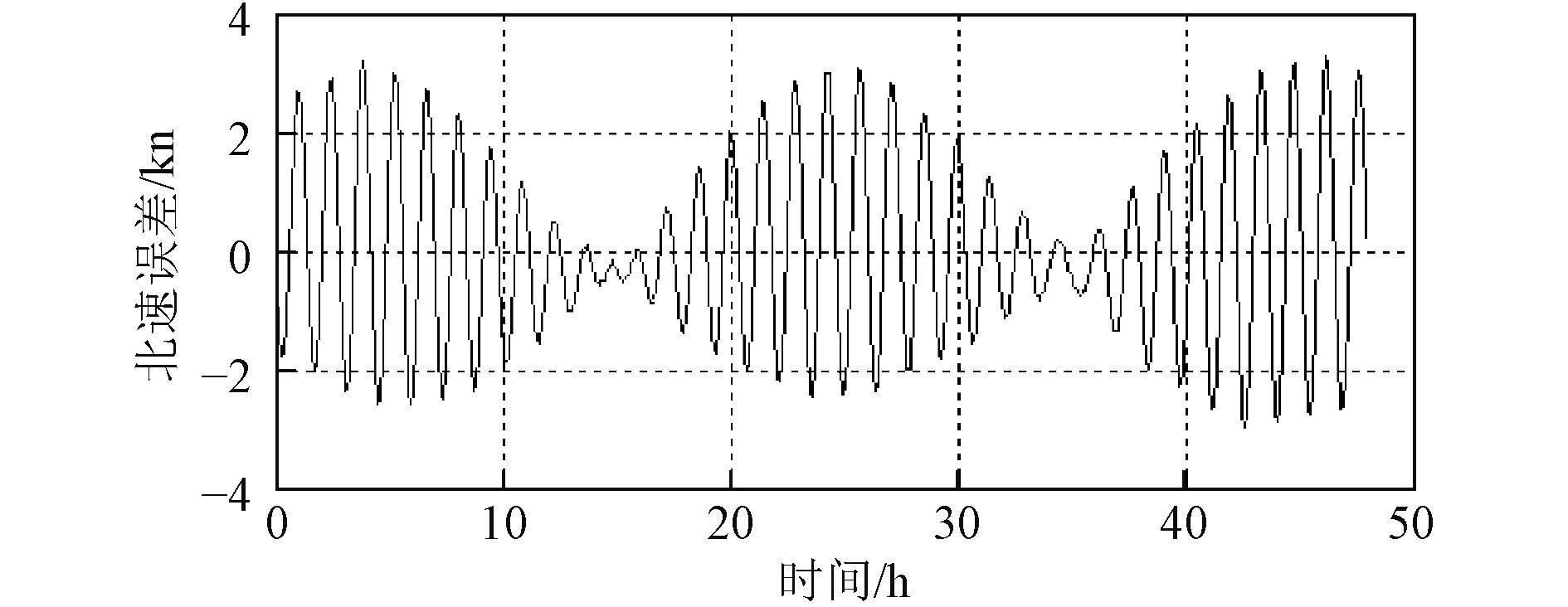
图 2 惯导北向速度误差 Fig. 2 Northward velocity error of INS |
根据图1和图2,当舰船处于稳定直航状态时,由于惯导加速度计零偏、标度因素误差、安装误差、初始姿态误差以及由于补偿由地球自转和舰船在地球表面运动引起的加速度不完全影响等因素的影响,惯导输出的等效北向加速度信息和北向速度误差并不为0,而是均呈现受傅科振荡调制的舒拉周期振荡误差特点,北向加速度振荡范围约为(−0.001 9 m/s2,0.001 9 m/s2),北向速度误差的振荡范围约为(−3.0 kn,3.2 kn)。
当舰船处于稳定直航状态时,认为航向航速不变,根据式(9)可知,惯导等效加速度信息与惯导速度误差呈现一一对应关系,因此,利用舰船稳定航行阶段时的加速度信息可实现对惯导水平姿态角误差进行估计,并实现误差补偿。
根据舰船稳定航行阶段的惯导等效加速度信息,利用式(9)可实时估计惯导水平姿态角误差,如图3所示。
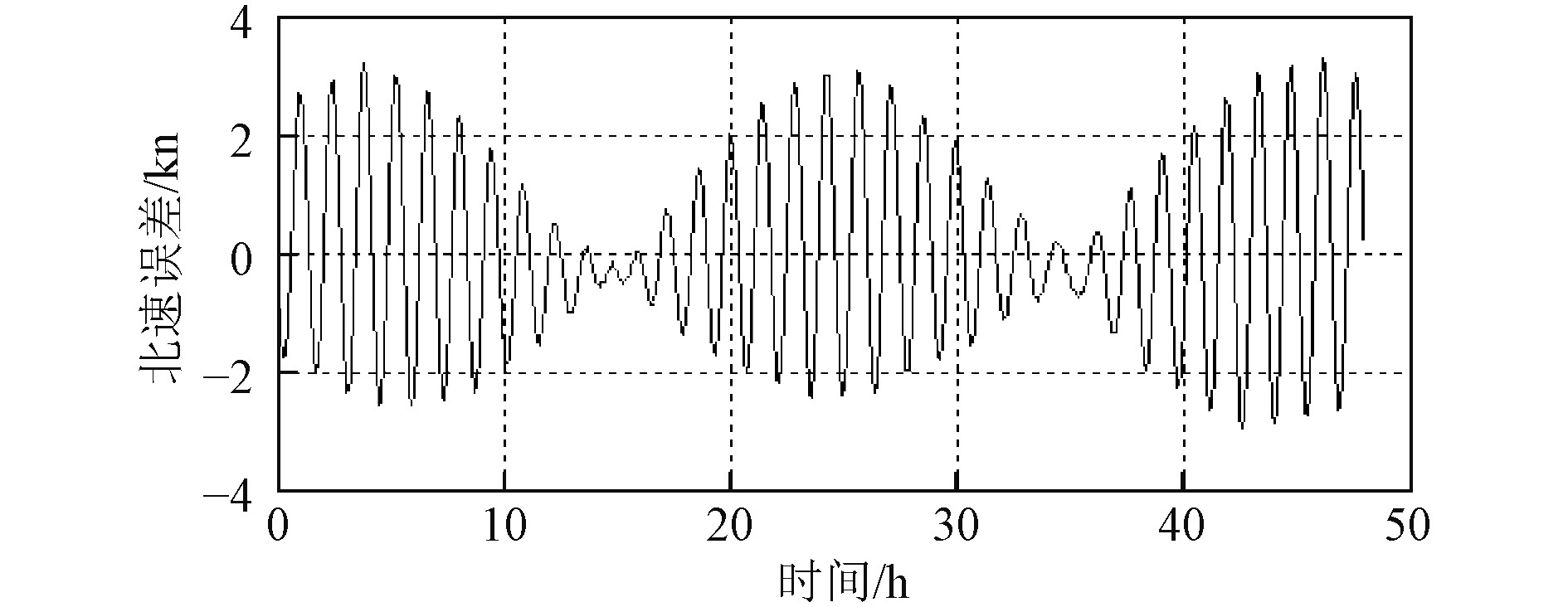
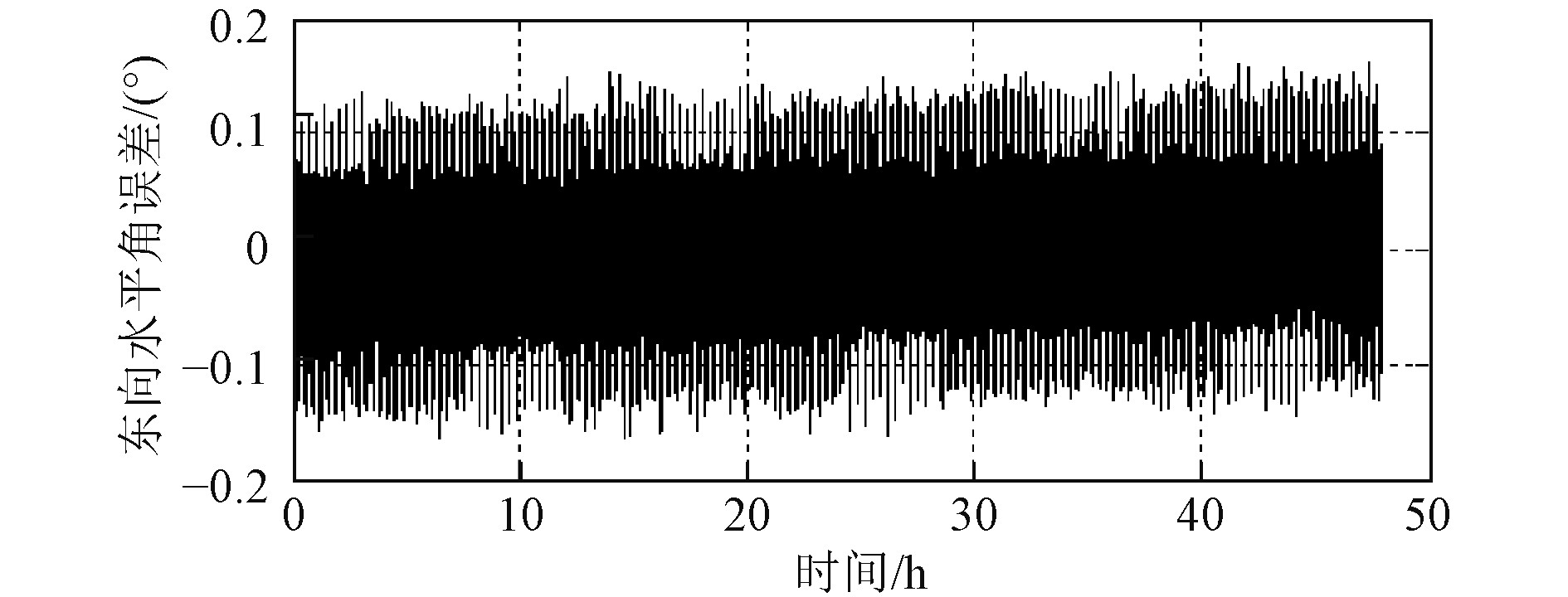
在图3中,实线为惯导实际东向水平姿态角误差曲线,是由计算机仿真获取;点虚线为根据惯导等效加速度信息,利用式(9)估计出的惯导东向水平姿态角误差曲线。根据图3,东向水平姿态角估计误差曲线与实际误差曲线基本重合,均呈现受傅科振荡调制的舒拉周期振荡误差特点利用估计出的惯导水平姿态角误差对惯导实际输出姿态角进行补偿,得到补偿后惯导水平姿态角误差曲线如图4所示。
|
图 3 东向水平姿态角误差 Fig. 3 Eastward horizontal attitude angle error |
|
图 4 补偿后惯导东向水平姿态角误差 Fig. 4 Compensated eastward horizontal attitude angle error |
根据图3和图4,惯导输出东向水平角实际误差振荡范围约为(−0.66',0.66'),经过补偿后,东向水平角误差振荡范围为(−0.16',0.16'),与补偿前惯导实际水平角误差相比,北向水平角误差最大值和振荡范围均减小了75.8%。
此外,根据图2和图3,在惯导傅科周期时间段内,北向速度误差最大值约为3.3kn,根据惯导东向速度误差最大值约为北向水平姿态角误差最大值的4.6倍这个特点,可估计出惯导东向水平姿态角误差最大值约为0.69',从而可验证在惯导傅科周期时间段内,惯导东向速度误差最大值约为北向水平姿态角误差最大值的4.6倍。利用此特点,根据惯导傅科周期时间段内的速度误差特点,实现对惯导水平姿态角误差范围的估计。
4 结 语在无外界校准导航信息条件下,利用舰船稳速直航状态下的实际加速度值近似为零的特点,分别建立了基于惯导等效水平加速度信息和惯导速度误差的水平姿态角误差评估模型,一方面可根据舰船稳速直航状态下惯导等效加速度实现对惯导水平姿态误差进行动态自主估计和补偿,另一方面也可根据在傅科周期时间段内的速度误差估计惯导水平姿态角误差的范围。仿真实验结果表明,提出的水平姿态误差动态自主评估与补偿方法,在不依赖外部导航信息条件下,实现了惯导水平姿态误差动态自主评估与补偿,能较大幅度提高惯导系统的水平姿态精度,对无外部导航校准信息情况下的舰船作战评估具有重要的实际应用价值。
下一步将在仿真实验的基础上,充分考虑海上复杂影响因素情况,结合舰船码头或实际海上动态航行中惯导实测数据,利用建立的惯导水平姿态误差评估模型,对海上动态条件下的惯导水平姿态误差进行估计。
| [1] |
周朝猛, 朱伟康, 张同双, 等. 基于星体测量的惯导水平姿态标定技术[J]. 中国惯性技术学报, 2009, 17(3): 253-257. ZHOU Chao-meng, ZHU Wei-kung, ZHANG Tong-shuang, et al. Horizontal attitude calibration technology of inertialnavigation based on star measurement[J]. Journal of Chinese Inertial Technology, 2009, 17(3): 253-257. |
| [2] |
张磊, 李辉, 韩涛, 等. 舰船武器系统姿态基准坞内标校新方法[J]. 中国惯性技术学报, 2013, 21(2): 275-280. ZHANG Lei, LI Hui, HAN Tao, et al. New method of dock calibration for naval vessel weapon system attitude reference[J]. Journal of Chinese Inertial Technology, 2013, 21(2): 275-280. DOI:10.3969/j.issn.1005-6734.2013.02.029 |
| [3] |
胡佩达, 高钟毓, 张嵘. 基于三轴摇摆台的高精度姿态试验系统[J]. 中国惯性技术学报, 2013, 21(2): 271-274. HU Pei-da, GAO Zhong-yu, ZHANG Rong. High accuracyattitude testing system based on three-axis test table[J]. Journal of Chinese Inertial Technology, 2013, 21(2): 271-274. DOI:10.3969/j.issn.1005-6734.2013.02.028 |
| [4] |
潘良, 赵文华, 刘新明, 等. 经纬仪测星评估惯导系统姿态角误差方法[J]. 中国惯性技术学报, 2011, 19(3): 369-373. PAN Liang, ZHAO Wen-hua, LIU Xin-ming, et al. Method of using theodolite's observation data of fixed star toevaluate INS's attitude accuracy[J]. Journal of Chinese Inertial Technology, 2011, 19(3): 369-373. |
| [5] |
傅中泽, 徐凯, 关劲, 等. 一种惯导系统航向测量精度的动态评估方法[J]. 中国惯性技术学报, 2014, 22(3): 416-420. FU Zhong-ze, XU Kai, GUAN Jin et al. Dynamic evaluation method of INS course measurement precision[J]. Journal of Chinese Inertial Technology, 2014, 22(3): 416-420. |
| [6] |
郭敬明, 何听, 魏仲慧, 等. 基于双星敏感器的船体姿态测量系统设计[J]. 光电子技术, 2014, 34(1): 5-9. GUO Jing-ming, HE Xin, WEI Zhong-hui, et al. The design of a ship attitude measurement system based on dual star sensors[J]. Optoelectronicl Technology, 2014, 34(1): 5-9. DOI:10.3969/j.issn.1005-488X.2014.01.002 |
| [7] |
王超, 朱海. 基于加速度计信息的单轴旋转惯导混合水平阻尼方案[J]. 大连海事大学学报, 2012, 38(4): 91-94. WANG Chao, ZHU Hai. Mixed level damping scheme of single-axial rotation of INS based on acceleration[J]. Journal of Dalian Maritime Universty, 2012, 38(4): 91-94. |
| [8] |
TITTERTON D H, WESTON J L. Strapdown inertial navigation technology[M].Lexington, Massachusetts, USA: Copublished by the American Institute of Aeronautics and Astronautics and the Institution of Electrical Engineers, 2004.
|
| [9] |
于旭东, 王宇, 张鹏飞, 等. 单轴旋转对惯导系统误差特性的影响[J]. 中国惯性技术学报, 2008, 16(6): 643-648. YU Xu-dong, WANG Yu, ZHANG Peng-fei, et al. Influence of single-axial rotation on INS error characteristics[J]. Journal of Chinese Inertial Technology, 2008, 16(6): 643-648. |
| [10] |
龙兴武, 于旭东, 张鹏飞. 激光陀螺单轴旋转惯性导航系统[J]. 中国惯性技术学报, 2010, 18(2): 149-154. LONG Xing-wu, YU Xu-dong, ZHANG Peng-fei. Single-rotatinginertialnavigation systemwithringlasergyroscope[J]. Journal of Chinese Inertial Technology, 2010, 18(2): 149-154. |
 2021, Vol. 43
2021, Vol. 43
