在现代海战中,水声对抗的效果很大程度上决定己舰的安全与否。目前反鱼雷技术主要集中在自我保护和软杀伤2个方面。其中声诱饵是各国海军广泛采用的武器装备之一[1-2]。
声诱饵的工作方式分为主动式和被动式2种。主动式声诱饵的主要工作原理是通过应答敌方的搜寻信号,模拟目标的发射特性,达到干扰敌方主动声呐航向的目的。被动式声诱饵可以连续发出与舰船辐射噪声相似的宽带噪声,诱骗敌方声呐认为是潜艇噪声[3]。声诱饵主要由发射阵、接收阵、以及电子舱组成。其中,电子舱是耐压壳体结构,主要有2个作用,一是作为发射接收装置的支撑体,二是作为电源和连接线的储藏体。图1分别为以色列Rafael公司的SCUTTER声诱饵和美国的AN/SLQ-25型声诱饵[4],其中接收发射阵置于电缆处。

|
图 1 声诱饵模型 Fig. 1 Acoustic bait model |
主动式声诱饵工作过程中发射信号的质量决定了器材的诱骗性能,而发射信号是由器材接收端接收信号经过信号处理得到的[1],因此,有必要探究影响接收信号的因素。
不存在电子舱的情况下,声波是典型的球面波衰减,接收信号波形和主动声呐发射信号波形只会有幅度上的差异,信号周期、脉宽等保持一致,只需对接收信号按照模拟潜艇目标的目标强度进行变换即可获得很好的诱骗能力。然而,实际工程中由于电子舱的存在,接收装置处于电子舱散射声场的近场范围,接收信号会严重受到电子舱散射声场的干扰,发生畸变。
本文主要探究诱饵电子舱的散射声场对接收信号的失真程度的影响。通过计算接收点在电子舱不同方位、不同距离以及选用不同壳体材料时有无电子舱存在接收到的时域信号的互相关系数来讨论信号失真程度,互相关系数越高表明信号失真程度越低,声诱饵性能越好。
1 理论基础 1.1 诱饵电子舱建模与散射声场计算COMSOL Multiphysics是一款具有多物理场直接耦合功能的有限元分析软件[5]。本文主要利用其中的声固耦合模块计算电子舱存在时的声场。
常见的声诱饵电子舱结构是一面为球冠的圆柱形轴对称结构(见图1),因此可以将其简化为二维轴对称的几何模型,相比直接计算三维模型,可节约大量计算时间。
建立声诱饵电子舱二维轴对称数值计算模型,如图2所示,包含简化的诱饵电子舱、计算水域和有吸声功能的完美匹配层。其中,电子舱模型圆柱体部分为长度为1 m,半径为0.1 m,球冠部分为半径等于圆柱半径的半球,整体壳厚度为0.02 m。为后续表述方便,将球冠一端称为“圆头”,另一段称为“平头”。
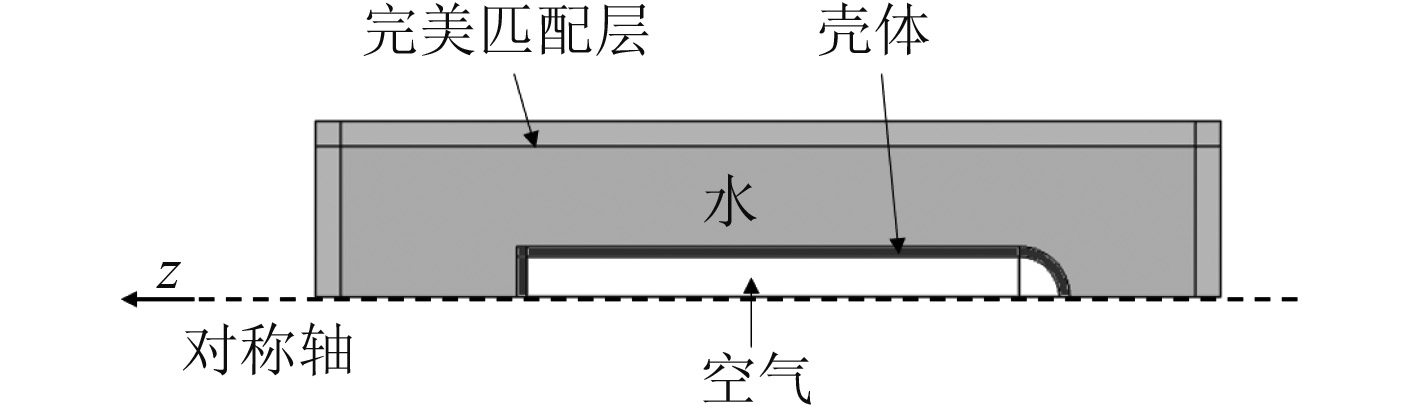
|
图 2 电子舱数值计算模型 Fig. 2 Numerical calculation model of electronic cabin |
采用二维轴对称计算,入射声波经过谐波展开后为:
| $p_m^{inc}(r,z) = {i^m}{e^{ikz\sin \phi }}{J_m}(kr\cos \phi )\text{。}$ | (1) |
其中
计算完成后,通过软件提供的后处理功能中的点计算可提取传递函数。其中表达式设为acpr.p_t时获取到的即为电子舱存在时的传递函数
将包含目标的声信道看作是一个线性系统,回波即为系统对入射信号的响应。设发射信号为
| $ \left\{ {\begin{array}{*{20}{l}} {S(\omega ) = FFT(s(t))}\text{,}\\ {{y_1}(t) = FF{T^{ - 1}}(S(\omega ) \times {H_1}(\omega ))}\text{,}\\ {{y_0}(t) = FF{T^{ - 1}}(S(\omega ) \times {H_0}(\omega ))}\text{。} \end{array}} \right. $ | (2) |
图3为20 kHz,0.2 ms单频信号沿平头入射,平头正前方轴线上0.2 m处有无电子舱的接收信号对比。其中,电子舱材料设置为钢,具体参数见表1。
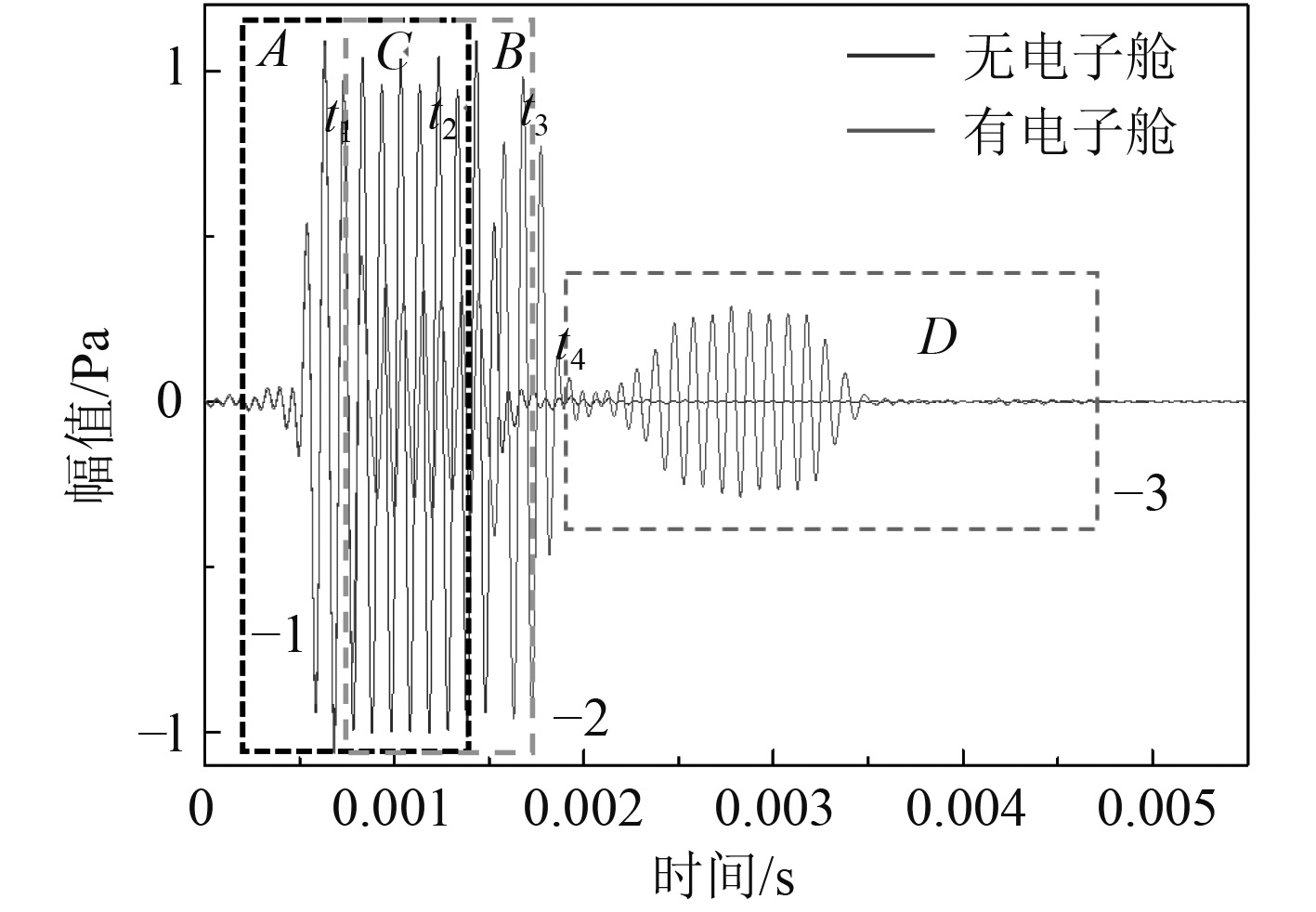
|
图 3 有无电子舱接收信号对比 Fig. 3 Comparison of signal received by electronic cabin |
|
|
表 1 材料参数表 Tab.1 Table of material parameter |
从图3可以看到,电子舱导致接收信号严重畸变。
相关分析[9]是在统计意义上表征2个或多个变量间的相关程度。在信号处理领域,通常通过计算互相关系数来分析信号的相关度[10]。
本文中通过计算电子舱存在时的接收信号
| $\rho ({y_1}(t),{y_0}(t)) = \frac{{\displaystyle\int_{{\rm{ - }}\infty }^\infty {{y_1}(t){y_0}(t){\rm d}t} }}{{\sqrt {\displaystyle\int_{{\rm{ - }}\infty }^\infty {{y_1}^2(t){\rm d}t} } \sqrt {\displaystyle\int_{{\rm{ - }}\infty }^\infty {{y_0}^2(t){\rm d}t} } }}\text{。}$ | (3) |
ρ的取值范围为[−1, 1],其绝对值越大表示信号之间相关性越强;反之相关性越弱;接近1表示正相关性强,接近−1表示负相关性强,当其等于0时表示信号之间完全不相关。一般认为:
理论上式(3)中时间需要取无限长,但是对于确定信号做相关分析时在有限长数据窗内仍然成立,本文只对包含目标信息的信号即A,B,C,D四部分进行分析。
对图3分析得到二者的相关系数为0.4491,可以看出,二者呈低度相关,说明接收信号被电子舱干扰后,仅有少量的敌方主动声呐发射信息,波形严重畸变。
2 仿真分析 2.1 接收点和电子舱距离的影响探究20 kHz,0.2 ms单频信号沿平头入射,接收点位于平头正前方轴线上时,其与电子舱的距离对接收信号失真度的影响。壳体为钢材料,距离电子舱0.005~4 m间隔为0.005 m的一组轴向接收点的散射声压以及相关系数结果分别如图4和图5所示。
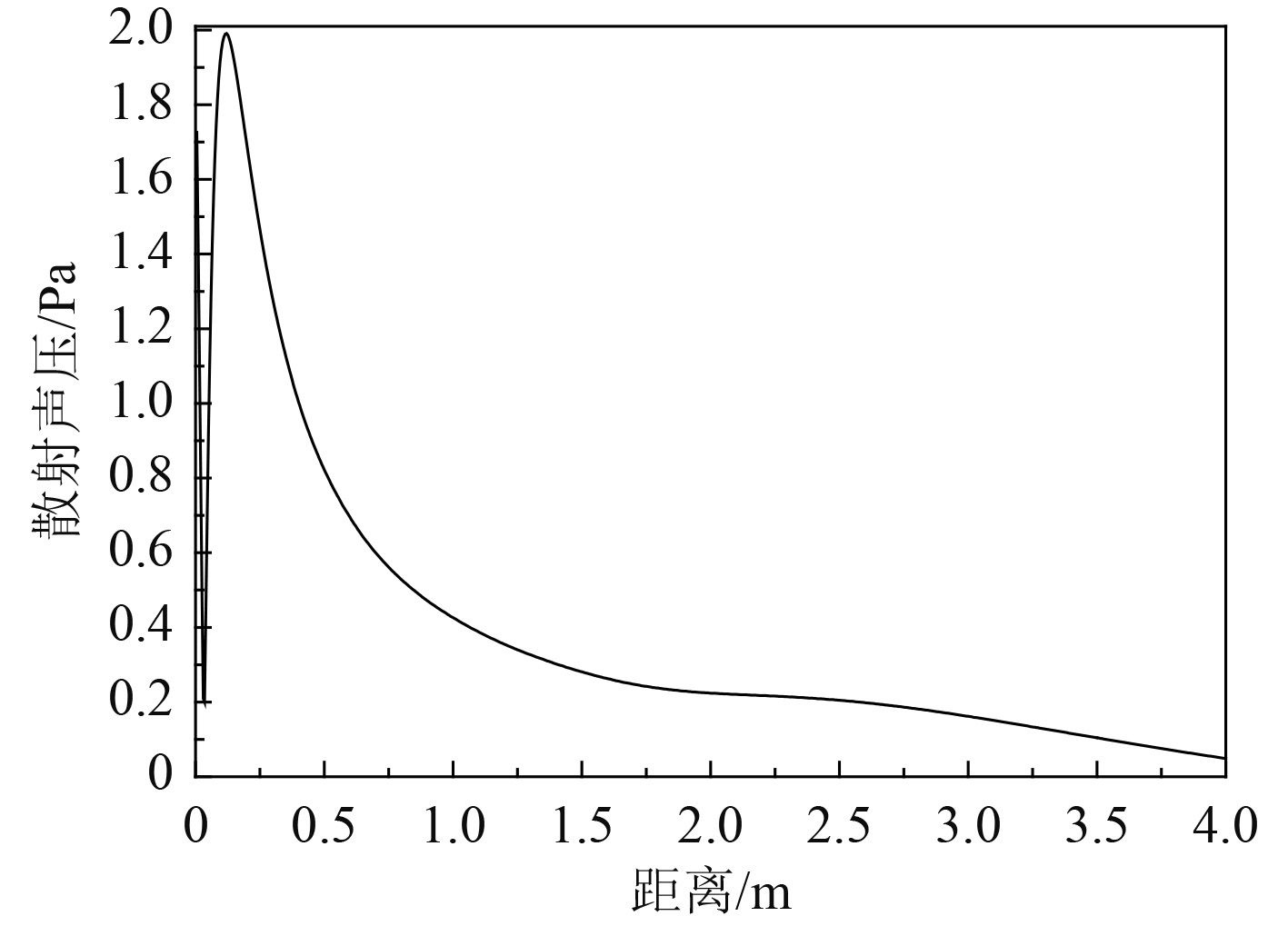
|
图 4 平头正前方散射声压随距离关系 Fig. 4 Scattering sound pressure with distance in front of the flat head |

|
图 5 平头正前方相关系数随距离关系 Fig. 5 Correlation coefficient with distance in front of flat head |
从图4可以看出,距离诱饵0.1 m以内时,散射声压先下降后迅速上升,这是由于各个几何反射点[12]的反射声波相位存在相反情况,叠加后导致幅值变小。在大于0.1 m后,有效反射点变少,散射声压值趋于稳定,随距离逐渐减弱。
从图5可以看出:
1)距离小于0.15 m时,相关系数出现较为激烈的上下震荡。由几何关系有,距离电子舱D m处直达波和几何回波的到达时间差
2)距离在0.15 m以上的时,直达波和几何回波完全分开,即C部分消失,此时作用的只有A,B和D。A部分不随距离变动,该部分信号呈正相关,且相关性较强,该部分信号在整体相关性贡献不随距离改变;B,D部分信号呈不相关状态,随着距离变化宽度不变,但到达时刻随距离向后移动,信号幅值会随距离衰减,因此该部分信号在整体相关性贡献中逐渐减弱。综上,距离在0.15 m以上的时,相关系数随距离的增加变大。
3)距离大于0.535 m时,直达波和几何回波相差3.6个脉宽,相关系数在0.8以上,信号呈高度相关,接收质量较好。
4)结合图5可以看到,相关系数和散射声压变化规律相反,散射声压越弱,接收信号质量越好,二者呈负相关。
2.2 接收端电子舱端部形状影响为探究接收点方位的影响,计算声波沿圆头入射时圆头正前方信号相关系数随距离的变化关系,并与上文计算结果对比,如图6所示。

|
图 6 接收点在两端结果对比 Fig. 6 Results comparison of receiving points at both ends |
可以看出,接收点在圆头正前方时,整体相关系数比在平头正前方高,且震荡区域小,震荡幅值范围窄。这是由于平头处接近于平板散射,其散射声场强[12],且边缘处同样存在对声波的反射,几何反射点多[13],因此接收点接收到的散射波较强,各处反射回来的波叠加后,更易形成相位波动,使相关系数震荡。相比之下,圆头处接近于球散射[12],其散射能力较平板弱,且没有突出的几何反射点,因此散射波更弱更平稳,其相关系数更强,接收信号质量更好。
2.3 壳体材料的影响应用控制变量法,计算壳体为橡胶材料的情况,具体材料参数见表1,得到结果与钢材料对比如图7所示。
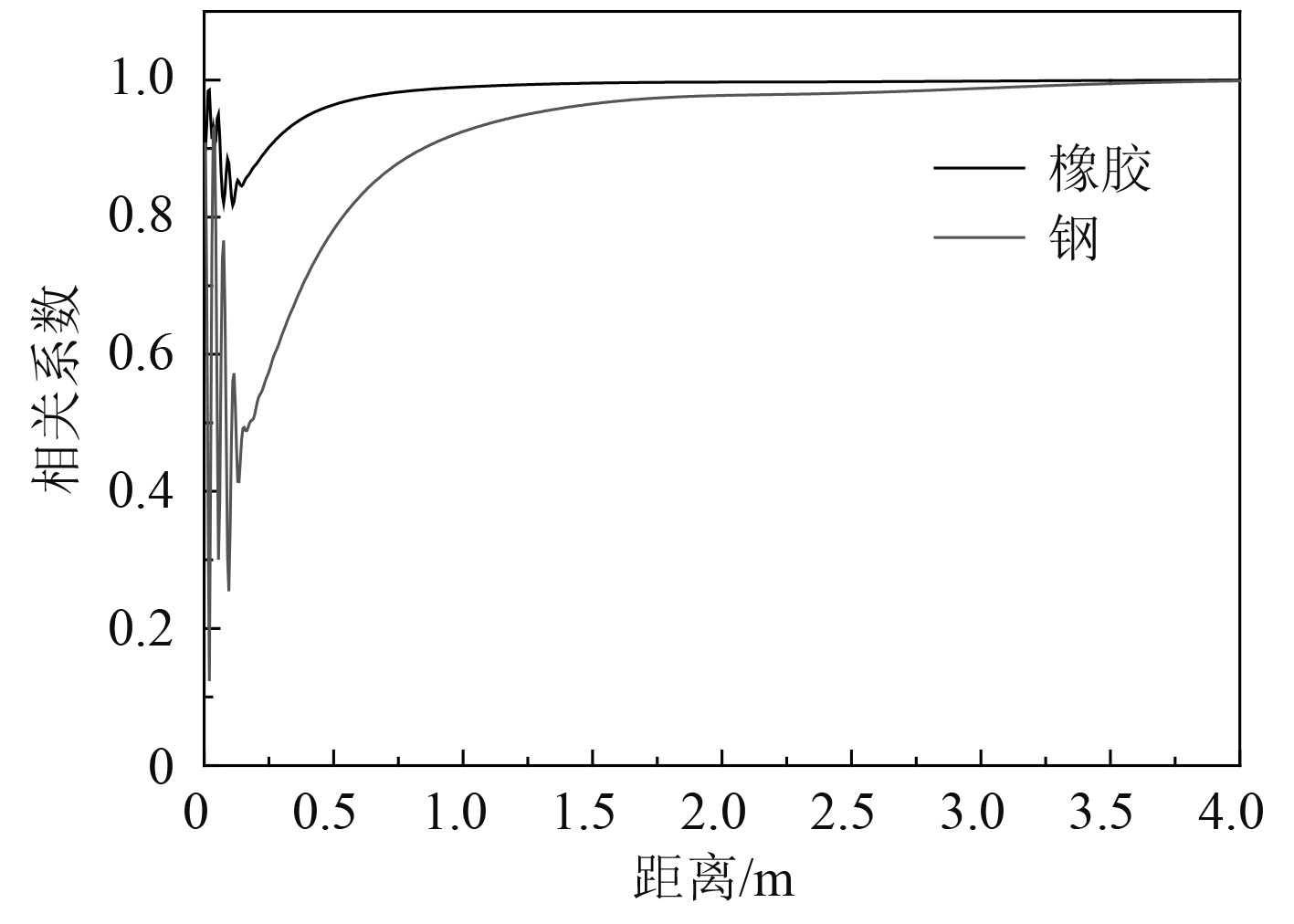
|
图 7 不同材料相关系数对比 Fig. 7 Comparison of correlation coefficients of different materials |
可以看到材料为橡胶时相关系数很高,均在0.8以上。由于橡胶材料具有吸声性能,导致其对声波的反射和散射能力很弱,即B,C,D三部分很弱,因此其接收的信号不易畸变,质量更好。
3 结 语本文结合有限元数值仿真和频域间接法获取了有无电子舱时的接收信号,并讨论了电子舱散射声场引起接收信号畸变的原因。利用相关分析法获取相关系数进而量化接收信号畸变程度。并对3种情况进行仿真,得到如下结论:
1)接收信号质量和散射声压呈负相关;
2)接收点距离电子舱越远,接收信号质量越高;
3)相同距离时,接收点置于圆头正前方比平头正前方接收信号质量高;
4)选取有吸声性能的壳体材料,可以有效降低电子舱散射导致的接收信号的畸变。
| [1] |
李本昌, 刘春跃, 郑援. 现代水声对抗装备发展及其对海战的影响[J]. 鱼雷技术, 2011, 19(6): 468-472. LI Ben-chang, LIU Chun-yue, ZHENG Yuan. Development of modern acoustic countermeasure equipments and its effect on sea warfare[J]. Torpedo Technology, 2011, 19(6): 468-472. DOI:10.3969/j.issn.1673-1948.2011.06.014 |
| [2] |
汪伟, 李本昌, 罗笛. 潜艇水声对抗及水声对抗器材的应用[J]. 指挥控制与仿真, 2008(5): 102-105. WANG Wei, LI Ben-chang, LUO Di. Acoustic warfare of submarine and application of acoustic countermeasure equipment[J]. Command Control and Simulation, 2008(5): 102-105. DOI:10.3969/j.issn.1673-3819.2008.05.029 |
| [3] |
孙仲阜. 水声对抗系统中声诱饵仿真研究[J]. 声学技术, 2003(2): 113-116. SUN Zhong-fu. Acoustical decoy simulation using underwater acoustical warfare simulation system[J]. Technical Acoustics, 2003(2): 113-116. DOI:10.3969/j.issn.1000-3630.2003.02.014 |
| [4] |
陈敬军. 鱼雷防御系统中软杀伤器材的现状及其发展趋势[J]. 声学技术, 2013(4): 342-348. |
| [5] |
MULTIPHYSICS C. Introduction to COMSOL Multiphysics®[J]. COMSOL Multiphysics, Burlington, MA, accessed Feb, 1998, 9: 2018. |
| [6] |
卢笛. 基于有限元原理的弹性目标声散射计算[D]. 哈尔滨: 哈尔滨工程大学, 2014. LU Di. Researches on acoustic scattering of elastic target on finite element methods[D]. Harbin: Harbin Engineering University, 2014. |
| [7] |
栾经德, 范军. 水中目标回波的时频分析方法研究[C]// 中国声学学会水声学分会2011年全国水声学学术会议论文集. 2011.
|
| [8] |
任鹏. 弹性圆柱壳体目标回波结构分析[D]. 哈尔滨: 哈尔滨工程大学, 2007.
|
| [9] |
江征风. 测试技术基础[M]. 北京: 北京大学出版社, 2007.
|
| [10] |
温永仙. 概率论与数理统计[M]. 北京: 高等教育出版社, 2010.
|
| [11] |
杨伟新, 王平, 雷沫枝, 等. EMD-PCA 与相关分析在航空发动机弹支动应力信号中的应用[J]. 噪声与振动控制, 2015, 35(6): 87-90. YANG Wei-xin, WANG Ping, LEI Mo-zhi, et al. Application of EMD-PCA and correlation analysis in dynamic stress signal analysis of the aero-engine elastic supporters[J]. Noise and Vibration Control, 2015, 35(6): 87-90. |
| [12] |
汤渭霖, 范军, 马忠成. 水中目标声散射[M]. 北京: 科学出版社, 2018.
|
| [13] |
姜姝. 水下目标回波几何亮点结构的形态学研究[D]. 哈尔滨: 哈尔滨工程大学, 2014. JIANG Yan. Morphological research on underwater target echo geometric highlight structure[D]. Harbin: Harbin Engineering University, 2014. |
 2021, Vol. 43
2021, Vol. 43
