智能化的发展首先体现在水下无人机器人、无人机、无人车的出现,随着智能化研究的深入无人水面艇随之而来并飞速进步,在军事领域技术已经较为成熟[1]。无人水面艇作为军事领域的重要研究对象,其在航行过程中的路径规划也十分关键,一般可分为2种类型:一种是全局路径规划,另一种是局部路径规划[2]。二者之间的主要区别是已知信息量的范围,全局路径规划是已知整个航行环境信息而局部路径规划则是只能根据传感器探测得到周围的环境信息[3]。传统的路径规划方法主要有人工势场法[4]、蚁群算法[5]、栅格法[6]等。智能化算法主要有模糊逻辑算法、神经网络、遗传算法以及混合算法等[7]。由于工作环境以及需要的不同,传统算法无法满足路径规划的需要因而许多研究者对算法进行了组合和改进。张玉奎[8]利用遗传算法和人工势场法对多种复杂的障碍物环境进行规划。王燕龙等[9]提出了一种基于航行安全权重,导频量和路径曲线平滑的改进A*算法。曹璐[10]针对多变因素和即时重要需求约束提出了一种基于Voronoi图和改进遗传算法的快速路径规划方法。陈超等[11]改进人工势场法来解决最小点问题。
本文在前人研究成果的基础上,以无人水面艇为例提出一种混合算法优化的全局路径规划方法,对环境中的可行区域使用A*算法预处理后使用遗传算法进行路径规划并对结果进行平滑处理获得适合快速安全行进的路线,并给出一种评价体系对规划结果进行定量的避障评价,评价结果显示通过混合优化算法规划出的路径更安全和平滑。
1 问题描述在全局路径规划中,无人艇航行环境已知,并且确定无人艇的位置[12],需要根据要求如耗时短、耗能少、路线距离小等[13]搜索出一条最适合当前要求的能够到达目标点的路径。本文在进行全局路径规划过程中选取使用的算法为能够对静态障碍物进行全局路径规划的遗传算法,但基本的遗传算法存在着早熟、收敛速度慢等问题[14],因此在基本的遗传算法上进行一定的改进,在规划出路线的同时进行一定的优化,并给出避障能力的评价指标。
1.1 应用平台“蓝信”号USV作为一种具有全自主和半自主控制的多功能智能化无人水面机器人由大连海事大学自主研发[15]。
船长7.02 m、型宽2.60 m、配备5.0 L排量191.1 kW的推进器、该船最大载荷1000 kg、航速最高可达35 kn、可持续航行180 n mile。艇上搭载有红外热成像系统、4G波段连续波导航雷达、前扫防碰撞声纳、海事卫星链路终端、多路差分GPS/BDS、姿态方位组合导航、高清视频和音频、VHF通信等多种传感器;配备自主研发的自主动态避碰控制器、自主导航运动控制器、多信息网络控制器和推进控制器等[16];“蓝信”号USV能够通过地面站设备操控无人船以较高的航行速度实现多种功能。
1.2 全局路径规划的快速平滑安全性问题随着现有各种算法的不断发展,采用单一方法虽然也能够实现路径规划,但是每种方法也都存在着一些不足和待解决的问题,因而不断出现各种改进及优化使得基础算法不断完善,得到更快更好的路径规划结果。遗传算法以其并行性和良好的全局寻优能力而著称,但由于算法中早熟和收敛速度慢等不足,因此需要对其进行改进优化。本文主要以遗传算法为主,同时使用A*算法进行搜索范围预处理,并对其规划出来的路线给出适当的评价函数,通过评价函数更直观的了解规划出的路线的避障能力。
2 全局路径规划算法介绍 2.1 A*算法A*算法作为智能化算法一种是典型的启发式算法,能够灵活方便解决问题[17]。A*算法主要是将搜索空间看作是一系列位置节点和连接它们的边,针对不同边长赋予相应的路径价值,通过搜索到达目标节点价值最小的节点序列来得到最短路径 [18]。
评价函数作为算法的核心,表达式为:
| $f(n) = g(n) + h(n)\text{。}$ | (1) |
式中:n为当前搜索到的节点位置;f(n)为估价函数,其中估价是指从起始位置经过节点n以最优路径到目标位置的价值;g(n)表示从初始位置以实际的最短路径到节点n的价值,如果n为起始位置,则g(n)=0;h(n)是“估算”节点n以最优路径到目标位置的价值。
2.2 遗传算法遗传算法由美国J. Holland教授在1975年提出,是一种模拟生物进化过程寻找最优解的智能搜索算法[19]。它以初始种群为基础,其中初始种群是某一随机产生的或是特定的,种群由若干经过基因编码的个体组成。按照适者生存和优胜劣汰的原则经过选择、复制、交叉、变异等操作并根据个体的适应度不断迭代计算从而引导种群的基因向最优解逼近[20]。迭代结束后,将最优个体的基因经过解码得到最优解或近似最优解[21]。遗传算法简单易用,容易得到满意结果,且适用于并行分布处理,在科学研究和工程领域得到普遍认可[22]。
遗传算法是基于染色体群的并行搜索,带有猜测性质的选择操作、交叉操作和变异操作,并且能够同时处理群体中的多个个体,能够减少陷入局部最优解的可能,此外具有自组织、自适应和自学习性,利用进化过程获得的信息自行组织搜索时适应度大的个体具有较高的生存概率,并获得更适应环境的基因结构。但是遗传算法通常的效率比其他传统的优化方法低,易过早收敛,而且对精度、可行度、计算复杂性等方面,还没有有效的定量分析方法。
2.3 人工势场法Khatib[23]针对配置空间提出了势场的概念。人工势场是将被控对象看作一个质点,其所在环境为二维欧式空间,对环境空间模拟潜在的引力场和斥力场,其中目标位置周围为吸引力场,障碍物周围为排斥力场 [24],环境中被控对象的运动虚拟为在受力场中的运动,障碍物产生斥力,目标则为引力,2种力产生的合力控制运动方向[25]。
3 全局路径规划的混合优化 3.1 全局路径规划的优化遗传算法之所以能被大量使用是因其并行性和良好的全局寻优能力等,但也饱受早熟和收敛速度慢等问题的困扰。收敛速度慢的原因有很多,例如随着搜索范围的不断扩大,生成的随机初始种群的可能性也越来越多,有些位置可能会出现在初始种群中,但在路径规划时,这些位置最终不会出现在可行路径,排除这些可行区域中的不通行区域,能够减少不必要的计算量。
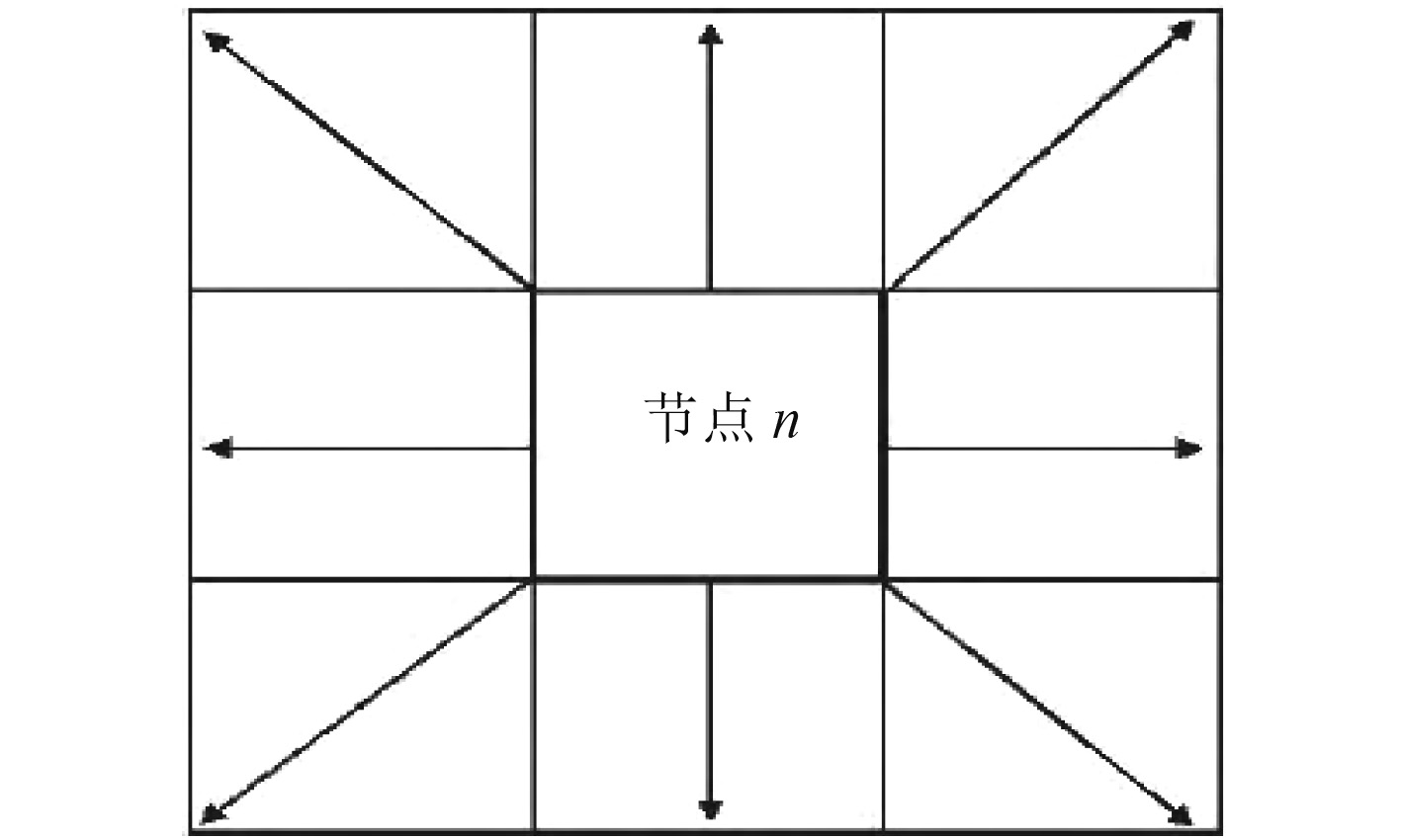
选择A*算法进行预处理是因为A*算法从当前节点出发向周围8个方向进行节点扩展,如图1所示。
|
图 1 A*算法扩展节点方向图 Fig. 1 A* algorithm extended node pattern |
8个节点选取“估算”价值最小的节点作为路径节点序列中第2个节点,然后对第2个节点进行相同操作直到目标节点,搜索出最短路径[26]。A*算法在规划过程中会有许多可行点作为规划结果而导致最终路径过于冗余,也会出现一些大角度的转折,因此在使用A*算法作为路径规划算法时需要对其进行改进优化,综上考虑选取A*算法作为预处理方法保证非全覆盖搜索后搜索到的可行栅格内包含最优路径。
A*算法对海图进行预处理主要是对给定的海图以及起始点和目标点进行搜索区域计算,栅格大小选取为海图的一个像素点,通过预处理缩小可行区域范围,并将搜索区域的范围读取出来作为遗传算法的初始种群范围。图2是以天津港的海图作为无人艇的航行环境,给定的起始点和目标点位置在图中以绿色点的形式显示,使用A*算法对环境进行预处理,红色区域为使用A*算法预处理后得到的可行区域范围,其中经过预处理后的可行区域约占整个海图可行区域的40%,减少了遗传算法的规划范围,提高了遗传算法全局路径规划效率。

|
图 2 A*预处理结果 Fig. 2 A* preprocessing results |
由于采用不同的海图以及设置的起始点和目标点存在差异,因此预处理过程搜索出的可行区域相对于原环境的海图来说能够减少一定的可行区域面积,但是具体减少的面积比例要根据实验环境中的可行区域以及对起始点和目标点的设定的不同而存在差异。
遗传算法中着重考虑的是适应度函数,在本文中选取的是最小路径代价、平均拐角值代价和碰撞威胁代价得到综合最小解 [27,28]。综合最小解
由于无人艇实际航行轨迹应为一条连续平滑的曲线,而进化遗传算法得到的可行路径是由浮点数所连接而成的折线段组成,因此要对结果进行平滑处理使其能够作为无人艇的航行路线。通过采用贝塞尔数学优化方法,可以将折线路径进行曲线优化[29]。
贝塞尔曲线普遍应用为矢量曲线,一般化的
| $\begin{split}B(t) = &\sum\limits_{i = 0}^n {\left(\begin{array}{*{20}{c}} n \\ i \end{array}\right){P_i}} {(1 - t)^{n - i}}{t^i} = \left(\begin{array}{*{20}{c}} n \\ 0 \end{array}\right){P_0}{(1 - t)^n}{t^0} +\\ &\left(\begin{array}{*{20}{c}} n \\ 1 \end{array}\right){P_1}{(1-t)^{n - 1}}{t^1}+ \cdots +\left(\begin{array}{*{20}{c}} n \\ {n - 1} \end{array}\right){P_{n - 1}}{(1-t)^1}{t^{n - 1}}+\\ &\left(\begin{array}{*{20}{c}} n \\ n \end{array}\right){P_n}{(1 - t)^0}{t^n}\text{。}\\[-20pt]\end{split}$ | (2) |
其中,B(t)表示由点
路径优化采用高阶贝塞尔曲线,阶数选取依据可行路径的浮点个数,从而得到光滑的连续路径。
本文提出的混合优化算法主要是对遗传算法的初始种群进行优化,对生成初始种群的范围进行缩小,在不影响最终路线的情况下,缩小搜索范围,使得混合优化后的算法能够快速有效的规划出适合无人水面艇安全航行的全局路线。
3.2 评价函数的优化本文提出一种对避障能力进行评价的方法,利用人工势场法的思想,将无人艇行进过程中的陆地岛屿等不可行区域看作斥力影响,目标点则看作引力影响,给出引力和斥力对无人艇的影响函数,最终得到评价函数。其中无人艇受到的斥力由当前行进的位置点到左右两侧的最近障碍点的斥力值之差来确定,斥力值需要分别计算左右两侧,通过下式计算得到:
| ${f_{re}} = \left\{ {\begin{array}{*{20}{c}} {100,0 \leqslant h \leqslant 3} \text{,}\\ {\dfrac{{100}}{h},3 < h < 150} \text{,}\\ {0,h \geqslant 150} \text{。} \end{array}} \right.$ | (3) |
式中:
| $h = \sqrt {{{({x_0} - {x_b})}^2} + {{({y_0} - {y_b})}^2}} \text{。}$ | (4) |
最终该位置点的斥力fr由式(3)分别计算出左侧障碍物的斥力值frel和右侧障碍物的斥力值frer,取两者之差的绝对值作为该点的斥力
| ${f_r} = \left| {{f_{rel}} - {f_{rer}}} \right|\text{。}$ | (5) |
无人艇受到的引力主要是目标点对当前行进的位置点的吸引,当前位置点离目标点越近,受到的引力值越大,受到的引力fa通过下式计算得到:
| ${f_a} = \left\{ {\begin{array}{*{20}{c}} {70,0 \leqslant H \leqslant 10} \text{,}\\ { - \dfrac{1}{{10}}H + 70,10 < H \leqslant 700} \text{,}\\ {5,H > 700} \text{。} \end{array}} \right.$ | (6) |
式中:H为行驶到当前规划路线时所在点(x0, y0)到目标点(xa, ya)的距离。
| $H = \sqrt {{{({x_0} - {x_a})}^2} + {{({y_0} - {y_a})}^2}} \text{,}$ | (7) |
评价函数作为无人艇受到的合力值,是整个规划的路线中每一个位置点的引力和斥力值之和后取平均值,而斥力在评价函数中是作为负值出现的,因此引入的评价函数为:
| $f = \frac{{\displaystyle\sum\limits_{k = 1}^n {{f_a}(k) - {f_r}(k)} }}{n}\text{。}$ | (8) |
其中:n为规划出的路线上所有点的个数。
评价函数评价的路径为经过混合算法得到的路径点使用贝塞尔曲线平滑处理后的路径,若经过平滑处理后的路线经过障碍物及其他不可行区域则重新进行全局路径规划。评价函数的值越高,说明经过平滑处理得到的可行路径能够保证在整个行进的过程中无人艇距离周围陆地及暗礁岛屿的距离都很充裕,能够较好地使用算法获得最优路径。
4 实验验证及结果分析 4.1 实验环境搭建本文在Matlab环境中基于天津港的海图针对无人艇进行了全局路径规划。首先对获取的电子海图进行加载,用Matlab读取电子海图的像素点信息,将彩色的海图进行图像处理,分离障碍物与可行进区域,设置起始点和目标点的位置,使用A*算法对规划路线区域进行预处理,缩小生成初始种群的范围。对缩小后的可行区域范围使用遗传算法进行路径规划并对规划后的路线进行平滑处理从而使规划出来的路线更符合船舶运动特性。最后对规划出来的路线进行避障评价,采用基于人工势场法的评价函数对规划路线的避障能力予以评价分析,以便更加显著地看出使用混合算法优化的路线具有更好地避障能力,具体流程如图3所示。

|
图 3 混合算法流程图 Fig. 3 Hybrid algorithm flowchart |
本文在Matlab上使用混合算法进行路径规划的同时,搭建了能够加载海图显示相关参数的QT平台。该平台能够加载典型航行区域的电子海图,并可以针对每个加载的海图设置相应的起点和终点经纬度,选择相应的算法进行路径规划。
4.3 实验结果及分析本文在Matlab上对天津港的海图进行了模拟仿真,仿真主要是以天津港为背景,结合天津港周围的海况以及暗礁岛屿绘制出天津港的环境,通过对周围的岛屿及陆地等无人艇不可能行驶的区域进行提取后,分别使用A*算法和混合算法对无人艇进行路径规划,使无人艇能够避开障碍物从设定的起始点到达目标点。
本文首先使用了路径规划较为广泛的A*算法对天津港的周围区域进行全局路径规划,设定起始位置和目标位置后使用A*算法进行规划并对规划出来的折线结果进行相同的贝塞尔曲线平滑处理,对最终的路径点进行避障结果评价。在进行平滑处理后得到的曲线会穿过障碍物致使无人艇无法航行,使用A*算法规划并进行平滑处理后得到的仿真结果如图4所示。

|
图 4 使用A*算法仿真图 Fig. 4 Simulation diagram using A* algorithm |
在使用A*算法进行路径规划的同时,本文也使用了混合优化算法对天津港附近海域进行了同样的路径规划,设定相同的起始点和目标点,得到的仿真结果如图5所示。由于起点和终点都位于不可行区域附近,结合仿真结果和评价值,说明规划出的路径能够正确避开障碍物及不可行区域抵达目标点。

|
图 5 使用混合算法仿真图 Fig. 5 Simulation diagram using a hybrid algorithm |
A*算法和混合算法都能够将电子海图给出的附近区域中的障碍物和可行区域信息提取出来,在设定起始点和目标点之后通过算法得到一条无碰撞航线,但是经过贝塞尔曲线平滑处理后,2种算法得到的路线有一些不同之处,依据避障评价函数对2种算法进行评价的结果如表1所示。其中安全距离为无人艇与周围障碍物之间的最小距离,避障评价为衡量算法规划出的路径对于无人艇平稳安全通过的能力。
|
|
表 1 A*算法与混合算法的对比 Tab.1 Comparison of A* algorithm and hybrid algorithm |
通过评价结果可以看到当确定无人艇航行环境以及起始点和目标点时,A*算法的规划路径穿越障碍物区域,这种路径是不能被采用的,本文所提出的混合算法可以规划出一条足够安全的路径。同时本文通过所提出的评价函数对不同算法规划出来的路线进行避障能力的评价,用数值直观地给出评价结果。通过以上仿真及评价函数的结果可以显著地看出使用混合优化算法比用A*算法规划的路线具有更好的避障能力,其生成的路径能够与周围障碍物保持相对较远的安全距离,使得船只能够更安全的通过障碍物区域抵达目标点。
5 结 语本文将A*算法应用到遗传算法中提出混合路径规划算法,首先A*算法预处理从起点到目标点进行大致范围搜索,减少遗传算法中计算的范围,然后使用遗传算法对起点到目标点的路线进行规划生成能够行进的路线,最后引入评价函数对规划出来的路线进行评价,评价函数的值越高,该路线的避障能力越强,最后选择最为合适的路线作为最优路线。在仿真过程中,使用能够提供周围障碍的图像并给出起始点和目标点,使用Matlab进行路径规划,并对规划出的路线进行评价,最终得到较为合适且便捷的行进路线。同时使用QT搭建界面显示的平台,加载相应的环境进行路径的设置和显示。在接下来的研究中路径规划算法不仅需要考虑行驶的天气性因素,还要对行驶中的其他各种干扰情况进行考虑。
| [1] |
VEERS J, BERTRAM V. Development of the USV multi-mission surface vehicle Ⅲ[C]//In 5th International Conference on Computer Application and Information Technology in the Maritime Industries, Leiden, The Netherlands, 2006: 299 − 314.
|
| [2] |
陈超, 唐坚. 基于可视图法的水面无人艇路径规划设计[J]. 中国造船, 2013(1): 135-141. |
| [3] |
CAO J, LI Y, ZHAO S, et al. Genetic-algorithm-based global path planning for AUV[C]//2016 9th International Symposium on Computational Intelligence and Design (ISCID). IEEE, 2016, 2: 79 − 82.
|
| [4] |
MONTIEL O, OROZCO-ROSAS U, SEPÚLVEDA R. Path planning for mobile robots using bacterial potential field for avoiding static and dynamic obstacles[J]. Expert Systems with Applications, 2015, 42(12): 5177-5191. DOI:10.1016/j.eswa.2015.02.033 |
| [5] |
王哲, 孙树栋, 曹飞祥. 动态环境下移动机器人路径规划的改进蚁群算法[J]. 机械科学与技术, 2013, 32(1): 42-46. |
| [6] |
李天成, 孙树栋, 高扬. 基于扇形栅格地图的移动机器人全局路径规划[J]. 机器人, 2010, 32(4): 547-552. DOI:10.3724/SP.J.1218.2010.00547 |
| [7] |
陈华, 张新宇, 姜长锋, 等. 水面无人艇路径规划研究综述[J]. 世界海运, 2015, 38(11): 30-33. |
| [8] |
张玉奎. 水面无人艇路径规划技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2008.
|
| [9] |
WANG Y, LIANG X, LI B, et al. Research and implementation of global path planning for unmanned surface vehicle based on electronic chart[C]//International Conference on Mechatronics and Intelligent Robotics. Springer, Cham, 2017: 534 − 539.
|
| [10] |
CAO L. Improved genetic algorithm for fast path planning of USV[C]//Ninth International Symposium on Multispectral Image Processing and Pattern Recognition (MIPPR2015). International Society for Optics and Photonics, 2015.
|
| [11] |
陈超, 耿沛文, 张新慈. 基于改进人工势场法的水面无人艇路径规划研究[J]. 船舶工程, 2015(9): 72-75. |
| [12] |
石鸿雁, 孙茂相, 孙昌志. 未知环境下移动机器人路径规划方法[J]. 沈阳工业大学学报, 2005(1): 63-69. DOI:10.3969/j.issn.1000-1646.2005.01.017 |
| [13] |
孙晓界. 无人水面艇实时路径规划系统研究[D]. 大连: 大连海事大学, 2016. SUN Xiao-jie. Research on real-time path planning system for unmanned surface vessel[D]. Dalian: Dalian Maritime University, 2016. |
| [14] |
王雷, 李明, 蔡劲草, 等. 改进遗传算法在移动机器人路径规划中的应用研究[J]. 机械科学与技术, 2017, 36(5): 711-716. |
| [15] |
范云生, 郭晨, 赵永生, 等. 时变漂角下USV直线路径跟踪控制器设计与验证[J]. 仪器仪表学报, 2016(11): 2514-2520. FAN Yun-sheng, GUO Chen, ZHAO Yong-sheng, et al. Design and verification of straight line path following controller for USV with time-varying drift angle[J]. Chinese Journal of Scientific Instrument, 2016(11): 2514-2520. DOI:10.3969/j.issn.0254-3087.2016.11.014 |
| [16] |
张斌, 郑中义. 以实习船为教学基地的校企联合新型授课模式研究[J]. 航海教育研究, 2018, 35(4): 85-88. |
| [17] |
刘纪磊, 王莉莉, 张兆宁. 基于RNP的A* 算法动态航路规划研究[J]. 航空计算技术, 2011, 41(2): 33-35. LIU Ji-lei, WANG Li-li, ZHANG Zhao-ning. Research on A* algorithm dynamic route planning based on RNP[J]. Aeronautical Computing Technique, 2011, 41(2): 33-35. DOI:10.3969/j.issn.1671-654X.2011.02.009 |
| [18] |
杨璐, 汪博涵, 张雪洁. 基于A*算法的AGV路径规划研究[J]. 公路与汽运, 2014(163): 47-49. |
| [19] |
HOLLAND J H. Adaptation in natural and artificial systems[M]. ANN Arbor: The university of Michigan Press, 1975: 45 − 47.
|
| [20] |
马永杰, 云文霞. 遗传算法研究进展[J]. 计算机应用研究, 2012(04): 1201-1206+1210. MA Yong-jie, YUN Wen-xia. Research progress of genetic algorithm[J]. Application Research of Computers, 2012(04): 1201-1206+1210. DOI:10.3969/j.issn.1001-3695.2012.04.001 |
| [21] |
孟祥杜. 无人船路径规划算法研究[D]. 天津: 天津理工大学, 2017. MENG Xiang-du. Research on path planning algorithm for unmanned ship[D]. Tianjin: Tianjin University of Technology, 2017. |
| [22] |
李连鹏, 苏中, 解迎刚, 等. 基于遗传算法的机器鱼水中路径规划[J]. 兵工自动化, 2015, 34(12): 93-96. DOI:10.7690/bgzdh.2015.12.024 |
| [23] |
KHATIB O. Real-time obstacle avoidance for manipulators and mobile robots[M]. Autonomous Robot Vehicles. Springer, New York, NY, 1986: 396-404.
|
| [24] |
LI D, WANG P, DU L. Path planning technologies for autonomous underwater vehicles-A review[J]. IEEE Access, 2019(7): 9745-9768. |
| [25] |
修彩靖, 陈慧. 基于改进人工势场法的无人驾驶车辆局部路径规划的研究[J]. 汽车工程, 2013, 35(9): 808-811. DOI:10.3969/j.issn.1000-680X.2013.09.011 |
| [26] |
孙炜, 吕云峰, 唐宏伟, 等. 基于一种改进 A* 算法的移动机器人路径规划[J]. 湖南大学学报 (自然科学版), 2017, 44(4): 94-101. SUN Wei, LV Yun-feng, TANG Hong-wei, et al. Mobile robot path planning based on an improved A* algorithm[J]. Journal of Hunan University(Natural Sciences), 2017, 44(4): 94-101. |
| [27] |
KANAKAKIS V, SPANOUDAKIS P, TSOURVELOUDIS N. Optimized design of an unmanned surface vehicle[C]//Elmar 09 International Symposium. IEEE, 2009.181 − 184.
|
| [28] |
NAEEM W. Evasive decision making in uninhabited maritime vehicles[C]//World Congress, 2011.12833 − 12838.
|
| [29] |
陈成, 何玉庆, 卜春光, 等. 基于四阶贝塞尔曲线的无人车可行轨迹规划[J]. 自动化学报, 2015(3): 486-496. CHEN Cheng, HE Yu-qing, BU Chun-guang, et al. Feasible trajectory generation for autonomous vehicles based on quartic bezier curve[J]. ACTA Automatica Sinica, 2015(3): 486-496. |
 2021, Vol. 43
2021, Vol. 43
