0 引　言

随着人工智能技术的不断发展，水面无人艇（Unmanned Surface Vehicle，USV）作为一种无人化与智能化作战平台，在军用和民用领域都有着广泛的应用前景。根据底层任务要求，水面无人艇需要具备在包含静态和动态障碍物的复杂海域环境下进行安全有效自主航行的能力。路径规划是无人艇自主航行的前提，是无人艇智能化程度的重要体现，也是无人艇研究领域的热点问题^[1-2]。

环境地图是开展路径规划任务的前提。一般来讲，水面无人艇在航行过程中，可以通过雷达、摄像机等传感设备获得船舶周围局部环境信息，还需要电子海图提供全局环境信息。环境地图通常由复杂几何图形构成，使得路径规划时大多数搜索算法不能被直接应用，并且地图的规模直接影响着路径规划的效率，因此需要对环境地图进行处理^[3-6]。栅格地图是最常用的处理及表达形式。格栅地图将环境表示为具有一定分辨率的方形栅格网，栅格根据是否被障碍物占据分为自由状态和占据状态，栅格之间相互独立。格栅地图创建简单，便于路径规划实现，因此被广泛应用于机器人、自动驾驶等领域。地图的格栅化有2个重要参数−地图尺寸和栅格大小。地图尺寸需要足够大，能覆盖自由航行区域，同时又希望尽可能小，提高存储以及计算的效率。显然，地图大小一定时，栅格的数量和栅格大小是成反比的。太小太精细的栅格会导致栅格的数量迅猛增长，急剧地降低路径规划的效率；太大的网格会提高路径规划的计算速度，但是会影响规划路径的精度。有学者提出了“有义地图率”的概念，讨论了栅格大小、传感器精度与有义地图率之间的关系；并提出了栅格准确度和栅格信息量为变量的代价函数来评估占据地图精度的方法^[7]。因此，选择合理的栅格尺度降低地图规模并尽量保持地图的边界特征，是栅格地图建模及提高路径规划效率的关键。

环境地图的格栅化降低了实际环境中障碍物的处理难度，因此基于栅格地图的搜索方法在路径规划中得到了广泛的关注。当规划环境稀疏时，可以采用深度优先搜索、广度优先搜索、Dijkstra算法^[8]等准确高效地找到全局最短路径。然而随着规划环境的规模和复杂度增加时，求解全局最优路径的计算量会急剧增加，此时精确算法很难在短时间内得到满意解。启发式搜索算法牺牲了求解质量换取计算速度，可以在较短时间内得到最优解。A*（A-star）算法由Dijkstra算法发展而来，是目前最常用，也是应用最广的一种启发式搜索算法^[9-12]。算法中加入了目标点到当前路径点的距离估计代价，综合考虑了从起点到当前路径点的距离以及经由路径点到达终点的距离来决定搜索的方向。A*算法主要用于静态栅格地图的最优路径搜索，通常有两方面的改进内容：提高搜索速度以及提高规划的可行性。目前，提高路径搜索速度的方法主要通过使用曼哈顿距离和对角线距离作为代价函数，引入决胜法来处理评价值相等的情况，同时进行跳跃点搜索、双向搜索等手段。

本文对环境地图的格栅化及路径规划进行研究，介绍了栅格地图建模方法，利用等效网格对障碍物边界区域网格进行改进，保证了规划环境的空间连通性。阐述了A*算法在栅格地图路径规划的实现流程，最后以某海域环境为例进行了仿真验证，对比分析了环境地图格栅化对路径规划的影响。

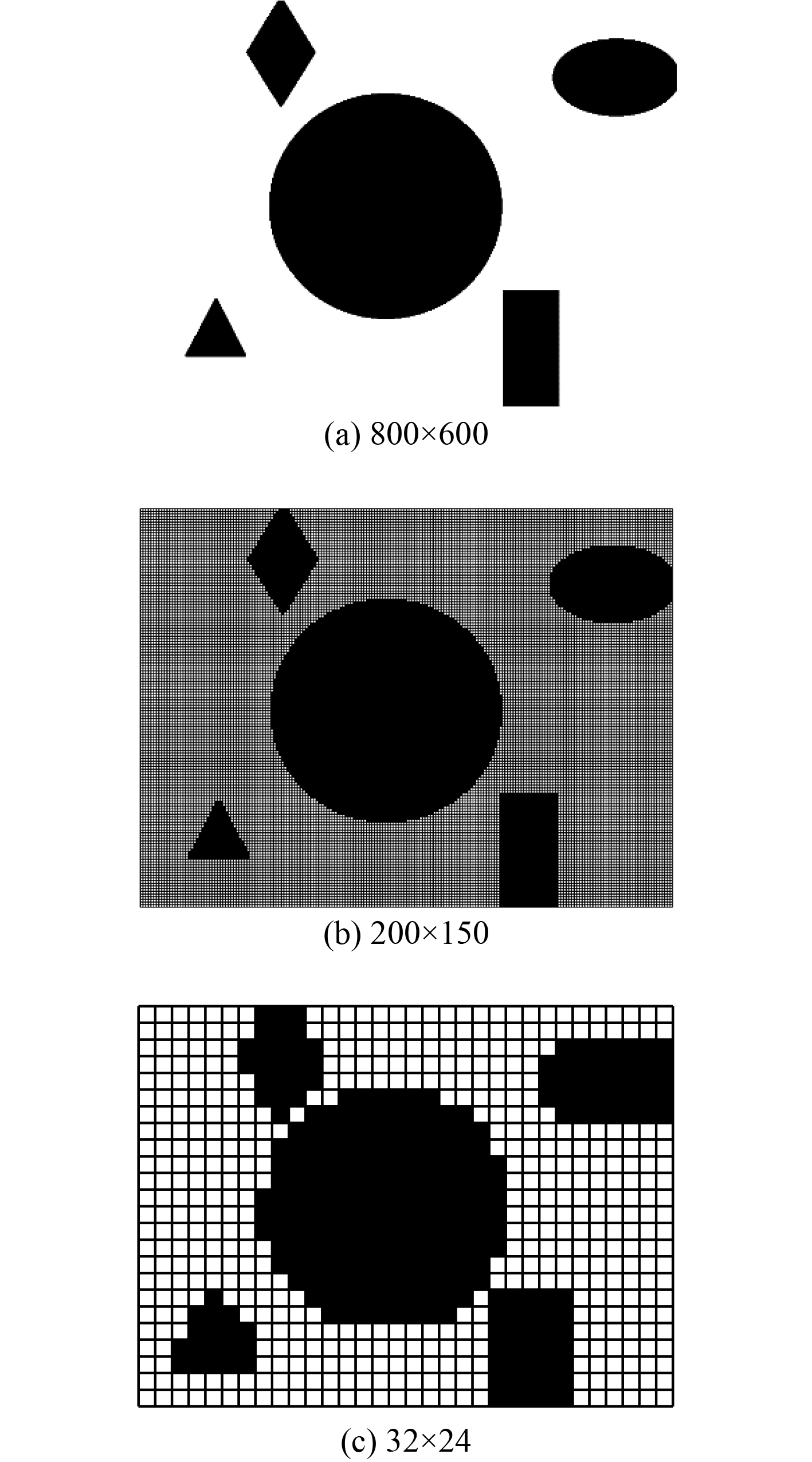
1 栅格地图建模

一般来讲，水面船舶在航行过程中，可以通过雷达、摄像机等传感设备来获得船舶周围局部环境信息，还需要根据电子海图来获取全局环境信息。这些环境信息无法直接应用到水面无人艇路径规划中，需要将电子海图转化为可被利用的环境模型。栅格法表述简单且容易实现，可以应用于不同的搜索算法，是目前地图建模中应用最为广泛的一种方法。通常，栅格法在处理路径规划问题时，利用栅格对规划环境空间进行划分，并用2种颜色（白与黑）或数字（1和0）将栅格分为可行区（自由栅格）与不可行区（障碍栅格）2种情况，同时对划分后的栅格进行编码，构建栅格地图模型。障碍栅格是环境中障碍物进过膨胀或者腐蚀处理后填充到栅格中形成的，黑色表示被障碍占据，白色表示空白区域，如图1所示。

栅格的分辨率（网格尺度）是栅格地图的特征体现。当栅格的分辨率过高时（网格尺度过小），栅格数量的急剧增加，使得路径规划计算存储量显著增加（图1（a）和图1（b）），而栅格的分辨率过低会导致规划区域特征过于粗糙，无法得到有效路径，甚至导致规划区域的连通性被破坏，使得路径规划失败（图1（c））。图1所示格栅地图中，障碍物边界在栅格内，该栅格就被处理为不可通行网格，这种极端的做法势必会影响规划地图的连通性，当网格尺度较大时尤为明显（图1（c））。可以看出，选取合理的栅格尺度是规划环境建模的关键，同时障碍物边界网格的处理也会影响规划空间的连通性。为寻求最大限度降低路径规划的复杂度并保证路径规划的成效，需要寻求网格尺度和规划区域特征之间的平衡，在降低规划空间规模的同时保证规划空间的连通性。岳伟韬等^[7]提出了“有义地图率”表征占据格栅地图准确度的概念，分析了栅格大小、有义地图率的影响。

为保证规划空间的局部特征及连通性，本文对障碍物边界采用等效网格来替代。类比多孔介质流动特性，设定一个阀值，当网格中障碍物占比大于阀值，则认为该网格是障碍栅格，不可通行；反之则认为该网格是自由网格，可通行。假设规划区域范围为 $X \times Y$ ，以尺度 $Scale$ 进行格栅化处理，则输出的栅格地图规模可表示为 $nx \times ny$ ，其中：

$\left\{ \begin{gathered} nx = ceil(X/Scale) \text{，} \\ ny = ceil(Y/Scale) \text{，} \\ \end{gathered} \right.$

(1)

障碍物 $Obs$ 在区域 $[i - 1:i,j - 1:j] \cdot Scale$ 所对应栅格 $(j,i)$ 的占据率为：

$Occupanc{y_{ji}} = \sum {{S_{Obs}}(i,j)} /{S_{i,j}}\text{，}$

(2)

设障碍占比阀值为 ${a_0}$ ，则栅格的状态可以通过下式确定：

$map = \left\{ \begin{gathered} 0,Occupanc{y_{j,i}} > {a_0} \text{，} \\ 1,Occupanc{y_{j,i}} < = {a_0} \text{。}\\ \end{gathered} \right.$

(3)

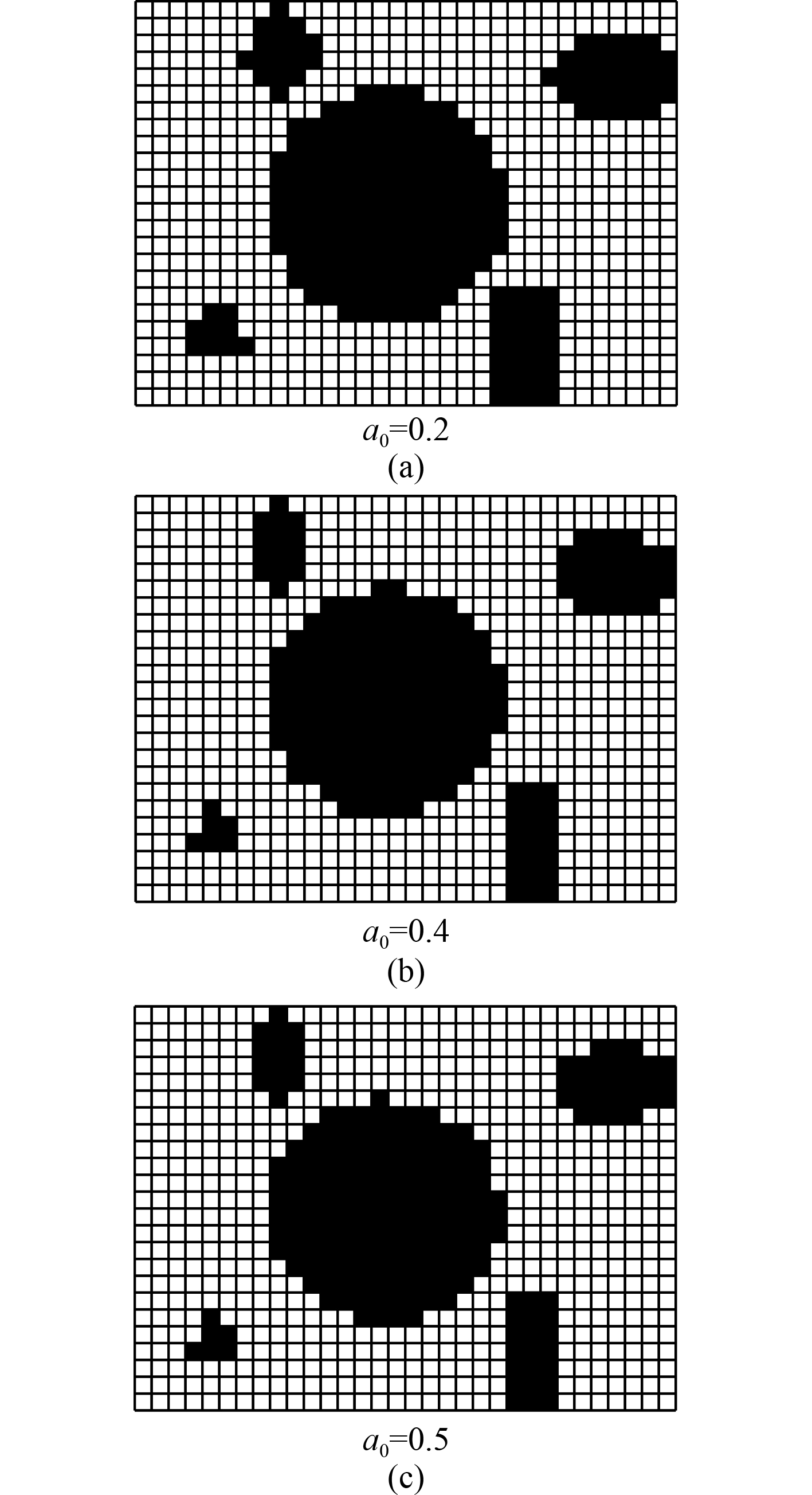
图2给出了图1（a）在较粗网格下不同阀值时的格栅地图，表1给出了不同阀值改进后的障碍物占比统计值。不难看出，自由空间与障碍物交界面网格的状态得到了显著改进，栅格地图在维持规划空间图形特征的同时连通性也得到了保障。需要注意的是，较小的阀值同样会导致边界处自由空间被占据，而较大的阀值会使得边界处障碍信息被抹掉。结合表1并参考二维多孔介质格子模型逾渗概率的临界值0.6，一般情况下障碍占比临界阀值 ${a_0}$ 可取为0.4来保持规划空间格栅化后的连通性特征。

2 A*算法

环境地图的格栅化处理降低了实际环境中障碍物处理的难度。当环境地图经格栅化转化为栅格地图，无人艇路径规划问题就转化为在栅格地图中寻找2个给定网格点之间的最优路径问题，可以通过基于栅格的搜索方法来解决。A*搜索算法是一种启发式的搜索算法，也是目前路径规划技术中最受欢迎的算法，在无人系统路径规划和路径寻优等领域有着广泛的应用。本文采用A*算法来进行最优路径的搜索。

A*算法是在Dijkstra 算法的基础上发展起来的，它通过构建以当前节点与起始节点两者间的实际距离代价加上当前节点与目标节点的预估代价的启发式评价函数来对当前节点进行对比筛选。在路径规划过程中，A*算法的评价函数如下式：

$ f({V_i}) = g({V_i}) + h({V_i})\text{。} $

(4)

其中： $f({V_i})$ 表示起始节点S经由当前节点 ${V_i}$ 和目标节点G构成的评价函数； $g({V_i})$ 表示起始节点S到当前节点 ${V_i}$ 的实际距离代价， $h({V_i})$ 表示当前节点 ${V_i}$ 与目标节点G之间的估算距离代价。 $f({V_i})$ 值越小，表示经由 ${V_i}$ 到达目标点G的总代价越小。A*算法具有超强的灵活性与适应性，根据不同的搜索任务可以设计针对性的代价函数。估算距离代价 $h({V_i})$ 属于启发函数，决定 A*算法效率的高低，在评价函数中起关键作用。若 $h({V_i})$ 为 0，就只有 $g({V_i})$ 起作用，A*算法简化为 Dijkstra算法。

对于启发函数的计算方法由很多种，对于栅格法建立的环境模型，传统的计算方法有2种，一种是欧氏距离估计，另外一种是曼哈顿距离估计。为了便于计算，在充分考虑算法效率的基础上，本文选取欧氏距离估计作为启发式评价函数。

欧氏距离估计：

$h({V_i}) = a \cdot \sqrt {{{({x_i} - {x_g})}^2} + {{({y_i} - {y_g})}^2}} \text{，}$

(5)

曼哈顿距离估计：

$ h({V_i}) = a \cdot \left(\left| {{x_i} - {x_g}} \right| + \left| {{y_i} - {y_g}} \right|\right)\text{。} $

(6)

其中当前节点 ${V_i}$ 的坐标为 $({x_i},{y_i})$ ，目标节点G的坐标为 $({x_g},{y_g})$ ， $a$ 表示单位长度代价，即正方形栅格的边长。从起点S到达目标点G，在栅格地图中搜索最优路径的流程如图3所示。

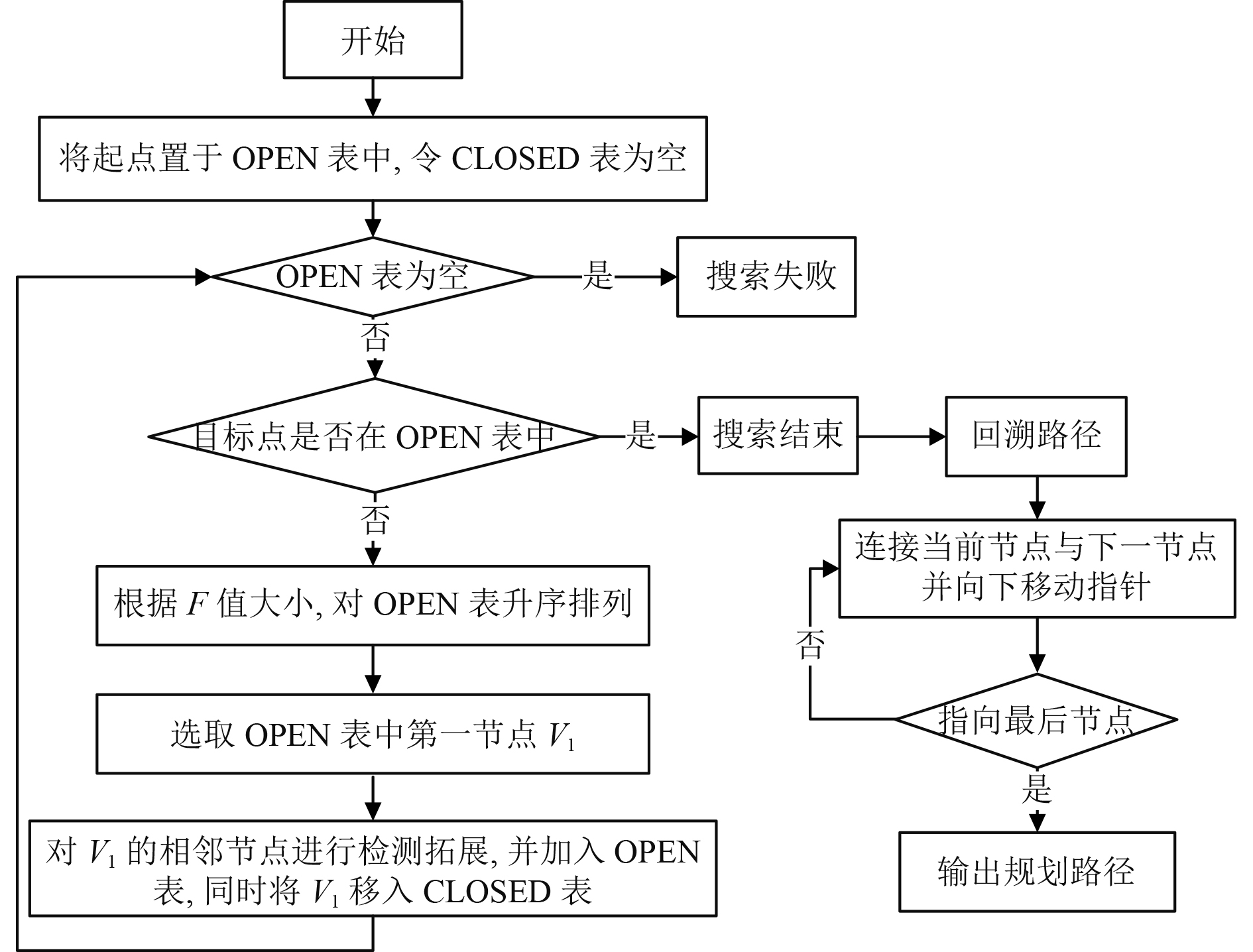
A*算法的搜索流程如图3所示。

3 仿真研究

为分析地图格栅化对路径规划的影响，以某海域地图为例进行路径规划仿真。规划环境地图区域范围为 $18\;{\rm km} \times 9\;{\rm km}$ ，假设水面无人艇需要从某水域自主航行至某水域，起点至目标点直线距离约 $12\;{\rm km}$ 。仿真环境用Matlab软件开发，并将水面无人艇简化为质点处理。图4为二值化地图，黑色范围表示陆地、岛屿等无人艇无法通行的区域，白色范围表示可以通行的水域。

二值化后地图规模约100万量级像素点，每个像素点代表距离约12.8 m。若将每个像素点作为栅格处理，地图规模庞大，不利于路径规划的高效实现，需要适当增大栅格尺度来降低栅格地图规模，并通过障碍物占比阀值来调节障碍物边界处栅格的状态。

图5～图7及表2给出了障碍物占比阀值为0.4时，不同栅格尺度时的规划路径图及结果统计。当栅格尺度变大时，栅格地图规模显著下降，路径规划的效率得到了提升，但栅格地图信息变得粗糙，规划路径结果差异显著。另外，从图5～图7对比可以看出，选择10个像素点作为网格尺度进行格栅化，在保证地图信息完整的同时，得到的规划路径与精细网格下的路径相近，并且规划效率得到了显著的提升。

图8～图11及表3给出了相同栅格尺度（10个像素点）下，不同障碍占比阀值时的规划路径及结果统计。不难看出，当前尺度格栅化后的环境地图基本都能保持原始地图区域特征，并且都能顺利完成路径规划任务，得到规划路径。但是随着障碍占比阀值的减小，交界面处的网格信息会有所不同，障碍物栅格会有所增加，减弱了规划区域的通行性，在狭窄航行区域尤为明显，同时路径规划所需的时间会明显增加。而从规划路径的结果对比可以看出，阀值大于0.4时，所得的规划路径几乎一致，所需花费时间也大致相同；当阀值小于0.4时，所得的规划路径差异明显，这从一定程度上说明障碍占比阀值取0.4可行。需要说明的是，障碍物占比阀值取得越小，允许栅格内部存在障碍物的可能性就越低，网格通行的成功率就越高，所获得的规划路径就更为安全。

4 结　语

环境地图建模是无人艇导航和路径规划的重要组成部分。本文主要讨论了网格尺度及障碍物边界处理对栅格地图建模及路径规划的影响，并以某海域为例进行了路径规划对比分析。结果表明：

1）选择适中的网格尺度和障碍占比阀值对环境地图进行格栅化，规划空间的图形特征能严格保持，利用A*算法可以快速高效地在规划空间求得规划路径；

2）大网格尺度会显著降低栅格地图的规模，提高路径规划的效率，但是可能降低规划地图的空间连通性，甚至会导致路径规划失败，因此需要通过障碍物占比阀值来适当地调节障碍物边界处网格的状态；

3）障碍占比阀值的大小影响着障碍物边界占据网格的状态，也会影响规划空间的连通性。当栅格尺度较大时，较大的阀值会提高规划空间的连通性；当栅格尺度较小时，较小的阀值会提高规划路径的安全性，但是会导致规划效率的降低。