2. 上海交通大学 核科学与工程学院,上海 200240
2. School of Nuclear Science and Engineering, Shanghai Jiaotong University, Shanghai 200240, China
两相流动是沸水堆、压水堆核电站普遍遇到的一种流动形式,其对于堆芯换热及其余热的排出具有十分重要的影响[1]。特别是对于堆芯流道以及蒸汽发生器内的换热管束而言,两相流动下的流动阻力和传热十分复杂,而且还有可能存在流动不稳定性,因此准确的预测计算两相流动下的流动阻力以及传热具有很重要的意义[2]。已有的大型系统程序如RELAP5,TRAC等,在数值求解两流体基本方程时,采用了许多本构关系式[3]。其中摩擦阻力关系式、物性状态方程、对流传热关系式均是在大量实验的基础上得到的,其准确性可以得到保证。然而,对于相间传热关系式,由于难以进行实验,所以其准确性尚需进行验证。
在开发一维系统程序时,发现根据流型计算的相间换热系数值往往过大,导致计算失败,因此有必要对相间换热系数值进行限制[4-5]。本文的研究重点是相间换热边界限制对于相间换热的影响。
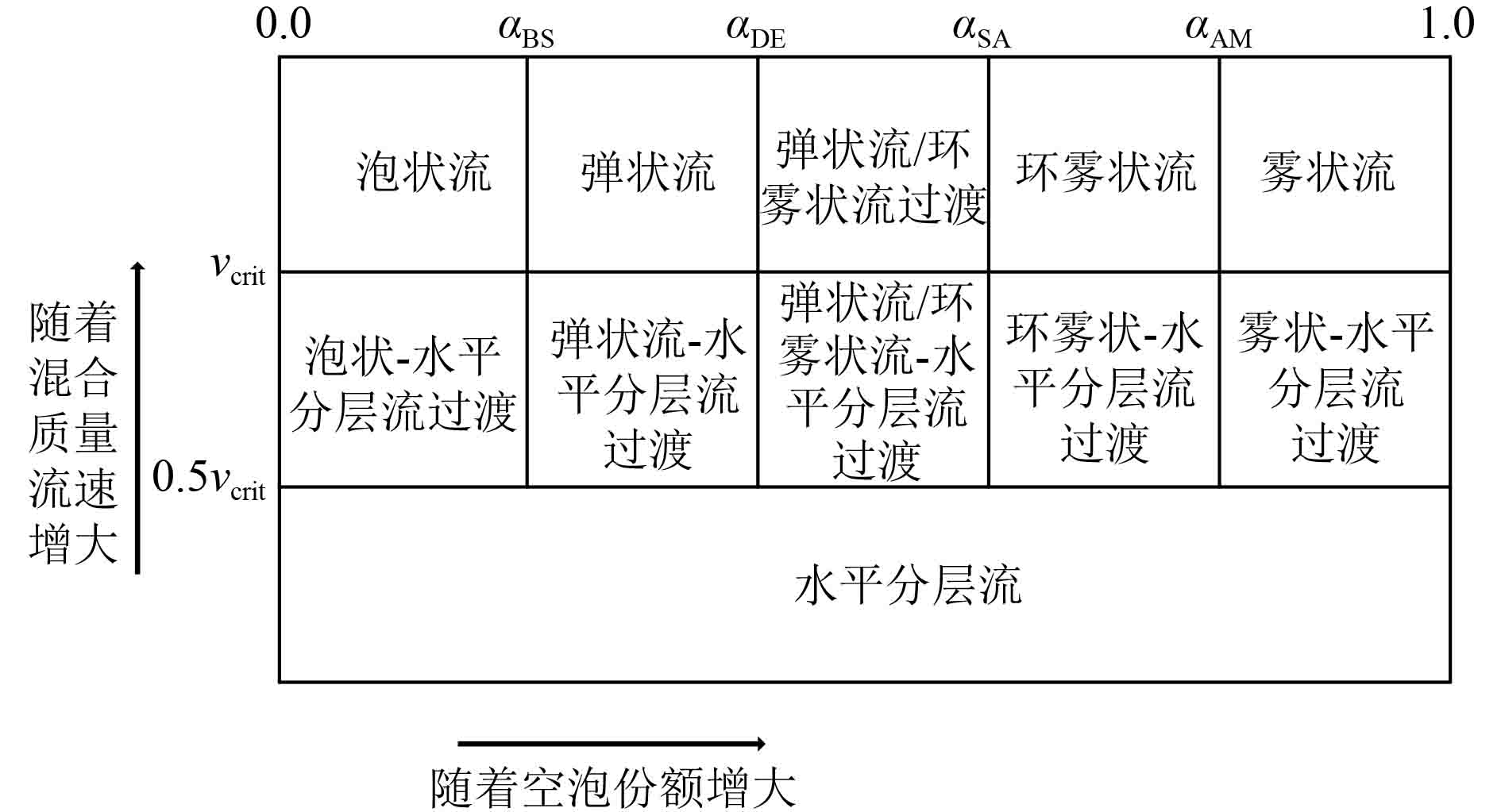
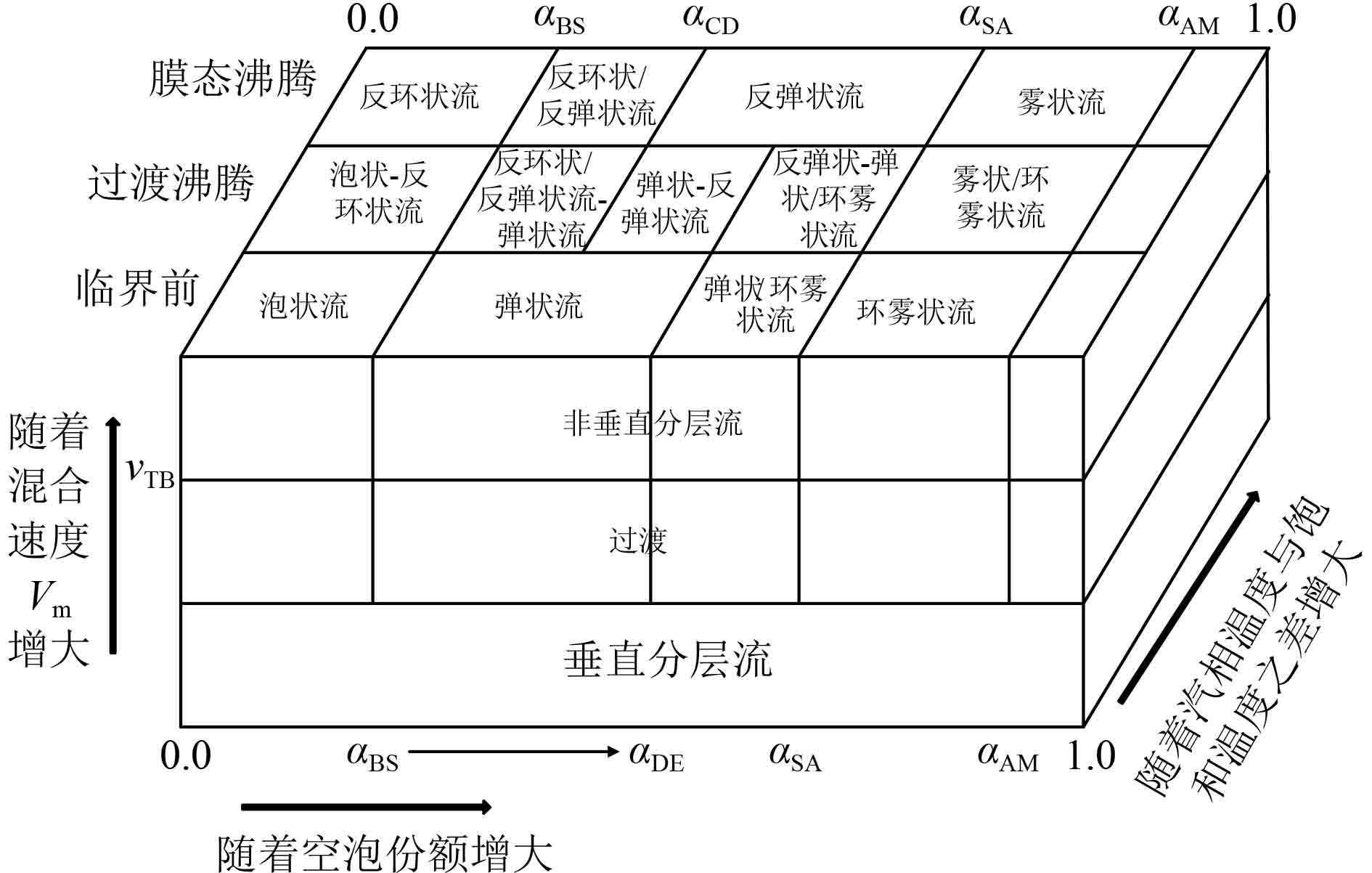
1 相间换热模型系统分析程序如RELAP5/MOD3.2对于两相相间传热的计算一般是先判断两相流型,然后根据两相流型进行相间传热关系式的选择和相间换热的计算。正在开发的COSINE程序参考RELAP5/MOD3.2两相流型的分类,根据管的倾角,将管内两相流型分为垂直和水平两大类。当管的倾角大于0°且小于45°时,在程序内部统一归类于水平管,当管的倾角大于等于45°且小于90°时,在程序内部统一归类于垂直管。水平管内流型分类和垂直管内流型分类如图1和图2所示。在计算时,根据管内不同的流型选择不同的相间传热计算关系式[6-8],相间换热关系式也是参考了RELAP5/MOD3.2程序。
|
图 1 水平流型图 Fig. 1 Horizontal flow pattern |
|
图 2 垂直流型图 Fig. 2 Vertical flow pattern |
为研究相间换热边界限制对于相间换热的影响,首先进行无边界限制时的两相流动计算。研究对象为水平管和垂直管内的单相水和水蒸汽的两相流动,水平管与垂直管的RELAP5节点图如图3和图4所示,其中管A和管B的控制体长度均为0.5 m。选取水平环形雾状流、垂直环形雾状流2种不同流型的工况进行计算,不同流型的计算条件如表1所示,其中液相过冷,汽相过热。

|
图 3 水平管节点图 Fig. 3 Horizontal pipe node diagram |

|
图 4 竖直管节点图 Fig. 4 Vertical pipe node diagram |
|
|
表 1 两种流型的计算条件 Tab.1 Calculation conditions of two flow patterns |
|
|
表 2 二种流型的计算结果(无换热系数边界限制) Tab.2 Calculation results of two flow patterns (no boundary limit of heat transfer coefficient) |
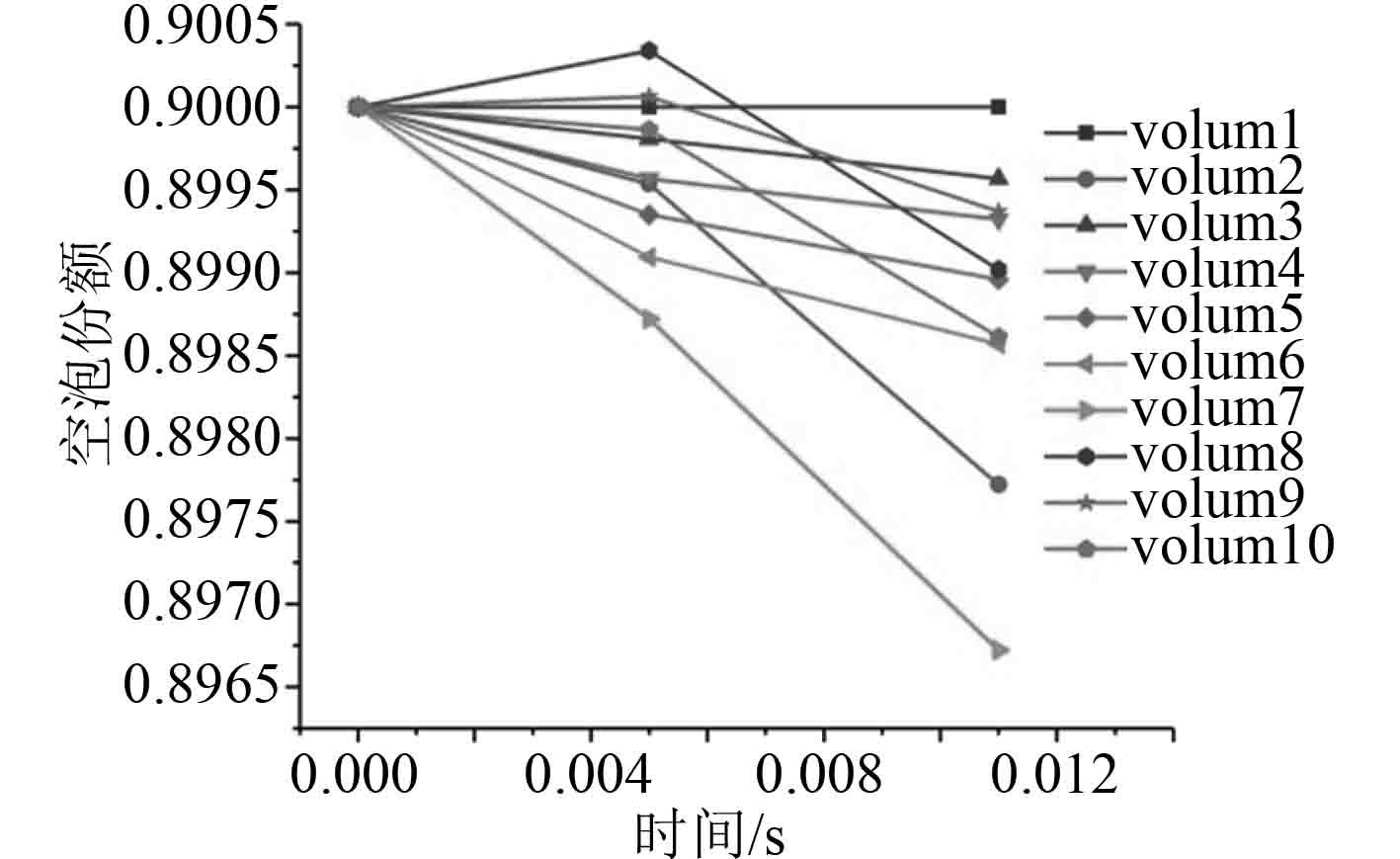
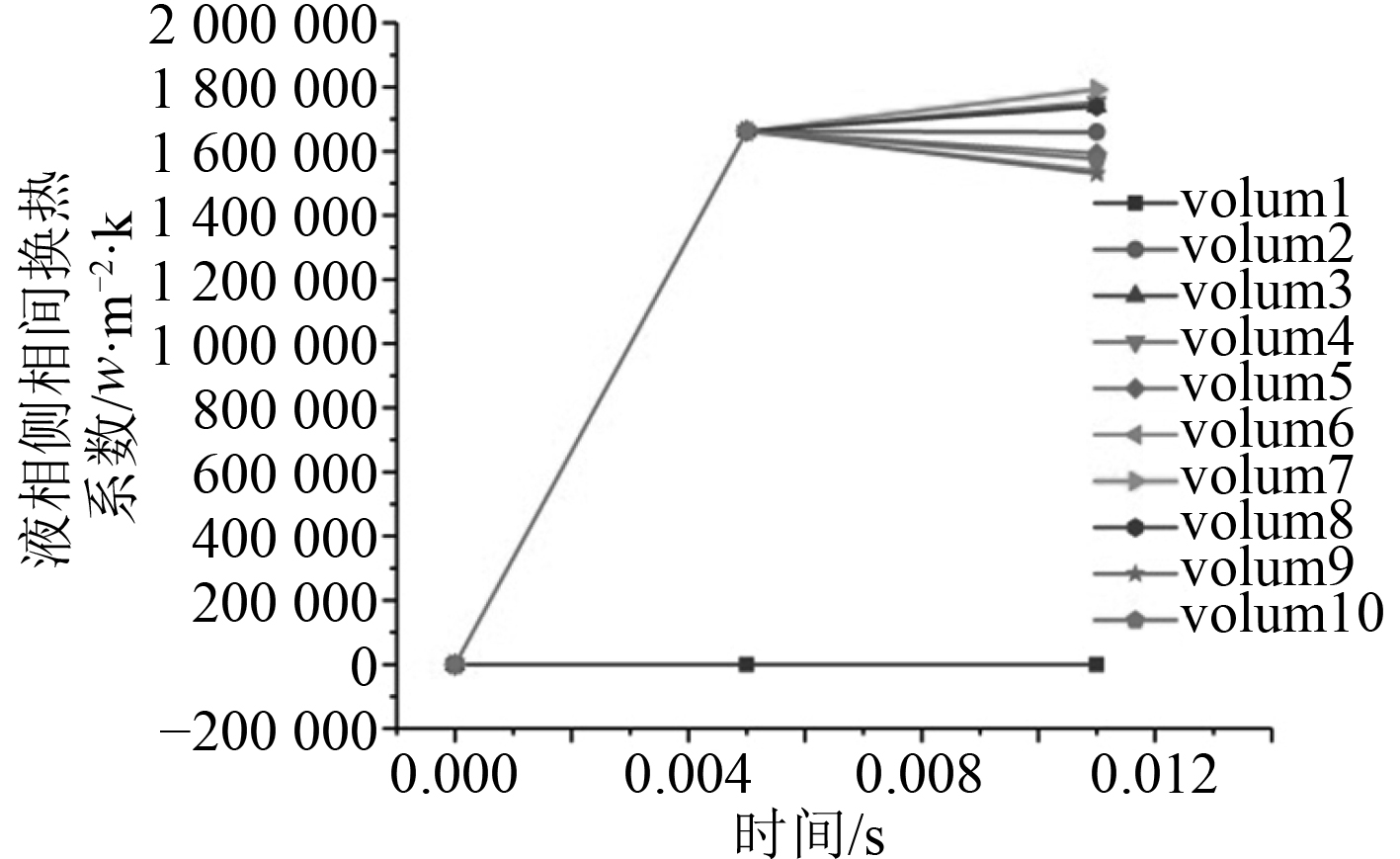
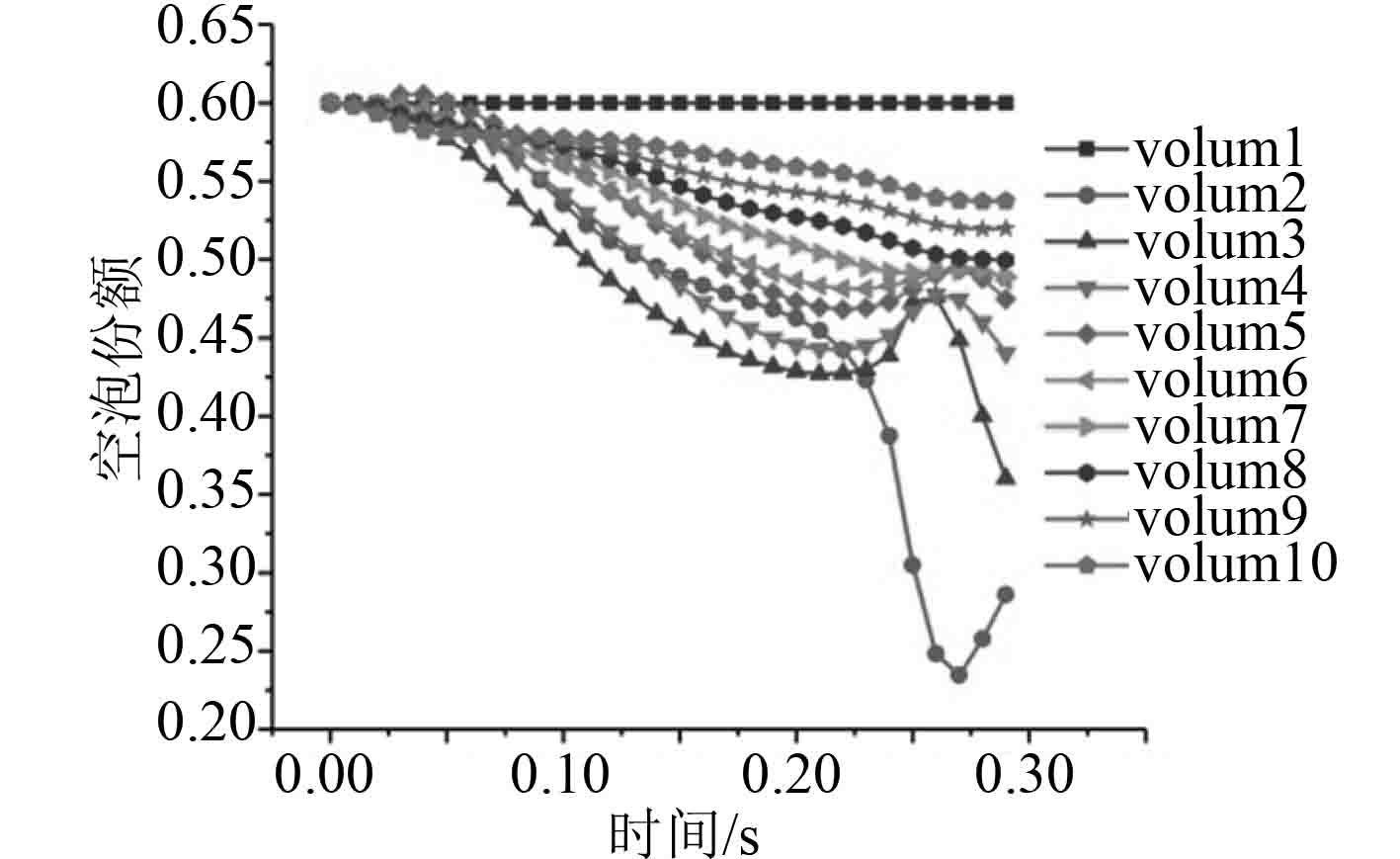
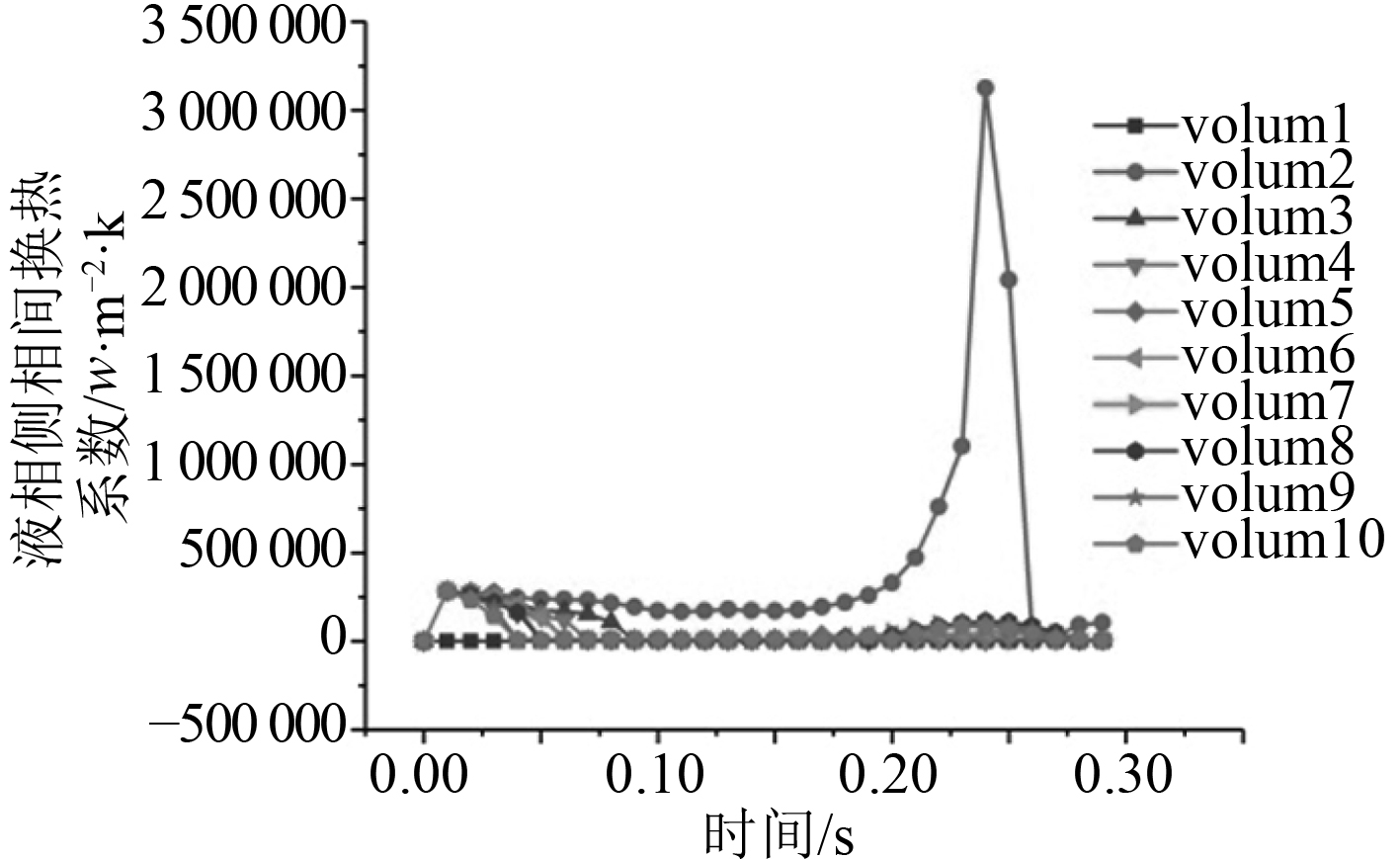
由图5~图8所示计算结果表明,二种流型均只能计算很短的时间,显示物性报错。调试程序后发现相间换热系数过大,相间换热系数均达到了10E6量级,从而导致汽相焓值出现负值,从而导致计算失败。
|
图 5 水平环雾状流空泡份额 Fig. 5 Bubble share of horizontal annular fog flow |
|
图 6 水平环雾状流液相侧相间换热系数 Fig. 6 Heat transfer coefficient between liquid phase and side of horizontal annular fog flow |
|
图 7 垂直环雾状流空泡份额 Fig. 7 Bubble share of vertical annular fog flow |
|
图 8 垂直环雾状流液相侧相间换热系数 Fig. 8 Heat transfer coefficient between liquid phase sides of vertical annular fog flow |
为了限制相间传热系数,使得计算结果趋于合理和计算的顺利进行,必须对相间传热系数的数值进行限制。参考 RELAP5/MOD3.2中的处理[8],对相间传热系数进行2个方面的限制。
1)液相侧相间传热系数最大值
当空泡份额逐渐接近于0或者1时,相间传热系数应该是一个小值,因此采用式(1)进行限制,从而使得空泡份额逐渐接近于0或者1时,相间传热系数能够趋向于一个小值。同时式(1)也限制了汽相的冷凝速率,当汽相冷凝速率过快时,将导致压力变化很快,此时会出现水物性报错。式(1)是利用COBRA程序计算N-type反应堆时采用的关系式,式中的系数17539,472.4,4.724均是假设值,472.4是气泡大小的假设,4.724是气泡大小的下限,17539是计算N-type反应堆时采用的传热系数的限制[8]。这3个数值均是对相间传热系数的最大值进行限制,因此有必要分析相间传热系数的最大值对两相流动相间传热的影响。
| $\begin{split} {{H}}_{{i}{f}}=&\mathrm{m}\mathrm{i}\mathrm{n}\Biggr\{{{H}}_{{i}{f}},17539\mathrm{m}\mathrm{a}\mathrm{x}\left[\mathrm{4.724,472.4}{\mathrm{\alpha }}_{\mathrm{g}}\left(1-{\mathrm{\alpha }}_{\mathrm{g}}\right)\right]\times\\ &\mathrm{m}\mathrm{a}\mathrm{x}\left[0,\mathrm{m}\mathrm{i}\mathrm{n}\left(1,\frac{{\mathrm{\alpha }}_{\mathrm{g}}-1.0\times {10}^{-10}}{0.1-1.0\times {10}^{-10}}\right)\right]\Biggr\} \text{。}\end{split} $ | (1) |
式中:
2)相间传热系数最小值
限定液相与汽相的相间传热系数的最小值为0。
3 液相侧相间传热系数最大值限制对于两相相间换热计算的影响加入上述二项相间换热系数限制后,2种流型工况还是不能顺利计算,因此表明所加的限制不能够有效的限制相间换热。图9和图10分别为在程序内添加相间换热限制后此时2种流型下控制体不同位置内液相侧和汽相侧相间换热系数、空泡份额的的对比。
|
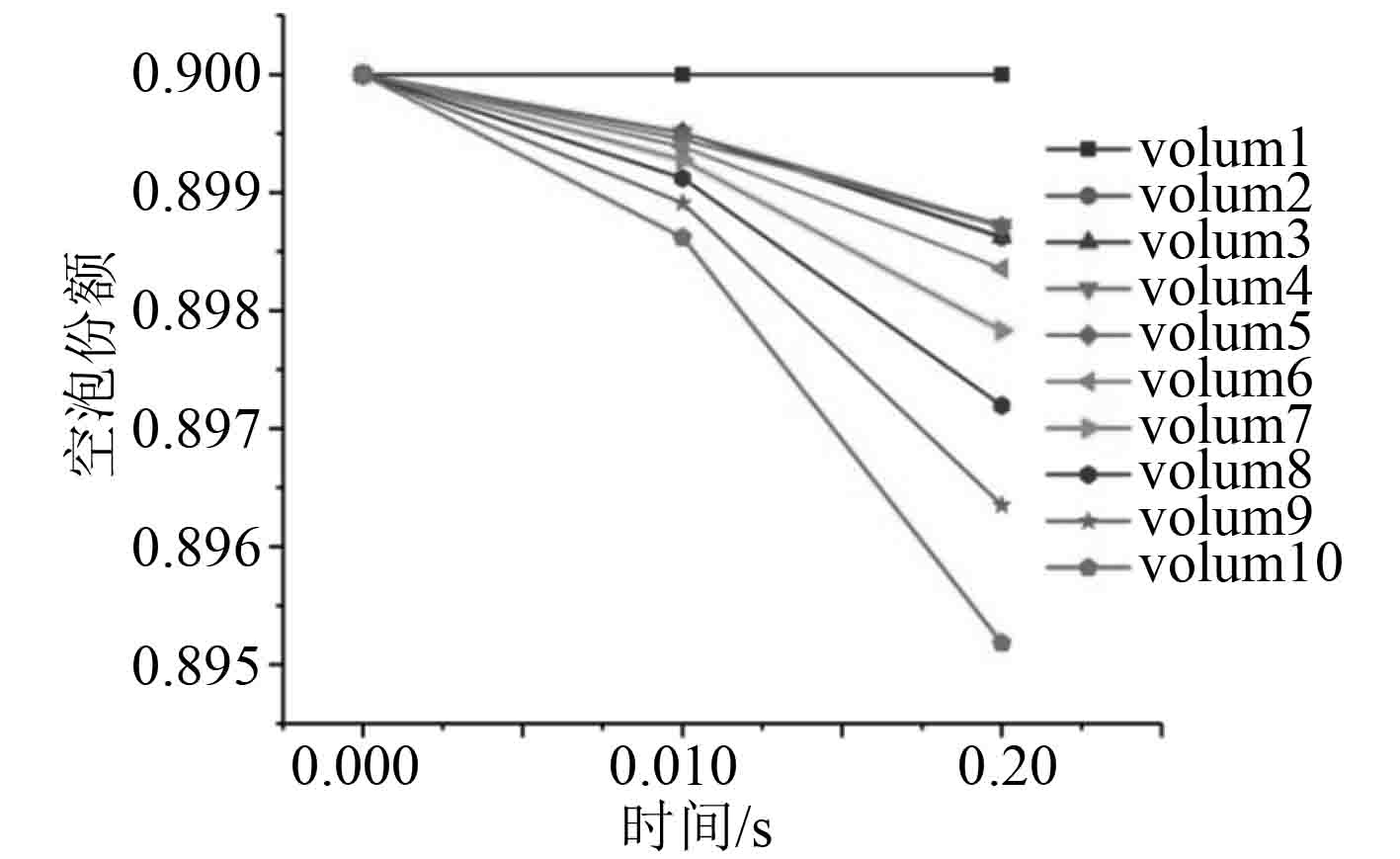
图 9 水平环雾状流空泡份额(加相间换热系数限制) Fig. 9 Bubble share of horizontal annular fog flow (limited heat transfer coefficient between phases) |
|
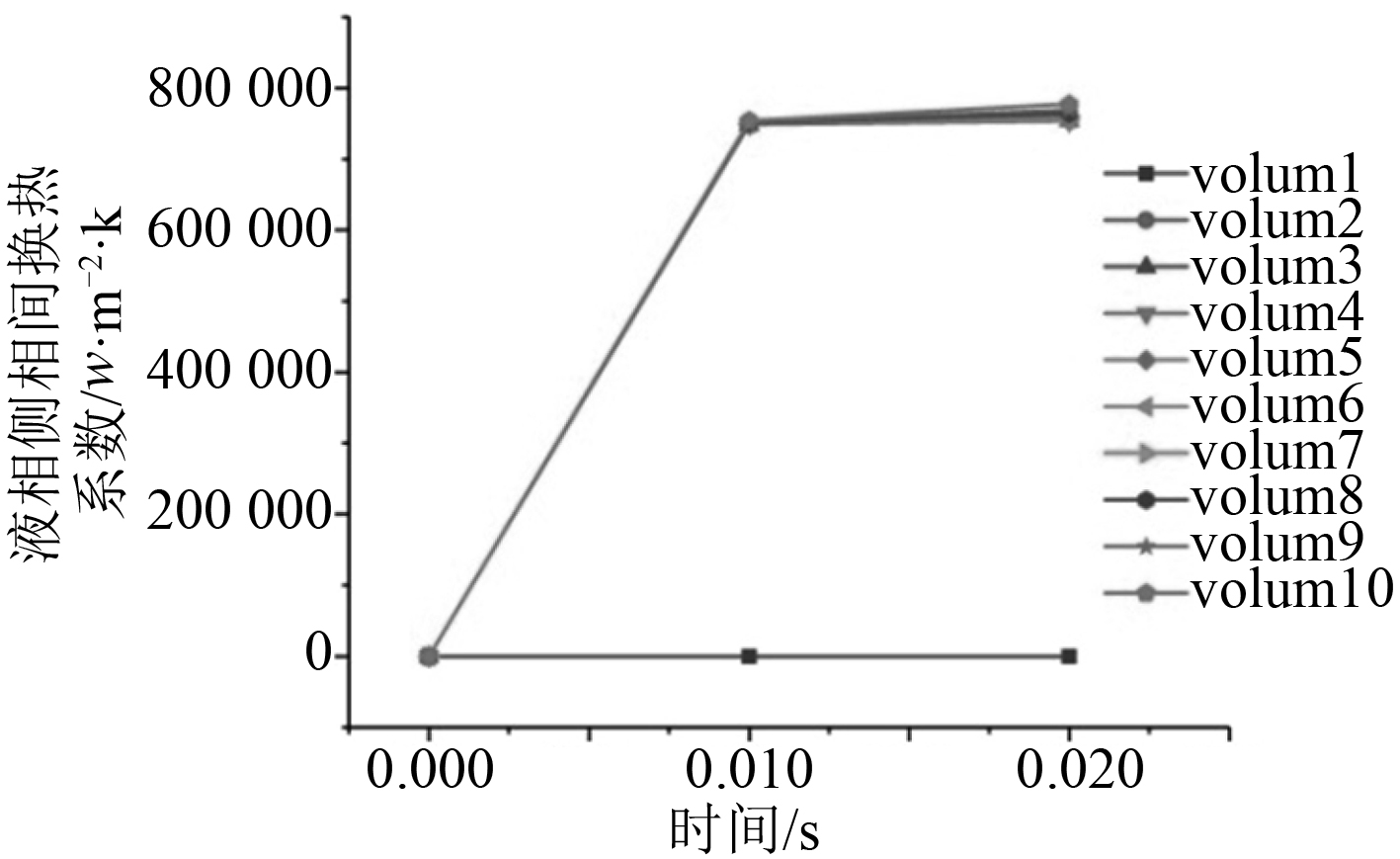
图 10 水平环雾状流液相侧相间换热系数(加相间换热系数限制) Fig. 10 Heat transfer coefficient between liquid phase side of horizontal annular fog flow (limit of heat transfer coefficient between phases) |
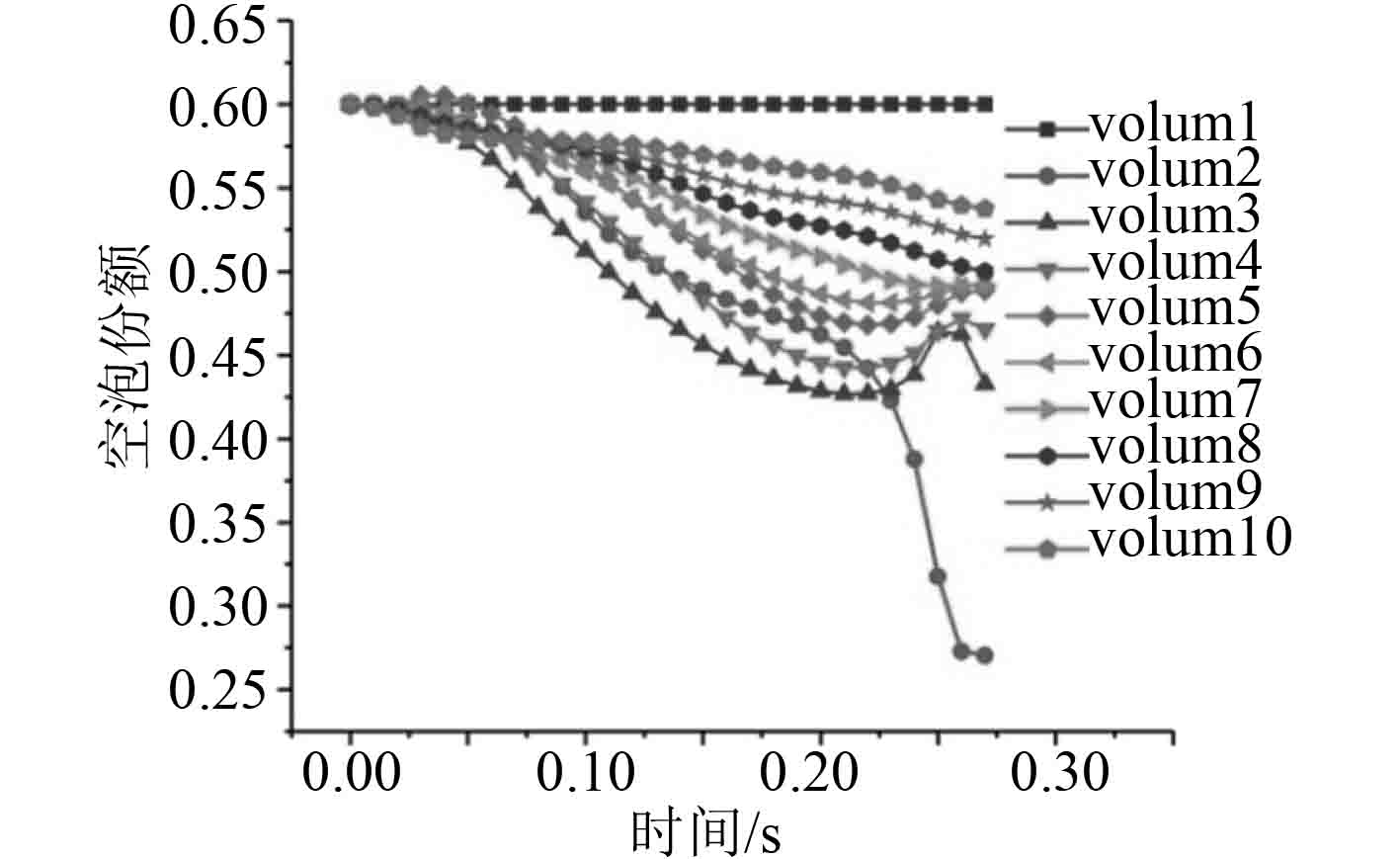
如图9~图12所示,在程序中添加对应的相间换热限制方程后,相应的相间换热系数减少了一个数量级,但是还是过大,导致程序计算时出现水物性错误,无法顺利计算。
|
图 11 垂直环雾状流空泡份额(加相间换热系数限制) Fig. 11 Bubble share of vertical annular fog flow (limited heat transfer coefficient between phases) |
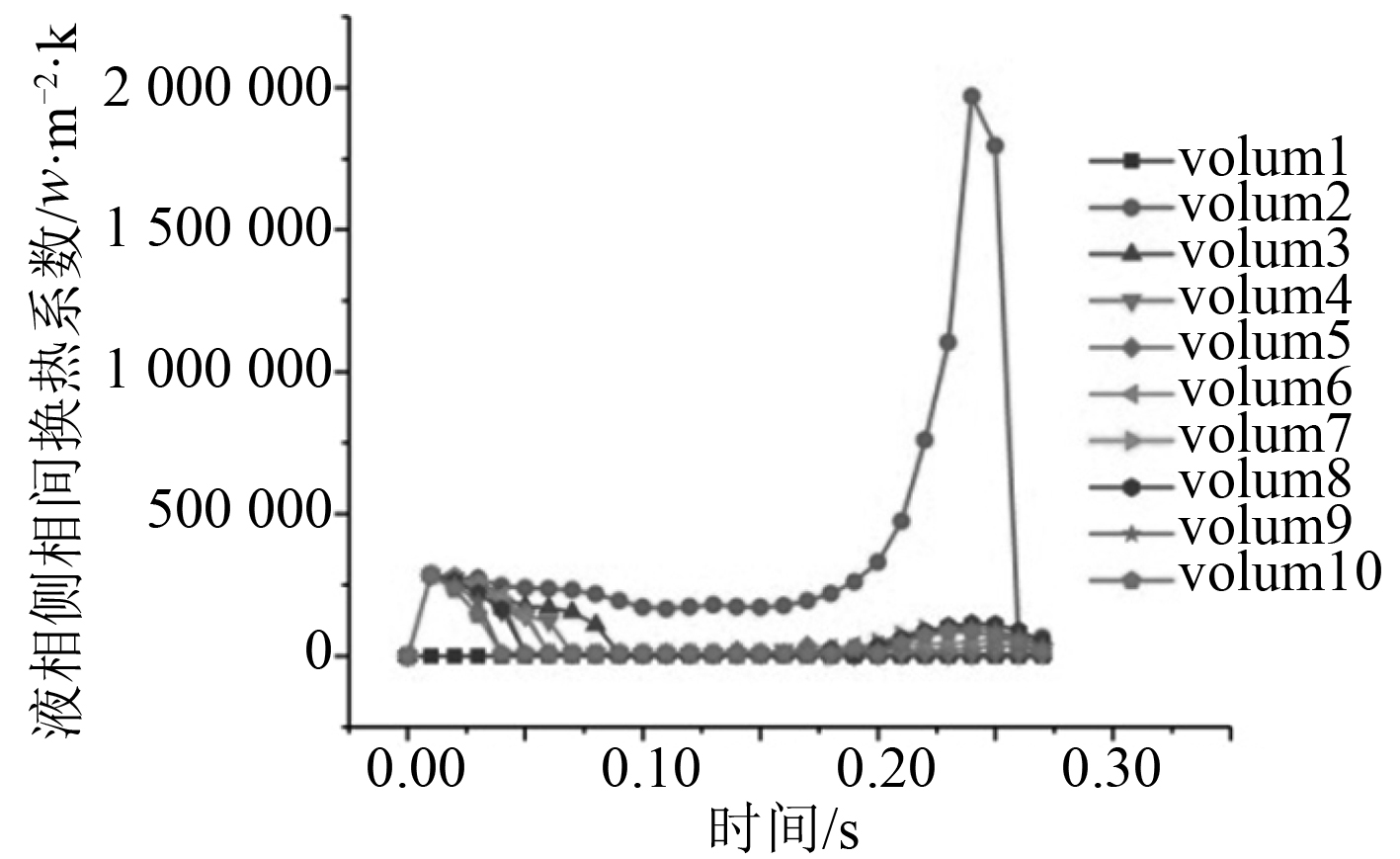
|
图 12 垂直环雾状流液相侧相间换热系数(加相间换热系数限制) Fig. 12 Heat transfer coefficient of liquid phase side of vertical annular fog flow (limit of heat transfer coefficient between phases) |
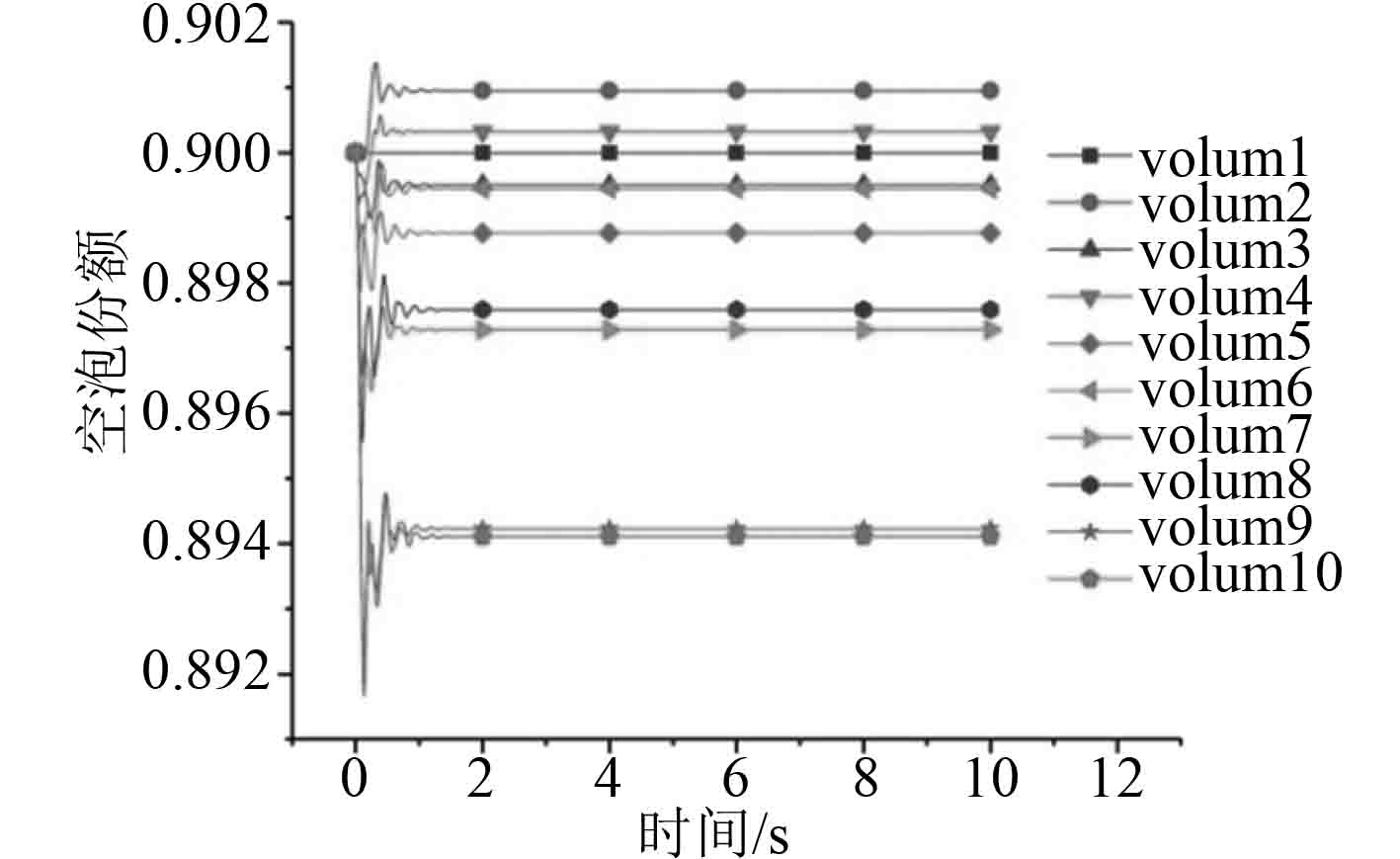
为了进一步分析相间换热系数对于相间换热的影响,对式(1)中的系数17539进行修改,通过不断减小该系数的值使得相间换热系数的值不断减少。现对水平环形雾状流,将系数17539修改为3539,3000,300进行计算,计算结果如图13~图18所示。随着相间换热系数的不断减少,程序计算越来越稳定。同时,对比图13、图15、图17可以看到,相间换热系数值对于空泡份额的计算几乎没有影响。
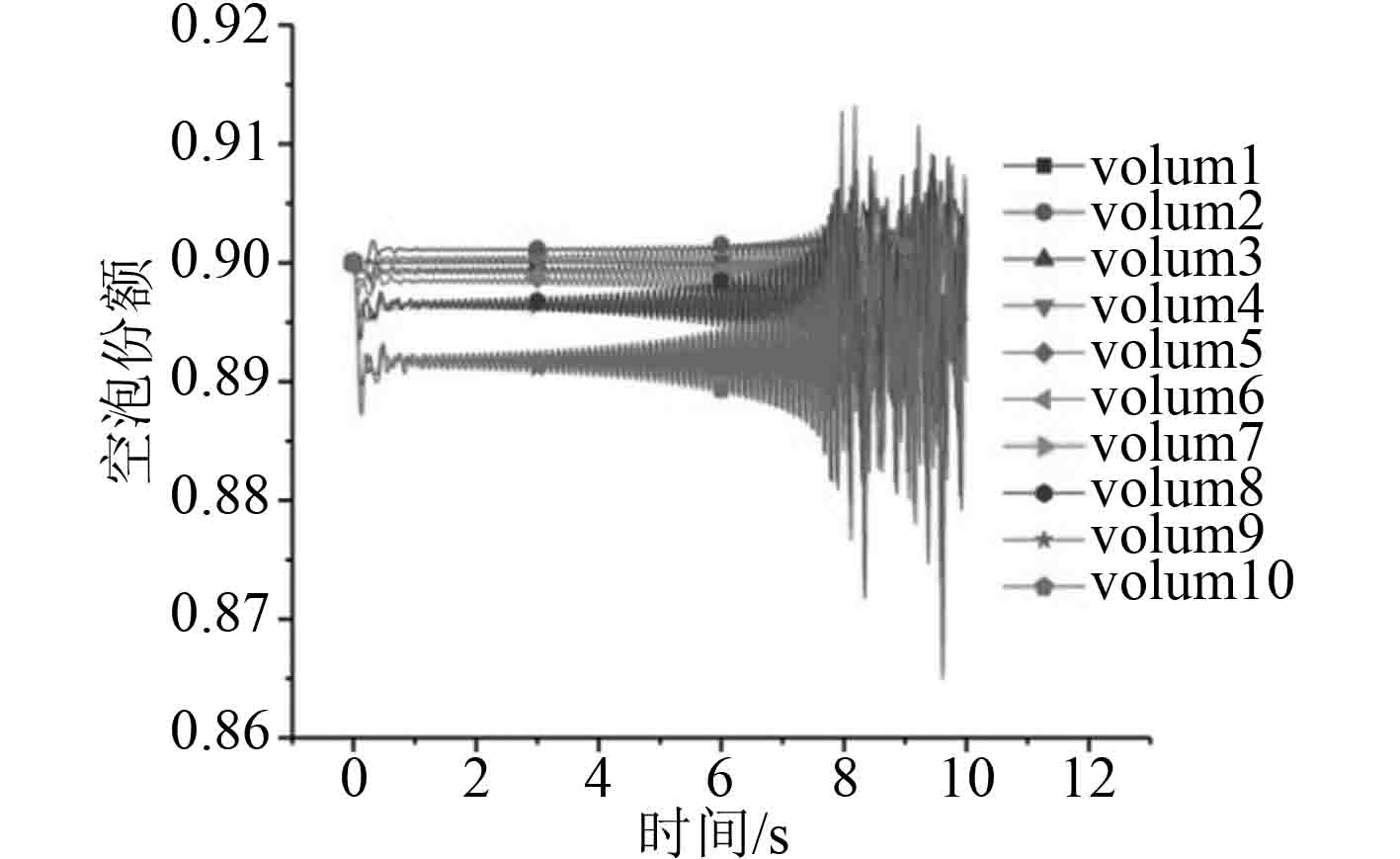
|
图 13 Hor-3539空泡分额 Fig. 13 Hor-3539 void fraction |
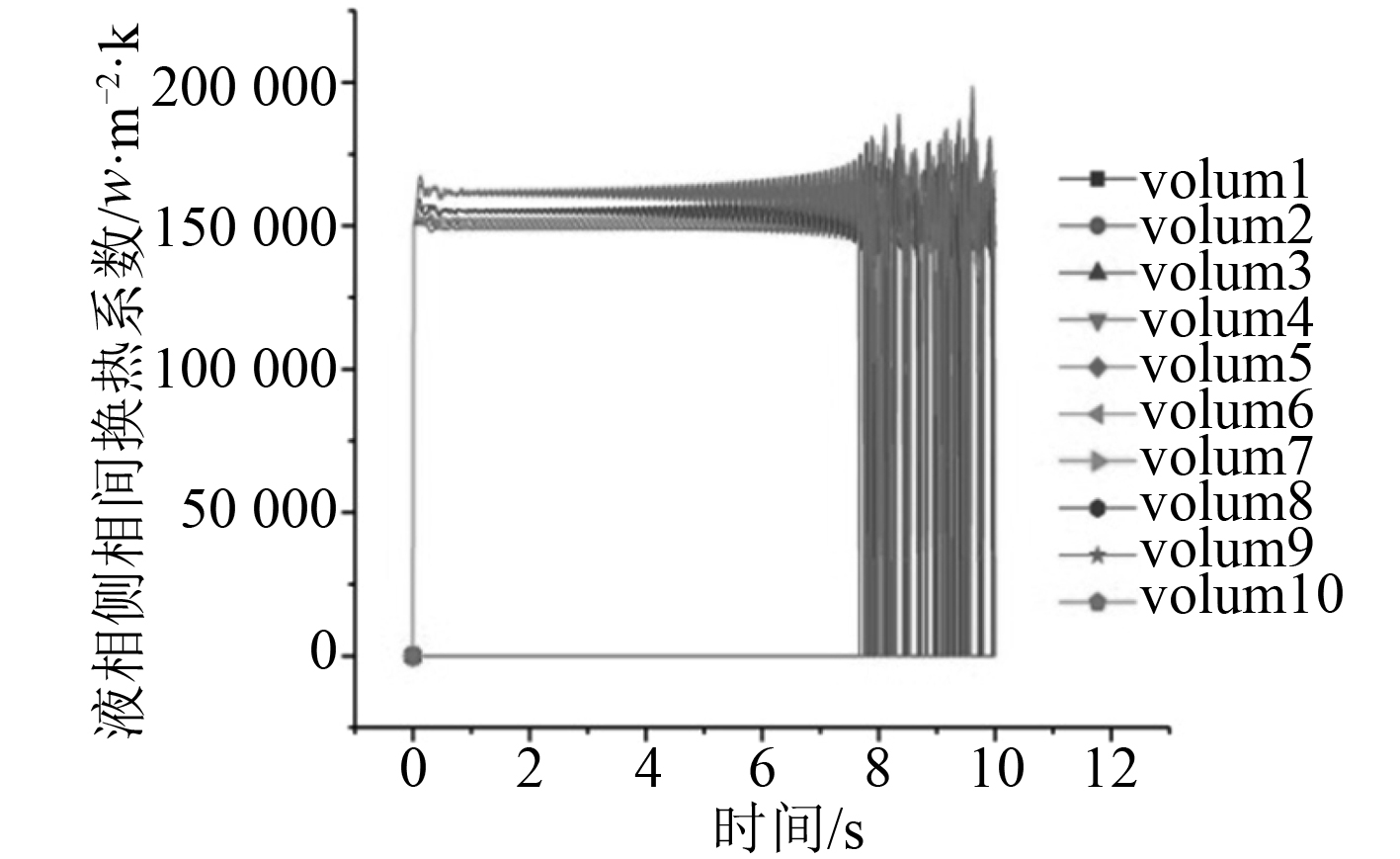
|
图 14 Hor-3539液相侧相同换热系数 Fig. 14 The same heat transfer coefficient on the side of Hor-3539 liquid phase |
|
图 15 Hor-3000空泡分额 Fig. 15 Hor-3000 void fraction |
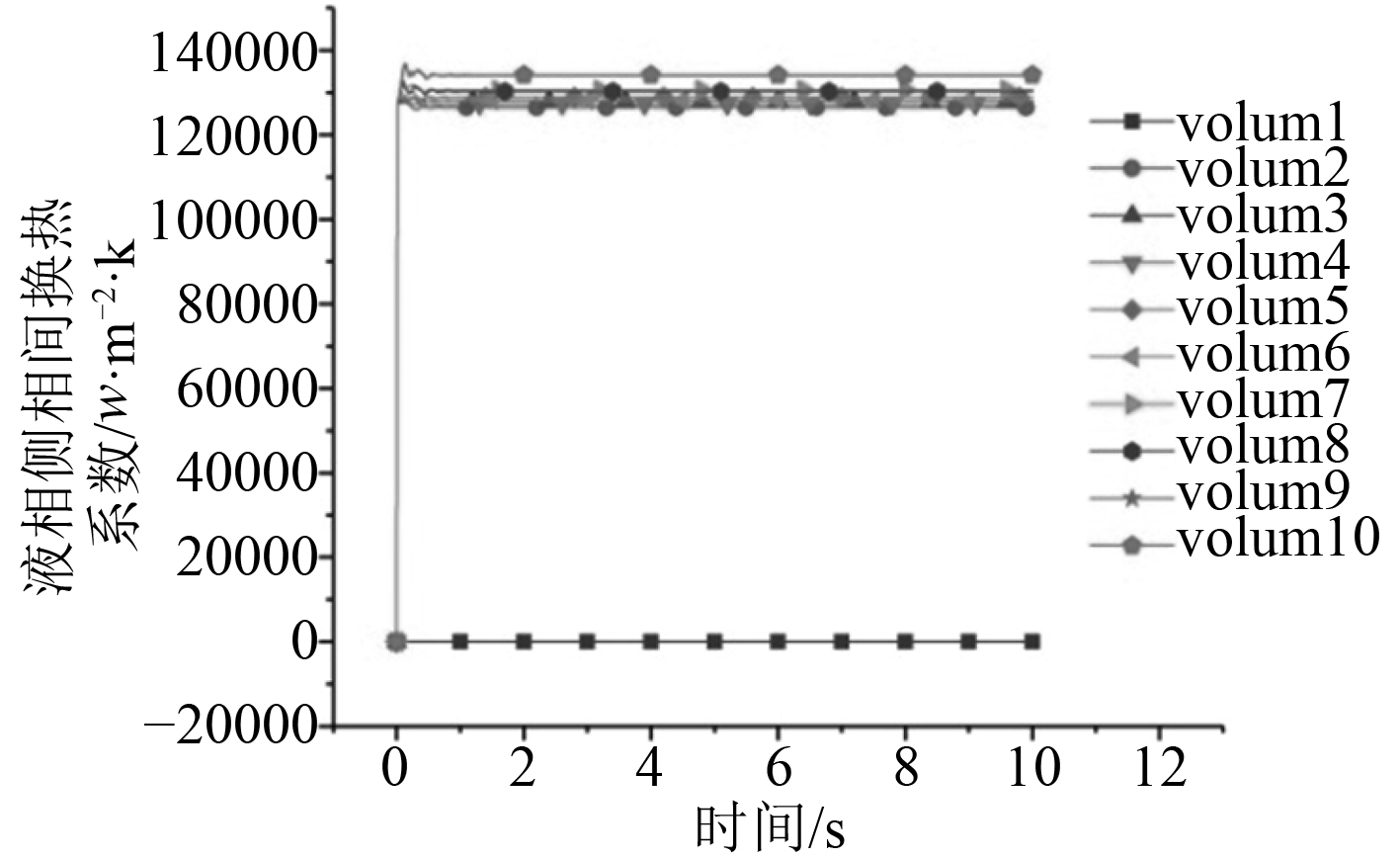
|
图 16 Hor-3000液相侧相同换热系数 Fig. 16 The same heat transfer coefficient on the side of Hor-3000 liquid phase |
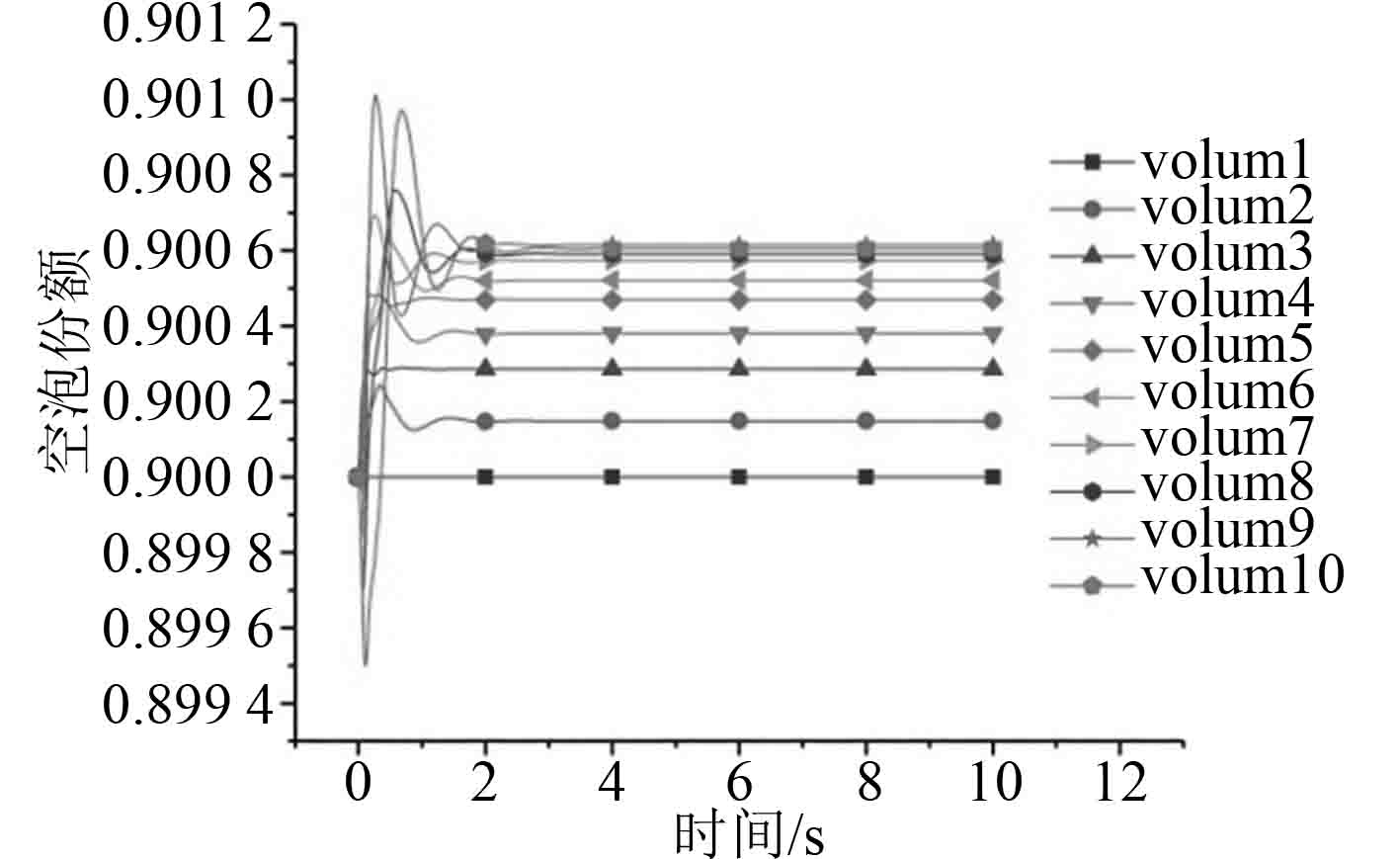
|
图 17 Hor-300空泡分额 Fig. 17 Hor-300 void fraction |
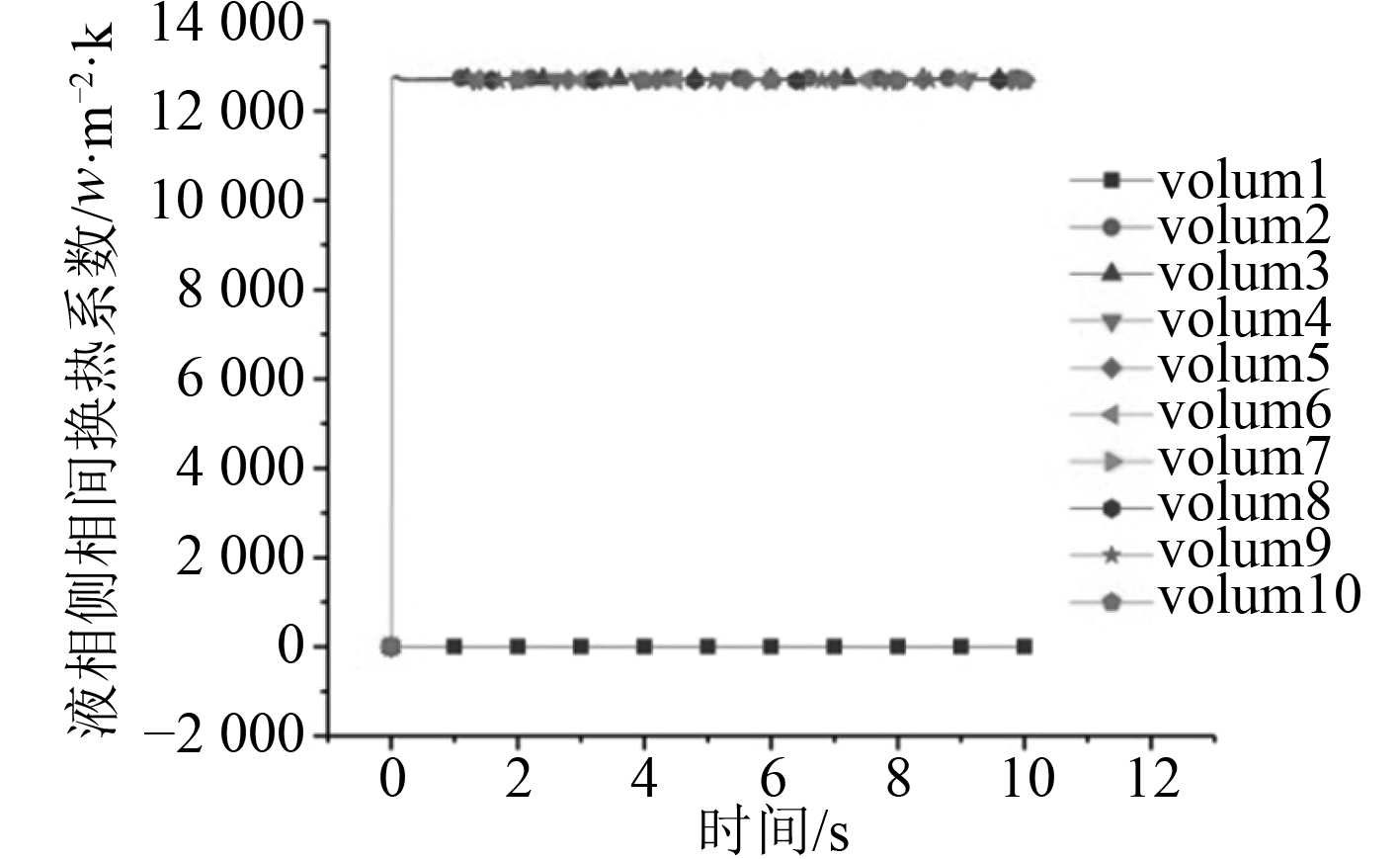
|
图 18 Hor-300液相侧相同换热系数 Fig. 18 he same heat transfer coefficient on the side of Hor-300 liquid phase |
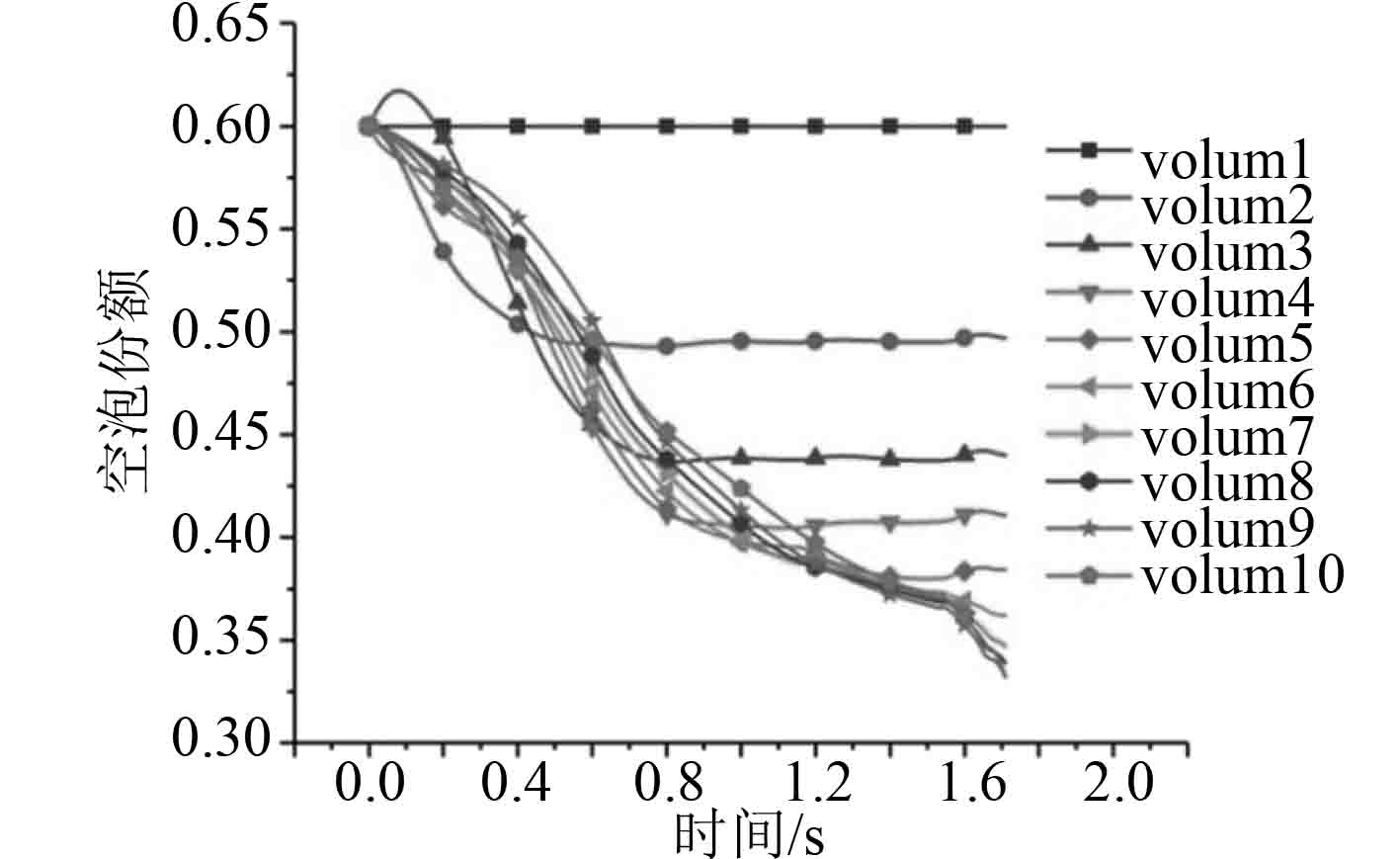
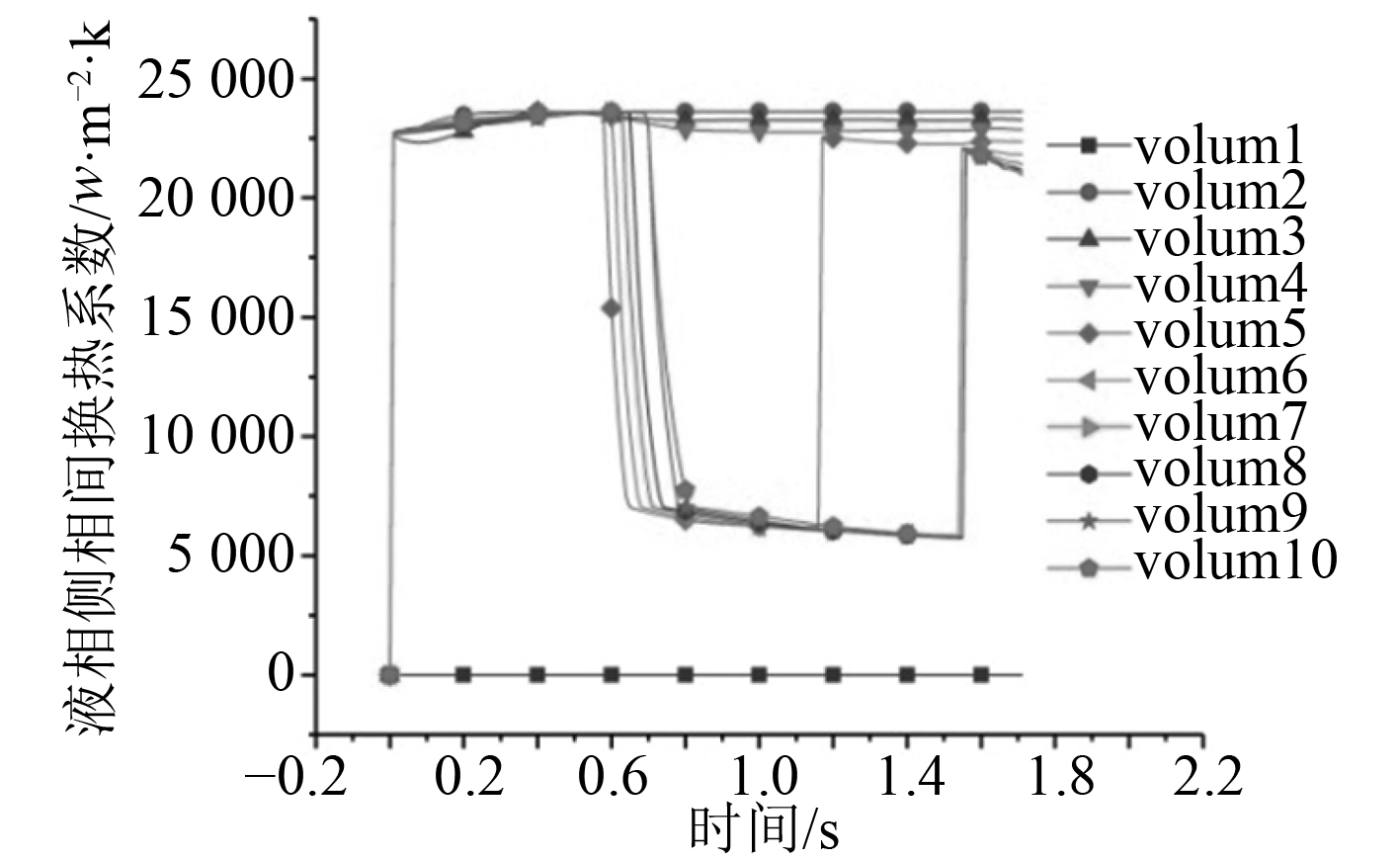
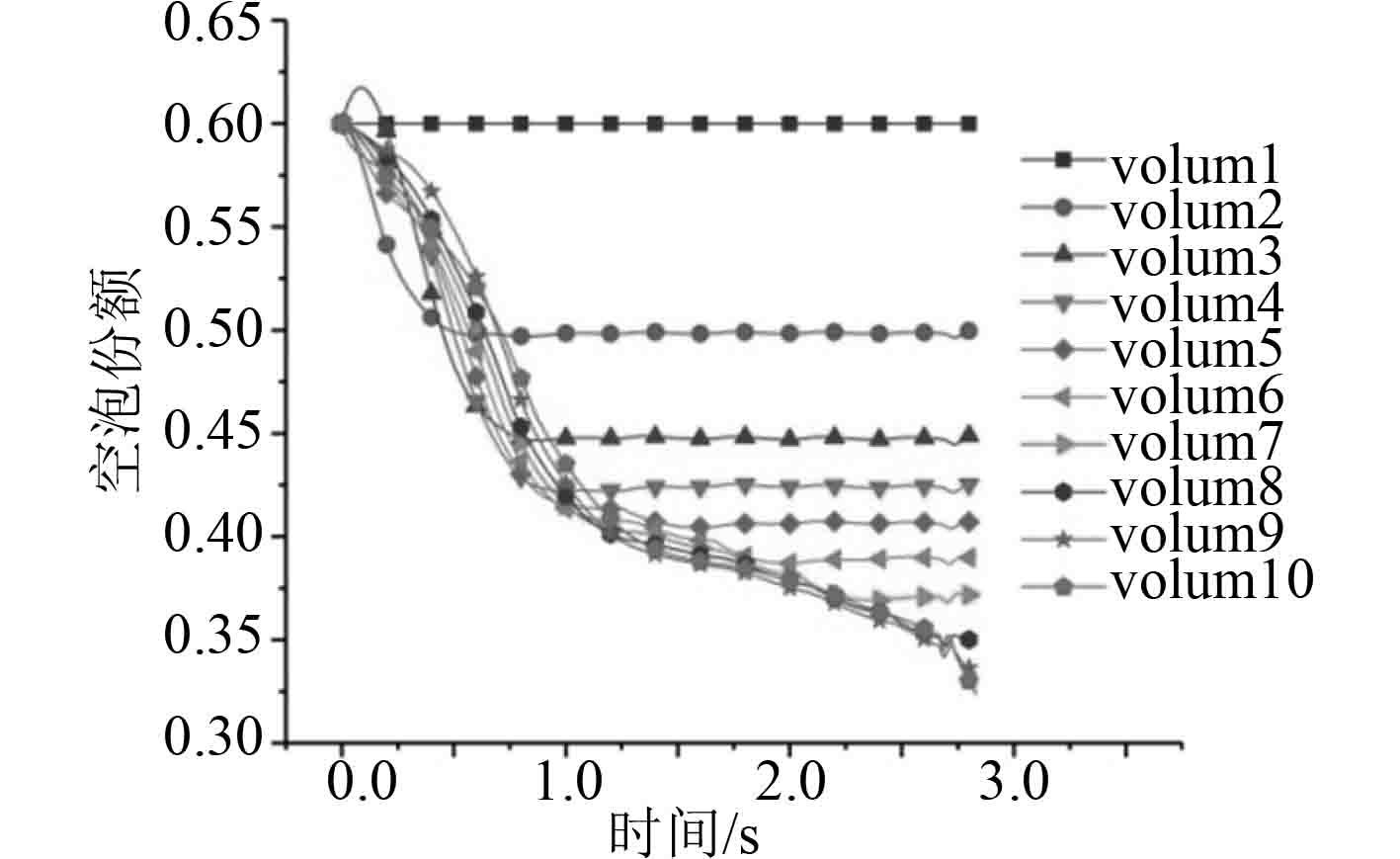
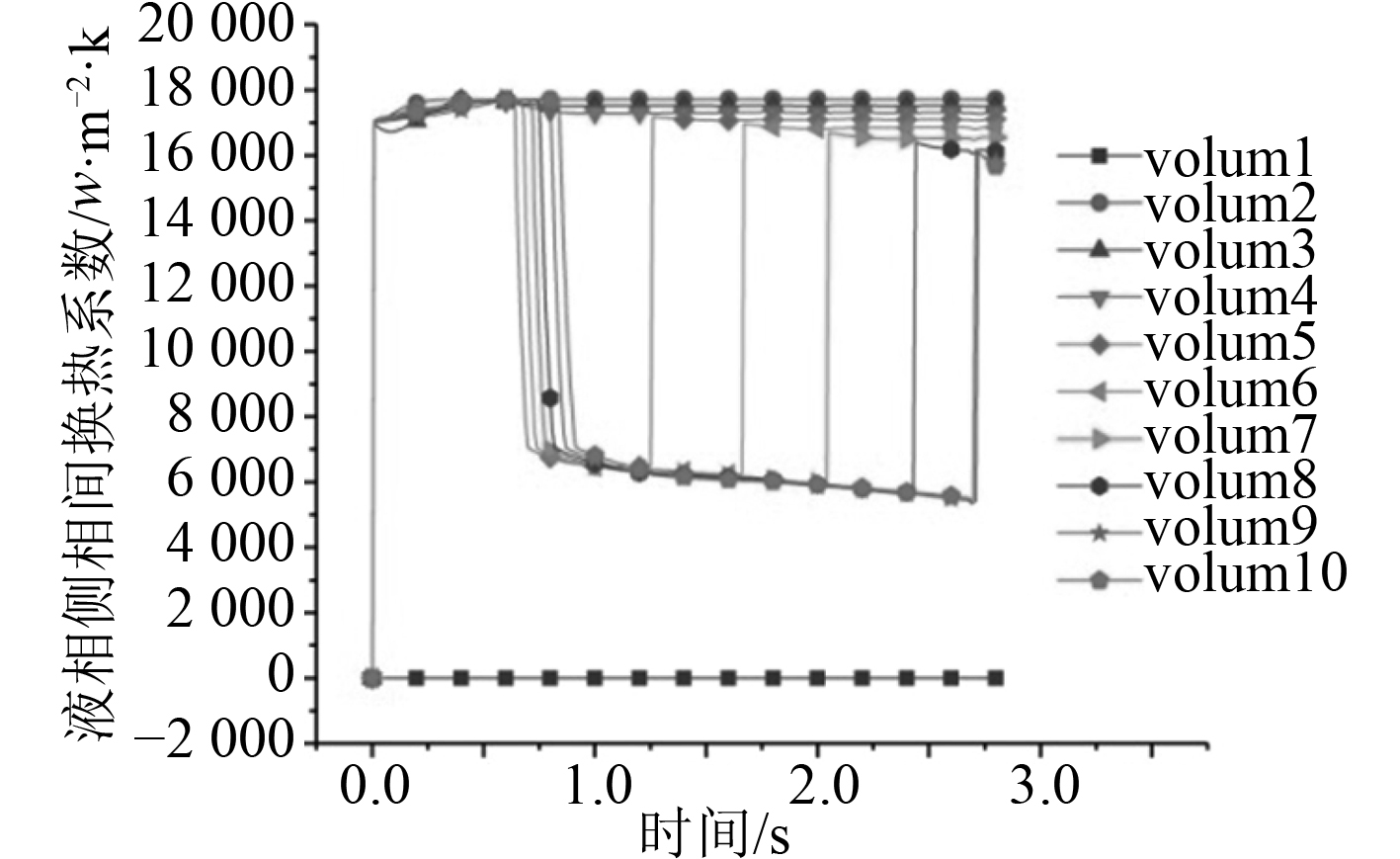
针对垂直环形雾状流,将系数17539修改为200,150,100,20进行计算,计算结果如图19~图26所示。从图20和图22可以看出,相间换热系数出现了强烈的振荡,该现象在图13和图14中更加明显。从图22~图26可以看到,当相间换热系数小到一定值后,计算趋于稳定。对比图11,图19,图21,图23,图25可以看出,相间换热系数的大小对于空泡份额的计算有很大的影响。
|
图 19 Vet-200空泡分额 Fig. 19 Vet-200 void fraction |
|
图 20 Vet-200液相侧相同换热系数 Fig. 20 The same heat transfer coefficient on the side of Vet-200 liquid phase |
|
图 21 Vet-150空泡分额 Fig. 21 Vet-150 void fraction |
|
图 22 Vet-150液相侧相同换热系数 Fig. 22 The same heat transfer coefficient on the side of Vet-150 liquid phase |
|
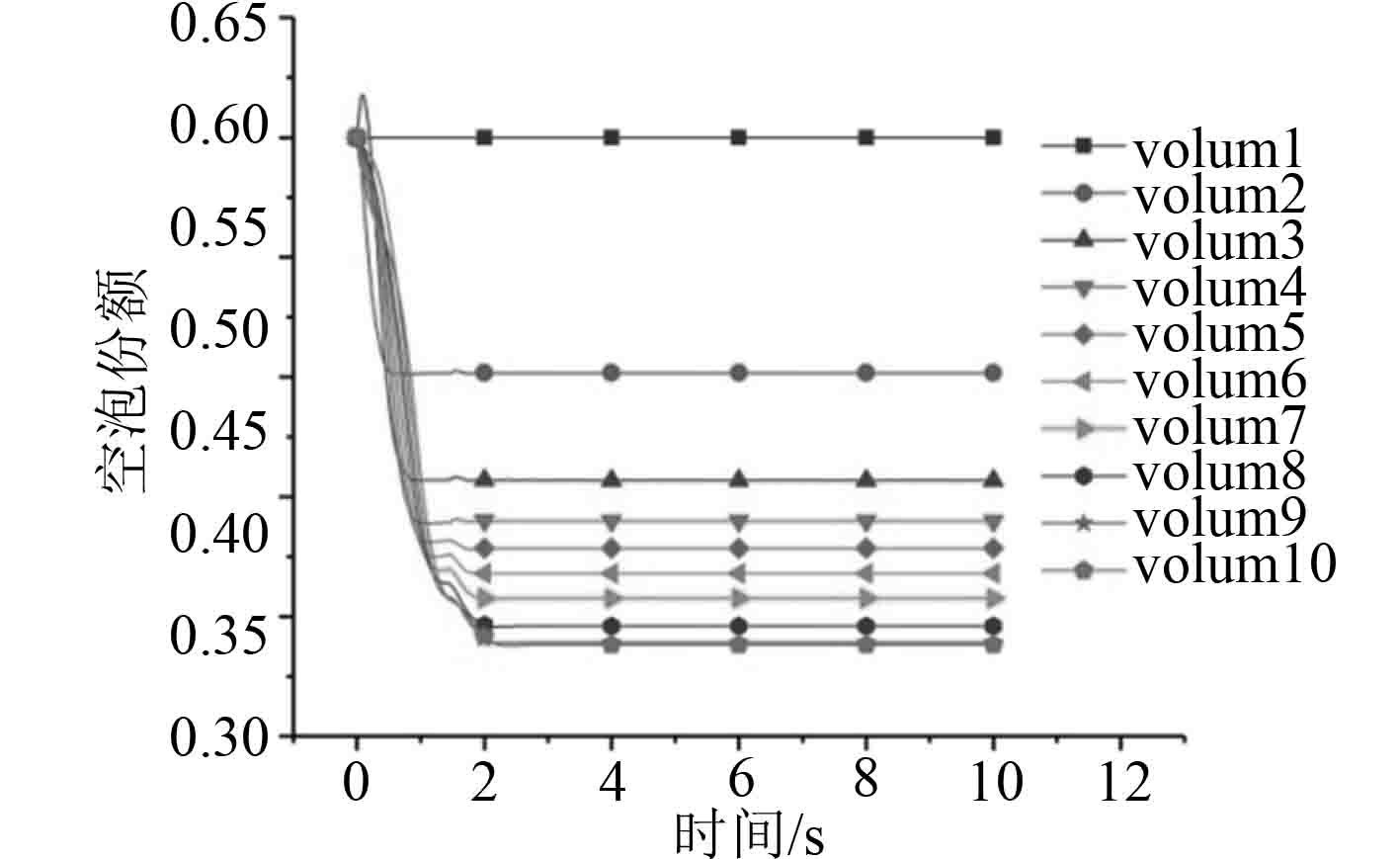
图 23 Vet-100空泡分额 Fig. 23 Vet-100 void fraction |
|
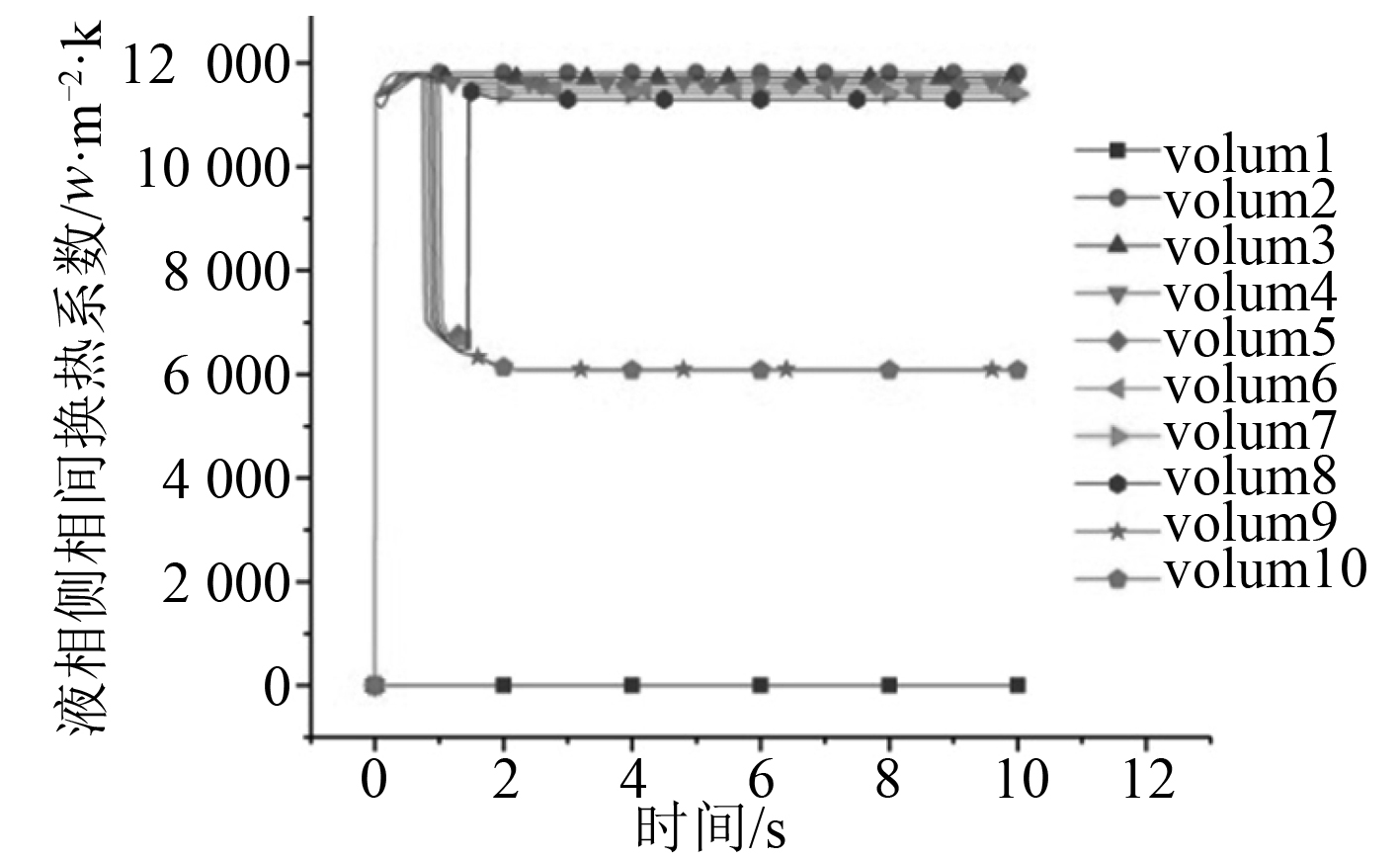
图 24 Vet-100液相侧相同换热系数 Fig. 24 The same heat transfer coefficient on the side of Vet-100 liquid phase |
|
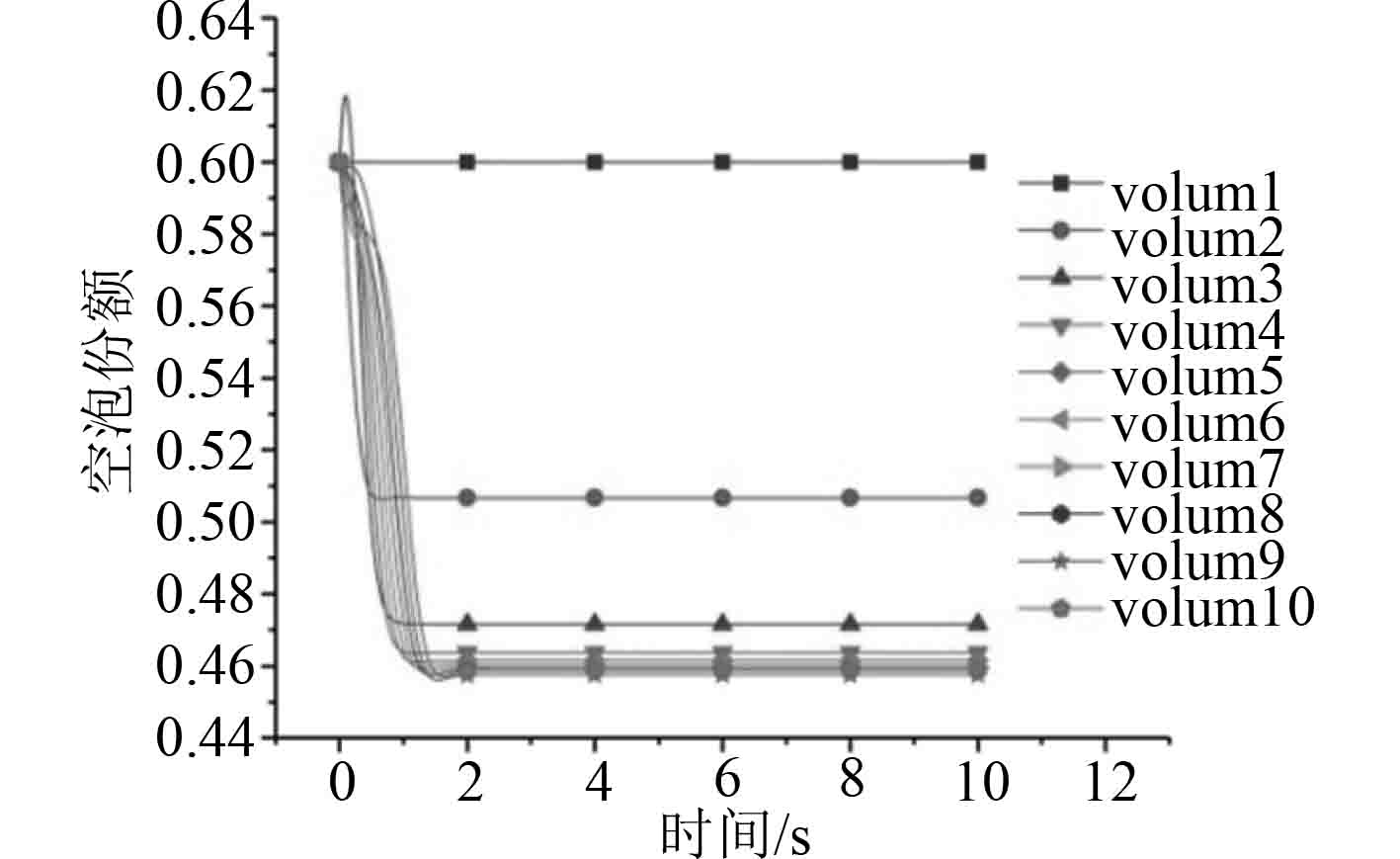
图 25 Vet-20空泡分额 Fig. 25 Vet-20 void fraction |
|
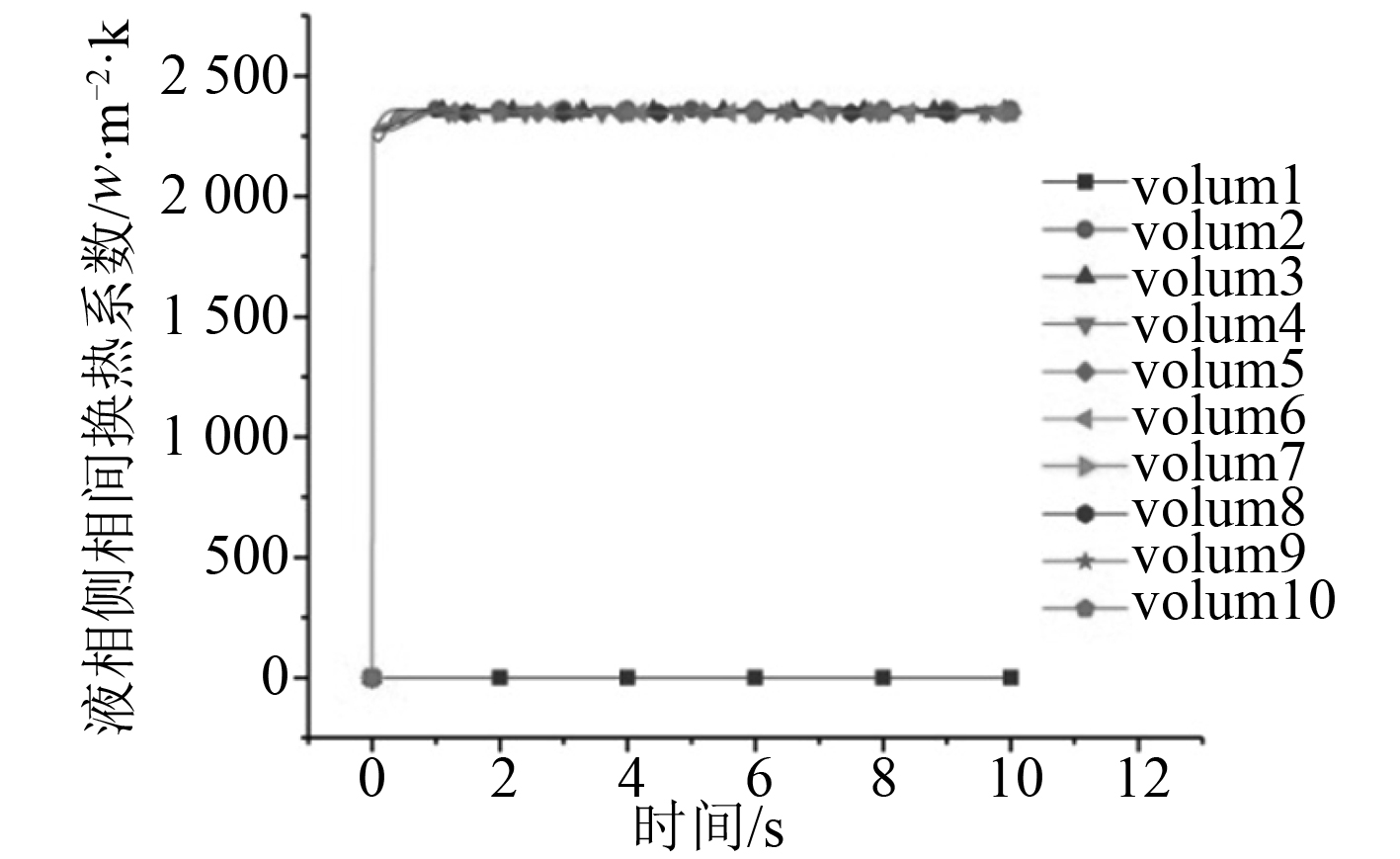
图 26 8Vet-20液相侧相同换热系数 Fig. 26 The same heat transfer coefficient on the side of Vet-20 liquid phase |
通过以上计算可以看到:
1)只采用RELAP5/MOD3.2的相间传热限制关系式(1)并不能保证两相流数值计算的稳定。
2)不同空泡份额下的计算结果表明,不同空泡份额下使得两相数值计算稳定的相间换热限制不一致,因此必须采用其他方法对相间换热系数值进行限制。
3)计算结果表明空泡份额在相间换热系数过大时导会快速变化,而图23和图25所示,在相间换热系数变小时,空泡份额变化不再剧烈,计算顺利进行。因此,可以考虑在相间传热限制关系式(1)基础上,当空泡份额变化剧烈时,对空泡分额变化率进行限制。
4)图13和图14表明,相间传热系数限制不恰当还会引起数值计算的振荡。因此有必要对相间换热系数的限制方式进一步深入研究。
| [1] |
俞冀阳, 贾宝山.反应堆热工水力学[M]. 北京: 清华大学出版社, 2011, 131−134.
|
| [2] |
冯可新, 彭敏俊, 徐宇翔. 核电站给水加热器建模仿真[J]. 原子能科学技术, 2014(2): 310-317. FENG Ke-xin, PENG Min-jun, XU Yu-xiang. Nuclear power plant feedwater heater modeling and simulation[J]. Atomic Energy Science and Technology, 2014(2): 310-317. DOI:10.7538/yzk.2014.48.02.0310 |
| [3] |
章旋, 茆荣, 曹建亭. 核电站全范围模拟机关键技术探讨[J]. 热力发电, 2011, 40(1): 16-18. ZHANG Xuan, MAO Rong, CAO Jian-ting. Discussion on key technology of full range simulator in nuclear power plant[J]. Thermal Power Generation, 2011, 40(1): 16-18. DOI:10.3969/j.issn.1002-3364.2011.01.016 |
| [4] |
林萌, 等. RELAP5作为核电站模拟器热工水力系统程序的改造[J]. 核动力工程, 2005(2): 125-129. LIN Meng, et al. RELAP5 as a nuclear power plant simulator thermal hydraulic system program transformation[J]. Nuclear Power Engineering, 2005(2): 125-129. DOI:10.3969/j.issn.0258-0926.2005.02.007 |
| [5] |
李美琳, 林萌, 杨燕华, 等. 应用于反应堆热工水力程序的核态沸腾传热关系式评价[J]. 核科学与工程, 2015(1): 36-42. LI Mei-lin, LIN Meng, YANG Yan-hua, et al. Evaluation of the relationship of nuclear state boiling heat transfer for reactor thermal hydraulic procedures[J]. Nuclear Science and Engineering, 2015(1): 36-42. |
| [6] |
LI, Y., M. LIN and Y. YANG. Coupling methods for parallel running RELAPSim codes in nuclear power plant simulation[J]. Nuclear Engineering and Design, 2016(297): 1-14. |
| [7] |
Nuclear Safety Analysis Division. RELAP5/MOD3.3 code manual volume I : Code structure, system models, and solution methods[M].US : Nuclear Regulatory Commission, 2001: 98−105.
|
| [8] |
The RELAP5 Code Development Team. RELAP5/MOD3 Code Manual[R]. NUREG/CR-5535-V1.1995: 213−215
|
 2021, Vol. 43
2021, Vol. 43
