在过去的数十年中,越来越多的国家致力于实现无人水下航行器(UUV)从试验室研究向蓝海应用的技术飞跃,使UUV凭借其具有的技术优势,在世界各国的海洋资源开发活动中正扮演着越来越重要的角色[1-2]。由于UUV通常具有航速低、航程长、低噪声、大深度的特征,从而对动力系统提出了静音、可快速启停等一系列要求,基于以上原因,蓄电池驱动的电动力系统成为现阶段UUV普遍采用的能源形式。然而,随着UUV关于航程、航速、航程等技术指标的不断提高,蓄电池在能量密度方面的技术瓶颈却迟迟无法突破[3],为UUV未来的应用前景蒙上了一层阴影。
近年来为了有效解决这一问题,行业内的众多专家纷纷致力于开发出具有高能量密度的动力形式以代替蓄电池,进一步提升UUV的工作性能。从现阶段的发展情况来看,以燃料电池为代表的新型高能量密度供电技术凭借转化效率、能量密度、循环寿命等方面的优势,被视为未来UUV使用的最佳能源形式[3-4]。然而值得注意的是,受到电化学转化速率制约,燃料电池存在响应滞后、输出特性软等缺点,若以燃料电池为系统中的唯一供能单元,将难以及时响应UUV的负载需求,还会在大幅度负载功率变化的条件下出现水淹电极、缺水,甚至催化剂中毒等极端情况,大大降低燃料电池效率、缩短燃料电池寿命,而这对执行长时间巡航任务的UUV来说是不可接受的。为了充分发挥出燃料电池的优势,许多学者对“燃料电池+能量存储装置”形式的混合动力系统进行了广泛的研究[5]。由于兼具2种能量单元的技术特点,混合系统有效弥补了过往单一能源在使用中存在的技术缺陷,极大改善了工作特性,因而被认为是未来UUV的最佳动力系统形式。
采用混合动力的UUV通常使用燃料电池作为主要能源,通过蓄电池平衡瞬时动态负载达到“削峰填谷”的效果,保证燃料电池始终工作在最优区间,从而优化系统工作特性。在这一思路下,系统需要设计出高效的能量管理策略实现混合能量单元之间的动态分配[6]。在实际应用中,为了提升控制效果,需要在算法设计过程中充分考虑负载需求、系统约束等因素,通过精确调节DCDC变换器的输出电流实现能量分配,从而保证动力系统工作在最优区间。近年来关于能量管理算法的研究百花齐放,专家学者们对诸如规则化方法[7-9]、最优化方法[10-12]、智能方法[13-14]等进行了分析对比和验证。极小值原理作为一种经典最优控制理论,最初由苏联数学家庞特里亚金提出,该方法通过将动态规划描述的约束优化转化为Hamilton无约束优化,同时将求解全局最优转化为求解局部最优[15]。从已有的研究工作中可以看到[16],相比于动态规划方法,极小值原理不需要整个航程信息作为先验知识,依靠当前时刻和过去时刻的信息就能完成局部优化问题求解,因而更适合于实时能量控制系统的开发。
1 燃料电池混合动力系统在燃料电池混合动力系统中,根据连接方式不同可分类为直接连接和间接连接。
在图1的结构中,在蓄电池和母线之间设置一个双向DCDC变换器,因此可以通过控制双向DCDC变换器对蓄电池进行充放电管理。但根据相关研究表明,这一结构虽然在母线电压调节上效果显著,但电压调节范围上却有所损失。除此之外,2个DCDC变换器的存在还使得系统无功功率增大,系统复杂度、重量及成本随之提高,这对内部空间本就狭小、重量控制精准、工作效率要求严苛的UUV使用造成了障碍。
|
图 1 间接匹配拓扑 Fig. 1 Indirect match topology |
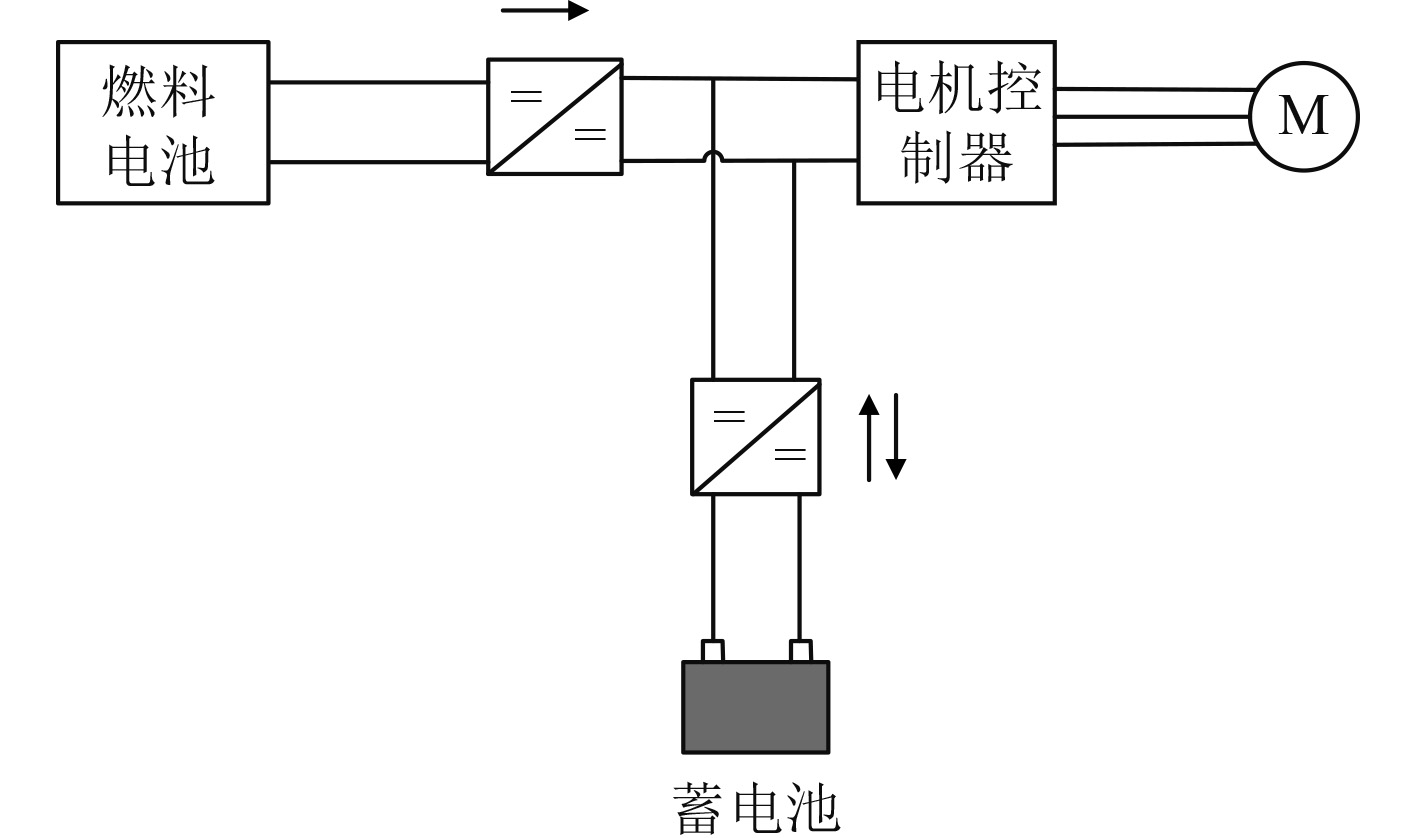
为了简化拓扑结构,提出如图2所示的拓扑结构,在这一结构中蓄电池不经过DCDC调压直接挂接在母线上,母线电压与蓄电池输出电压保持一致。该型拓扑的优势在于燃料电池能够充分发挥长时间工作的特点,平稳工作在更加高效的状态,从而延长其使用寿命[17]。同时由于只使用了一个DCDC,减小了系统的无功功率损耗,能够实现控制对象少、转换效率高的目标,更适合在UUV动力系统中进行应用。

|
图 2 直接匹配拓扑 Fig. 2 Direct match topology |
不同于大巴上使用的氢-空燃料电池,UUV上使用的氢-氧燃料电池使用纯氧作为氧化剂,因而导致其阴极内部压力分布也有所不同。此外,氢氧电堆中质子交换膜厚度增加、排水流道不同等因素会导致电堆的输出特性也有所不同[18],在建立氢-氧燃料电池的数学模型的过程中,为了简化数学运算过程,通常会对电堆做出如下合理假设[19-24]:
1)理想的气体流动过程;
2)液相流体的不可压缩流动;
3)流体流动为层流;
4)电解质、电极和双极性材料各向同性且均匀分布;
5)阳极内水蒸汽压力是饱和蒸汽压力的50%,阴极内水蒸汽压力和饱和蒸汽压力一致;
6)反应气体为纯氢、纯氧。
根据燃料电池的电化学理论,单片燃料电池的输出电压可描述为能斯特方程与活化极化、欧姆极化的差值,如下式:
| ${V_{cell}} = {E_{energy}} - {V_{act}} - {V_{ohm}}\text{,}$ | (1) |
其中的能斯特分量
| ${E_{nernst}} = \left[ \begin{split} {E_0} -& 0.85\times{10^{ - 3}}({T_{body}} - 298.15) + \\ & \frac{{R{T_{body}}}}{{2F}}\ln [{p_{{H_2}}}\times{({p_{{O_2}}})^{0.5}}] \end{split} \right]\text{,}$ | (2) |
| ${V_{act}} = - \{ {\xi _1} + {\xi _2}{T_{body}} + {\xi _3}{T_{body}}\ln {C_{{O_2}}} + {\xi _4}{T_{body}}\ln I\} \text{,}$ | (3) |
| ${C_{{H_2}}} = 9.174\times{10^{ - 7}}{p_{{H_2}}}\exp \left(\frac{{ - 77}}{{{T_{body}}}}\right)\text{,}$ | (4) |
| ${C_{{O_2}}} = 1.97\times{10^{ - 7}}{p_{{O_2}}}\exp \left(\frac{{498}}{{{T_{body}}}}\right)\text{,}$ | (5) |
| ${V_{ohm}} = I\times{R_{\operatorname{int} }}\text{,}$ | (6) |
| ${R_{\operatorname{int} }} = \frac{{{r_{mem}}\times{t_{mem}}}}{{{A_{cell}}}}\text{,}$ | (7) |
| ${r_{mem}} = \frac{{181.6[1 + 0.03J + 0.062{{({T_{body}}/303)}^2}{J^{2.5}}]}}{{[\gamma - 0.634 - 3J]\exp [4.18(({T_{body}} - 303)/{T_{body}})]}}\text{。}$ | (8) |
其中:
进一步根据热力学理论,可结合环境工作温度根据式(9)~式(11)计算出对应的饱和蒸汽压力
| $ {Log(p_{{H_2}O}^{sat}) = \left( {\begin{array}{*{20}{c}} {2.95\times{{10}^{ - 2}}({T_{body}} - 273.15) - } \\ {9.18\times{{10}^{ - 5}}{{({T_{body}} - 273.15)}^2} + } \\ {1.44\times{{10}^{ - 7}}{{({T_{body}} - 273.15)}^3} - 2.18} \end{array}} \right)\text{,}}$ | (9) |
| ${p_{{H_2}}} = 0.5p_{{H_2}O}^{sat}\left[\frac{1}{{X_{{H_2}O}^{channel}\exp \left(\dfrac{{1.653J}}{{T_{body}^{1.334}}}\right)}} - 1\right]\text{,}$ | (10) |
| ${p_{{O_2}}} = p_{{H_2}O}^{sat}\left[\frac{1}{{X_{{H_2}O}^{channel}\exp \left(\dfrac{{4.192J}}{{T_{body}^{1.334}}}\right)}} - 1\right]\text{。}$ | (11) |
根据以上分析计算可知,燃料电池输出电压可以根据以上计算得出的单片燃料电池电压
| ${V_{stack}} = {N_{cell}}\times {V_{cell}}\text{。}$ | (12) |
内阻模型是一种在蓄电池相关研究中广泛应用的数学模型,它通过将蓄电池等效为一个理想电压源和电阻的串联准确描述蓄电池的实际工作效果,其原理图如图3所示。
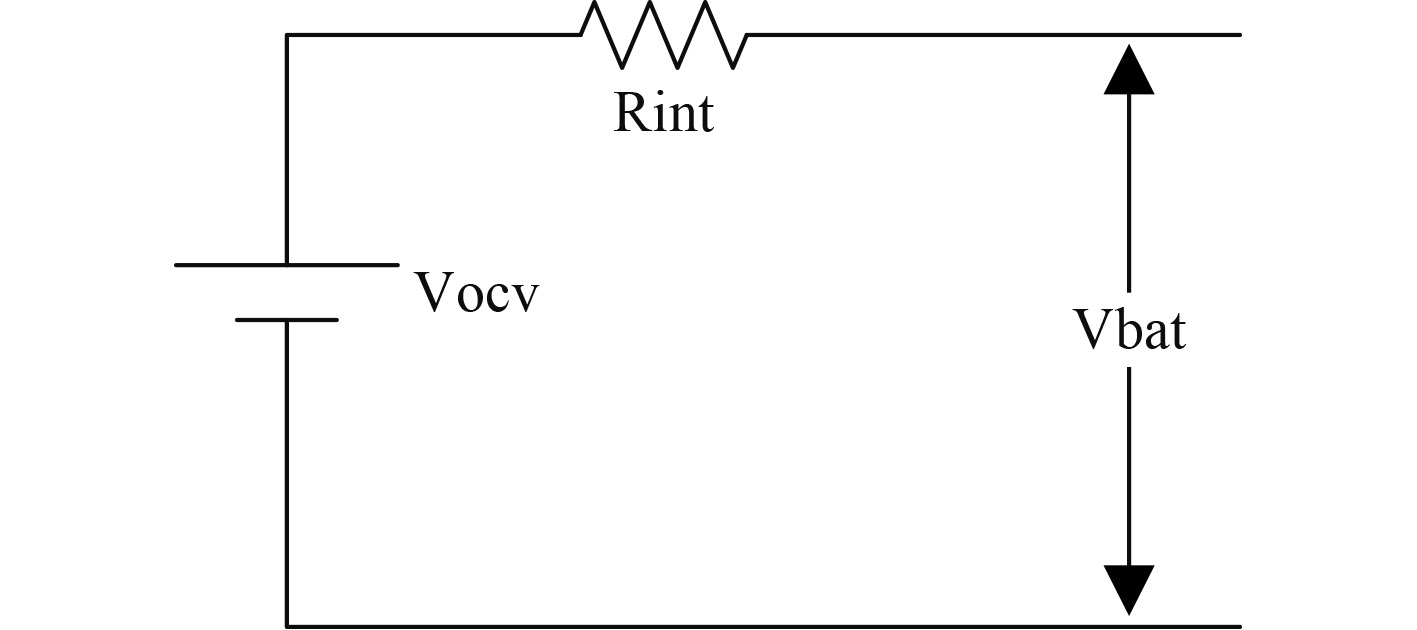
|
图 3 内阻模型 Fig. 3 Internal resistance model |
根据相关研究成果可知,蓄电池的等效内阻在充电、放电过程中是不断变化的,具体数值和电池的荷电状态(state of charge, SOC)相关。通常当蓄电池的输出功率取为P时,数学模型中对应的电流、电压可根据式(13)和式(14)求解得到:
| ${I_{bat}} = \frac{{{V_{ocv}} - \sqrt {V_{ocv}^2 - 4{R_{\operatorname{int} }}P} }}{{2{R_{\operatorname{int} }}}}\text{,}$ | (13) |
| ${V_{bat}} = {V_{ocv}} - {R_{\operatorname{int} }}{I_{bat}}\text{。}$ | (14) |
式中的蓄电池开路电压
| ${V_{ocv}} = \left\{ \begin{array}{l} {f_1}(SOC),{\rm {charg}} e \text{,} \\ {f_2}(SOC),{\rm{discharg}} e \text{,} \\ \end{array} \right.$ | (15) |
| ${R_{\operatorname{int} }} = \left\{ \begin{array}{l} {f_3}(SOC),{\rm{charg}} e \text{,} \\ {f_4}(SOC),{\rm{discharg}} e \text{。} \\ \end{array} \right.$ | (16) |
进一步分析可知,蓄电池当前时刻的SOC可由它的初始值
| $SOC = SO{C_0} - \int_0^t {\frac{{{I_{bat}}}}{{{Q_{bat}}}}{\rm d}t} \text{。}$ | (17) |
作为一项在最优控制领域得到广泛应用和充分验证的数学方法,极小值原理能够给出提供约束条件下全局最优问题的必要条件。虽然不是充分条件,但最优解必定在这些极值点当中,且满足必要条件的极值点数有限,因此可以通过对比直观的得到问题的最优解[25]。综上所述,最优问题可定义为寻找一组能够使系统方程
| $J(u) = \varPhi [x({t_f}),{t_f}] + \int_0^{{t_f}} {L[x(t),u(t),t]} {\rm d}t\text{。}$ | (18) |
式中的
| $H[x(t),u(t),\lambda (t),t] = L[x(t),u(t),t] + {\lambda ^{\rm T}}(t)f[x(t),u(t),t]\text{。}$ | (19) |
式中的Lagrange乘子
| ${\dot x^*}(t) = \frac{{\partial H}}{{\partial \lambda (t)}}[{x^*}(t),{u^*}(t),\lambda (t),t]\text{,}$ | (20) |
| $\dot \lambda (t) = - \frac{{\partial H}}{{\partial {x^*}(t)}}[{x^*}(t),{u^*}(t),\lambda (t),t]\text{,}$ | (21) |
| $H[{x^*}(t),{u^*}(t),\lambda (t),t] \leqslant H[x(t),u(t),\lambda (t),t]\text{。}$ | (22) |
极小值原理通过构建Hamilton方程将全局最优问题转化为带有等式和不等式约束的局部最优问题,因而在UUV混合动力系统的能量管理策略中,极小值方法能够快速的寻找出满足约束的极值,从而进一步筛选出能够使性能指标最小的最优解。
2.2 极小值在能量管理中的应用燃料电池汽车在工程化应用中为了尽可能降低使用成本、增加续航能力、控制系统体积,大都采用直接从外部吸入空气作为氧化剂的氢-空燃料电池。UUV作为长时间工作在水下的无人系统,无法在任务中从外部环境获取空气,因此必须使用自身携带的纯氢、纯氧为燃料电池提供所需的能量。由于UUV内部空间狭小、氢氧储量有限,因而设计出最优的能量控制策略将能大大提高系统工作效率和能量利用率,从而增大工作半径、延长续航时间。具体到混合动力系统中,可以将UUV全航程所消耗的氢气总量最小作为优化目标。由于蓄电池内阻效应的存在,其在充电-放电过程中必然存在一定的能量损失,因此在混合系统工作中应尽量减少使用燃料电池向蓄电池充电的过程,并充分合理的使用蓄电池内部储备的能量,从而降低使用的氢气总量。在本文提出的能量管理策略中,利用等效氢耗量方法将蓄电池的输出能量折算为等效的氢气消耗量,从而实现功率分配任务下的氢耗量优化。根据以上分析便可以建立起UUV能量管理系统的优化目标方程如下:
| $J = \min \sum {({{\dot m}_{bat}} + {{\dot m}_{fc}})}\text{。} $ | (23) |
同时需要满足以下约束条件:
1)SOC(0)=SOCH;
2)SOC(
3)SOCL<SOC(t)<SOCH,
4)Pbat
5)
结合系统特性和理论分析,可进一步建立起动力系统的状态方程如下:
| $\dot x = S\dot OC = - \frac{{{I_{bat}}}}{{{Q_{bat}}}}\text{。}$ | (24) |
式中:
| ${I_{bat}} = \frac{{{V_{oc}} - \sqrt {V_{oc}^2 - 4{R_{\operatorname{int} }}{P_{bat}}} }}{{2{R_{\operatorname{int} }}}}\text{。}$ | (25) |
式中:
此外,蓄电池的等效氢耗量
| ${\dot m_{bat}} = {P_{bat}}{({\eta _{chg}}{\eta _{dis}})^{ - \operatorname{sgn} ({P_{bat}})}}\text{。}$ | (26) |
在得到以上方程后,就可以构建起实时系统中完成功率调节的总体思路,即控制器在每个采样时刻把负载需求功率作为输入量,将DC/DC变换器的输出功率
| $H = {\dot m_{bat}} + {\dot m_{fc}} - \lambda *\frac{{{I_{bat}}}}{{{Q_{bat}}}}\text{。}$ | (27) |
由此就将整个航程下的全局优化问题转化为局部优化问题,而对应的电堆最优输出功率也应该满足以下条件方程:
| $S\dot OC(t) = \frac{{\partial H}}{{\partial \lambda }} = - \frac{{{V_{oc}}(SOC) - \sqrt {V_{OC}^2(SOC) - 4{R_{\operatorname{int} }}{P_{bat}}} }}{{2{R_{\operatorname{int} }}{Q_{bat}}}}\text{,}$ | (28) |
| $\dot \lambda (t) = - \frac{{\partial H}}{{\partial SOC}} = \frac{{\lambda (t)}}{{{Q_{bat}}}}\times \left(\frac{{\partial {I_{bat}}}}{{\partial {V_{oc}}}}\times \frac{{\partial {V_{oc}}}}{{\partial SOC}} + \frac{{\partial {I_{bat}}}}{{\partial {R_{\operatorname{int} }}}}\times \frac{{\partial {R_{\operatorname{int} }}}}{{\partial SOC}}\right)\text{。}$ | (29) |
通常情况下,蓄电池内阻随SOC的变化趋势要远小于输出电流随开路电压的变化趋势,因此可合理假设内阻阻值为常数,则式(29)可进一步整理得:
| $\dot \lambda (t) = {\rm{ - }}\frac{{\lambda (t)}}{{{Q_{bat}}}}\times \frac{{{I_{bat}}}}{{\sqrt {V_{oc}^2(SOC) - 4{R_{\operatorname{int} }}{P_{bat}}} }}\times \frac{{\partial {V_{oc}}}}{{\partial SOC}}\text{。}$ | (30) |
在每个采样时刻,控制器都会计算得到能够使当前时刻的Hamilton方程达到最小的最优控制量
| $P_{dc}^* = \arg \min H\text{,}$ | (31) |
由此就可以根据动力系统的负载需求功率和约束条件,求出当前时刻的最优蓄电池输出功率为:
| $ P_{bat}^* = {P_{req}} - P_{dc}^*,{P_{bat}} \in [{P_{bat,\max }},{P_{bat,\min }}]\text{。} $ | (32) |
UUV的实时在线控制系统需要计算得到当前时刻的最优控制,而不需要探寻不同时刻最优控制之间的数学关系,因此多采用数值化方法求解能量管理问题。在求解过程依据极小值方法建立的Hamilton方程时,则通常首先将最优控制问题转化为一个两点边值问题,再使用数值化方法迭代求解。作为求解差分方程问题的经典数值化方法,打靶法在很多问题求解中得到广泛应用,而对Hamilton方程应用打靶法的核心步骤就是寻找最优协变量初始值
| $\left\{ \begin{array}{l} {\lambda _i} = {\lambda _0},i = 1 \text{,} \\ {\lambda _i} = {\lambda _1} + \delta ,i = 2 \text{,} \\ {\lambda _i} = {\lambda _{i - 1}} - ({\lambda _{i - 1}} - {\lambda _{i - 2}})\times\\ \qquad \dfrac{{SO{C_{i - 1,{t_f}}} - SO{C_{{t_f}}}}}{{SO{C_{i - 1,{t_f}}} - SO{C_{i - 2,{t_f}}}}},i = 3,4,\cdots \text{。} \\ \end{array} \right.$ | (33) |
式中:
在求解过程中,蓄电池的SOC和协变量
| $SOC_i^{k + 1} = SOC_i^k + S\dot OC*\Delta t\text{,}$ | (34) |
| $\lambda _i^{k + 1} = \lambda _i^k + \dot \lambda *\Delta t\text{。}$ | (35) |
综上所述,根据每次计算偏差值就可以建立起来一套基于实时数据的数值化迭代算法。在求解过程中,每一个瞬时时刻均可以通过计算得到一个Hamilton值从而组成一个向量,而其中的最小元素所在位置对应该时刻DCDC输出功率向量中的最优功率输出值
UUV作为水下攻防系统的重要组成单元通常工作在特定的循环工况下,这时燃料电池混合动力系统就要在任务执行阶段及时满足能量和功率需求。不同于陆上行驶的车辆,UUV在功率变化通常较为温和,同时不具备利用制动装置回收能量的条件。由此可见,最优能量管理策略将会对提高UUV系统的能源利用率具有非常重要的作用。
为了充分验证基于极小值原理能量管理策略的有效性,将利用某小型UUV的典型功率曲线开展模拟计算,并对计算结果进行深入分析。观察如图4所示功率曲线可以看出,整个航程由多个周期循环组成,整个续航时长约6000 s,其中UUV在同时供应测绘、探测、航行所需的能量时,峰值功率可达到8000 W,最后混合动力系统和极小值原理的具体参数如表1所示。

|
图 4 负载功率循环曲线 Fig. 4 Load power cycling curves |
|
|
表 1 系统参数 Tab.1 System parameters |
从图5~图7所展示的变化曲线可以清晰看出,随着协变量初值
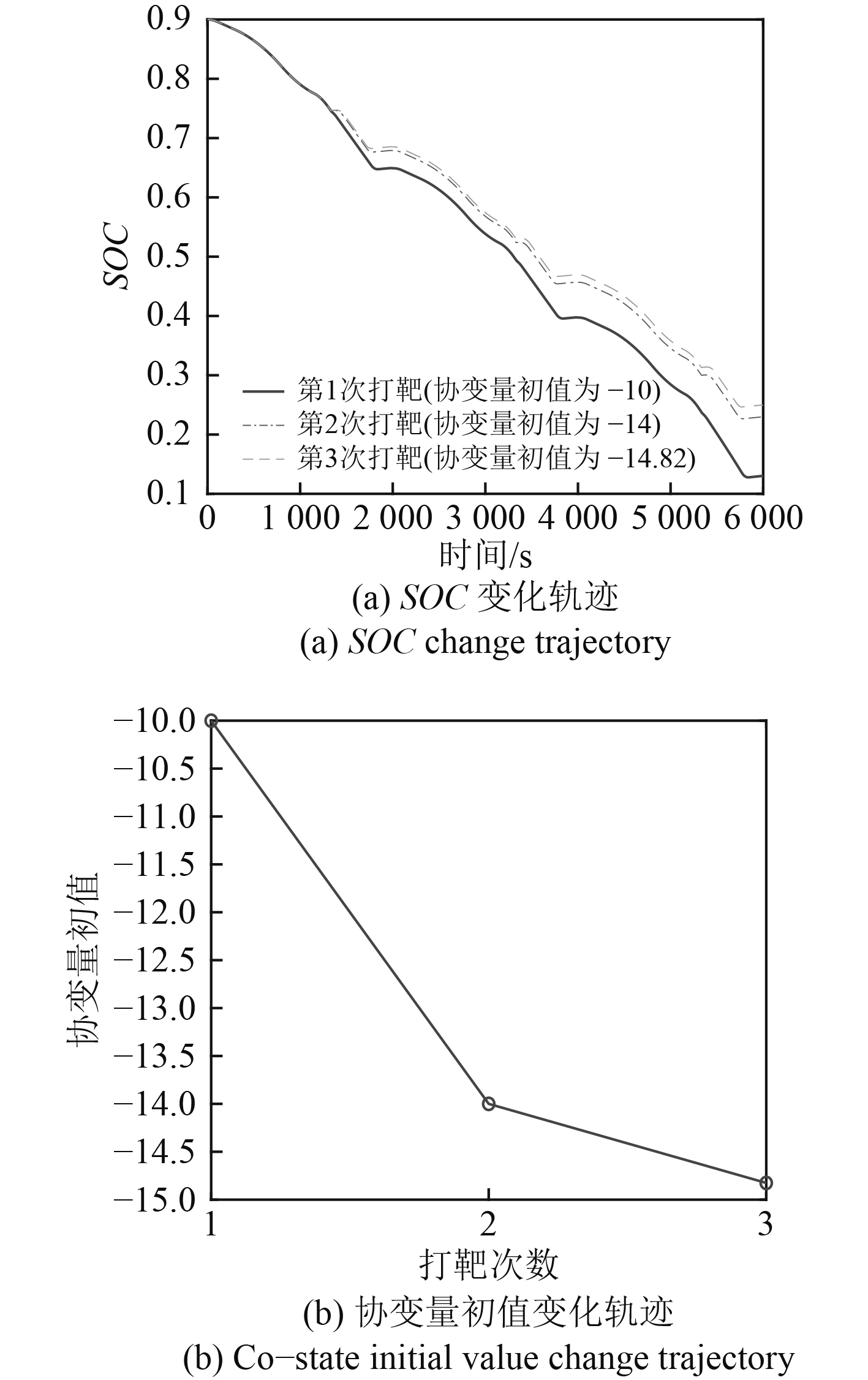
|
图 5 协变量初值 Fig. 5 Co-state initial value |

|
图 6 协变量初值 Fig. 6 Co-state initial value |
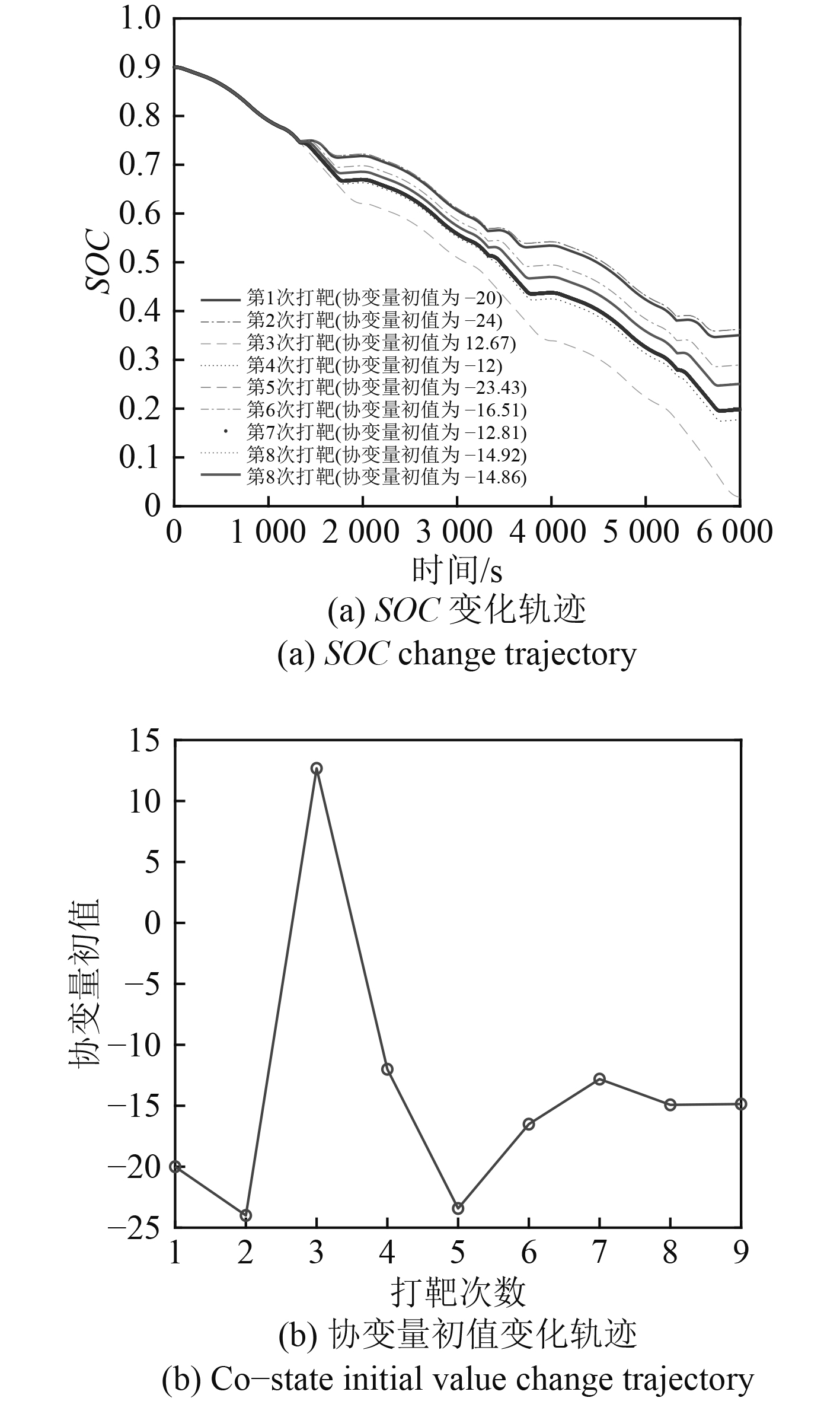
|
图 7 协变量初值 Fig. 7 Co-state initial value |
从仿真计算结果可以看到,本文建立的极小值控制算法能够精确控制UUV航行任务过程中的能量分配,从而使得蓄电池SOC从初始状态持续下降至允许范围内的最小值。正是由于在航行过程中充分利用了蓄电池内部存储的能量,相应减少了燃料电池的工作变化频次和工作总时长。由于蓄电池在输出同等功率或能量时的等效氢耗量低于燃料电池,因此系统的等效总消耗量得到了有效控制。
进一步来看,图5~图7所示的打靶过程尽管初始协变量不同,但是最终都收敛至最优协变量所处的某个邻域内(

|
图 8 协变量最优轨迹 Fig. 8 Optimal co-state trajectory |
本文从燃料电池的输出特性入手,对极小值原理在混合动力系统的能量管理领域的应用进行了分析,以实现等效氢耗量最小为目标,通过建立Hamilton方程求出了满足约束条件的最优能量数值解计算方法。为了验证方法的可行性,在报告最后利用某小型UUV典型功率负载曲线完成了模拟计算,结果显示提出的能量控制策略能够实现在线实时能量最有分配,使得系统的等效氢气消耗量最小化,蓄电池SOC达到预期值。
1)针对UUV工作场景的特征,分析氢氧燃料电池和氢空燃料电池工作特性差异,提出了将等效氢耗量作为混合动力系统能量管理的优化方向;
2)在分析极小值原理的数学特性后,将UUV能量管理系统的约束优化问题转化为Hamilton方程,从而把求解全局最优解转变为求解局部最优解,为实现在线能量控制提供了可能;
3)针对实时系统中解析解不利于计算的缺陷,提出了使用数值化方法求解Hamilton方程的思路。算法将SOC作为目标量,蓄电池输出电流作为控制量,通过使用数值优化方法迭代优化协变量初始值,最终求解出最优协变量初值和轨迹,实现UUV上不同能量单元之间的实时最优能量调节。
极小值原理的应用大大提高了系统的能量转换效率,而且改变了以往动态规划法或神经网络法不适用于实时系统的不足,可用于未来UUV混合动力系统的能量管理开发。
| [1] |
钱东, 赵江, 杨芸. 军用UUV发展方向与趋势(上)−美军用无人系统发展规划分析解读[J]. 水下无人系统学报, 2017, 25(2): 1-30. QIAN D, ZHAO J, YANG Y. Development trend of military UUV(I): A review of U. S. military unmanned system development plan[J]. Journal of Unmanned Undersea Systems, 2017, 25(2): 1-30. |
| [2] |
陈强, 张林根. 美国军用UUV现状及发展趋势分析[J]. 舰船科学技术, 2010, 32(7): 129-134. CHEN Q, ZHANG G L. Analysis of current situational development trend of US military UUV[J]. Ship science and technology, 2010, 32(7): 129-134. DOI:10.3404/j.issn.1672-7649.2010.07.026 |
| [3] |
严浙平, 吴越媛. UUV闭式循环燃料电池系统与推进功率匹配控制[J]. 化工学报, 2011, 62(1): 170-178. YAN Z P, WU Y Y. Control strategy for power matching between closed-loop circulation fuel cell system and UUV propulsion system[J]. Journal of Chemical Industry and Engineering(CHINA), 2011, 62(1): 170-178. |
| [4] |
ALAAELDEEN M. E. Ahmed, DUAN Wen-yang. Over on the development of Autonomous underwater vehicles (AUVS). Journal of ship mechanics, 2016, 20(6): 768−787.
|
| [5] |
贾同国, 王银山与李志伟, 氢能源发展研究现状. 节能技术, 2011.29(3): 第264−267页.
|
| [6] |
陈龙, 王晓亮, 盘朝奉, 等. 燃料电池混合动力车能量管理策略研究[J]. 重庆交通大学学报(自然科学版), 2014, 33(1): 149-152. CHEN L, WANG X L, PAN Z F, et al. Energy management strategy for fuel cell hybrid electric vehicles[J]. Journal of Chongqing Jiaotong University(Natural Sciences), 2014, 33(1): 149-152. |
| [7] |
SCHOUTEN NJ, SALMAN MA, KHEIR NA. Fuzzy logic control for parallel hybrid vehicles[J]. IEEE T Contr Syst T 2002, 10(3): 460e8.
|
| [8] |
YAN F, WANG J. Hybrid electric vehicle model predictive control torque-split strategy incorporating engine transient characteristics. IEEE T Veh Technol 2012, 61(6): 2458−67.
|
| [9] |
周雅夫, 连静, 李启迪. ISG混合动力电动汽车控制策略研究[J]. 仪器仪表学报, 2009, 6(30): 1164-1168. ZHOU Y F, LIAN J, LI Q D. Control strategy of integrated starter/generator hybrid electric vehicle[J]. Chinese Journal of Scientific Instrument, 2009, 6(30): 1164-1168. |
| [10] |
XU L, LI J, HUA J, LI X, OUYANG M. Optimal vehicle control strategy of a fuel cell/battery hybrid city bus. Int J Hydrogen Energy 2009, 34: 7323−33.
|
| [11] |
PAGANELLI G, DELPRAT S, GUERRA TM, RIMAUX J, SANTIN JJ. Equivalent consumption minimization strategy for parallel hybrid powertrains[C]//In: IEEE vehicular technology conference, Birmingham Al, US 2002, May 6−9. p. 2076−81.
|
| [12] |
SCIARRETTA A, BACK M, GUZZELLA L. Optimal control of parallel hybrid electric vehicles[J]. IEEE T Control System 2004, 12(3): 352−63.
|
| [13] |
ZHANG Xiaohui, LIU Li , DAI Yueling, et al. Experimental investigation on the online fuzzy energy management of hybrid fuel cell/battery power system for UAVs. International journal of hydrogen energy, 43(2018): 10094−10103.
|
| [14] |
MOHAMMADIAN M, TAGHI BATHAEE SM, MEHDI ANSAREY MSM. Neuro-genetic energy management for hybrid fuel cell power train. In: IEEE conference on cybernetics and intelligent systems, Singapore 2004, Dec 1−3: 1043−1048.
|
| [15] |
HOU C, OUYANG M, XU L, et al. Approximate Pontryagin′s minimum principle applied to the energy management of plug-in hybrid electric vehicles[J]. Applied Energy, 2014, 115: 174−189.
|
| [16] |
隗寒冰, 刘小飞, 彭志远. 考虑发动机排气背压阈值的柴电混合动力汽车最优控制[J]. 控制理论与应用, 2017, 4(34): 533-540. HUAI H B, LIU X F, PENG Z Y. The optimal control of plug-in diesel hybrid electric vehicle with considering the threshold of exhaust back pressure[J]. Control Theory & Applications, 2017, 4(34): 533-540. |
| [17] |
徐梁飞, 李相俊, 华剑锋, 等. 燃料电池混合动力参数辨识及整车控制策略优化[J]. 机械工程学报, 2009, 45(2): 56-61. XU L F, LI X J, HUA J F, et al. Parameter identification and control strategy optimization of hybrid fuel cell powertrain[J]. Journal of mechanical engineering, 2009, 45(2): 56-61. DOI:10.3901/JME.2009.02.056 |
| [18] |
LEE Chien-Hsing, YANG Jian-Ting. Modeling of the Ballard-Mark-V proton exchange membrane fuel cell with power converters for applications in autonomous underwater vehicles[J]. Journal of Power Sources, 196(2011): 3810−3823.
|
| [19] |
WANG C , NEHRIR M H , SHAW S R. Dynamic models and model validation for PEM fuel cells using electrical circuits[J]. IEEE Transactions on Energy Conversion, 2005, 20(2): 442−451.
|
| [20] |
AMPHLETT, J. C. Performance Modeling of the Ballard Mark IV Solid Polymer Electrolyte Fuel Cell[J]. Journal of The Electrochemical Society, 1995, 142(1): 9.
|
| [21] |
Amphlett J C, Mann R F, B. A. Peppley, et al. A model predicting transient responses of proton exchange membrane fuel cells. Journal of Power Sources, 1996, 61(1-2): 183−188.
|
| [22] |
KHAN M J, IQBAL M T. Dynamic modelling and simulation of a fuel cell generator[J]. Fuel Cells, 2005, 5(1): 97-104.
|
| [23] |
NGUYEN, T. V, WHITE R. E. A water and heat management model for proton Exchange-Membrane fuel cells[J]. Journal of the Electrochemical Society, 140, 2178-2186.
|
| [24] |
ROWE A , LI X. Mathematical modeling of proton exchange membrane fuel cells[J]. Journal of Power Sources, 2001, 102(1−2): 82−96.
|
| [25] |
秦大同, 曾育平, 苏岭, 等. 基于近似极小值原理的插电式混合动力汽车实时控制策略[J]. 机械工程学报, 2015, 51(2): 134-140. QIN D T, ZENG Y P, SU L, et al. Plug-in hybrid vehicle’s real-time control strategy based on approximate Pontryagin’s minimum principle[J]. Journal of Mechanical Engineering, 2015, 51(2): 134-140. DOI:10.3901/JME.2015.02.134 |
 2021, Vol. 43
2021, Vol. 43
