船舶噪声主要由机械噪声、推进系统噪声和水动力噪声3部分叠加而成[1]。随着机械设备隔振技术和低噪声推进器的快速发展,船舶低速航行时,推进系统噪声和水动力噪声可以得到有效抑制,机械噪声便成了主要声源,直接影响静音型水面舰船、潜艇的声隐身性能。船舶海水冷却系统流量大、两端直接与海洋环境相通,是机械噪声的重要组成部分,海水系统中泵、阀等元件的机械振动不仅沿着管壁结构经支吊架传递至船结构,还会沿着管内的水介质经通海口直接向舷外辐射噪声,传递路径相对复杂,控制难度大。近年来,减振接管[2]、管路弹性支吊架[3]的广泛应用极大地改善了管系向船体的振动传递,而通过管内水介质传递通道引起的声辐射已经成为海水管路噪声控制的重点。董自虎等[4]利用Fluent软件对船用通海阀内流场进行了仿真计算,根据其可视化结果分析了影响通海阀性能和产生噪声的原因,并提出了改进模型。张冠军[5]以双层加筋板为对象,应用(FEM/BEM)方法和FEM/AML方法,对水下结构物的辐射噪声进行了分析对比,验证了FEM/AML直接声振耦合计算方法的准确性及高效性。
海水冷却系统噪声主要由流体脉动力产生的流噪声和海水泵等相连设备的工作噪声组成,设备工作噪声工程上主要通过提高严控设备指标,提高选型要求来改善。本文采用基于Helmholtz方程的FEM/AML方法,以船舶海水冷却系统舷侧阀出口管路为对象,针对其额定工作状态下的流噪声进行预报研究,并对比不同舷侧阀水下深度、出口管径对流噪声的影响,为海水冷却系统的降噪设计指明方向。
1 控制方程有限元法(FEM)求解流噪声的思路是对Helmholtz方程进行数值求解[6]。在流体域中任何位置
| $ {\nabla }^{2}{p}\left({x},{y},{z}\right)+{{k}}^{2}\cdot {p}\left({x},{y},{z}\right)=-{j}{{\rho }}_{0}{{\omega}}\cdot {q}\left({x},{y},{z}\right) \text{。}$ | (1) |
式中:q为频率ω=2πf的源项分布;k=ω/c=2πf为声波数;ρ0是环境流体质量密度。边界条件满足:
1)压力边界条件
| $ p=\stackrel-p \text{,}$ | (2) |
2)法向速度边界条件Ων
| $ {\rm{\nu }}_n=\frac{j}{{\rm{\rho }}_{0}\rm{\omega }}\frac{\partial p}{\partial n}={\overline{\rm{\nu }}}_n\text{,} $ | (3) |
3)法向阻抗条件
| $ p=\overline{\rm{Z}}\cdot {\rm{\nu }}_n=\frac{{j}\overline{\rm{Z}}}{{\rm{\rho }}_{0}\rm{\omega }}\frac{\partial {p}}{\partial {n}} \text{。}$ | (4) |
式中:
有限元法可以真实地模拟声场的低频波动特性,进行全域计算,相对于边界元法结果更加准确,在求解内声场和声辐射方面有极大的优势[7]。
自动匹配层方法(AML)[7]是在完美匹配层(AML)基础上发展而来。PML方法在结构物表面的有限元声学网格上建立一种有限元匹配层,运用有限元方法对该匹配层离散插值,解析传导到该匹配层上的声压数据。根据结构物形状不同,采用PML方法手动建立合适模型的工作量巨大,AML方法的出现,只需指定结构物有限元声学网格的AML属性及匹配层厚度,在声学网格与计算域之间会自动生成完美匹配层。AML方法不仅大大减少了建立有限元模型的工作量,亦能根据计算频率的要求,生成网格尺寸大小合适的有限元匹配层。对于计算水下结构物在流场中的低频声学特性,AML方法速度更快,效率更高。
2 计算模型及方法 2.1 计算模型某船机舱右舷海水冷却舷侧阀管路如图1所示,舷侧阀出口位置水线下1000 mm。

|
图 1 海水冷却舷侧阀管路图 Fig. 1 The piping diagram of SW system |
柴油发电机冷却水和主机冷却水出口合并后从舷侧阀排出,各设备流量、管径等参数如表1所示。
|
|
表 1 冷却系统参数表 Tab.1 The data table of SW system |
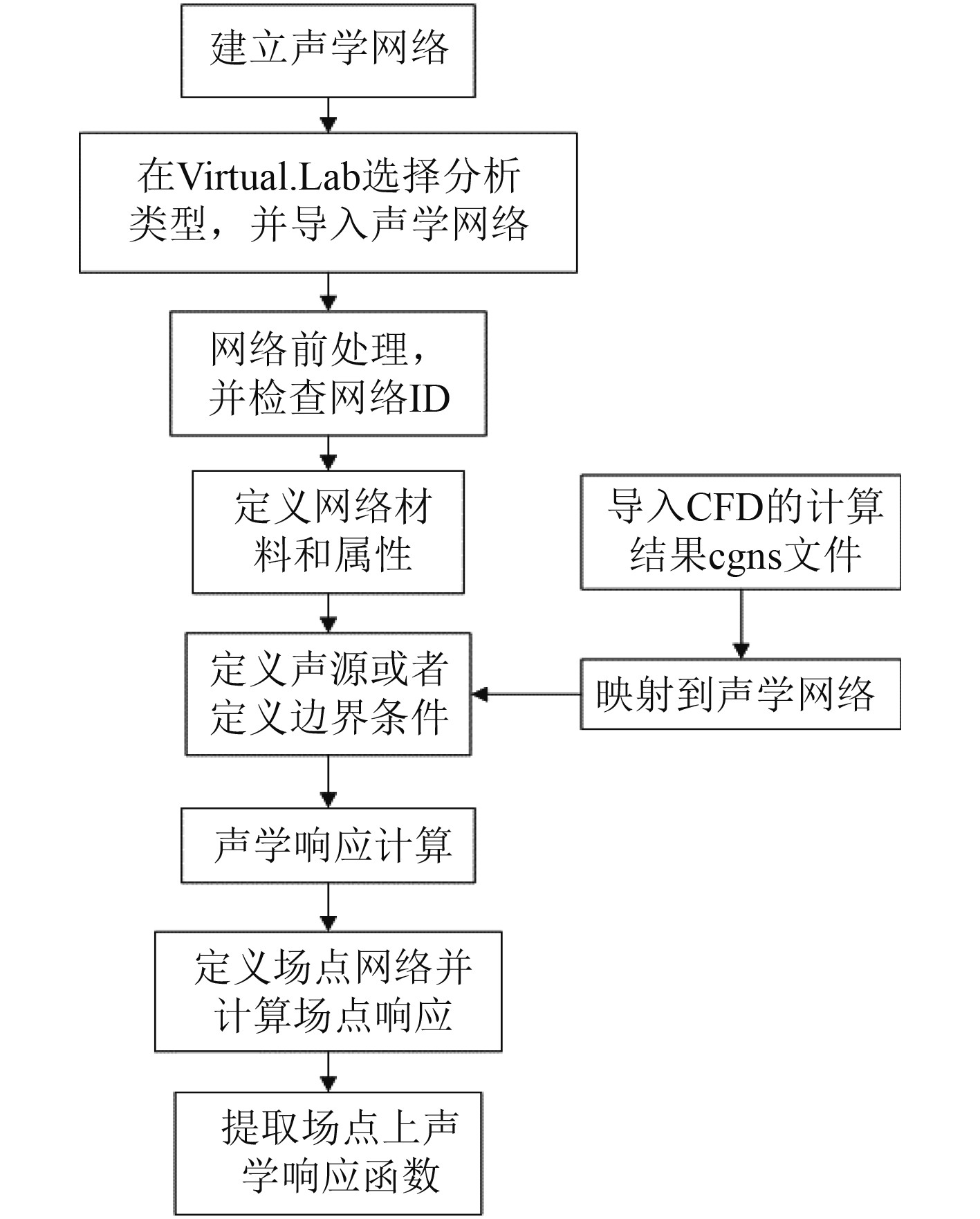
通过Fluent对模型进行稳态分析,计算收敛后以稳态流场为初场进行瞬态计算,并导出流固耦合面的压力脉动数据。通常来说,流场中的压力脉动有体积分布的四极子声源和表面分布的偶极子声源,低马赫数下,四极子声源可以忽略,偶极子是系统主要噪声源[8]。因此,将脉动压力映射至声学网格,进行傅里叶变换后作为偶极子噪声源导入 Virtual. Lab中,采用FEM/AML法进行声场计算,计算流程如图2所示。
|
图 2 计算流程图 Fig. 2 The block diagram of calculation |
利用Ansysicemcfd将图1模型划分六面体-四面体混合网格,将网格导入Fluent,流场求解采用基于压力的求解器,运用SST k-Ω湍流模型,边界条件如表2所示。
|
|
表 2 流场计算边界条件 Tab.2 The boundary conditions of flow calculation |
稳态计算收敛之后,先取大时间步长进行瞬态计算,待流场压力脉动稳定后取小时间步长进行计算,得到分析频率和频率分辨率适宜的流场压力时域数据,管路稳态压力分布计算结果如图3所示。

|
图 3 管路稳态压力分布图 Fig. 3 The steady-state pressure distribution of SW system |
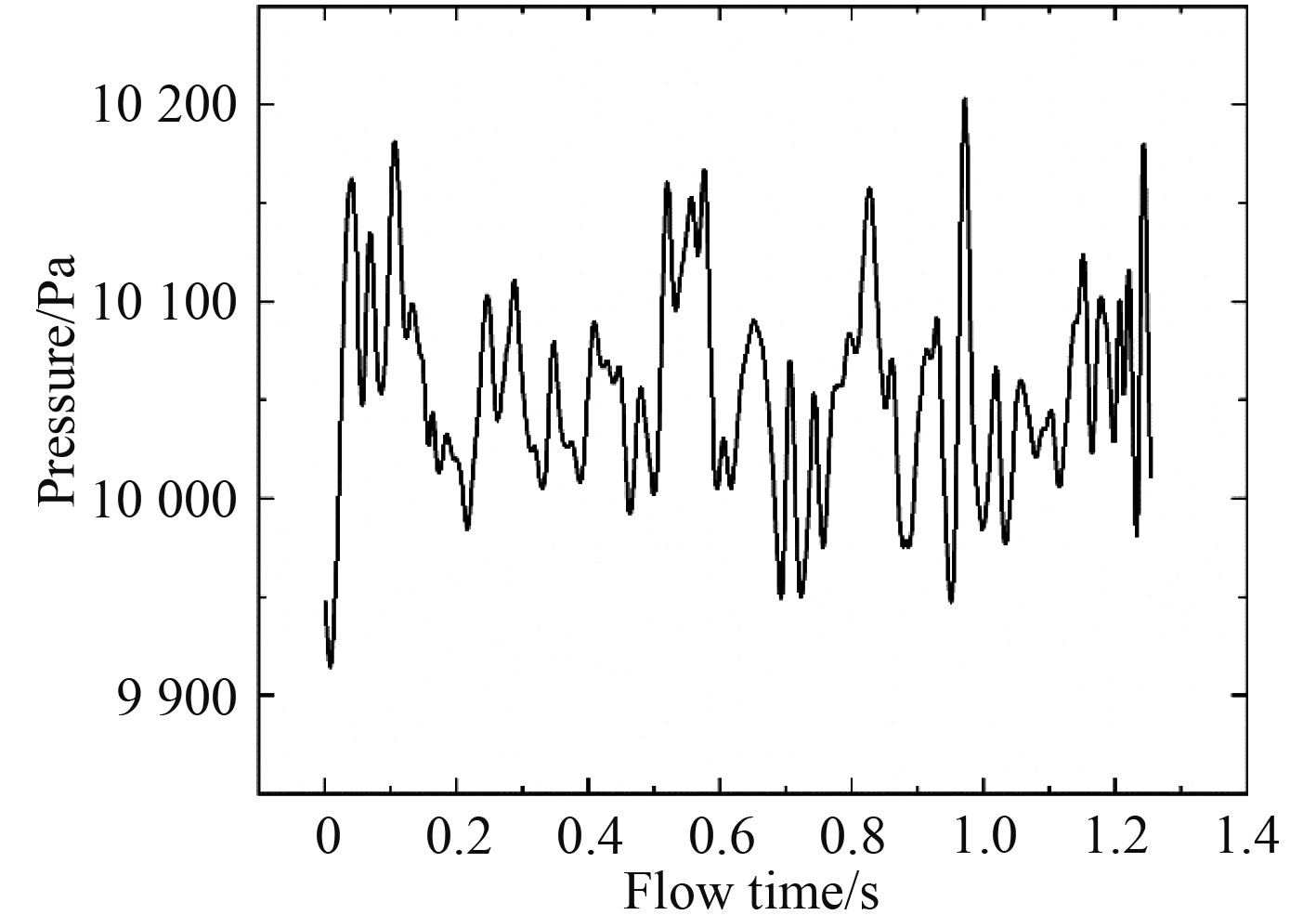
以稳态计算结果为初场,计算流场的瞬态计算,分析频率上限2500 Hz,频率分辨率5 Hz。取舷侧阀出口中心点为压力检测点,该点的压力时间历程曲线如图4所示。
|
图 4 舷侧阀出口中心点的压力-时间曲线 Fig. 4 The pressure-time curve of discharge valve |
将流场计算得到的计算结果导入LMS Virtual Lab软件的声学有限元模块中,将其转化为等效声源,运用AML(自动匹配边界层)技术可以根据声学有限元声辐射边界以及物理模型自动定义吸收层和吸收系数,进而进行无限空间域声学计算。声场计算模型包含声学网格和场点网格。声学网格采用四面体单元,网格尺寸0.02 m,满足计算需求。场点网格包括:如图5所示的离出口正前方1 m和50 m的声场观测点和以离出口正前方1 m为中心的指向性场点,该指向性场点以X轴正方向为法向,Y轴正向为0°,自右向左逆时针为正向,场点间隔为1°,半径为10 m;如图6所示以舷侧阀出口轴线作为对称轴,互相相交垂直的平面场点。

|
图 5 舷侧阀管段场点网格 Fig. 5 The field point grid of discharge valve pipe |

|
图 6 舷侧阀管段场点网格局部放大 Fig. 6 The partial magnification grid discharge valve pipe |
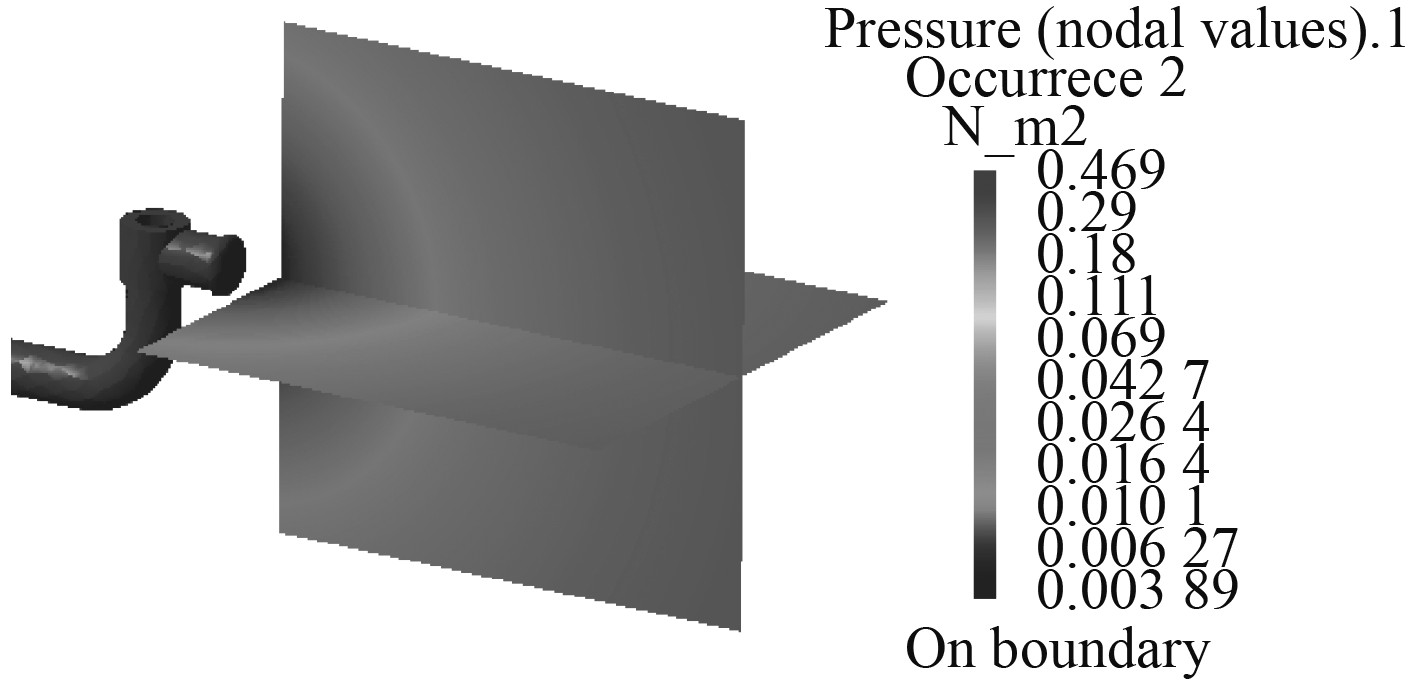
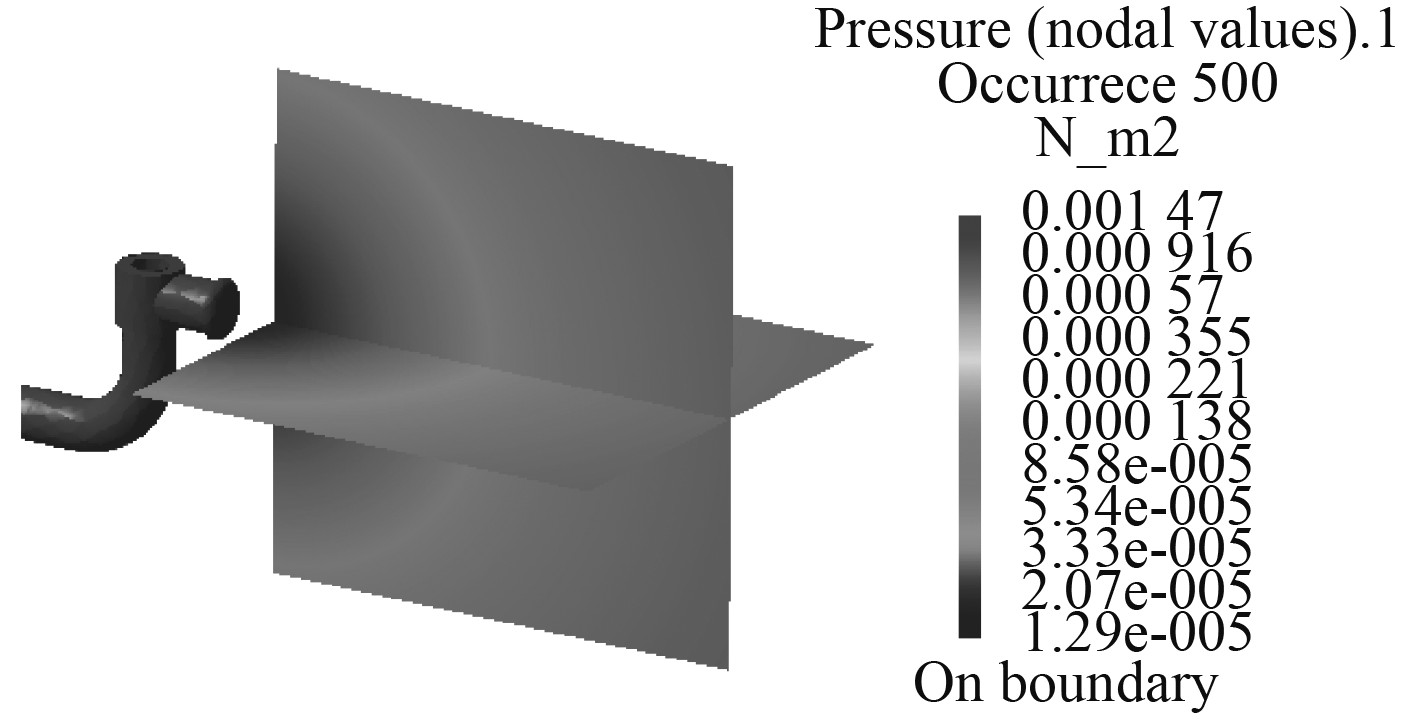
计算得到如图7~图10所示的对应50 Hz,100 Hz,1000 Hz和2500 Hz的辐射声压云图。

|
图 7 舷侧阀辐射噪声云图(50 Hz) Fig. 7 The acoustic pressure distribution of of discharge valve(50 Hz) |
|
图 8 舷侧阀辐射噪声云图(100 Hz) Fig. 8 The acoustic pressure distribution of of discharge valve(100 Hz) |

|
图 9 舷侧阀辐射噪声云图(1000 Hz) Fig. 9 The acoustic pressure distribution of of discharge valve(1000 Hz) |
|
图 10 舷侧阀辐射噪声云图(2500 Hz) Fig. 10 The acoustic pressure distribution of of discharge valve(2500 Hz) |
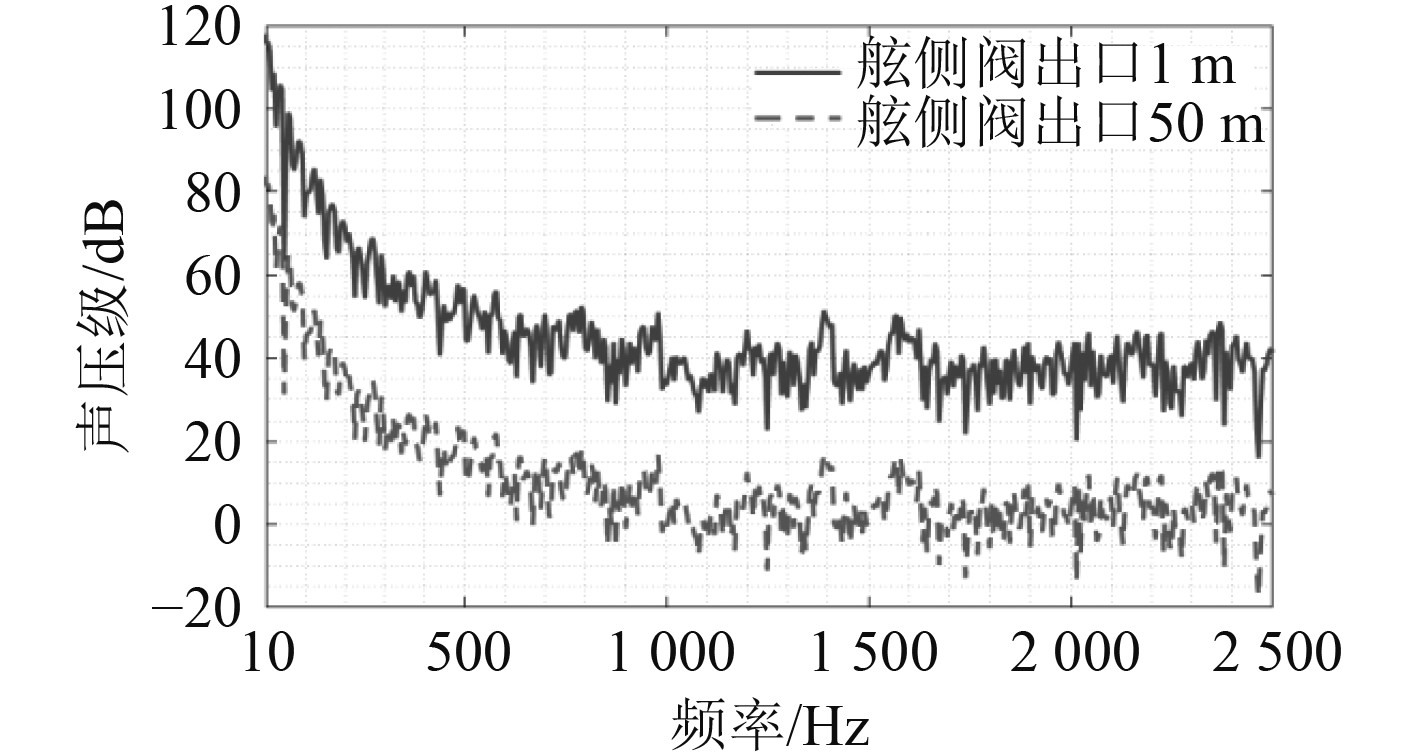
计算得到舷侧阀出口正前方1 m以及50 m处的声压级频谱图11所示。
|
图 11 舷侧阀出口1 m和50 m处的声压级频谱(参考声压1 μPa) Fig. 11 The acoustic pressure spectrum of discharge valve 1 m and 50 m(Reference sound pressure 1 μPa) |
从图11可以看出,舷侧阀出口1 m处的最大声压级约为120 dB,出口50 m处最大声压级约为85 dB。随着频率增加,声压级整体呈下降趋势,500 Hz以后,声压幅值下降趋于平缓。表3为舷侧阀出口1 m和50 m处各分频段及通频段声压级,可以发现舷侧阀水下声辐射主要集中在低频。
|
|
表 3 舷侧阀出口1 m和50 m处各分频段及通频段声压级对比(参考声压1 μPa) Tab.3 The sound pressure of discharge valve 1 m and 50 m (Reference sound pressure 1 μPa) |
为确定舷侧阀水下排出口位置、出口管径对海水冷却系统流噪声的影响,提出优化方案2和方案3。与原方案的对比如表4所示。
|
|
表 4 对比方案参数表 Tab.4 The data table of comparing programmes |

|
图 12 方案2舷侧阀出口1 m和50 m处的声压级频谱(参考声压 1 μPa) Fig. 12 The programme 2 acoustic pressure spectrum of discharge valve 1 m and 50 m(Reference sound pressure 1 μPa) |
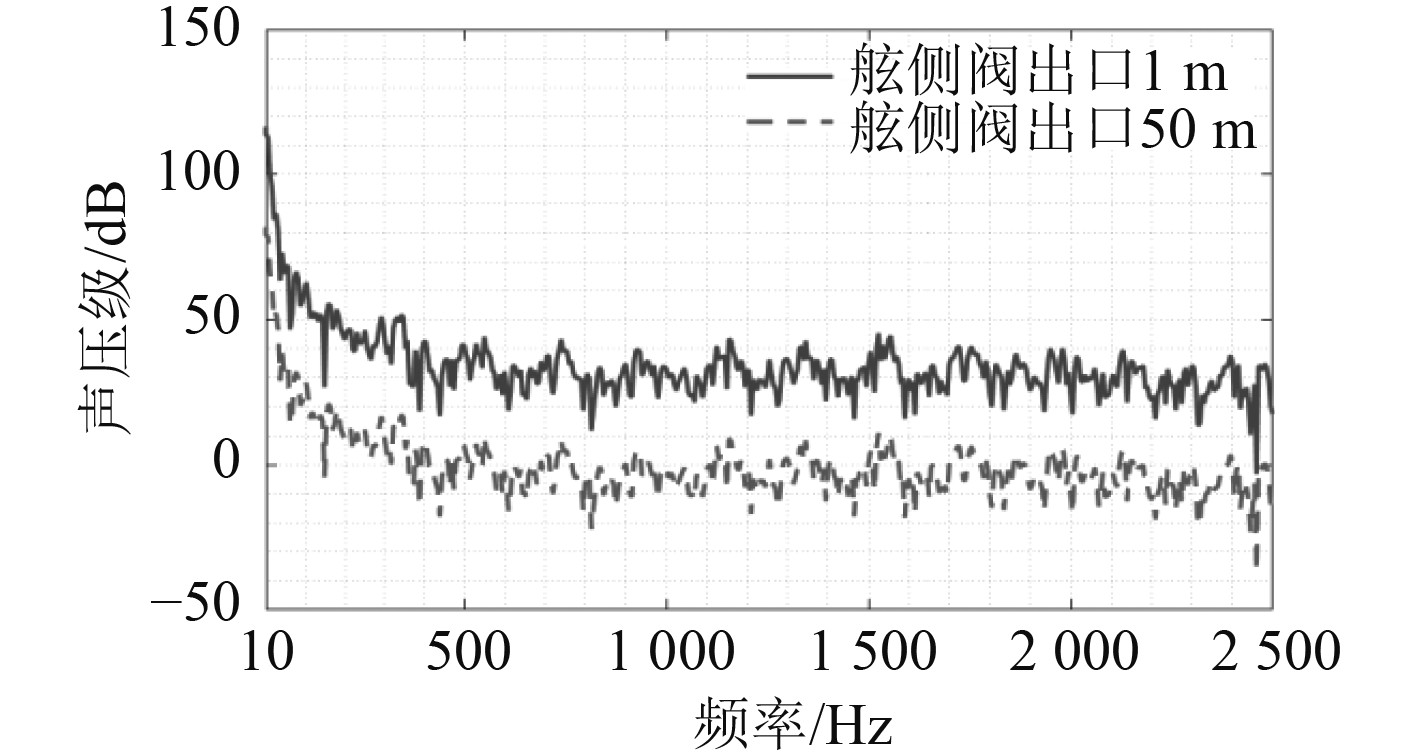
|
图 13 方案3舷侧阀出口1 m和50 m处的声压级频谱(参考声压 1 μPa) Fig. 13 The programme 3 acoustic pressure spectrum of discharge valve 1 m and 50 m(Reference sound pressure 1 μPa) |
各方案舷侧阀出口1 m和50 m处各分频段及通频段声压级对比如表5和表6所示。
|
|
表 5 各方案舷侧阀出口1 m处各分频段及通频段声压级对比(参考声压 1 μPa) Tab.5 The sound pressure contrast of discharge valve 1 m (Reference sound pressure 1 μPa) |
|
|
表 6 各方案舷侧阀出口50 m处各分频段及通频段声压级对比(参考声压 1 μPa) Tab.6 The sound pressure contrast of discharge valve 50 m (Reference sound pressure 1 μPa) |
通过对比可以发现,舷侧阀管段管径选用DN150、舷侧排出口位于水线下1 m的方案3在全频段都具有最低的流噪声声压级。由此可见,增大管径可以降低海水冷却系统流噪声。方案2在低频段的声压级高于原方案,说明舷侧阀出口水深减小会导致辐射声压的增大。
6 结 语本文采用FEM/AML的方法,海水冷却系统舷侧阀出口管路的流场环境进行了模拟,基于流场模拟计算数据开展了舷侧阀出口辐射噪声研究,对比了不同舷侧阀水下深度、出口管径对水下流噪声的影响,得到以下结论:
1)海水冷却系统舷侧阀水下流噪声以低频为主,随着频率增加,声压级整体呈下降趋势,500Hz以后,声压幅值下降趋于平缓。
2)通过增大舷侧阀管径、降低排出口水下位置等措施可以降低系统流噪声,对静音型水面舰船、潜艇的海水冷却系统降噪设计具有重要的参考意义。
| [1] |
何祚镛. 水下噪声及其控制技术进展和展望[J]. 应用声学, 2002, 21: 26-34. HE Zuo-yong. Review of some aspects of underwater noise including its control techniques and Its prospect[J]. Applied Acoustics, 2002, 21: 26-34. DOI:10.11684/j.issn.1000-310X.2002.01.007 |
| [2] |
胡家雄 2005. 关于潜艇橡胶减振接管隔振效果的思考[C].
|
| [3] |
蔡标华, 俞健, 白亚鹤. 舰船系统管路弹性减振设计与试验[J]. 舰船科学技术, 2011, 33: 61-64. CAI Biao-hua, YU Jian, BAI Ya-he. Design of elastic damping vibration on warship piping and its testing research[J]. Ship Science and Technology, 2011, 33: 61-64. DOI:10.3404/j.issn.1672-7649.2011.06.015 |
| [4] |
董自虎, 李超. 某船用通海阀流道优化仿真分析研究[J]. 舰船电子工程, 2016, 36: 95-100. DONG Zi-hu, LI CHAO. Marine valve flow optimization simulation analysis and research[J]. Ship Electronic Engineering, 2016, 36: 95-100. DOI:10.3969/j.issn.1672-9730.2016.07.024 |
| [5] |
张冠军, 朱翔, 李天匀, 等. 水中双层加筋板结构的声振耦合特性[C]//中国造船工程学会船舶力学学术委员会第八次全体会议, 2014.
|
| [6] |
张跃, 郑轶, 王振, 等. 基于 LES 和 FEM/AML 方法对潜标结构流噪声预报研究[J]. 海洋技术学报, 2018(12): 22-27. ZHANG Yue, ZHENG Zhi, WANG Zhen, et al. Numerical simulation for flow noise of subsurface buoy with LES and FEM/AML method[J]. Journal of Ocean Technology, 2018(12): 22-27. |
| [7] |
DE Lang-he, Koen, et al. Advanced simulation techniques for vehicle acoustic panel loading predictions, including FEM AML and Fast Multipole BEM (FMBEM).[C] Internoise 2011.
|
| [8] |
刘翠伟, 李玉星, 王武昌, 等. 输气管道气体流经阀门气动噪声产生机理分析[J]. 振动与冲击, 2014, 33(2): 152-157. LIU Cui-wei, LI Yu-xing, WANG Wu-chang, et al. Analysis on the mechanism of aero-acoustic noise generated by gas flow through valves of natural gas pipelines[J]. Journal of Vibration and Shock, 2014, 33(2): 152-157. DOI:10.3969/j.issn.1000-3835.2014.02.029 |
 2021, Vol. 43
2021, Vol. 43
