2. 海军装备部重大专项装备项目管理中心,北京 100071
2. Project Management Center of Major Special Equipment of Navy, Beijing 100071, China
舰船通道设计[1-3]是舰船总布置设计的重要任务之一,通道直接影响人流、物流及损管等设计的合理性。通道布置设计应能便于作战行动、人员流通、物品运送和设备搬运等各种活动的进行;流通路线应尽量短、直而流畅,并保证所有舱室和部位都可达,这就涉及通道的设计和验证。良好的通道设计不仅可以提高船舶人流、物流的效率,而日有助于损管工况下人员的紧急流通,使舰船及早恢复战斗力和生命力。
舰船舱室、人员和部门较多,各种工况下人员部署和调度复杂。在舰船遭受导弹、鱼雷等攻击时,通道可能遭受损害,无法通行。针对此类问题,利用网络流优化算法开展舰船通道网络完整工况和损害工况下的流量分析。网络流优化(Network Flow Optimazition)是一种寻找最优解的成熟应用数学方法,本文通过网络流优化搭建了包含兵舱、雷达室、指挥室和武器室等节点的简化通道网络,对此网络建立数学模型并进行战斗部署下人员流动模拟。为模拟舰船通道N-1损害工况,依次对各段通道损害时的网络流进行了仿真。仿真结果对通道设计和生命力设计具有一定的参考意义。
1 网络流模型 1.1 模型定义网络[4]是一个各条边都有权值和方向的图,网络的每一条边拥有一个最大的容量u,即该条边可以容纳的最大流量,x是流过该边的实际流量,且总有
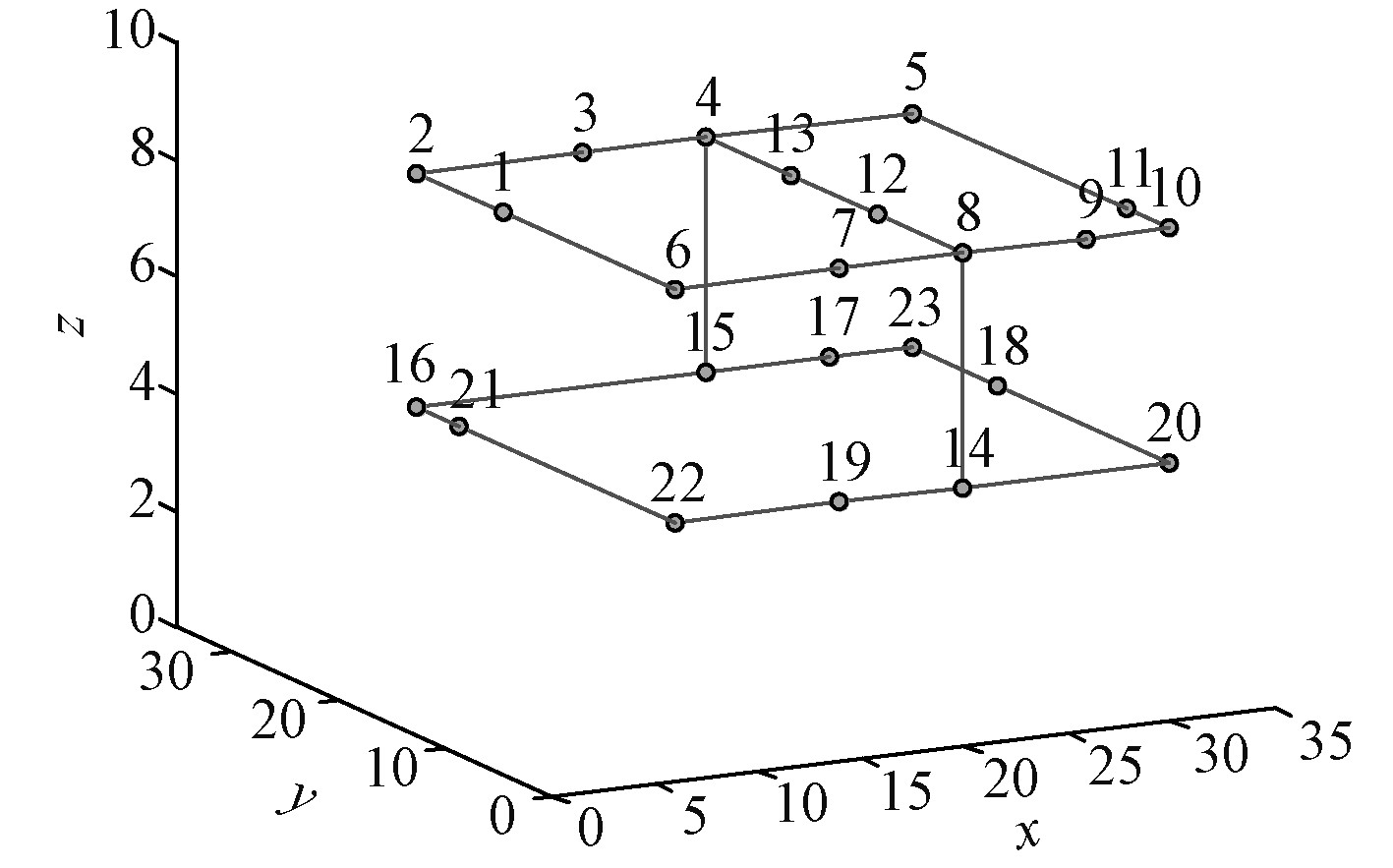
搭建包含兵舱、雷达室、指挥室和武器室等节点的2层甲板简化通道网络[5-6],如图1所示,模拟战斗部署下12名士兵从兵舱前往各站位过程。简化的通道网络包含23个节点,各节点在实船位置(简化示例)及站位设置如表1所示。由节点连接的弧如表2所示,该网络包含26条弧,弧的方向为1表示为正向流,2表示为逆向流,3表示为双向流,通道网络的弧均为双向流。所有弧的最大容量初步设置为8人。
|
图 1 简化通道网节点分布图 Fig. 1 Simplified channel network node distribution |
|
|
表 1 通道网节点 Tab.1 Channel network nodes |
|
|
表 2 通道网弧列表 Tab.2 Channel network arc list |
针对创建的网络,以每个弧的人流量为设计变量,以各节点遵循能量守恒的连续性方程和各弧满足容量限制为约束,以网络通行总距离为优化目标,进行网络流优化。具体表达式为:
Min
St
其中:
利用分枝定界法[7-8]求解此类整数线性规划问题,分枝定界法(branch and bound)用于求解纯整数或混合的整数规划问题。在20世纪60年代由Land Doig和Dakin等提出。这种方法灵活且便于用计算机求解,目前已经成功运用于求解生产进度问题、旅行推销员问题、工厂选址问题、背包问题及分配问题等。
该算法对有约束条件的最优化问题(其可行解为有限数)的所有可行解空间恰当地进行系统搜索。通常把全部解空间反复地分割为越来越小的子集,称为分枝,并对每个子集内的解集计算一个目标下界(对于最小值问题),这称为定界。在每次分枝后,若某个已知可行解集的目标值不能达到当前的界限,则将这个子集舍去。这样,许多子集不予考虑,这称为剪枝。其思路具体如下:有最大化的整数规划问题A,与它相应的线性规划问题时B。从解问题B开始,若其最优解不符合A的整数条件,那么B的最优目标函数必是A的最优目标函数z*的上界,记作z¯;而z的任意可行解的目标函数值将是z的一个下界z_。分枝界定法就是把B的可行域分成子区域的方法。逐步减小z¯和增大z_。最终求到z*。
本文在Matlab中进行求解[9-10],计算结果如图2所示。图中无流量通道硬虚线表示,有流量弧的流量通过线宽表示。

|
图 2 完整通道网络流量图 Fig. 2 Complete channel network flow chart |
在舰船遭受打击时,网络中的节点或弧会受到损害,这里对网络中一个节点或弧受到损害时(即N-1工况)的网络流进行计算,可以通过依次设置

|
图 3 通道网络N-弧4流量图 Fig. 3 Channel network N-arc4 flow chart |
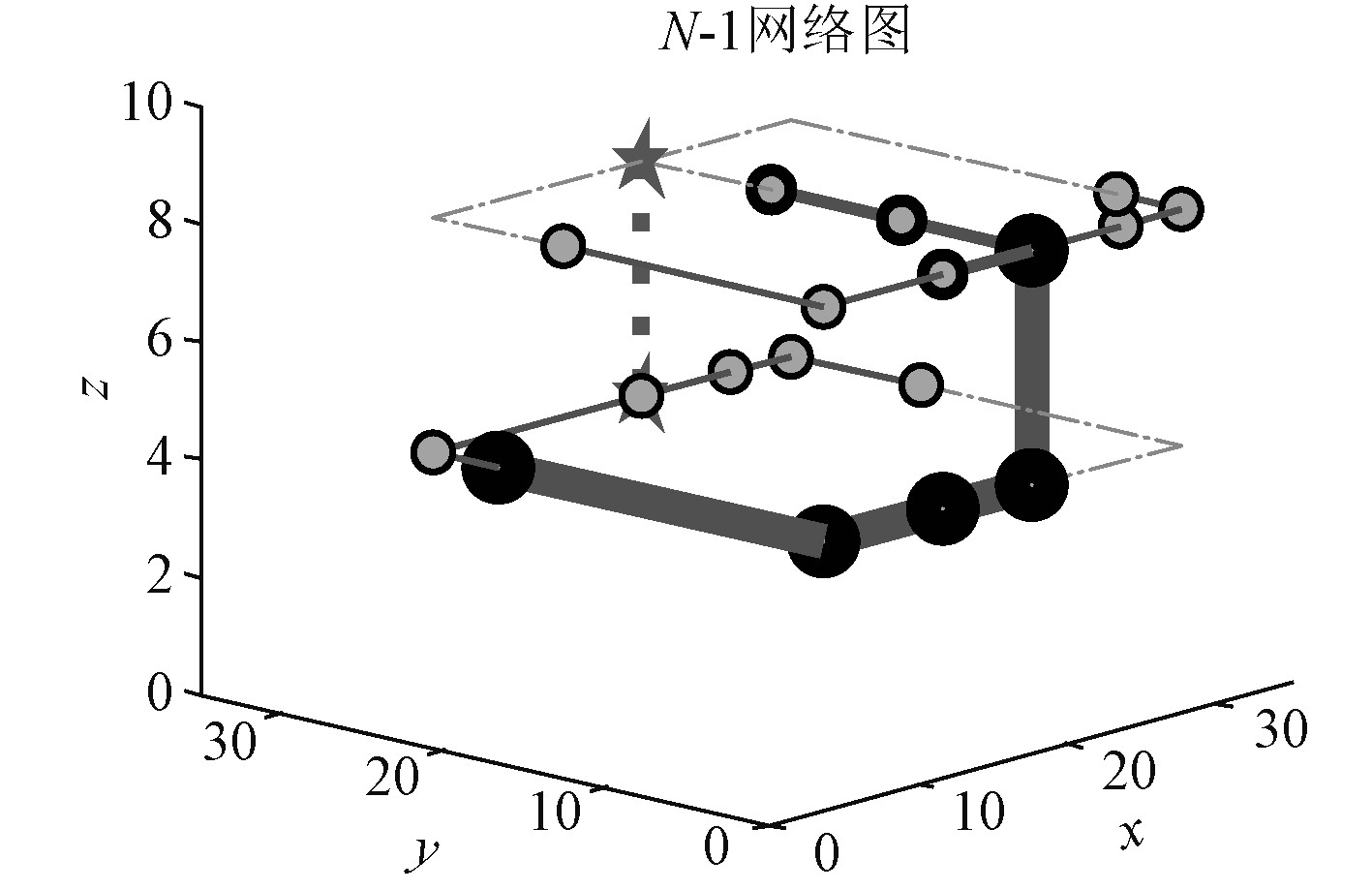
|
图 4 通道网络N-弧7流量图 Fig. 4 Channel network N-arc7 flow chart |

|
图 5 通道网络N-弧14流量图 Fig. 5 Channel network N-arc14 flow chart |
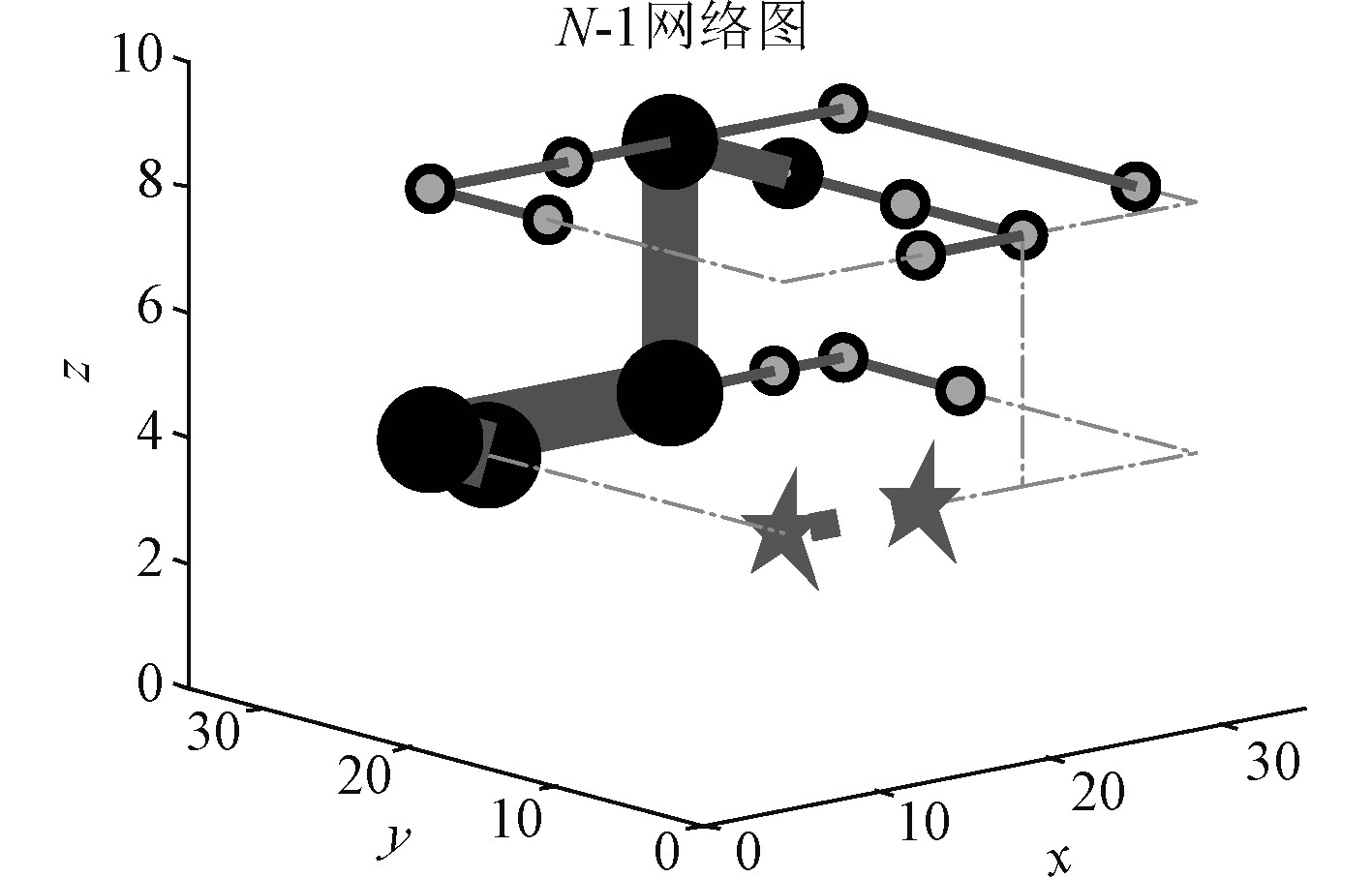
|
图 6 通道网络N-弧25流量图 Fig. 6 Channel network N-arc25 flow chart |
对于网络中一个弧受到损害(即N-1工况)时各弧的最大网络流如图7所示。图2~图7对应的各弧网络流数值如表3所示。由于弧为双向流,单向流最大容量8人,表3中可以看出双向流的容量和最大为12人。
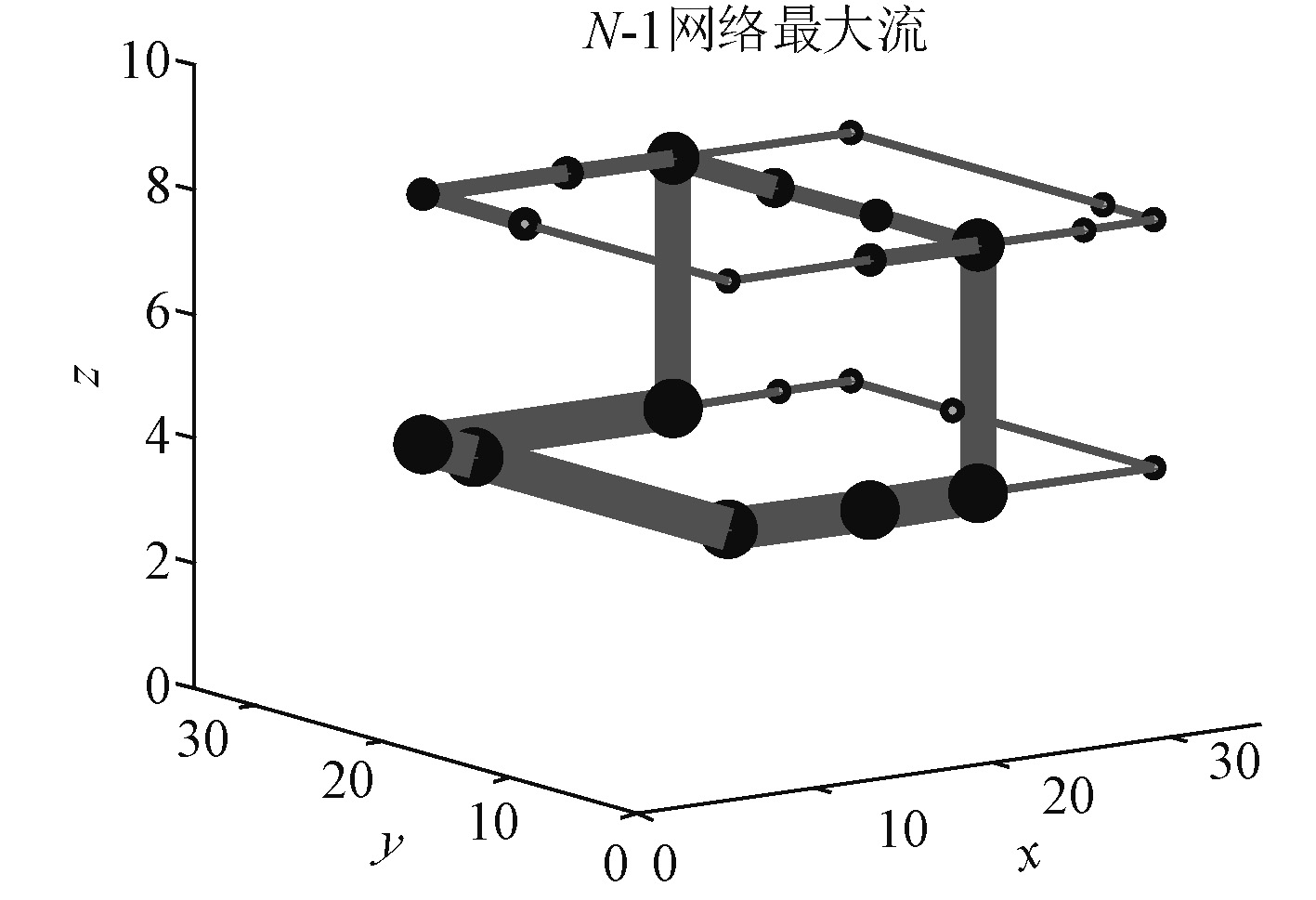
|
图 7 通道网N-1工况最大网络流 Fig. 7 Channel network N-1 maximum network flow |
|
|
表 3 各典型工况网络流 Tab.3 Network flow of each typical working condition |
通过计算结果可以对通道设计进行验证和完善,如是否满足N-X损害工况的生命力设计要求,是否含有冗余通道可以删减等。结果显示,本文提出的通道网络可以满足N-1损害工况下的生命力设计,各弧最大网络流均大于0,无冗余弧,通道的容量可以参照计算结果开展相关设计,以降低通行距离和总体资源。
3 结 语本文在舰船简化通道网的基础上,建立以通行距离最小为目标的网络流模型,利用分枝定界法开展网络流优化。依次对完整网络和N-1损害工况下网络进行了优化求解,结果显示,本文的模型和算法能够快速、良好地反映通道网络流量分布,可为通道网的设计、验证和完善提供依据,可对网络N-1损害工况进行求解,计算结果可为通道网生命力设计和损管决策和操作提供依据。
| [1] |
余为波, 吴晓光, 王涛, 等. 基于最短路径算法的舰船通道逃逸路线研究[J]. 中国舰船研究, 2008, 3(2): 16-20. DOI:10.3969/j.issn.1673-3185.2008.02.005 |
| [2] |
余为波, 王涛. 基于图论的舰船通道路线优化[J]. 中国舰船研究, 2008, 3(1): 18-22. DOI:10.3969/j.issn.1673-3185.2008.01.005 |
| [3] |
王文全, 黄胜, 胡玉龙, 等. 舰船通道布局优化模型及其粒子群算法[J]. 武汉理工大学学报, 2012, 34(9): 52-56. DOI:10.3963/j.issn.1671-4431.2012.09.012 |
| [4] |
BREFORT D, SHIELDS C. An architectural framework for distributed naval ship systems [J] Ocean Engineering, 147: 375–385, 2018.
|
| [5] |
PARSONS. Application of a distributed system architecture framework to naval ship concept and requirements exploration (C&RE)[C]//Intelligent Ships Symposium, ANSE ISS 2019, Philadelphia, PA, April 2019.
|
| [6] |
ROBINSON, K. Modeling distributed naval ship systems using architecture flow optimization [J] Ocean Engineering, Virginia Tech, 2018.
|
| [7] |
段毅, 谭贤四, 曲智国, 等. 基于分支定界法的相控阵雷达事件调度算法[J]. 电子学报, 2019, 47(6): 1309-1315. DOI:10.3969/j.issn.0372-2112.2019.06.018 |
| [8] |
张晗, 陈晓晓, 魏禧辰, 等. 基于分支定界法的整数规划问题研究与应用[J]. 赤峰学院学报: 自然科学版, 2019, 35(4): 20-23. |
| [9] |
TRAPP T. Shipboard integrated engineering plant survivable network optimization[D]. Massachusetts Institute of Technology, 2015.
|
| [10] |
IBM. IBM ILOG CPLEX Optimization Studio CPLEX User's Manual Version 12 Release 6. USA: International Business machines Corp, 2014.
|
 2021, Vol. 43
2021, Vol. 43

