2. 湖北省电力勘测设计院有限公司,湖北 武汉 430040
2. Powerchina Hubei Electric Engineering Co. Ltd., Wuhan 430040, China
随着船舶大型化、高速化的发展趋势,全球船舶总数量、总吨位迅速增长,船舶平均可航面积减小,航行环境愈发复杂,这一系列因素导致船舶碰撞、搁浅、触礁等事故频发,严重威胁船舶航行安全和海洋生态环境。尽管全球定位系统、自动雷达标绘辅助系统、自动识别系统等航海装备逐渐升级换代,但是受人为判断失误、恶劣气象条件以及复杂通航环境等因素的影响,船舶碰撞事故仍时有发生,并且在船舶交通流量密集的水域经常会出现多船会遇的复杂局面。为减少船舶碰撞事故的发生,各海运大国相继开展船舶智能避碰决策的研究。而实时准确地获取船舶碰撞危险度一直是船舶智能避碰领域的核心和难点问题,并且在多船会遇局面下,船舶间碰撞危险度也是确定船舶避让行动优先级的重要评定指标。
船舶碰撞危险度(Collision Risk Index,CRI)是船舶避碰领域的一个基本概念[1-2],其表示船舶间发生碰撞的可能程度,取值在0~1之间。由于碰撞危险度具有模糊性和不确定性,目前国际上尚未形成统一的评判方法。船舶碰撞危险度确定方法的发展历程可以分为4个阶段,第1阶段是围绕宏观碰撞危险度,主要基于交通流理论,通过统计特定水域某段时间内船舶碰撞事故的发生频率来评价碰撞危险度。第2阶段从微观的角度出发,通过驾驶员的行为和心理所确定的船舶领域范围来评价船舶的碰撞危险度。主要的研究成果包括英国学者Goodwin的船舶领域模型[3]。第3阶段主要是综合考虑
本文为了解决多船避碰决策过程中船舶间避让行动优先权问题,提出一种基于模糊集合理论的船舶碰撞危险度确定模型。通过建立船舶碰撞参数模型,实时地计算出船舶运动过程中的
模糊理论是美国控制专家查德(L. A. Zadeh)于1965年首次提出的,旨在解决模糊问题。模糊性是相对于精确性而言的,所谓模糊就是概念的外延不明确、不清晰。其实,模糊是普遍存在的,如在日常生活中人们经常使用泾渭不分明的语言,另外在文章中关于某些术语的定义等都存在着模糊的现象。模糊数学作为一门新的数学方法,经过多年专家学者积累的卓越成果,已经取得了迅猛的发展。目前,模糊理论已广泛应用在人工智能、医学、人文、社科等众多领域。
船舶碰撞危险度实际上等同于“船舶在某种航行环境下与来船发生碰撞的危险程度”这个模糊集合的隶属函数,论域为“航行船舶所有可能发生的会遇局面”。因此,运用模糊集合理论来确定船舶间碰撞危险度是一种行之有效的方法。
1.2 船舶碰撞参数模型
|
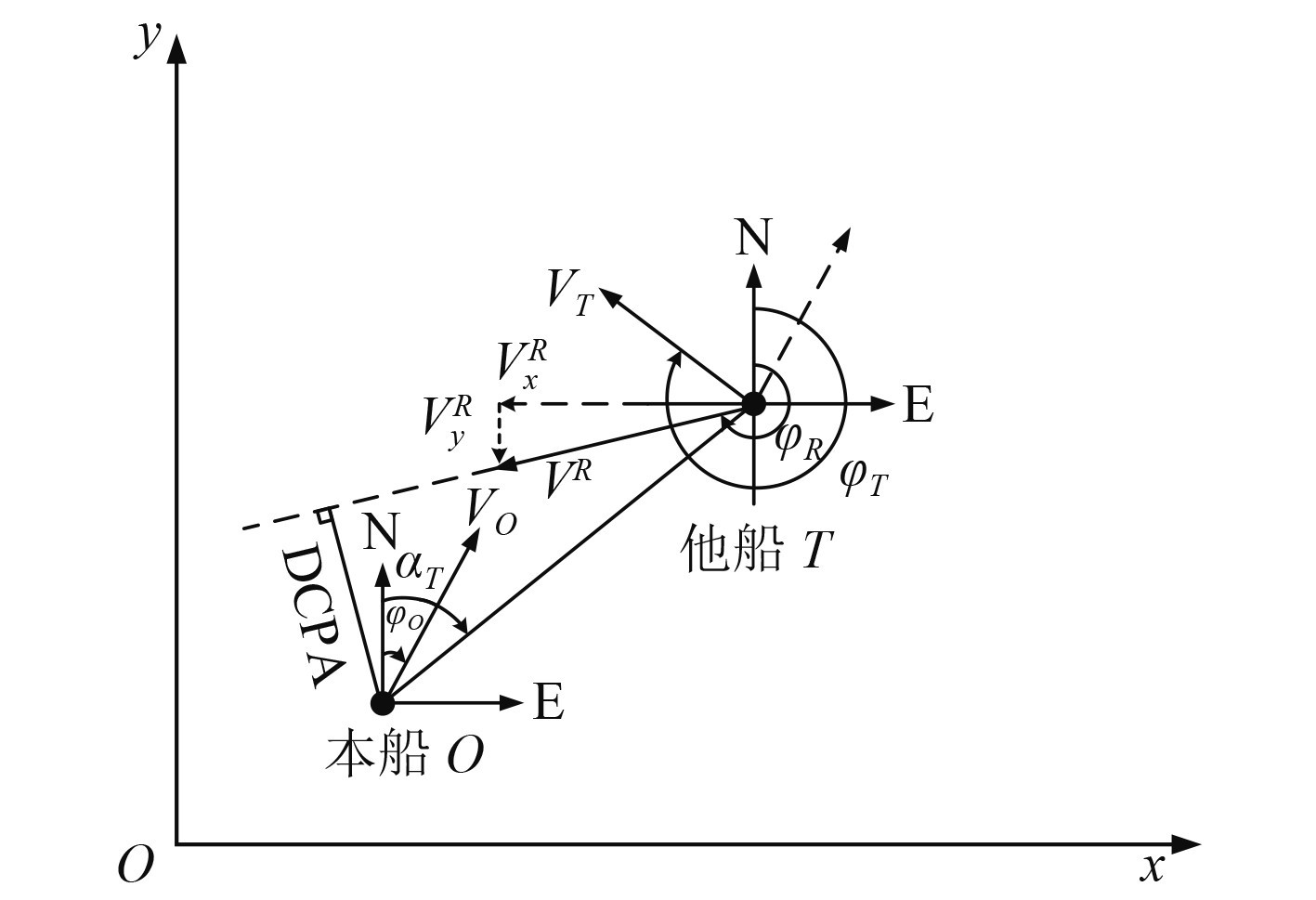
图 1 船舶碰撞参数示意图 Fig. 1 Schematic diagram of ship collision parameters |
1)则本船与他船的距离
| ${D_R} = \sqrt {{{({x_T} - {x_O})}^2} + {{({y_T} - {y_O})}^2}} {\text{。}} $ | (1) |
2)他船相对本船的运动速度
| ${v^R} = \sqrt {{{(v_x^R)}^2} + {{(v_y^R)}^2}}{\text{。}} $ | (2) |
其中:
3)他船相对本船的运动速度
| ${\phi _R} = \left\{ \begin{array}{l} \qquad\qquad 0{\text{,}}\qquad\qquad\quad v_x^R = 0,{\rm{ }}v_y^R \geqslant 0{\text{,}}\\ \qquad\qquad\text{π}{\text{,}} \qquad\qquad\quad v_x^R = 0,{\rm{ }}v_y^R < 0{\text{,}}\\ {\alpha _1} - {\mathop{\rm arc}\nolimits}\;{\rm{tan(}}v_y^R/v_x^R){\text{,}}\qquad v_x^R \ne 0{\text{。}} \end{array} \right. $ | (3) |
其中:若
4)他船相对于本船的真方位
| ${\alpha _T} = \left\{ \begin{array}{l} \qquad\qquad 0{\text{,}} \qquad\qquad\quad \Delta x = 0,{\rm{ }}\Delta y \geqslant 0{\text{,}}\\ \qquad\qquad \text{π}{\text{,}} \qquad\qquad\quad \Delta x = 0,{\rm{ }}\Delta y < 0{\text{,}}\\ {\alpha _2} - {\mathop{\rm\;arc}\nolimits}\;{\rm{tan(}}\Delta y/\Delta x{\rm{){\text{,}}\;\;\;\;\;\;}}\Delta x \ne 0{\text{。}} \end{array} \right. $ | (4) |
其中:
因此,若
| $\begin{split}&{D}^{CPA}(t)={D}_{R}·\mathrm{sin}\left({\phi }_{R}-{\alpha }_{T}-\text{π} \right){\text{,}}\\ &{T}^{CPA}(t)=\frac{{D}_{R}·\mathrm{cos}\left({\phi }_{R}-{\alpha }_{T}-\text{π} \right)}{\left|{v}_{ij}^{R}\right|}{\text{。}}\end{split} $ | (5) |
船舶间的碰撞参数
在航海实践中,船舶通过配备的自动识别系统、自动雷达标绘仪等助航设备可以准确地获取目标船的运动状态信息,并且基于建立的船舶碰撞参数计算模型可进一步快速地确定船舶间的
| $ {{\mathit{\boldsymbol{U}}}}=\left\{DCPA,TCAP,D,\beta ,K\right\}{\text{。}}$ |
为了对船舶碰撞危险度的各影响因素进行准确的评价,建立碰撞危险度各因素评价集,其评价集如下:
| $ {{\mathit{\boldsymbol{V}}}}=\left\{很高VD{ };高D{ };一般N{ };低S{ };很低VS\right\}\text{。}$ |
为了便于量化,现将各评价因素划分等级,如表1所示。
|
|
表 1 碰撞危险度各因素评判等级 Tab.1 Judgment level of collision risk index factors |
1)
| $\begin{split}&{R^{DCPA}}\left( x \right) = \\ &\left\{ {\begin{array}{*{20}{c}} 1{\text{,}}&{DCPA < DCP{A_0}}{\text{,}}\\ {0.5\left(1 - \sin \dfrac{\text{π} }{{{{\rm{\mu}} _1}}}\left(x - \dfrac{{{{\rm{\mu}} _2}}}{2}\right)\right)}{\text{,}}&{DCP{A_0}{\rm{ }} \leqslant DCPA < DCP{A_1}}{\text{,}}\\ 0{\text{,}}&{DCP{A_1} \leqslant DCPA}{\text{。}} \end{array}} \right.\end{split} $ | (6) |
其中:
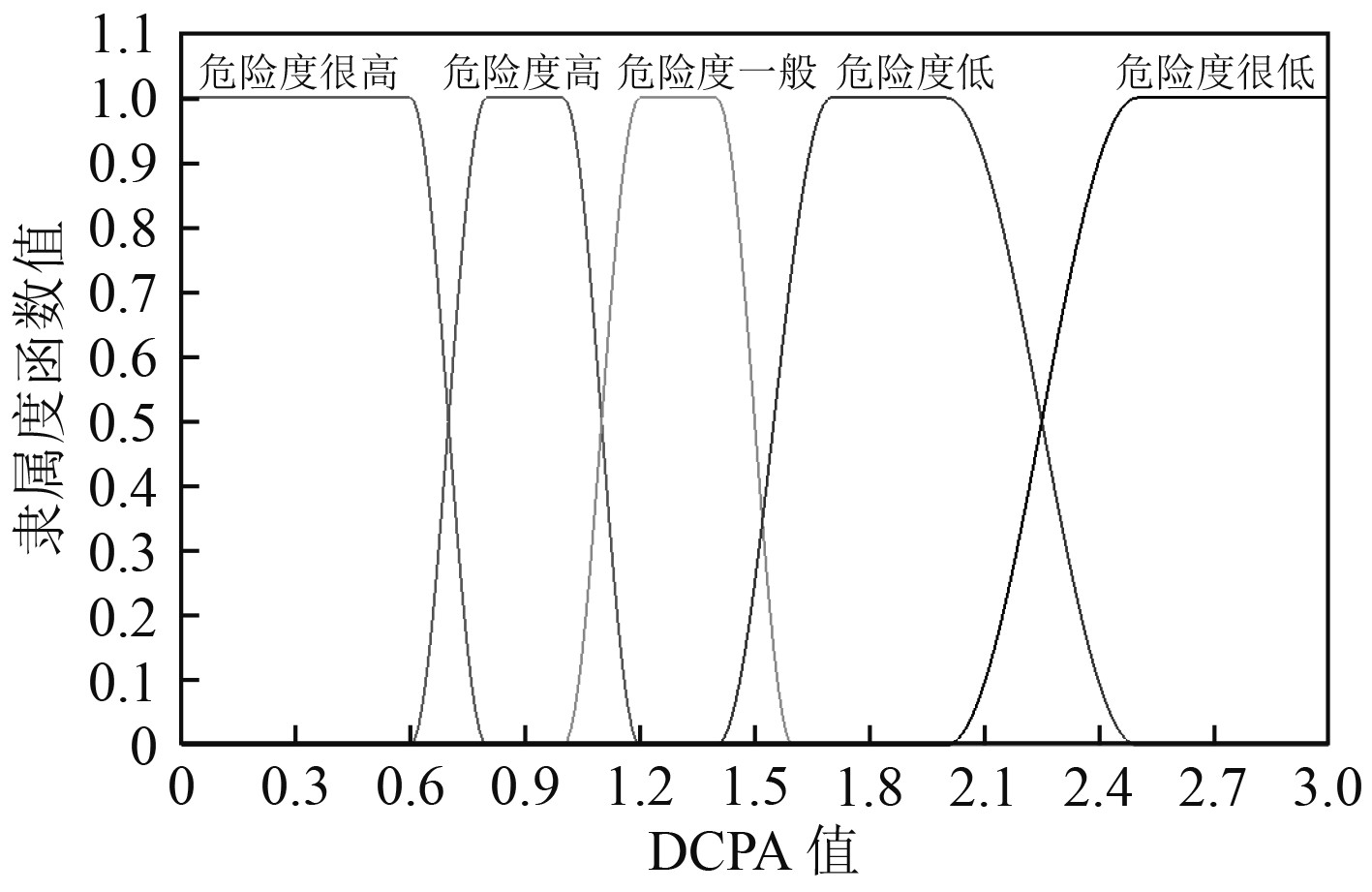
船舶间
|
图 2
|
2)
| $\begin{split}&{R^{TCPA}}\left( x \right) = \\ &\left\{ {\begin{array}{*{20}{c}} 1{\text{,}}&{TCPA < TCP{A_0}{\text{,}}}\\ {0.5\left(1 - \sin \dfrac{\text{π} }{{{{\rm{\delta }} _1}}}\left(x - \dfrac{{{{\rm{\delta }} _2}}}{2}\right)\right)}{\text{,}}&{TCP{A_0}{\rm{ }} \leqslant TCPA < TCP{A_1}}{\text{,}}\\ 0{\text{,}}&{TCP{A_1} \leqslant TCPA}{\text{。}} \end{array}} \right. \end{split} $ | (7) |
其中:
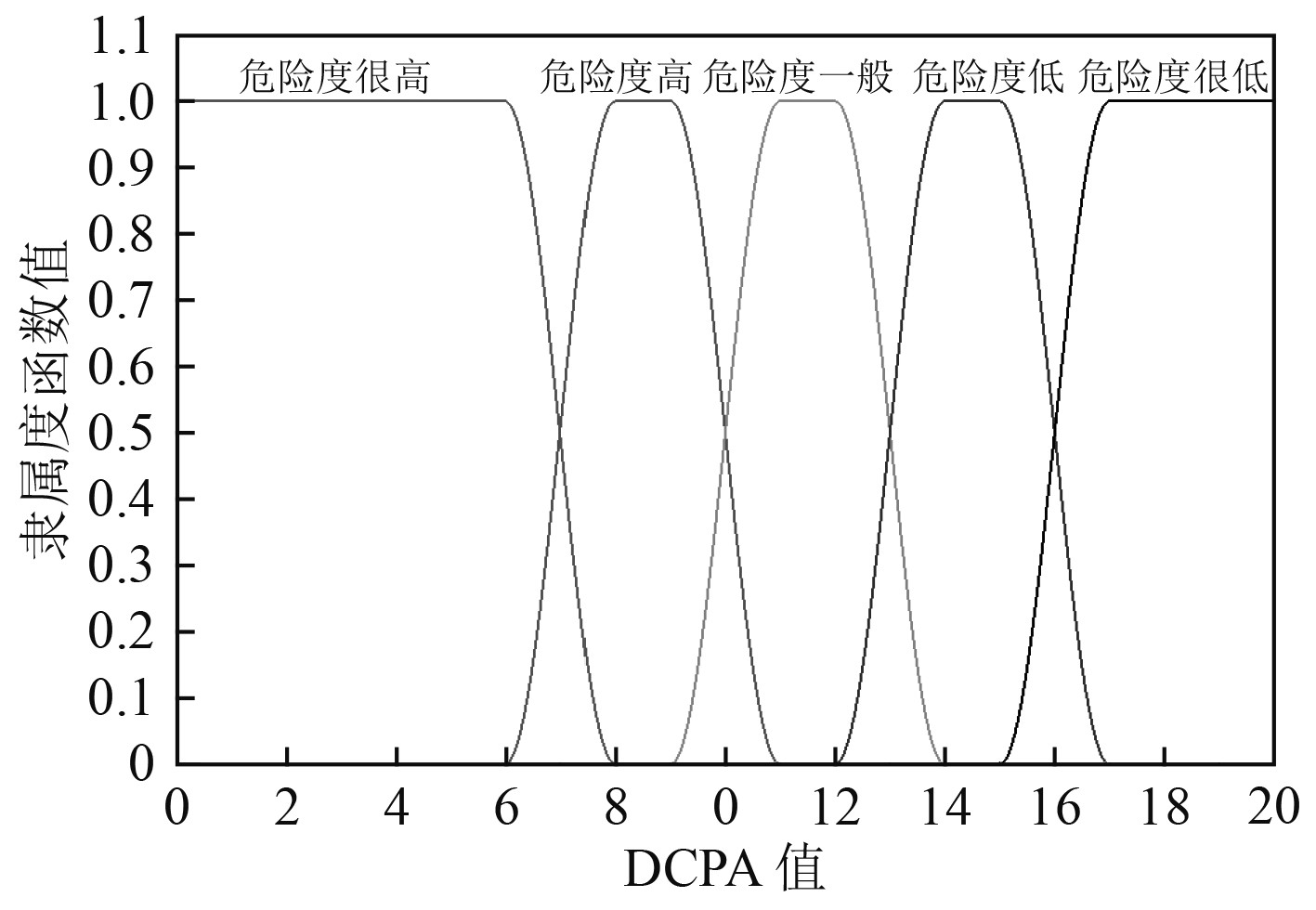
根据统计表明,当
|
图 3
|
3)船间距离
| ${R^D}\left( x \right) = \left\{ {\begin{array}{*{20}{c}} 1{\text{,}}&{D < {D_0}{\text{,}}}\\ {0.5\left(1 - \sin \dfrac{\text{π} }{{{{\rm{\omega }} _1}}}\left(x - \dfrac{{{{\rm{\omega }} _2}}}{2}\right)\right)}{\text{,}}&{{D_0}{\rm{ }} \leqslant D < {D_1}}{\text{,}}\\ 0{\text{,}}&{{D_1} \leqslant D}{\text{。}} \end{array}} \right. $ | (8) |
其中:
两船的相对位置距离越近,则船舶间的碰撞危险度越高。当

|
图 4
距离
|
4)相对方位
通过对船舶会遇态势进行分析,将来船的方位划分为6个区域:
|
|
表 2 船舶方位危险等级评价标准 Tab.2 Evaluation criteria for ship bearing danger level |
根据避碰经验,当来船位于本船19°左右时,本船感受到的碰撞危险程度最大;当来船位于本船199°左右时,本船感受到的碰撞危险程度最小。因此,建立来船相对方位的隶属度函数如下式:
| $\begin{split}&{R^\beta }\left( x \right){\rm{ = }}\frac{{17}}{{44}}\left[ {\cos ({\beta _0} - \beta ) + \sqrt {{{\cos }^2}({\beta _0} - \beta ) + \frac{{440}}{{289}}} } \right]{\text{,}}\\ &{\rm{0}}^\circ \leqslant \beta \leqslant 360^\circ{\text{。}}\end{split} $ | (9) |
其中:
5)船速比
若两船同时采取转向避碰行动(假定其他影响因素相同),若在同样的距离上对来船造成相同的
| ${R^K}\left( x \right) = 1/\left( {1 + {{\left( {\frac{{{K_0}}}{K}} \right)}^2}} \right){\text{。}} $ | (10) |
其中,定义船速比
建立相应的评价标准如表3所示。
|
|
表 3 船速比危险等级评价标准 Tab.3 Evaluation criteria for ship speed ratio danger level |
根据确立的船舶碰撞危险度因素集
| $\begin{split}{{\mathit{\boldsymbol{W}}}} =& \left[ {{W_{DCPA}},{W_{TCPA}},{W_D},{W_\beta },{W_K}} \right] = \\ &\left[ {0.36,0.32,0.14,0.10,0.08} \right]{\text{。}}\end{split}$ |
基于船舶碰撞危险度各影响因素的隶属度函数,建立目标船对本船的碰撞危险度评价矩阵
| $\begin{split}{{\mathit{\boldsymbol{R}}}} =& \left\{ \begin{array}{l} {R^{DCPA}}\\ {R^{TCPA}}\\ {R^D}\\ {R^\beta }\\ {R^K} \end{array} \right. =\\ &\left[ {\begin{array}{*{20}{c}} {R_{VD}^{DCPA}}&{R_D^{DCPA}}&{R_N^{DCPA}}&{R_S^{DCPA}}&{R_{VS}^{DCPA}}\\ {R_{VD}^{TCPA}}&{R_D^{TCPA}}&{R_N^{TCPA}}&{R_S^{TCPA}}&{R_{VS}^{TCPA}}\\ {R_{VD}^D}&{R_D^D}&{R_N^D}&{R_S^D}&{R_{VS}^D}\\ {R_{VD}^\beta }&{R_D^\beta }&{R_N^\beta }&{R_S^\beta }&{R_{VS}^\beta }\\ {R_{VD}^K}&{R_{D}^K}&{R_{N}^K}&{R_{S}^K}&{R_{VS}^K} \end{array}} \right]{\text{。}} \end{split} $ |
通过将各因素的评判矩阵、权重矩阵以及危险等级评价集
| $ CRI=W\cdot R\cdot V{\text{。}} $ | (11) |
为了验证本文提出的碰撞危险度模型的有效性,分别设置两船交叉会遇以及多船交叉会遇2种会遇局面,并初始化船舶运动参数,运用Matlab软件进行仿真实验。
1)两船交叉会遇态势
随着船舶的运动,时刻存储其运动信息,并基于建立的碰撞危险度模型对两船的碰撞危险度实时计算。两船交叉局面初始运动参数如表4所示,其运动轨迹及碰撞危险度变化如图5所示。
|
|
表 4 两船交叉局面初始运动参数 Tab.4 Initial motion parameters in two-ship crossing situation |

|
图 5 两船运动轨迹及船舶碰撞危险度变化 Fig. 5 Two-ship motion trajectory and change of ship collision risk index |
图5表示了2艘船舶处于交叉会遇态势下的船舶运动轨迹以及船舶间碰撞危险度的变化。初始时刻,根据船舶的运动参数进行计算,他船对本船的碰撞危险度数值为0.41,本船对他船的碰撞危险度数值为0.39。随着船舶相互驶近,两船间的碰撞危险度逐渐增大。在T=8时,两船间的碰撞危险度超过安全阈值0.5,其分别为0.53和0.51。根据船舶避碰基本常识,在该时刻船舶应采取最有利于避碰的行动。若两船继续航行,船舶间碰撞危险度将继续增大,其中他船对本船的碰撞危险度最大为0.78,本船对他船的碰撞危险度最大为0.77。在T=21时,碰撞危险度曲线陡然下降,此时两船间的
2)多船交叉会遇局面
通过增加会遇船舶的数量,并分别计算他船对本船的碰撞危险度,进一步模拟多船局面下船舶间的碰撞危险度变化。各船舶初始运动参数如表5所示,船舶运动轨迹及碰撞危险度变化曲线如图6所示。
|
|
表 5 多船交叉局面初始运动参数 Tab.5 Initial motion parameters in multi-ship crossing situation |
从图6可知,在初始时刻,船舶1对本船的碰撞危险度最大,船舶2对本船的碰撞危险度最小。随着船舶继续保持初始航向航行,船舶1对本船的碰撞危险度增长缓慢,并稳定在最大值0.71。在T=13时,船舶1对本船的碰撞危险度曲线陡然下降,两船间TCPA小于零,表明两船已驶过最近会遇点。而船舶3对本船的碰撞危险度则一直处于增长趋势,并逐渐超过船舶2的危险度大小,在T=17时达到最大值0.85。这意味着船舶3和本船在初始时刻若保向保速航行,两船会遇将会出现紧迫局面。尽管船舶2与本船呈正交航行态势,但两船间的碰撞危险度最大为0.53,并且该状态持续时间短,两船迅速驶过最近会遇点。因此,通过该碰撞危险度变化曲线,可以预测多船局面下两两船舶间的碰撞危险度变化趋势,使得本船可以综合多艘船舶的影响选择合适的避碰目标和避碰时机采取避碰行动。

|
图 6 多船运动轨迹及船舶碰撞危险度变化 Fig. 6 Multi-ship motion trajectory and change of ship collision risk index |
本文根据船舶碰撞危险度的模糊特性,将模糊集合理论引入到船舶碰撞危险度模型的确定研究中。通过建立船舶碰撞危险度影响因素集、评价集以及确定各影响因素的隶属度函数,运用模糊综合评价建立了船舶碰撞危险度计算模型,并分别设置两船交叉会遇以及多船交叉会遇2种会遇局面进行仿真实验。仿真结果表明,建立的碰撞危险度模型不仅可以实时地计算船舶间碰撞危险度并预测其变化趋势,还能够有效地解决多船会遇局面下船舶避碰行动优先级问题。因此,在本文研究成果的基础上,下一步将开展多船避碰决策算法的研究。
| [1] |
MEI J H, ARSHAD M R, TANG J R. Collision risk assessment based artificial potential field approach for multi-ships avoidance[J]. INDIAN JOURNAL OF GEO-MARINE SCIENCES, 2019, 48(7SI): 1037-1047. |
| [2] |
胥文, 胡江强, 尹建川, 等. 基于模糊理论的船舶复合碰撞危险度计算[J]. 舰船科学技术, 2017, 39(7): 78-84. XU Wen, HU Jiang-qiang, YIN Jian-chuan, et al. Composite evaluation of ship collision risk index based on fuzzy theory[J]. Ship Science and Technology, 2017, 39(13): 78-84. |
| [3] |
GOODWIN E. M.. A statistical study of ship domains[J]. Journal of Navigation, 1975, 28(3): 413-426. |
| [4] |
DAVIS P. V, DOVE M J, STOCKEL C T.. A computer simulation of marine traffic using domains and arenas[J]. Journal of Navigation, 1980, 33(2): 215-222. DOI:10.1017/S0373463300035220 |
| [5] |
PERERA L P, CARVALHO J P, SOARES C G. Fuzzy logic based decision making system for collision avoidance of ocean navigation under critical collision conditions[J]. Journal of Marine Science & Technology, 2011, 16(1): 84-99. DOI:10.1007/s00773-010-0106-x |
| [6] |
AHN J, RHEE K, YOU Y. A study on the collision avoidance of a ship using neural networks and fuzzy logic[J]. Applied Ocean Research, 2012, 37: 162-173. DOI:10.1016/j.apor.2012.05.008 |
| [7] |
贾立校. 船舶碰撞危险度模型应用与验证[J]. 舰船科学技术, 2016, 38(10): 16-18. JIA Li-xiao. Application and validation of ship collision risk model[J]. Ship Science and Technology, 2016, 38(10): 16-18. |
| [8] |
刘茹茹, 胡勤友. 一种主观的船舶碰撞危险度评价模型[J]. 上海海事大学学报, 2012, 33(1): 41-44. LIU Ru-ru, HU Qin-you. Subjective evaluation model of ships’ collision risk[J]. Journal of Shanghai Maritime University, 2012, 33(1): 41-44. DOI:10.3969/j.issn.1672-9498.2012.01.009 |
| [9] |
陈建华, 陈红卫, 刘科. 基于模糊神经网络的一种船舶碰撞危险度计算方法[J]. 舰船科学技术, 2008(2): 135-138. CHEN Jian-hua, CHEN Hong-wei, LIU Ke. A method of estimating ship collision risk based on fuzzy neural network[J]. Ship Science and Technology, 2008(2): 135-138. DOI:10.3404/j.issn.1672-7649.2008.02.027 |
| [10] |
陈立家. 海上多目标船智能避碰辅助决策研究[D]. 武汉: 武汉理工大学, 2011. CHEN Li-jia. Study on multiple objective decision making in collision avoidance at sea[D]. Wuhan: Wuhan University of Technology, 2011. |
| [11] |
薛彦卓, 魏伊, 孙淼. 基于避碰重点船算法的多船避碰模拟[J]. 大连海事大学学报, 2014, 40(1): 13-16. XUE Yan-zhuo, WEI Yi, SUN Miao. Simulation of multi-ship collision avoidance with avoidance key ship algorithm[J]. Journal of Dalian Maritime University, 2014, 40(1): 13-16. DOI:10.3969/j.issn.1006-7736.2014.01.004 |
 2021, Vol. 43
2021, Vol. 43
