0 引　言

随着我国经济的快速发展，海上运输量逐年大幅度增长，船舶碰撞事故时有发生，因此出于海洋环保的需要，必须将沉船携带或装载的大量燃油或液体危险化学品回收，否则会造成严重的海洋污染事件。由于沉船结构与海底环境的复杂，此类水下作业需要封堵、开孔、切割、抽液等各类应急处置工具及遥控式作业型水下机器人（ROV） 进行协同作业。在作业过程中不同的工具往往需要使用不同的接口，因此需要操作员使用ROV搭载的机械手完成相关接口的变换及对接工作。

目前水下连接器对接作业过程中，主要由操作员根据ROV搭载的摄像设备传回的视频在母船上远程操控机械手完成相关作业，这种作业方式存在的主要问题是摄像设备传回的视频多为二维视频，操作员难以直观地判断水下连接器是否对齐，是否可以对接。由于缺少了深度这一维度的信息，不得不由操作员依据自身的经验在实际水下空间多次尝试完成作业，或者由操作员借助多个摄像设备传回不同角度的二维视频进行作业，但是这样的作业方式需要操作员作业时同时关注多个视频画面，操作员操作难度较大，要求操作员有较高的操作水平。

随着计算机视觉技术的发展，视觉定位技术得到了越来越广泛的应用。视觉定位技术根据使用摄像机的数目分为单目、双目和多目视觉定位技术。目前使用的单目视觉技术要求已知目标物的尺寸，因此只适用于形状规则的简单目标物中；双目视觉定位相对于单目定位可以更精确地重现目标物的三维坐标，更好地模拟人类双眼视物的过程；双目视觉定位相对于多目定位更加简单易行。因其具有非接触测量、自动化程度高等优点，在机器人定位、智能工厂等^[1]领域取得了很好的应用效果。在水下工程领域，殷莉甜^[2]设计了基于双目视觉的水下焊接系统，并在水箱中进行了初步试验，分析了水质与测量距离对定位精度的影响；王从政^[3]设计了应用于核电站的燃料组件变形检测系统，该系统可以测量核电站燃料组件的长度，较好地监控燃料组件的变形情况；盛明伟^[4]提出了一种基于双目视觉的水下测距方法，并在水池中对水下机械手进行了测距实验，以上研究大多关注被测对象的位置或三维坐标等信息，对于姿态的研究较少。

针对水下连接器对接工作的特殊性，为提高该作业的效率，降低操作人员作业难度，本文首先根据水下连接器的颜色特征确定检测范围，之后在检测范围中以水下连接器为模板进行初步定位，然后根据水下连接器端面的成像特点检测椭圆特征，并进行双目匹配获得相关三维点坐标，最后计算得出水下连接器的位姿，从而为操作员完成对接工作提供参考。

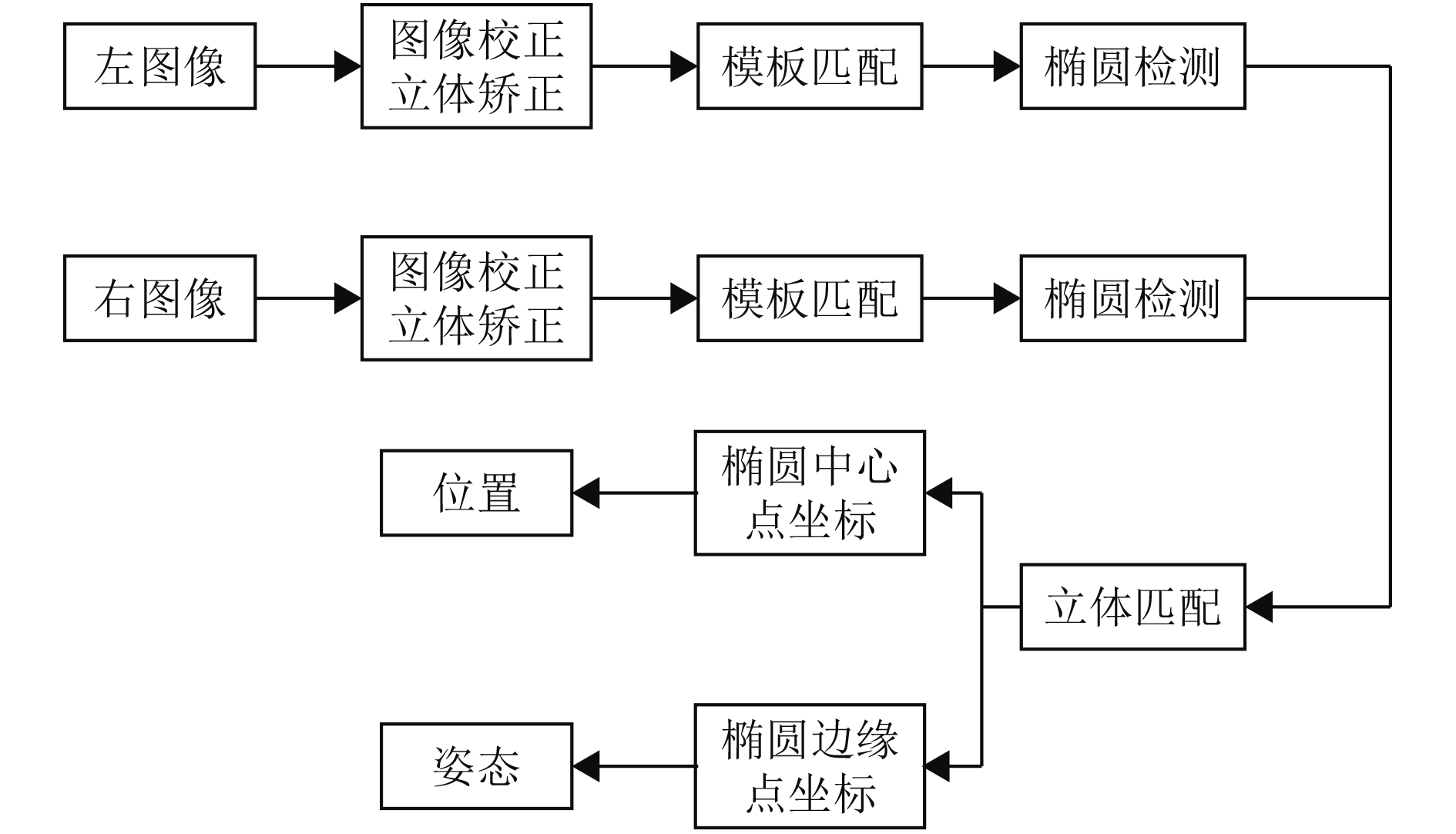
1 原理与方法

本文设计的方法首先根据水下连接器的颜色特征确定检测范围，之后在检测范围中以水下连接器为模板进行初步定位，然后根据水下连接器端面的成像特点检测椭圆特征，并进行双目匹配获得相关三维点坐标，最后分别计算得出水下连接器的位姿。相关流程如图1所示。

1.1 双目测量原理

双目立体视觉根据三角测量法，即对2台摄像机进行标定，获取其内、外参数之后，通过左、右视图中的一对同名像素点，获取其对应的空间三维坐标。

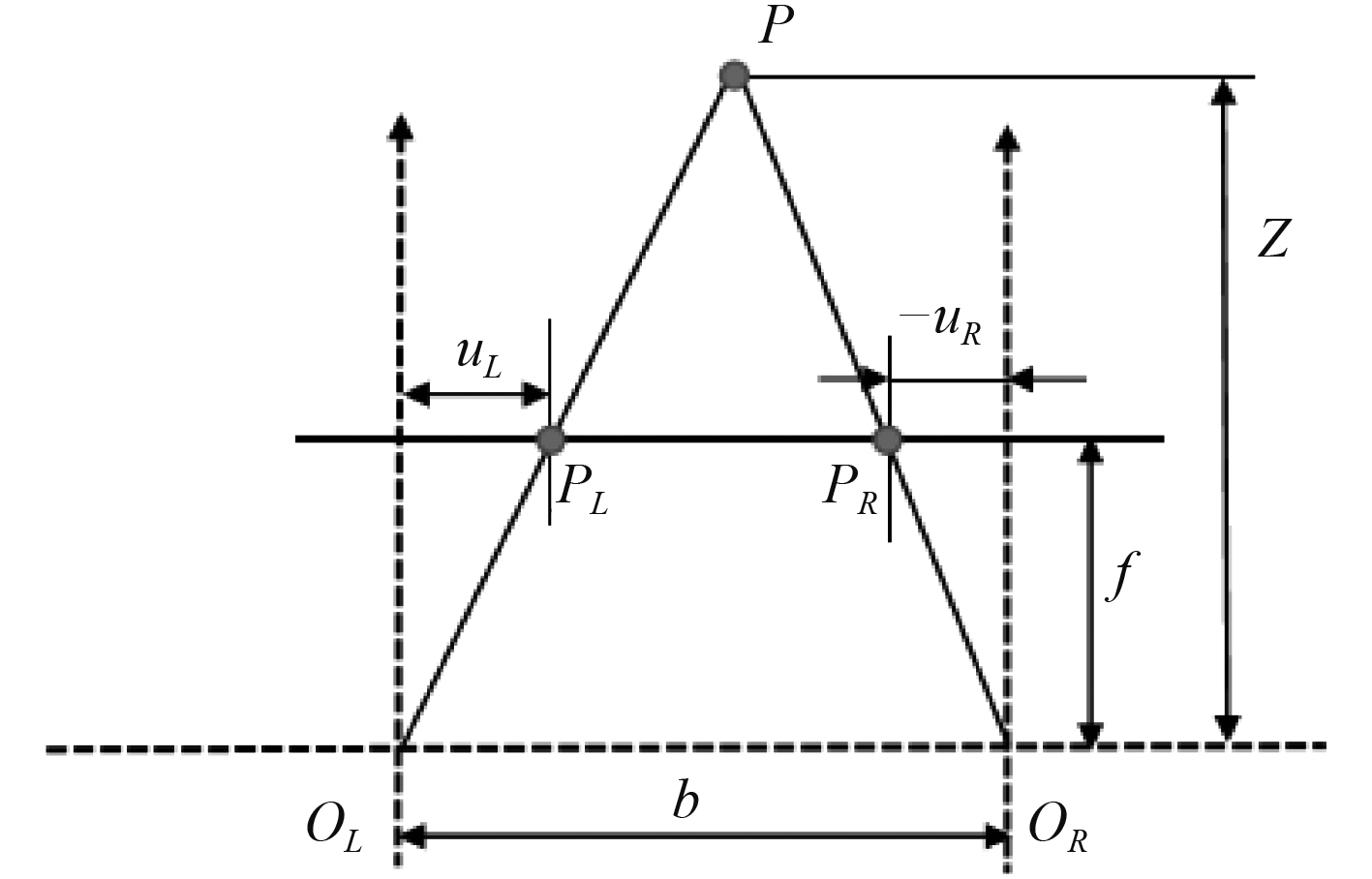
如图2所示， $O{}_L$ ， ${O_R}$ 分别是左右相机的光心， ${P_L}$ ， ${P_R}$ 分别是空间点 $P$ 在左右相机上的成像点， $b$ 是左右相机之间的距离，即基线长度， $f$ 是相机的焦距。

根据三角形相似，有

$\frac{{z - f}}{z} = \frac{{b - {u_L} + {u_R}}}{b}{\text{，}}$

(1)

整理，得

$z = \frac{{fb}}{{{u_L} - {u_R}}}{\text{，}}$

(2)

根据相机的小孔成像模型，

$x = \frac{{z{u_L}}}{f}{\text{，}}$

(3)

$y = \frac{{z{v_L}}}{f}{\text{。}}$

(4)

其中， ${u_L}$ , ${v_L}$ 是点 $P$ 在左相机成像平面的坐标（通常情况下坐标系以左相机为准）。

1.2 标定与校正

理想情况下的摄像机小孔成像模型要求相机光轴在图像的中心，并且相机在 $x$ ， $y$ 方向的缩小系数应保持一致，但是实际情况下，相机制造过程中不可避免存在器件误差与安装误差，这种误差由相机的内参数描述。此外，为了获得更好的成像效果，相机中往往要加入透镜，这会导致相机成像的畸变。为了消除这些影响，需要对相机进行标定获得相机的内参数及畸变系数，从而进行图像校正。另一方面，双目相机在安装过程中造成的位姿误差以及基线长度需要用外参数描述。因此还需对双目相机进行立体标定，并用立体标定得到的外参数进行立体校正从而保证左右图像的对应点在同一水平极线。

本文采用OpenCV开源库对双目相机进行标定及立体标定^[5]，并对图像进行校正及立体校正^[6]。如图3所示，左图像棋盘格点 $A$ 及其对应点右图像棋盘格点 $A'$ 不在同一水平极线上，经过图像校正后，左图像棋盘格点 $B$ 及其对应点 $B'$ 在同一水平极线上。

1.3 位置测量算法

水下连接器接口端面存在一系列圆形插孔，这些插孔可以作为图像模板匹配的特征进行初步定位。模板匹配是一种常用的模式识别方法，它将需要检测的物体作为模板图像，从左至右、从上至下地计算模板图像与原图像重叠的子图像之间的匹配度，最终在原始图像中选择匹配度最大的子图像作为匹配结果。考虑到水下连接器在原始图像中较小，对原始图像进行模板匹配计算代价较大，本文首先根据水下连接器的颜色特征在原始图像上选定部分检测范围，之后进行模板匹配，从而达到加速计算的目的。

此外，考虑到拍摄角度的影响，水下连接器接口端面在成像时会被投影为椭圆，因此本文采用椭圆检测算法^[7]获得椭圆中心的图像坐标，图4展示了使用该算法在水下作业中对水下连接器进行椭圆检测的结果。之后根据式（2）～式（4）可以得出椭圆中心的三维坐标，最后以椭圆中心的三维坐标作为水下连接器接口的位置坐标。

1.4 姿态测量算法

本文以水下连接器端面法向量为准描述水下连接器的姿态信息。理论上3个不共线的点可以确定一个平面，但在实际中，这样做容易导致平面法向量受少数点误差的影响存在较大误差。因此需要根据之前检测的特征椭圆的一系列边缘点的三维坐标拟合水下连接器的端面法向量。

为了获得椭圆边缘点的三维坐标，需要进行边缘点选取与立体匹配。如图5所示，本文采取的选点策略：在完成图像校正与立体校正的图像中，以纵坐标为准每隔一定距离在左图像上选择一系列边缘点 ${P_1}$ ， ${P_2}\cdots {P_n}$ ，同时在右图像相同纵坐标处选择与左图像边缘点的横坐标相近的点作为左图像的匹配点。此外，考虑到边缘取点的均衡性，相邻水平线上的点分别取在椭圆的左半部分和右半部分。

根据这一系列边缘点的三维坐标拟合平面，本质上是一个最优化问题，即求出这一系列点 ${P_i}(i = 1, $ $ 2, \cdots ,n)$ 到某个平面 $ax + by + cz + d = 0$ 的距离 ${d_i}$ 之和最小，其中平面法向量取单位向量，则有 ${a^2} + {b^2} + {c^2} = 1$ 。

$\begin{split} \min \sum {d_i^2} = &\min \sum {\frac{{{{{\rm{(}}a{x_i} + b{y_i} + c{z_i} + d{\rm{)}}}^{\rm{2}}}}}{{{a^2} + {b^2} + {c^2}}}} =\\ &\min \sum {{{(a{x_i} + b{y_i} + c{z_i} + d)}^2}}{\text{，}}\\ &{\rm{s.t.}}\;{{a^2} + {b^2} + {c^2} = 1} {\text{。}}\end{split} $

(5)

其中， $(a,b,c)$ 为待拟合平面的法向量，即水下连接器的姿态， $({x_i},{y_i},{z_i})$ 为点 ${P_i}$ 的三维坐标。

由于这一系列点 $ （{x}_{i},{y}_{i},{z}_{i})$ 的平均值 $ （\overline{x},\overline{y},\overline{z})$ 在拟合的平面上，即 $a\bar x + b\bar y + c\bar z + d = 0$

故有

$\begin{split} \min \sum &{{{(a{x_i} + b{y_i} + c{z_i} + d{\rm{)}}}^{\rm{2}}}} =\\ & \min \sum {{\rm{[}}a{x_i} + b{y_i} + c{z_i} - } (a\bar x + b\bar y + c\bar z){]^2} =\\ &\min \sum {{{[a({x_i} - \bar x) + b({y_i} - \bar y) + c({z_i} - \bar z){\rm{]}}}^{\rm{2}}}}{\text{，}} \end{split} $

(6)

定义

${\mathit{\boldsymbol{A}}} = \left[ {\begin{array}{*{20}{c}} {{x_1} - \bar x}&{{y_1} - \bar y}&{{z_1} - \bar z}\\ {{x_2} - \bar x}&{{y_2} - \bar y}&{{z_2} - \bar z}\\ {\cdots}&{\cdots}&{\cdots}\\ {{x_n} - \bar x}&{{y_n} - \bar y}&{{z_n} - \bar z} \end{array}} \right],\;{\mathit{\boldsymbol{X}}} = \left[ {\begin{array}{*{20}{c}} a\\ b\\ c \end{array}} \right],\;{\mathit{\boldsymbol{X}}} = \left[ {\begin{array}{*{20}{c}} a\\ b\\ c \end{array}} \right]{\text{，}}$

(7)

则 ${\rm{min}}{\displaystyle\sum {{\rm{[}}a({x_i}-\bar x)+b({y_i}-\bar y)+c(z} _i}-\bar z){{\rm{]}}^{\rm{2}}}=\min {\left\| {{\mathit{\boldsymbol{AX}}}} \right\|^2}$ 。

对 ${\mathit{\boldsymbol{A}}}$ 做奇异值分解： ${\mathit{\boldsymbol{A}}} = {{\mathit{\boldsymbol{UD}}}}{{\mathit{\boldsymbol{V}}}^{\rm{T}}}$ ，其中 ${\mathit{\boldsymbol{U}}}$ 和 ${\mathit{\boldsymbol{V}}}$ 为酉矩阵，从而

$\begin{split}\min {\left\| {{\mathit{\boldsymbol{AX}}}} \right\|^2} = &\min {\left\| {{{\mathit{\boldsymbol{UD}}}}{{{\mathit{\boldsymbol{V}}}}^{\rm{T}}}{{\mathit{\boldsymbol{X}}}}} \right\|^2} = \min {\left\| {D{{{\mathit{\boldsymbol{V}}}}^{\rm{T}}}{{\mathit{\boldsymbol{X}}}}} \right\|^2} =\\ & \min {({{{\mathit{\boldsymbol{V}}}}^{\rm{T}}}{{\mathit{\boldsymbol{X}}}})^{\rm{T}}}{{{\mathit{\boldsymbol{D}}}}^{\rm{T}}}{{\mathit{\boldsymbol{D}}}}({{{\mathit{\boldsymbol{V}}}}^{\rm{T}}}{{\mathit{\boldsymbol{X}}}}){\text{。}}\end{split}$

(8)

其中： ${{{\mathit{\boldsymbol{V}}}}^{\rm{T}}}{{\mathit{\boldsymbol{X}}}}$ 是列向量，且 $\left\| {{{\mathit{\boldsymbol{V}}}^{\rm{T}}}{\mathit{\boldsymbol{X}}}} \right\| = 1$ 。 ${{\mathit{\boldsymbol{D}}}^{\rm{T}}}{\mathit{\boldsymbol{D}}}$ 是对角矩阵，假设对角元素是降序排列的，那么当且仅当 ${{\mathit{\boldsymbol{V}}}^{\rm{T}}}{\mathit{\boldsymbol{X}}} = $ $ {\left[ 0\;\; 0\;\; 1 \right]^{\rm{T}}}$ 时，目标函数取最小值。此时， ${\mathit{\boldsymbol{X}}} = [ 0\;\; 0 \;\; 1]^{\rm{T}}{\mathit{\boldsymbol{V}}}$ 。

由此可以根据水下连接器端面的椭圆边缘点坐标计算得出水下连接器的姿态。

2 实验与结果分析

为了验证本文方法位姿测量算法的有效性，设计并搭建了水下连接器位姿测量实验装置。该实验装置主要包括水箱、棋盘格标定板、水下连接器、固定装置及支柱，其中支柱与固定装置可以保证水下连接器的端面与棋盘格标定板处于同一平面。由于棋盘格标定板的格点可以方便的识别从而获得其三维坐标，因此棋盘格标定板可以作为测量的基准。

2.1 位置测量实验

在位置测量实验中，以棋盘格左上角格点为起点水下连接器中心点为终点，通过双目立体匹配分别求出水下连接器中心坐标与棋盘格左上格点坐标，根据两点距离公式求出其距离，并与实测距离进行比较。之后，调整水下连接器的位置，进行多次实验，相关实验数据如表1所示。

2.2 姿态测量实验

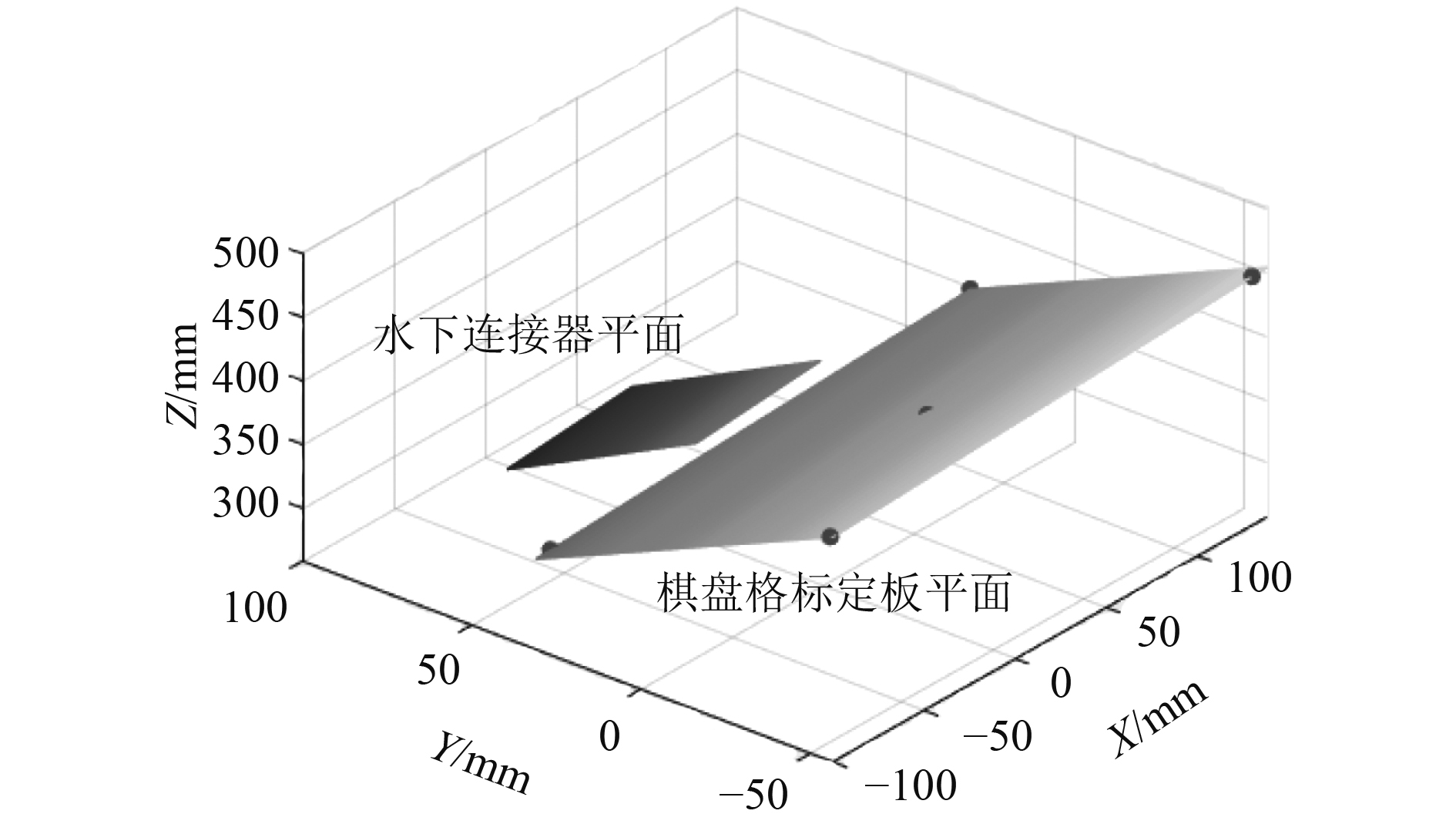
在姿态测量实验中，保持水下连接器端面与实验平台平面重合，改变双目相机的拍摄视角，从而模拟水下连接器的不同姿态。为验证本文算法的有效性，以棋盘格标定板法向量为基准，将其与本文算法计算得出的水下连接器法向量相比较，相关实验数据如表2所示，其中误差为两向量的夹角。图6展示了第4次实验两平面在三维空间的情况。

2.3 实验结果与误差分析

经过实验验证，本文设计的方法可以获得水下连接器在对接过程中的位姿信息，其中位置测量平均误差1.28%，姿态测量平均误差3.5°，从而为水下连接对接提供参考。其中误差的主要来源有：1）投影椭圆拟合误差，由于实验中水下连接器防水层存在一定厚度，投影椭圆实质上是椭圆环，因此会对椭圆检测造成干扰；2）相机标定误差，相机标定得到的内参数往往带有误差，通常情况下，在画面的中间成像效果会更好一些，表1中第3及第4次实验水下连接器在画面中间时误差较小也验证了这一点。

3 结　语

水下连接器对接作业是水下工程作业的重要环节，目前该作业主要由操作员根据水下摄像机传回的视频进行远程作业，这种作业方式存在操作难度大，依赖操作员经验的问题。为此本文将双目视觉测量技术用于水下连接器的对接作业，实验结果表明本文位姿测量方法在水下机械手作业范围内误差满足相关对接要求，可以较好地为水下连接器对接作业提供参考。