2. 浙江海洋大学,浙江 舟山 316022;
3. 银川能源学院,宁夏 银川 750105
2. Zhejiang Ocean University, Zhoushan 316022, China;
3. Yinchuan Energy Institute, Yinchuan 750105, China
国际海事组织IMO(International Maritime Organization)针对航运业温室气体排放制定了技术性国际海运GHG(Greenhouse Gas)条例[1-2]。同时,全球航运业市场低迷,竞争激烈,节能减排成为航运研究的重点。船舶纵倾优化是IMO推荐的船舶节能减排技术手段之一,可以在不改变船舶航速和载重量的情况下,通过调节船舶在航行中的纵倾角,减小其航行阻力。与其他节能减排的方法相比,具有成本低、易实现和效果佳等优点。由于受限于船型原因,很少有学者进行这方面的工作。
研究方法通常有模型试验和CFD(Computational Fluid Dynamics)数值计算,邵世明等[3]和邱斌彬等[4]通过对水池实验和实船试航数据证明了纵倾优化的有效性。宋磊等[5]、Coraddu等[6]和童骏等[7]以CFD方法和数据分析的方法,对于肥大型船舶纵倾优化进行了研究。集装箱船近年来大型化和快速化趋势日益明显,并且多以班轮运输方式运营,对纵倾优化的研究与应用有更多的需求。本文以标准船模KRISO Container Ship (KCS)集装箱船为对象,利用STAR-CCM+ RANS求解器对集装箱船纵倾优化进行数值研究,提出集装箱船经济航速时的最佳纵倾角,为集装箱船在实际营运中最佳纵倾操作提供建议。
1 船型尺度及特征本文选取KCS标准集装箱船进行研究,此船型是由韩国海洋与海洋工程研究所提供的比较研究船型,此船型具有大量实验和模拟数据可供检验和验证,是ITTC推荐船型之一。KCS集装箱实船船垂线间长230 m,型宽32.2 m,设计吃水10.8 m,设计航速为24 kn。为与实验数据进行对比,本文采用缩尺比为λ=31.6的模型,模型如图1所示,具体参数如表1所示。本文所用实验数据来源于KRISO和东京CFD研讨会。

|
图 1 船体几何模型 Fig. 1 Geometry model of ship's hull |
|
|
表 1 船模主要参数 Tab.1 Main parameters of ship's model |
采用RANS控制方程组,包括连续性方程和动量守恒方程,其不可压缩流体无量纲RANS方程的张量形式为:
| $\frac{{\overline {\partial {u_i}} }}{{\partial {x_i}}} = 0{\text{,}}$ | (1) |
| $\begin{split} \frac{{\partial \overline {{u_i}} }}{{\partial t}} + \overline {{u_j}} \frac{{\partial \overline {{u_i}} }}{{\partial {x_j}}} + \frac{{\partial \overline p }}{{\partial {x_i}}} - \frac{1}{{\operatorname{Re} }}\frac{{{\partial ^2}{u_i}}}{{\partial {x_j}\partial {x_j}}} - \frac{\partial }{{\partial {x_j}}}( - \overline {u_i'u_j'} ) = 0 {\text{。}} \end{split} $ | (2) |
式中:ui为雷诺平均速度分量;P为压强;
湍流模型计算中采用Realizable
考虑到计算效率,计算时采用的是对称模型,以船模中纵剖面为对称面。为避免计算域边界对计算的影响,本文根据以往研究者的经验[8],计算域入口在船首上游1.5Lpp,出口在船尾下游2.5Lpp,侧面距离船侧2Lpp,顶部距离自由液面1.5Lpp,底部距离船底表面2Lpp处,计算域设置如图2所示。边界条件设置如表2所示。

|
图 2 计算域设置 Fig. 2 Computational domain setting |
|
|
表 2 边界条件设置 Tab.2 Boundary condition setting |
为方便调整船舶纵倾,节省网格划分的工作量,对于船舶纵倾优化的研究采用重叠网格(Overset mesh)技术。计算域被分为背景区域和重叠区域。背景区域和重叠区域采用切割体网格进行网格划分,并为捕捉自由液面和准确的计算船舶周围流场,对自由液面和网格重叠的区域进行网格局部加密,船体周围的边界层网格采用棱柱层网格进行划分,并在船首和船尾流场的复杂区域进行局部网格加密,以捕获更多流动细节。
Realizable

|
图 3 计算域网格 Fig. 3 Computational domain grid |
计算域网格的划分与边界条件设置对计算求解精度与稳定性有很大影响[10],对初始状态为平吃水的KCS船模在不同傅汝德数下的船舶阻力进行计算,验证网格、边界条件和求解技术的准确性,并将总阻力、纵倾和下沉量的计算值与2015年东京研讨会[11]提供的实验结果进行对比。船舶总阻力系数Ct表达式为:
| ${C_t} = \dfrac{{{R_t}}}{{\dfrac{1}{2}\rho {U^2}{S_w}}}{\text{。}}$ | (3) |
式中:Rt为船舶总阻力;U为船模速度;ρ为水密度;SW为船模的湿表面积。
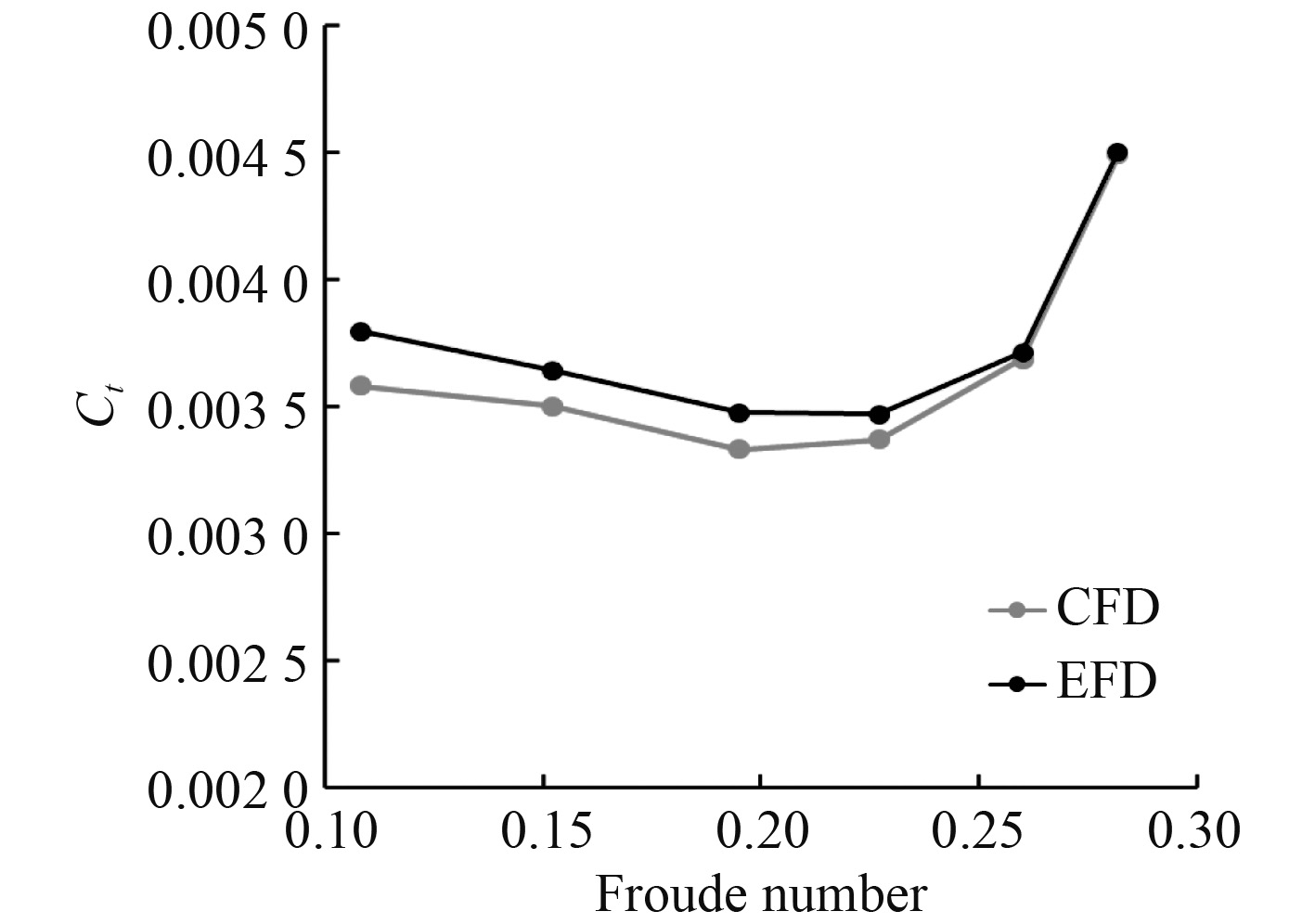
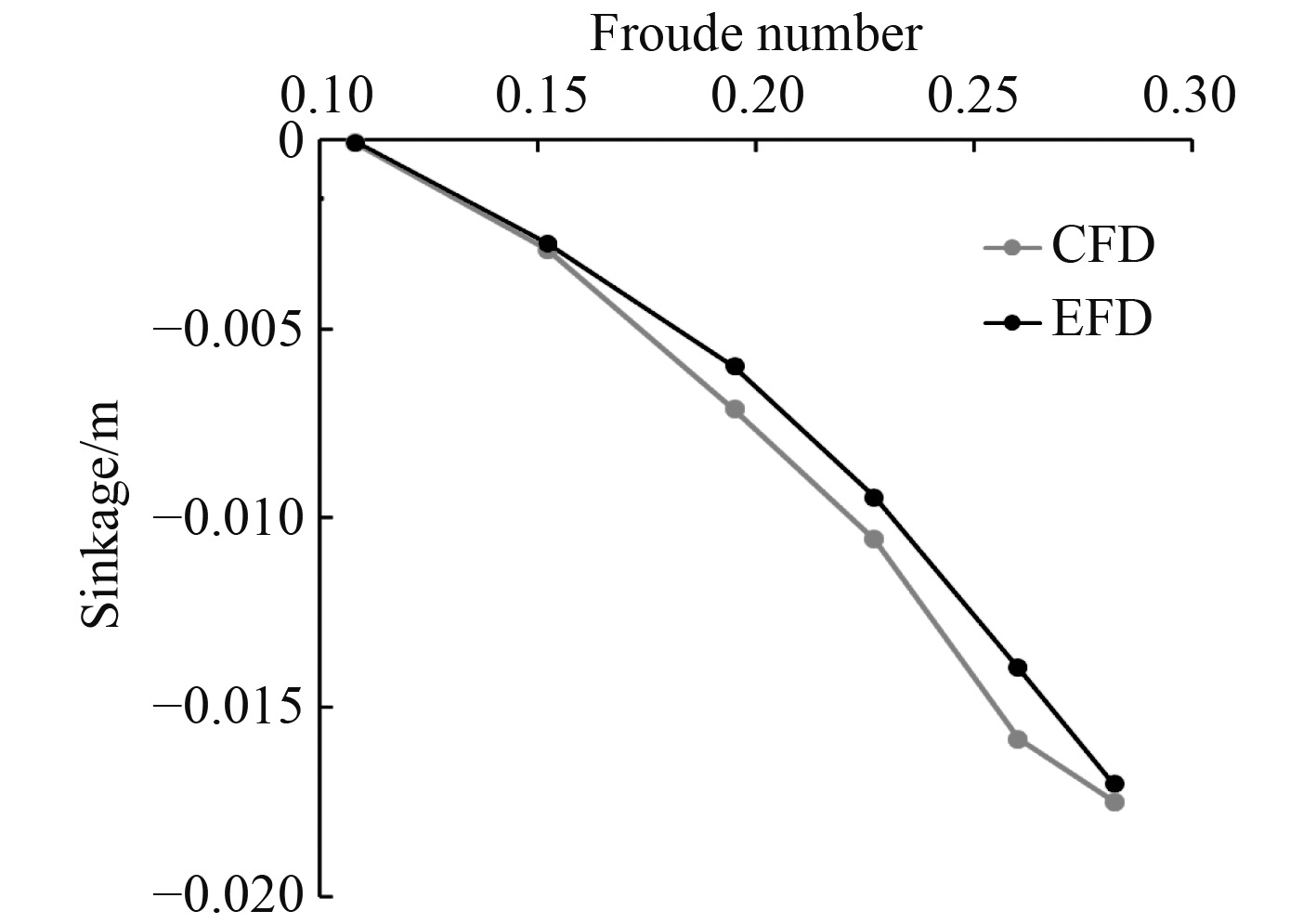
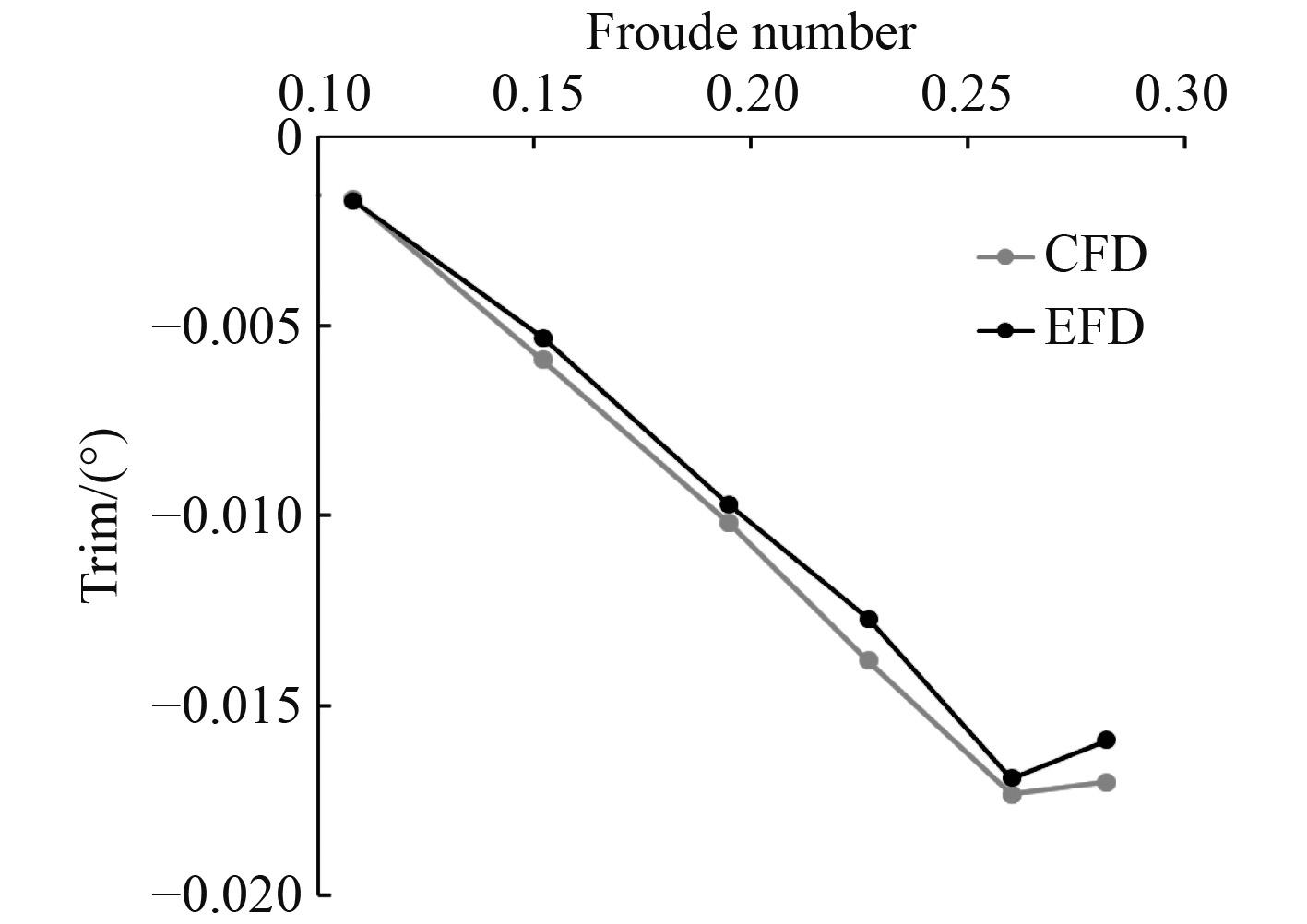
总阻力、纵倾和下沉量的数值计算结果与实验数据对比如图4~图6所示,通过图中数据对比,总阻力、纵倾和下沉量的计算值与实验数据十分接近,证明本文方法可以进行纵倾优化的数值计算。
|
图 4 总阻力系数对比 Fig. 4 Comparison of total drag coefficient |
|
图 5 下沉量对比 Fig. 5 Subsidence contrast |
|
图 6 纵倾对比 Fig. 6 Contrast of trim |
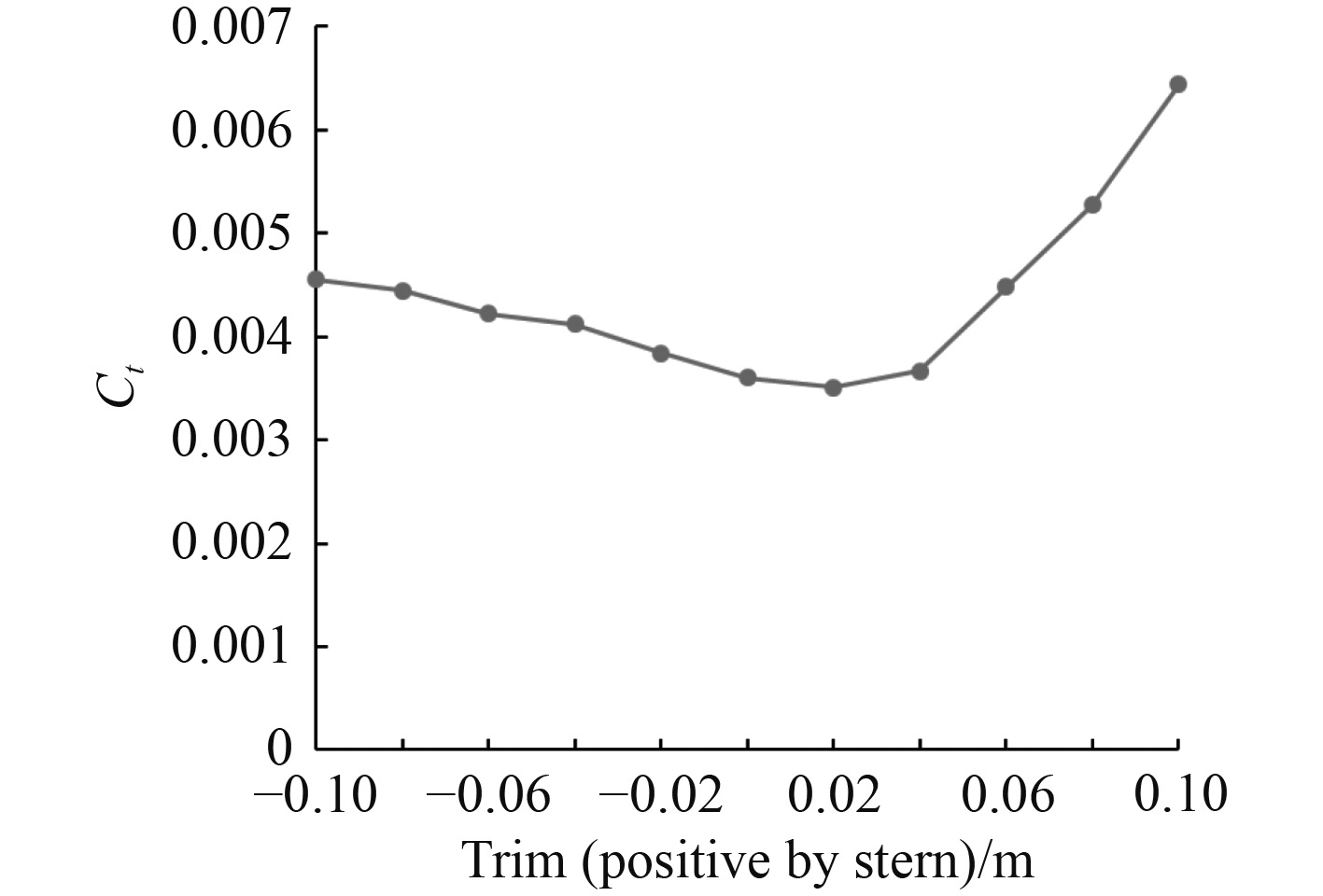
采用验证后的网格划分和数值方法,对不同纵倾条件下的KCS船模进行阻力计算,吃水状态为满载吃水0.34 m,纵倾值调节范围从0.02~0.1 m的尾倾和0.02~0.1 m的首倾,纵倾每次调节幅度为0.02 m,航速为Fn=0.227的经济航速。各纵倾状态下的船舶总阻力如图7所示,负值为首倾,正值为尾倾。
|
图 7 各纵倾下总阻力系数 Fig. 7 Total drag coefficient at each trim |
在经济航速时,以最大阻力值为基准,纵倾优化导致的阻力变化率如表3所示。
|
|
表 3 阻力变化率 Tab.3 Rate of resistance change |
与平吃水状态相比,当船舶处于首倾状态时,船舶总阻力随着首倾的增加而增加,当船舶处于尾倾状态时,随着船舶尾倾状态的增加,船舶总阻力先减小,当尾倾超过0.02 m后,船舶总阻力开始明显增加。最佳纵倾值为尾倾0.02 m,其阻力与阻力最大时相比减少约45.48%,阻力减小非常明显。考虑到船舶尾倾时,其螺旋桨推进效率更高,其节能减排的效果更好。
为分析不同纵倾下总阻力发生变化的原因,将总阻力Rt分为摩擦阻力Rf和剩余阻力Rr[12],阻力及其系数表达式如下:
| ${R_t} = {R_f} + {R_r}{\text{,}}$ | (4) |
| ${C_f} = \frac{{{R_f}}}{{\frac{1}{2}\rho {U^2}{S_w}}}{\text{,}}$ | (5) |
| ${C_r} = \frac{{{R_r}}}{{\frac{1}{2}\rho {U^2}{S_w}}}{\text{,}}$ | (6) |
| ${C_t} = {C_f} + {C_r}{\text{。}}$ | (7) |
|
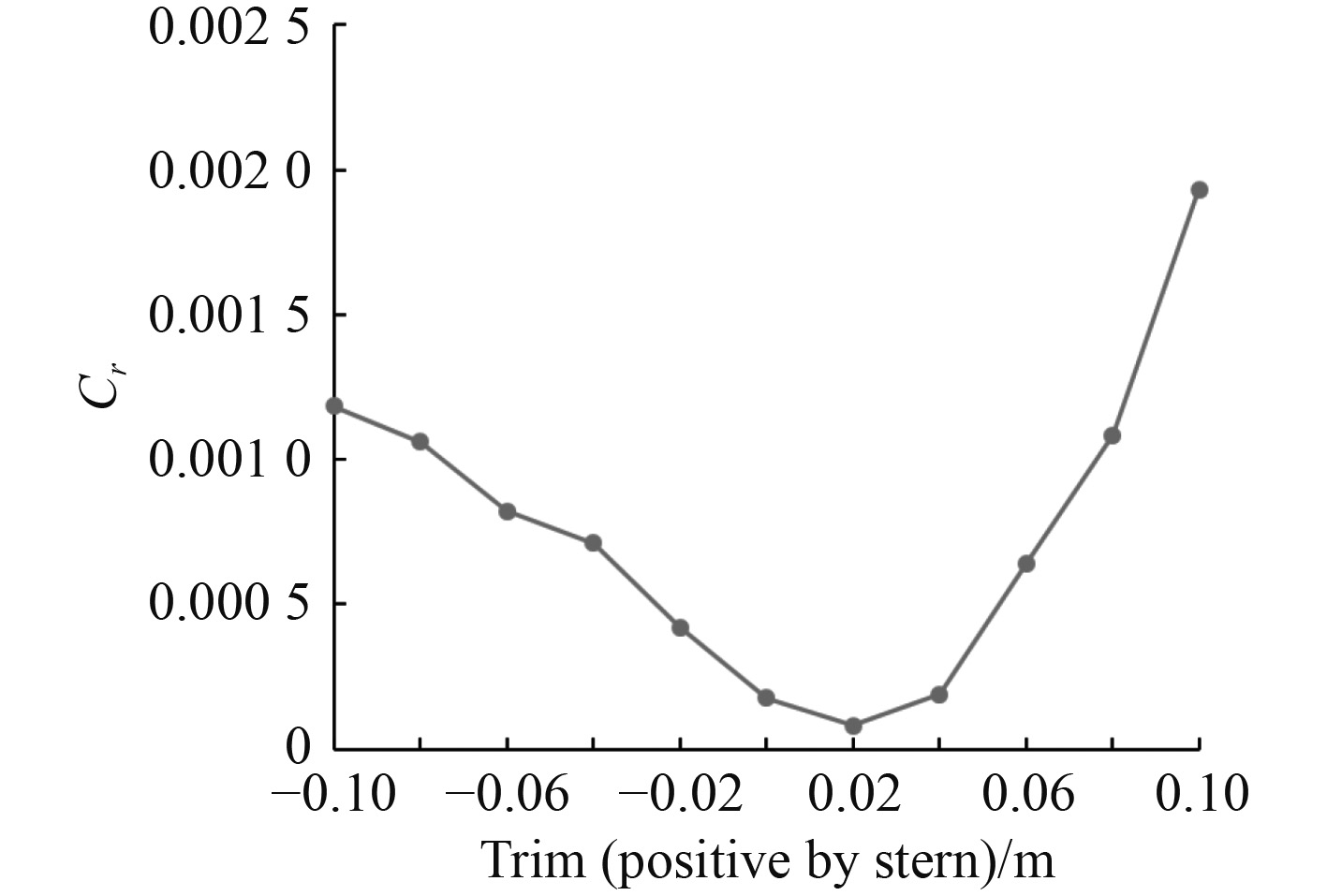
图 8 各纵倾下剩余阻力系数 Fig. 8 Coefficient of residual resistance at each trim |
|
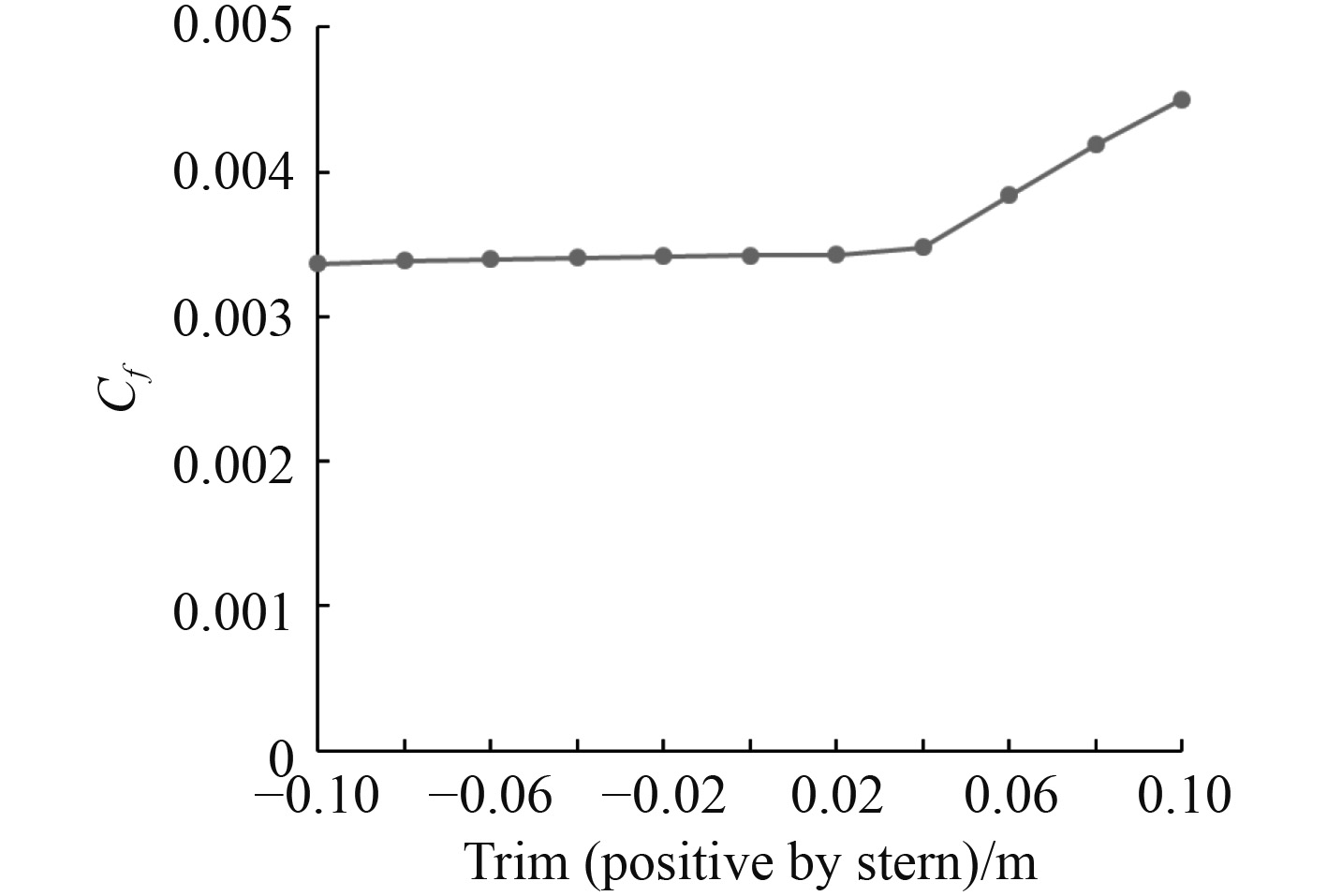
图 9 各纵倾下摩擦阻力系数 Fig. 9 Coefficient of frictional resistance at each trim |
通过图中数据,发现剩余阻力系数在船舶首倾和尾倾状态下,都随着纵倾值的增加,剩余阻力系数增加,尾倾状态比首倾状态剩余阻力增加明显。而摩擦阻力系数在船舶首倾状态时,随着首倾增加,摩擦阻力系数缓慢减少,当船舶尾倾时,随着尾倾的增加,摩擦阻力系数先平缓增加,后明显增加。可以看出,在首倾时,剩余阻力的变化决定了不同纵倾下总阻力的变化趋势,而在尾倾时,剩余阻力和摩擦阻力共同决定了不同纵倾下总阻力的变化趋势。这是由于船舶阻力与排水量、水深、船速和纵倾角有关。船舶在排水量一定的情况下,改变纵倾角,船舶水下部分几何形状发生改变,船体水线形状和水线长度、浮心位置、船首来流、船尾去流也相应改变,且尾倾时较首倾时变化更大,导致船舶航行时阻力发生改变。
4 结 语本文通过对调节纵倾来改善船舶总阻力的原理进行分析,以标准船模KCS集装箱船为对象进行船模阻力实验,采用RANS方法和Realizable
1)采用RANS方法和Realizable
2)排除水深影响,KCS集装箱船在不改变船舶航速、载重量的前提下,仅通过纵倾调节可以使船舶阻力达到最小,节能减排的作用明显;
3)试验以及仿真计算中所得减阻数据和结论可以为KCS集装箱船舶以及类似船舶的实际运营提供指导,船舶纵倾优化是一种不需要改变船体构造、不附加安装设备的节能方式,不仅不降低船舶载货量、不降低航速、易于实施,并且效果显著。
| [1] |
ENDRESEN, SORGARD E, BEHRENS H L, et al. A historical reconstruction of ships' fuel consumption and emissions[J]. Journal of Geophysical Research Atmospheres, 2007, 112(D12). |
| [2] |
BUHAUG, CORBETT J J. ENDRESEN, et al. Second IMO GHG study 2009[J]. Mepc, 2009. |
| [3] |
邵世明, 王云才, 钱章义, 等. 高速排水型艇的初始纵倾对阻力影响的试验研究[J]. 上海交通大学学报, 1996(10): 136-140. |
| [4] |
邱斌彬. 船舶纵倾优化[J]. 中国船检, 2014(2): 70-74. |
| [5] |
宋磊, 涂海文, 谢文雄, 等. 散货船纵倾阻力研究[J]. 舰船科学技术, 2016, 38(12): 48-52. |
| [6] |
CORADDU A, ONETO L, BALDI F, et al. Vessels fuel consumption forecast and trim optimisation: A data analytics perspective[J]. Ocean Engineering, 2017, 130: 351-370. DOI:10.1016/j.oceaneng.2016.11.058 |
| [7] |
童骏, 涂海文, 孙江龙. 船舶纵倾优化减阻数值模拟研究[J]. 自然科学版, 2018, 48(7). |
| [8] |
YANG L, ZHU P, QIN Z. Numerical analysis of ship hull resistance considered trims[C]//The 24th International Ocean and Polar Engineering Conference. International Society of Offshore and Polar Engineers, 2014.
|
| [9] |
张师帅. 计算流体动力学及其应用: CFD软件的原理与应用[M]. 武汉: 华中科技大学出版社, 2011.
|
| [10] |
邓锐, 黄德波, 周广利, 等. 影响船舶阻力计算的部分CFD因素探讨[J]. 船舶力学, 2013(6): 616-624. DOI:10.3969/j.issn.1007-7294.2013.06.004 |
| [11] |
Tokyo 2015 Workshop. [Online] 2015. http://www.t2015.nmri.go.jp/.
|
| [12] |
姜次平, 邵世明. 船舶阻力[M]. 上海: 上海交通大学出版社, 1985.
|
 2021, Vol. 43
2021, Vol. 43

