船舶的优化设计理论及技术在降低船舶建造成本和提高船舶整体性能方面已经卓有成效,其研究成果已经广泛地应用到散货、集装箱及油轮等船型的优化设计中。船体结构重量是关乎船舶经济性和环保性的重要因素,是衡量船舶设计方案优劣的重要指标。对于超大型油船,船体所受的静水弯矩是影响船体结构重量的重要因素,而货油舱分舱方案直接决定了静水载荷的大小和分布情况,从而影响静水弯矩的大小。因此,以较小静水弯矩为目标的分舱优化已成为船舶优化设计的重要研究方向。
尚宝国[1]重点研究超大型油船压载舱的分舱优化,考虑到超大型油船最大的中拱弯矩通常发生在压载出港时所有压载舱全满的URS11校核工况,针对性地提出一种压载舱分舱优化方案,实现降低船体最大静水中拱弯矩的目标。张建波等[2]针对变边舱分舱对降低总纵弯矩的影响进行了研究,通过对比筛选,得到一型可同时降低航行中拱与中垂弯矩、在港中拱弯矩的变边舱分舱方案。顾柳婷等[3]以船型、主尺度以及货油舱总舱容确定为前提条件,以静水弯矩最小为优化目标,并以满足意外溢油量和假定溢油量、破损稳性、完整稳性以及浮态等要求为限制条件,利用“穷举法”进行货油舱横舱壁位置的优化。袁永生等[4]针对散货船型,在NAPA中进行二次开发,程序实现以各货舱长度为变量快速生成分舱方案,以此建立22种分舱方案,通过比较各分舱方案的弯矩剪力极值,选定最优方案。
遗传算法是一种通过模仿自然界的选择与遗传的机理来搜索最优解的方法,目前逐步在船舶工程各领域获得应用。该方法在航线优化、压载水交换、主尺度确定、舱室布置、浮态和稳性计算以及结构优化等方面均获得良好应用[5]。本文将探索以NAPA三维设计软件为平台,通过二次开发实现分舱方案的参数化建模以及装载工况的自动计算。在此基础上,利用遗传算法进行以横舱壁位置为变量的静水弯矩最小为目标的分舱优化。
1 参数化分舱目前船舶设计中,设计者通常是在TRINBON或者NAPA等三维设计软件中,通过可视化手动建模或者利用写命令的方式进行分舱建模。这种方式建模周期较长,效率低,并且由于建模过程较为复杂,容易出错。因此,无法通过该方式实现大量的分舱方案研究。
本文应用NAPA的二次开发功能[6],实现以货舱区域横舱壁位置为变量的参数化分舱建模。若某VLCC货油舱区域分成n个货油舱段,则货舱区域各横舱壁位置为x(bh1), x(bh2), x(bh3), ……, x(bh(n-1))。在货油舱区域以外的其他舱室定义完成之后,给定各横舱壁位置数值,运行便可生成分舱模型。若修改横舱壁位置数值,运行后便可生成一个新的分舱模型。
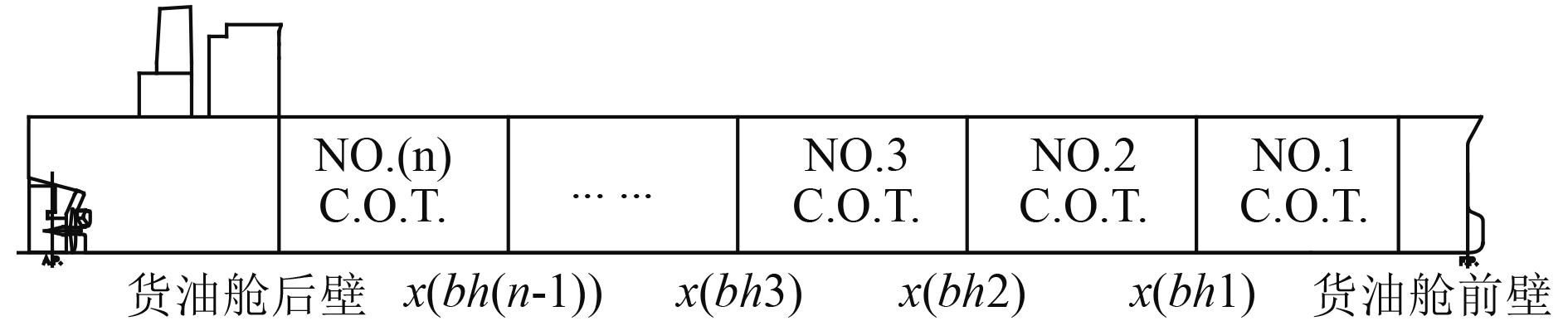
2 基于遗传算法的优化模型 2.1 设计变量本文的重点是VLCC货油舱的分舱优化设计。船舶主尺度、总布置、货舱数量及分舱型式是设计前提条件。当首尾防撞舱壁确定以后,货油舱长度由机舱长度决定,而机舱长度取决于机舱的布置需求。因此,可假设货油舱区域最前端舱壁和最后端舱壁的位置固定,只有货油舱区域内横舱壁位置可变。假设货油舱区域分成n个货油舱段,则优化参数为中间各横舱壁位置x(bh1), x(bh2), x(bh3), …… x(bh(n-1)),具体优化参数如图1所示。
|
图 1 优化参数示意图 Fig. 1 Optimization variable diagram |
相比静水剪力,静水弯矩是决定船体结构重量的主导因素,因此选择船体梁所受的静水弯矩最小作为优化目标。在一定的装载工况下,船体梁静水弯矩的大小主要取决于货物重量分布、船体结构自身重量分布以及船体所受浮力分布等因素的影响[3]。VLCC货油舱区域横舱壁位置的移动,主要是导致货舱区域货油以及压载水重量分布的变化,进而使得船体梁受到的静水弯矩变化。
通常VLCC需要考虑60多种装载工况,如果对所有工况都进行配载计算,将花费较长时间,遗传算法优化工程花费时间较长,不实用。而一般静水弯矩较大的极端工况主要是几种典型的装载工况。因此,为了提高优化效率,选择容易产生静水弯矩极值的几种典型装载工况进行配载计算。本文考虑的典型工况有:
1)夏季吃水均值满载出港、中途、到港状态;
2)设计吃水均值装载出港、中途、到港状态;
3)正常压载出港、中途、到港状态;
4)重压载出港、中途、到港状态;
5)H-CSR要求的针对部分压载的空满校核(URS11要求)。
船体梁受到的静水弯矩包括中拱弯矩和中垂弯矩。在NAPA中完成工况配载后,计算可得到沿船长各截面处所受到的弯矩值,负值的为中垂弯矩,正值的为中拱弯矩。中拱弯矩和中垂弯矩同时影响船体重量,因此,本文同时考虑中拱弯矩和中垂弯矩的优化。最终选择中拱弯矩和中垂弯矩极大值的绝对值,然后取二者的平均值BMave,作为优化目标。
2.3 优化流程遗传算法是模拟自然界生物遗传和进化过程而形成的一种全局优化搜索算法。首先经过种群初始化能得到一组初始种群,在种群中搜索局部最优解保存作为全局最优解,并对种群个体作选择、交叉、变异等操作得到下一代的种群。下一代种群中的局部最优解比较全局最优解并取代之,如此循环进化得到最终的最优解的个体。
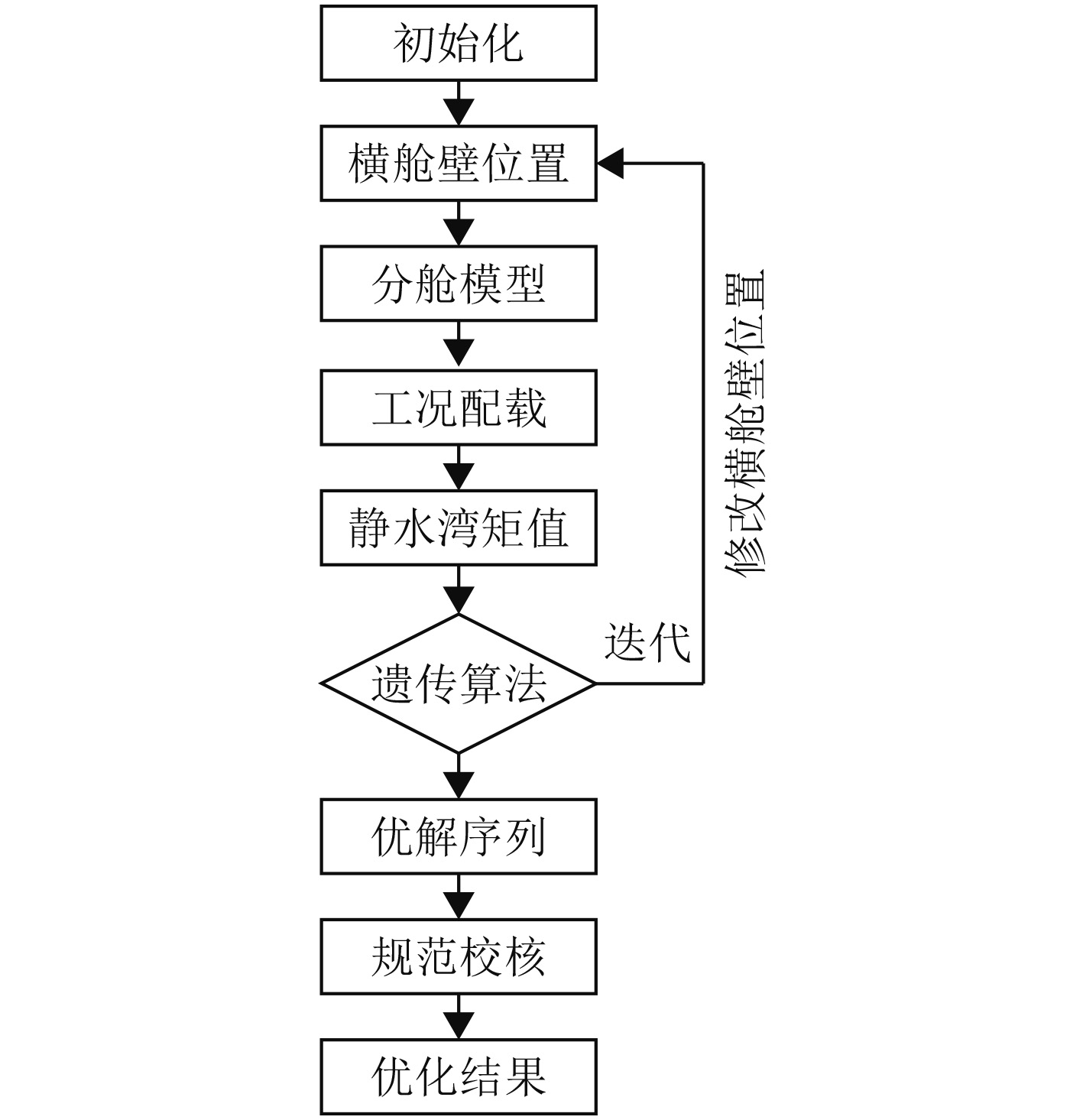
首先根据设计经验或参考母型船设定横舱壁初始位置,并根据规范要求及生产工艺限制设定变量的上下限。初始化是根据初始横舱壁位置生成初始分舱模型,并进行工况配载,计算得到初始BMave。遗传算法通过评估BMave进行设计变量的选择、交叉、变异,从而修改横舱壁位置,进而重新建模计算。如此循环迭代,直到优化得到满足条件的最优解或者达到迭代代数限制。遗传算法分舱优化流程如图2所示。
|
图 2 优化流程 Fig. 2 The process of optimization |
通过遗传算法优化,可得到关于横舱壁位置的一组最优解序列。但是根据有关规范公约规定,VLCC分舱还必须满足意外溢油量和假定溢油量、完整稳性以及破损稳性等方面的要求。最后对最优解序列按照倒序进行上述规范校核,剔除不满足要求的解,便可以得到优化结果。
3 VLCC优化计算实例 3.1 优化船型以32万吨VLCC为研究对象,进行分舱优化,其主参数见表1。
|
|
表 1 船型主参数表 Tab.1 Main dimensions of the ship |
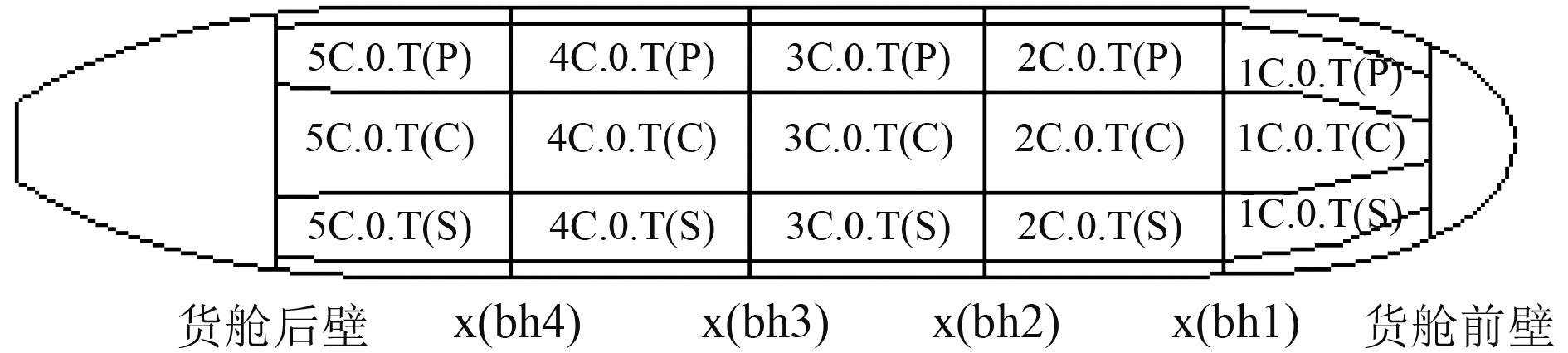
该型VLCC采用双底双壳结构,整个货油舱区域通过4道中间横舱壁、2道内壳纵舱壁以及2道中间纵舱壁,分成5个中货油舱和5对边货油舱。该型VLCC货油舱分布如图3所示。
|
图 3 某32万吨VLCC货油舱分布示意图 Fig. 3 Subdivision diagram of 320 K VLCC |
其中遗传算法的主要控制参数为群体规模、交叉概率、变异概率,研究表明合理参数范围为:种群规模M,20~100;交叉概率Pc,0.4~0.9;变异概率Pm,0.001~0.01[7]。本文遗传算法主要控制参数群体规模、交叉概率、变异概率,分别取值为20,0.9,0.01。
考虑实例船型装卸货操作便利性要求,限制2号、3号和4号货油舱舱长相同,仅1号和5号货油舱舱长可各不相同。因此,该实例优化设计变量简化为x(bh1)和x(bh4)。合理的设计变量取值范围可以提高遗传算法的搜索效率,并且确保得到足够有效的可行解。设计变量设定如表2所示。
|
|
表 2 横舱壁位置初始设定 Tab.2 Initial setting of transverse bulkheads |
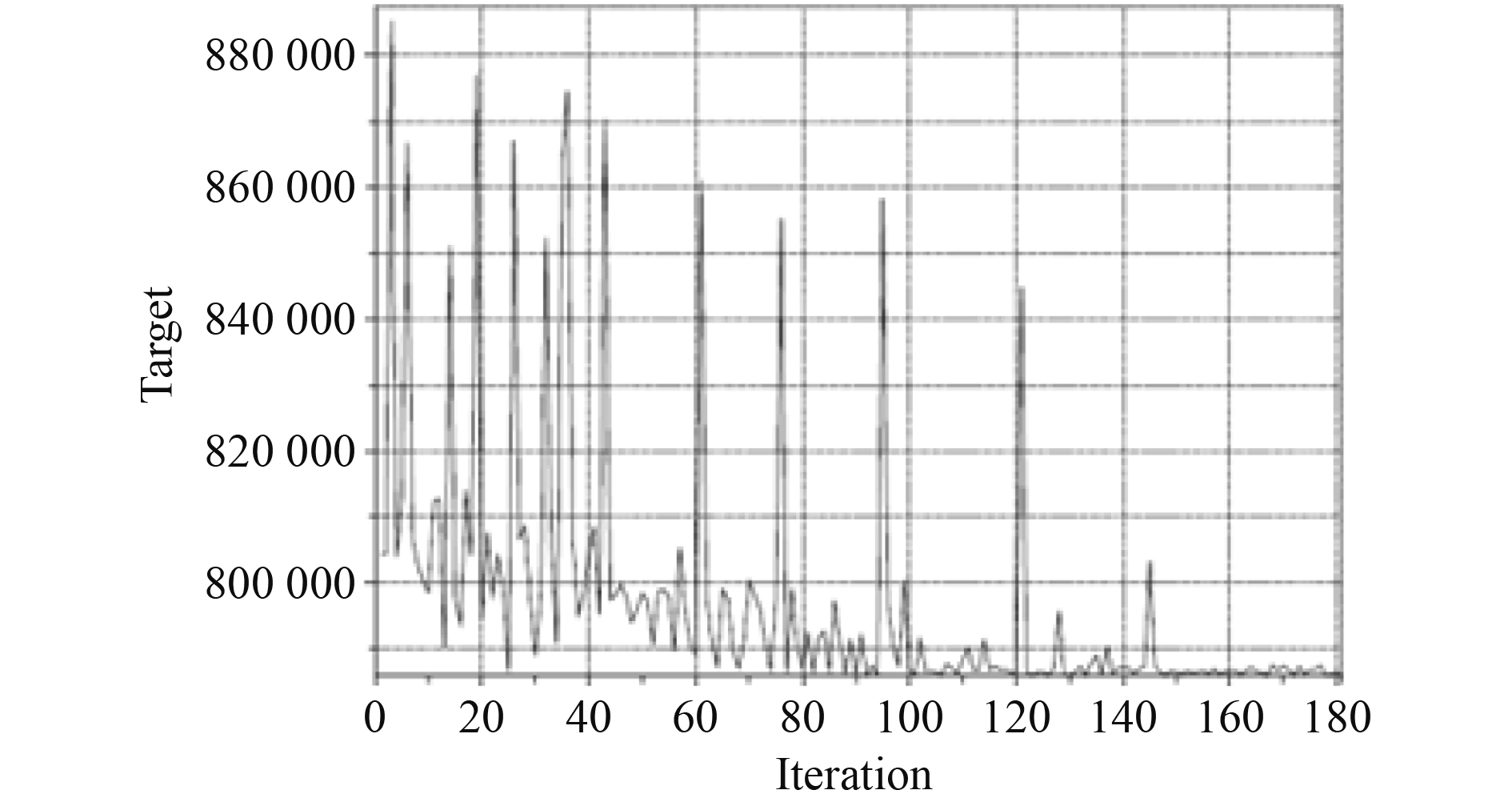
针对上述优化模型,利用遗传算法搜索最优解,优化目标随迭代过程变化如图4所示。
|
图 4 遗传算法优化过程 Fig. 4 Genetic algorithm optimization process |
随遗传迭代前进,优化目标呈减小趋势,并且最后趋于稳定。经校核,优化结果满足浮态、完整稳性、破损稳性、意外溢油量和假定溢油量等方面的要求。优化结果与初始值对比如表3所示,静水弯矩BMave经过优化,减小2.3%。
|
|
表 3 优化结果对比表 Tab.3 Comparison of the optimized result |
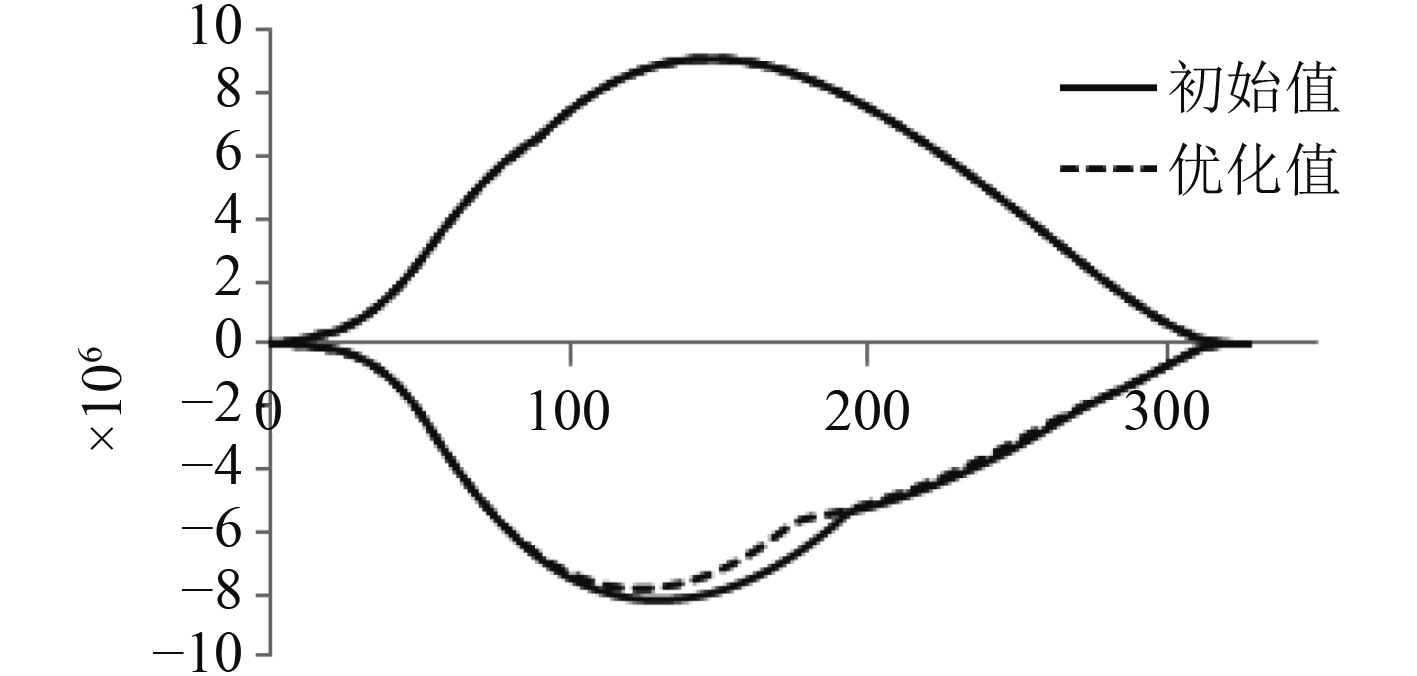
对比优化前后各典型工况弯矩极值包络线,如图5所示。
|
图 5 优化前后弯矩包络线对比图 Fig. 5 The bending moment envelop before and after optimization |
从图5可以看出,横舱壁位置优化对于各工况中拱弯矩极值包络线影响非常小,理论分析是因为中拱弯矩包络线由货舱区域所有压载舱均满的压载工况决定,而横舱壁位置的变化对该典型工况的静水弯矩几乎无影响;通过遗传算法优化,各典型工况中垂弯矩极值包络线整体明显减小。
4 结 语针对超大型油船,本文建立了以横舱壁位置为变量的参数化分舱建模方法,大大提高了建模效率,降低了人为差错率。同时,参数化分舱建模也是引入全局优化算法的前提条件。本文将遗传算法应用到超大型油船的横舱壁位置优化中,从而进行全局搜索最优解,大大提高了优化效率以及优化结果的质量。目前的分舱还处于经验决定或者采用局部优化策略等方式,因此,基于遗传算法的全局优化思路值得向分舱优化的其他领域推广应用,如双壳宽度优化,艏尖舱舱容优化等。
| [1] |
尚保国. 超大型油船压载水舱分舱的优化研究[J]. 船舶, 2011(6): 18-22. DOI:10.3969/j.issn.1001-9855.2011.06.005 |
| [2] |
张建波, 强兆新, 郝金凤, 等. 超大型油船分舱方案优化设计研究[J]. 中国造船, 2017(1): 125-134. DOI:10.3969/j.issn.1000-4882.2017.01.015 |
| [3] |
顾柳婷, 夏利娟, 刘奕谦. “穷举法”在油船货油舱分舱优化设计中的应用[J]. 船舶工程, 2017(3): 27-48. |
| [4] |
袁永生, 封毅, 苗文举, 等. 降低总纵弯矩的散货船分舱优化设计技术研究[J]. 舰船科学技术, 2015, 37(8): 40-44. DOI:10.3404/j.issn.1672-7649.2015.08.009 |
| [5] |
吕振望, 马坤, 姜彭, 等. 基于提高舰船不沉性的分舱优化[J]. 中国造船, 2015(3): 108-115. DOI:10.3969/j.issn.1000-4882.2015.03.012 |
| [6] |
NAPA. NAPA Manual[M]. 2019.
|
| [7] |
雷英杰. 遗传算法工具箱及应用[M]. 西安: 西安电子科技大学出版社, 2005.
|
 2021, Vol. 43
2021, Vol. 43
