2. 中国人民解放军驻葫芦岛地区军事代表室,辽宁 葫芦岛 125000
2. Huludao Military Representatives of the PLA, Huludao 125000, China
现代潜艇操纵面的设计已经不仅仅满足于操纵能力的要求,隐身性、安全性等性能愈受重视。传统的十字舵潜艇广泛应用的同时,X舵潜艇也被诸多潜艇强国采用。实际应用X舵潜艇的国家主要有荷兰、澳大利亚、以色列、瑞典、德国、日本和法国。从其外观设计上可以发现:X舵设计为全动舵,底部有很小的基座,几何尺寸上不超过艇宽,与艇体纵中剖面成45°交叉布置。从国外X舵成功应用以及目前的广泛应用趋势,表明其必然有相比于十字舵巨大优势。为探究X舵的优势,推进X舵在我国潜艇上的实际应用,国内许多学者做了大量的研究工作。
国外比较有参考意义的一些资料来源于欧洲防务署制定的由意大利和挪威负责的关于潜艇尾操纵面的X型布置与十字型布置操纵性与稳定性的CFD仿真研究项目。国内学者对X型尾操纵面的布局做出了一些基础性的理论研究工作。2003年胡坤等[1]提出等效舵角转换的设计理念,建立起了X型与十字型尾操纵面的数学关系模型,降低了人工操纵的难度;2006年王京齐等[2]对X舵操纵特性做了初步的分析并潜艇尾操纵面发展状况进行了研究,主要概述了十字型和X型尾操纵面之间的区别,提出了X型尾操纵面的优势,为其理论设计提供了重要依据;2007年胡坤等[3]概括了X舵发展概况并对其操纵特性做了初步分析;2008年胡坤等[4]进一步对X舵与十字舵舵角相互转换的数学模型进行了模拟分析,论证了等效舵角方法的有效性。此外,2006年李艳等[5]在数值模拟带附体潜艇的尾流场时,利用SUBOFF标模和在其基础上将尾操纵面旋转 45°得到的X舵潜艇的尾流场,得出二者尾流场相差不大;2017年张露等[6]利用CFD方法对SUBOFF模型2种设计的水动力性能进行了初步的数值计算,得出由十字舵直接变化旋转45°得到的X舵潜艇升力性能更优。
针对X舵的稳定性相关工作还没有开展这一问题,在原有十字舵潜艇的基础上设计X舵潜艇,并分析二者的航向稳定型性差异。
1 SUBOFF模型的数值模拟及验证静态模拟同平面运动机构(PMM)模拟相结合可以方便快速求取与潜艇方向稳定性相关的水动力导数。利用SUBOFF标模的相关实验数据对表1中数值模拟结果做全面验证分析,从而考核湍流模型、网格划分、边界条件等物理参数设置。分析得到的结果可以为后续数值模拟做铺垫,增强模拟结果的可信度。
|
|
表 1 模拟矩阵 Tab.1 Simulation matrix |
计算模型利用SBUOFF AFF-8(见图1)与SUBOFF_HSCR(见图2)潜艇模型,SUBOFF潜艇模型由美国泰勒舰船研究中心(DTRC)设计,泰勒水池以SUBOFF模型做了大量系列试验,SBUOFF AFF-8是其中带有指挥台围壳以及4个尾部操纵面的模型,习惯称其为全附体。实际上,还有装有导流管以及支架的SUBOFF,文中称其为SUBOFF_HSCR。SBUOFF AFF-8主艇体长L为4.356 m,其中前体长1.016 m,平行中体长2.229 m,后体长1.111 m,最大直径2R=0.508 m;指挥台围壳长0.368 m,高0.460 m,上部覆有2:1椭圆形横截面的顶盖;截面为NACA0020的4个尾操纵面十字型对称布置在尾部,顶端弦长0.152 m,。SUBOFF_HSCR在艇尾部分增加了X型支架和导管(Ring wing No.1),详细的几何特征可以查看Groves报告[7]。

|
图 1 SUBOFF AFF-8 模型 Fig. 1 Model of SUBOFF AFF-8 |

|
图 2 SUBOFF_HSCR尾部 Fig. 2 Stern of SUBOFF_HSCR |
SUBOFF AFF-8的主附体表面压力系数,尾流场状况的实验数据全面;SUBOFF_HSCR在垂直面与水平面稳定性与操纵性研究的数据全面。可以分别利用2个模型来做相关数值模拟结果的可行性验证分析。
1.2 计算方法以及计算域网格划分利用STAR-CCM+流体力学计算软件,采用RANS方法,湍流模型利用SST
网格的设置大体上参考文献[8],并依据式(1)和式(2)做适当调整。其中,
| $\Delta y = L\Delta {y^ + }\sqrt {80} \operatorname{Re} _L^{ - 13/14}{\text{,}}$ | (1) |
| ${\delta _0} = 0.035L\operatorname{Re} _L^{ - 1/7}{\text{。}}$ | (2) |

|
图 3 SUBOFF AFF-8 中纵剖面网格 Fig. 3 The longitudinal mesh of SUBOFF AFF-8 |

|
图 4 SUBOFF_HSCR网格 Fig. 4 The mesh of SUBOFF_HSCR |
斜航数值模拟包括水平面变漂角以及垂直面变攻角2种,DTRC所公布的 SUBOFF实验资料详细记录了斜航相关的数据,为验证数值模拟的准确性提供了途径。
由于潜艇左右对称,侧向力
| $\left\{ \begin{gathered} {Y'} = Y_v'{v'} + Y_{vvv}'{v^{'3}}{\text{,}} \\ {N'} = N_v'{v'} + N_{vvv}'{v^{'3}}{\text{,}} \\ \end{gathered} \right.\left\{ \begin{gathered} {Y'} = Y/0.5\rho {V^2}{L^2} {\text{,}} \\ {N'} = N/0.5\rho {V^2}{L^3}{\text{,}} \\ {v'} = v/V {\text{。}} \\ \end{gathered} \right.$ | (3) |
其中
计算结果同试验值比较,如表2所示。
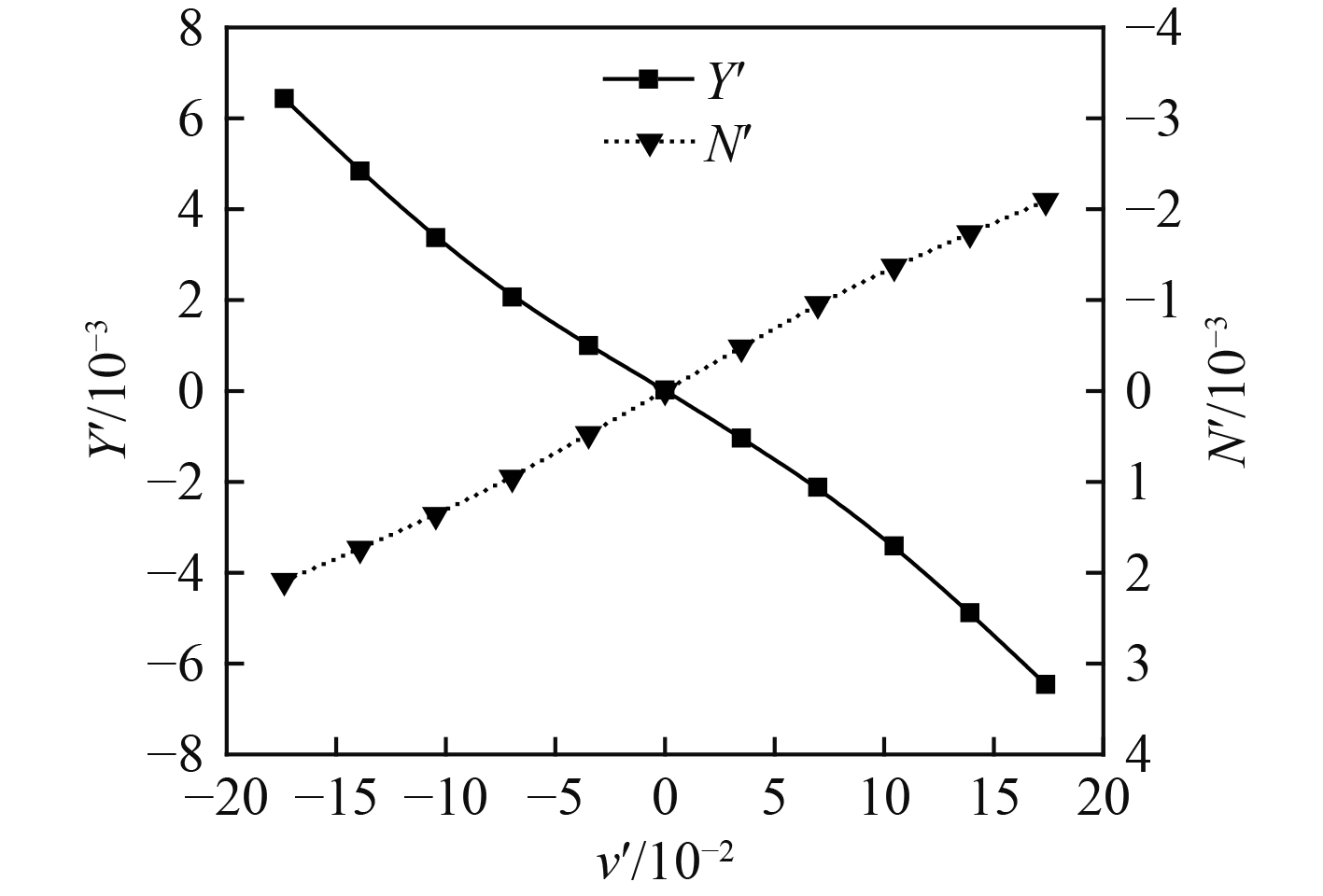
|
图 5 侧向力与摇首力矩系数计算值 Fig. 5 Calculated results of lateral force and yaw moment |
|
|
表 2 水平面速度导数CFD结果同实验值比较 Tab.2 Comparison of horizontal velocity derivative between CFD and experiment |
对于潜艇在垂直面的水动力方程可写为:
| $\left\{ \begin{gathered} {{\rm{Z}}'}=Z_0'+Z_w'{w'}+Z_{www}'{w^{'3}} {\text{,}} \\ {M'}=M_0'+M_w'{w'}+M_{www}'{w^{'3}} {\text{,}} \\ \end{gathered} \right.\left\{ \begin{gathered} {Z'}=Z/0.5\rho {V^2}{L^2}{\text{,}} \\ {M'}=M/0.5\rho {V^2}{L^3}{\text{,}} \\ {w'}=w/V {\text{。}} \\ \end{gathered} \right.$ | (4) |
其中,
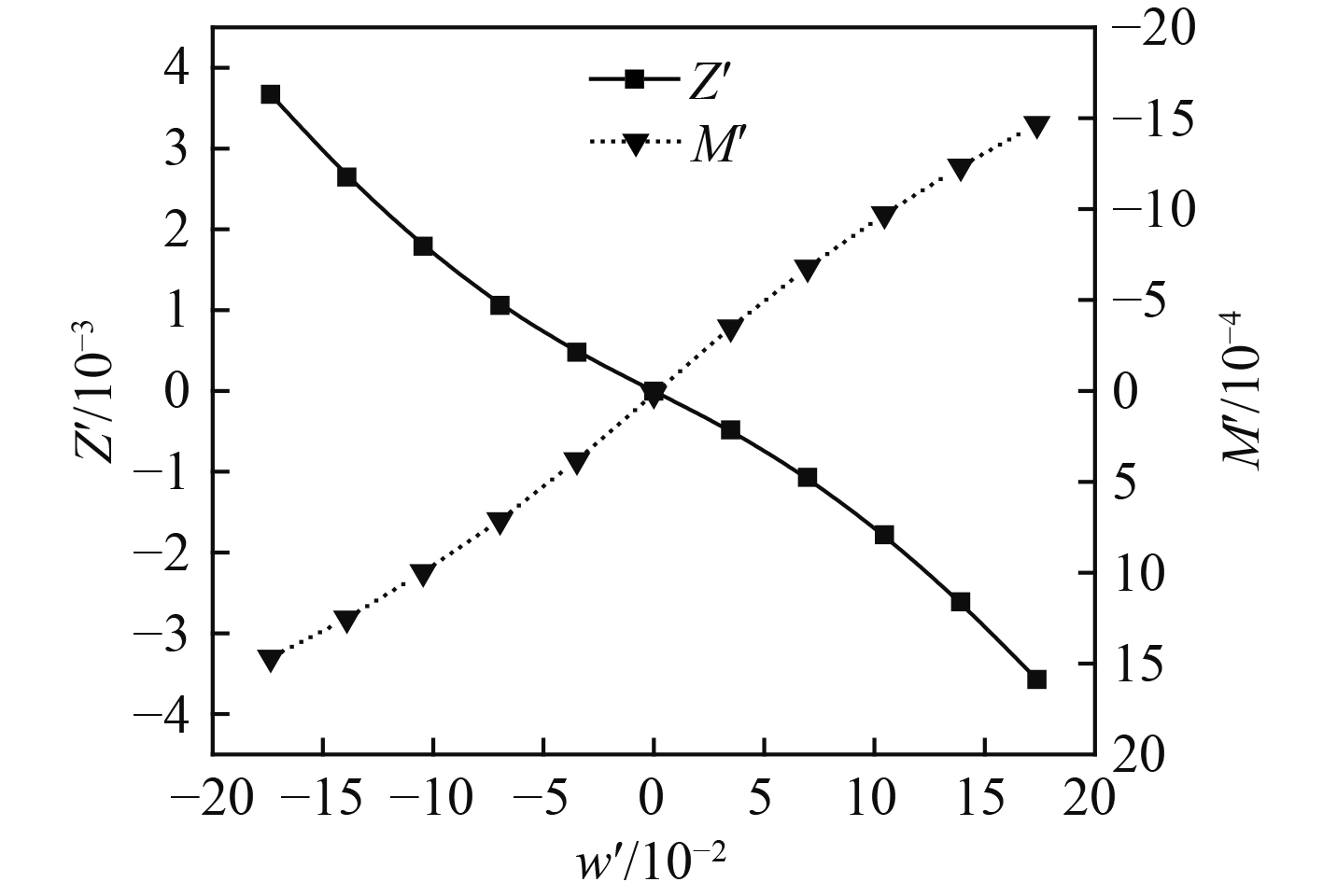
|
图 6 垂向力与纵倾力矩系数计算值 Fig. 6 Calculated results of vertical force and pitch moment coefficient |
计算结果同试验值比较结果如表3所示。
|
|
表 3 垂直面速度导数CFD结果同实验值比较 Tab.3 Comparison of vertical velocity derivative between CFD and experiment |
纯首摇这一运动用于求解艇体的旋转水动力导数,对潜艇的运动形式要求较高。相比于Fluent流体力学计算软件,STAR-CCM+在模拟纯首摇运动时更加智能。只需要勾选纯首摇选项,设置首摇频率、前进速度、横向振荡幅值就可以模拟出这一运动。纯首摇(俯仰)运动轨迹如图7所示。
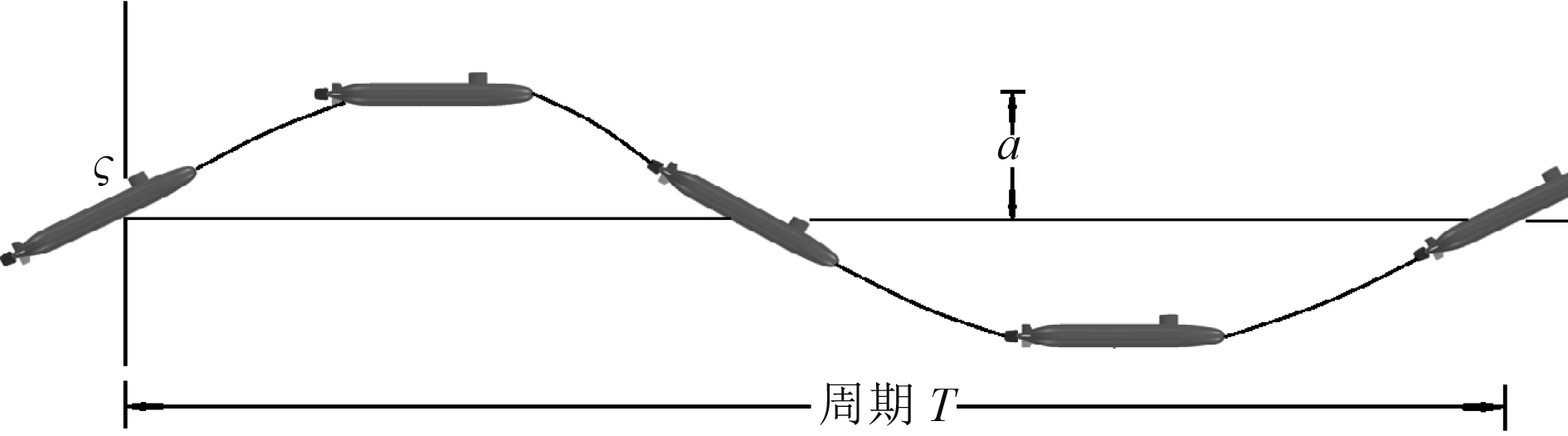
|
图 7 潜艇纯首摇俯仰(俯仰)运动轨迹 Fig. 7 Trajectory of submarine during pure yawing (pitching) test |
|
|
表 4 纯首摇水动力导数CFD结果与实验值比较 Tab.4 Comparison of hydrodynamic derivative of pure yaw motion between CFD and experiment |
根据诸多研究给出的水动力导数对以水动力导数为基准的数学模型仿真研究结果,本文中对水动力导数的求解精度满足工程需要,可以指导目标艇的研究设计。
1.6 水平面稳定性验证分析为了分析潜艇在水平面的稳定性,DTRC报告定义水平面稳定性指数如下:
| ${G_h} = 1 - N_v'(Y_r' - {m'})/\left[ {{Y_v}'(N_r' - {x_G}'{m'})} \right]\text{。}$ | (5) |
将求得的水动力导数代入稳定性衡准公式(3)得到表5。
|
|
表 5 稳定性指数 Tab.5 Stability index |
表中负值表示潜艇的布置不具备方向稳定性,泰勒水池实验值为计算结果提供了有力的支撑。尽管计算结果同实验值有一定误差,但基于同一种方法、同一套网格来分析不同布置下潜艇的稳定性是可行的。
2 X舵潜艇与十字舵潜艇航向稳定性分析用于分析的基准模型为某型潜艇。以基准艇(见图8)为基础设计了X舵潜艇(见图9),在主艇体以及其他附体相同的情况下,舵的投影面积对潜艇的稳定性起到决定性作用。在设计X舵潜艇时,保持X舵与十字舵具有相同的正投影面积,以建立在航向稳定性上的比较基础。此外,X舵采用全动舵形式:对于十字舵潜艇来说,较大的垂直舵面积较小的稳定翼面积对稳定性和机动性都是有利的。同样,X舵在设计上采用全动舵的形式可以充分兼顾稳定性和机动性能。

|
图 8 某十字舵潜艇 Fig. 8 A c-rudder submarine |

|
图 9 X舵潜艇 Fig. 9 X-rudder submarine |
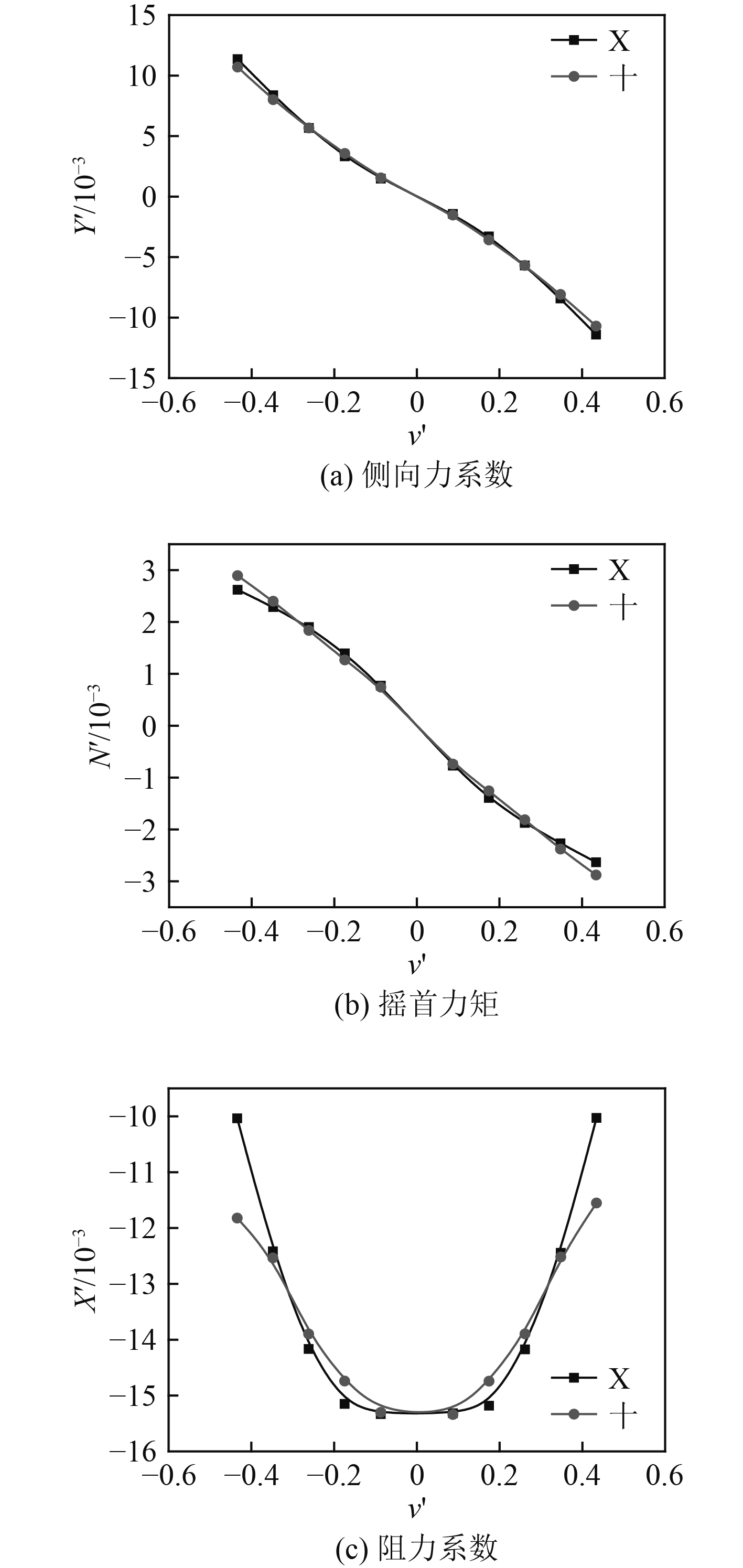
|
图 10 十字舵与X舵潜艇水动力系数计算值 Fig. 10 Calculated results of hydrodynamic coefficients of the c-rudder and x-rudder submarine |
设计时以十字舵潜艇的水平操纵面(水平舵和稳定翼组合体)为基础,将其旋转45°,再沿着舵轴方向三维缩放至不超艇宽的最大位置,最后根据投影面积将舵沿着艇轴方向进行二维缩放。这个过程保证了舵梢至舵根相应比例位置舵型不变,弱化了设计过程对单独舵水动力特性的影响。X型尾操纵面舵轴的位置接近舵的水动力中心,对实际舵轴的选择具有参考意义。
2.1 数值模拟结果|
|
表 6 水平面速度导数CFD结果 Tab.6 The CFD results of horizontal velocity derivative |
|
|
表 7 垂直面速度导数CFD结果 Tab.7 The CFD results of vertical velocity derivative |
稳定性是潜艇的固有属性,需满足一定的设计要求。为了综合分析2种尾操纵面构型潜艇的直线稳定性,利用潜艇的直线稳定性指数
| ${C_H} = \frac{{N_r'}}{{Y_r' - m'}} - \frac{{N_v'}}{{Y_v'}}{\text{。}}$ | (6) |
其中,
指数
表 8的结果说明了潜艇稳定性指数允许有较小的负值。这是因为实际潜艇的操纵经验表明,为了追求潜艇的灵活性,并不要求潜艇是静稳定的,甚至于航向稳定性指数也不一定为正,可以是一定的负值。一般来说,在设计时根据文献[11]给出建议:
|
|
表 9 稳定性指数分析 Tab.9 Analysis of stability index |
由计算结果可知,X舵的设计使得潜艇的倾覆力臂增加,对潜艇的方向稳定性不利。但X舵潜艇的稳定力臂增加更多,对潜艇的航向稳定性产生较大的有利影响。综合来看,X舵潜艇相对于十字舵潜艇的稳定性增加0.22960。从设计上对2种构型航向稳定性产生差异的原因进行深入分析:
1)尾操纵面远离艇体水动力中心,其构型对潜艇稳定性影响大;
2)X舵采用全动舵式的设计、对角化的布置,增加了舵的迎流面积,使得潜艇在零舵角有漂角来流时潜艇首部更易向来流方向旋转。通过水平面变漂角模拟求解结果体现的就是这一点,这个原因使得X舵潜艇相比于十字舵潜艇倾覆力臂增加;
3)当潜艇受到扰动,操纵面相对来流产生攻角,X舵相比于十字舵的更大迎流面积,并且4个舵同时产生恢复性的舵力,使其恢复力臂更大。
综合结果表明:X舵潜艇虽然变得容易被侧向来流扰动了,但一旦潜艇方向改变便会产生更大的恢复力矩,使得潜艇快速稳定下来,快速稳定的潜艇在新的航向上保持直线航行。本文设计的X舵潜艇,满足航向稳定性要求,并可以增加航向稳定性。
| [1] |
胡坤, 宗方勇, 庞晓楠. X舵潜艇等效舵角转换装置设计研究[J]. 船海工程, 2003(6): 19-21. DOI:10.3963/j.issn.1671-7953.2003.06.008 |
| [2] |
王京齐, 李亚楠. 潜艇X型艉操纵面的操纵特性[J]. 船海工程, 2006, 35(2): 1-3. DOI:10.3963/j.issn.1671-7953.2006.02.001 |
| [3] |
胡坤, 徐亦凡, 王树宗. 潜艇X舵发展概况及其操纵控制特性分析[J]. 中国造船, 2007, 48(2): 130-136. DOI:10.3969/j.issn.1000-4882.2007.02.017 |
| [4] |
胡坤, 王树宗. 水下航行体X型正交舵控制参数设计研究[J]. 船海工程, 2008, 37(3): 127-131. DOI:10.3963/j.issn.1671-7953.2008.03.038 |
| [5] |
李艳, 姚震球. 带附体潜艇艉流场的数值模拟与验证[J]. 自然科学版, 2006(2): 7-12. |
| [6] |
张露, 肖昌润, 焦玉超. 十字舵与X舵潜艇的水动力性能数值比较[J]. 舰船科学技术, 2017, 39(7): 24-28. |
| [7] |
GROVES N C, HUANG T T, CHANG M S. Geometric characteristics of DARPA SUBOFF models[R]. Report DTRC/SHD1298-01, 1989.
|
| [8] |
叶金铭, 张凯奇, 于安斌. 基于STAR-CCM+的全附体潜艇艉流场数值分析[J]. 海军工程大学学报, 2017, 29(4): 53-58. |
| [9] |
GJB64.2-85潜艇船体规范及编制说明书. 北京: 国防科工委, 1985.
|
| [10] |
现代潜艇技术与战术. 海军装技部舰艇部, 1991.
|
| [11] |
R K 伯切尔. C V 贝茨. 潜艇设计教程. 今日潜艇, 1988.
|
 2021, Vol. 43
2021, Vol. 43
