自二战以来,水下特种作战在各国海军的水下攻防作战中越来越受到重视。这一作战方式主要通过微型特种潜艇或蛙人输送艇将作战人员隐蔽送至敌方港口、海上经济设施等重要目标并对其实施侦察破袭等任务[1],曾多次在历史上留下辉煌战绩。在此种作战方式里,为便于隐蔽,输送艇的尺寸远小于常规潜艇[2],目前各国用于特种作战的微型特种潜艇(或蛙人输送艇)长度一般都较短,搭乘人员为2~8人。
在执行上述任务的过程中,特种作战人员全员离艇前需考虑将艇停靠在近海底的固定位置以便于作战人员寻艇返回。一个可靠的方法是作战人员驾乘潜艇航行至目标海底区域上方,然后通过增减压载来调节潜艇的负浮力进行下潜,最终在水下坐底并可借助锚固定。下潜的过程中,潜艇的速度会受到由于自身向下运动而引起的流体动力影响,流体动力产生的纵倾力矩也可能会改变潜艇的姿态甚至导致失控,对艇内人员造成生命威胁,这需要潜艇在下潜前预设控制好首、尾水舱内的进水量,以平衡下潜时产生的流体阻力及纵倾力矩,维持艇体姿态稳定。
针对潜艇的运动研究,水下实物试验费用高昂,需要耗费大量人力及物力,计算流体力学技术的快速发展让数值计算模拟在船舶运动及流场分析的研究中得到广泛应用。Pan等[3]通过拘束模及数值模拟方法得到了潜艇模型的水动力系数等参数;B.PULL[4]比较了全附体潜艇模型分别应用SST
直接数值模拟法(Direct Numerical Simulation, DNS)是最为基本的湍流研究方法,但计算量非常大,会占用大量计算成本。本文采用雷诺平均法(Reynolds-averaged Navier-Stokes, RANS)模拟求解潜艇在稳态条件下的流场,湍流模式选用SST
SUBOFF为美国国防预研规划署(DARPA)和大卫·泰勒研究中心(DTRC)设计的潜艇试验模型,本文选用其中带有指挥围壳和4个尾翼的AFF-8全附体潜艇模型为研究对象。
该潜艇模型分前中后3段,分别长1.016 m,2.229 m,1.111 m,中段上方有一指挥围壳,围壳上部有一外凸形顶盖,4个尾翼截面为NACA0020翼型,呈十字型分布在尾部,基本几何参数见表1,其他详细几何特征数据参见文献[7],利用三维制图软件绘制几何模型如图1所示。
|
|
表 1 潜艇模型几何数据 Tab.1 Geometric data of submarine model |

|
图 1 SUBOFF AFF-8全附体模型 Fig. 1 The full appendage model of SUBOFF AFF-8 |
为便于运动仿真求解,对仿真条件做出如下假设:
1)视水为不可压缩流体;
2)潜艇表面光滑无缝隙;
3)潜艇无动力做稳定下潜运动,即水平速度为0,垂向速度恒定。
2 计算域及网格划分 2.1 计算域尺寸为了模拟潜艇稳态下潜的流场,进行数值仿真时需要建立一个合适大小的计算域。由于流动关于潜艇的纵剖面对称,所以本文只采用一半模型进行模拟,建立计算域尺寸为3 L×3 L×L,如图2所示。

|
图 2 计算域大小和边界条件 Fig. 2 Computational domain and boundary conditions |
网格形式主要选取表面重构、自适应切割体网格及棱柱层网格对计算域及艇体表面进行网格划分。表面重构可以为潜艇表面生成良好的面网格;切割体网格技术保证了六面体网格的优良性;棱柱层网格主要在潜艇近壁面生成贴体网格;同时进一步对计算域中艇所在位置的水平方向和垂直方向上的网格体积细化,围壳和尾翼的表面和附近区域也做了网格加密处理,最终生成的网格如图3,总网格数约为180万。

|
图 3 计算域体网格及艇表面网格 Fig. 3 Mesh for submarine surface and computation domain |
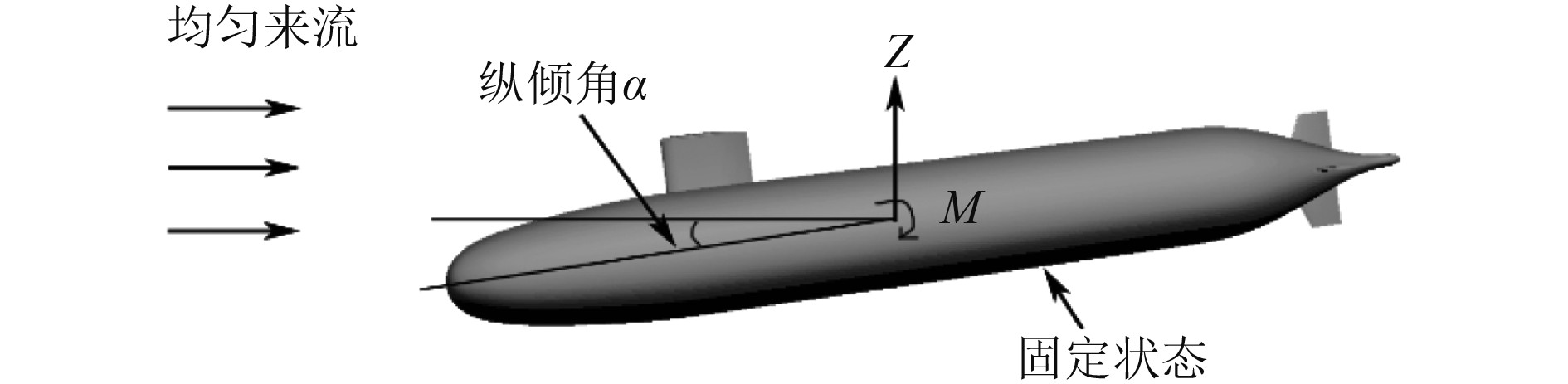
为验证上述方法的可行性,此处参考文献[5]中的方法,开展处于固定状态下的潜艇模型纵倾角在−10°~10°范围内,前向来流速度
|
图 4 前向来流示意图 Fig. 4 Sketch for the flow |
为了便于对比分析,定义潜艇在前向来流时所受到的垂向力系数、垂向力矩系数如下[5]:
| $\left\{ \begin{gathered} Z' = Z/(0.5\rho U_\infty ^2L_{PP}^2){\text{,}} \\ M' = M/(0.5\rho U_\infty ^2L_{PP}^3){\text{。}} \\ \end{gathered} \right.$ |
式中:
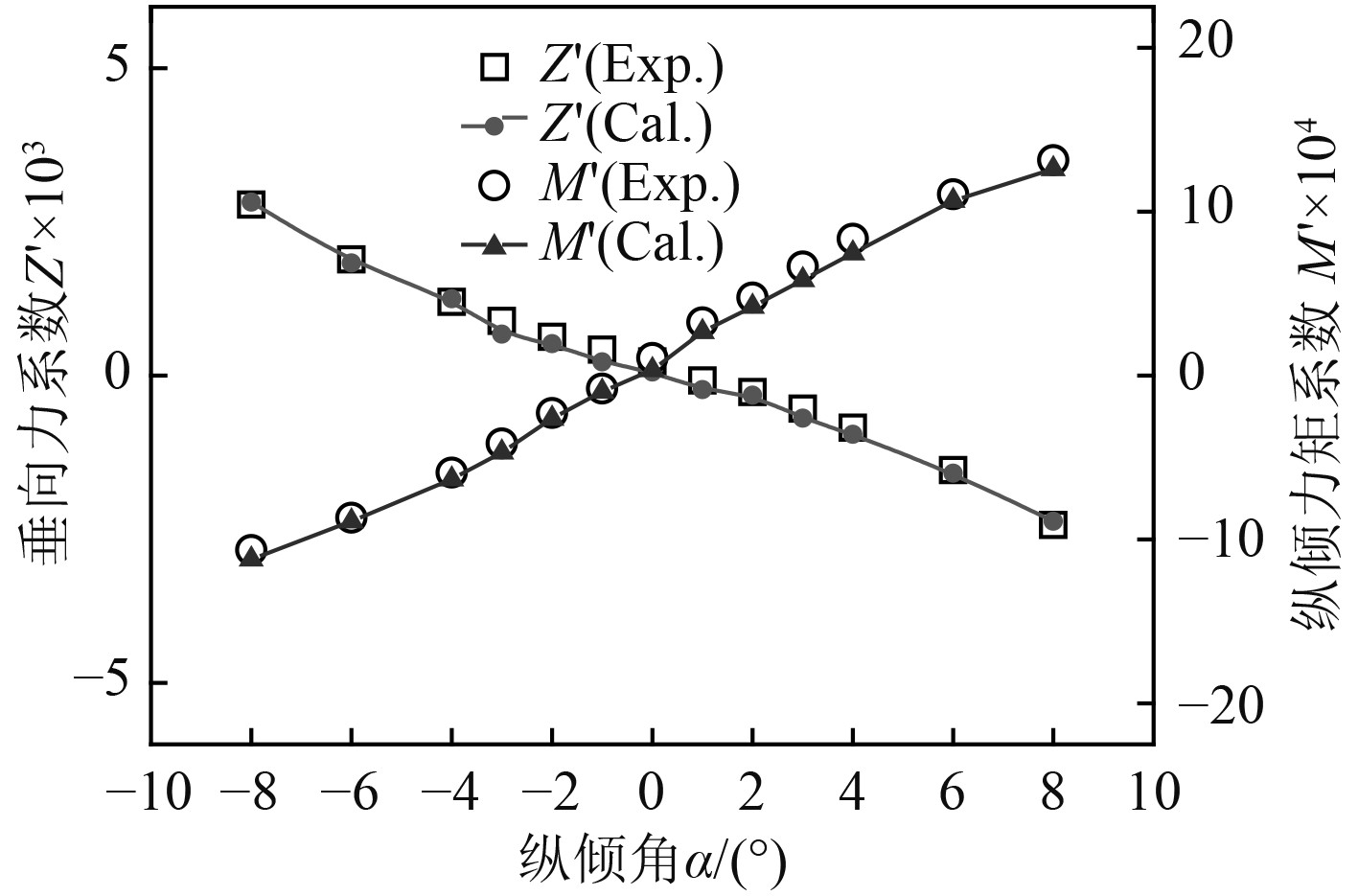
对比仿真与试验的结果如图5所示,试验值由文献[8]的报告图中读出,可能存在少许读数误差。从图5可以看出两者结果较为接近,计算误差在可接受范围内。因此下面继续做潜艇在稳态下潜状态下的仿真计算。
|
图 5 垂向力系数及纵倾力矩系数仿真值与试验对比 Fig. 5 Comparison of simulation values and test values of vertical force coefficient and trim moment coefficient |
执行特种任务的微型特种潜艇或蛙人输送艇与常规潜艇不同之处除了尺寸大小不一致外,还有特种艇在执行特种任务中需下潜停泊在近海底,这一过程下潜的速度不能过快,以避免潜艇一头“扎”进海底导致艇无法再离底返回或对艇结构造成损伤,同时还可以保障艇内人员安全。
本文主要是对潜艇以不同纵倾角在不同下潜速度下的稳态下潜开展数值模拟,研究其在稳态下潜过程中受到的垂向阻力及纵倾力矩与纵倾角及下潜速度的关系。
蛙人输送艇中有一类湿式艇,艇内人员处于水下开放环境中,对下潜速度要求不超过15 m/min即0.25 m/s。所以仿真计算取3种大小的速度,分别为0.25 m/s,0.5 m/s和1 m/s。而潜艇尾部有易损附体,为了保护尾部结构,一般选择首倾下潜,所以这里仿真计算纵倾角范围取−2°~8°,间隔2°, 2°附近间隔取1°。
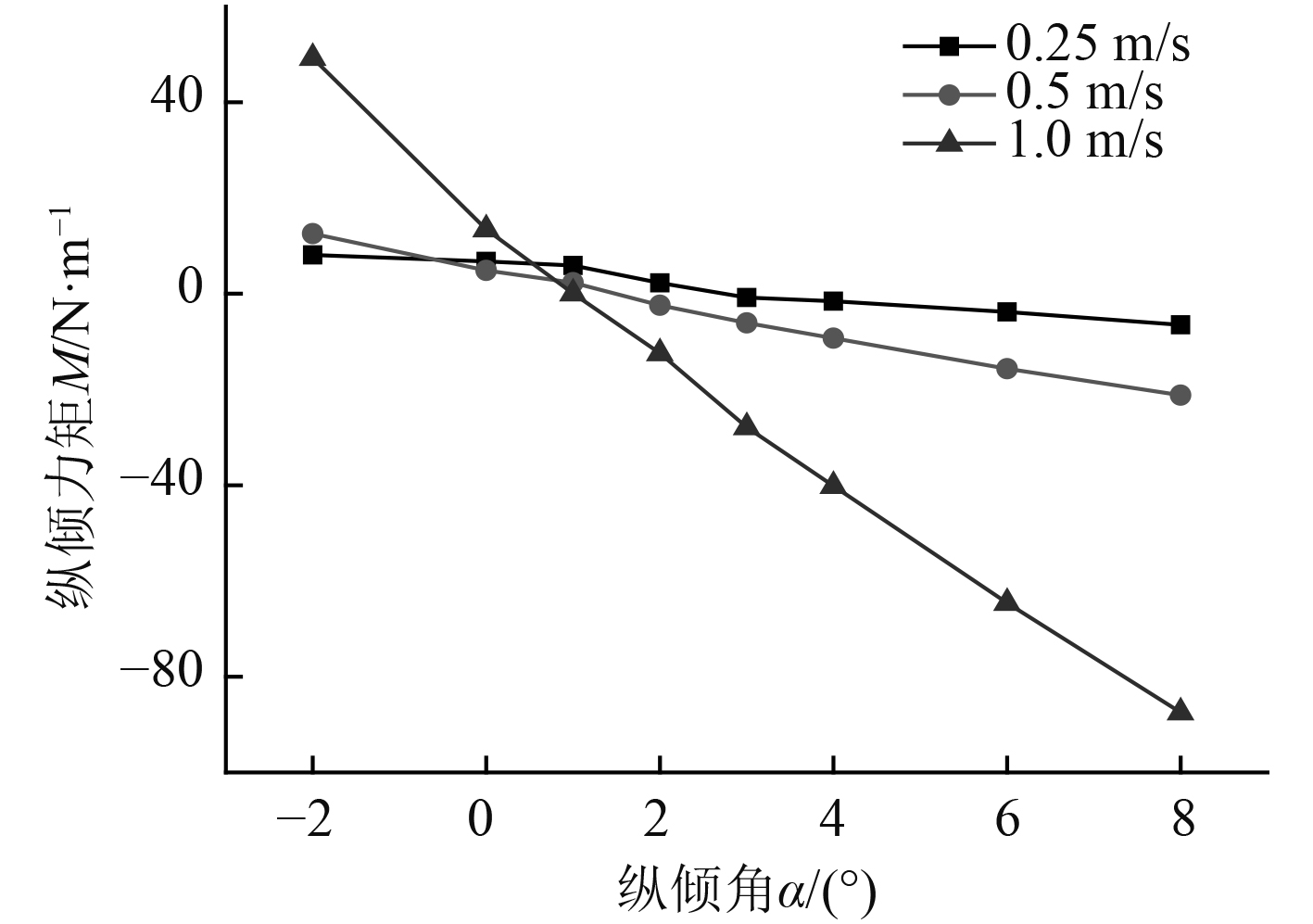
4.2 结果分析假定潜艇做稳态下潜,在仿真中模型固定不动,即相对而言潜艇受到垂向均匀来流,仿真得到的垂向阻力及纵倾力矩结果如图6和图7所示。从图中可以看出潜艇受到的垂向力随下潜速度的增加而增加,下潜速度不变时,纵倾角在−2°~8°范围内小幅度增减对垂向力的大小无太大影响,但其受到的纵倾力矩变化较大。可知潜艇在稳态下潜中,水舱注排水要注重调节纵倾力矩,以免对控制造成不利影响,尤其是潜艇实物在下潜时受到的力及力矩会更大,所以在控制中更应注意注首、尾排水量的调节。

|
图 6 不同速度、纵倾角下的垂向力 Fig. 6 Vertical forces at different speeds and trim angles |
|
图 7 不同速度、纵倾角下的纵倾力矩 Fig. 7 Trim moment at different speeds and trim angles |
潜艇以0°纵倾角状态在不同速度下潜时受到的力矩均为正值,即受到的纵倾力矩会造成潜艇有首倾的趋势,随着纵倾角的加大,这一力矩会对其产生反作用使其产生尾倾的趋势来抵消纵倾角继续扩大的效果。如果不加以控制,这可能会有一个动态平衡的过程,但在浅水域内,由于下潜距离较短,潜艇在下潜时还是要控制好首、尾水舱的注水量以调节流体对其产生的纵倾力矩,从而保持自身的稳定状态。
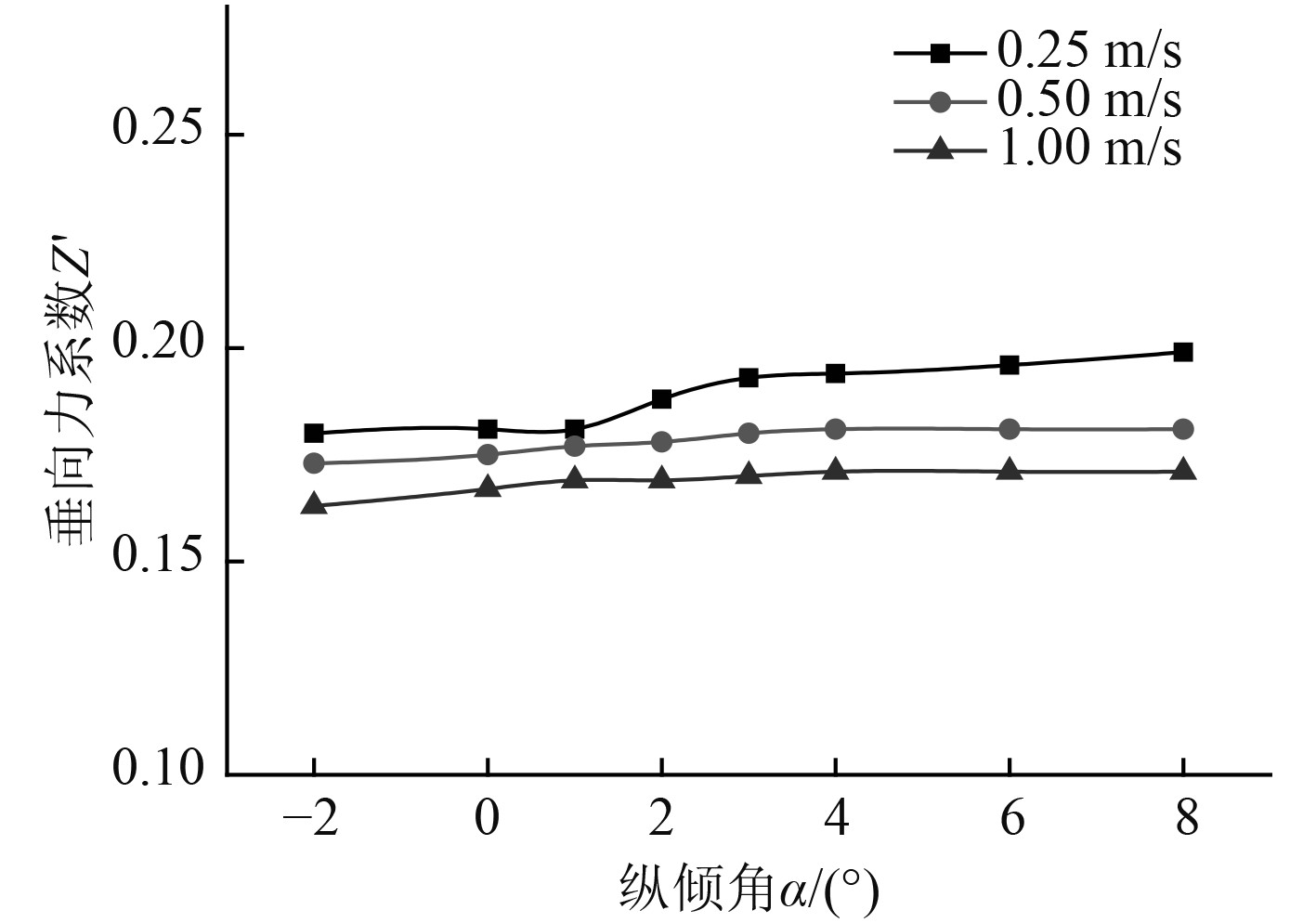
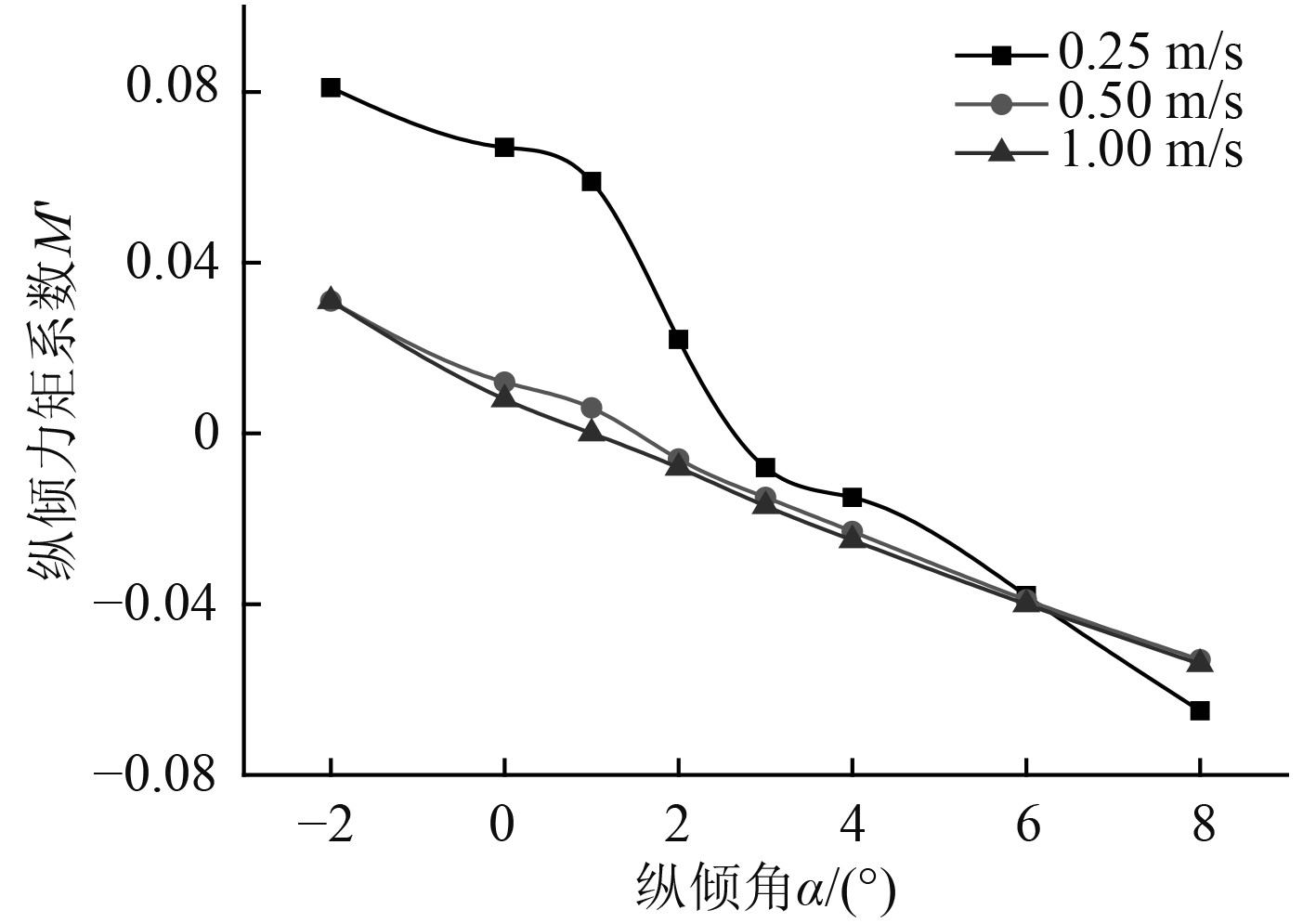
将潜艇在下潜过程中受到的垂向力及纵倾力矩无量纲化,结果如图8和图9所示。从无量纲化的结果图来看,垂向的阻力系数随着速度的增大而减小,但随潜艇纵倾角的增大而增大,纵倾力矩系数的绝对值也随潜艇首倾时纵倾角的增大而增大。从图中也可以看出垂向力系数曲线和纵倾力矩曲线在0°纵倾角附近有明显波动,说明在此处的数值模拟可能不够精确,后续可以提高网格精度再进行深入分析。
|
图 8 不同速度、纵倾角下的垂向力系数 Fig. 8 Vertical force coefficients at different velocities and trim angles |
|
图 9 不同速度、纵倾角下的垂向力矩系数 Fig. 9 Vertical moment coefficients at different velocities and trim angles |
从前面的分析来看,潜艇纵倾角不变时,下潜速度越大,使潜艇发生尾倾的纵倾力矩也越大。图10为潜艇在8°纵倾角下以3种速度下潜的表面压力对比,可以看出艇体最大受力点主要集中在艇体下表面,首部在横剖面附近的压力最小。这是因为此处区域流速较大,产生了一个相对负压,使得首段有一部分下表面压力小于上表面的压力。虽然水平尾翼下表面与来流几乎垂直,受力较大,但面积过小,且潜艇尾段较首段细,最终还是会产生一个尾倾的纵倾力矩。

|
图 10 8°纵倾角压力对比云图 Fig. 10 Cloud diagram of pressure contrast at 8° caster Angle |
本文基于STAR-CCM+软件对SUBOFF AFF-8全附体潜艇模型以8种纵倾角姿态在3个不同速度下的稳态下潜状态进行了仿真,得到以下结论:
1)该潜艇模型受到的垂向力随下潜速度的增加而增加,下潜速度不变时,纵倾角在-2°~8°范围内小幅度增减对垂向力的大小无太大影响,但其受到的纵倾力矩变化较大,所以潜艇下潜时注排水需着重注意调节首、尾水舱力矩的平衡;
2)该潜艇模型以0°纵倾角状态在不同速度下潜时,受到的力矩均为正值,但也要控制好首、尾水舱的注水量以调节流体对其产生的纵倾力矩,从而保持自身的稳定状态。
3)垂向的阻力系数随着下潜速度的增大而减小,但随潜艇纵倾角的增大而增大,纵倾力矩系数的绝对值也随潜艇首倾时纵倾角的增大而增大。
| [1] |
滕俊, 郭万海, 刘冬利. 国外海军水下特种作战研究[J]. 舰船电子对抗, 2012, 35(4): 39-42. DOI:10.3969/j.issn.1673-9167.2012.04.011 |
| [2] |
周超, 王庆胜, 李卓禹. 外军水下特种作战装备体系研究[J]. 水雷战与舰船防护, 2020, 3(1): 52-57. |
| [3] |
PAN Y C, ZHOU Q D, ZHANG H X. Numerical simulation of rotating arm test for prediction of submarine rotary derivatives[J]. Journal of Hydrodynamics, 2015, 27(1): 68-75. DOI:10.1016/S1001-6058(15)60457-7 |
| [4] |
BULL P. The validation of CFD predictions of nominal wake for SBUOFF fully appended submarine geometry[C]. Proceedings of 21st Symposium on Naval Hydrodynamics. Trondheim: Lohner, 1996.
|
| [5] |
周广礼, 董文才, 欧勇鹏. 潜艇应急上浮六自由度运动及黏性流场数值模拟[J]. 国防科技大学学报, 2017, 39(2): 199-206. |
| [6] |
LARSSON L, RAVEN H. Ship resistance and flow[M]. New York, USA: Society of Naval Architects and Marine Engineering, 2010.
|
| [7] |
GROVES N C, HUANG T T, CHANG M S. Geometric characteristics of DARPA SUBOFF models(DTRC model numbers 5470 and 5471): DTRC/SHD1298-01[R]. [S. l. : s. n. ], 1989.
|
| [8] |
RODDY R F. Investigation of the stability and control characteristics of several configurations of the DARPA SUBOFF model (DTRC model 5470) from captive-model experiments[R]. Maryland, USA: David Taylor Research Center, 1990.
|
 2021, Vol. 43
2021, Vol. 43
