加筋板结构是船舶、航空航天领域最为常用的结构类型之一。对于此类结构,当结构受力达到材料屈服强度后,其仍有一定的承载能力,直至载荷水平达到其极限强度。在加筋板结构设计中,极限状态(ULS)设计已经被公认为优于传统的许用应力方法,因为前者能更真实反映结构的安全极限[1]。加筋板结构在服役年限中不可避免遭受不同种类的损伤,裂纹损伤就是影响结构失效行为的重要因素之一。在加筋板结构中,裂纹经常在焊接和应力集中区域萌生,例如在加强筋和底板的交接处。在加筋板寿命周期中,这些裂纹可能在不同载荷状态下扩展,结果形成不同的尺寸和位置。
按载荷形式的不同,含裂纹加筋板的剩余强度问题可分为压缩载荷下加筋板的屈曲强度、拉伸载荷下加筋板的极限强度和剪切载荷下加筋板的剩余强度。对于此类问题,传统的有限元方法是将裂纹建立成类似于狭缝的几何模型,并在裂纹尖端进行网格加密,从而将断裂力学问题简化为一般静力学问题。Sadek等[2]用数值模拟的方法分析了含裂纹加筋板在压缩应力下的屈曲特性,分析中考虑了裂纹的演化发展;Cao等[3]根据欧洲规范EN1990,EN1991和EN1993,对环向和经向制造裂纹的圆形钢筒仓的屈曲性能进行了评估;Duc等[4]通过数值模拟计算,建立了基于裂纹有限元分析的静稳定板模型。Brighenti等[5]研究了裂纹损伤对拉伸、压缩、剪切载荷下的矩形板屈曲强度的影响,其中裂纹长度、裂纹方向和材料泊松比是变化的,结果表明裂纹方向垂直拉伸和压缩载荷方向时是最危险的工况。Margaritis Y等[9]研究了含裂纹加筋板的极限和失效响应,详细检查了裂纹闭合对结构响应的作用。Paik等[10]对完整和含裂纹加筋板的极限剪切强度进行了数值研究,并基于完整加筋板方程发展了预报含裂纹加筋板的极限剪切强度方程。Saad-Eldeen等[11]对含中心椭圆开口和封闭裂纹的薄壁钢板剩余强度进行了试验研究,试验中的试件是从服役期中的实际结构构件中取得的,而不是新建试件。
与传统的一般静力学分析方法相比,J积分方法具有以下优势:一是不需要建立裂纹模型,而是从断裂力学机理出发,直接定义裂尖和裂纹方向,这更加符合裂纹模型的实际情况;二是J积分方法避开了直接求解裂端塑性应力场的困难。Cherepanov[6]和Rice[7]各自独立提出了一种与积分路径无关的J积分,用于综合度量裂端应力应变场强度。它对弹塑性断裂力学发展起到了重要的作用。
通过以上文献可以看出,以前的研究主要关注含裂纹结构在典型拉伸载荷下的失效行为或塑性屈曲强度评估。含裂纹结构在轴向拉伸下的剩余极限强度在近年来得到了广泛关注,但是该领域的研究仍然是有限、不充分的。因此,需要进行更多的研究来更深理解含裂纹缺陷结构构件的失效行为。本文的主旨在于发现含裂纹损伤的加筋板在单调轴向拉伸下的极限强度行为。假定板横向裂纹位于加筋板内截面,或只位于板单元上,或位于板单元和加强筋上。需要指出的是,本文不考虑裂纹扩展和断裂相关的临界裂纹长度。
加筋板材料为Q345B高强度钢,为了达到目的,进行了含一系列不同尺寸、位置裂纹加筋板在单轴拉伸载荷下的非线性弹塑性大变形分析。
1 力学分析方法 1.1 J积分及其有限元列式J积分理论避开了直接计算裂纹尖端附近的弹塑性应力、应变场,而用远场J积分作为表示裂纹尖端应力应变集中特征的平均参量。对于二维问题,J积分可定义为[3]:
| ${J} = \int_\Gamma {\left( {Wd{x_2} - {T_i}\frac{{\partial {u_i}}}{{\partial {x_1}}}} \right){\rm{d}}s\text{。}} $ | (1) |
其中:
在线弹性断裂力学中,J积分与应力强度因子KI有如下关系式:
| $J = K_I^2/E'{\text{。}}$ | (2) |
式中:对于平面应力,弹性模量
可以解析证明,J积分与积分路线
由于J积分与选择的路径无关,并能描述裂纹尖端的应变状态。这一特点使J积分计算可以在离开高应力、高应变梯度的裂纹尖端区外的任意回线进行。对于二维体的J积分列式可以写为[11]:
| $\begin{split} {\rm{J}} = & 2\int_y {\left( {W - {\sigma _{11}}\frac{{\partial u}}{{\partial x}} + {\sigma _{12}}\frac{{\partial v}}{{\partial x}}} \right){\rm{d}}y} -\\ &2\int_x {\left( {W - {\sigma _{22}}\frac{{\partial v}}{{\partial x}} + {\sigma _{12}}\frac{{\partial u}}{{\partial x}}} \right){\rm{d}}x} {\text{。}} \end{split} $ |
其中:
| $W = \frac{G}{{1 - V}}\left[ {\mathop \varepsilon \nolimits_{11}^2 + 4v\mathop \varepsilon \nolimits_{11} \mathop \varepsilon \nolimits_{22} + 2(1 - v)\mathop \varepsilon \nolimits_{12}^2 + \mathop \varepsilon \nolimits_{22}^2 } \right]{\text{。}} $ |
将平面上定义的二维J积分沿着裂纹缝线逐点积分可得裂纹线的三维J积分为:
| $\begin{split} \overline {\rm{J}} =& \int_L {J\left( s \right)\lambda \left( s \right){\rm{d}}s} = \\ & \mathop {\lim }\limits_{\Gamma \to 0} \int_{{A_i}} {\lambda \left( s \right)n \cdot \left( {\omega I - \sigma \cdot \frac{{\partial u}}{{\partial X}}} \right) \cdot q{\rm{d}}A} {\text{。}} \end{split} $ |
式中:L为裂纹缝线长度;dA为包绕裂纹缝线的圆柱曲面上的面积微元,
J积分的计算必须采用数值积分,如果回线经过单元积分点,可以采用有限元中的高斯积分策略。从远离裂纹尖端的应力场、应变场计算J积分,只能在无体力、初始应变和裂纹表面拉力情况下能用。当有体力或初始应变时,J积分要加入封闭表面的积分。此时路径无关性将丧失,必须从完整的应力和应变结果中计算,包括裂纹尖端的高应力区。
J积分的主要优点是不需要用很细的网格对裂纹尖端区进行分析。路径无关性的非线弹性材料也存在,真实的弹塑性材料与非线弹性材料类似。J积分也可以用于描述弹塑性材料的裂纹尖端的应力场和应变场,材料用增量塑性理论描述并不允许有卸载,以免W的加载历程相关性,J值的增量可以从每个载荷步的应力和应变增量计算得到。
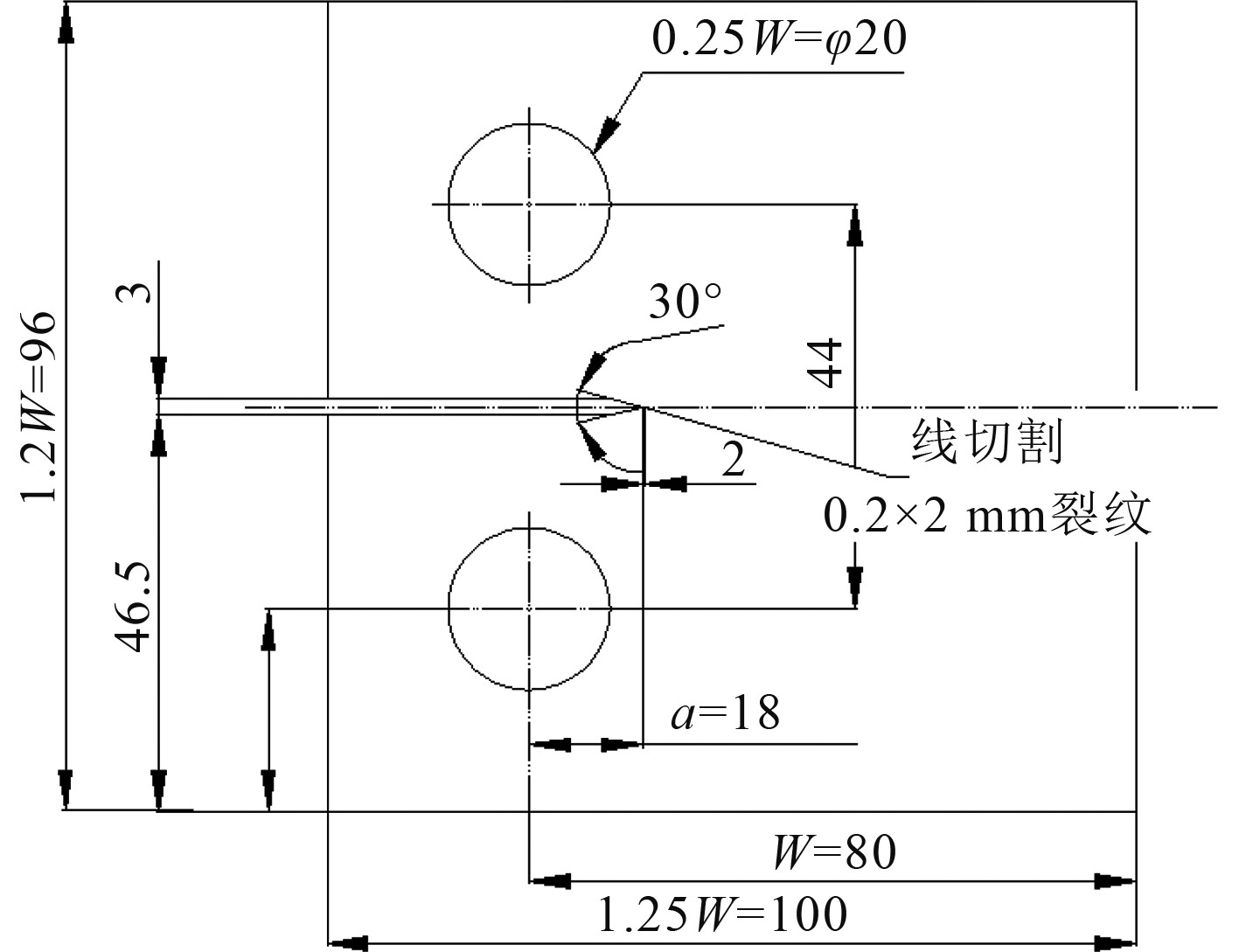
1.2 精度验证算例以紧凑拉伸(CT)式样为例进行说明,材料选用304不锈钢,厚度为5 mm,对其进行单项拉伸,CT式样尺寸如图 1所示。为了效验计算结果的准确性,将各方法的计算结果与(2)式用应力强度因子法计算的理论值做比较。根据上述计算J积分的方法,对该实例进行计算,结果如图 2所示。
|
图 1 CT试样尺寸 Fig. 1 Dimension of the CT specimen |
|
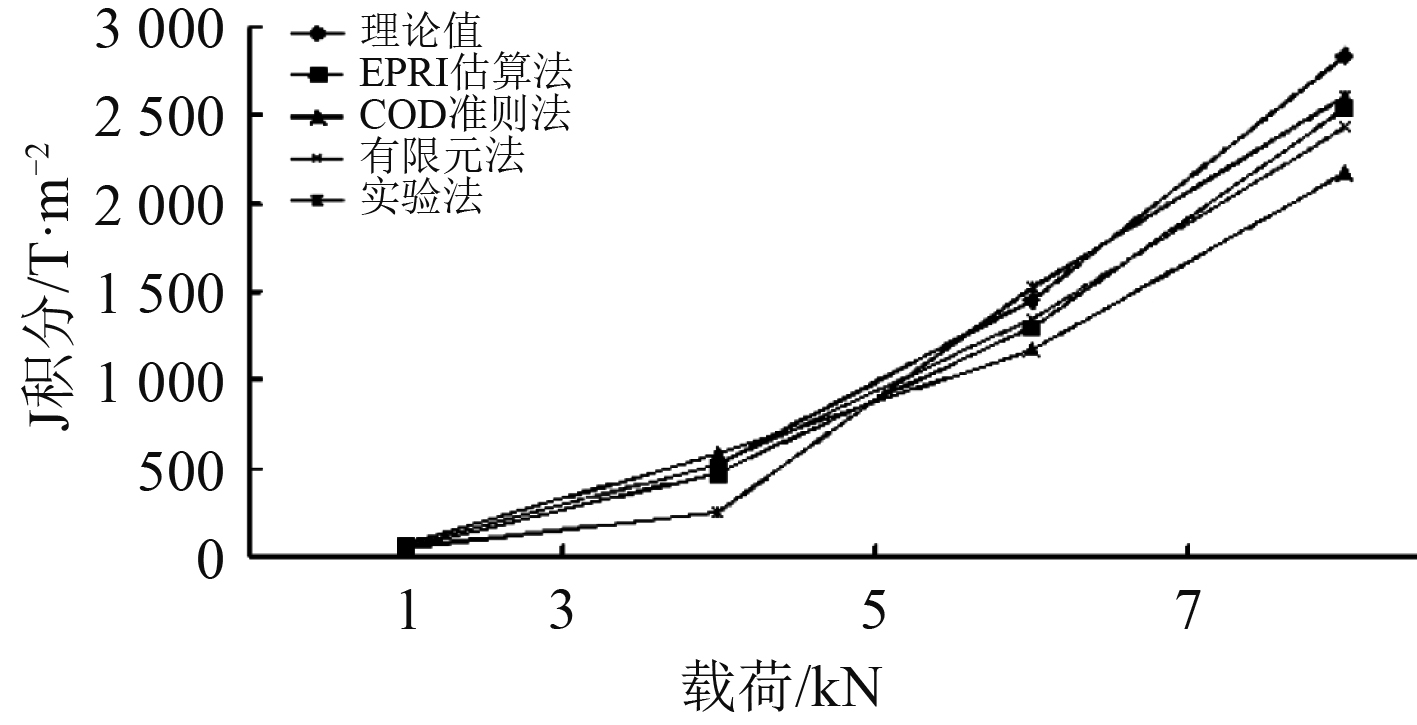
图 2 J积分计算结果图 Fig. 2 The scheme of J-integral calculation result |
由图 2可知,各种J积分计算方法的结果具有相同的增长趋势且相差不大,通过与理论值的对比,验证了各种常用J积分计算方法的准确性与可行性。
1.3 有限元模型 1.3.1 几何和材料本文的分析对象为含2根加强筋(截面对称)和1个板单元的加筋板,其长细比范围为4~6,如图 3所示。在图 3中,板的尺寸用

|
图 3 加筋板的模型尺寸 Fig. 3 Model dimension of the stiffened-panel |
|
|
表 1 加筋板的几何特征 Tab.1 Geometrical features of the stiffened-panel |
其中长细比β是控制加筋板屈曲/失效行为的重要参数,定义如下[13]:
| $\beta = b/t\sqrt {{\sigma _s}/E} {\text{。}} $ |
其中:b为板宽;t为板厚;
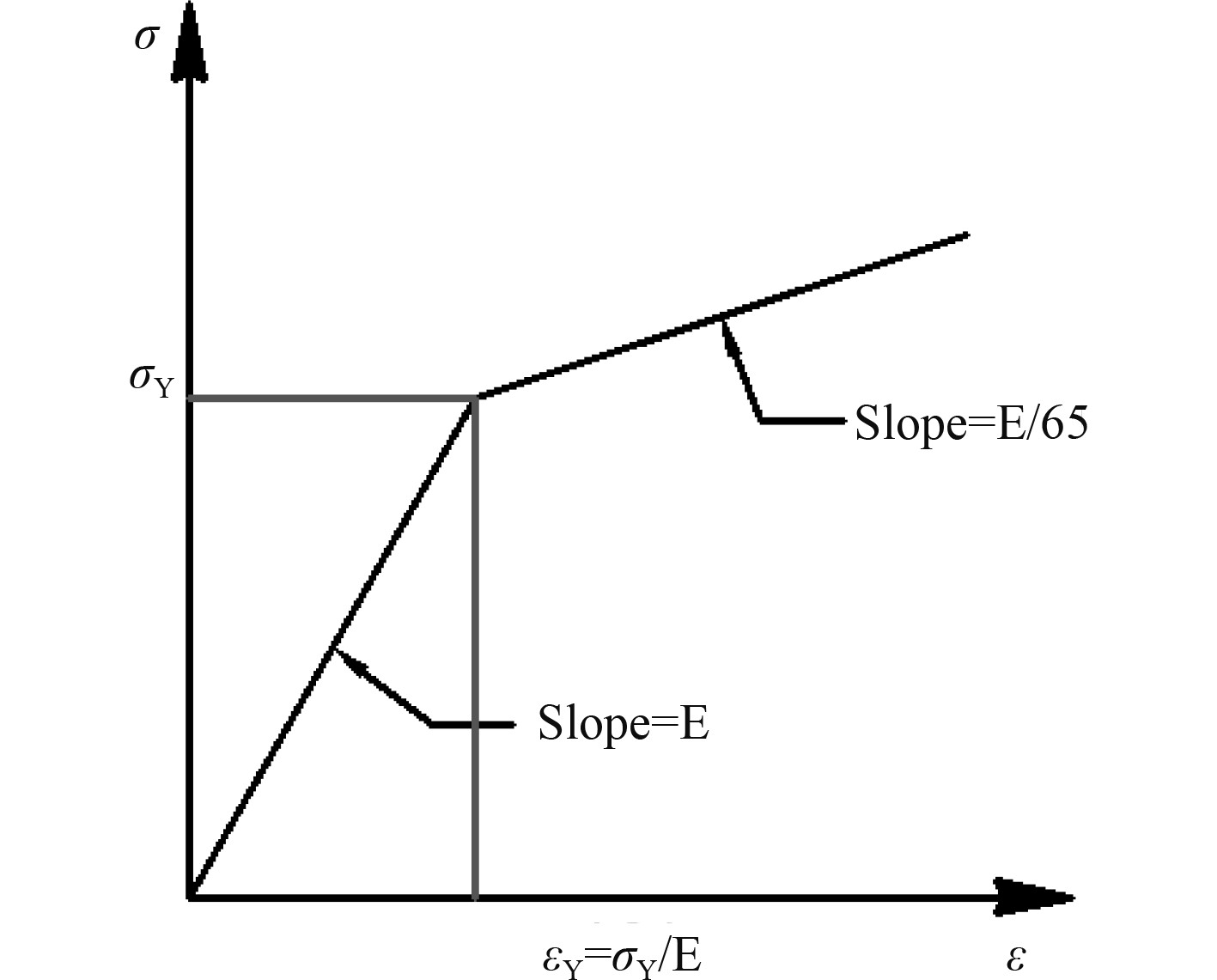
本文使用的材料为Q345B钢。一般来说,钢结构具有应变硬化正切模量
|
图 4 材料的理想弹塑性应力-应变行为 Fig. 4 Ideal elastic-plastic stress-strain behavior of the material |
|
|
表 2 Q345B钢材料属性汇总 Tab.2 A summary of Q345B steel material properties |
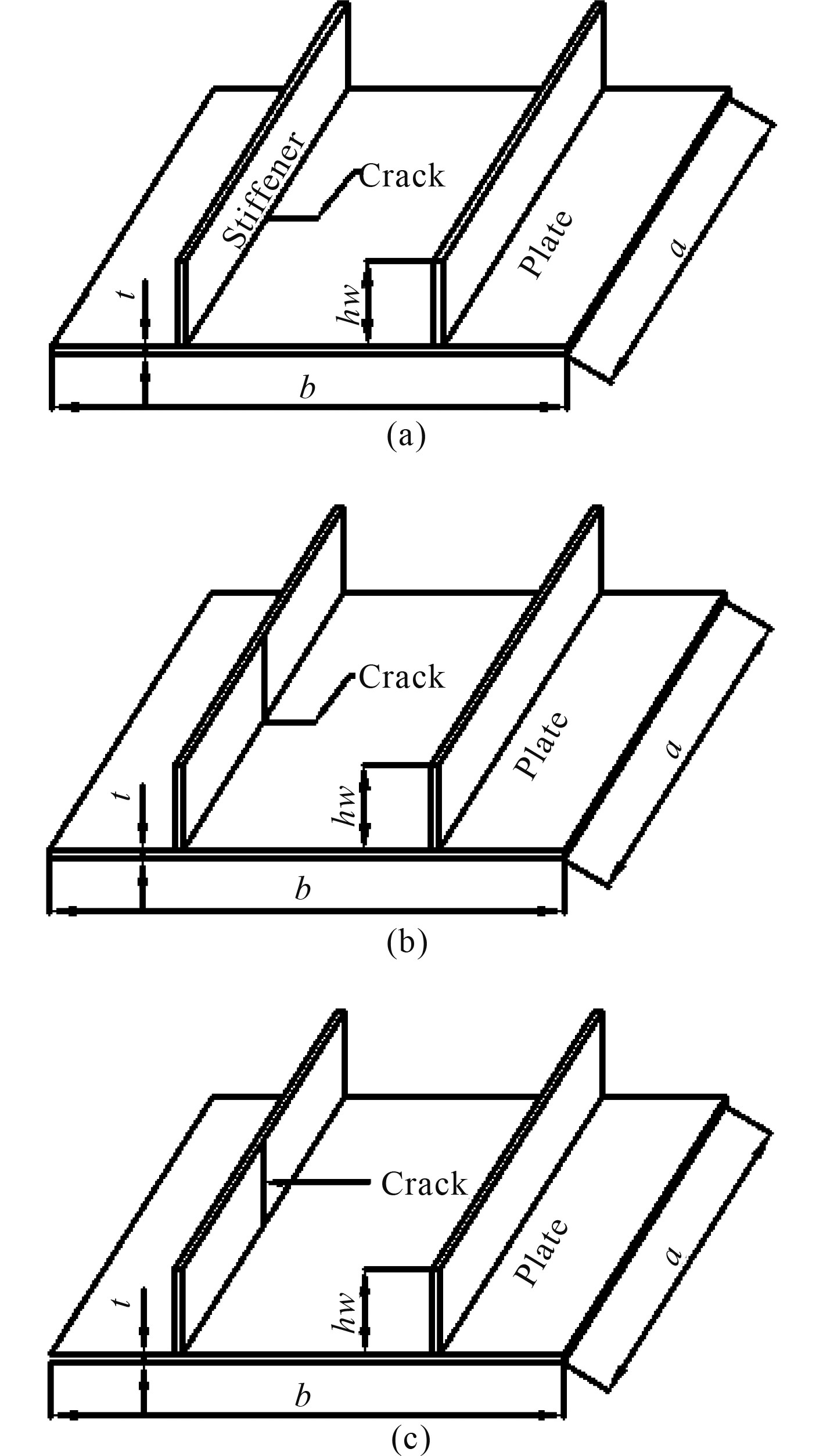
为了考虑裂纹的不同位置,本文应用了3种不同的模型,如图 5所示。这些模型按裂纹位置分类,如裂纹只在底板上,裂纹在底板和加强筋上,裂纹只在加强筋上。
|
图 5 3种裂纹模型 Fig. 5 3 types of crack models |
裂纹在加筋板中的深度取决于多种因素,其中裂纹深度等于板厚时最为危险。在工程中,在相对较薄的加筋板中,裂纹一般被认为贯穿板厚。因此,在本文研究中,底板和加强筋上的裂纹都假设贯穿厚度。在所有的3种模型中,不论裂纹在底板上还是加强筋上,都沿板的横向。为了考虑不同裂纹长度,假设加筋板上的裂纹长度c是对应板宽的某一特定比例,其比值c/b的变化范围为0.05~0.15,而图5(b)和图5(c)中在加强筋上的裂纹长度等于加强筋高度。表 3描述了本文考虑的不同几何参数。
|
|
表 3 FE模型几何参数值汇总 Tab.3 A summary of FE models’ geometrical parameters |
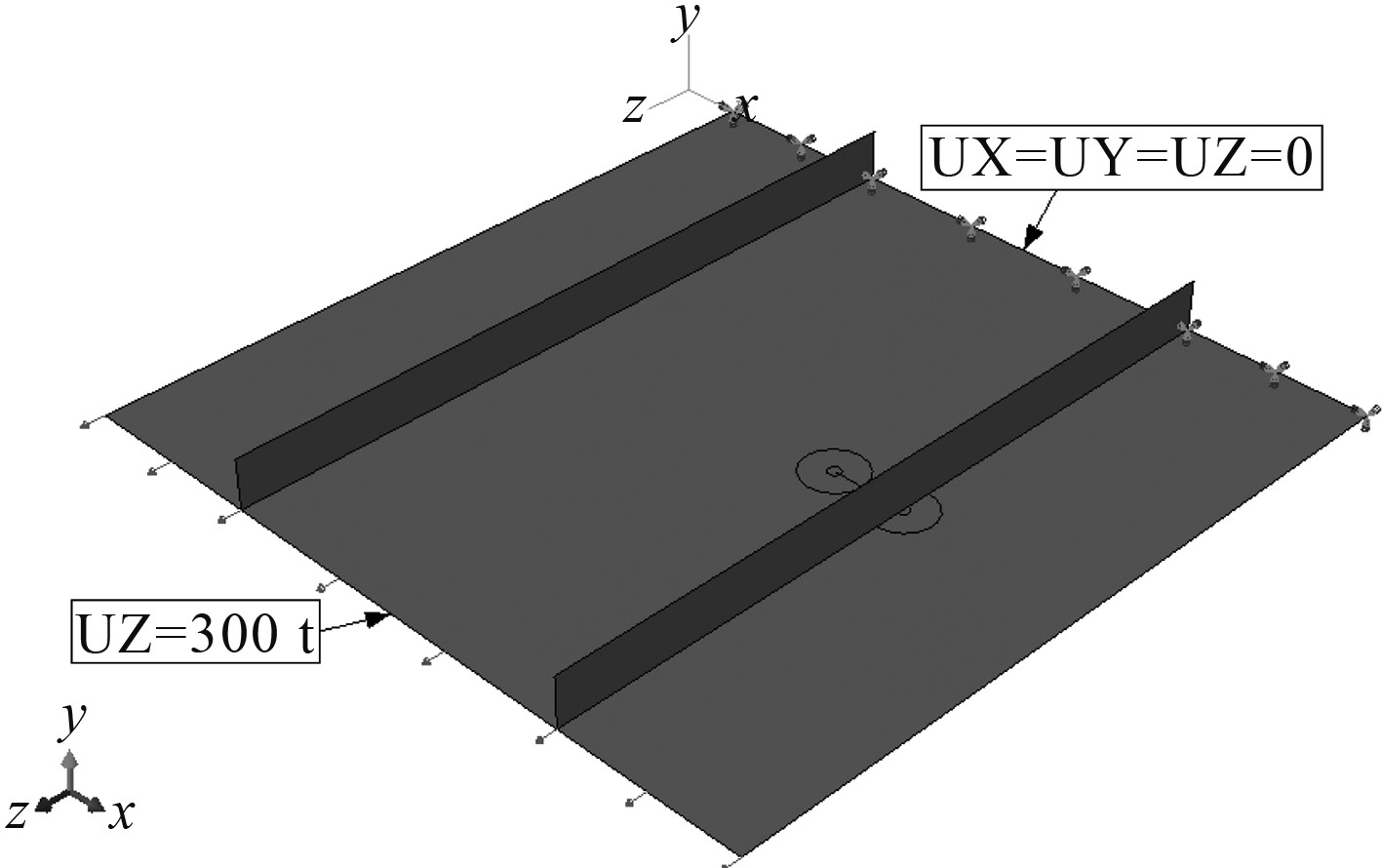
在进行FE分析之前,在FE模型上施加合适的边界条件尽可能合理模拟结构实际响应是十分重要的。一个常规的方法是在极限状态评估中在横向边缘施加简支或夹持边界条件。本文主要关注的是加筋板在单轴拉伸载荷下的极限强度。通常认为加筋板横剖面会受到均匀的拉伸外载荷力,可采用位移控制的方式来实现加筋板均匀轴向载荷的逐步加载。图 6描述了含裂纹加筋板模型的载荷和边界条件,其中t为时间。
|
图 6 含裂纹加筋板载荷和边界条件 Fig. 6 Loads and BCs of the stiffened-panel with cracks |
结构极限强度计算是非线性问题。在本文的研究中,含裂纹加筋板的失效行为和极限强度评估使用有限元软件Abaqus,评估中同时考虑几何和材料非线性。在Abaqus包含可使用的单元库中,选择8节点S8R单元来离散加筋板模型。S8R适合属于加筋板结构范畴的适度薄壁壳结构。其适合线性、大应变和大转动非线性应用。
在FE分析中,计算精度和速度在很大程度上取决于单元大小或网格密度。网格尺寸必须足够精细来捕捉含裂纹加筋板的屈曲/塑性失效行为。另一方面,更为精确的网格引起更大的计算代价。从这一点来说,必须进行精度和计算时间的平衡。对于含裂纹加筋板,精确网格必须分配在局部裂纹区域来模拟更早的屈服和由于应力集中引起的高应力梯度。
进行不同网格尺寸的收敛性研究决定相对合适的非线性有限元分析网格模型。最终,沿板宽方向b和板长方向a的壳单元数目指定为20。对于加强筋腹板在高度方向
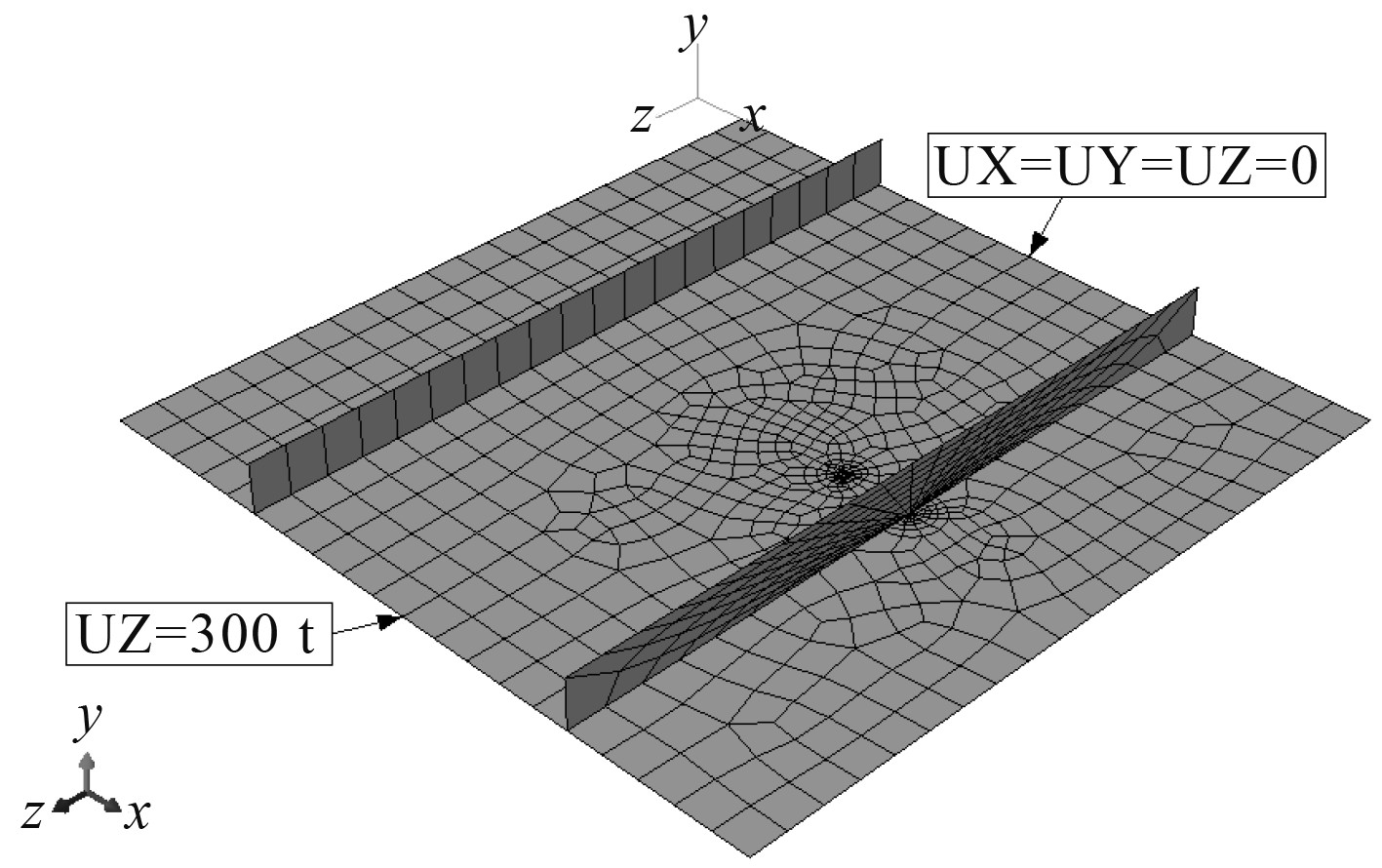
|
图 7 含裂纹加筋板网格实例 Fig. 7 Mesh example of the stiffened-panel with cracks |
使用Abaqus有限元软件进行一系列弹塑性大变形分析研究含裂纹加筋板在单轴拉伸载荷下的失效行为。在分析中,使用牛顿-拉普生方法来解决非线性控制方程,考虑上文描述的3种裂纹模型。而且改变裂纹长度和板厚来研究其对含裂纹加筋板极限强度特性的影响。
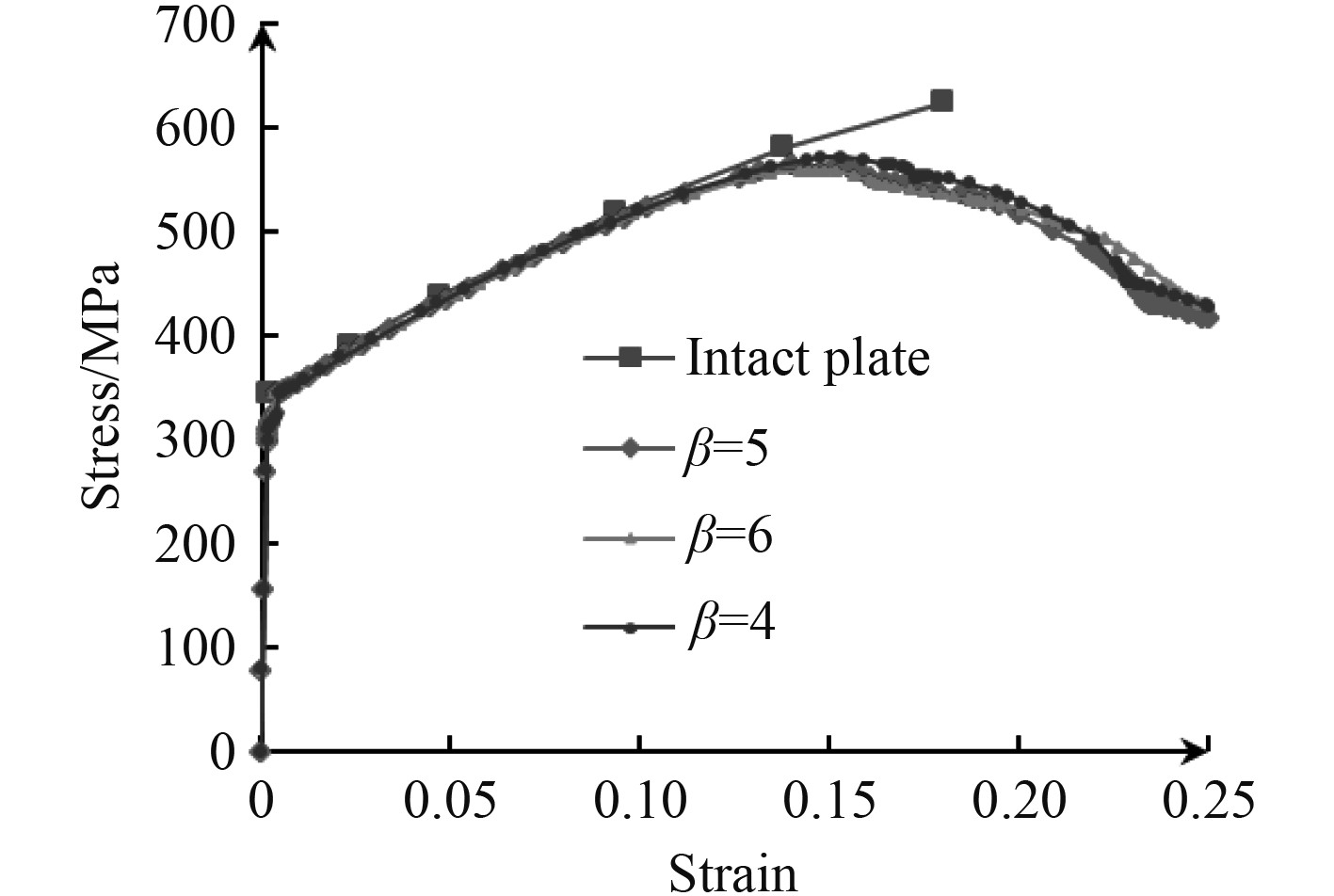
2.1 长细比的影响考虑表 3中所列的不同板厚来研究其对含裂纹加筋板极限强度特性的影响。选择裂纹长度c/b=0.1和裂纹纵向位置固定于加筋板的中横剖面。将加载试验中采集的轴向荷载和轴向拉伸变形进行换算,即将轴向荷载除以实测的试件截面积,得到截面的平均应力值;将轴向拉伸变形除以试件的实测初始长度,得到试件的平均应变值[15],图 8给出了不同长细比的模型(a)应力-应变曲线(裂纹长度c/b=0.1)。图中也包含了相关无裂纹损伤完整加筋板作为参考模型。应力-应变曲线的峰值即为加筋板的极限拉伸强度,当载荷水平达到该值时,含裂纹加筋板的应力云图(以β=5为例)如图 9所示。可以看出,当载荷水平达到含裂纹加筋板极限强度时,加筋板中横剖面几乎所有单元的等效米塞斯应力都达到材料的抗拉强度,加筋板失去抗拉能力。
|
图 8 不同长细比的模型(a)应力-应变曲线(裂纹长度c/b=0.1) Fig. 8 The stress-strain curve of Model (a) with different slenderness (crack length c/b=0.1) |

|
图 9 含裂纹加筋板的应力云图(β=5) Fig. 9 The stress distribution of the stiffened-panel with cracks(β=5) |
为了测量裂纹损伤对加筋板极限拉伸强度的影响,将结果与相关无裂纹损伤完整加筋板进行对比是必要的。从这一点出发,引入极限强度缩减系数,如下式:
| $R = {\sigma _u}/{\sigma _{u0}\text{。}}$ |
其中:
3种长细比下极限强度缩减系数分别为0.914,0.902,0.895,含裂纹加筋板极限拉伸强度随加筋板长细比的增大略有减小,说明当加筋板厚度越大,裂纹损伤对加筋板极限强度的影响越明显。总体来看,加筋板长细比对极限强度的影响不大,这是因为在本文的算例中,当加筋板板厚增大时,裂纹深度也随之增大,表明含贯穿型裂纹的加筋板在单轴拉伸载荷下的剩余强度对加筋板长细比不敏感。
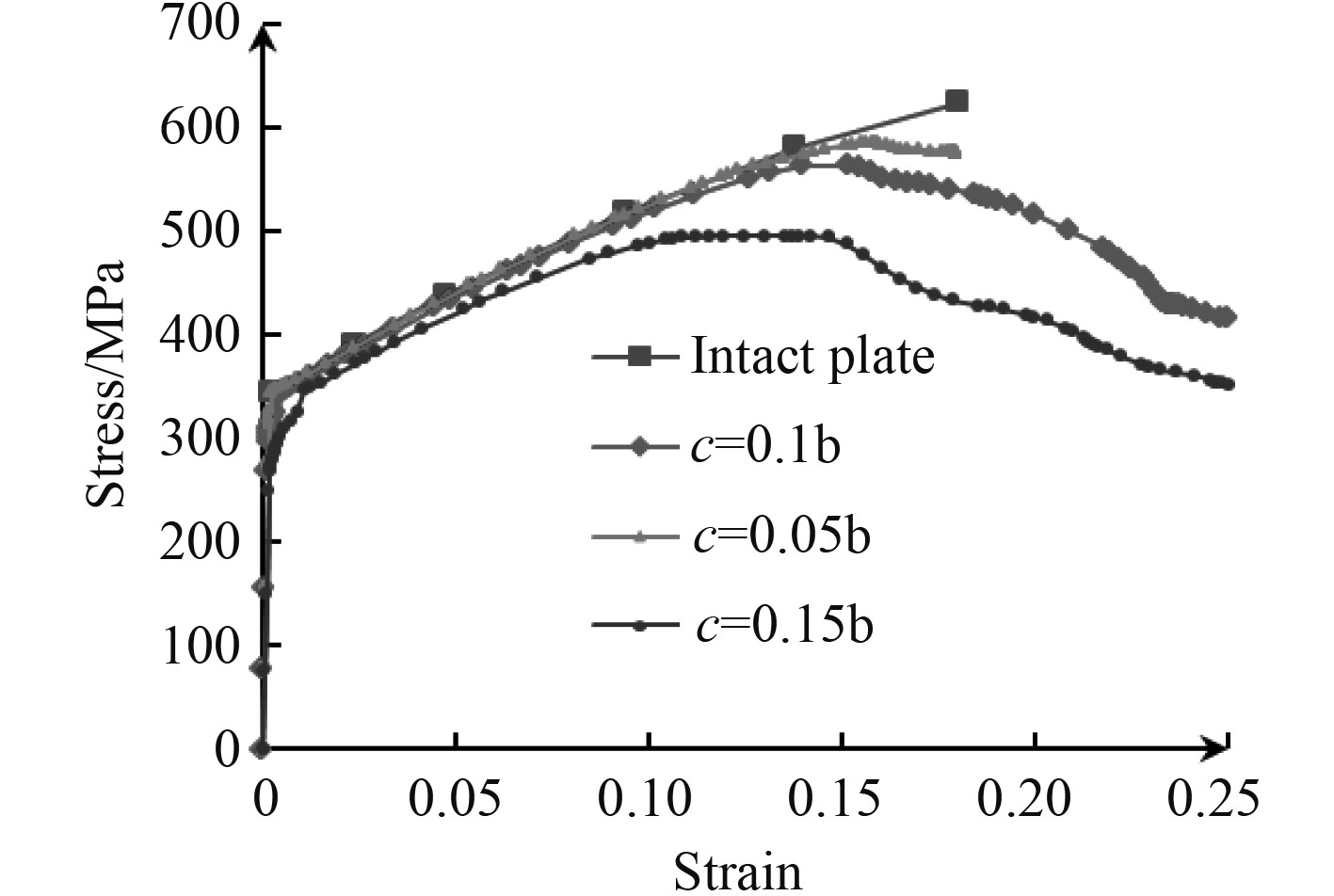
2.2 裂纹长度的影响为了研究裂纹长度对加筋板失效行为的影响,选择板厚为10 mm,裂纹位于加筋板中横剖面的工况,改变底板上裂纹的长度。加强筋上没有裂纹。图 10演示了裂纹长度对应力-应变关系的影响。可知裂纹长度的增加影响加筋板结构响应,极限强度和剩余强度都随裂纹长度的增大而减小。而且,从图中还可以看出极限应变(失效点应变)随裂纹长度的增大而减小(3种工况下极限应变分别为0.158,0.152,0.142)。3种裂纹长度下极限强度缩减系数分别为0.939,0.902,0.793,含裂纹加筋板极限拉伸强度随裂纹长度的增大而减小,且减小的幅度逐渐增大,说明含裂纹加筋板在单轴拉伸载荷下的极限强度对裂纹长度较为敏感。
|
图 10 裂纹长度对应力-应变关系的影响 Fig. 10 The influence of crack length on the stress-strain behavior |
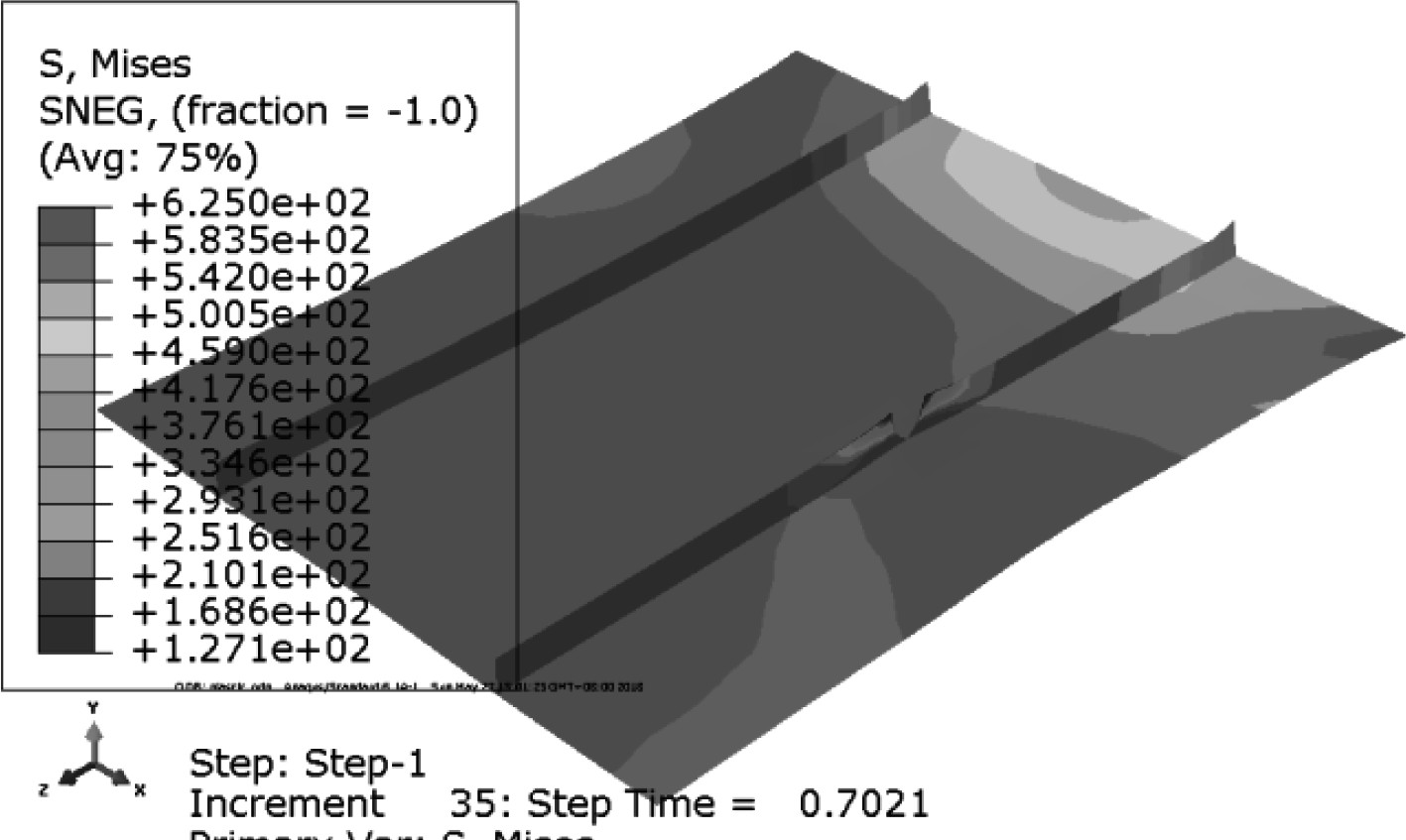
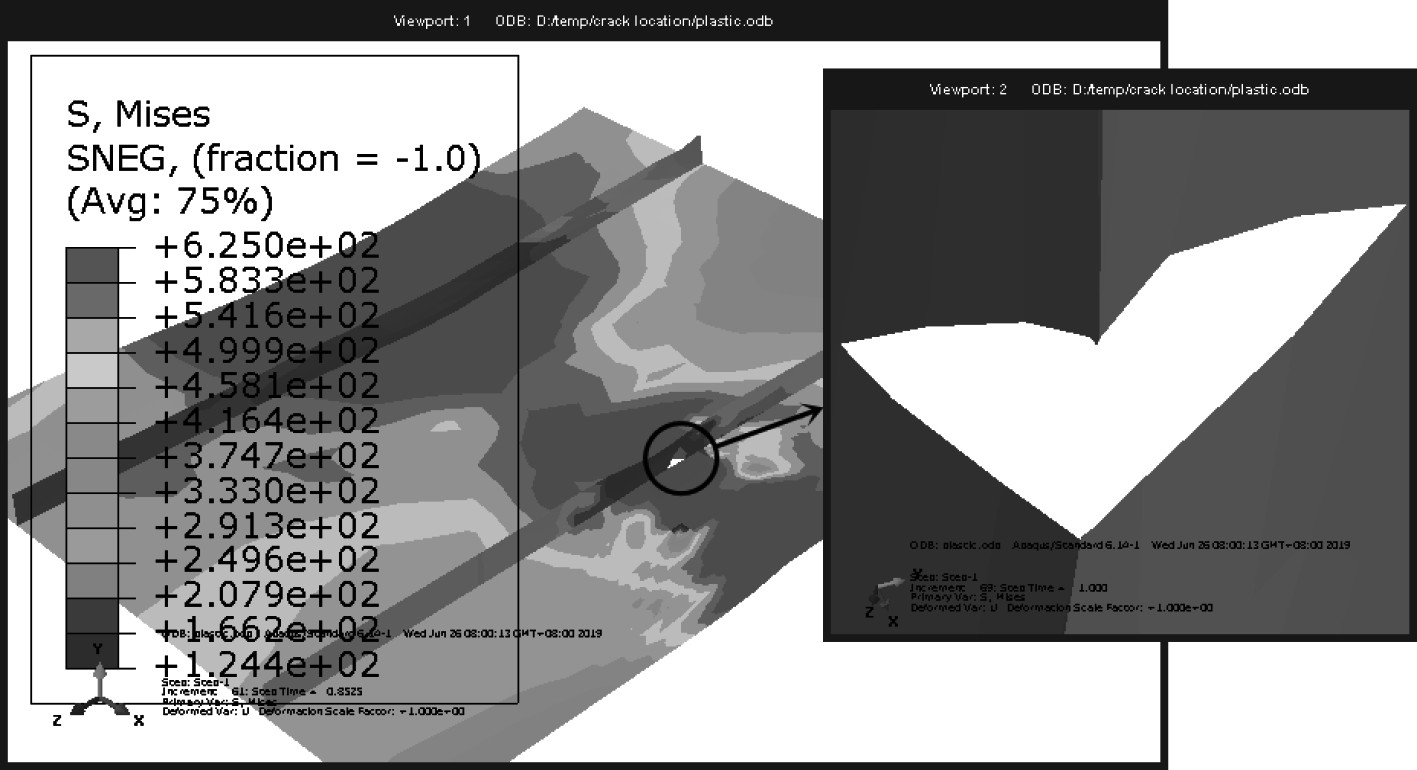
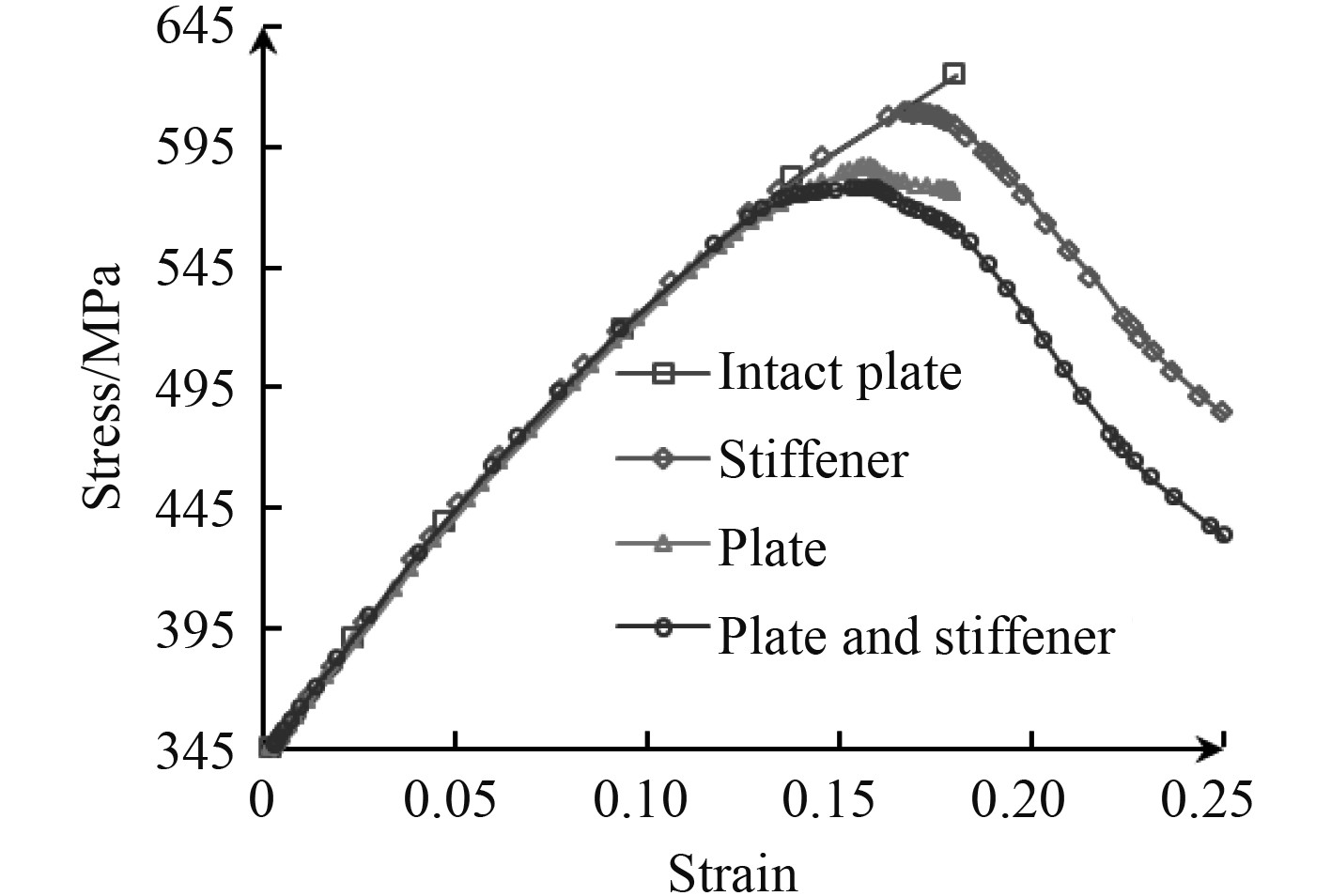
为了检查裂纹位置对含裂纹加筋板极限强度行为的影响,设计了裂纹只出现在底板上、裂纹只出现在加强筋上、裂纹同时出现在底板和加强筋上3组仿真试验。图 11和图 12分别为裂纹在加强筋上和裂纹同时在底板和加强筋上时的应力云图,图 13为3种工况下含裂纹加筋板应力-应变曲线。3种工况下极限强度缩减系数分别为0.939(裂纹只出现在底板上)、0.975(裂纹只出现在加强筋上)、0.924(裂纹同时出现在底板和加强筋上),说明加强筋上的裂纹对含裂纹加筋板极限强度的影响小于底板上的裂纹,而裂纹同时出现在底板和加强筋上时对含裂纹加筋板极限拉伸强度的影响最大。这是因为裂纹只位于底板和加强筋上时,裂纹区域在单轴拉伸载荷下的变形都受到加强筋或底板的限制,而裂纹同时位于底板和加强筋上时,裂纹在底板和加强筋相交的位置能够自由变形。
|
图 11 裂纹在加强筋上时的应力云图 Fig. 11 The stress distribution when the crack locates on the stiffener |
|
图 12 裂纹同时在底板和加强筋上时的应力云图 Fig. 12 The stress distribution when the crack locates on both the stiffener and the plate |
|
图 13 三种工况下含裂纹加筋板应力-应变曲线 Fig. 13 The stress-strain curve of the stiffened-panel with cracks under 3 different cases |
本文建立了一系列不同长细比、不同裂纹长度、不同裂纹位置的含裂纹加筋板有限元模型,基于J积分理论对含裂纹加筋板在单轴拉伸载荷下的极限强度进行了计算分析,得到以下结论:
1)长细比对含贯穿型裂纹的加筋板在单轴拉伸载荷下的剩余强度影响不大;
2)含裂纹加筋板极限拉伸强度随裂纹长度的增大而减小,且减小的幅度逐渐增大,极限拉伸强度对裂纹长度较为敏感;
3)加强筋上的裂纹对含裂纹加筋板极限强度的影响小于底板上的裂纹,而裂纹同时出现在底板和加强筋上时对含裂纹加筋板极限拉伸强度的影响最大。
本文在进行含裂纹加筋板极限强度计算时没有考虑裂纹扩展,这或多或少与实际情况存在一定的差异。裂纹扩展对含裂纹加筋板极限强度的影响,是下一步研究的方向。
| [1] |
CHONG Cui, PING Yang, CHUANG Li, et al. Ultimate strength characteristics of cracked stiffened plates subjected to uniaxial compression[J]. Thin-Walled Structures, 2017, 113: 27-38. DOI:10.1016/j.tws.2017.01.003 |
| [2] |
SALEM Cherif Sadek, TAMINE tawfik. Buckling of cracked plate reinforced[J]. Procedia Structural Integrity, 2016, 1: 234-241. DOI:10.1016/j.prostr.2016.02.032 |
| [3] |
QING Shuai CAO, Yang ZHAO, LI Xing, er al. Nonlinear buckling of cylindrical steel silos with fabrication cracks[J]. Powder Technology, 2019, 353: 219-229. DOI:10.1016/j.powtec.2019.04.080 |
| [4] |
NGUYEN-Xuan H. et al. (eds.), Proceedings of the International Conference on Advances in Computational Mechanics 2017, Lecture Notes in Mechanical Engineering, https://doi.org/10.1007/978-981-10-7149-2_3
|
| [5] |
李群, 欧卓成, 陈宜亨. 高等断裂力学[M]. 北京: 科学出版社, 2017: 27.
|
| [6] |
CHEREPANOV. G. P.. Cracks propagation in continuous media.[J]. Journal of Applied Mathematics and Mechanics, 1967, 31(31): 503-512. |
| [7] |
RICE. J. R. A path independent integral and the approximate analysis of strain concentration by notches and cracks ASME[J]. Journal of Applied Mechanics, 1968, 35(2): 379-386. DOI:10.1115/1.3601206 |
| [8] |
R. BRIGHENTI, A. CARPINTRRI. Buckling and fracture behaviour of cracked thin plates under shear loading[J]. Mater. Des, 2011, 32: 1347-1355. DOI:10.1016/j.matdes.2010.09.018 |
| [9] |
MARGARITIS Y., TOULIOS M... The ultimate and collapse response of cracked stiffened plates subjected to uniaxial compression[J]. Thin-Walled Struct, 2012, 50: 157-173. DOI:10.1016/j.tws.2011.09.008 |
| [10] |
PAIK J.K. FANG Wang, B.J. Kim, CUI Weicheng, et al. Ultimate shear strength of intact and cracked stiffened panels[J]. Thin-Walled Struct, 2015, 88: 48-57. DOI:10.1016/j.tws.2014.12.001 |
| [11] |
S. SAAD-ELDEEN, Y. GARBATOV, C. GUEDES SOARES. Experimental compressive strength analyses of high tensile steel thin-walled stiffened panels with a large lightening opening[J]. Thin-Walled Structures, 2017, 113: 61-68. DOI:10.1016/j.tws.2017.01.005 |
| [12] |
孙丹丹, 陈红火.全新Marc实例教程与常见问题解析[M].第二版.北京:中国水利水电出版社, 2016:334.
|
| [13] |
刘伯运, 周晓松, 张岳林. 考虑焊接残余应力的船体板结构屈曲强度[J]. 船海工程, 2017, 46(6): 6-11. LIU Bo-yun, ZHOU Xiao-song, ZHANG Yue-lin. Buckling strength of hull plate structure considering welding residual stress[J]. Marine Engineering, 2017, 46(6): 6-11. DOI:10.3963/j.issn.1671-7953.2017.06.002 |
| [14] |
M. R. KHEDMATI, M. M. ROSHANALI, Z. H. M. E. NOURIi. Strength of steel plates with both-sides randomly distributed with corrosion wastage under uniaxial compression. Thin-Walled Structures 49(2011)325−342.
|
| [15] |
袁焕鑫.焊接不锈钢轴心受压构件局部稳定和相关稳定性能研究[D].北京: 清华大学, 2014: 95. YUAN Huan-xin. Local stability and related stability of welded stainless steel axially compressed members[D]. Beijing: Tsinghua University, 2014: 95. |
 2021, Vol. 43
2021, Vol. 43
