0 引 言 传统的油船结构设计中,横向强框和横舱壁水平桁端部设置有大肘板,其远离面板区域的应力水平普遍较低,结构利用效率较低。根据油船轻量化设计的趋势[1-3],货舱区横向强框和横舱壁水平桁端部拓扑优化后呈现出类似斜撑杆的轻型结构[4-5],应力水平较低的区域布置较大的开孔。这种斜撑杆结构已经在多型油船中进行了实船上应用,并有效减轻了船体结构重量。
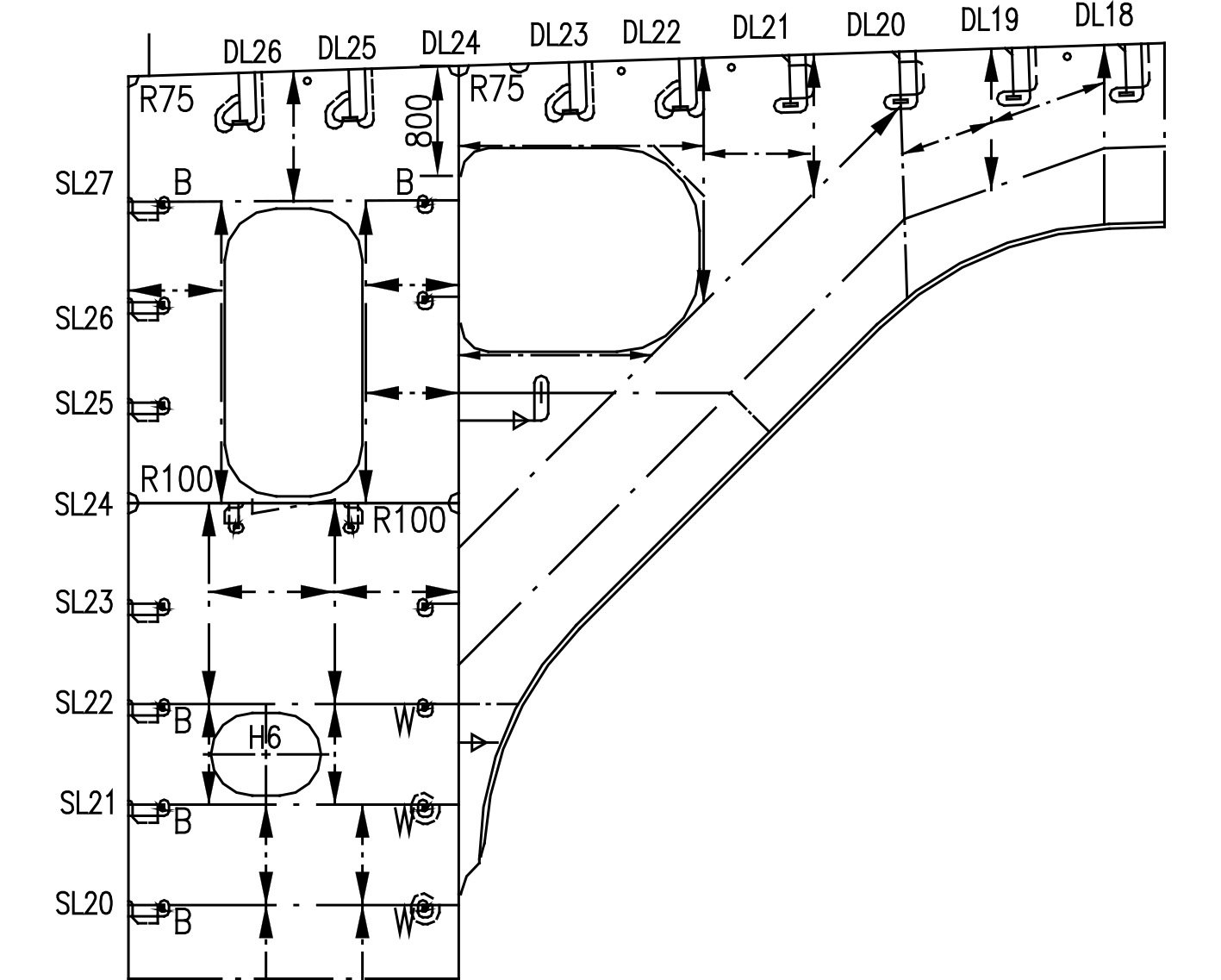
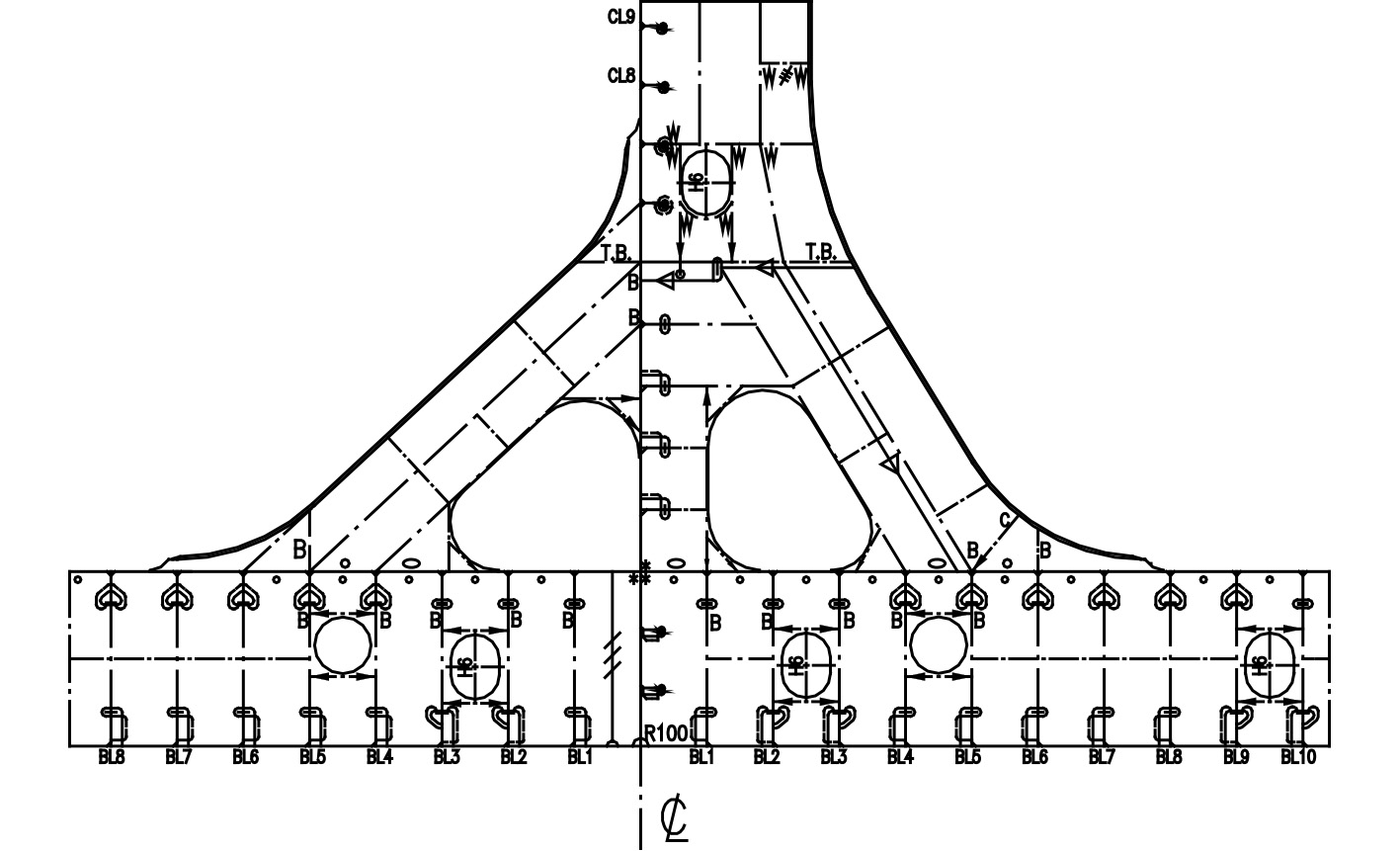
油船货舱区结构中,在以下位置采用了斜撑杆结构:甲板强横梁与舷侧强框架连接处、横舱壁水平桁与舷侧平台连接处、纵舱壁垂直桁与船底肋板连接处,如图1~图3所示。船体主要支撑结构通过斜撑杆相连并相互传递载荷,同时斜撑杆承受了较大的轴向载荷。斜撑杆成为相连的主要支撑结构的弹性支撑,一方面其轴向载荷对船体主要支撑结构的应力分布产生较大的影响,另外还需要根据斜撑杆的轴向载荷评估其自身屈服和屈曲强度[6]。
在设计初始阶段,往往需要对斜撑杆的多种设计方案进行比较,这就要求快速得到不同设计方案下斜撑杆的轴向载荷。目前还没有相关规范(包括HCSR)和标准适用于计算斜撑杆的轴向载荷,利用拓扑优化技术能够得到较优的设计方案,但是时间成本相对较高。
本文通过建立相关结构力学模型,快速得到斜撑杆轴向载荷的理论值,并与有限元计算结果进行比较,验证了相关力学模型及理论结果的有效性,最后对影响斜撑杆轴向载荷的主要因素进行了分析。这些工作能够为初始设计阶段优化斜撑杆结构的布置和尺寸提供一定的指导。
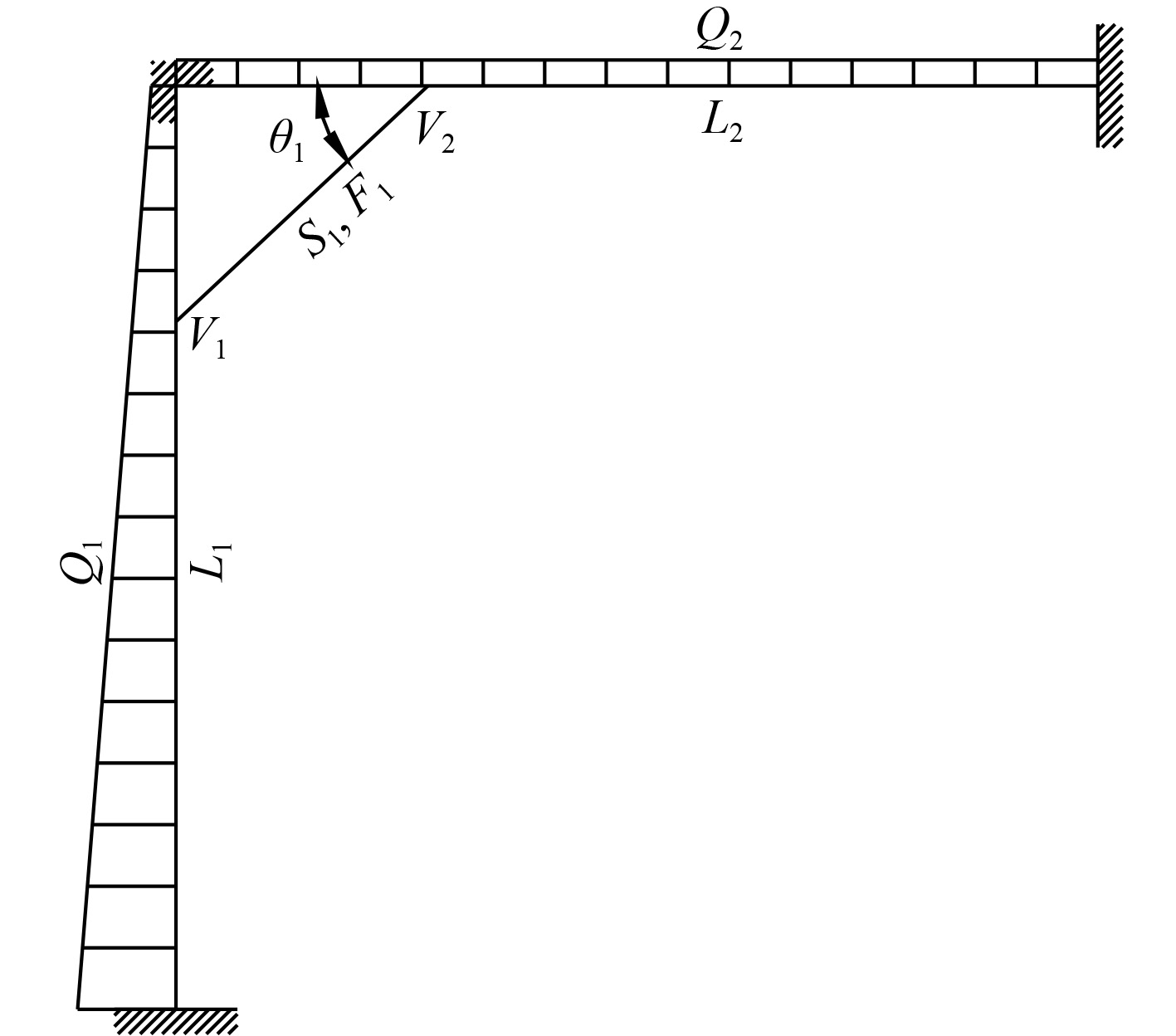
1 斜撑杆结构力学模型 1.1 力学模型A 首先以甲板强横梁与舷侧强框处结构为基础建立力学模型A,如图4所示。舷侧强框承受梯型载荷,甲板强横梁承受均布载荷。假设舷侧强框和甲板强横梁两端刚性固定,不考虑斜撑杆的弯曲效应。
${L_1}$
和
${L_2}$
分别为舷侧强框和甲板强横梁的弯曲跨距,
${I_1}$
和
${I_2}$
分别为舷侧强框和甲板强横梁的惯性矩;
${Q_1}$
和
${Q_2}$
分别为舷侧强框和甲板强横梁承受的横向载荷,
${Q_1}$
向右为正,
${Q_2}$
向下为正;
${S_1}$
,
${A_1}$
和
${F_1}$
分别为斜撑杆的有效长度、横截面积和轴向载荷,轴向拉力为正;
${v_1}$
和
${v_2}$
分别为舷侧强框和甲板强横梁在斜撑杆支撑点处的扰度,
${v_1}$
向右为正,
${v_2}$
向下为正;
${x_1}$
和
${x_2}$
分别为斜撑杆支撑点到舷侧强框与甲板强横梁交点的距离;
${\theta _1}$
为斜撑杆与水平方向的角度。
根据单跨梁理论,结构承受的横向载荷、斜撑杆轴向载荷和斜撑杆支撑点处位移之间关系的简化形式如下式:
|
${v_1}\cos ({\theta _1}) + {v_2}\sin ({\theta _1}) = {F_1}{\gamma _1}{\text{,}}$
|
(1) |
|
${Q_1}{\alpha _1}{\rm{ - }}{F_1}\cos ({\theta _1}){\beta _1} = {v_1}{\text{,}}$
|
(2) |
|
${Q_2}{\alpha _2} - {F_1}\sin ({\theta _1}){\beta _2} = {v_2}{\text{。}}$
|
(3) |
求解式(1)~式(3)联立的方程组,可以得到斜撑杆的轴向载荷为:
|
${{F}_{1}}={\left( {{Q}_{1}}{{\alpha }_{1}}\cos {{\theta }_{1}}+{{Q}_{2}}{{\alpha }_{2}}\sin {{\theta }_{1}} \right)}/{\left( {{\gamma }_{1}}+{{\cos }^{2}}\theta {}_{1}{{\beta }_{1}}+{{\sin }^{2}}\theta {}_{1}{{\beta }_{2}} \right)}{\text{。}}$
|
(4) |
其中:
|
${\gamma _1} = {S_1}/\left( {{A_1}E} \right){\text{,}}$
|
|
${\alpha _1} = \alpha ({x_1})L_1^3/(60E{I_1}){\text{,}}$
|
|
${\alpha _2} = \gamma ({x_2})L_2^3/(24E{I_2}){\text{,}}$
|
|
${\beta _1} = \beta ({x_1})L_1^3/(3E{I_1}){\text{,}}$
|
|
${\beta _2} = \beta ({x_2})L_2^3/(3E{I_2}){\text{。}}$
|
横舱壁水平桁与舷侧平台处结构类似于上述力学模型A,
${L_1}$
和
${L_2}$
分别为横舱壁水平桁和舷侧平台的弯曲跨距,不同之处为横舱壁水平桁承受均布载荷,上述公式中的
${\alpha _1}$
应根据承受均布载荷的单跨梁计算,
${\alpha _1} = \gamma ({x_1})L_1^3/(24E{I_1})$
。
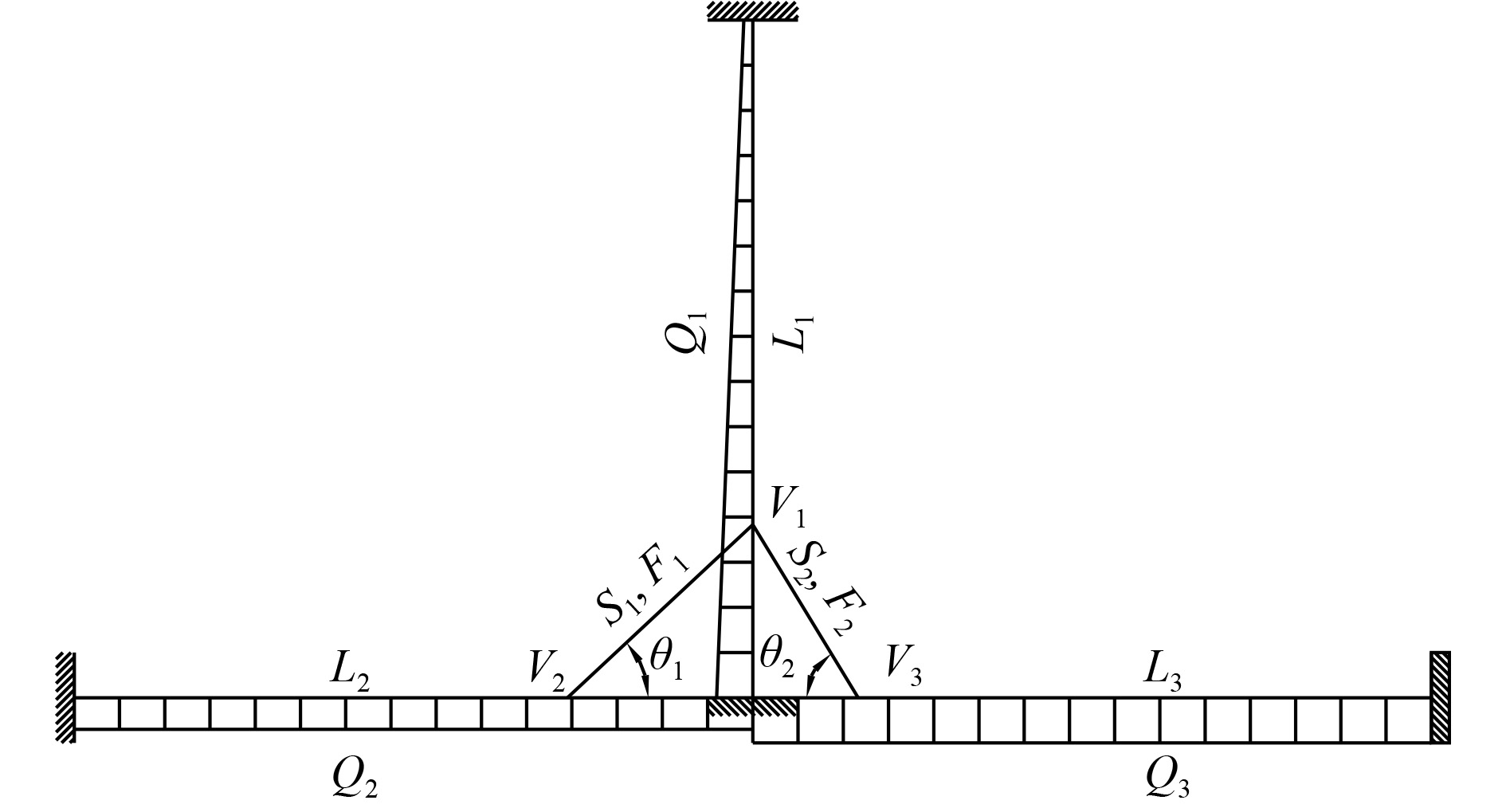
1.2 力学模型B 中纵舱壁垂直桁和船底肋板处结构比较复杂,左右两舷各有一个斜撑杆结构,据此建立力学模型B,如图5所示。中纵舱壁垂直桁承受梯型载荷,双层底肋板承受均布载荷,左右舷肋板承受的均布载荷可以不同(模拟不同的装载工况),左右两舷斜撑杆的布置和尺寸可以不同。假设垂直桁和肋板两端刚性固定,不考虑斜撑杆的弯曲效应。
${L_1}$
,
${L_2}$
和
${L_3}$
分别为中纵舱壁垂直桁和左右两舷肋板的弯曲跨距,
${I_1}$
,
${I_2}$
和
${I_3}$
分别为中纵舱壁垂直桁和左右两舷肋板的惯性矩;
${Q_1}$
,
${Q_2}$
和
${Q_3}$
分别为中纵舱壁垂直桁和左右两舷肋板承受的横向载荷,
${Q_1}$
向右为正,
${Q_2}$
和
${Q_3}$
向下为正;
${S_1}$
,
${A_1}$
,
${F_1}$
和
${S_2}$
,
${A_2}$
,
${F_2}$
分别为左右舷2个斜撑杆的有效长度、横截面积和轴向载荷,轴向拉力为正;
${v_1}$
,
${v_2}$
和
${v_3}$
分别为中纵舱壁垂直桁和左右两舷肋板在斜撑杆支撑点处的扰度,
${v_1}$
向右为正,
${v_2}$
和
${v_3}$
向下为正;
${x_1}$
,
${x_2}$
和
${x_3}$
分别为斜撑杆支撑点到垂直桁与肋板交点的距离;
${\theta _1}$
和
${\theta _2}$
分别为2个斜撑杆与水平方向的角度。
根据单跨梁理论,结构承受的横向载荷、斜撑杆轴向载荷和斜撑杆支撑点处位移之间关系的简化形式如下式:
|
${v_1}\cos ({\theta _1}) + {v_2}\sin ({\theta _1}) = {F_1}{\gamma _1}{\text{,}}$
|
(5) |
|
$ - {v_1}\cos ({\theta _2}) + {v_3}\sin ({\theta _2}) = {F_2}{\gamma _2}{\text{,}}$
|
(6) |
|
$ {Q}_{1}{\alpha }_{1}+({F}_{2}\rm{cos}({\theta }_{2})-{F}_{1}\rm{cos}({\theta }_{1})){\beta }_{1}={v}_{1}{\text{,}}$
|
(7) |
|
${Q_2}{\alpha _2} - {F_1}\sin ({\theta _1}){\beta _2} = {v_2}{\text{,}}$
|
(8) |
|
${Q_3}{\alpha _3} - {F_2}\sin ({\theta _2}){\beta _3} = {v_3}{\text{。}}$
|
(9) |
求解式(5)~式(7)联立的方程组,可以得到2个斜撑杆的轴向载荷分别为:
|
${F_1} = \frac{{CD - BE}}{{AD - {B^2}}}{\text{,}}$
|
(10) |
|
${F_2} = \frac{{BC - AE}}{{AD - {B^2}}}{\text{。}}$
|
(11) |
其中:
|
$\begin{split} &A = {\gamma _1} + {\cos ^2}{\theta_1}{\beta _1} + {\sin ^2}{\theta_1}{\beta _2}{\text{,}} \\ &B = \cos {\theta_1}\cos \theta {}_2{\beta _1}{\text{,}} \\ &C = {Q_1}{\alpha _1}\cos ({\theta _1}) + {Q_2}{\alpha _2}\sin ({\theta _1}){\text{,}} \\ &D = {\gamma _2} + {\cos ^2}\theta {}_2{\beta _1} + {\sin ^2}\theta {}_2{\beta _3}{\text{,}} \\ & E = {Q_1}{\alpha _1}{\rm{cos}}({\theta _2}){\rm{ - }}{Q_3}{\alpha _3}{\rm{sin}}({\theta _2}){\text{,}} \end{split} $
|
|
${\gamma _1} = {S_1}/\left( {{A_1}E} \right){\text{,}}$
|
|
${\gamma _2} = {S_2}/\left( {{A_2}E} \right){\text{,}}$
|
|
${\alpha _1} = \alpha ({x_1})L_1^3/(60E{I_1}){\text{,}}$
|
|
${\alpha _2} = \gamma ({x_2})L_2^3/(24E{I_2}){\text{,}}$
|
|
${\alpha _3} = \gamma ({x_3})L_3^3/(24E{I_3}){\text{,}}$
|
|
${\beta _1} = \beta ({x_1})L_1^3/(3E{I_1}){\text{,}}$
|
|
${\beta _2} = \beta ({x_2})L_2^3/(3E{I_2}){\text{,}}$
|
|
${\beta _3} = \beta ({x_3})L_3^3/(3E{I_3}){\text{。}}$
|
2 理论计算结果验证 应用上文建立的2个力学模型,基于MARIC开发的114K载重原油船(单纵舱壁),分别计算典型位置处斜撑杆轴向载荷理论值,包括甲板强横梁与舷侧强框架间斜撑杆、纵舱壁垂直桁与船底肋板间斜撑杆、横舱壁水平桁与舷侧平台间斜撑杆,并与有限元计算结果进行比较。
基于散货船和油船共同结构规范(HCSR),对于同一装载模式,航行工况和港内工况下结构承受的压力载荷大小不同但载荷形式类似,因此只对港内工况不同装载模式下斜撑杆轴向载荷结果进行比较,其结论同样适用于航行工况。针对不同位置处的斜撑杆,选取港内工况下典型的装载模式进行计算,HCSR港内工况下各装载模式如图6所示[7]。
2.1 甲板强横梁与舷侧强框处结果 基于图6中B8载荷工况对甲板强横梁与舷侧强框处斜撑杆的轴向载荷理论值进行验证,选取最靠近货舱舱长中点处横向强框的有限元结果和理论值进行比较。斜撑杆轴向载荷的有限元结果根据有限元应力水平得出。
斜撑杆的有效长度在撑杆截面的中心线处量取,斜撑杆的有效截面积在其截面积最小位置处量取,主要支撑结构的弯曲跨距不考虑所计算斜撑杆的减跨作用。计算参数如表1所示,比较结果如表2所示。
表 1(Tab. 1)

表 1 计算输入参数
Tab. 1 Input parameter of calculation
| 舷侧强框架 |
|
甲板强横梁 |
|
斜撑杆 |
| Q1/kN·m−1 |
L1/m
|
I1/cm4 |
x1/m
|
Q2/kN·m−1 |
L2/m
|
I2/cm4 |
x2/m
|
θ1/(°)
|
S1/m
|
A1/cm2 |
| 350 |
15.6 |
7.2E+6 |
4.2 |
|
9.1 |
15.7 |
1.3E+6 |
4.35 |
|
45 |
6.15 |
239 |
|
表 1 计算输入参数
Tab.1 Input parameter of calculation
|
表 2(Tab. 2)

表 2 计算结果比较
Tab. 2 Comparision of calculation
| 斜撑杆轴向载荷 |
| 理论值/kN |
有限元结果/kN |
误差/% |
| 1074 |
1013 |
5.7 |
|
表 2 计算结果比较
Tab.2 Comparision of calculation
|
2.2 横舱壁水平桁与舷侧平台处结果 基于图6中B8载荷工况对横舱壁水平桁与舷侧平台处斜撑杆的轴向载荷理论值进行了验证,计算参数如表3所示,比较结果如表4所示。
表 3(Tab. 3)

表 3 计算输入参数
Tab. 3 Input parameter of calculation
| 舷侧平台(距基线5990 mm) |
| Q1/kN·m−1 |
L1/m
|
I1/cm4 |
x1/m
|
| 900 |
4.48 |
5.6E+6 |
4.48 |
| 横舱壁水平桁(距基线5990 mm) |
| Q2/kN·m−1 |
L2/m
|
I2/cm4 |
x2/m
|
| 900 |
14.7 |
4.5E+6 |
4.44 |
| 斜撑杆 |
| θ1/(°)
|
S1/m
|
A1/cm2 |
|
| 45 |
6.28 |
361 |
|
|
表 3 计算输入参数
Tab.3 Input parameter of calculation
|
表 4(Tab. 4)

表 4 计算结果比较
Tab. 4 Comparision of calculation
| 斜撑杆轴向载荷 |
| 理论值/kN |
有限元结果/kN |
误差/% |
| 4332 |
4654 |
−7.4 |
|
表 4 计算结果比较
Tab.4 Comparision of calculation
|
由于舷侧平台受到舷侧强框和底边舱斜板的有效支撑,舷侧平台侧向变形很小,计算参数中舷侧平台的跨距
${L_1}$
取为和
${x_1}$
相同,使得斜撑杆在与舷侧平台相交处的位移为零,模拟实际情况。
2.3 中纵舱壁垂直桁和肋板处结果 中纵舱壁垂直桁和肋板处有左右2个斜撑杆,不同装载模式下斜撑杆的受力有很大的不同。考虑港内工况下所有的装载模式,包括图6中B8,B9,B10和B11四种装载模式,对中纵舱壁垂直桁和肋板处斜撑杆的轴向载荷理论值进行验证,同样选取最靠近货舱舱长中点处横向强框的有限元结果和理论值进行比较。计算参数如表5所示,比较结果如表6所示。
表 5(Tab. 5)

表 5 计算输入参数
Tab. 5 Input parameter of calculation
| 纵舱壁垂直桁 |
|
左舷肋板 |
|
左舷斜撑杆 |
| L1/m
|
I1/cm4 |
x1/m
|
|
L2/m
|
I2/cm4 |
x2/m
|
|
${\theta _1}$
/(°)
|
S1/m
|
A1/cm2 |
| 17.1 |
5.6E+6 |
3.83 |
|
14.8 |
4.9E+6 |
4.1 |
|
43 |
5.61 |
318 |
|
表 5 计算输入参数
Tab.5 Input parameter of calculation
|
表 5(Tab. 5)

| 右舷肋板 |
|
右舷斜撑杆 |
|
${L_3}$
/m
|
${I_3}$
/cm4 |
${x_3}$
/m
|
|
${\theta _2}$
|
${S_2}$
/m
|
${A_2}$
/cm2 |
| 13.9 |
4.9E+6 |
3.28 |
|
59 |
3.89 |
378 |
|
|
表 5(Tab. 5)

| 载荷工况 |
Q1/kN·m−1 |
Q2/kN·m−1 |
Q3/kN·m−1 |
| B8 |
0 |
598 |
598 |
| B9 |
475 |
598 |
−170 |
| B10 |
−475 |
−170 |
598 |
| B11 |
0 |
−512 |
−512 |
|
|
表 6(Tab. 6)

表 6 计算结果比较
Tab. 6 Comparision of calculation
载荷
工况
|
左舷斜撑杆轴向载荷 |
|
右舷斜撑杆轴向载荷 |
理论值/
kN
|
有限元结果/
kN
|
误差/% |
理论值/
kN
|
有限元结果/
kN
|
误差/% |
| B8 |
2460 |
2532 |
−3 |
|
3040 |
2706 |
11 |
| B9 |
3750 |
3986 |
−6.3 |
|
−2030 |
−2296 |
−13.1 |
| B10 |
−1990 |
−2214 |
−11 |
|
4200 |
3937 |
6.3 |
| B11 |
−2110 |
−2363 |
−12 |
|
−2600 |
−2600 |
0.0 |
|
表 6 计算结果比较
Tab.6 Comparision of calculation
|
由以上有限元和理论值的比较结果可以看出,根据本文建立的力学模型得到的斜撑杆轴向载荷理论值和有限元结果的误差在一定范围内,验证了2个力学模型及理论结果的有效性。通过理论计算能够方便快速的得到斜撑杆的轴向载荷,进而对优化斜撑杆结构的布置和尺寸有一定的指导作用。
3 斜撑杆轴向载荷影响因素分析 根据斜撑杆轴向载荷的理论计算式(4)可知,斜撑杆的轴向载荷主要与斜撑杆的刚度和角度、支撑点位置、相连的主要支撑结构的刚度及其承受的载荷有关。主要支撑结构的刚度及其承受的载荷一定的情况下,可以计算出最优的斜撑杆角度和支撑点位置。
相同条件下,斜撑杆的轴向载荷越大,表明斜撑杆的效率越高,对相连结构的支撑越有效,可以认为斜撑杆布置相对较优。
3.1 斜撑杆角度对轴向载荷的影响 计算斜撑杆不同角度下其轴向载荷时,斜撑杆一端的位置保持不变,另一端的位置和斜撑杆的长度随斜撑杆角度的变化而变化,其他计算参数保持不变。针对114K载重原油船横舱壁水平桁(距基线5990 mm)和舷侧平台处斜撑杆、甲板强横梁和舷侧强框处斜撑杆和纵舱壁垂直桁和左舷肋板处斜撑杆分别选取典型的载荷工况进行计算分析。
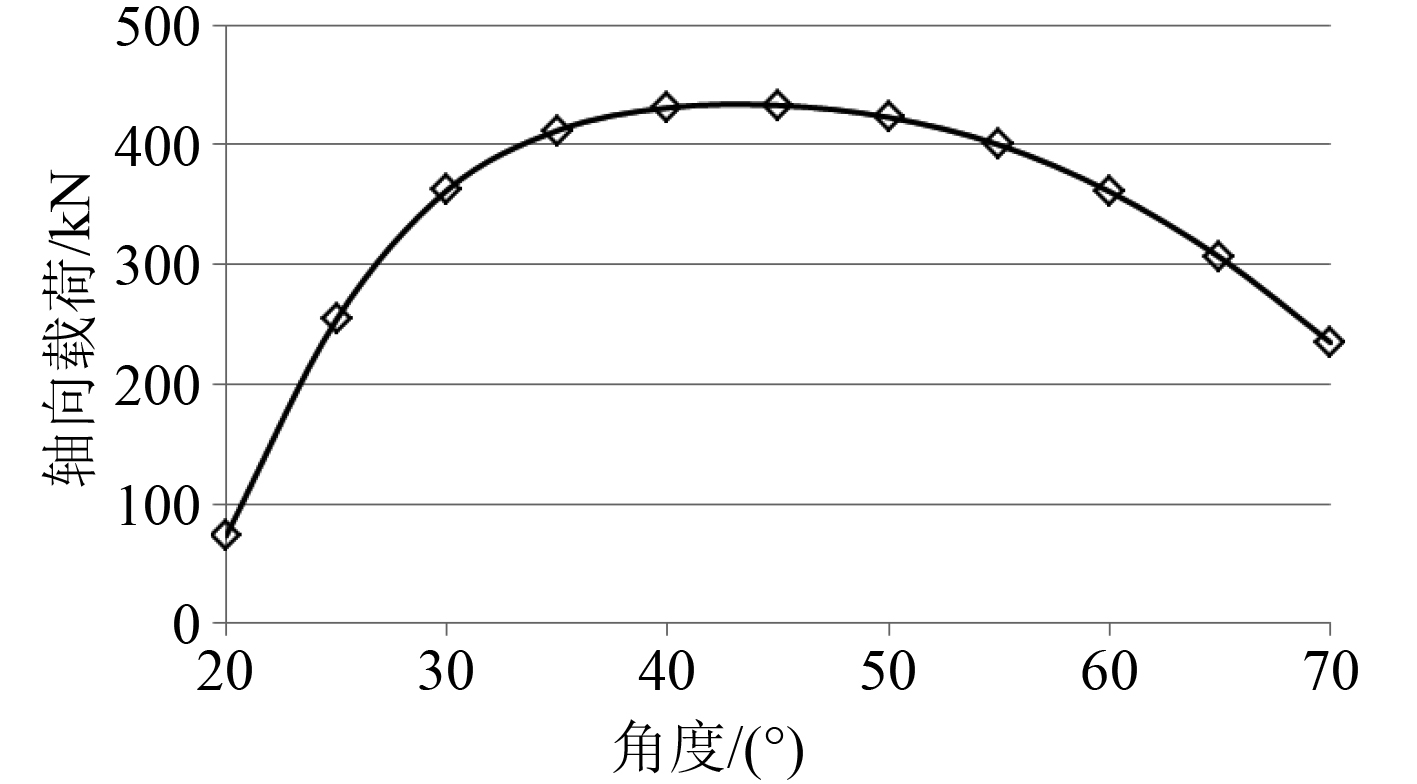
B8载荷工况下横舱壁水平桁(距基线5990 mm)和舷侧平台处斜撑杆角度对其轴向载荷的影响如图7所示。可以看出,当斜撑杆的角度近似为45°时,斜撑杆的轴向载荷达到最大值,斜撑杆的效率较高,这与114K原油船斜撑杆的实船设计角度一致。不同的船型和载荷工况下最优的斜撑杆设计角度可能不同,需要根据具体情况进行计算分析。
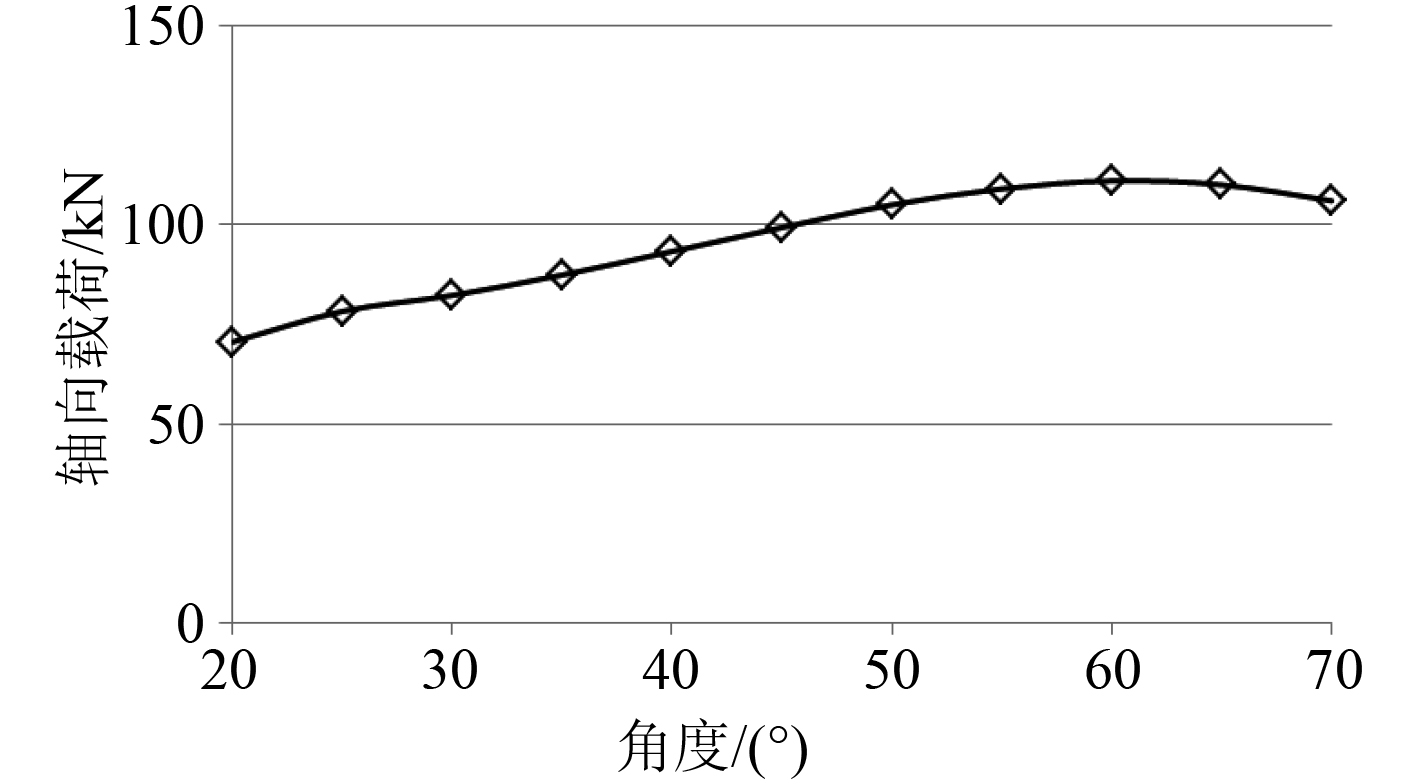
B8载荷工况下甲板强横梁和舷侧强框处斜撑杆角度对其轴向载荷的影响,如图8所示。可以看出,当斜撑杆的角度约为60°时,斜撑杆的轴向载荷达到最大值。
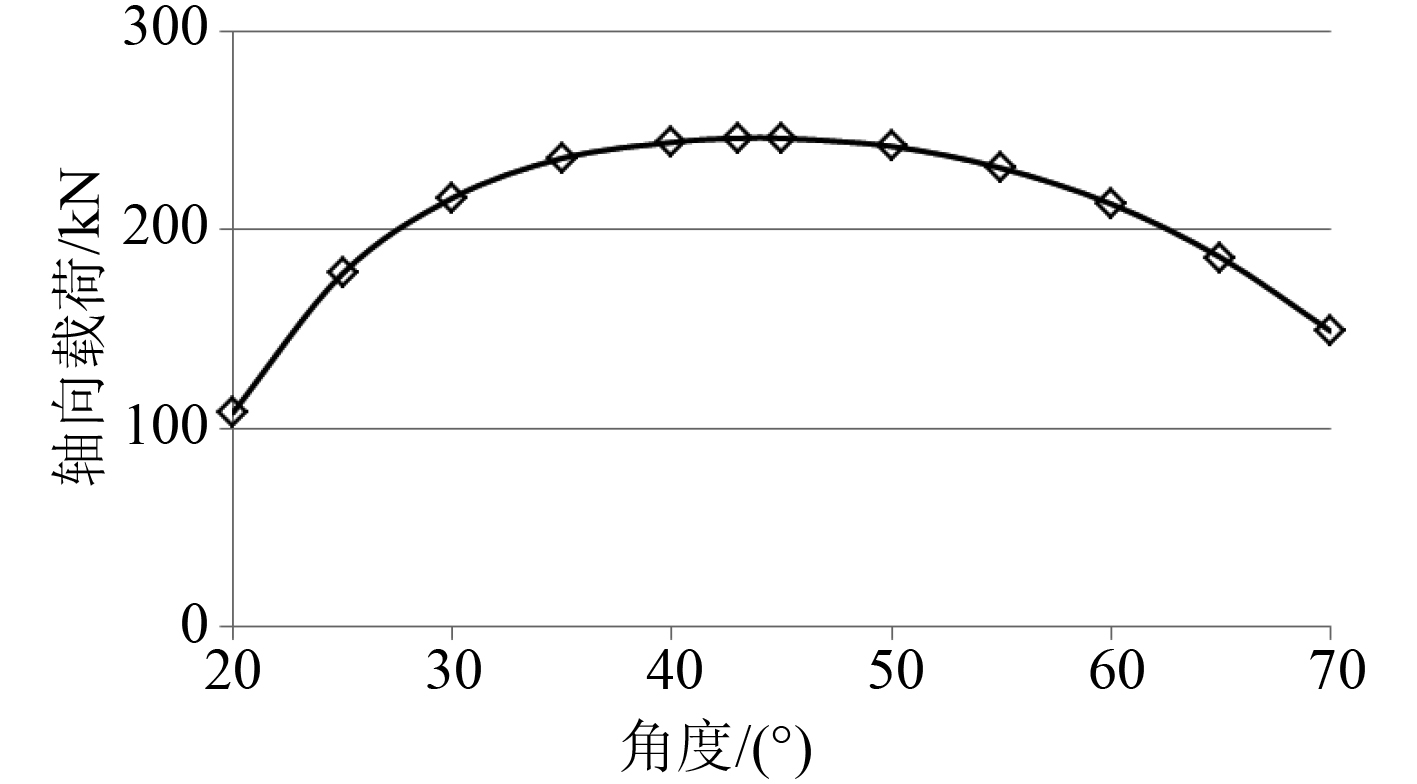
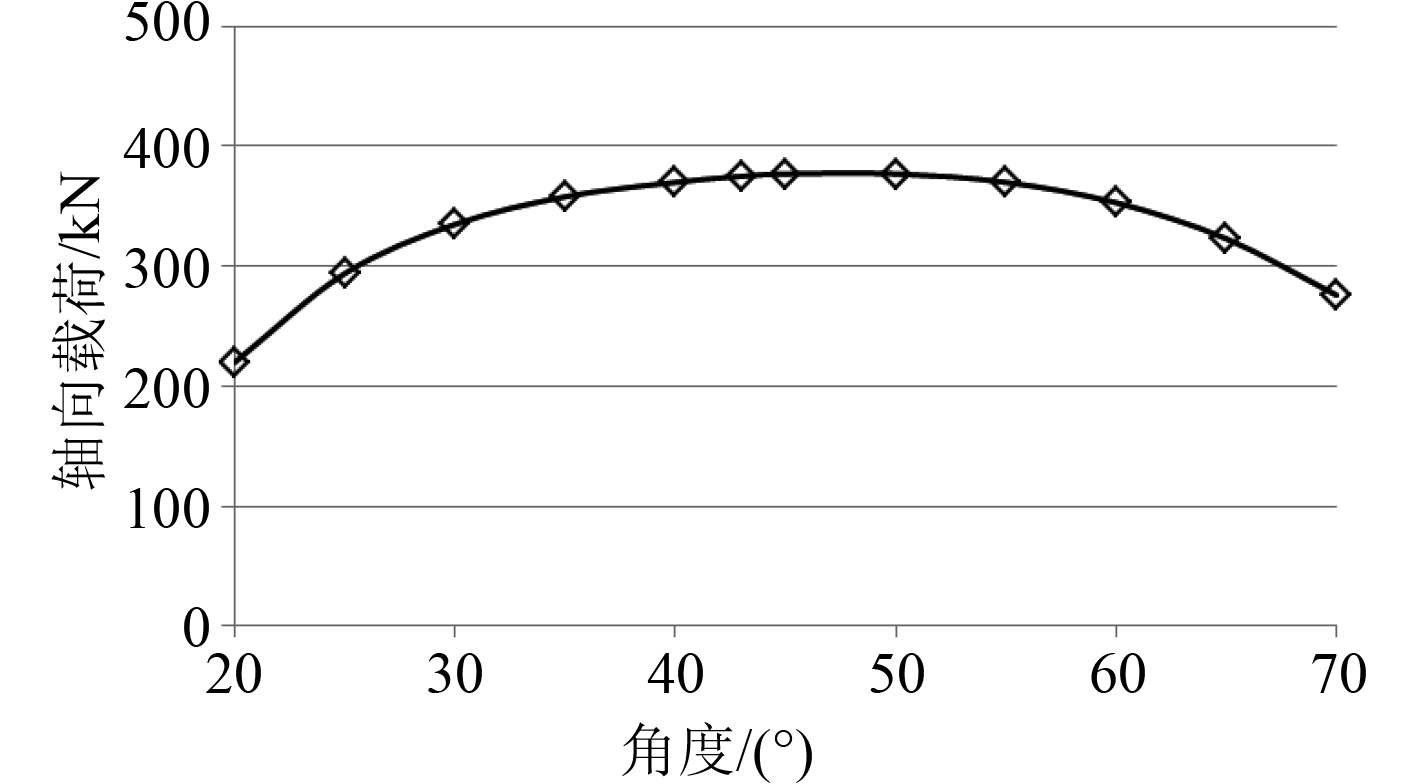
B8和B9载荷工况下纵舱壁垂直桁和左舷肋板处斜撑杆角度对其轴向载荷的影响,分别如图9和图10所示。可以看出,当斜撑杆的角度约为45°时,2种工况下斜撑杆的轴向载荷都达到最大值,与114K原油船斜撑杆的实船设计角度基本一致。
3.2 斜撑杆支撑点位置对轴向载荷的影响 计算斜撑杆不同支撑点位置下其轴向载荷时,斜撑杆长度随支撑点位置的变化而变化,斜撑杆的轴向刚度(斜撑杆截面积和长度之比)、斜撑杆角度和其它参数保持固定不变。可以得到斜撑杆支撑点位置对其轴向载荷的影响。
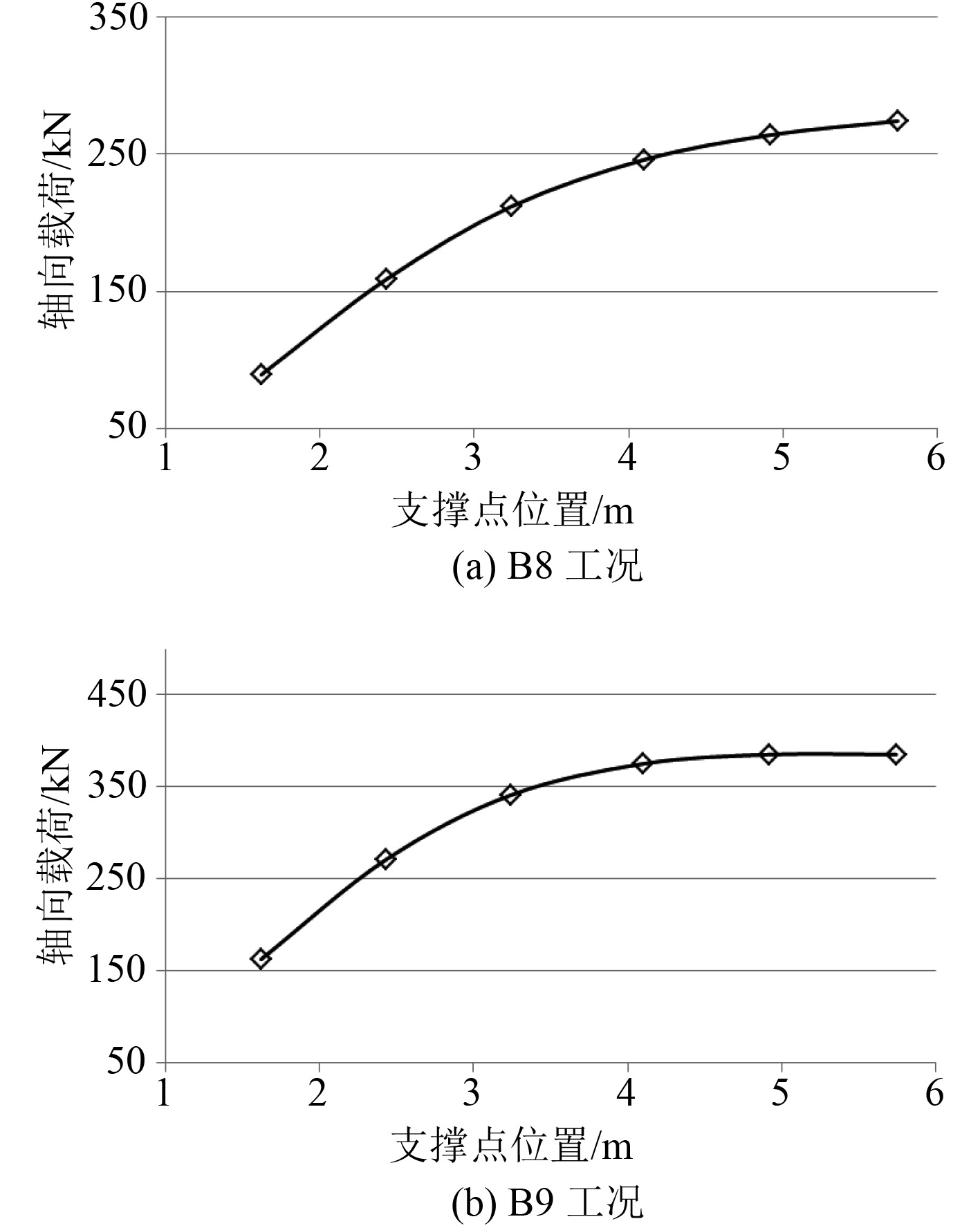
B8载荷工况下横舱壁水平桁(距基线5990 mm)和舷侧平台处斜撑杆支撑点位置对其轴向载荷的影响如图11所示。B8和B9载荷工况下纵舱壁垂直桁和左舷肋板处斜撑杆支撑点位置对其轴向载荷的影响如图12所示。
可以看出,随着支撑点与主要支撑构件端部之间距离的增加,斜撑杆的轴向载荷也逐渐增加,但是其增加的幅度逐渐变缓。在实船设计中,需要综合考虑斜撑杆的效率和其他因素来确定支撑点的位置。
4 结 语 油船轻量化设计中,端部大肘板优化为类似斜撑杆的轻型结构,斜撑杆承受了较大的轴向载荷,在设计初始阶段,需要快速得到不同设计方案下斜撑杆的轴向载荷,来指导斜撑杆结构的优化设计。
1)本文针对典型位置处的斜撑杆结构,建立2个力学模型,得到斜撑杆轴向载荷的理论值,并与有限元计算结果进行比较,验证了相关力学模型及理论结果的有效性,能够为初始设计阶段优化斜撑杆结构的布置和尺寸提供一定的指导。
2)针对114K油船典型载荷工况下斜撑杆角度对其轴向载荷的影响进行计算分析,结果表明横舱壁水平桁端部斜撑杆和纵舱壁垂直桁端部背部斜撑杆的角度近似为45°时,斜撑杆的轴向载荷达到最大值,斜撑杆的效率较高,与114K油船的实船设计角度一致。
3)同样对114K油船典型载荷工况下斜撑杆支撑点位置对其轴向载荷的影响进行计算分析,结果表明随着支撑点与主要支撑构件端部之间距离的增加,斜撑杆的轴向载荷也逐渐增加,但是其增加的幅度逐渐变缓。
4)根据斜撑杆轴向载荷的理论计算公式可知,斜撑杆的轴向载荷主要与斜撑杆的刚度和角度、支撑点位置、相连的主要支撑结构的刚度和承受的载荷有关。不同船型和载荷工况下,最优的斜撑杆设计角度和支撑点位置可能不同,需要根据具体情况进行计算分析。
5)优化后的斜撑杆布置方案下,斜撑杆承受的轴向载荷相对比较大,因此在设计中要特别关注斜撑杆的局部屈曲和整体屈曲问题。



 2021, Vol. 43
2021, Vol. 43
