水下承压结构作为大型焊接结构,残余应力不可忽略[1]。研究表明,残余应力对水下承压结构的承载性能及疲劳性能均会产生不利影响[2-3]。因此,准确掌握水下承压结构残余应力规律可为结构服役安全性评估及结构残余应力消除提供支撑和依据[4]。
在众多残余应力测试方法中,盲孔法因其适用性强、操作简便、检测精度高等优点而得到了广泛应用[5]。一般采用三轴直角应变花进行残余应力测试[5-9],基于三轴等角应变花的残余应力测试鲜有报道。文中采用等轴三角应变花针对高强度钢锥柱结合结构试验模型进行残余应力测试。首先,对等轴三角应变花的应变释放系数完成了有限元标定和塑性修正,得到了塑性修正后的应变释放系数;然后,根据测试得到的各残余应力测点的释放应变值,结合塑性修正后的应变释放系数计算得到了锥柱结合结构典型测点的残余应力值。
文中的研究工作可为基于三轴等角应变花的残余应力测试提供参考;同时,测试得到的锥柱结合结构典型测点的残余应力分布规律可为水下承压结构安全性评估和残余应力消除提供支撑,具有一定工程意义。
1 盲孔法测量残余应力基本原理文献[5-9]描述了盲孔法测量残余应力的基本原理:在结构或构件残余应力场内任意一点处钻一盲孔,此时盲孔附近将产生微弱释放应变,其数值大小与被释放处的残余应力相对应,采用应变花测出这种释放应变后,即可利用相应残余应力计算式确定测点处的残余应力情况。
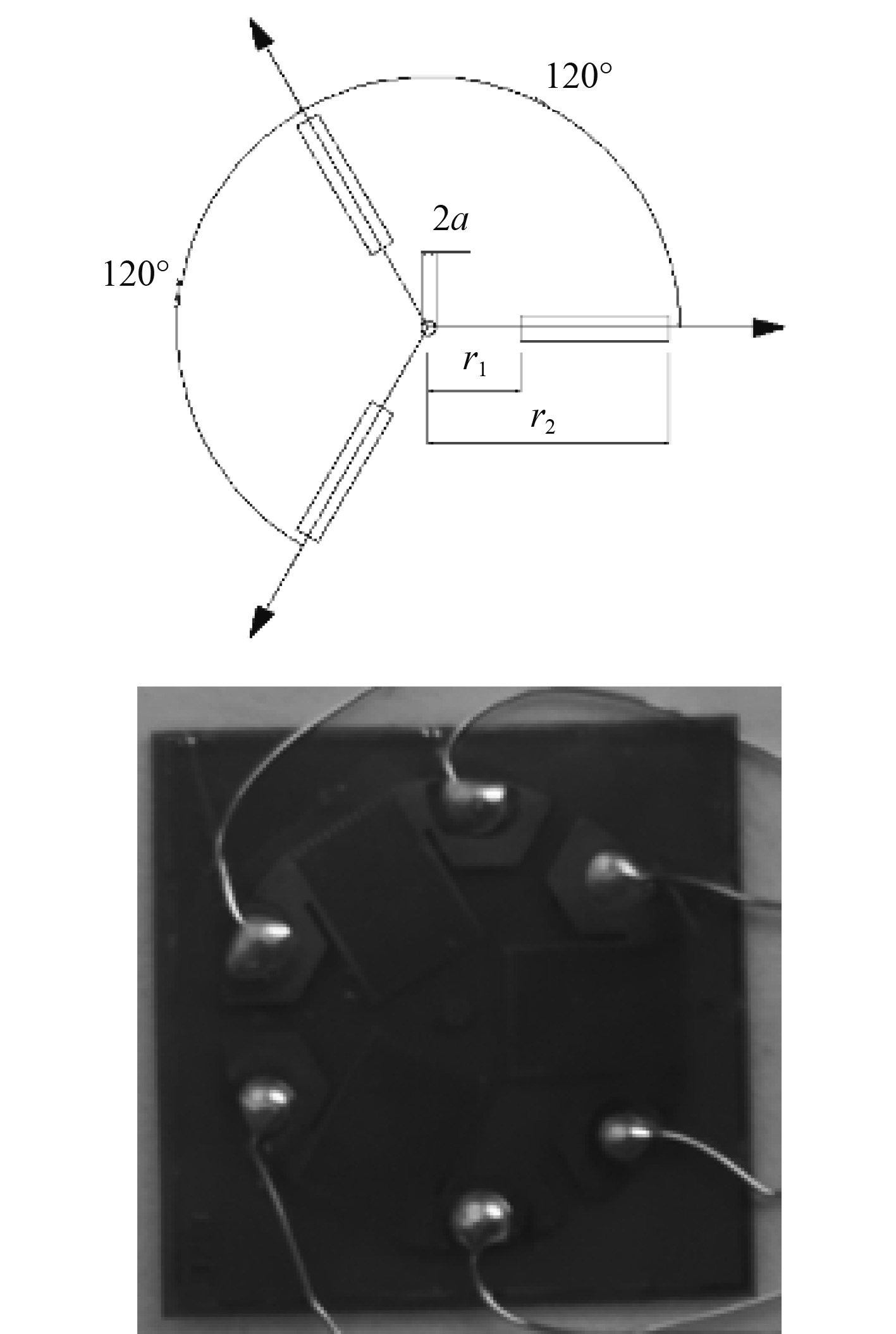
本次试验用三轴等角应变花示意如图1所示。应变花中3个应变计夹角均成120°,分别记为0°,120°,240°应变计(逆时针)。
|
图 1 三轴等角应变花 Fig. 1 Triaxial equiangular strain gauge |
文献[10]中给出的三轴等角应变花主应力、主应变和夹角计算式,给出基于三轴等角应变花的残余应力计算相关式如下:
| $ \begin{split}{\sigma }_{{1,2}}=&\frac{\left({\varepsilon }_{0}+{\varepsilon }_{120}+{\varepsilon }_{240}\right)}{A}\pm \\ &\frac{\sqrt{\dfrac{{\left({\varepsilon }_{120}-{\varepsilon }_{240}\right)}^{2}}{3}+{\left({\varepsilon }_{0}-\dfrac{{\varepsilon }_{0}+{\varepsilon }_{120}+{\varepsilon }_{240}}{3}\right)}^{2}}}{B} \end{split}{\text{,}}$ | (1) |
| $\begin{split}{\varepsilon }_{{1,2}}=&\frac{\left({\varepsilon }_{0}+{\varepsilon }_{120}+{\varepsilon }_{240}\right)}{3}\pm \\ &\sqrt{\frac{{\left({\varepsilon }_{120}-{\varepsilon }_{240}\right)}^{2}}{3}+{\left({\varepsilon }_{0}-\frac{{\varepsilon }_{0}+{\varepsilon }_{120}+{\varepsilon }_{240}}{3}\right)}^{2}} \end{split}{\text{,}}$ | (2) |
| $ \mathrm{t}\mathrm{a}\mathrm{n}2\theta =\frac{1}{\sqrt{3}}\frac{{\varepsilon }_{120}-{\varepsilon }_{240}}{{\varepsilon }_{0}-\dfrac{1}{3}({\varepsilon }_{0}+{\varepsilon }_{120}+{\varepsilon }_{240})} {\text{。}}$ | (3) |
式中:
盲孔法测量结构残余应力的关键点在于准确获取应变释放系数,而应变释放系数与钻孔孔径、应变花尺寸及被测材料的弹性模量有关,一般可通过理论计算、拉伸试验标定或拉伸试验数值仿真标定得到[5-6]。标定原理如下:
对拉伸试样施加单向应力场(
| $ \left\{\begin{array}{c}\sigma =\dfrac{1}{A}\left({\varepsilon }_{0}+2{\varepsilon }_{240}\right)+\dfrac{2}{3B}\left|{\varepsilon }_{0}-{\varepsilon }_{240}\right|{\text{,}}\\ 0=\dfrac{1}{A}\left({\varepsilon }_{0}+2{\varepsilon }_{240}\right)-\dfrac{2}{3B}\left|{\varepsilon }_{0}-{\varepsilon }_{240}\right|{\text{。}}\end{array}\right. $ | (4) |
由式(4)可得:
| $ \left\{\begin{array}{c}A=2({\varepsilon }_{0}+2{\varepsilon }_{240})/\sigma {\text{,}}\\ B=4\left|{\varepsilon }_{0}-{\varepsilon }_{120}\right|/3\sigma{\text{。}} \end{array}\right. $ | (5) |
将0°和240°方向应变计测得的释放应变
采用有限元法标定残余应力应变释放系数。拉伸试样尺寸为120 mm×60 mm×12 mm,盲孔及应变花尺寸取为实际尺寸,如表1所示。表中参数
|
|
表 1 有限元模型尺寸 Tab.1 Finite element mode dimension |
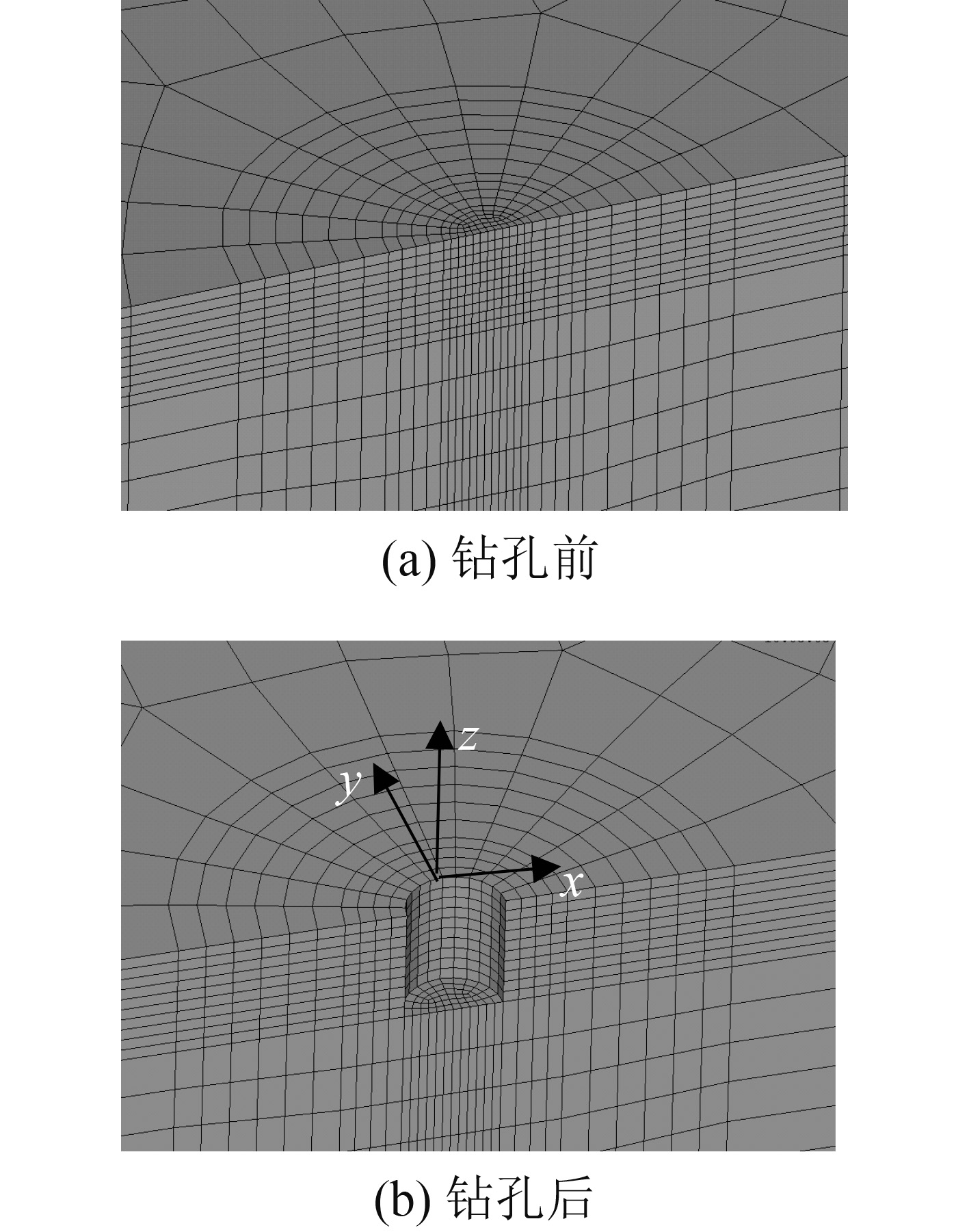
采用Ansys中的SOLID45体单元建立拉伸试样有限元模型。考虑对称性,建立1/2模型进行计算,对称面施加对称约束,模型长度方向一端刚性固定,另一端施加均布拉伸载荷。钻孔前、后盲孔附近有限元模型如图2所示。
|
图 2 有限元模型 Fig. 2 Finite element model |
对钻孔前、后有限元模型分别施加1 MPa,10 MPa,100 MPa,200 MPa,300 MPa,400 MPa,500 MPa和600 MPa单轴拉伸载荷
| $ {\varepsilon }_{0}={\varepsilon }_{0}^{'}-{\varepsilon }_{0}^{0} {\text{,}}$ | (6) |
| $ {\varepsilon }_{90}={\varepsilon }_{90}^{'}-{\varepsilon }_{90}^{0} {\text{,}}$ | (7) |
| $ {\varepsilon }_{120}={\varepsilon }_{120}^{'}-{\varepsilon }_{120}^{0}{\text{。}} $ | (8) |
式中:
结合式(5)、式(6)、式(8)可求得不同拉伸载荷
|
|
表 2 释放应变及应变释放系数计算结果 Tab.2 Release strain and strain release coefficients calculation results |
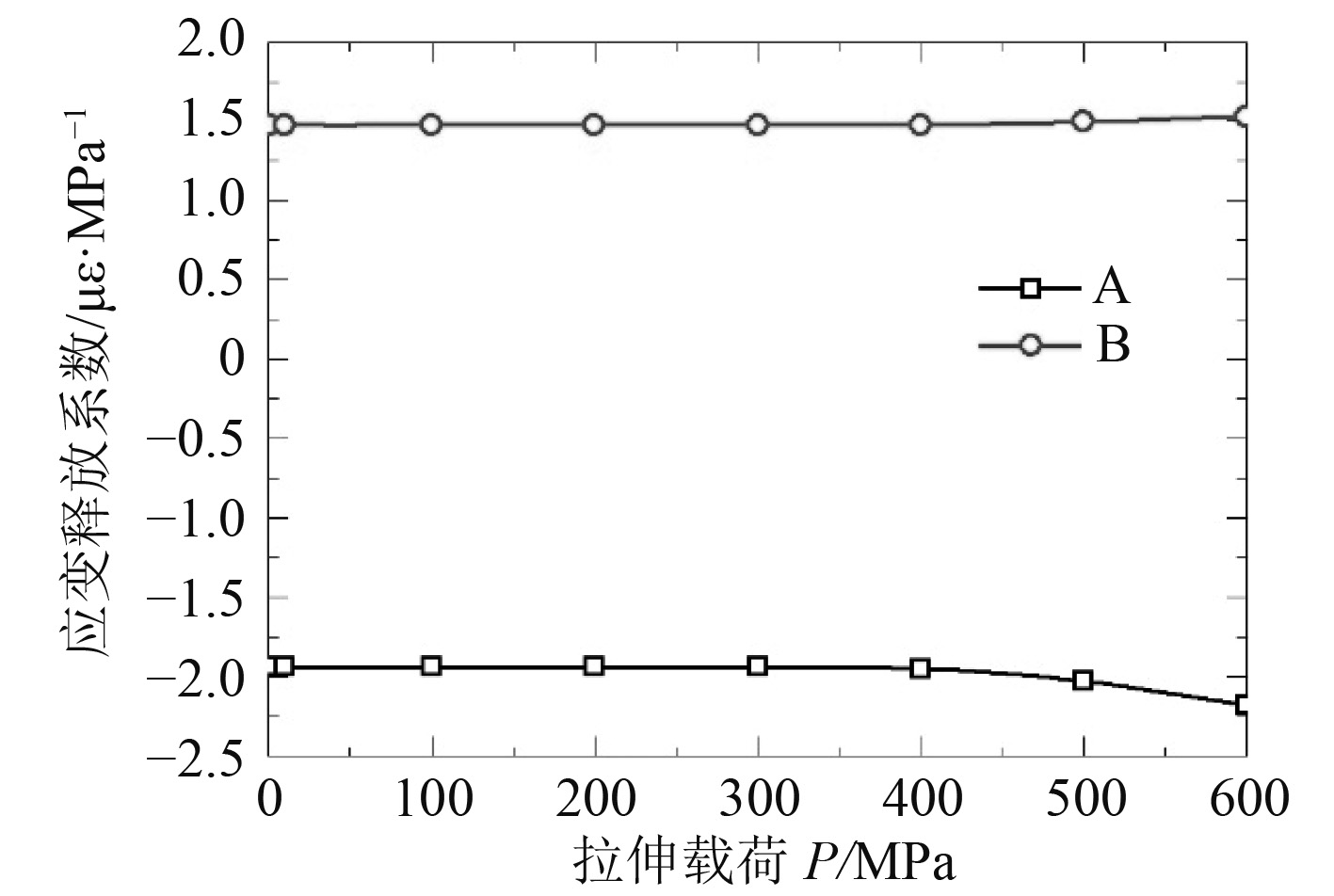
应变释放系数随应力变化曲线如图3所示。
|
图 3 应变释放系数-应力曲线 Fig. 3 Curves of strain release coefficients varying with calibration stress |
由图3可知,均布拉伸载荷
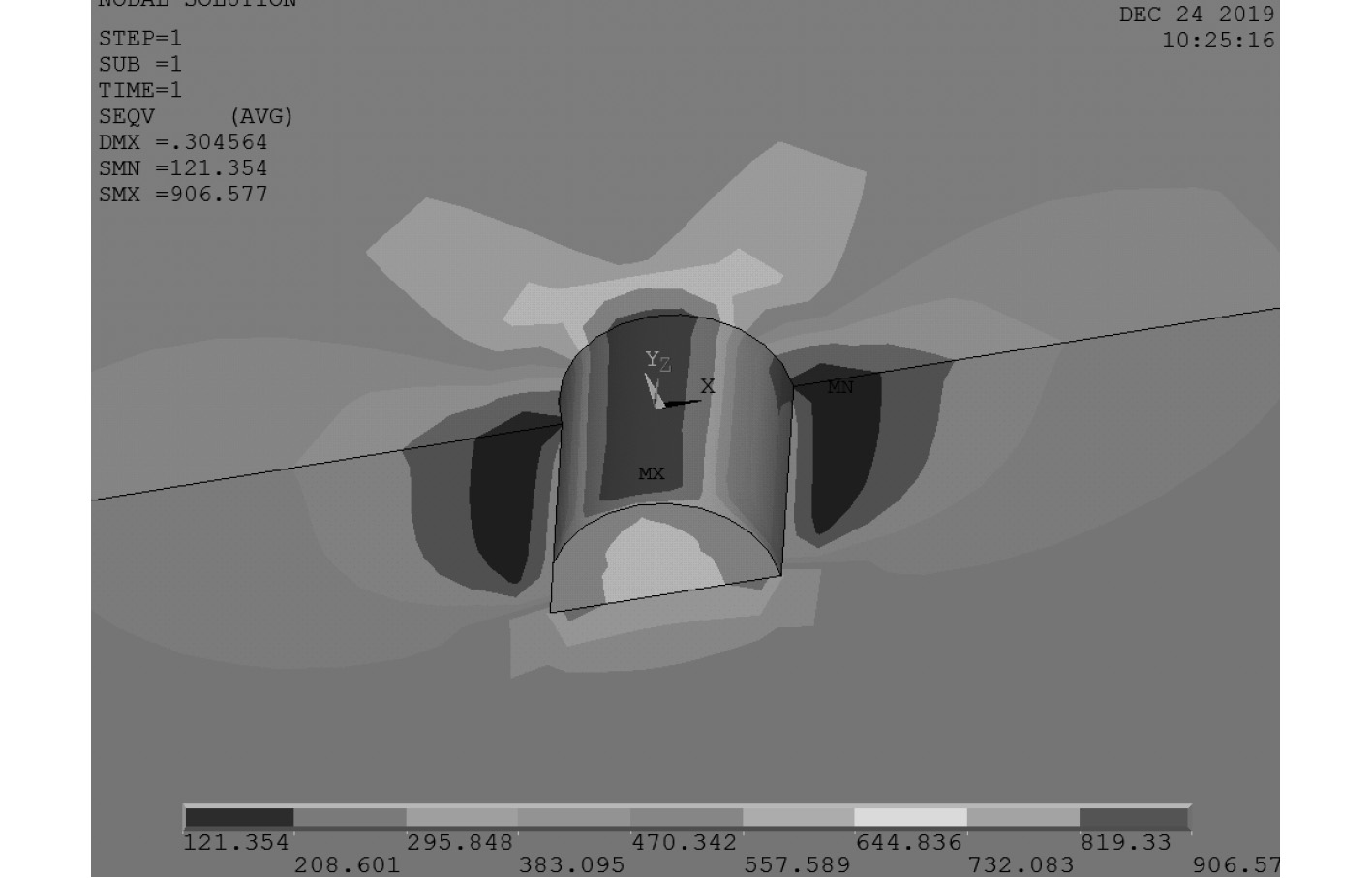
研究表明,盲孔法测量时不能忽略孔边塑性应变引起的附加应变影响[5]。本文同样采用基于形状改变能参量
|
图 4 孔边出现应力集中 Fig. 4 Hole-edge stress concentration |
| $ S = \left( {1 + {\upsilon ^2} - \upsilon } \right)\left( {\varepsilon _1^2 + \varepsilon _2^2} \right) - \left( {1 - {\upsilon ^2} - 4\upsilon } \right){\varepsilon _1}{\varepsilon _2}{\text{。}}$ | (9) |
式中:
|
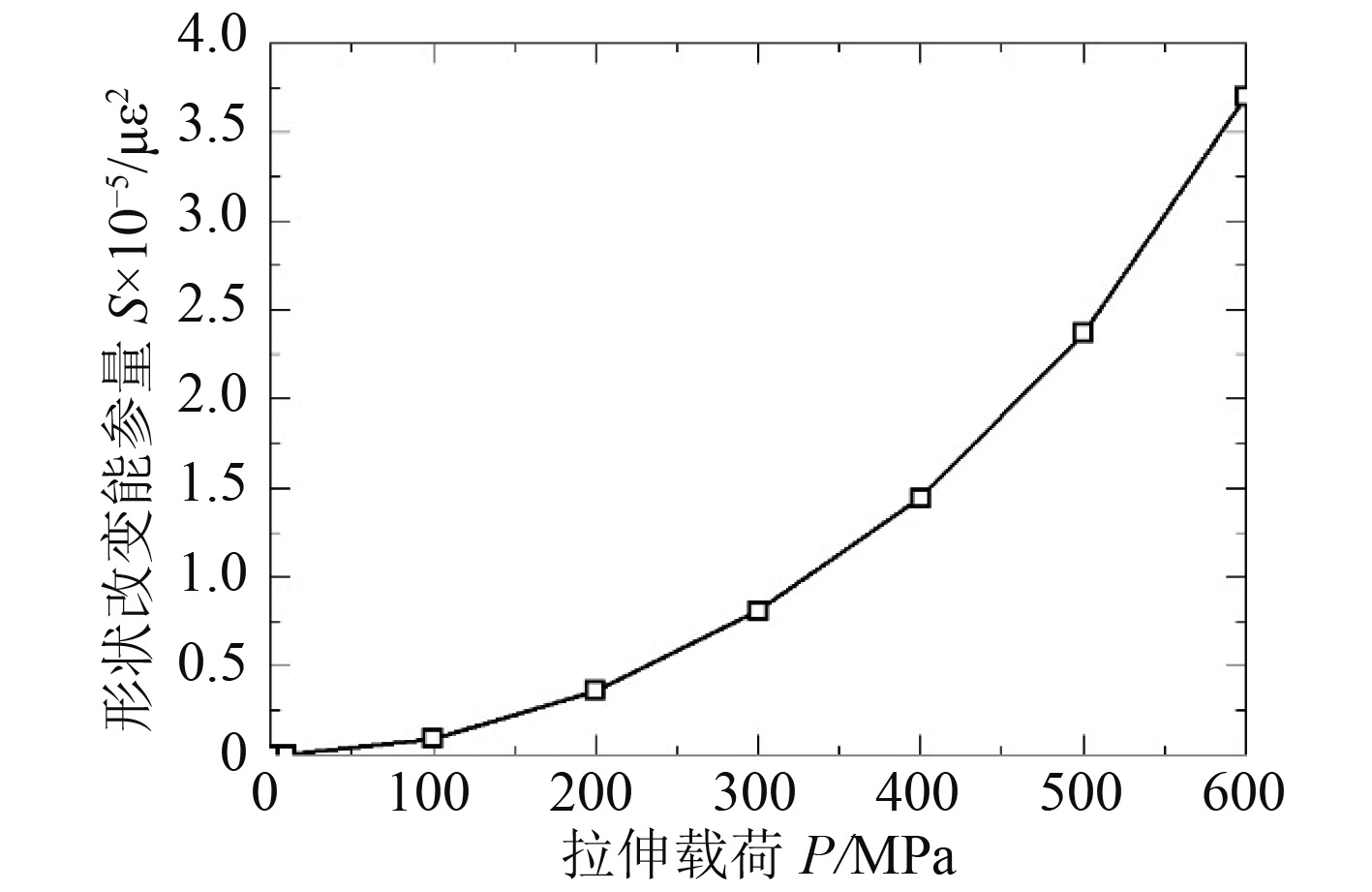
图 5 孔边形状改变能参量与标定应力关系曲线 Fig. 5 Curve of shape deformation energy parameter varying with calibration stress |
由图5可知,
建立
|
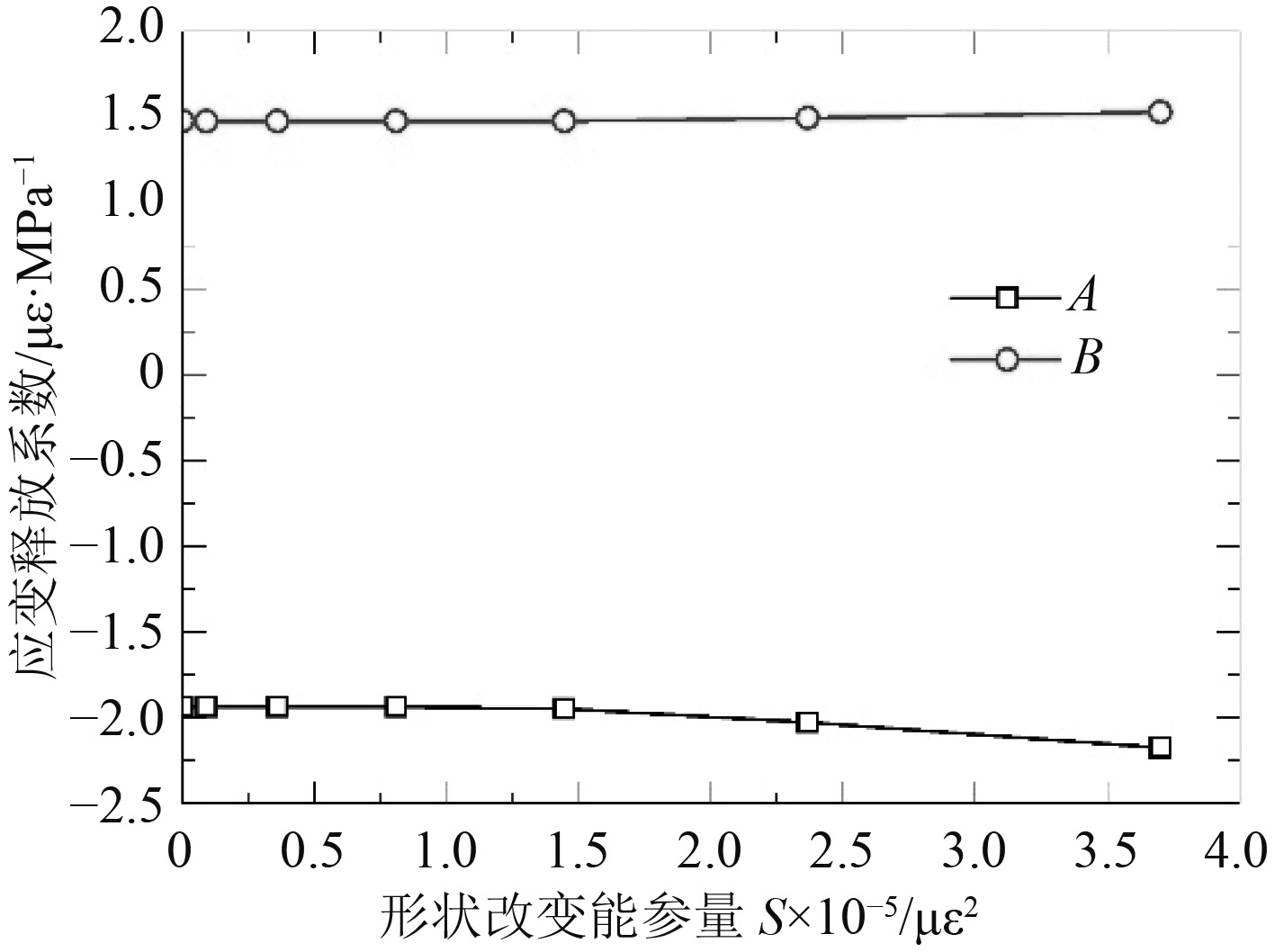
图 6 形状改变能参量与应变释放系数关系曲线 Fig. 6 Curves of strain release coefficients varying with shape deformation energy parameter |
对图6中关系曲线进行线性拟合,可得修正后的应变释放系数
| $ A = \left\{ {\begin{array}{*{20}{l}} { - 1.934}{\text{,}}&{S \leqslant 1.443 \times {{10}^{ - 5}}}{\text{,}}\\ { - 0.102S - 1.795}{\text{,}}&{S > 1.443 \times {{10}^{ - 5}}}{\text{。}} \end{array}} \right.$ | (10) |
| $ B = \left\{ {\begin{array}{*{20}{l}} {1.476}{\text{,}}&{S \leqslant 1.443 \times {{10}^{ - 5}}}{\text{,}}\\ {0.0228}{\text{,}}&{S + 1.444S > 1.443 \times {{10}^{ - 5}}}{\text{。}} \end{array}} \right.$ | (11) |
完成应变释放系数的有限元标定工作后进行水下承压结构残余应力测试。
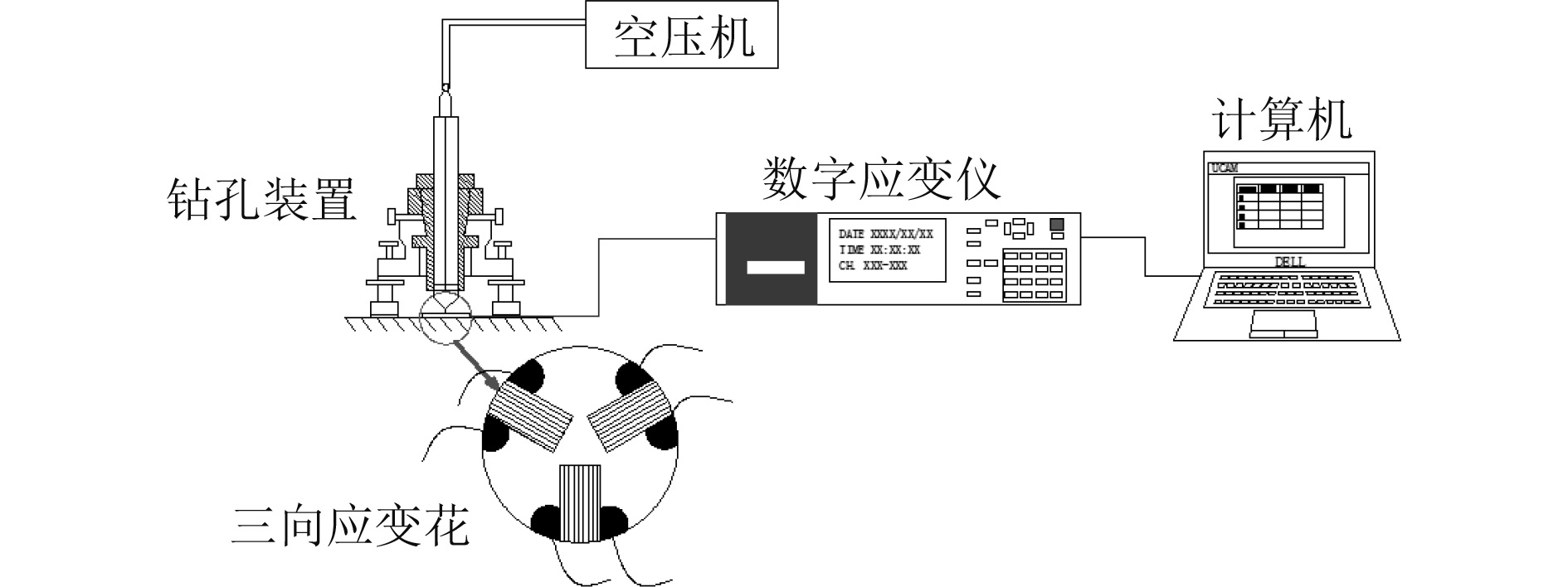
3.1 测试设备残余应力测试仪器包括UCAM-60B数字测量系统、RS200高速透平铣孔装置、H2.31.016 #38高速铣孔钻头以及三轴等角应变花(型号LC-BE350-3CD-K,电阻值350.3±0.3 Ω,灵敏系数2.07±1%)。
残余应力测试系统示意如图7所示。
|
图 7 残余应力测量系统示意图 Fig. 7 Schematic of residual stress measurement system |
锥柱结合结构试验模型材料为800 MPa级高强度钢。在模型内表面凸锥-大圆柱壳环焊缝附近布置3处残余应力测点,受测试设备及结构形式限制,第1个测点距离焊缝根部20 mm,其余各测点相隔20 mm。
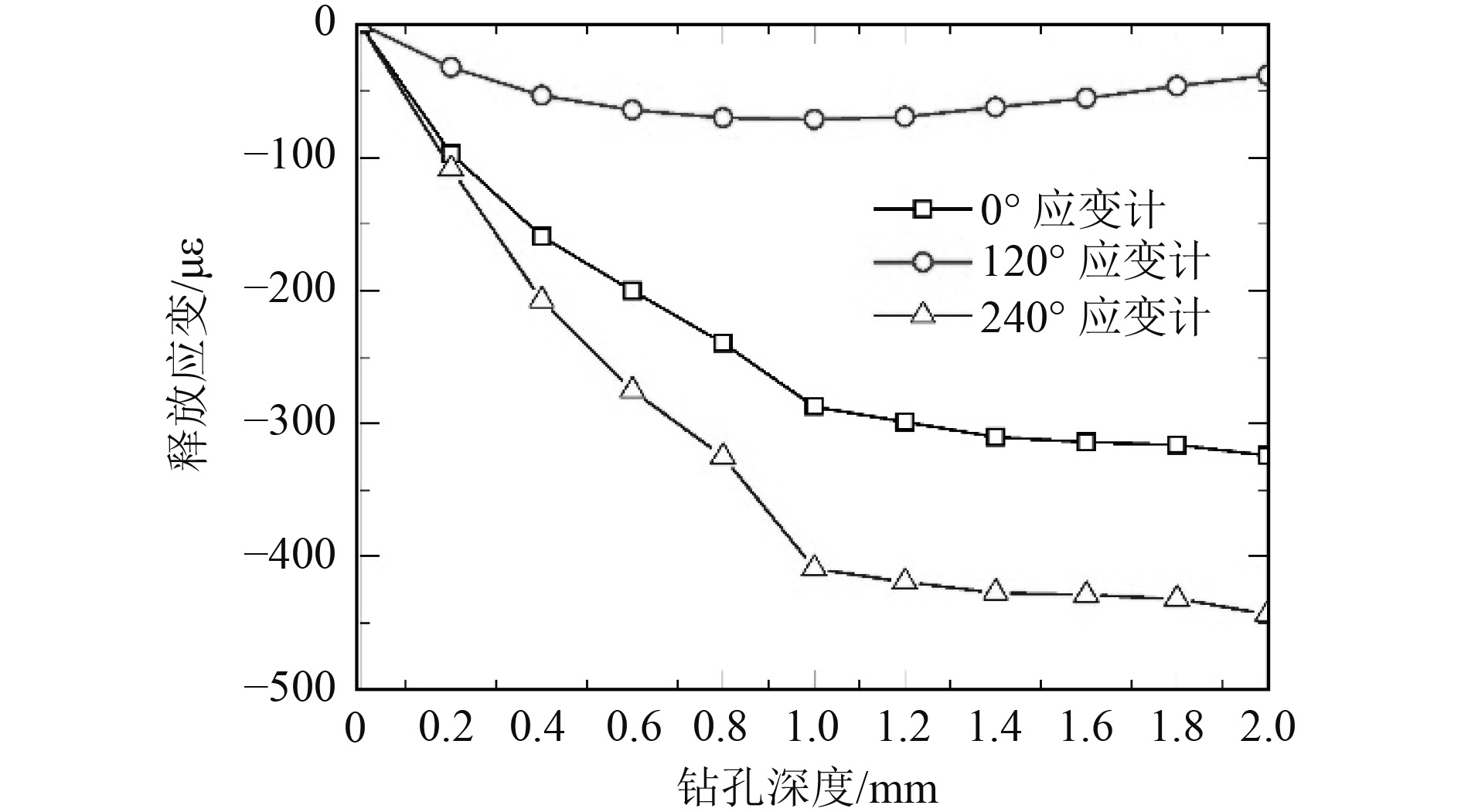
3.2 测试结果以0.2 mm为步长,采集0~2.0 mm钻孔深度下的释放应变值。图8给出了最靠近焊缝的残余应力测点释放应变与钻孔深度曲线。
|
图 8 测点1释放应变-钻孔深度曲线 Fig. 8 Strain release curves of measuring point 1 |
测试测得释放应变值后,便可计算得到各测点残余应力情况。
1)将2.0 mm钻孔深度处的3个方向释放应变值代入式(2)中计算各测点释放主应变值;2)将各测点释放主应变值代入式(9)中计算形状改变能参量
|
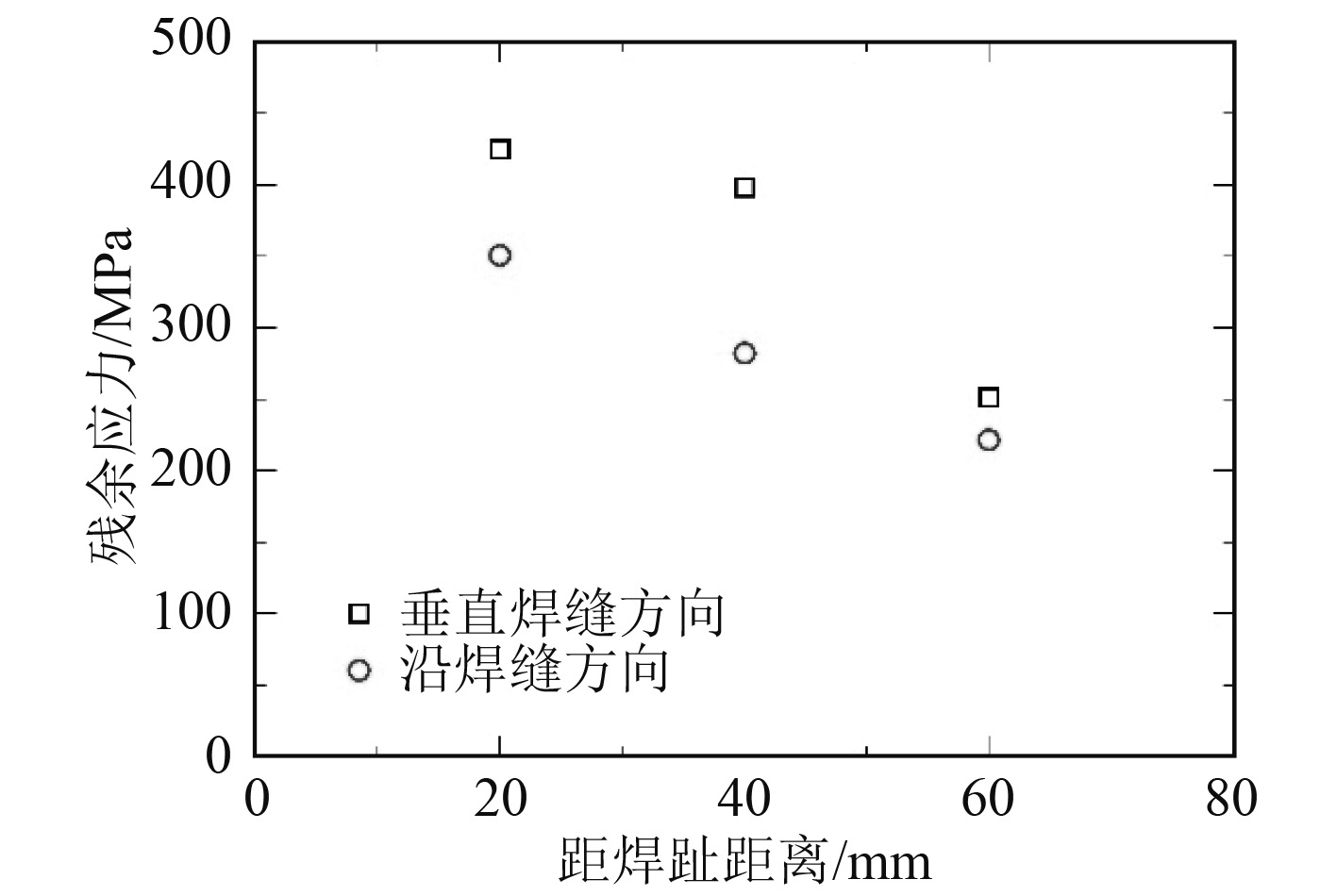
图 9 水下承压结构残余应力实测值 Fig. 9 Residual stress test results |
由图9可知:测点距离焊趾越远,垂直焊缝方向和沿焊缝方向残余应力值越低,符合预期;环焊缝内表面测点纵向残余应力极值为425 MPa(距离焊缝20 mm处,约0.5
本文对等轴三角应变花的应变释放系数完成有限元标定和塑性修正并得到塑性修正后的应变释放系数,为基于三轴等角应变花的残余应力测试提供了参考;采用塑性修正后的应变释放系数计算得到了水下承压结构环焊缝内表面测点残余应力情况,测试结果表明,距离焊缝20 mm处纵向残余应力约0.5
| [1] |
李良碧, 万正权, 王自力, 等. 高强度钢耐压锥柱壳体焊接残余应力数值分析[J]. 中国造船, 2010, 51(3): 128-137. LI LB, WAN ZQ, WANG ZL, et al. Numerical analysis of welding residual stress on high strength steel cone-cylinder pressure hull[J]. Shipbuilding of China, 2010, 51(3): 128-137. DOI:10.3969/j.issn.1000-4882.2010.03.015 |
| [2] |
张震. 焊接残余应力对耐压结构极限承载能力影响研究[D]. 无锡: 中国船舶科学研究中心, 2017. ZHANG Z. Influence of welding residual stress on ultimate strength of pressure structure[D]. Wuxi: China Ship Scientific Research Center, 2017. |
| [3] |
卞如冈, 崔维成, 万正权, 等. 焊接残余应力对疲劳寿命影响的定量研究[J]. 船舶力学, 2011, 15(7): 776-783. BIAN RG, CUI WC, WAN ZQ, et al. A quantitative stud on the effect of welding residual stress on fatigue life[J]. Ship Mechanics, 2011, 15(7): 776-783. DOI:10.3969/j.issn.1007-7294.2011.07.010 |
| [4] |
吴国庆, 王永军, 张震, 等. 船用高强度钢焊接残余应力测量技术研究[J]. 船舶工程, 2016, 38(3): 59-64. WU GQ, WANG YJ, ZHANG Z, et al. Research on test method for welding residual stress of marine high-tensile steel[J]. Ship Engineering, 2016, 38(3): 59-64. |
| [5] |
苏礼季, 周广涛, 刘洪生. 盲孔法测LY12铝合金焊接残余应力时应变释放系数的标定及塑性修正[J]. 机械工程材料, 2016, 40(4): 48-53. SU LJ, ZHOU GT, LIU HS. Calibration and plastic correction on strain release coefficients in welding residual stress measurement of LY12 aluminum alloy by blind-hole method[J]. Materials and Testing, 2016, 40(4): 48-53. DOI:10.11973/jxgccl201604012 |
| [6] |
马小明, 欧清扬. 盲孔法测曲面残余应力时释放系数的数值模拟[J]. 华南理工大学学报(自然科学版), 2019, 47(12): 25-31. MA XM, OU QY. Numerical simulation for hole-drilling strain gage method applied on curved surface[J]. Journal of South China University of Technology, 2019, 47(12): 25-31. |
| [7] |
张涛, 王志宇, 李晓磊. T形接头钢板焊接残余应力试验研究[J]. 建筑结构学报, 2018, 39(S2): 128-134. ZHANG T, WANG ZY, LI XL. Experimental study on welding residual stress of T-joint steel plate[J]. Journal of Building Structures,, 2018, 39(S2): 128-134. |
| [8] |
甘世明, 韩永全, 陈芙蓉, 等. 基于弹性模量变化的7A52铝合金VPPA-MIG复合焊接残余应力测试[J]. 焊接学报, 2019, 40(5): 13-17+23+161. GAN SM, HAN YQ, CHEN FR, et al. 7A52 aluminum alloy VPPA-MIG hybrid welding residual stress testing based on elastic modulus variation[J]. Transactions of the China Welding Institution, 2019, 40(5): 13-17+23+161. |
| [9] |
侯海量, 朱锡, 刘润泉. 盲孔法测量焊接残余应力应变释放系数的有限元分析[J]. 机械强度, 2003, 25(6): 632-636. HOU Hai-liang, ZHU Xi, LIU Run-quan. FEM analysis on the strain release factors for measuring welding residual stresses using blind-hole method[J]. Journal of Mechanical Strength, 2003, 25(6): 632-636. DOI:10.3321/j.issn:1001-9669.2003.06.009 |
| [10] |
张如一, 沈观林, 李朝弟. 应变电测与传感器[M]. 北京: 清华大学出版社, 1999.
|
 2021, Vol. 43
2021, Vol. 43
