0 引　言

实际海战中，舰船一旦沾染核生化武器袭击带来的放射性物质，如果得不到有效防护则会迅速丧失战斗能力^[1-2]。早在2011年3月11日，日本福岛电站发生核泄漏扩散，导致前来救援的美国“里根”号航母受到了轻微污染，不得不撤出危险地带并及时进行清洗^[3]。与此同时，舰船无论是遭受袭击还是日常训练均极易发生火灾。据统计，美国自拥有航母以来就已经发生过近20起大型火灾事件^[4]，造成巨大人员和设备损失。面对这些突发危险，目前舰船一般采用水幕系统（CMWDS）进行防护，水幕系统通过安装的水幕喷头持续喷水、形成水幕帘覆盖船身，形成隔离带，降低舰船沾染核物质颗粒物以及火灾扩大的风险。而传统水幕喷头结构内部流道直通，无复杂形状，喷口通过在喷头侧壁切割开口形成，开口数目为一道或者多道，此结构下的流体流经流道，经喷口喷射出的水幕射程短、覆盖面积小、隔离效果差。因此，研制喷射速度快、喷射距离远、水幕隔离防护效果好、性能提高显著的水幕喷头显得尤为重要。

1 喷头结构优化设计

传统的舰船水幕喷头内部结构简图如图1 （a）所示。该喷头内部水流道中空，出水口设置在通道侧壁，采用切割方式在喷头流道侧壁切割出一道喷口。如图1（a）中1位置处所示，喷头采用预先铸模和后期切割加工的方式制造，在内流道喷口进水处与侧壁面形成一个直角。根据流体流动规律，当喷嘴口突然收窄，流体在该处会形成高速射流，而此结构棱角突出、无法很好给流经该处的流体提供速度变化的过渡，高速射流直接在直角处与壁面剧烈摩擦，动能损失剧大，极大降低射流最终离开喷口的速度。故在1位置处预设倒角，使得流道内流体流动更加平滑，减少流体动能损耗。如图1（a）中2位置处所示,喷头流道孔通径在2位置处突然增大，而实际流体以一定速度运动过程中，从2处位置进入一个通径更大的流道，根据伯努利原理可知，流体运动速度会在此处发生突变，从而影响流体最终离开喷嘴时的射流速度。

针对上述问题，对其进行优化后的水幕喷头内部流道结构如图1（b）所示，即在图1（a）中1位置处进行3 mm的弧形倒角过渡设计，同时对图1（a）中2位置处变径流道作直通处理。基于激光选区熔化制造技术（SLM）对喷头进行一体化制造，优化成型后的喷头结构实物模型如图2所示。

2 数值模拟与计算 2.1 数学模型

目前国内外对喷头射流这类气液两相流动过程主要采流体体积（VOF）模型和拉格朗日多相模型进行分析^[5-9]。水幕喷头在实际工作状态下，射流形成的水幕帘在空气中的物理形态更多是一种以连续相的水幕薄膜存在，而非雾化的离散相液滴存在，而流体体积（VOF）模型较好地描述这一水和空气互不相容连续运动的状态，因此这里采用STAR-CCM+软件中流体体积（VOF）模型求解射流过程气液这2种不混溶流体流的控制方程。而流体运动主要遵循质量守恒、动量守恒、能量守恒这三大定律，根据实际工作环境，把水视作不可压缩流体，水喷射过程中的热交换可忽略不计，故可以不考虑能量守恒方程，因此最终采用的流体体积（VOF）模型主要控制方程如下：

质量守恒方程为

$ \frac{\partial \rho }{\partial t}+\frac{\partial }{\partial {x}_{i}}\left(\rho {\mu }_{i}\right)=0\text{。} $

(1)

式中： $ \rho $ 为流体密度，本文中液体为水； $ t $ 为时间； $ {\mu }_{i} $ 为流体速度沿 $ i $ 方向分量； $ {x}_{i} $ 为 $ i $ 方向坐标。

动量守恒方程为

$ \frac{\partial }{\partial t}\left(\rho {\mu }_{i}\right)+\frac{\partial }{\partial {x}_{j}}\left(\rho {\mu }_{i}{\mu }_{j}\right)=-\frac{\partial p}{\partial {x}_{i}}+\frac{\partial {\tau }_{ij}}{\partial {x}_{i}}+\rho {g}_{i}+{F}_{i} \text{。}$

(2)

式中： $ {F}_{i} $ 为体积力； $ {\tau }_{ij} $ 为应力矢量；P为流体微元体上压力，其他参数含义见式（1）。

STAR-CCM+软件中提供的K-Epsilon 湍流模型有标准、标准两层、可实现、可实现的两层等9种类型，其中可实现的K-Epsilon两层模型可为网格提供最大灵活性，计算更加精确，本文选用可实现的K-Epsilon两层模型。

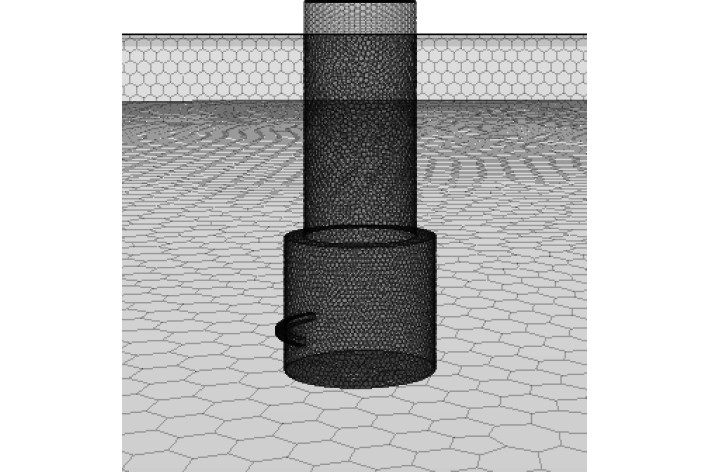
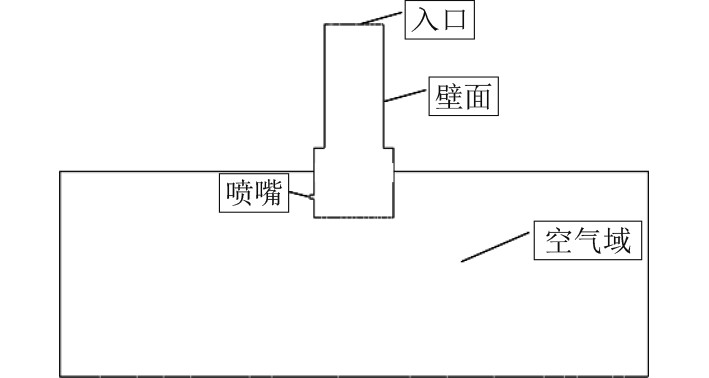
2.2 数值模型

为保证数值模拟结果精确，对流体运动变化剧烈的喷头出口处网格进行细化处理，图3为计算流体区域网格划分示意图。由图可看出喷头流道以及出口处网格较为密集，空气域网格相对稀疏，最终整个模型网格总数目为954452。喷头的射流模型边界条件设置如图4所示，喷头进口端采用压力进口，流道表面设置为壁面无速度滑移和质量渗透，外部空气域设置为压力出口类型，出口表压为0 MPa。计算域的网格模型由喷头内部流体域和外部空气域两部分组成，空气域为高1m、半径5m的圆柱体。为确保运算效率和结果精度，软件采用表面重构、基于六面体网格的切割体网格生成器，对于过渡区域采用棱柱层网格生成器，棱柱层数为5层。

2.3 模型验证

为确认数值模拟的可靠性，先对不同压力下的水幕喷头出口截面处速度进行试验测试和数值模拟，通过比较试验和数值模拟的多组数据结果，验证数值模型可靠性，图5（a）为试验进行时的水压表、图5（b）为试验现场。

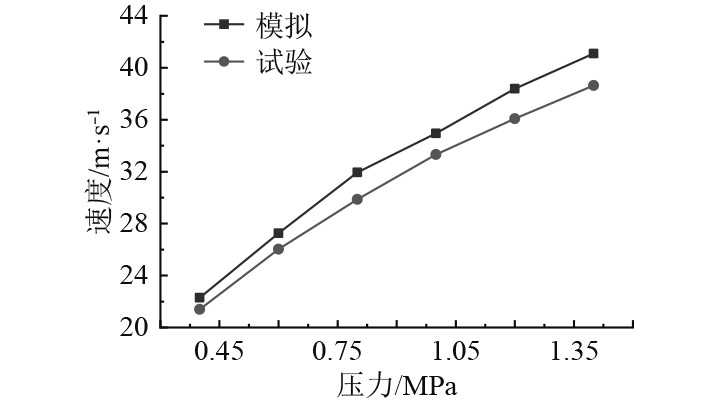
图6为不同压力下，喷头出口截面处速度曲线。由图可知，在不同工作压力下，喷头出口截面处，试验测得的速度值与数值模拟测得的速度值均随着压力的增大而增大，并且两者的变化趋势较接近。

同时由图可知，试验测得的速度值均小于数值模拟测得的速度值，经过分析，这是因为尽管数值模拟中考虑了金属壁面粗糙度的影响，将粗糙度设为3.2 $ \mathrm{\mu }\mathrm{m} $ ，但实际数值模拟计算过程中，设定的网格尺寸最小量级为 $ 1\times {10}^{-4} $ m，远大于设定粗糙度量级的 $ 1\times {10}^{-6} $ m，故粗糙度的影响在数值计算过程中无法准确的反映，导致数值模拟值与试验值相比较大。但若将网格尺寸设定为粗糙度的量级，则将极大增加计算时间，最终考虑到计算效率和计算精度，网格尺寸量级仍设为 $ 1\times {10}^{-4} $ m。由表1可知，试验和数值模拟值之间的误差均小于7%，表明该数值模型计算是可靠的，能够为下一步准确模拟喷头喷射性能提供保证。

3 结果与分析 3.1 水幕喷头水流速度对比分析

图7和图8分别为水幕喷头在同一压力工况下，其优化前后的喷头射流速度对比。从图7和图8的速度分布云图以及标量轴的数值可知，优化后的水幕喷头射流速度显著提升，水流速度分布轨迹也更加分散，这是因为喷头出口截面射流速度越大，与空气形成的速度差越大，空气与水之间的剪切力也越大，水流越容易撕裂破碎分散为水滴。

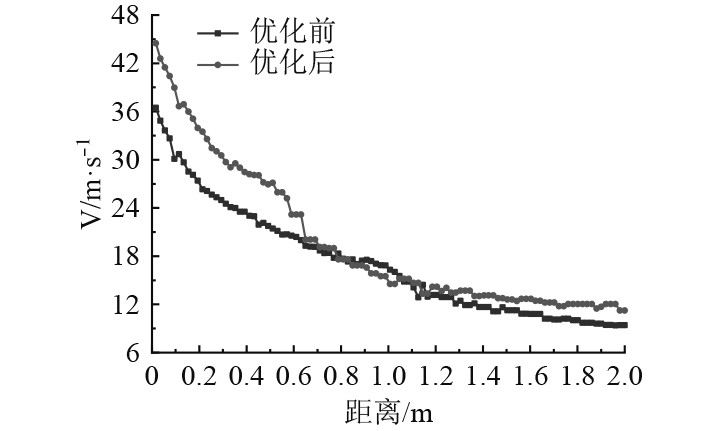
图9为1 MPa工作压力下，射流形成的水幕帘在距离喷头出口截面2 m范围内速度分布情况。由图可知，优化后在2 m范围区间内，水幕喷头在各测点的速度整体大于优化前，这意味着优化后的水流离开喷头获得了更大的初始动能。随着喷射距离的增大，因空气阻力的作用，水流速度逐渐衰减，当距离增大到2 m时，水流受到的空气阻力开始接近重力从而形成动态平衡，速度变化减缓并趋于稳定。

图10为喷头出口处表面平均速度随压力变化曲线。由图可知，优化后的水幕喷头出口处表面平均速度远高于优化前。如表2所示，其速度的提升幅度均值在23%左右。同时，喷头出口表面平均速度也在随着压力的增大而逐渐放缓，可以预知压力增大到一定时候，喷头出口表面平均速度值的增加会趋于收敛。

3.2 水幕喷头体积流量对比

图11为不同工况压力下，优化前后水幕喷头的体积流量曲线。可以看出，随着压力增大，优化前水幕喷头的体积流量从39.26 L/min增加到73.64 L/min，而优化后该喷头的体积流量从48.99 L/min增加到91.93 L/min。经过对比可知，在各个压力工况下，优化后的喷头在单位时间内射流体积流量均得到显著增加，这表明优化后的喷头内部流道结构喷射性能得到了较好的提升。

3.3 水幕喷头流量系数对比

工程中喷头的流量特性一般采用流量系数K来表示，已知流量系数公式：

$ {K}=Q/\sqrt{10P} \text{。}$

(3)

式中： $ {{K}} $ 为流量系数；Q为体积流量，L/min； $ P $ 为压力，MPa；

根据公式，可以计算求出优化前后水幕喷头的流量系数K，为减小偏差，表3对不同工况压力下的流量系数进行求解并取平均值，如表3所示。

由表3可以看出，不同工况压力下，优化前水幕喷头的流量系数为19.71，而优化后喷头的流量系数为24.54，优化后喷头的流量系数有明显的提高，说明提出的优化方案可显著改善喷头内部流道结构的流畅性，减少了水流在离开喷头出口时的动能损耗，使得水流射程更远、水幕帘覆盖面积更广泛。

4 结　语

本文对传统舰船水幕喷头进行了优化设计，采用数值模拟研究了水幕喷头工作过程中气液两相流动，同时对优化前后的喷头喷射性能进行比较研究，获得结论如下：

1）数值模拟过程中测得的喷头出口平均速度均大于实际试验测得，这是因为数值模拟未能很好考虑粗糙度影响或者粗糙度设置过小，故实际试验值会略微小于数值模拟值。

2）工作压力一定，沿喷头出口轴线方向，水流速度随距离增加而减小，受到的空气阻力也在减小，当水流受到的空气阻力接近重力时将会处于动态平衡，速度变化趋于平稳。

3）同尺寸大小喷嘴，水流出口速度随压力增大而增大，但是速度增加会趋于放缓，可以预知压力增大到一定时候，喷头出口处射流速度的增加会趋于收敛。

基于激光选区熔化制造技术（SLM）一体化优化成型的喷嘴结构，其水流射速、流量、流量系数等性能指标均得到显著提高，本文研究对舰船水幕喷头增材优化设计与工程应用具有重要的参考价值。