2. 高新船舶与深海开发装备协同创新中心,上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
螺旋桨激振力所引起的尾部振动一直是船舶振动的一个关注点,其减振方法之一是在尾部设置避振穴,以减小螺旋桨表面力向船体的传递[1]。避振穴的研究最早可以追溯到20世纪50年代,最初是用于解决螺旋桨直径与桨叶间隙的矛盾,主要应用于内河小型船舶,后逐渐推广到内河大中型船舶和海船[2-3]。马佐璋、黄孟浩和高宪智等[4-7]通过结构模型试验、快艇阻力试验以及2次实艇试验,研究了避振穴对高速船快速性的影响、橡胶板的强度和变形等问题,认为避振穴可有效减少高速大马力船的尾部振动,并且对船舶的航态和阻力影响不大。李昌龙等[8-9]设计的钟形减振穴增大了叶梢间隙并利用橡胶吸收振动能量,在一艘双桨平底船上取得了满意的减振效果。1988年日本川崎重工[10]设计出一种利用舱内空气层和小孔阻尼起减振作用的开孔水舱避振穴,分析了底板开孔率、空气层厚度等参数的影响,并通过实船试验验证了其对叶频和倍叶频表面力显著的减振效果。吴卫国、翁长俭等[11-13]进一步根据隔振原理得出阻尼舱发挥作用的条件,使激励频率与等效弹性系统固有频率的比值大于
此前对避振穴的研究多从试验方面着手,缺少数值和理论方面的探讨。本文结合气囊隔振原理,采用Abaqus非线性有限元方法建立了避振穴隔振模型,并对其隔振特性进行了数值分析,探讨避振穴深度、初始内压和橡胶板厚度等参数的影响。
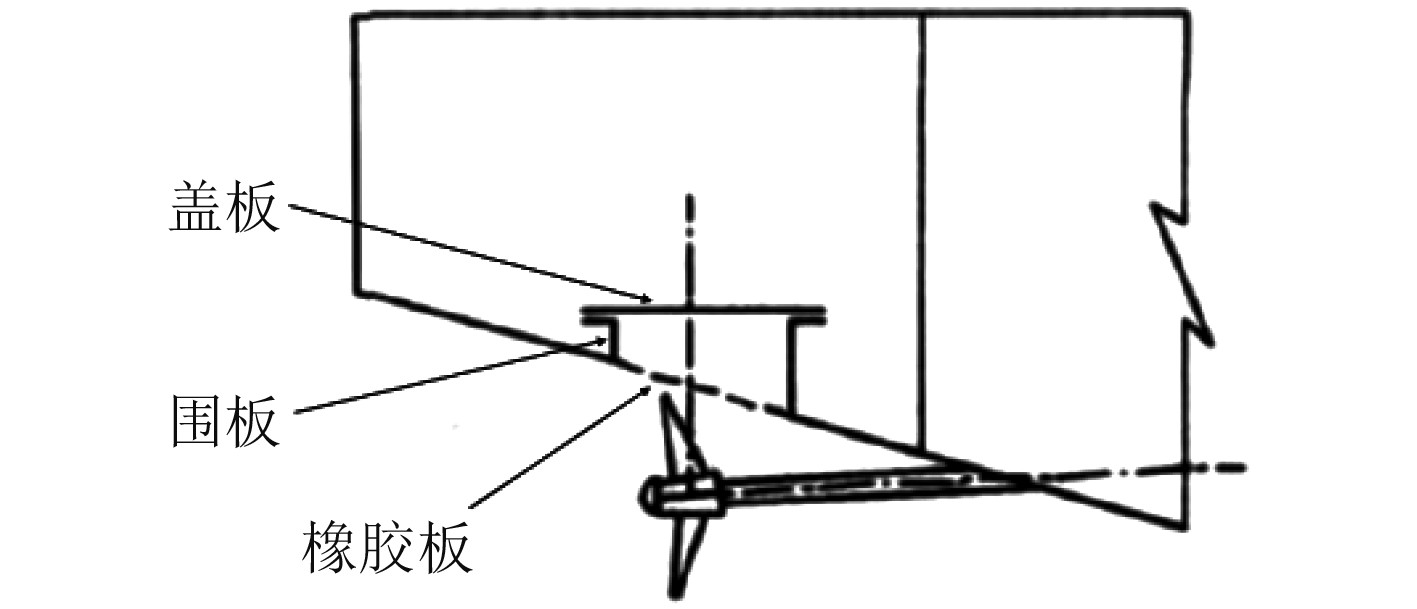
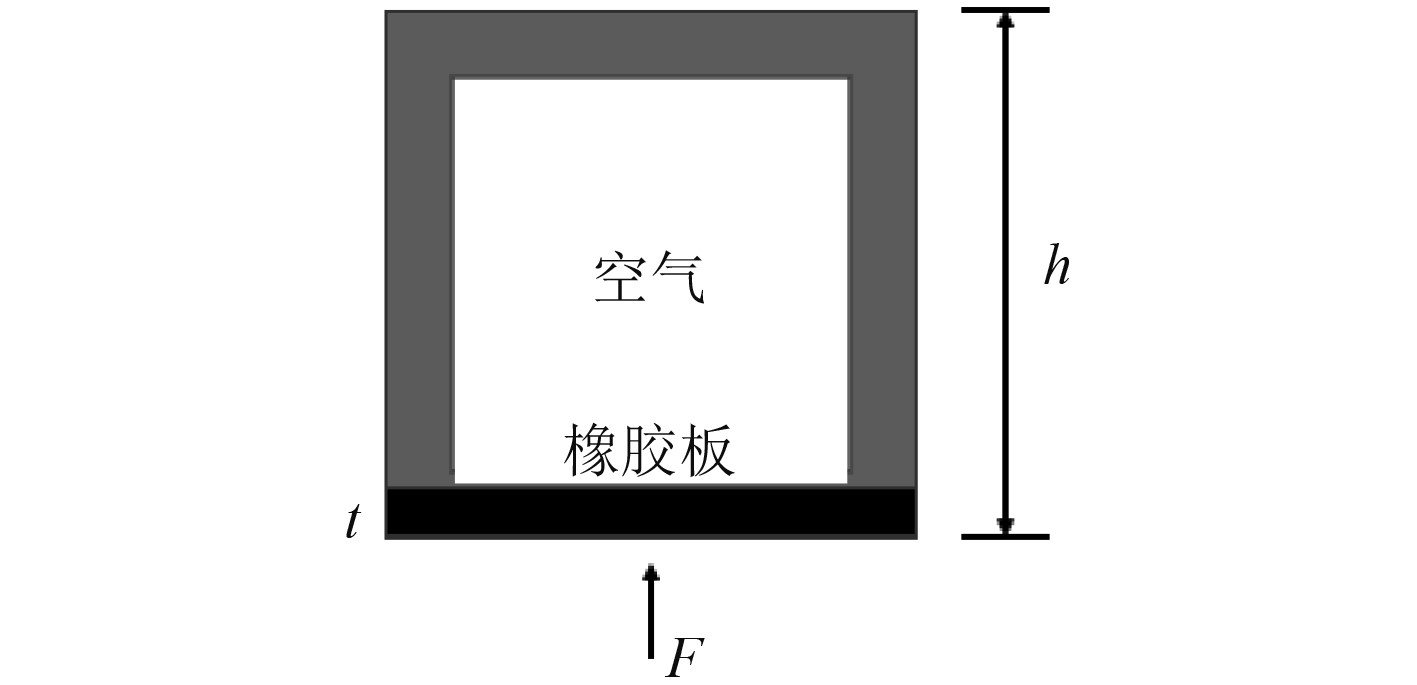
1 避振穴有限元仿真方法避振穴是通过在螺旋桨上方的船体外板开孔,开孔处覆盖橡胶膜,并设置围井盖板构成的具有减振作用的封闭气室,如图1所示。可将其看作是布置在振源和船体结构之间,用以减弱螺旋桨激振向船体传递的一个弹性隔振系统,其减振原理可由图2所示的橡胶-空气隔振系统来表示。该系统由橡胶底板、钢制围板和盖板以及内部密封空气组成,在外部激励F的作用下,橡胶板发生弹性变形,内部气体压缩,二者产生恢复力从而实现隔振和缓冲作用。在橡胶板面积确定的情况下,深度h决定了结构的容积,内部的加压空气起着重要的承载作用,橡胶板厚度t则是影响橡胶板弹性变形重要参数。
|
图 1 避振穴 Fig. 1 The anti-vibration cave |
|
图 2 橡胶-空气隔振系统 Fig. 2 Rubber-air vibration isolation system |
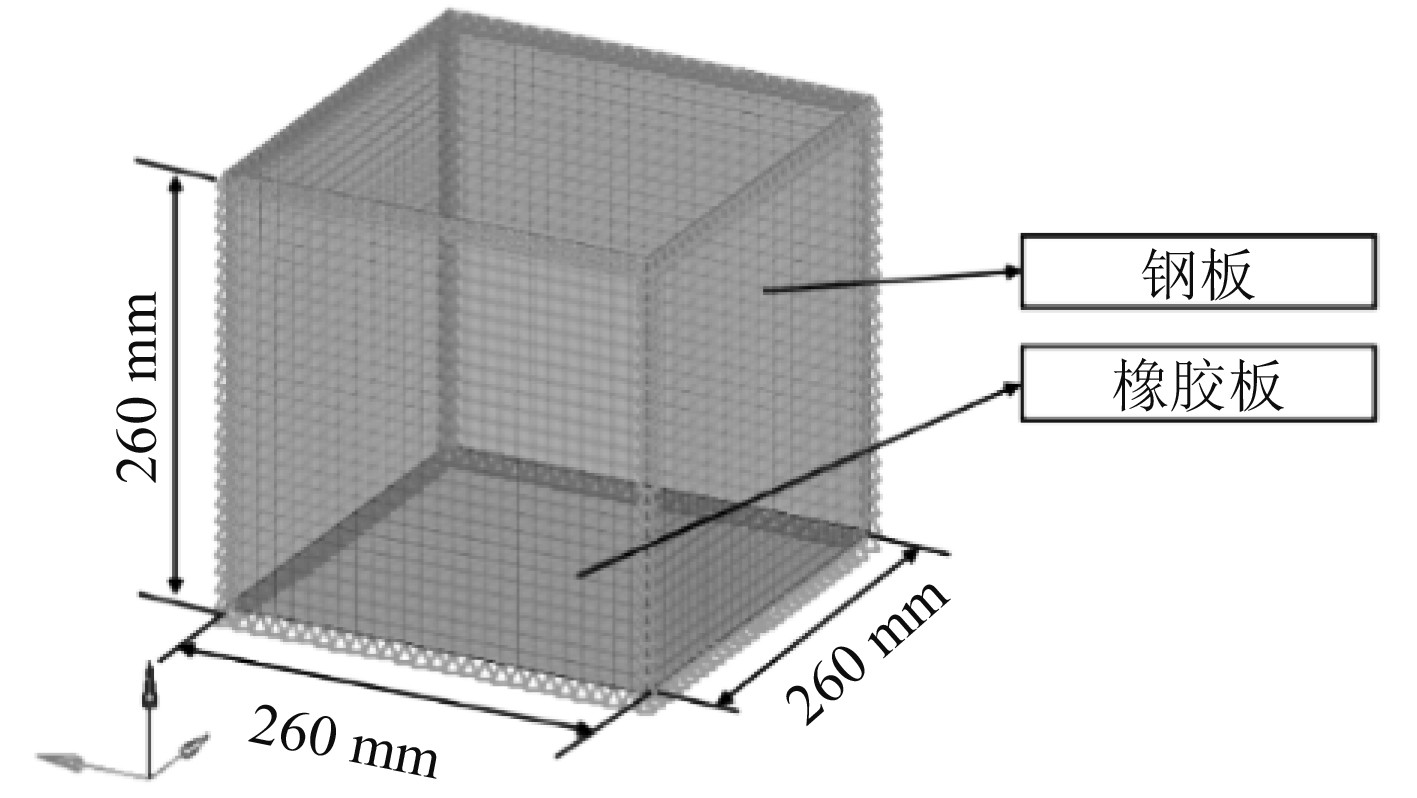
基于前述橡胶-空气隔振系统,建立一个立方体密闭气室有限元计算模型如图3所示。采用Abaqus中流体腔功能来模拟密闭气室结构,该功能适用于气体填充结构的建模和力学响应预测[15]。橡胶底板和钢板均采用四节点板单元S4R模拟,空气采用三维四节点单元F3D4模拟,空气单元表面与板单元共用节点。钢板厚度为10 mm,橡胶板厚度为厚度为1.5 mm。空气体积模量为1.01×10–1 MPa,密度为1.2×10–12 t/mm3。约束条件为橡胶板四边固定,钢板框架各边简支。
|
图 3 密闭气室有限元模型 Fig. 3 Air-filled cavity finite element model |
橡胶板是避振穴中承受外载荷并吸收能量的重要部件。作为一种各向同性、近似不可压缩的超弹性材料[16],在变形过程中其应力是瞬时应变的非线性函数。其力学特性常用Mooney-Rivlin应变势能模型描述:
| $ W={C}_{10}\left({I}_{1}-3\right)+{C}_{01}({I}_{2}-3)\text{。} $ |
式中:W为应变势能;C10和C01为超弹性材料系数,一般通过材料试验数据拟合确定。根据文献[17]中的试验拟合数据取C10=0.253216,C01=0.4709,橡胶材料密度为1.43×10–9 t/mm3。
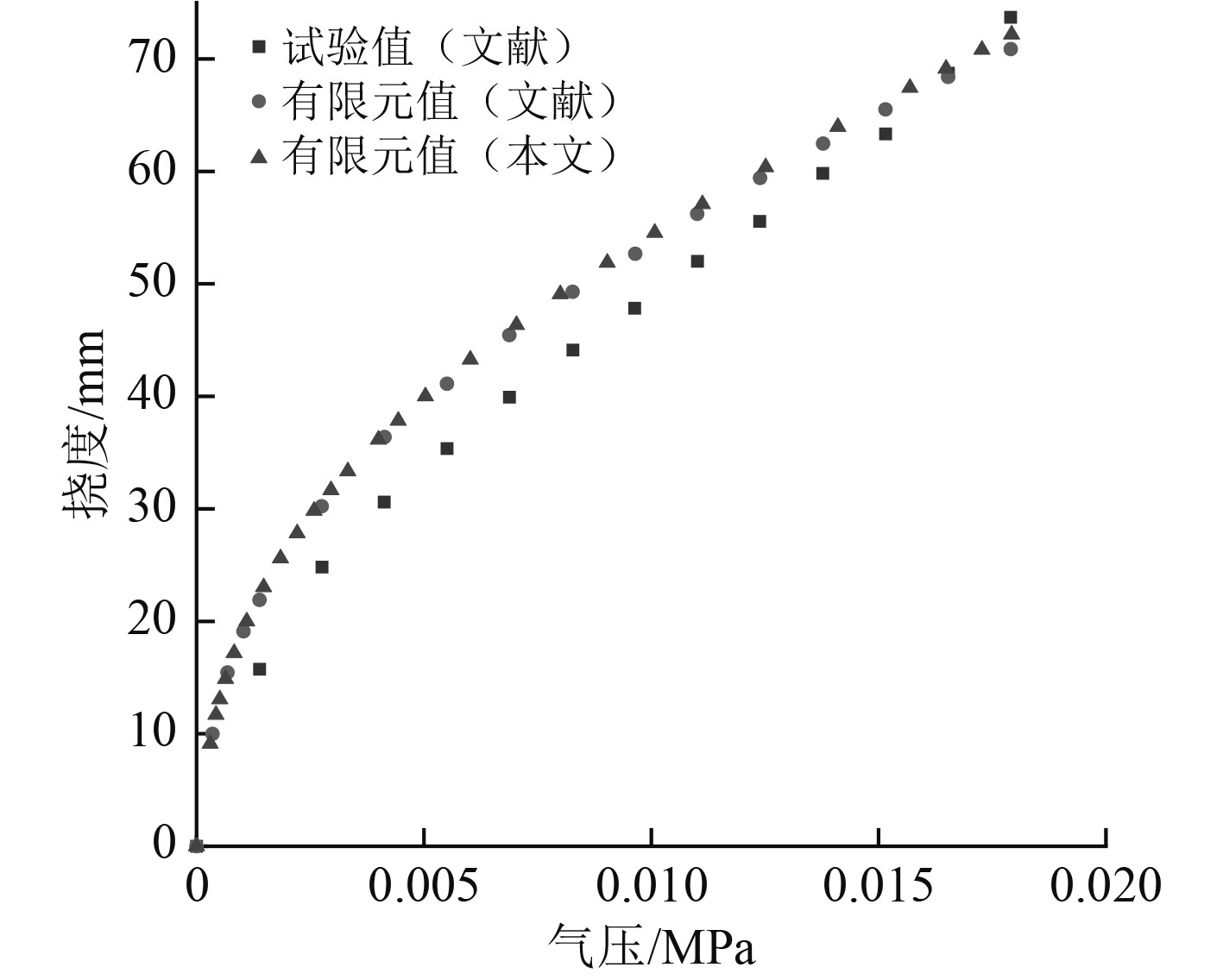
1.3 充气过程仿真为使避振穴进入工作状态,需要先进行充气加压,此过程涉及到橡胶板的材料非线性和大变形带来的几何非线性问题。Abaqus中通过将一个分析步分解为多个增量步,在每个增量步中进行多次迭代的方式求解非线性问题。对图3所示模型进行充气过程模拟,内部气压从0逐渐增加到0.02 MPa,整个加压过程分为5个分析步,共96个增量步。绘出橡胶板中心点的z向变形挠度随气压变化曲线,并与文献[17]的结果进行比较,如图4所示。结果表明,随着气压缓慢增加,橡胶板中心点的z向挠度逐渐增大,变化趋势起先较为急剧后渐渐平缓。相比于试验结果,有限元模拟的橡胶板偏于柔韧,但总体上还是吻合的较好。在大变形的情况下,Mooney-Rivlin模型能较好模拟橡胶材料的非线性特性。
|
图 4 橡胶板中心点静挠度随气压变化曲线 Fig. 4 Static deflection of the rubber plate measured at the center as function of pressure |
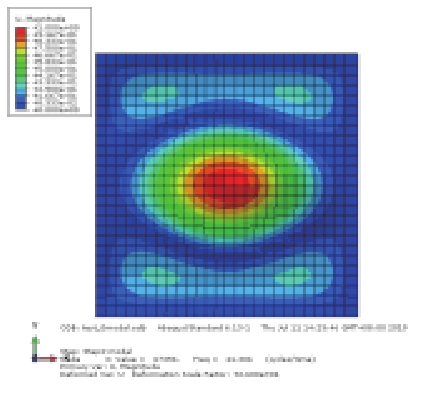
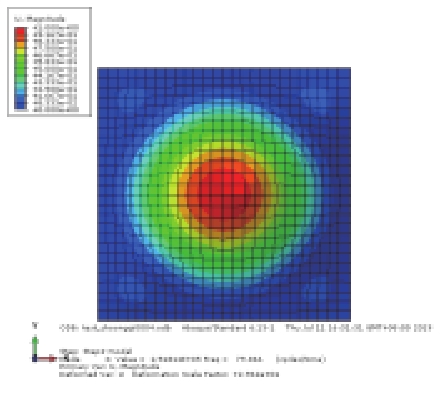
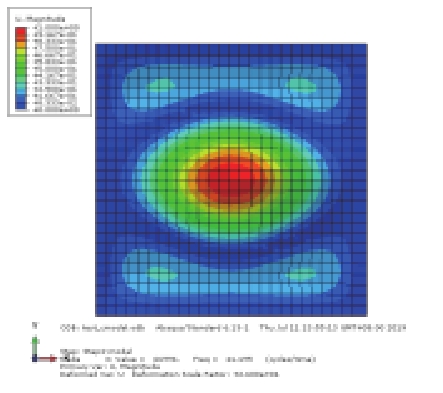
避振穴结构中橡胶底板相对于钢制围板和顶板而言较柔,故其低阶模态主要体现为橡胶板的振动。首先对四边固支的橡胶薄板进行模态分析,采用Lanczos方法提取前4阶模态频率并与文献[17]中结果对比如表1所示,其中m, n分别表示振型沿x, y方向的半波个数,可以发现本文的计算结果和文献结果吻合较好。
|
|
表 1 橡胶板模态分析结果 Tab.1 Modal results for rubber plate |
探讨内部空气对气室结构固有频率和振型的影响。由于避振穴中橡胶板是水下部分船壳板的替代部件,还需考虑静水压力的影响。分析如下4种情况:
1)橡胶板;
2)橡胶板+空气,无初始内压;
3)橡胶板+空气,存在初始内压;
4)橡胶板+空气,存在初始气压,橡胶板底部施加静水压力。
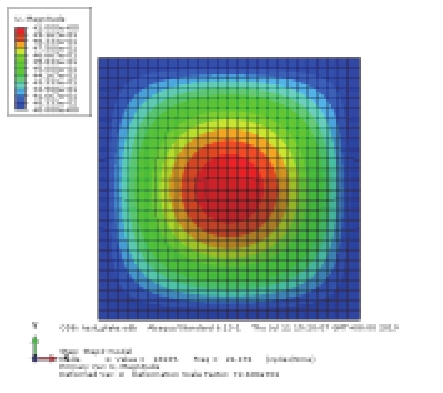
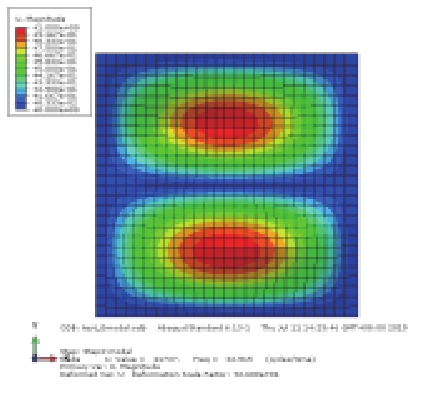
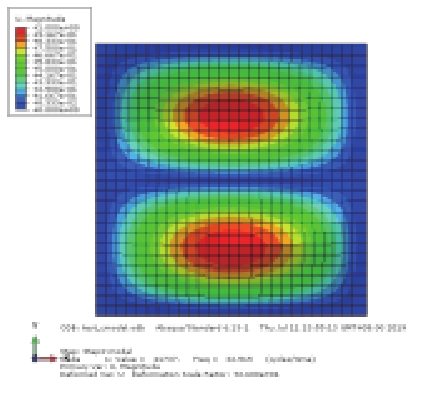
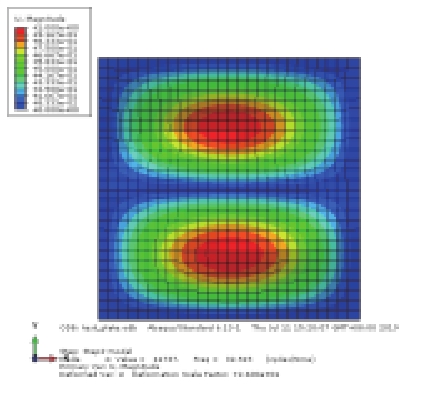
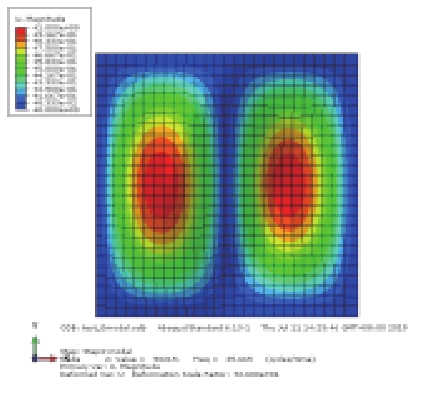
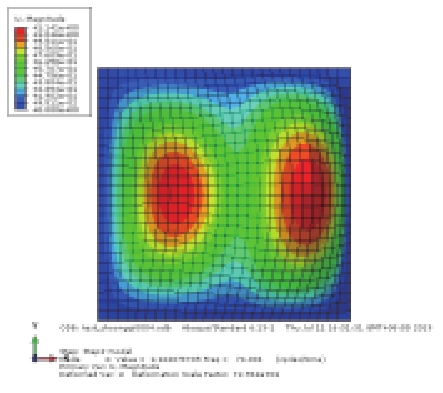
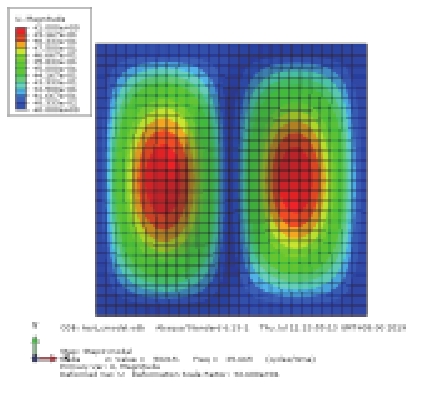
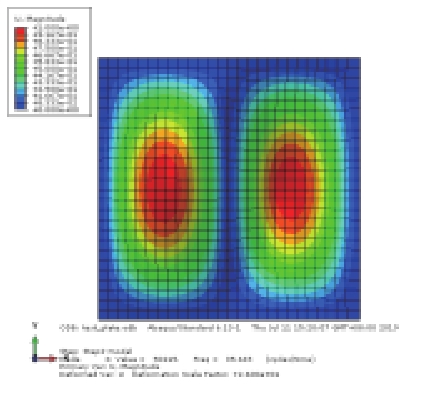
对上述4种情况进行模态分析比较,其中静水压力通过表面力的方式施加,静水压力与初始气压均取0.004 MPa,前3阶模态结果见表2(只显示避振穴底部橡胶板的振型)。比较工况1和工况2的振型结果可知,内部空气的存在对橡胶板的部分模态产生了影响,引起气室体积变化较大的奇-奇模态难以被激发,由第1阶(21.49 Hz)提高到第3阶(41.31 Hz),而其余振型基本不受影响;比较工况2和工况3的振型结果可知,加压空气将引起橡胶板的自振频率提高;对比工况2和工况4可知,内部气压与橡胶底板外部大小相同的静水压力的影响抵消,振动情况基本与未加压的状态一致,其中奇-奇模态的固有频率略有降低。
|
|
表 2 避振穴橡胶板模态分析结果对比 (Hz) Tab.2 Comparison of modal results for air-filled cavity |
计算避振穴结构在单位激励力下的频率响应,分析其深度(比)、初始内压和橡胶板厚度对振动响应的影响。激励力以节点力的形式添加,大小为1N,施力点为橡胶底板的中心,激励频率范围为0~1440 Hz。结构的模态阻尼比
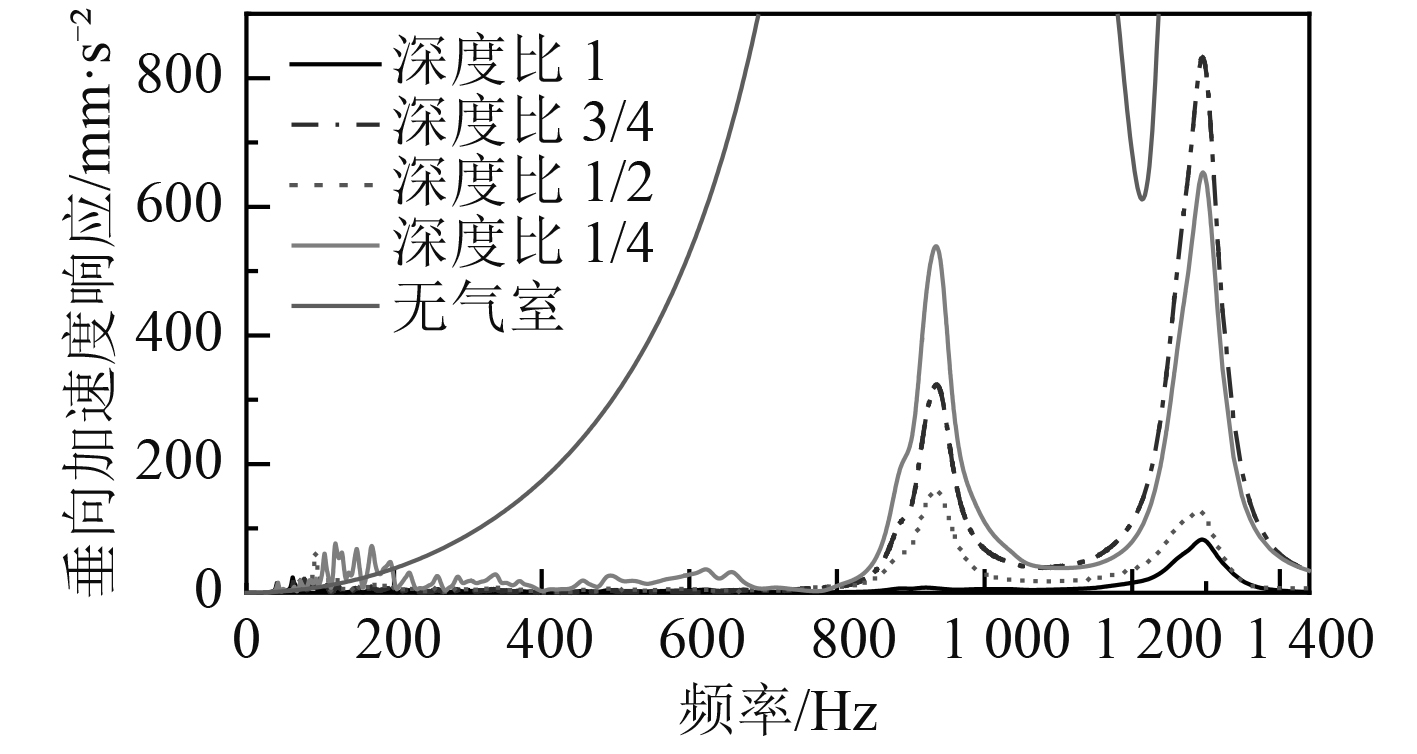
深度h是避振穴结构的一个重要尺寸参数。为避免对船舶尾部原结构较大的改动,其深度不宜过大,若太浅又可能导致橡胶板振幅较大时接触到盖板,影响隔振效果。保持其他条件不变,分别取h为0 mm,65 mm,130 mm,195 mm,260 mm(深度比为0,1/4,1/2,3/4,1)5个深度值进行计算,其中深度为0表示无气室的原结构。评价点的加速度响应曲线如图5所示。可以看出添加隔振气室后,低频段(0~200 Hz)出现了较多共振峰,此时的振动响应要高于初始结构。在渡过低频共振区后,气室结构的振动响应比起原结构有显著降低。随着深度的减小,在原结构的前2个共振峰处(941.1 Hz和1299.0 Hz处),评价点的响应呈现先增加后减小的趋势,深度比为1时响应值最小,其次是深度比1/2,深度比为1/4和3/4时响应相对较大。综上,1/2深度比时减振效果较好,且对原结构的改动较小。
|
图 5 气室深度对振动响应的影响 Fig. 5 The effect of h on vibration response |
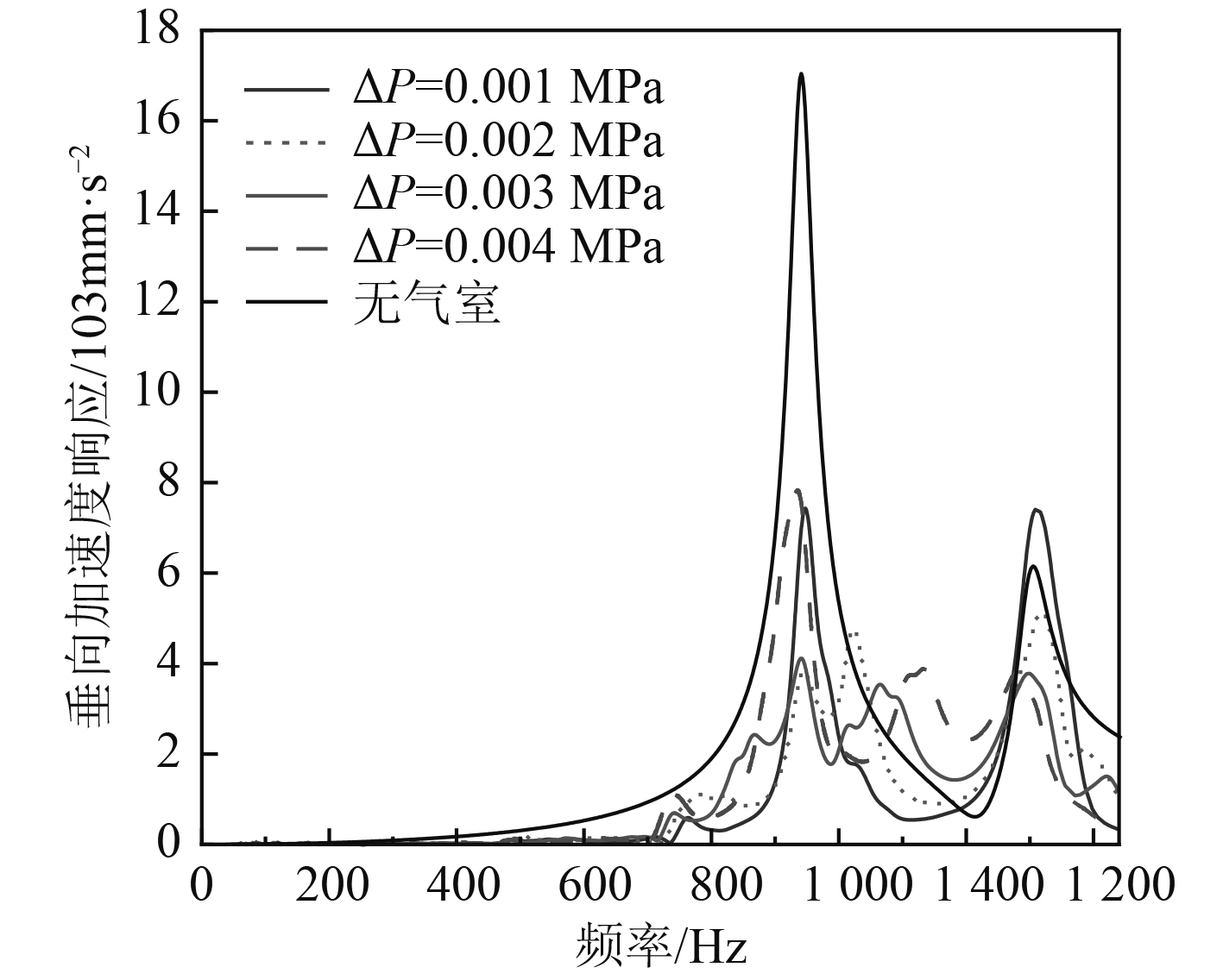
分析初始气压值对振动响应的影响,设置一系列初始内压值P0=0.005~0.008 MPa进行计算。由于橡胶板底部还受到0.004 MPa的静水压力作用,气室结构内外的压力差相应地为ΔP=0.001~0.004 MPa。评价点的加速度响应曲线如图6所示,随着气压差ΔP的增大,评价点的振动响应先增大后减小。在0.001 MPa和0.004 MPa时响应较大,而在0.002和0.003 MPa时响应较小,约为前者的一半。随着初始气压的增大,橡胶板中心点在同样激励下的位移响应减小。如图7所示,无气压差时最大位移为24.45 mm,增压0.001 MPa后最大值降为12.09 mm。
|
图 6 初始内压对加速度响应的影响 Fig. 6 The effect of P0 on acceleration response |

|
图 7 初始内压对橡胶底板位移响应的影响 Fig. 7 The effect of P0 on displacement response |
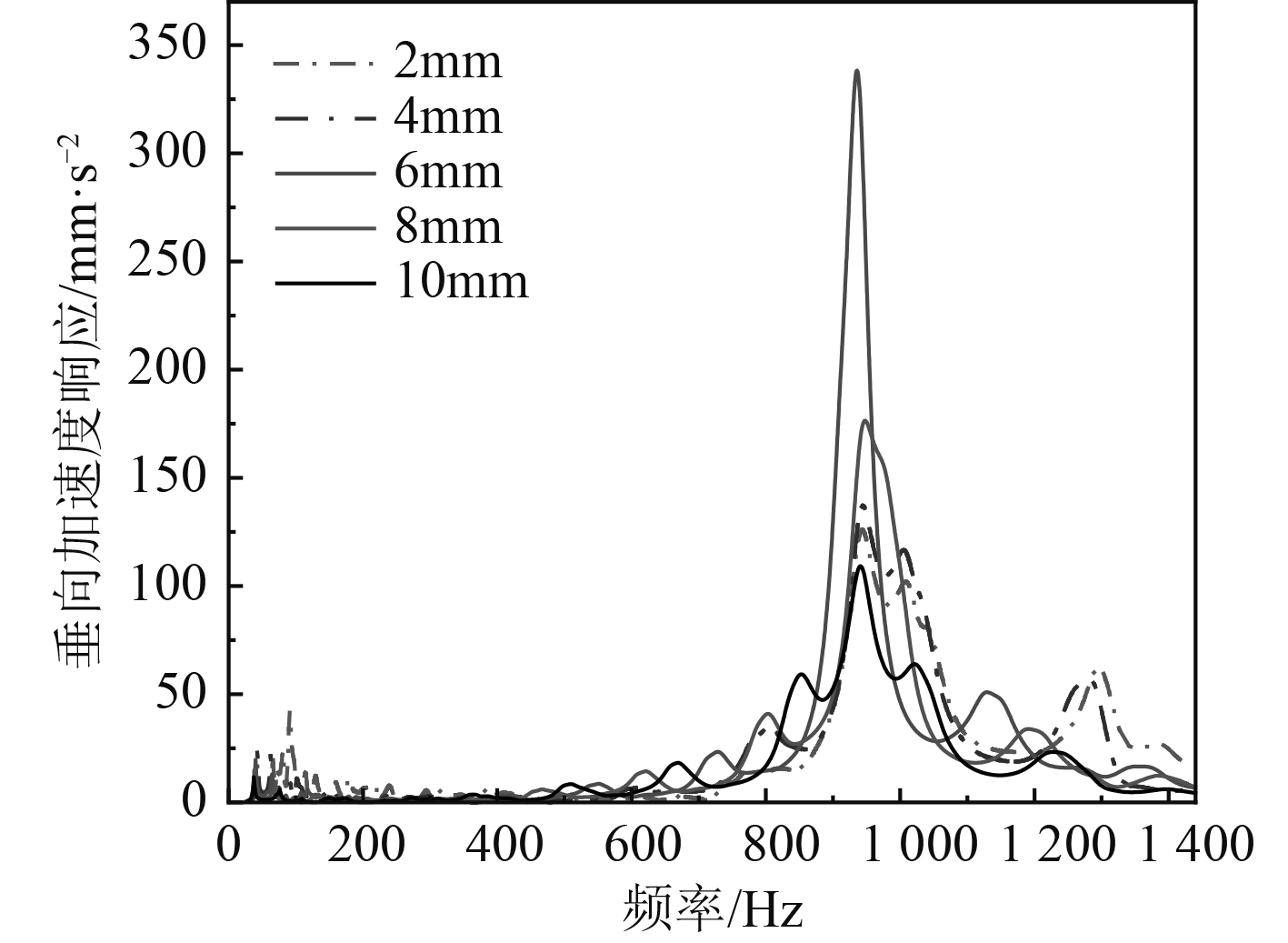
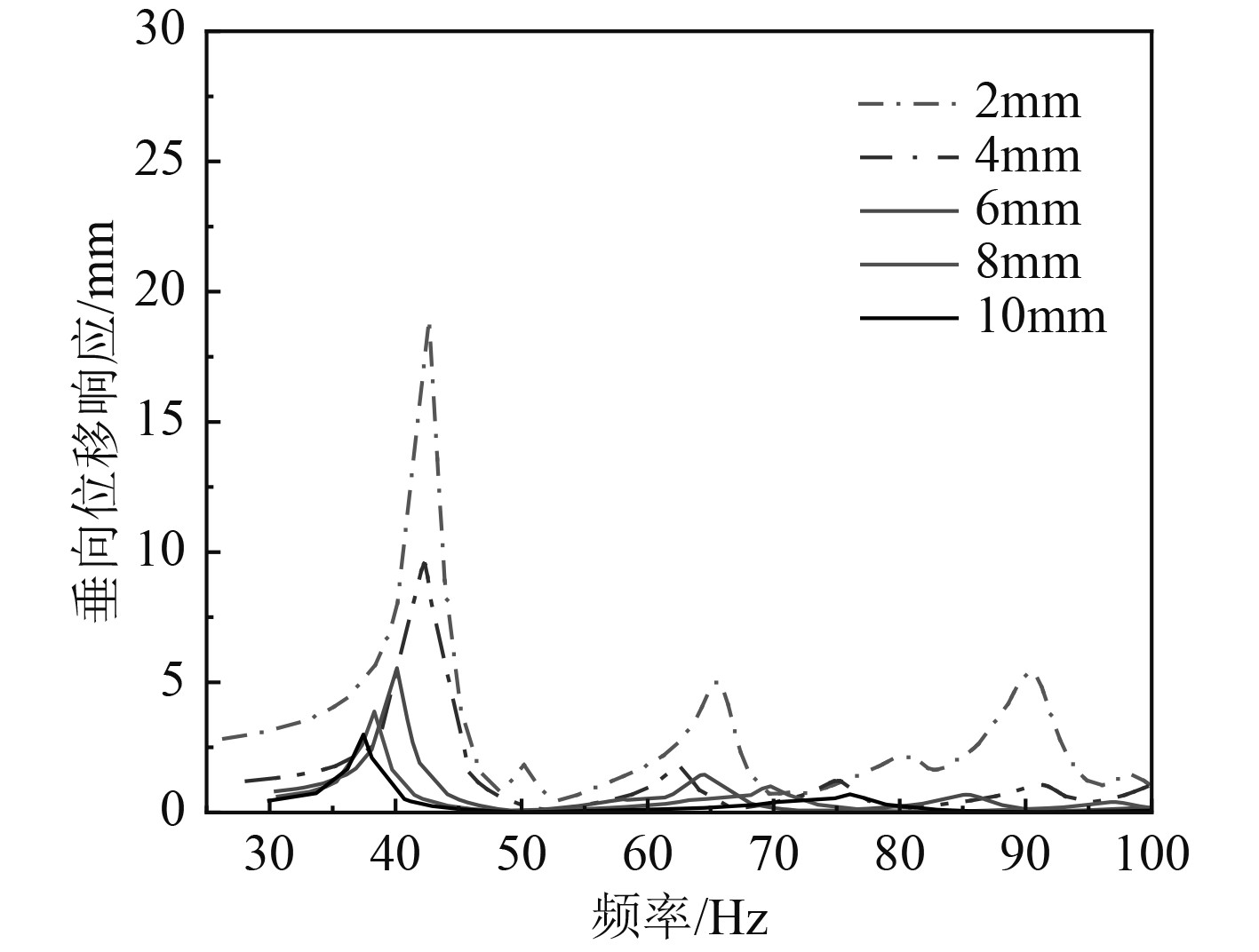
分析橡胶板厚度对气室振动特性的影响。分别取板厚为2~10 mm进行计算,评价点的加速度响应曲线如图8所示。可以看出,随着厚度的增加,峰值响应先增大后减小,在厚度为2 mm,4 mm和10 mm时响应较小,而在厚度为6 mm和8 mm时响应较大。橡胶底板中心点的位移响应曲线如图9所示,橡胶底板的固有频率随着厚度的增加而降低,从43 Hz逐渐降为37 Hz。位移响应也逐渐降低,从约20 mm降低到3 mm,可见橡胶底板厚度的增加也可以降低其动力位移响应。
|
图 8 橡胶板厚度对加速度响应的影响 Fig. 8 The effect of t on acceleration response |
|
图 9 橡胶板厚度对底板位移响应的影响 Fig. 9 The effect of t on displacement response |
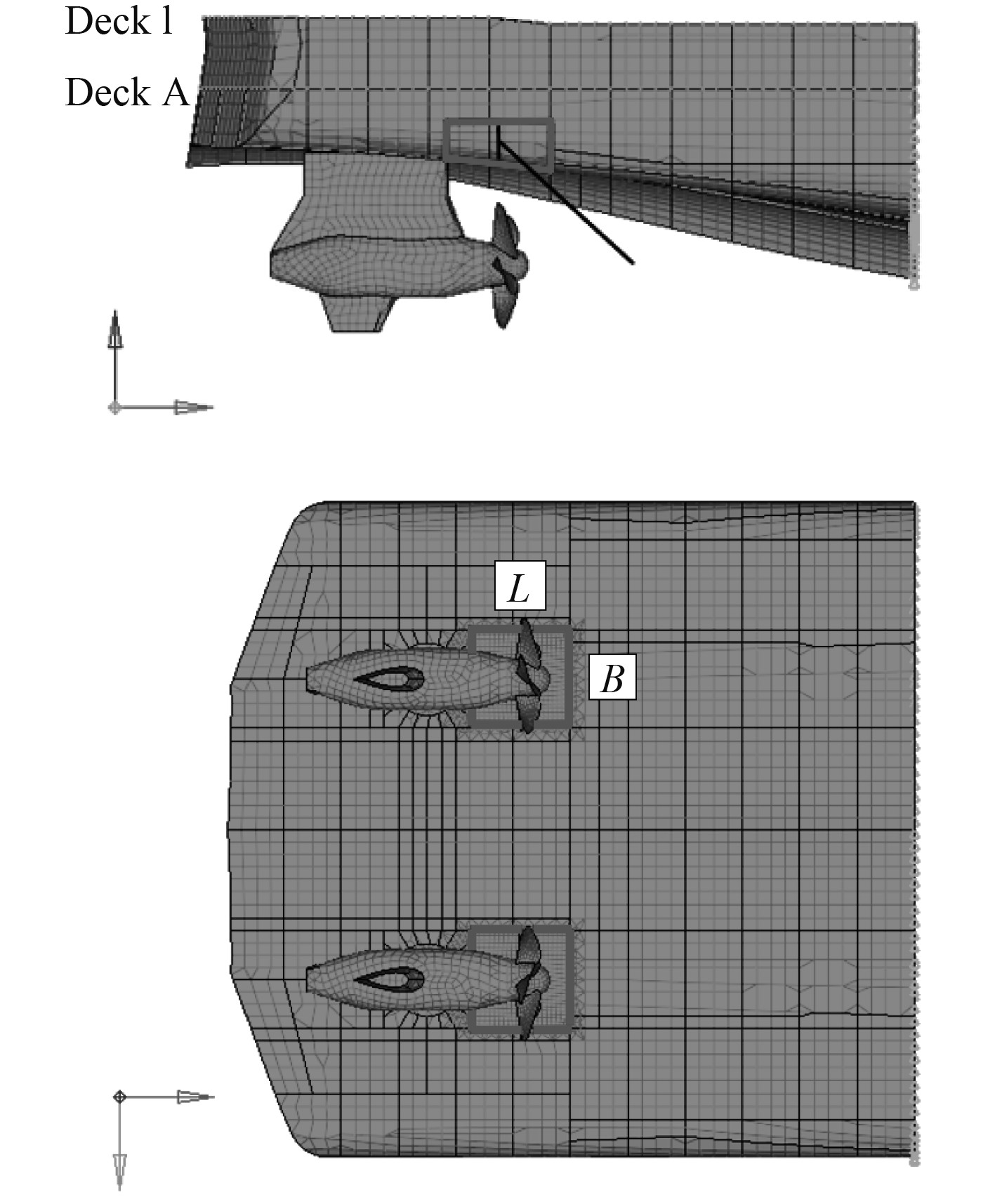
为进一步探讨避振穴的隔振机理和隔振性能,将其应用于尾部模型。如图10所示,在某双桨船尾部进行避振穴的布置。计算模型取船尾部分,截断边界处施加固支约束条件,上层建筑通过质量点的方式施加于2层甲板(1甲板与A甲板)上。有限元模型网格尺寸为700 mm,在避振穴的底部橡胶板处局部加密为200 mm。
|
图 10 实船尾部避振穴布置 Fig. 10 The anti-vibration cave arrangement at ship stern |
螺旋桨脉动压力主要作用区域为螺旋桨盘面之前0.1D,分布范围为D×D的区域[18],螺旋桨直径D=5980 mm,在此区域的正上方进行局部结构修改。避振穴长宽尺寸取为L=4900 mm,B=4800 mm,此区域的船底板换成橡胶板,自船底板向上挖出深度为h的空腔。橡胶板厚t取原船底板厚度25 mm,材料属性同第2节。避振穴所在部位吃水约0.37 m,此处船底外板所承受的静水压力约为0.004 MPa。相应的,避振穴内初始气压P0设为0.004 MPa。
3.2 避振穴对总体振动的影响计算原模型以及3种避振穴深度尾部模型的前5阶总体振动固有频率,如表3所示。可以看出,避振穴的改造对尾部总体振动的影响较小。随着深度的增加,固有频率略有下降,首阶固有频率最大降低幅度仅为0.7%。
|
|
表 3 不同深度比避振穴尾部模型的总体振动固有频率(Hz) Tab.3 Comparison of global natural frequencies for different depth ratio |
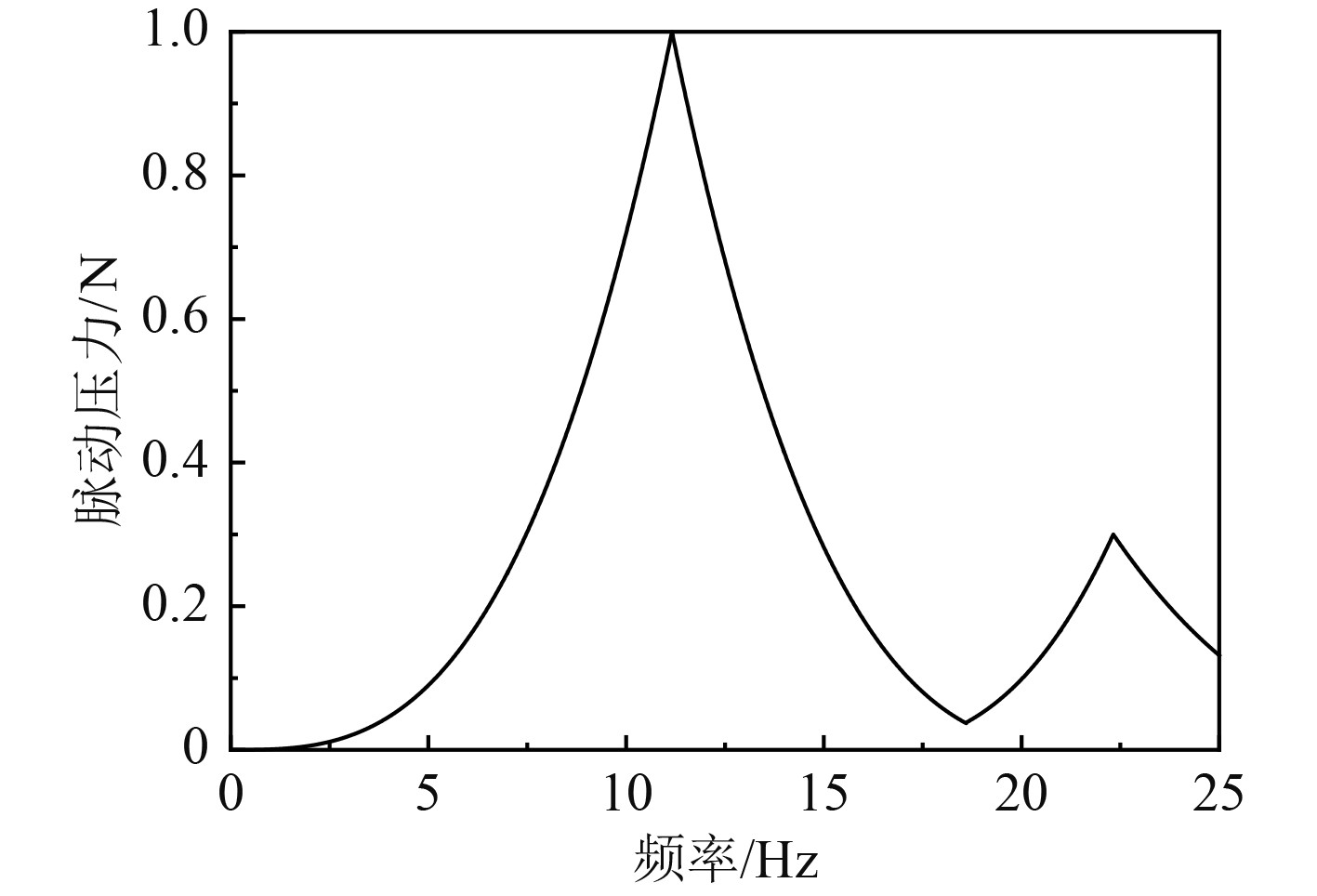
取避振穴深度比为1/2,对改造前后的尾部模型进行频率响应计算。螺旋桨脉动激励的叶频与倍叶频分别为11.16 Hz和22.32 Hz,作用于船底D×D的区域范围。脉动压力幅值随频率变化,在叶频和倍叶频处为峰值,在峰值两侧呈三次方衰减,如图11所示。
|
图 11 归一化脉动压力随频率变化曲线 Fig. 11 The normalized pressure curve |
关注A甲板的振动响应情况,原尾部模型A甲板上最大响应出现于双桨中部及后方区域,故选取此部位如图12所示的4个点作为响应评价点:Node343600位于中剖面与尾封板交界处,Node34222位于两舵后方偏左舷位置,Node343526位于两舵中间位置,Node343120位于两舷避振穴区域中部。

|
图 12 A甲板上评价点位置 Fig. 12 Evaluation points on Deck A |
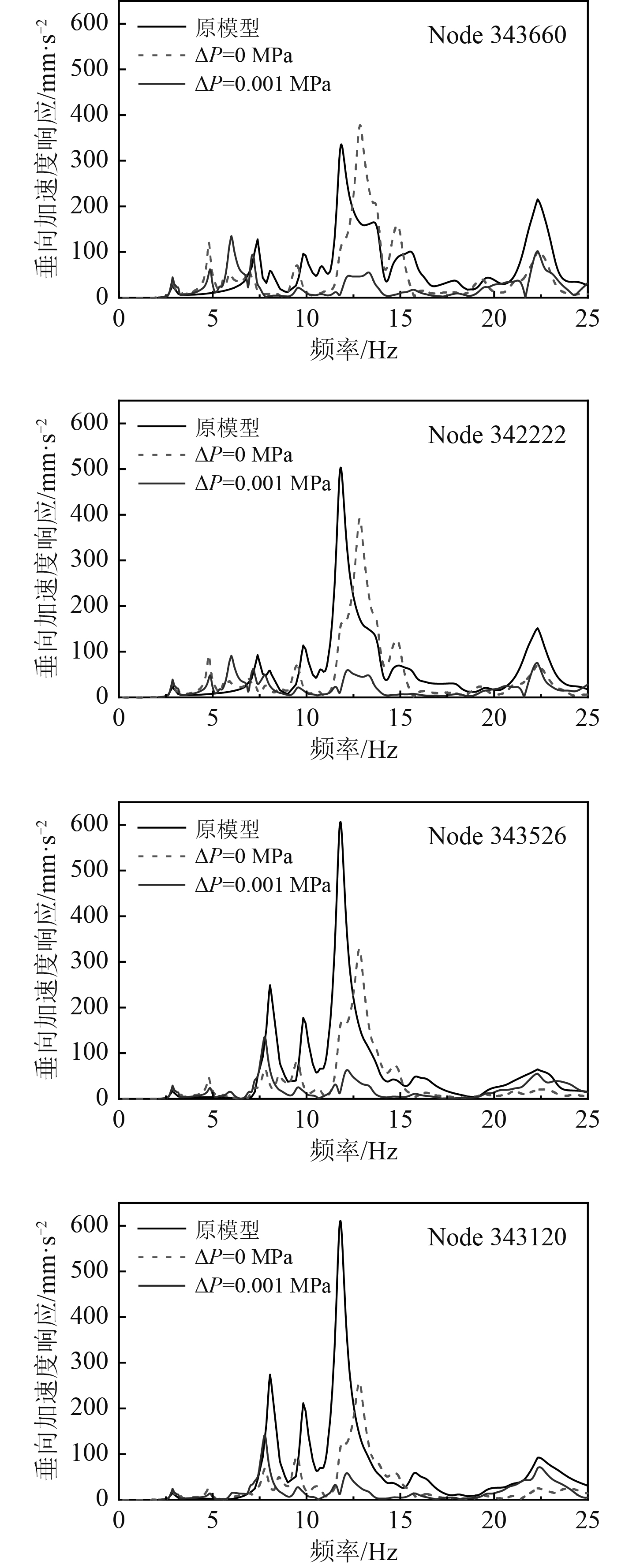
计算评价点在脉动激励下的垂向加速度响应,并考虑增压0.001 MPa的影响,结果如图13所示。可以看出,在低频段(0~7 Hz)除了船尾低阶总体振动的共振峰,避振穴结构的响应曲线出现新的共振峰,使得此频段的响应值增大。但在叶频和倍叶频附近频段(7~25 Hz)的响应有较大程度的降低,叶频处的共振峰右移。其中Node34222在叶频处的响应降低了约22%,Node343526的叶频响应降低了约46%,Node343120的叶频响应降低了约58%。位于中剖面和尾封板交界处的Node343600在叶频处的响应略有提高,约12%。避振穴内加压0.001 MPa后,低频共振区域新的共振峰处响应略有降低,叶频处响应值显著降低。
|
图 13 A甲板评价点的加速度响应(气压影响) Fig. 13 Acceleration response of evaluation points on deck A for different pressure |
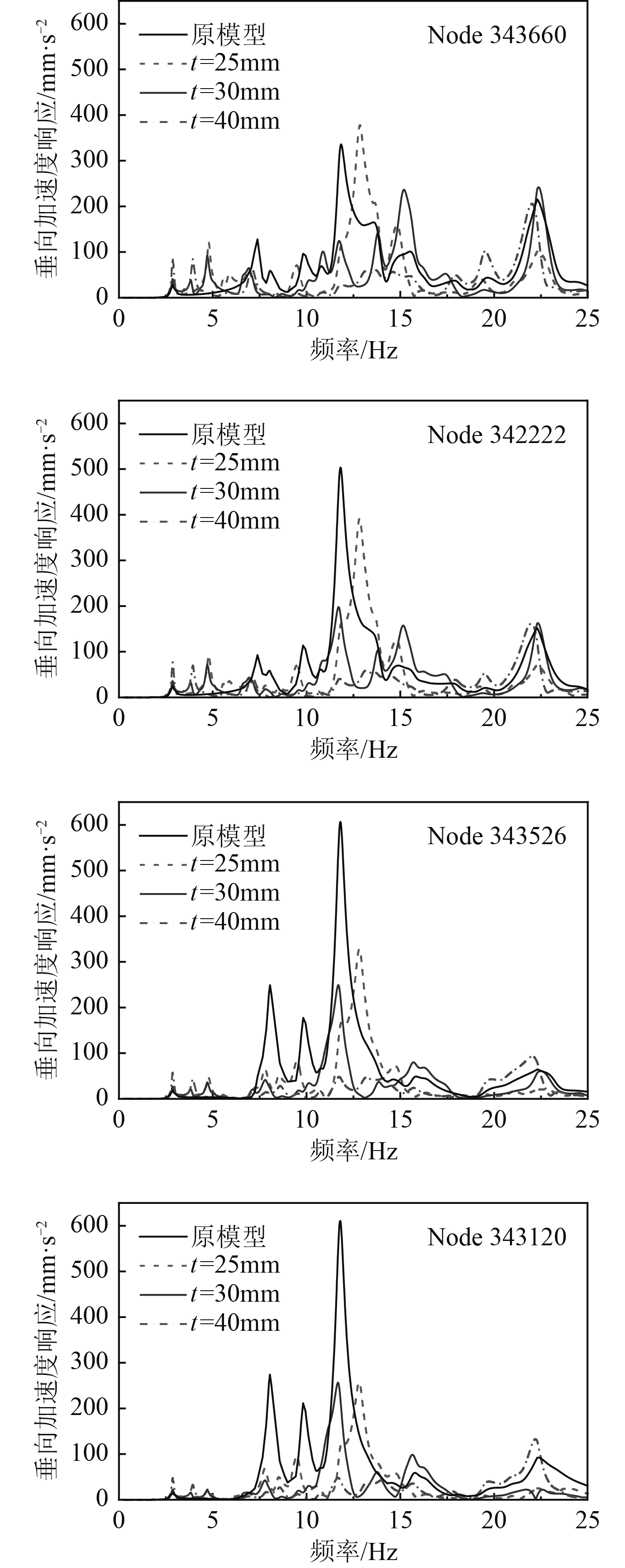
改变橡胶底板厚度,分别取t=25 mm,30 mm,40 mm进行计算。计算结果如图14所示。橡胶板厚度增大引起自身固有频率的降低,低频区域新出现的共振峰发生左移,且峰值降低。随着板厚增加,各评价点在叶频处的响应均有较显著的降低,而在倍叶频处的响应略微提高。
|
图 14 A甲板评价点的加速度响应(板厚影响) Fig. 14 Acceleration response of evaluation points on deck A for different rubber plate thickness |
本文通过非线性有限元方法分析避振穴的隔振性能和参数影响。结果表明:避振穴相对于尾部结构具有较低的自振频率,在叶频和倍叶频处具有显著的减振效果,但在低频共振区会产生新的共振峰使得振动响应增大;避振穴深度不必取的过深,深度比1/2甚至更浅亦能取得较好的减振效果;提高避振穴气压值或增大橡胶板厚度能改变避振穴自身固有频率,降低其在低频共振区带来的影响。
| [1] |
金咸定, 夏利娟. 船体振动学[M]. 上海: 上海交通大学出版社, 2011.
|
| [2] |
翁长俭, 吴学仁, 吴卫国, 等. 新型避振穴研究[J]. 中国造船, 1996(4): 51-56. Weng Changjian, Wu Xueren, Wu Weiguo, et al. A study of a new type of cave for damping[J]. Shipbuilding of China, 1996(4): 51-56. |
| [3] |
张平, 于全虎. 船舶减振降噪措施简析[J]. 江苏船舶, 2010, 27(3): 2-4. Zhang Ping, Yu Quanhu. Brief discussion on ship vibration reduction and noise reduction[J]. Jiangsu Ship, 2010, 27(3): 2-4. |
| [4] |
马佐璋, 黄孟浩, 肖熙, 等. “避振穴”对减小船舶尾部振动的效果[J]. 上海交通大学学报, 1980(2): 5-17. Ma Zuozhang, Huang Menghao, Xiao Xi, et al. The effect of the anti-vibration cave on reducing ship′s vibration[J]. Journal of Shanghai Jiaotong University, 1980(2): 5-17. |
| [5] |
高宪智, 肖熙. “避振穴”的减振效能[J]. 上海交通大学学报, 2000(1): 108-110. Gao Xianzhi, Xiao Xi. Vibration absorbing effect of anti-vibration cave on reducing ship′s vibration[J]. Journal of Shanghai Jiaotong University, 2000(1): 108-110. |
| [6] |
黄孟浩, 马佐璋, 肖熙, 等. “避振穴”对减小快艇艉部振动效能的试验研究[J]. 舰船科学技术, 1980(7): 1-12. Huang Menghao, Ma Zuozhang, Xiao Xi, et al. Experiment study on vibration absorbing effect of anti-vibration cave on reducing speed boat′s vibration[J]. Ship Science and Technology, 1980(7): 1-12. |
| [7] |
高宪智, 马佐璋. 多孔型“避振穴”装置的减振性能研究[J]. 实验室研究与探索, 1993(3): 53-56. Gao Xianzhi, Ma Zuozhang. Study on vibration absorbing effect of anti-vibration cave with multihole[J]. Research and Exploration in Laboratory, 1993(3): 53-56. |
| [8] |
李昌龙, 庄和埙, 甘列松. 钟形减振穴的设计研究[J]. 中国造船, 1985(1): 63-70. Li Changlong, Zhuang Hexun, Gan Liesong. Study and design of bell type anti-vibration device[J]. Shipbuilding of China, 1985(1): 63-70. |
| [9] |
李昌龙, 庄和埙, 甘列松. 大功率双桨船的一种新型减振装置——钟形减振穴[J]. 舰船科学技术, 1985(4): 1-10. Li Changlong, Zhuang Hexun, Gan Liesong. A new damping device for high-power twin-propeller ship—bell type anti-vibration device[J]. Ship Science and Technology, 1985(4): 1-10. |
| [10] |
Tadao Yamano, Hodaka Shimizu. Reduction System of Afterbody Vibration due to Surface Force: Mechanism and Effect for Model and Ship[J]. Kansai Soc. N. A, 1989(211): 157-166. |
| [11] |
吴卫国, 翁长俭, 吴学仁, 等. 新型避振穴减振机理研究[J]. 武汉造船, 1997(5): 34-37. Wu Weiguo, Weng Changjian, Wu Xueren, et al. Study on vibration reduction mechanism of cave for damping[J]. Wuhan Shipbuilding, 1997(5): 34-37. |
| [12] |
吴学仁, 翁长俭. 新型避振穴的模型试验[J]. 武汉交通科技大学学报, 1997(3): 18-20. Wu Xueren, Wen Changjian. Model Experiment of cave for damping[J]. Journal of Wuhan Transportation University, 1997(3): 18-20. |
| [13] |
翁长俭. 我国船舶振动冲击与噪声研究近年进展[J]. 中国造船, 2001(3): 70-86. Weng Changjian. Recent development in field of ship vibration shock and noise research in China[J]. Shipbuilding of China, 2001(3): 70-86. |
| [14] |
王强, 邬卡佳, 刘雪莹, 等. 一种基于聚氨酯的船舶避振穴及安装方法[P]. 中国: CN102351034B, 2015-01-14.
|
| [15] |
ABAQUS Theory Guide 3.8. 1, HKS Co. Ltd.
|
| [16] |
刘文玺, 周其斗. 基于非线性有限元法的橡胶隔振器构型优化[J]. 船舶力学, 2014, 18(4): 434-440. Liu Wenxi, Zhou Qidou. Study on configuration optimization of rubber isolator by nonlinear FEM[J]. Journal of Ship Mechanics, 2014, 18(4): 434-440. |
| [17] |
AMABILI M., BALASUBRAMANIAN P., BRESLAVSKY I. D., et al.. Experimental and numerical study on vibrations and static deflection of a thin hyperelastic plate[J]. Journal of Sound and Vibration, 2016, 385: 81-92. DOI:10.1016/j.jsv.2016.09.015 |
| [18] |
中国船级社. 船上振动控制指南[M]. 北京: 人民交通出版社, 2000.
|
 2021, Vol. 43
2021, Vol. 43