0 引　言

三组元推进剂是热动力鱼雷近期发展所能采用的最佳推进剂之一，比例控制器是实现三组元推进剂精确配比的关键部件^[1]，其本质是3个具有共同转速的标准容积计量装置。研究人员^[2-4]以往通过理论分析和经验来计算各因素对于比例控制器比例精度的影响，对于内部流场研究则相对较少。

计算流体力学为预测比例控制器的性能提供了重要途径^[5]。本文以比例控制器燃料路为研究对象进行流场数值模拟，利用Pumplinx软件所具备的泵阀模板快速实现不同叶片和不同间隙下的网格划分，分析不同进出口压差及叶片与定子内表面间隙^[6]工况下对于比例控制器燃料路流量、压力脉动和转动速度等影响。

1 流量理论分析

比例控制器是以马达形态工作的叶片式容积计量装置^[7]，其运动计量原理如图1所示。

根据图中 $xoy$ 坐标，定子圆上某点的矢径 $\rho \left( \theta \right)$ 为转角的 $\theta $ 函数。逆时针方向为正转向。设 ${\rm{d}}t$ 时间转过了 ${\rm{d}}\theta $ 角度，压油区由 $acfd$ 变为 $a'c'f'd'$ ，容积缩小量为 $acc'a'$ 与 $dff'd'$ 之差。由于 $\Delta abc$ 与 $\Delta a'b'c'$ 面积近似相等，故 $acc'a'$ 的面积 ${S_1}$ 近似相等于 $bcc'b'$ ，可按 $d\theta $ 角度下的圆环面积公式计算。同理， $dff'd'$ 的面积 ${S_2}$ 近似相等于 $mff'm'$ 的面积。

$\mathop s\nolimits_1 \approx \frac{1}{2}\left[ {{\rho ^2}\left( \theta \right) - {r^2}} \right]{\rm{d}}\theta \text{，}$

(1)

$\mathop s\nolimits_2 \approx \frac{1}{2}\left[ {{\rho ^2}\left( {{\theta _2}} \right) - {r^2}} \right]{\rm{d}}\theta \text{，}$

(2)

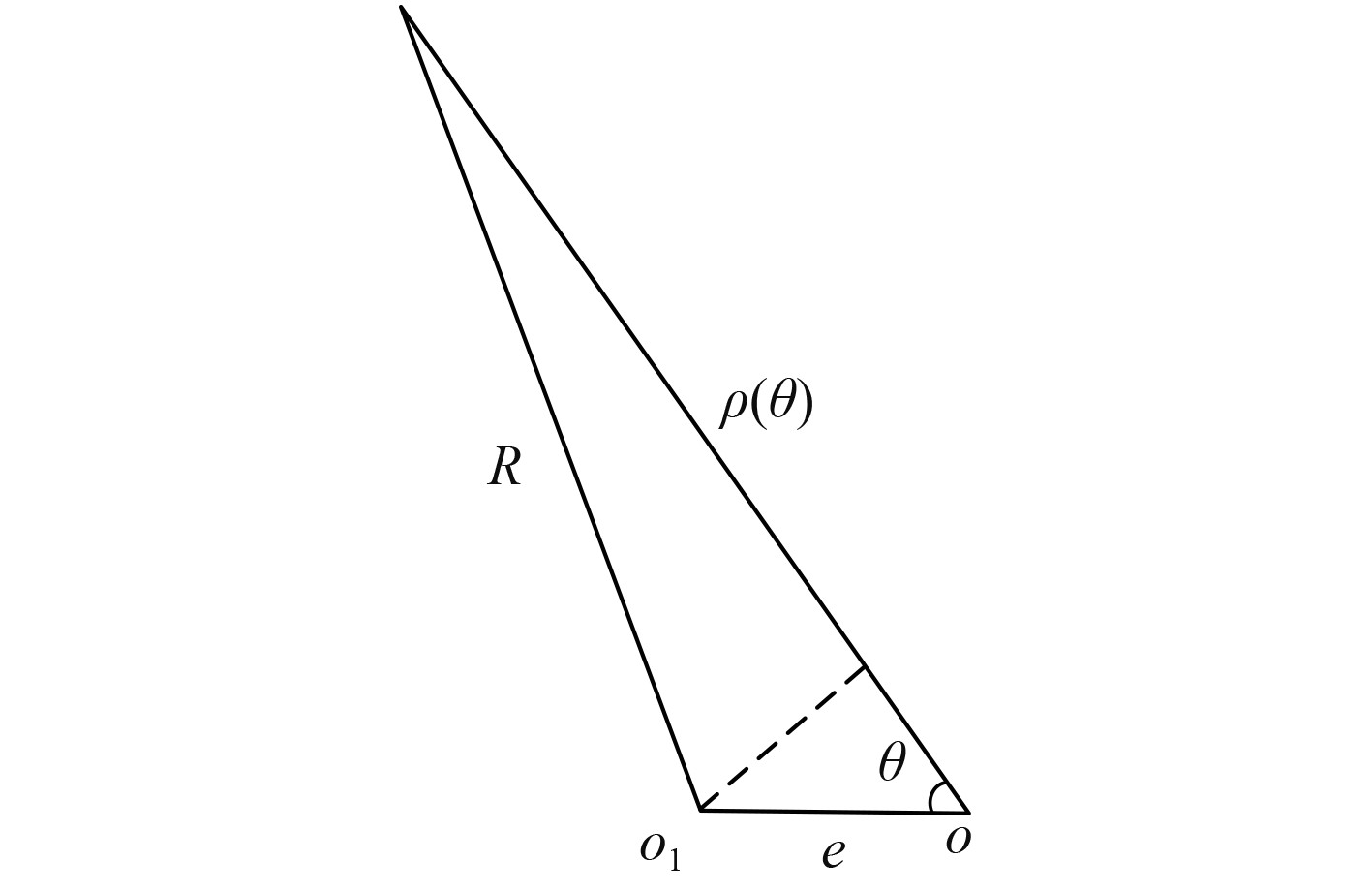
由图2可见， $\rho \left( \theta \right)$ 可表示为：

$\rho (\theta ) \approx e\cos \theta + \sqrt {{R^2} - {e^2}{{\sin }^2}\theta } \text{，}$

(3)

将 ${\theta _2} = \theta + \text{π} $ 代入得瞬时流量为：

$\begin{split} {Q_{ir}}{\rm{ }} = &\frac{{{\rm{d}}V}}{{{\rm{d}}t}} = \frac{1}{2}B\omega \left[ {{\rho ^2}\left( \theta \right) - {\rho ^2}\left( {{\theta _2}} \right)} \right] =\\ & \frac{1}{2}B\omega {R^2} \cdot 4\frac{e}{R}\cos \theta = \\ & {{ 2}}eBR\omega \cos \theta \text{。} \\ \end{split} $

(4)

式中： $- \dfrac{\beta }{2} \leqslant \theta \leqslant \dfrac{\beta }{2}$ ， $\beta = \dfrac{{2\text{π} }}{z} = \dfrac{\text{π} }{2}$ 。可知：

$\begin{split} & {({Q_{ir}})_{\max }} = 2eBR\omega \text{，} \\ & {({Q_{ir}})_{\min }} = 2eBR\omega \cos \frac{\text{π} }{4} \text{。} \end{split} $

(5)

可知，叶片由 $- \dfrac{\beta }{2}$ 到 $\dfrac{\beta }{2}$ 产生了一次最大流量和一次最小流量，即流量脉动了一次，脉动频率 $f = \dfrac{{4n}}{{60}}$ 。

2 湍流模型和数值方法 2.1 湍流模型

对于流体机械流动通常Re>10⁵，流动状态多处于湍流流动。本文采用流体机械领域最为普遍应用的k-ε模型。

2.2 数值方法

Pumplinx中采用有限体积法对划分的非结构化网格进行求解，对于控制方程的离散求解，在时间空间上采用2阶迎风格式，选择SIMPLEC (Semi–implicit method for pressure-linked equation Consistent)算法求解离散方程，由于计算不涉及空化模型，故收敛速度相对较快。

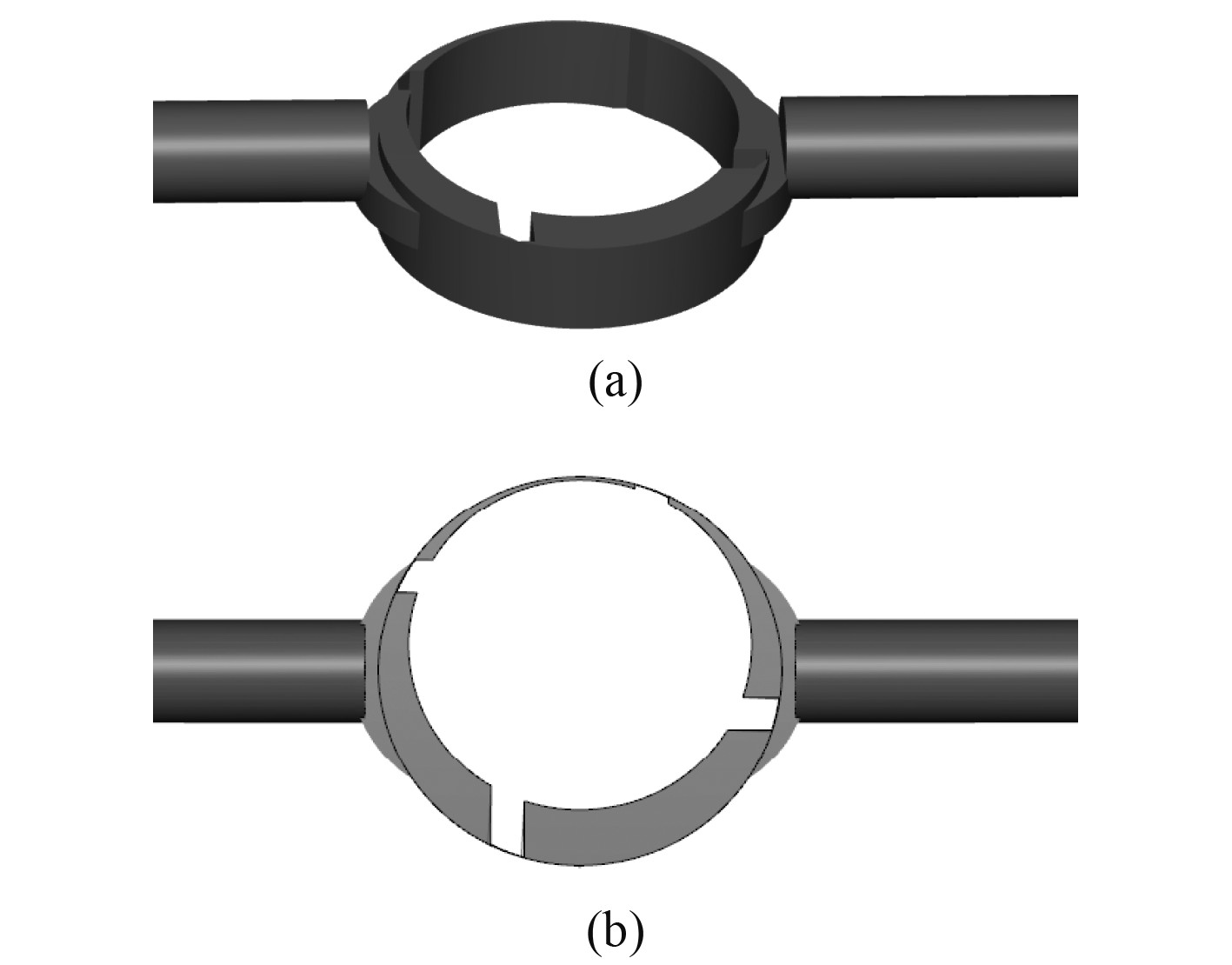
3 流体模型及网格划分 3.1 研究对象流体域提取

比例控制器在运转过程中，两叶片间的工作腔内部压力是动态变化的。本文所述的比例控制器单路与以往的偏心叶片泵形式有所不同，流量进口不再是通过配流盘进入，而是直接通过径向入口进入。单路的内流体域如图3(a)所示，主要包括进出口段、导油槽及偏心叶片旋转部分。

由于比例控制器的特殊结构形式^[7]决定了影响其内泄漏的最主要因素是径向间隙，即叶片顶部与定子之间的距离，故该流道模型忽略了轴向间隙，并针对叶片顶部接触对流体模型做一定简化，由图3(a)所示的线接触简化为图3(b)所示的面接触方式，同时也忽略叶片底部腔内高压区及打孔螺钉等微小部分。最终提取的比例控制器燃料路流体模型如图3(b)所示。

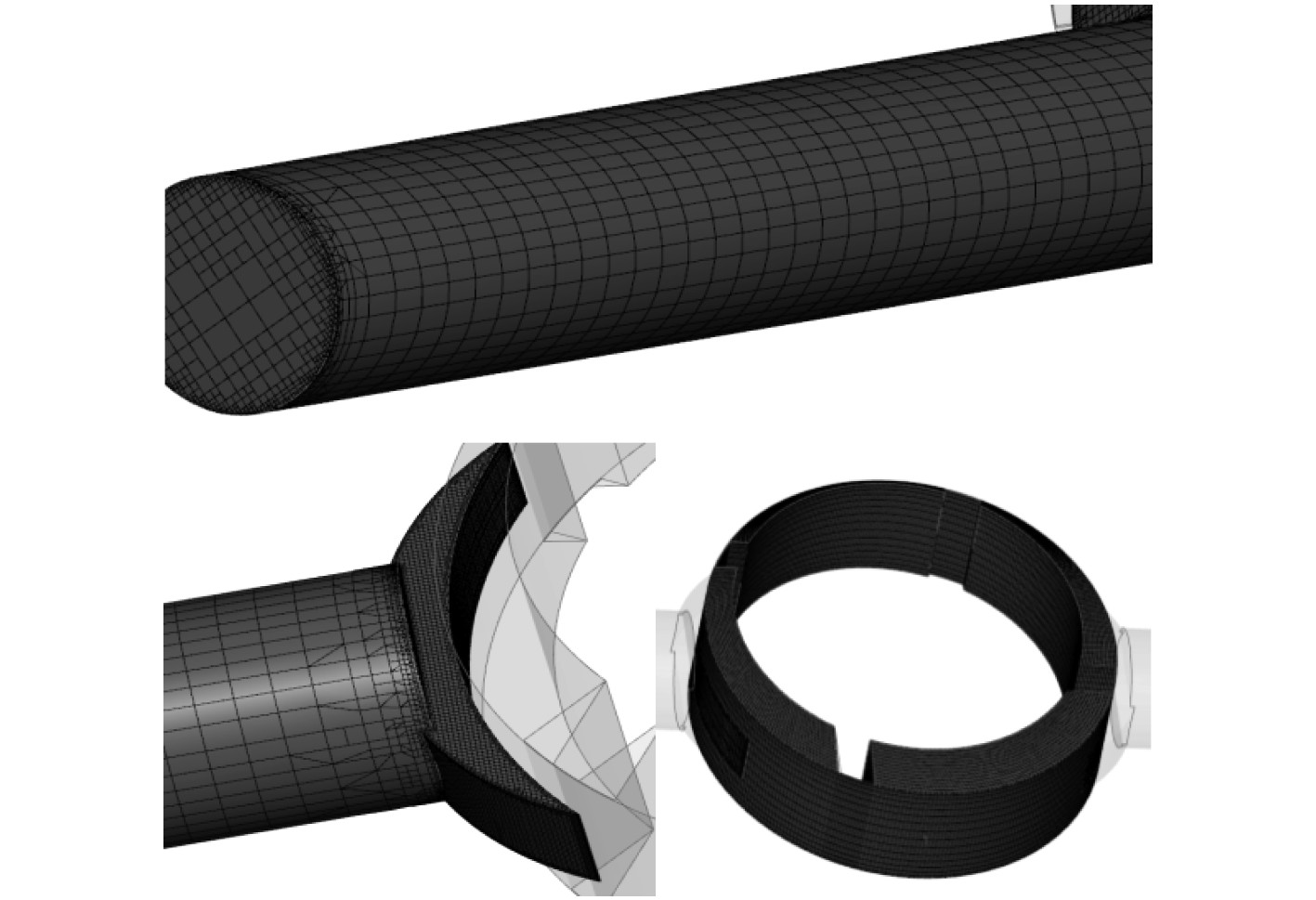
3.2 网格划分

采用Pumplinx内置的网格模板对模型进行网格划分，对于入口段和出口段运用基于自适应二叉树算法(CAB)建立笛卡尔网格，同时针对导油槽附近的网格进行局部加密；对于旋转区域采用自带的叶片泵模板，通过设置转动壁面、静止壁面、旋转中心和叶片数等就可以自动生成转子区域的网格，对于微米级别的叶顶径向间隙，划分5个节点即4层网格。网格划分结果如图4所示，整个流体域网格总数约54万。

3.3 从动旋转设置

比例控制器是以马达形态工作的，通过Pumplinx内置的旋转机械模板对比例控制器进行从动模拟，由内置的自由度模块根据流体冲击力的大小等属性来计算转子的转速。转子力平衡方程为：

$I\frac{{{\rm{d}}{}^2\theta }}{{{\rm{d}}{t^2}}} = {\tau _{hydrodynamic}} - {\tau _{damping}} + {\tau _{additional}} + {\tau _{friction}}\text{，}$

(6)

式中：

${\tau _{hydrodynamic}} = \Sigma {\tau _{pressure}} + \Sigma {\tau _{shear}}\text{，}$

${\tau _{damping}} = {D_\tau } \cdot \omega \text{，}$

${\tau _{friction}} = \mu \cdot N\text{。}$

式中： ${D_\tau }$ 为阻尼系数， $\ \mu $ 为摩擦系数。

计算流体域入口条件设置为压力入口，静压2.0 MPa，出口条件设置为压力出口，转子转动惯量经计算为 $9.0 \times {10^{ - 5}}\;{\rm{kg}} \cdot {{\rm{m}}^2}$ 。

4 计算结果分析 4.1 阻尼系数设定

为使模型尽可能真实模拟比例控制器内部流场情况，模型中使用阻尼系数 ${D_\tau }$ 模拟被动旋转时的阻力矩。取叶片顶部间隙为60 µm，参照比例控制器冷态实验数据进行校准，过程中模型以水为流体介质，工作温度20 ℃，密度998 kg/m³，动力粘度0.00101 Pa·s，考虑到比例控制器转速较低(<600 r/min)，计算不涉及空化模型。对不同工况下的流体模型进行计算模拟，通过计算分析得到，当阻尼系数设置为0.003时，可大致满足试验过程中的压差-转速数据关系，流场仿真结果与试验数据对比如图5所示。

4.2 比例控制器仿真结果分析 4.2.1 压差对比例控制器影响分析

以单组元比例控制器为研究对象，流体介质为OTTO-II，入口压力2.0 MPa，叶片径向端部与定子内壁的配合间隙为0.06 mm，阻尼系数0.003，研究压差对于比例控制器性能的影响。

表1给出了不同工作压差下比例控制器内部流场的仿真结果。可知：随着工作压差的增大，比例控制器的流量和转速均随之增大；随工作压差的增大，比例控制器流量与工作压差间并不是严格的线性关系，转速与工作压差间也不是严格的线性关系；随着比例控制器前后工作压差的提高，其容积效率逐渐降低，比例控制器内泄漏增大，但在工作区间内比例控制器内泄漏量总体差距不大，泄漏量上下变化范围在计量腔室容积的1.5%以内。

图6为不同工作压差下比例控制器转速随时间的变化情况。可知，比例控制器的转速随时间呈周期性变化。随着工作压差逐渐变大，比例控制器流量和转速均变大。但随着前后压差的逐渐增大，比例控制器的转速脉动程度变化不大。流量的脉动程度随压差的变化关系如图7所示。可知，随着工作压差的逐渐增大，流量脉动幅值也逐渐增大，且随着转速增大，脉动周期变短，脉动频率升高。这与第一节理论分析结果相符。

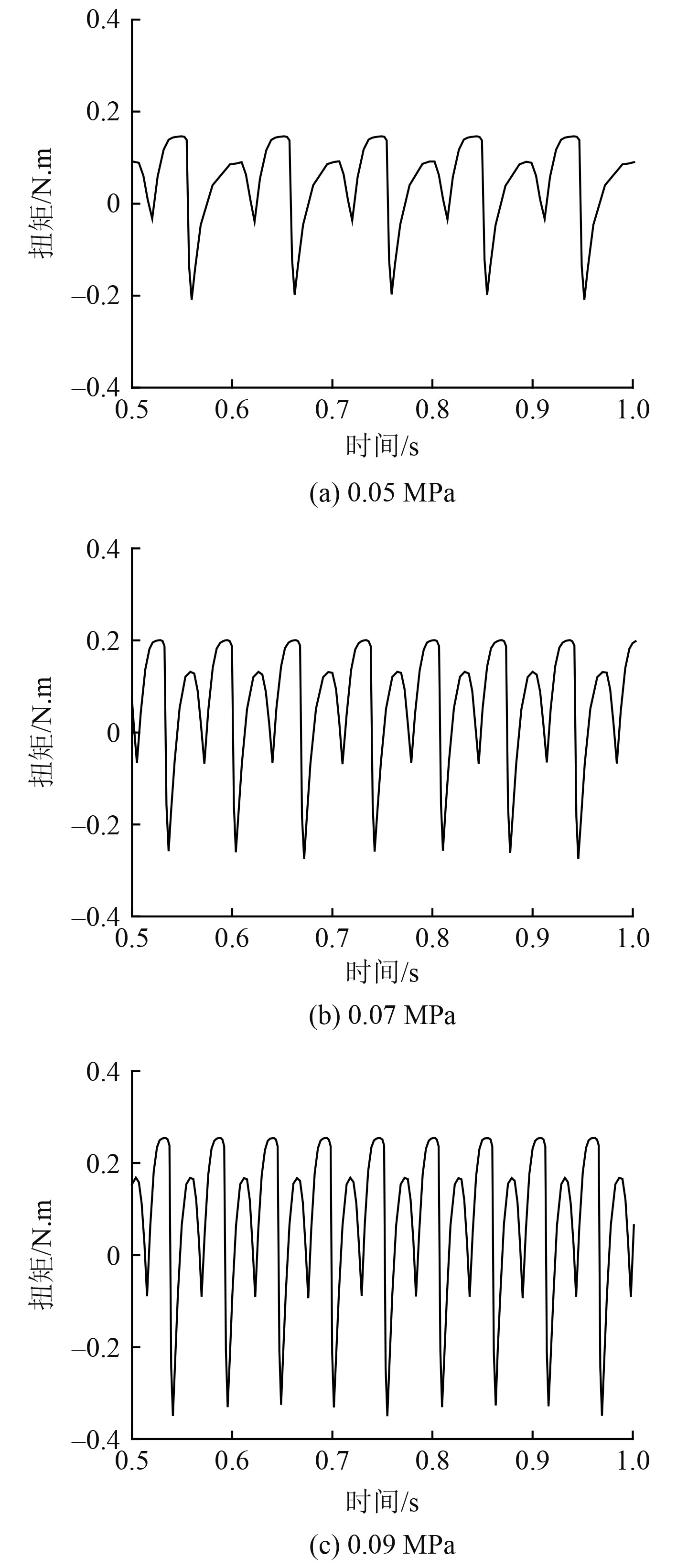
图8给出了工作压差改变时叶片所受流体扭矩随着时间的变化情况。可知，随着压差增大，扭矩脉动幅值增大，同时扭矩的平均值也随压差的增大。

4.2.2 不同径向间隙对比例控制器影响分析

不同于端面间隙对于叶片泵性能影响最大（端面泄漏约占内泄漏总量的70%～80%），比例控制器则因其特殊的构造导致影响其内泄漏最大的原因为径向间隙（即叶片径向顶部到定子内壁的距离）。以单组元比例控制器为研究对象，流体介质为OTTO-II，入口压力2.0 MPa，出口压力1.95 MPa，阻尼系数设为0.003，分别分析叶片与定子内壁配合间隙0～0.1 mm时比例控制器内部的流场特性。

表2给出了不同配合间隙下比例控制器的一些性能参数。

研究可知，在径向间隙为0时，前后压差0.5 MPa下，内部流场仿真发散，即此时比例控制器的转速为0，可知无法推动比例控制器转动。在径向间隙为20 µm时，比例控制器同样转动失败。当其径向间隙增至40 µm时，比例控制器开始转动，但存在着一定程度的正反转过程，转速存在正负脉动变换，由于其内部扭矩波动导致。当比例控制器径向间隙增至60 µm时，转速明显提高，完全消除反转现象；当径向间隙增至80 µm时，相应的转速增大，脉动幅度大幅降低。增至100 µm后，转速脉动幅度再次大幅下降，转速增加。

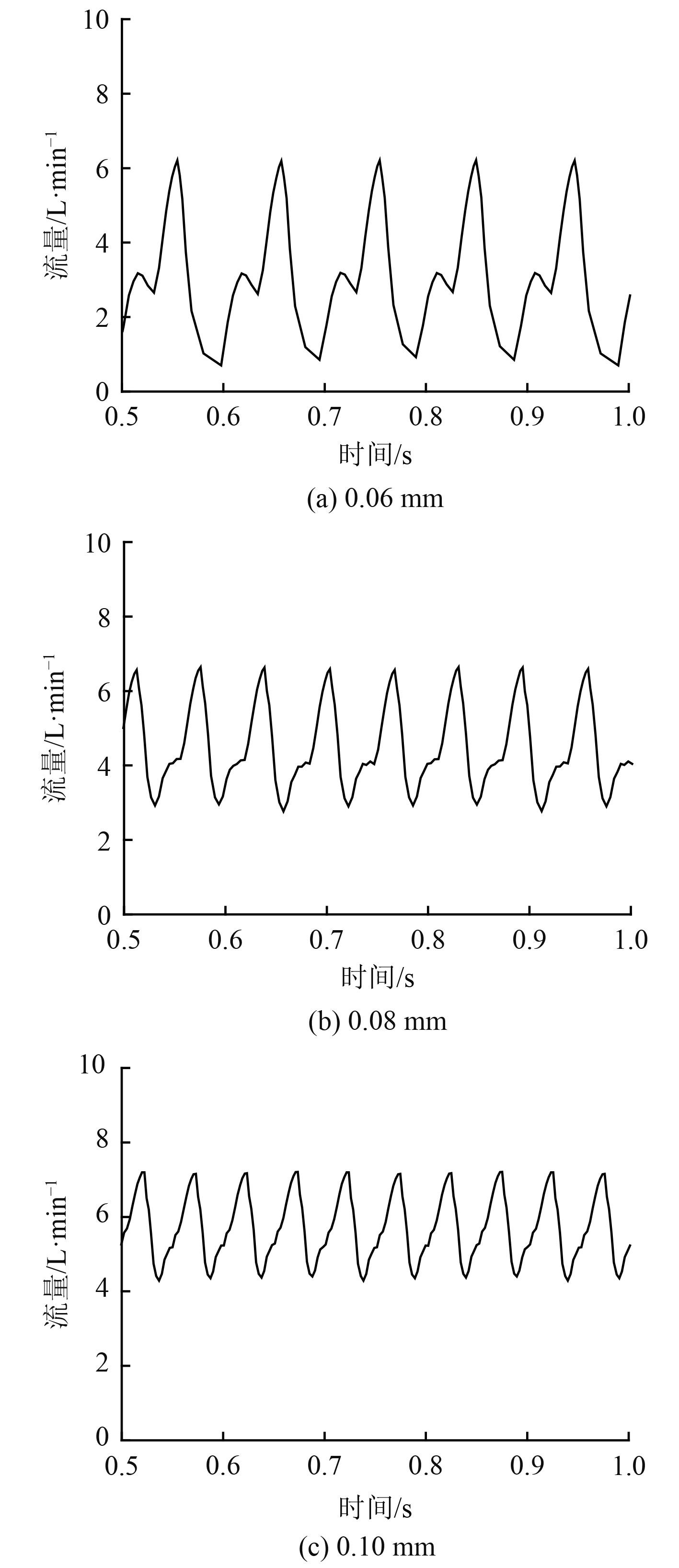
图9为不同配合间隙情况下比例控制器内部流场仿真结果。可知，配合间隙的大小对于比例控制器性能影响巨大，随着叶片顶部间隙变大，比例控制器转速脉动情况大幅度降低，转动平稳性大幅提高，且间隙变大，比例控制器转速升高。相比于压差，影响比例控制器转动平稳性的主要因素是叶片顶部间隙的大小，同时过小的径向间隙则会造成比例控制器卡滞，影响比例控制器工作，径向间隙的选取是比例控制器的关键所在。间隙同样会对比例控制器出口的流量脉动造成影响，由图9可以看出，随着径向间隙的增大，比例控制器流量升高，流量脉动幅度大幅减少，可得适当的增加比例控制器间隙对于比例控制器的转动是有利的。图10为不同间隙下转动叶片受流体扭矩随时间的变化情况，可知随着径向间隙增大，叶片所受扭矩均值升高，且随着转速升高，扭矩变化频率加大。同时在不同的间隙下，所受最大扭矩基本相等，扭矩最小值由于间隙的增大而升高，这是由于径向间隙的增大导致不同腔室间流动增加，大幅降低了闭死腔室在向前转动时突然接通压油腔的高压油时的瞬间反冲作用，而这种周期性的高压液冲击则会导致流量和压力脉动。同理，闭死容积内的高压液在接通低压出口时，会将容积内的高压液瞬时喷出，突然泄压，也会造成一定的流量脉动和压力脉动。

综上，可知在相同的边界条件下，比例控制器的转速会随着间隙的提高而增加，同时间隙的提高也有利于减少瞬时流量脉动和转速脉动。但间隙提升后，由高压区向低压区的泄漏量增加，每循环流量减少。因此要综合考虑间隙对比例控制器的影响。

4.2.3 叶片数目对于比例控制器影响分析

为了评估腔室数量对比例控制器的影响，针对不同叶片数目下的新转子对比例控制器进行性能分析。以单组元比例控制器为研究对象，流体介质为水，入口压力2.0 MPa，出口压力1.95 MPa，径向配合间隙60 µm，阻尼系数设为0.003，分别模拟了4，5，6三种叶片数目结构形式比例控制器流动情况。

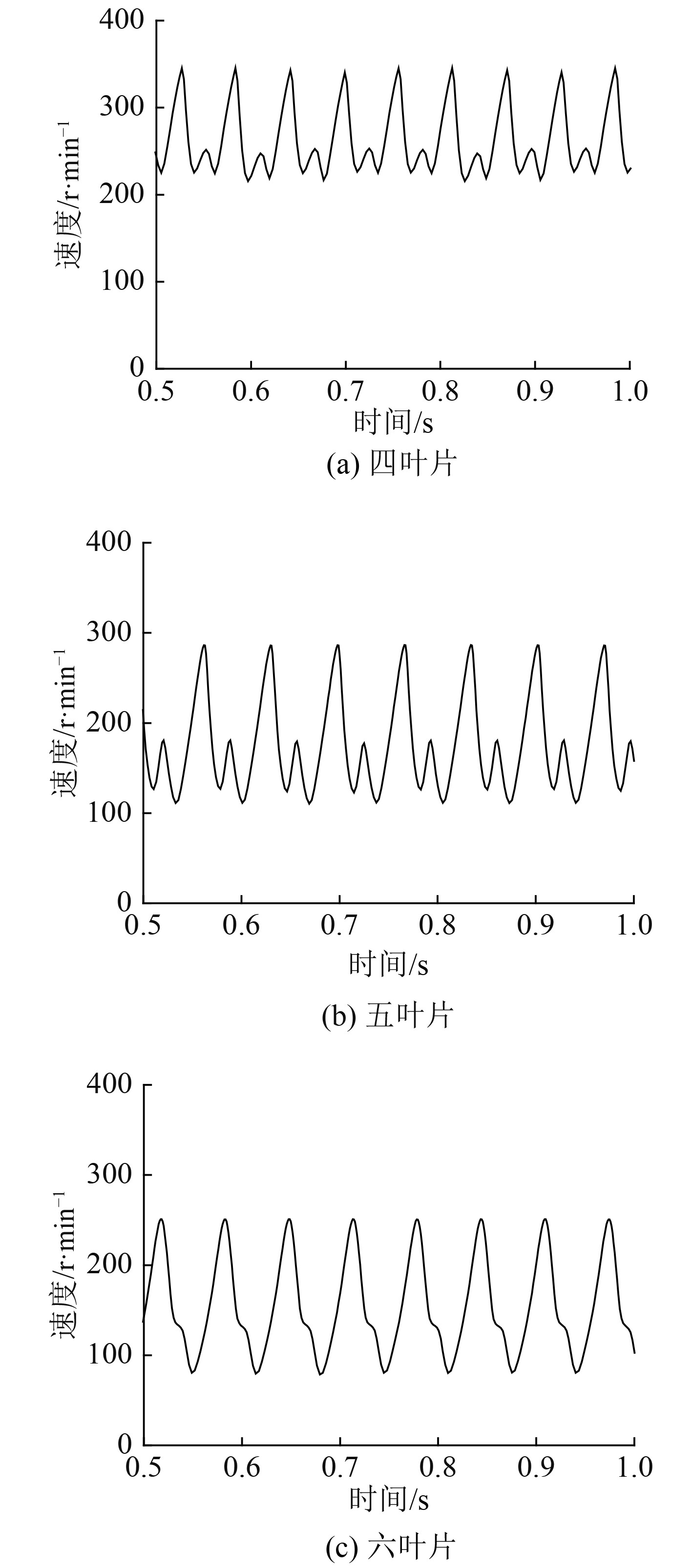
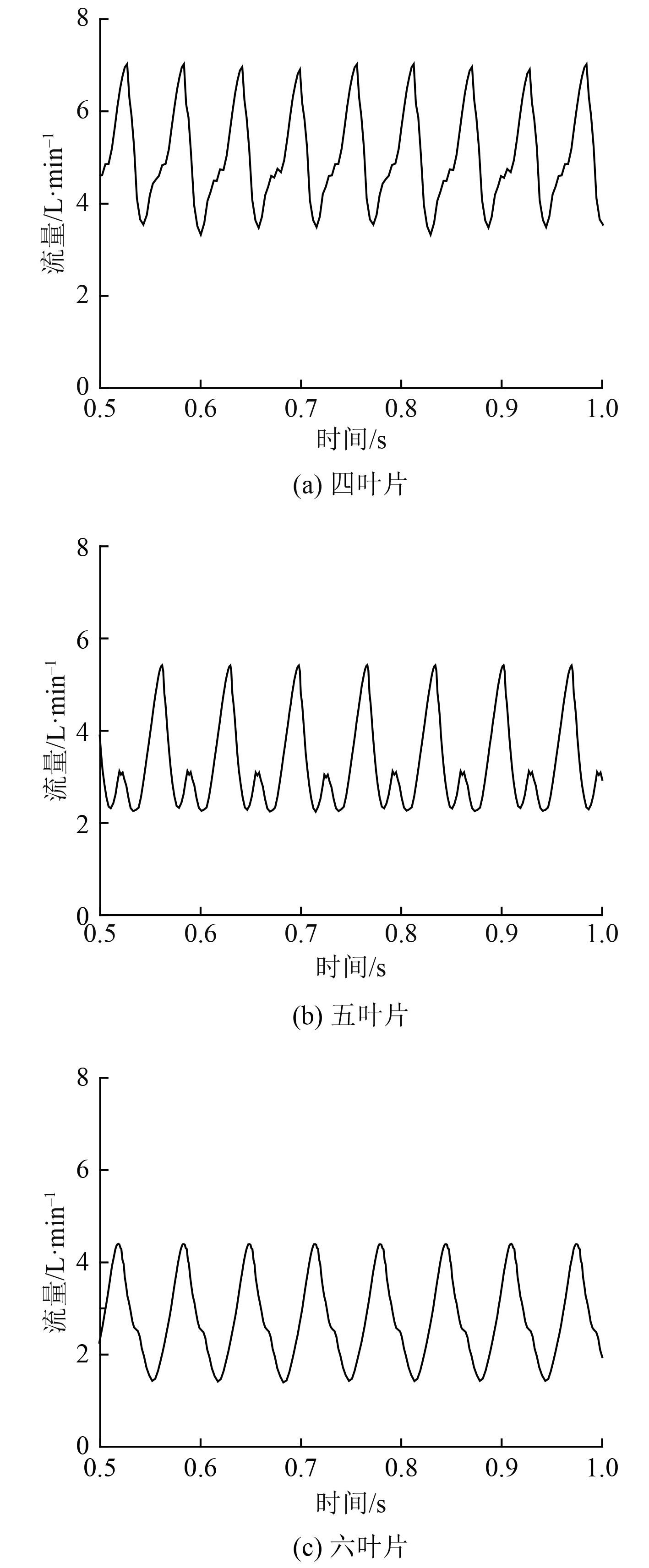
分析图12可知，叶片数目对于比例控制器性能的影响是巨大的。随着叶片数目增多，比例控制器转速降低，同时转速脉动程度也发生不同变化；随着叶片数目增多，比例控制器转速脉动幅度增大，且叶片数目为奇数时的转速脉动幅值大于叶片数目为偶数时的转速脉动幅值。同时，由图13可得，比例控制器的流量随叶片数目增多呈变小趋势，但流量脉动幅度随叶片数目改变而变化不大，均为3.5L/min左右，且叶片数目为偶数时流量均匀性要好于叶片数目为奇数时。综上可知，叶片数目的增多并不能改善比例控制器的流量和转速脉动情况，相反会加剧脉动，且会造成转速降低等不良效果。同时由于更多的叶片与转子和定子接触，造成机械效率的降低。因此，目前来说比例控制器的最优叶片数目为4。

5 结　语

本文通过对比例控制器内部流场分析，得到以下结论：

1)比例控制器转速和流量均随时间呈脉动变化情况。随着压差增大，转速脉动情况基本不变，流量与扭矩脉动幅值增加，且随着压差增大，比例控制器容积效率降低，泄漏增加。

2)间隙对于比例控制器启动有影响巨大，过小间隙由于闭死腔室内流体介质的无法流动而影响启动。间隙越小，比例控制器流量和转速、叶片所受扭矩脉动幅值越大，间隙增大后比例控制器转速提升，流量、扭矩、转速脉动情况大幅降低，但泄漏量增加。

3)叶片数目为偶数时比例控制器流量、转速脉动情况明显好于叶片数目为奇数时，同时叶片数目增多会占据腔室内一定容积，转速降低，导致排量降低。目前最优叶片数目为4。