0 前　言

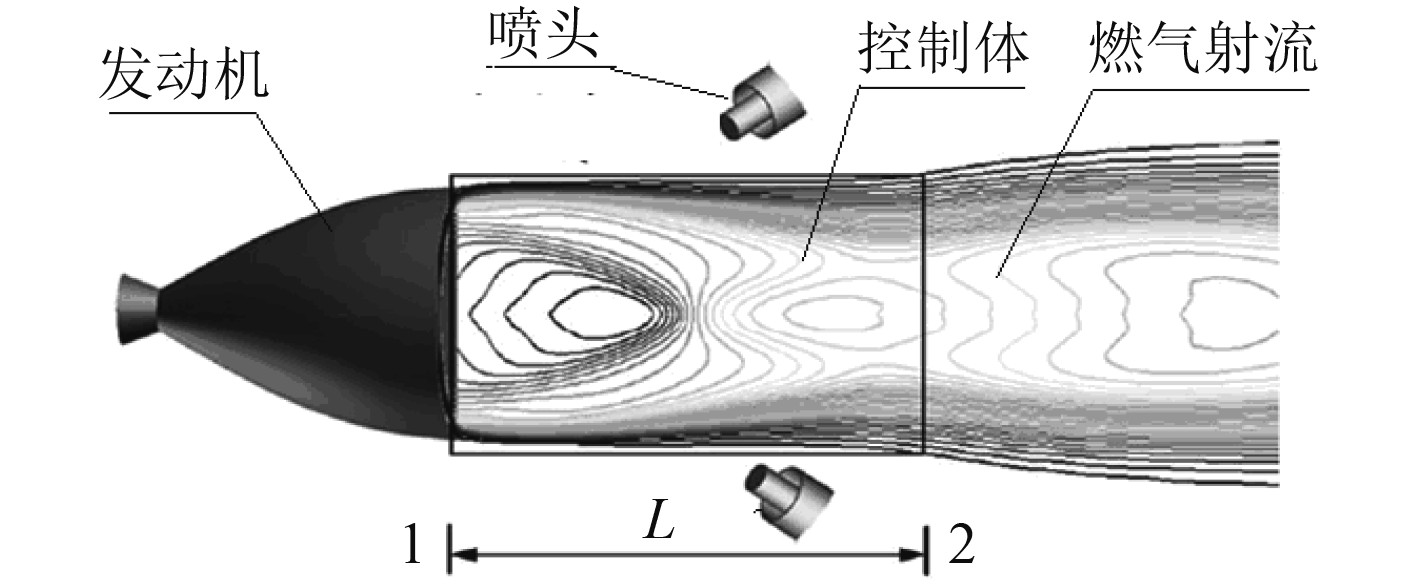
舰船弹库是舰船上储存弹药的舱室，不同弹库储存的弹药类型不同，舰载导弹平时储存在弹库内。舰载导弹自身带有固体火箭发动机，内部携带有大量的固体推进剂。导弹中的固体推进剂处于一种相对稳定的状态，当受到机械强冲击、爆炸冲击波、高温、静电等袭扰时，会发生意外点火，火箭发动机会在短时间内向外喷射高温、高压、高速燃气射流；燃气射流温度超过1000 ℃，速度超过2000 m/s，喷射出燃起流从十几千克到几十千克不等。舰船弹库是一个密闭空间，导弹在短时间内意外点火后，造成周围弹药处于高温高压下，极易发生殉爆，同时会使得弹库内部空间的压力急剧升高，造成弹库发生爆炸。李士军等^[1-2]先后研究了导弹意外点火时弹库泄压排气过程、喷洒抑制剂的影响。国外舰船弹库中一般均配置注水系统，例如“鞑靼人”舰空导弹库、MK41导弹库、MK48导弹库等。注水系统是通过注水喷头向意外点火的导弹发动机燃气射流中注入高压水，以便降低火箭发动机燃气射流温度，避免导弹发动机在弹库中意外点火时的高温燃气对周围弹药、舰船设备和船体造成损伤，如图1所示。我国国军标GJB 4000-2000第7组武器发射装置和保障系统721.5.3.4条弹库安全性中规定：发射装置的弹库应根据需要选用喷淋降温、强排风、注水、灭火措施，但是没有给出设计方法和设计指标。

国内外研究向火箭发动机注水的主要目的是为了降低火箭发动机噪声，张彬乾等^[3]通过大量试验研究了亚、超音速射流噪声场的分布规律及影响因素，分析了射流噪声源产生的机理，为后面研究射流噪声抑制技术打下了基础；徐悦等^[4]分析了火箭燃气射流噪声的气动特性，利用喷水试验探讨了喷水对火箭发动机点火时燃气的喷水降噪效果以及影响喷水降噪的因素；马宏伟等^[5]对单兵火箭燃气射流噪声进行了实验研究，获得了燃气射流噪声近场的分布规律，同时应用小波变换方法处理燃气射流噪声数据。张磊等^[6]对单兵火箭燃气射流噪声抑制进行了试验研究。Thomas^[7]通过试验验证了喷水能有效地抑制燃气射流噪声，并讨论了影响喷水降噪的关键因素；Kandula^[8-9]对注水抑制噪声进行了试验研究。

1 注水问题假设条件

根据具体问题进行物理假设：

1）发动机尾喷管出口处的压力为常量；

2）射流和射流混合物气体符合理想气体定量，采用理想气体状态方程，气体常数近似一致，且液滴均匀分布在控制体内的气体混合物中；

3）液滴在控制体内的分布均匀；

4）射流中的液滴直径相同；

5）液滴中的温度相同，不存在温度梯度，处于饱和状态即 ${T_{sat}} = 393{\rm{K}}$ ；

6）气体和水的热力学特性与温度无关；

7）水滴的拖拽力和传热相关，通过公式表示；

8）控制体的轴向长度取值为发动机尾喷管直径的2倍，即 $ n = L /{d_j} = 2$ ，确保控制体取在发动机射流中的核心区，发动机射流核心区的长度采用经验公式 $ x_t / d_j = 3.45{\left( {1 + 0.38{M_{je}}} \right)^2}$ 表示，式中 ${M_{je}}$ 为发动机尾喷管气流的Ma数；

9）液滴为刚性球体，不会受气流作用发生变形；

10）忽略辐射热传导作用和由于水的冲击碰撞、破碎消耗的能量。

2 控制方程

根据图2，建立控制界面1和界面2之间的连续方程、动量方程、能量方程和理想气体状态方程：

${\rho _{j1}}{u_{j1}}{A_{j1}} = {\rho _{j2}}{u_{j2}}{A_{j2}} - \eta {\dot m_W}\text{，}$

(1)

${\rho _{j2}}u_{j2}^2{A_{j2}} - {\rho _{j1}}u_{j1}^2{A_{j1}} = - {F_d} + \eta {\dot m_W}{u_p}\text{，}$

(2)

$\begin{split}&{\dot m_{j2}}\left( {{c_{pj}}{T_{j2}}+\frac{{u_{j2}^2}}{2}} \right) =\\ &{\dot m_{j1}}\left( {{c_{pj}}{T_{j1}}+\frac{{u_{j1}^2}}{2}} \right) - {F_d}{u_p}+\eta {\dot m_W}{T_p}{c_{pl}}\text{，}\end{split}$

(3)

${\rho _{j1}}{R_{j1}}{T_{j1}} = {\rho _{j2}}{R_{j2}}{T_{j2}}\text{。}$

(4)

式中： ${\dot m_W}$ 为水沿轴向的质量流率； ${F_d}$ 为液滴拖拽力； ${u_p}$ 为液滴速度； $\eta $ 为蒸发的水质量份数； ${c_{pl}}$ 为液体的比定压热容； ${\dot m_W}$ 为进入燃气流中的水总质量流率； ${\dot m_{Wt}}$ 为水喷嘴喷出的水总质量流率，变量下标1和2 代表控制体两侧侧面。

进入燃气流中的水质量流率和喷水总的质量流率之间的为 ${\dot m_W} = {\dot m_{Wi}}N$ ， $N$ 为喷头数量。

3 控制体两侧的参数比

将质量守恒方程式（1）代入动量守恒方程式（2），通过变换，可以得到控制体两侧射流速度之比：

$\frac{{{u_{j2}}}}{{{u_{j1}}}} = \frac{1}{{1 + \eta \dfrac{{{{\dot m}_W}}}{{{{\dot m}_{j1}}}}}} \cdot \left( {1 - \frac{{{F_d}}}{{{\rho _{j1}}u_{j1}^2{A_{j1}}}} + \frac{{\eta {{\dot m}_W}{u_p}}}{{{\rho _{j1}}u_{j1}^2{A_{j1}}}}} \right)\text{，}$

(5)

式（5）中右侧括号中的第二项可以写作：

$\varphi = \frac{{{F_d}}}{{{\rho _{j1}}u_{j1}^2{A_{j1}}}} = \frac{1}{2}{N_p}{C_D}\frac{{{A_P}}}{{{A_{j1}}}}{\left( {1 - \frac{{{u_p}}}{{{u_{j1}}}}} \right)^2}\text{，}$

(6)

式中， ${C_D}$ 为拖拽系数，拖拽力 ${F_d}$ 表达式为：

${F_d} = \frac{1}{2}{\rho _{j1}}{\left( {{u_{j1}} - {u_p}} \right)^2}{C_D}{A_{PT}}\text{，}$

(7)

${N_p} = \frac{3}{2}\left( {\frac{{\dot m}}{{{{\dot m}_{j1}}}}} \right) \cdot \left( {\frac{{{\rho _{j1}}}}{{{\rho _p}}}} \right) \cdot {\left( {\frac{{{{\rm d}_{j1}}}}{{{{\rm d}_p}}}} \right)^3} \cdot n\left( {1 - \eta } \right)\text{，}$

(8)

将式（5）代入式（4）可以改写为：

$\varphi = \psi \cdot \left( {\frac{{{{\dot m}_W}}}{{{{\dot m}_{j1}}}}} \right)\left( {1 - \eta } \right)\text{，}$

(9)

式中， $\psi = \dfrac{3}{4}n{C_D} \cdot \left( {\dfrac{{{\rho _{j1}}}}{{{\rho _p}}}} \right) \cdot {\left( {\dfrac{{{{\rm d}_{j1}}}}{{{{\rm d}_p}}}} \right)^3}{\left( {\dfrac{{{{\operatorname{Re} }_p}}}{{{{\operatorname{Re} }_{j1}}}}} \right)^2}$ ； ${{Re} _p}$ 为液滴的雷诺数 ${{Re} _p} = \dfrac{{{\rho _{j1}}\left( {{u_{j1}} - {u_p}} \right){{\rm d}_p}}}{{{\mu _{j1}}}}$ ； ${{Re} _{j1}}$ 为燃气流的雷诺数 ${{Re} _{j1}} = \dfrac{{{\rho _{j1}}{u_{j1}}{{\rm d}_{j1}}}}{{{\mu _{j1}}}}$ 。

式（3）中右边括号内第三项可以改写为雷诺数形式表示：

$\frac{{\eta {{\dot m}_W}{u_p}}}{{{\rho _{j1}}u_{j1}^2{A_{j1}}}} = \eta \left( {\frac{{{{\dot m}_W}}}{{{{\dot m}_{j1}}}}} \right)\left[ {1 - \frac{{{{\operatorname{Re} }_p}}}{{{{\operatorname{Re} }_{j1}}}} \cdot \frac{{{{\rm d}_{j1}}}}{{{{\rm d}_p}}}} \right]\text{，}$

(10)

将式（6）和式（8）代入式（3）中可得：

$\begin{split}\frac{{{u_{j2}}}}{{{u_{j1}}}} = &\frac{1}{{1 + \eta \dfrac{{{{\dot m}_W}}}{{{{\dot m}_{j1}}}}}}\left[ {1 - \psi \cdot \left( {\frac{{{{\dot m}_W}}}{{{{\dot m}_{j1}}}}} \right)\left( {1 - \eta } \right)} \right.+ \\ &\left. { \eta \left( {\frac{{{{\dot m}_W}}}{{{{\dot m}_{j1}}}}} \right)\left( {1 - \frac{{{{\operatorname{Re} }_p}}}{{{{\operatorname{Re} }_{j1}}}} \cdot \frac{{{{\rm d}_{j1}}}}{{{{\rm d}_p}}}} \right)} \right]\text{，}\end{split}$

(11)

由能量守恒式（3）和质量守恒式（1），可得到控制体进出口界面上的温度比值：

$\begin{split}\frac{{{T_{j2}}}}{{{T_{j1}}}} =& \frac{1}{{\left( {1 + \eta \dfrac{{{{\dot m}_W}}}{{{{\dot m}_{j1}}}}} \right)}}\left[ {1 + \frac{{u_{j1}^2}}{{2{c_{pj}}{T_{j1}}}} - \frac{{{F_d}{u_p}}}{{{{\dot m}_{j1}}{c_{pj}}{T_{j1}}}}} \right. +\\ &\left. { \frac{{\eta {{\dot m}_W}{T_p}{c_{pl}}}}{{{{\dot m}_{j1}}{c_{pj}}{T_{j1}}}}} \right] - \frac{{u_{j2}^2}}{{2{c_{pj}}{T_{j1}}}}\text{，}\end{split}$

(12)

根据气体等熵方程，可得：

$\frac{{u_{j1}^2}}{{2{c_{pj}}{T_{j1}}}} = \frac{{\gamma - 1}}{2}M_{j1}^2\text{，}$

(13)

$\frac{{u_{j2}^2}}{{2{c_{pj}}{T_{j1}}}} = {\left( {\frac{{{u_{j2}}}}{{{u_{j1}}}}} \right)^2}\left( {\frac{{\gamma - 1}}{2}} \right)M_{j1}^2\text{，}$

(14)

式中， $M_{j1}^{}$ 为超声速气体的当地马赫数 $M_{j1}^{} = \dfrac{{{u_{j1}}}}{{\sqrt {\gamma {\rm{R}}{T_{ji}}} }}$ ，R为气体常数。

将式（6）、式（8）、式（11）和式（12）代入式（10），可得：

$\begin{split}\frac{{{T_{j2}}}}{{{T_{j1}}}} =& \frac{1}{{\left( {1 + \eta \dfrac{{{{\dot m}_W}}}{{{{\dot m}_{j1}}}}} \right)}}\left[ {1 + \frac{{\gamma - 1}}{2}M_{j1}^2 - \psi \cdot \left( {\frac{{{{\dot m}_W}}}{{{{\dot m}_{j1}}}}} \right)\left( {1-\eta } \right)\frac{{{u_{j1}}{u_p}}}{{{c_{pj}}{T_{j1}}}}} \right. +\\ &\left. { \frac{{\eta {{\dot m}_W}{T_p}{c_{pl}}}}{{{{\dot m}_{j1}}{c_{pj}}{T_{j1}}}}} \right] - {\left( {\frac{{{u_{j2}}}}{{{u_{j1}}}}} \right)^2}\left( {\frac{{\gamma - 1}}{2}} \right)M_{j1}^2\text{，}\\[-18pt]\end{split}$

(15)

由理想气体状态方程的假设，可得 $\frac{{{\rho _{j2}}}}{{{\rho _{j1}}}} = \frac{{{T_{j1}}}}{{{T_{j2}}}}$ ，则控制体两侧气体马赫数之比：

$\frac{{M{a_{j2}}}}{{M{a_{j1}}}} = \frac{{\dfrac{{{u_{j2}}}}{{{c_{j2}}}}}}{{\dfrac{{{u_{j1}}}}{{{c_{j1}}}}}} = \frac{{{u_{j2}}}}{{{u_{j1}}}} \cdot \sqrt {\frac{{\gamma R{T_{j1}}}}{{\gamma R{T_{j2}}}}} = \frac{{{u_{j2}}}}{{{u_{j1}}}} \cdot \sqrt {\frac{{{T_{j1}}}}{{{T_{j2}}}}} \text{。}$

(16)

4 方程中的参数计算

式（5）中的拖拽系数与拖拽力成正比，直接影响拖拽力的大小。 ${C_D}$ 是与 ${{Re} _p}$ 数有关的函数，研究表明^[8]，当Re数很小( ${\operatorname{Re} _p} \leqslant 0.1$ )时，粘性力占主导地位，惯性力可以忽略不计，此时的流动为蠕动流，称为Stokes流动，拖拽系数 ${C_D}$ 为： ${C_D} = \dfrac{{24}}{{{{\operatorname{Re} }_p}}}$ ；当 ${{Re} _p}$ 数增大时，惯性力变得越来越重要而不能被忽略，根据不同的 ${{Re} _p}$ 数的使用范围，许多学者提出了相关的经验公式，本项目采用White^[7]提出的采用Spalding拖拽系数修正的公式 ${C_D} = {C_{D0}}\dfrac{1}{{1 + B}}$ ， ${C_{D0}} = \dfrac{{24}}{{{{\operatorname{Re} }_p}}} + \dfrac{6}{{1 + \operatorname{Re} _p^{0.5}}} + 0.4$ ， $B = $ \dfrac{{{h_{fg}}}}{{{C_{pj}}\left( {{T_{j1}} - {T_{sat}}} \right)}}$ ， ${h_{fg}}$ 为水的汽化潜热， ${T_{sat}}$ 为水的饱和温度。

气体传给液滴群的热量为：

${q_g} = \text{π} {N_p}{N_u}k{d_p}\left( {{T_{je}} - {T_p}} \right)\text{，}$

(17)

式中， ${N_p}$ 为液滴数量， ${N_u}$ 为修正Nusselt系数，计算式为 ${N_u} = {N_{u0}}\dfrac{{1 + B}}{B}$ ， ${N_{u0}} = 2 + 0.6\operatorname{Re} _p^{0.5}{\Pr ^{0.33}}$ ， $Pr $ 为Prandtl数，其表达式为 $Pr = \dfrac{{{C_{pl}}{\mu _{pl}}}}{k}$ ， ${C_{pl}}$ 为水的定压比热容， ${\mu _{pl}}$ 为水的粘度系数， $k$ 为水的热传导系数。

注水后液体的汽化部分的吸热量 ${q_p} = \eta {\dot m_w}{h_{fg}}$ ，应和式（15）相等，并考虑雷诺数，可得：

$\frac{1}{\eta } = 1 + \frac{{Pr }}{{{ N}u}} \cdot \frac{{{{{Re} }_{j1}}}}{{{{\left( {\dfrac{{{d_{j1}}}}{{{d_p}}}} \right)}^2}}} \cdot \frac{1}{{\dfrac{3}{2} \cdot \left( {\dfrac{{{\rho _{j1}}}}{{{\rho _p}}}} \right)n}}\left[ {\frac{{{h_{fg}}}}{{{c_{pj}}\left( {{T_{je}} - {T_{sat}}} \right)}}} \right]\text{，}$

(18)

式（16）说明在控制体内，水的汽化蒸发比例与发动机喷出的气体质量流率和注水的质量流率无关。

5 控制体内的不变量

根据雷诺数、式（8）和式（16），令 $C_{1}= $ \dfrac{{Re}_{j 1}}{\left({\rm d}_{j 1} / {\rm d}_{p}\right)^{2}} \cdot \dfrac{1}{\rho_{j 1} / \rho_{p}}$ ， ${C_2} = \dfrac{{{{{Re} }_p}}}{{{{{Re} }_{j1}}}} \cdot \dfrac{{{{\rm d}_{j1}}}}{{{{\rm d}_p}}}$ ， ${C_3} = \dfrac{{{\rho _{j1}}}}{{{\rho _p}}} \cdot {\left( {\dfrac{{{{\rm d}_{j1}}}}{{{{\rm d}_p}}}} \right)^3} \cdot $ \dfrac{{{{{Re} }_p}}}{{{Re} _{j1}^2}}$ ，则这三式的关系是相关的，即存在： ${C_2} = $ {C_1}{C_3}$ 。通过上述三式，可得：

$\frac{d_{j 1}}{d_{p}}=\sqrt{\frac{1}{C_{1}} \cdot \frac{\operatorname{Re}_{j 1}}{\rho_{j 1} / \rho_{p}}}\text{，}$

(19)

$\operatorname{Re}_{p}=C_{2} \frac{\operatorname{Re}_{j 1}}{{\rm d}_{j 1} / {\rm d}_{p}}\text{。}$

(20)

6 算例分析

以某导弹发动机参数为例进行计算分析。发动机燃气射流总温 ${T_0} = 3\;300\;{\rm K}$ ，喷管出口直径为 ${d_{j1}} = 0.2\;{\rm m}$ ，定压比热 ${C_{pj}} = {\rm{1\;773}}{\rm{.5J/}}\left( {{\rm{kg}} \cdot {\rm{K}}} \right)$ ，气体常数 ${{R}} = {\rm{305\;J/}} $ \left( {{\rm{kg}} \cdot {\rm{K}}} \right)$ ，绝热指数 $k = 1.21$ ，定容比热 ${C_{vj}} = 1\;465.7{\rm{J/}} $ \left( {{\rm{kg}} \cdot {\rm{K}}} \right)$ ，燃气流初速为 ${u_{j1}} = 2\;500\;{\rm{m/s}}$ ，喷管出口处气体密度 ${\rho _{j1}} = 0.356\;5\;{\rm{kg/{m^3}}}$ ，喷管喷出的气体质量流率 ${\dot m_{j1}} = 28\;{\rm{kg/s}}$ 。喷管出口燃气流温度 ${T_{j1}} = {T_0} - \dfrac{{u_{j1}^2}}{{2{C_{pj}}}} = $ 1\;538\;{\rm K}$ 。气体粘性系数 $\mu $ 由Sutherland公式确定：

${\mu _{j1}} = {\mu _0}{\left( {\dfrac{{{T_{j1}}}}{{273}}} \right)^{1.5}}\dfrac{{273 + C}}{{{T_{j1}} + C}}\text{。}$

式中： ${\mu _0} = 1.711 \times {10^{ - 5}}\;{\rm N}/{{\rm m}^2}$ ， $C = 122K$ ，经计算可得 ${\mu _{j1}} = 5.444 \times {10^{ - 5}}\;{\rm N}/{{\rm m}^2}$ 。

水的密度为 ${\rho _p} = 1\;000\;{\rm{kg}}/{{| {\rm{m}}}^3}$ ，注水压力在0.6MPa，喷头连接管路的水流速度为5 m/s，喷头通径为35 mm，单个喷头的出水量为4.3 kg/s，假设安装2个喷头，喷入水的速度为 $31.6\;{\rm{m/s}}$ 。水的汽化潜热 ${h_{fg}} = $ 2.256\;6 \times {10^6}\;{\rm{J/kg}}$ ，定压比热容为 ${C_{pl}} = 4\;220\;{\rm{J/kg}}$ ，标准大气压下水的饱和温度为 ${T_{sat}} = 373K$ ，水的热传导系数为 $k = 0.58\;{\rm W}/\left( {{\rm m} \cdot {\rm K}} \right)$ ， ${\mu _{pl}} = 1.01 \times {10^{ - 3}}\;{\rm{Pa }}\cdot {\rm s}$ ，水的温度为 ${T_p} = 293\;{\rm{K}}$ （20 ℃）。

液滴直径在 ${M_{j1}} = 1.45$ 时， ${C_1} = 5$ ， ${C_2} = 0.05$ ， ${{Re} _{j1}} = 1.3 \times {10^6}$ ， ${{Re} _p} = 2.1$ ， ${{\rm d}_{j1}}/{{\rm d}_p} = 3.13 \times {10^4}$ ， $\eta = $ 0.49$ ， ${T_{j1}} = 852K$ ， ${{Re} _p} = 2.1$ ， ${\operatorname{Re} _{j1}} = 31300$ ， $\dfrac{{{u_{j1}} - {u_p}}}{{{u_{j1}}}} = $ \dfrac{1}{{19.6}}$ ，液滴速度为： $\dfrac{{{u_p}}}{{{u_{j1}}}} = 95\% $ 。

本算例中的 ${u_p}$ 取值为喷管出口处燃气射流速度 ${u_{j1}}$ 的95%， ${u_p} = {u_{j1}} \times 0.95 = 2\;375\;{\rm{m/s}}$ 。

一般液滴的直径在 ${10^{ - 6}}\;{\rm m}$ 量级，液滴直径为 ${d_p} = $ 2 \times {10^{ - 6}}\;{\rm m}$ ，则 $\dfrac{{{d_{j1}}}}{{{d_p}}} = \dfrac{{0.2}}{{2 \times {{10}^{ - 6}}}} = 1 \times {10^5}$ 。可计算得到喷入水的蒸发率 $\eta = 73.08{\text{%}} $ ，温度变化关系式为：

$\begin{split}\frac{{{T_{j2}}}}{{{T_{j1}}}} = &\frac{1}{{\left( {1 + \eta \xi } \right)}}{\left[ {2.156 - 2.46 \cdot \xi \left( {1 - \eta } \right) + 0.453\eta \xi } \right]^2} -\\ & 1.156{\left( {\frac{1}{{1 + \eta \xi }}} \right)^2} \cdot \left[ {1 - 1.13\xi \left( {1 - \eta } \right) + 0.95\eta \xi } \right]\text{。}\end{split}$

(21)

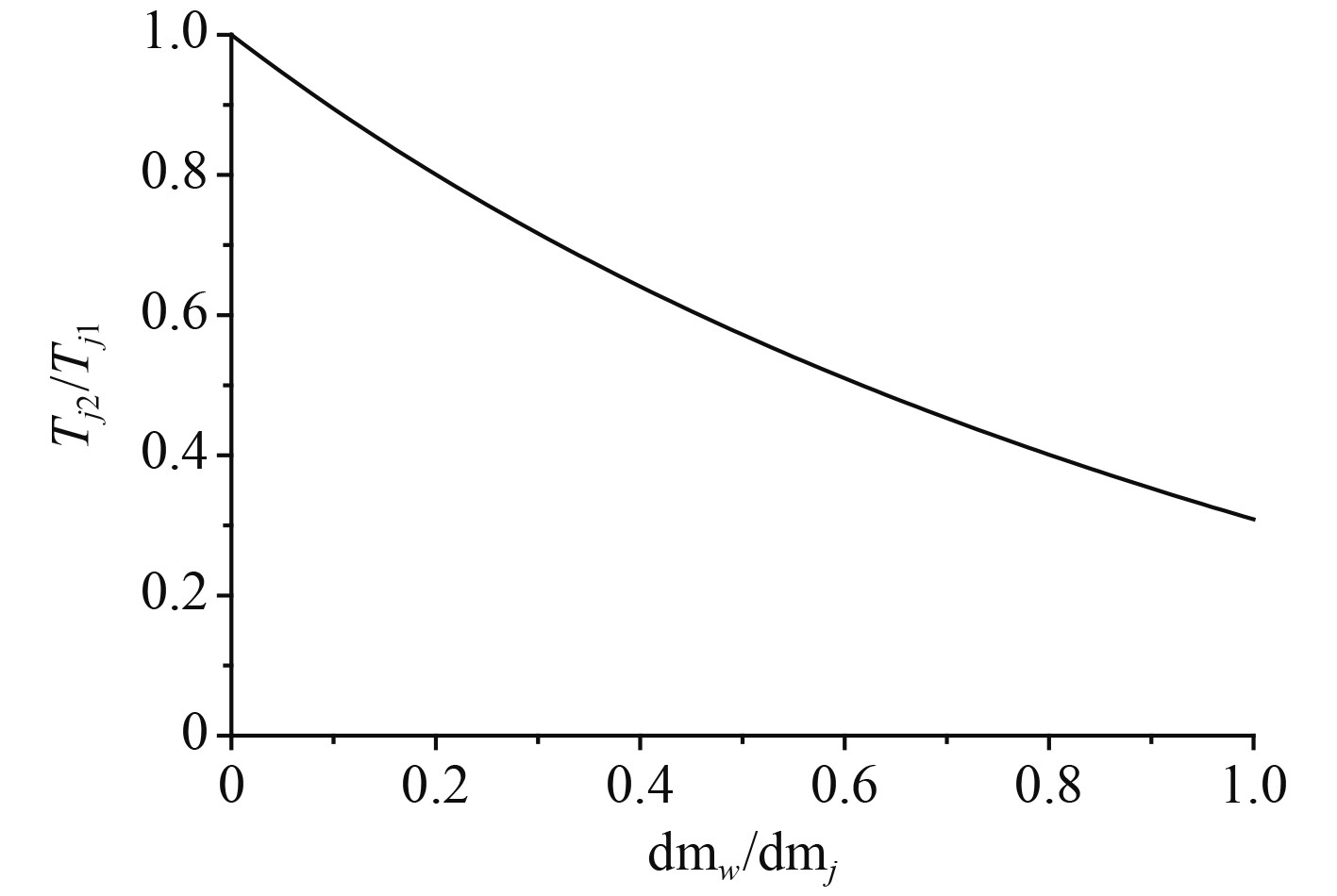
在蒸发量 $\eta = 73.08{\text{%}} $ 的条件下，喷入水的质量流率和燃气流质量流率比值对燃气温度的影响如图3所示。

7 结　语

本文采用参数比拟法，充分考虑了水射流形成的液滴及液滴汽化影响，提出注水量与燃气流场温度的计算方法，并通过算例进行了计算分析。该方法可为注水系统的设计提供理论支持和计算方法。