2. 武警海警总队山东支队青岛大队,山东 青岛 266033
2. Qingdao Brigade, Shandong Branch of the Armed Police Marine Police Corps, Qingdao 266033, China
平台式惯性导航系统是自主式导航系统,能够为舰船精确导航,是现代舰船上不可或缺的重要装备[1-5]。惯性导航系统维保人员必须具备熟练的技能,才能高质量完成导航系统的日常维保、维修操作。由于平台式惯导系统实装操作、维修等训练存在着风险大、成本高、周期长、设备寿命降低等方面的问题,还容易受到气象、海况等条件的限制[6-9]。因此,研制成本较低的平台式惯性导航系统模拟器用于维保人员的训练,可大幅度降低人员训练成本,提高训练效率。通过模拟器对学员进行操作、维修训练和考核,不但可以弥补理论与实践环节在衔接过程中脱节的问题,还可以使学员充分掌握实际操作程序和方法,大大地提高训练效果。模拟器以船用平台式惯导系统为对象,要求具备不亚于实装体验的真实的系统基本操作和常见及特殊故障诊断排除方面的教学、训练以及考核等基本功能,为学员提供真实体验。
轨迹发生器通过对舰船航行轨迹的模拟,可以为惯导模拟器提供惯性测量器件(Inertial Measurement Unit,IMU)的输出,是整个惯导模拟器软件部分的关键。一个能够模拟舰船操舵使用情况下真实航路的轨迹发生器,是实现模拟器后续进行组合导航模式工作,故障检测工作模拟的基础。目前比较常见的轨迹发生器分为:数值式轨迹发生器与解析式轨迹发生器2种。严恭敏等[10]为捷联惯导设计了一种基于数值式轨迹发生器的,通过输入运动时间,运动类型以及所需的加速度,角速度等信息,可以得到相对应的IMU参数,是非常经典的轨迹发生器。文献[11]为更好的对飞行器用的捷联惯导进行仿真,提高仿真精度,根据需要定义运动轨迹特性用以计算轨迹期间载体的速度和角速度变化量,采用数字积分算法的逆过程分步计算轨迹过程中的姿态、位置、速度以及惯性传感器的积分增量等导航参数,取得较好效果。文献[12]从飞机的运动特性出发,根据飞机常见的机动模式,模拟了飞机的俯仰机动、平飞以及协调转弯等情况,利用惯性导航算法对轨迹进行了重构,得到了较为符合飞行实际情况的轨迹与与之对应的IMU参数。文献[13]指出了数值式轨迹发生器会积累误差的问题,导致轨迹发生器精度难以满足高精度导航系统的要求,提出了高精度的全解析式飞行轨迹生成方法。
当前大部分轨迹发生器的研究都是针对捷联惯导与飞行器展开的,对于舰船使用的指北方位平台式惯导的轨迹发生器研究不多。设计一种能够应用于船用指北方位平台式惯导模拟器的轨迹发生器是一个亟待解决的问题。本文将基于舰船航行的实际,结合指北方位平台式惯导的特点,为模拟器设计一种解析式轨迹发生器软件,操作人员只需要设置起点与终点,以及必要的参数就可以生成与之相对应的轨迹以及IMU参数。在实验部分,通过在模拟器中设置位置点生成IMU参数并通过惯导解算模块得到惯导自主、组合模式下的导航参数,证明设计方法的有效性。
1 解析式轨迹方程舰船在大海中航行不同于飞机,不但运动速度相比于飞机较慢,加速度也难以达到较大数值,而且也无法像飞机一样在较短的时间内完成转弯等大航向改变的机动,也不存在较大幅度无规律的纵横摇。因此,在轨迹发生器的设计时,整个航行轨迹以直线航行为主,若遇到起点与终点航向不一致的情况,则进行转向机动以调整舰船的航向。这样就将整个轨迹分解为了匀速直线运动,匀变速直线运动与匀速圆周运动3种情况的组合。因此,只需要规定每一小段中的起点与终点,运动时间以及必要的运动参数就可以生成相对应的轨迹方程。下面将对这3种运动模式的模型进行介绍。各式中,为纬度
匀速直线运动是舰船航行过程中最为常见的一种航行模式,通常的经济航速为10~20 kn,为了提高轨迹发生器的精度,不能将地球表面认为是平面,使用平面上的两点间距离公式,而是使用球面的距离公式
| $s=R \cdot \arccos [cos{\lambda _0}\cos {\lambda _1}\cos ({L_0}-{L_1})+\sin {\lambda _0}\sin {\lambda _1}]\text{。}$ | (1) |
式中:
为了降低对轨迹设置的要求,防止出现无法在设置时间内从起点到达终点导致轨迹发生器出现错误的情况,选择通过操作人员输入起始点,根据式(1)计算的距离与前段轨迹结束时的速度,后台计算运动时间,根据式
通过航向对合速度进行分解可以得到东向与北向速度。
| $\left\{\begin{array}{l}L\left(t^{\prime}\right)=L_{0}+\left(L_{1}-L_{0}\right) t /\left(t^{\prime}\right) ,\\ \lambda\left(t^{\prime}\right)=\lambda_{0}+\left(\lambda_{1}-\lambda_{0}\right) t /\left(t^{\prime}\right){\text{。}}\end{array}\right.$ | (2) |
式中:
这样就实现通过输入起点坐标为
与匀速直线运动类似,为防止出现由于设置匀变速运动时间与设置的起止点的距离不合理,使得加速度过大导致失真的问题。在匀变速直线运动模型中,通过设置加速度大小的方式来求解速度与运动时间。
根据
| $\left\{\begin{array}{l} L(t') = {v_{L0}}{t'} + \dfrac{1}{2}a{t^{'2}} , \\ \lambda (t') = {v_{\lambda 0}}{t'} + \dfrac{1}{2}a{t^{'2}} ,\\ v(t') = {v_0} + at' {\text{。}} \\ \end{array} \right.$ | (3) |
式中:
这样就实现通过输入起点坐标为
舰船的圆周运动主要有2种情况,一种情况是由于地形或者航线要求等原因需要圆周运动或者通过圆周运动进行避障,另一种是由于航向的改变,需要通过一定圆心角的圆周运动来调整。
1)匀速圆周机动
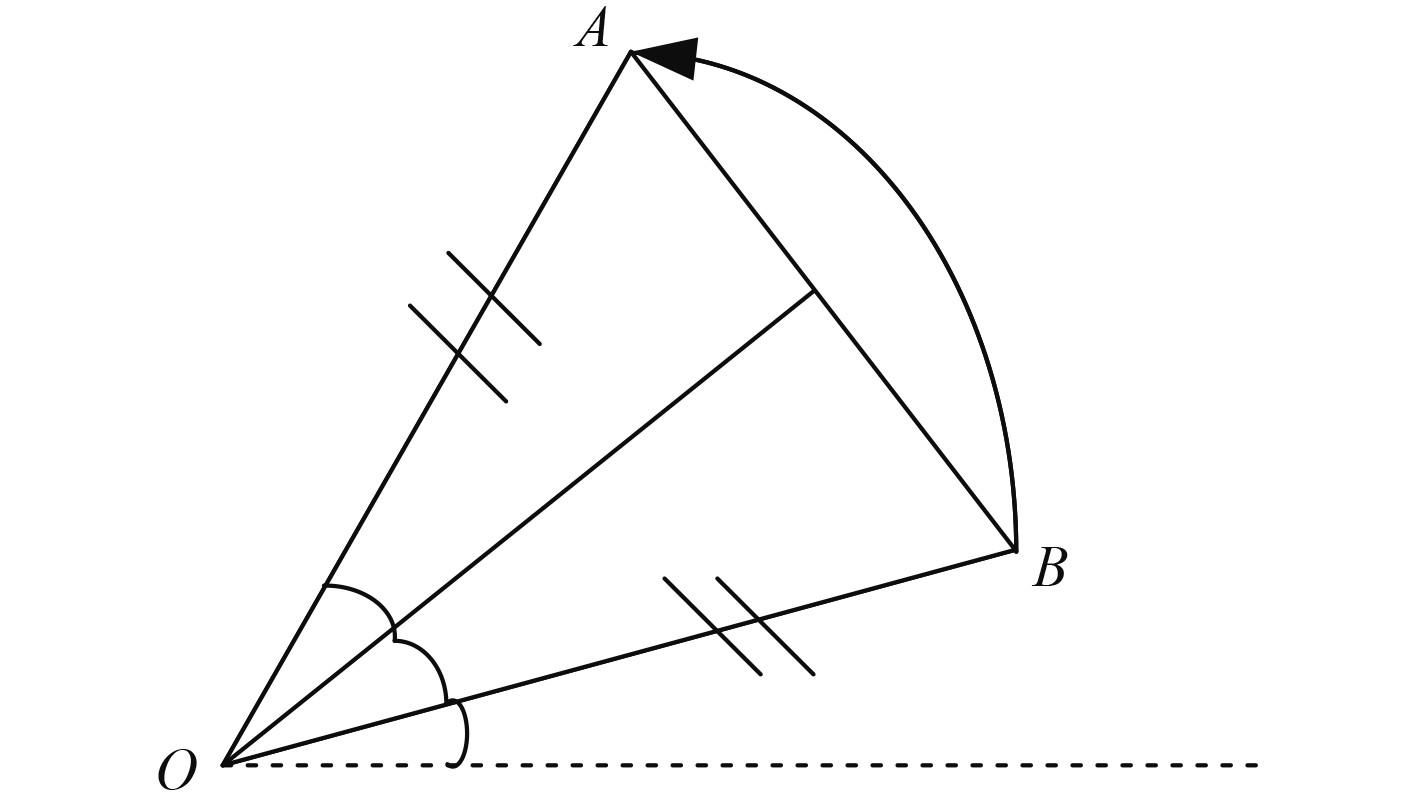
匀速圆周机动将轨迹起止点作为圆弧的起止点,由起点航向与起止点位置计算相关参数。由几何关系可以知道,圆心一定位于起点
|
图 1 匀速圆周机动几何关系示意图 Fig. 1 Geometric relationship of uniform circular motion |
图中,B点与A点是圆周运动的起始点,O点为根据起始点位置推算出的圆心位置。根据等腰三角形的性质与圆的几何性质,可以得到相对应的解析式方程。
| $\left\{\begin{array}{l} L({t'}) = {L_2} + r\sin [\omega ({t'}) + \alpha ] ,\\ \lambda ({t'}) = {\lambda _2} + r\cos [\omega ({t'}) + \alpha ]/cos({L_1}) ,\\ \omega = \dfrac{v}{r} ,\\ t =\dfrac{{\alpha r}}{\omega } {\text{。}} \end{array} \right.$ | (4) |
这样就实现通过输入起点坐标为
2)调整航向的匀速圆周运动
调整航向的匀速圆周运动与圆周运动类似,只是圆周运动的起始点不是轨迹的起止点。此外,根据经验以及方便简化计算,调整航向的圆周运动设计转弯半径
| $\alpha = \left\{ \begin{array}{l} \left| {\left| {\arctan ({K_1})} \right| - \left| {\arctan ({K_2})} \right|} \right|,{K_1}*{K_2} < 0 , \\ \left| {\left| {\arctan ({K_1})} \right| + \left| {\arctan ({K_2})} \right|} \right|,{K_1}*{K_2} > 0 {\text{。}}\\ \end{array} \right.$ | (5) |
对于转弯的起止点问题,起点即位于
|
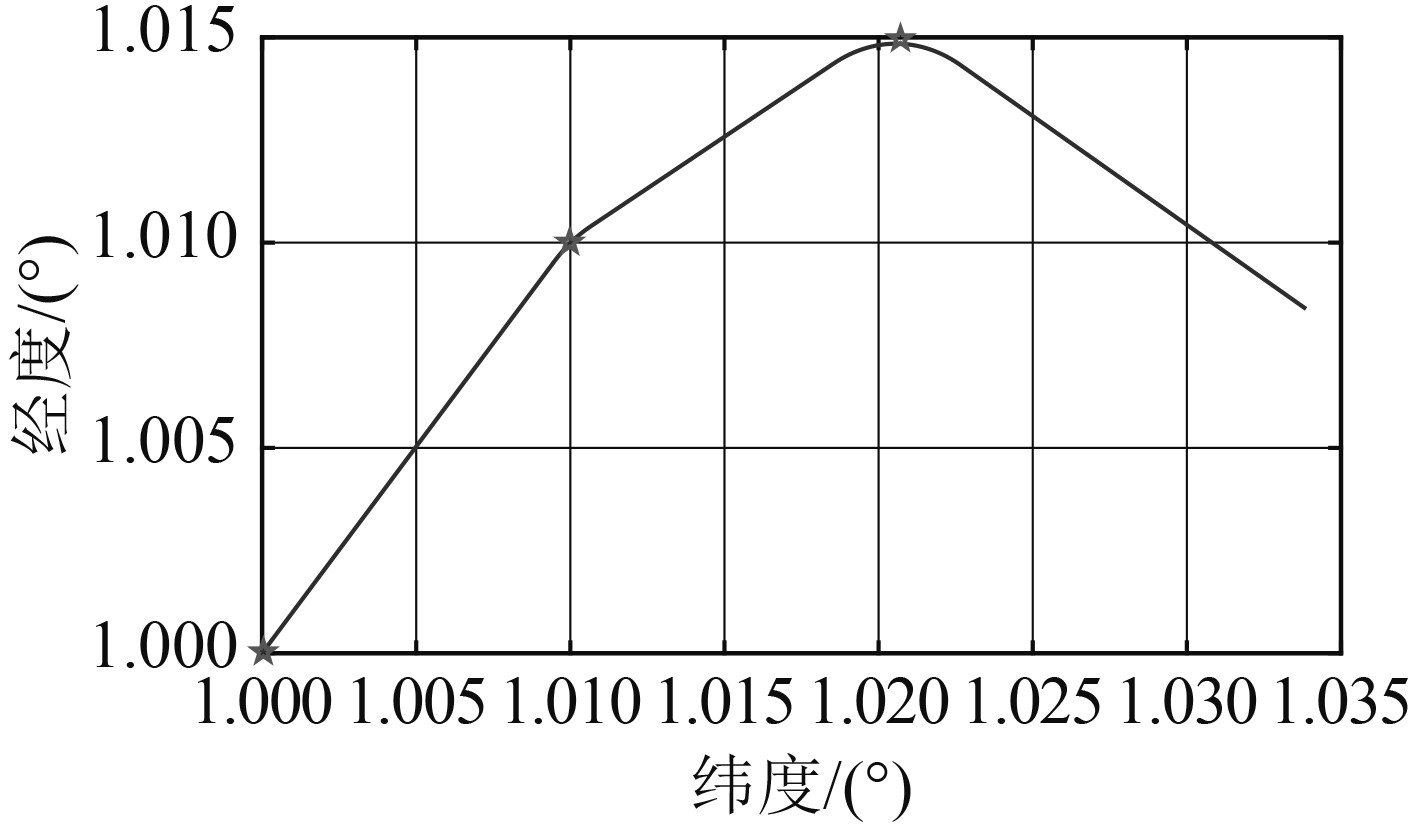
图 2 调整航向的匀速圆周运动轨迹 Fig. 2 Uniform circular motion track of course adjustment |
图中星点为给出的轨迹点,可以清楚看到,在点(1.01,1.01)与(1.022,1.015)处,由于轨迹点导致的航向调整,使得轨迹在十分逼近轨迹点的位置有一个转弯,使得航向调整得到轨迹下一点的航向。
这样,对于复杂海洋中航行的舰船的轨迹规划,就可以分解为以上几种解析式方程的组合。
2 IMU参数计算轨迹发生器除了具有航路规划的作用,在平台式惯导模拟器中,由于平台式惯导模拟器并不存在陀螺仪和加速度计,还有一项重要的作用就是模拟IMU的输出。无论是惯导的对准、解算、组合都需要IMU的参数作为基础。因此,在轨迹发生器的设计中,除了要给出轨迹的解析式方程,还需要给出与之相对应的IMU参数计算方法。指北方位平台式惯导由3个单自由度积分陀螺仪作为平台角运动敏感控制元件,从而使得平台系跟踪地理系。平台上还安装有东向、北向加速度计。
2.1 加速度计算惯导的解算是通过加速度计测得的比力,通过积分得到速度与位置。轨迹发生器为了能够生成东向与北向的加速度计参数,需要对速度与位置微分得到相对应的比力,下面给出东向与北向的加速度计算方法。
首先得到速度的计算公式如下:
| $\left\{ \begin{array}{l} {v_E} = \dot \lambda {R_N}\cos L ,\\ {v_N} = \dot L{R_M} , \\ \end{array} \right.$ | (6) |
式中:
这样通过对速度进行微分就可以计算出加速度计提供的不含加速度计零偏的输出信息:
| $\left\{ \begin{array}{l} {a_E} = \dot v_E^{} - \left(2{\omega _{ie}}\operatorname{sin}L + \dfrac{{v_E^{}}}{{{R_N}}}\tan { L}\right)v_N^{} ,\\ {a_N} = \dot v_N^{} + \left(2{\omega _{ie}}\operatorname{sin}L + \dfrac{{v_E^{}}}{{{R_N}}}\tan { L}\right)v_E^{} {\text{。}}\\ \end{array} \right.$ | (7) |
式中:
捷联式惯导通过计算
航向角:
| $ \psi =\left\{ \begin{array}{l} arctg({v}_{E}/{v}_{N}),{v}_{N}>0且{v}_{E}>0,\\ 2\pi +arctg({v}_{E}/{v}_{N}),{v}_{N}>0且{v}_{E}<0,\\ \pi +arctg({v}_{E}/{v}_{N}),{v}_{N}<0{\text{。}}\end{array}\right.$ | (8) |
为了更真实模拟船用指北方位平台式惯导的情况,加入符合正弦曲线的横摇,以模拟海浪的舰船姿态上的作用与影响。
3 实验分析为检验轨迹发生器设计的合理性与实用性。现将设计的船用解析式轨迹发生器嵌入到指北方位平台式惯导模拟器软件系统中。
通过对该软件系统输入参数,就可以让操作人员实现对某型船用指北方位平台式惯导的操作,维护与故障诊断方面的训练。
根据设置的位置点,轨迹发生器生成相对应的轨迹与轨迹相对应的加速度计输出信息以及姿态角信息。以此为基础,通过惯导解算模块,输出舰船的实时姿态,位置与速度。
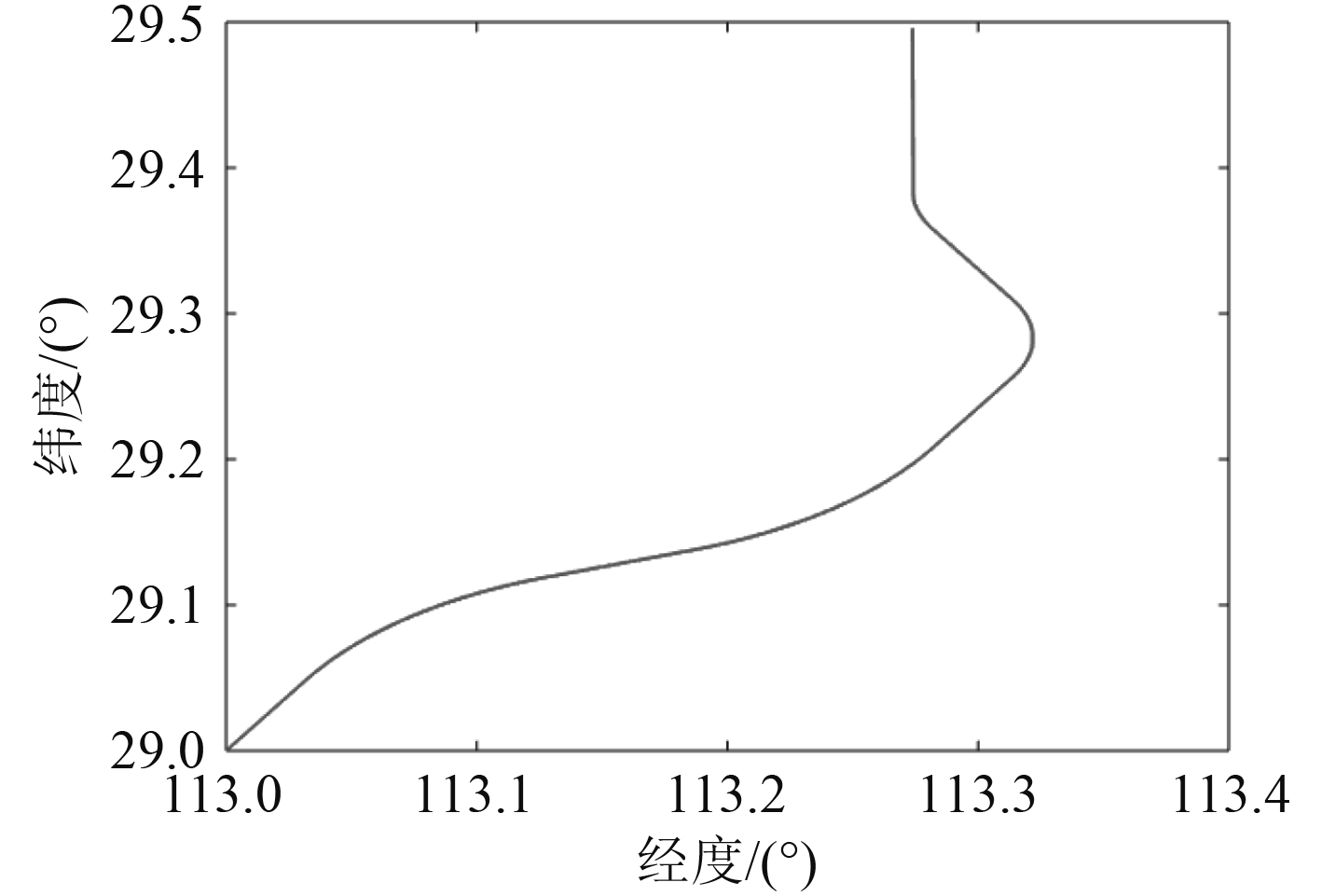
图3为通过设置几个位置坐标,并选择航行模式由船用指北方位平台式惯导模拟器中的轨迹发生器生成的一段航行轨迹,模拟从武汉长江出发的航行,为了更有效说明轨迹发生器设计的有效性,在轨迹点的设计与选取中,要求轨迹尽可能的复杂,包含多种情况。输入的几个坐标位置是(29°,113°),(29.04°,113.06°),(29.12°,113.13°),(29.15°,113.21°),(29.17°,113.28°),(29.27°,113.34°),(29.36°,113.28°),(29.49°,113.28°)。其中在(29°,113°)至(29.04°,113.06°)设置为匀加速直线运动,将航速从0加速至12 kn。(29.04°,113.06°)至(29.12°,113.13°)设置为匀速圆周运动模拟长江地理流向。(29.12°,113.13°)至(29.15°,113.21°)为匀速直线运动,(29.15°,113.21°)至(29.17°,113.28°)段为匀速圆周运动。(29.17°,113.28°)至(29.27°,113.34°)至(29.36°,113.28°)至(29.49°,113.28°)是2.3节中提到的需要调整航向而进行匀速圆周运动匀速直线运动的情况,以此为依据生成IMU参数。
|
图 3 轨迹发生器生成轨迹 Fig. 3 Track generator generating track |
在自主工作模式下,某型平台式惯导的陀螺漂移为0.003°/h,加速度计零偏为0.005 g,输出频率100 Hz。在组合工作模式下,加入GPS系统组成组合导航系统,输出频率为10 Hz,水平位置误差<10 m,采用松组合的方式,使用卡尔曼滤波进行计算。噪声设置如下:
| $ \begin{cases}{\boldsymbol{P}_0} = {\rm{diag}}\left( {\left[ {{\boldsymbol{P}_{{q_0}}};{\boldsymbol{P}_{{v_0}}};{\boldsymbol{P}_{{p_0}}};{\boldsymbol{P}_{{\varepsilon _0}}}} \right]} \right),\\ {\boldsymbol{P}_{{q_0}}} = {[3.0462{e^{ - 4}},3.0462{e^{ - 4}},3.0462{e^{ - 4}}]^{\rm{T}}},\\ {\boldsymbol{P}_{{v_0}}} = {[0.01,0.01]^{\rm{T}}},\\ {\boldsymbol{P}_{{p_0}}} = {[2.4582{e^{ - 14}},2.4582{e^{ - 14}}]^{\rm{T}}},\\ {\boldsymbol{P}_{{\varepsilon _0}}} = {[2.3504{e^{ - 11}},2.3504{e^{ - 11}},2.3504{e^{ - 11}}]^{\rm{T}}}, \end{cases}$ | (9) |
| ${\boldsymbol{Q}_0}{\rm{ = }}{\rm{diag}}{\left( {\left[ {0.001;0.001;0.1;0.1} \right]} \right)^2},$ | (10) |
| $\begin{cases}{\boldsymbol{R}_0} = {\rm{diag}}{\left( {\left[ {{\boldsymbol{R}_{{v_0}}};{\boldsymbol{R}_{{p_0}}}} \right]} \right)^2},\\ {\boldsymbol{R}_{{v_0}}} = {[0.001,0.001]^{\rm{T}}},\\ {\boldsymbol{R}_{{p_0}}} = {\left[2.4582{e^{ - 14}},2.4582{e^{ - 14}}\right]^{\rm{T}}}{\text{。}} \end{cases}$ | (11) |
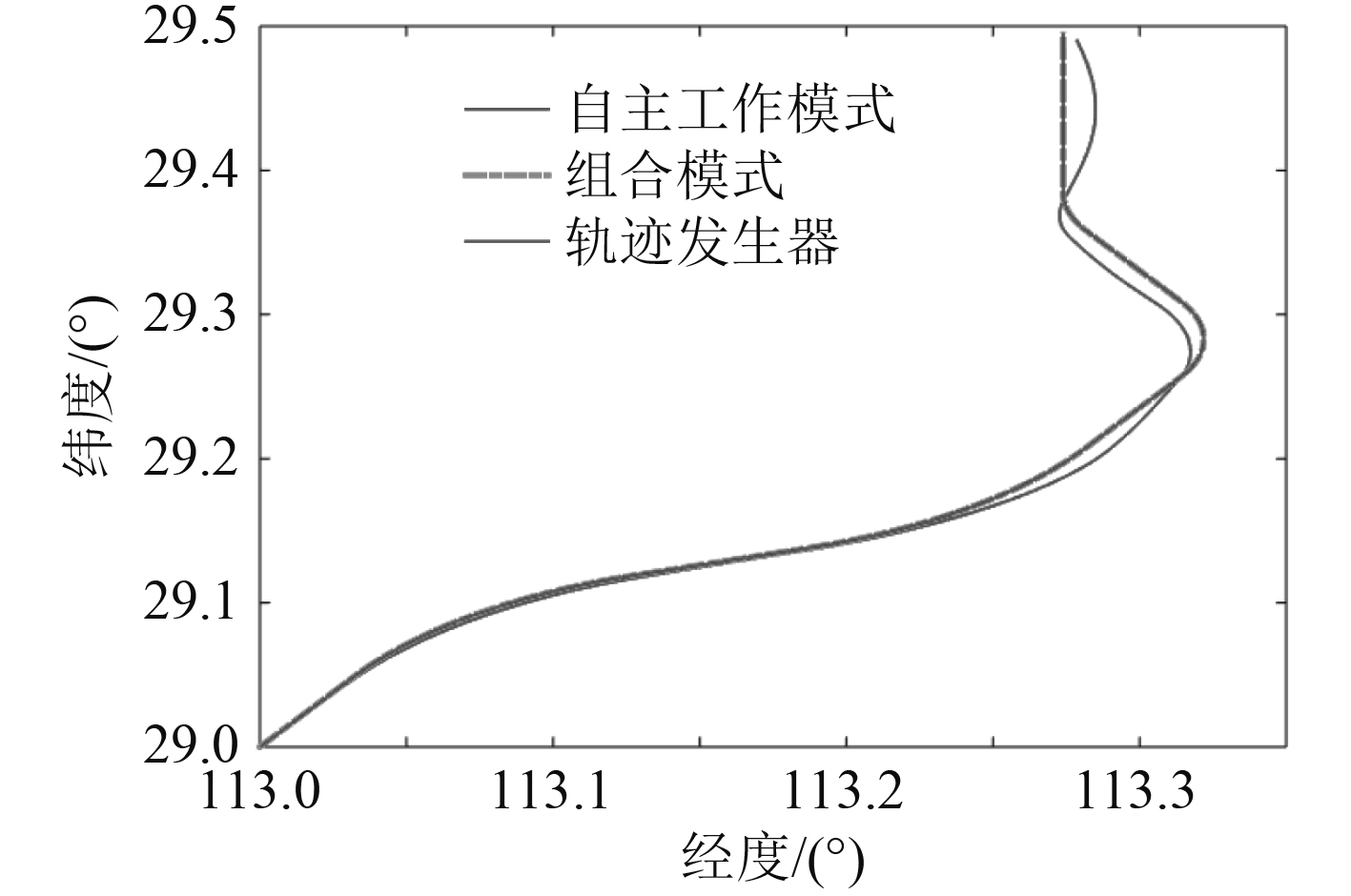
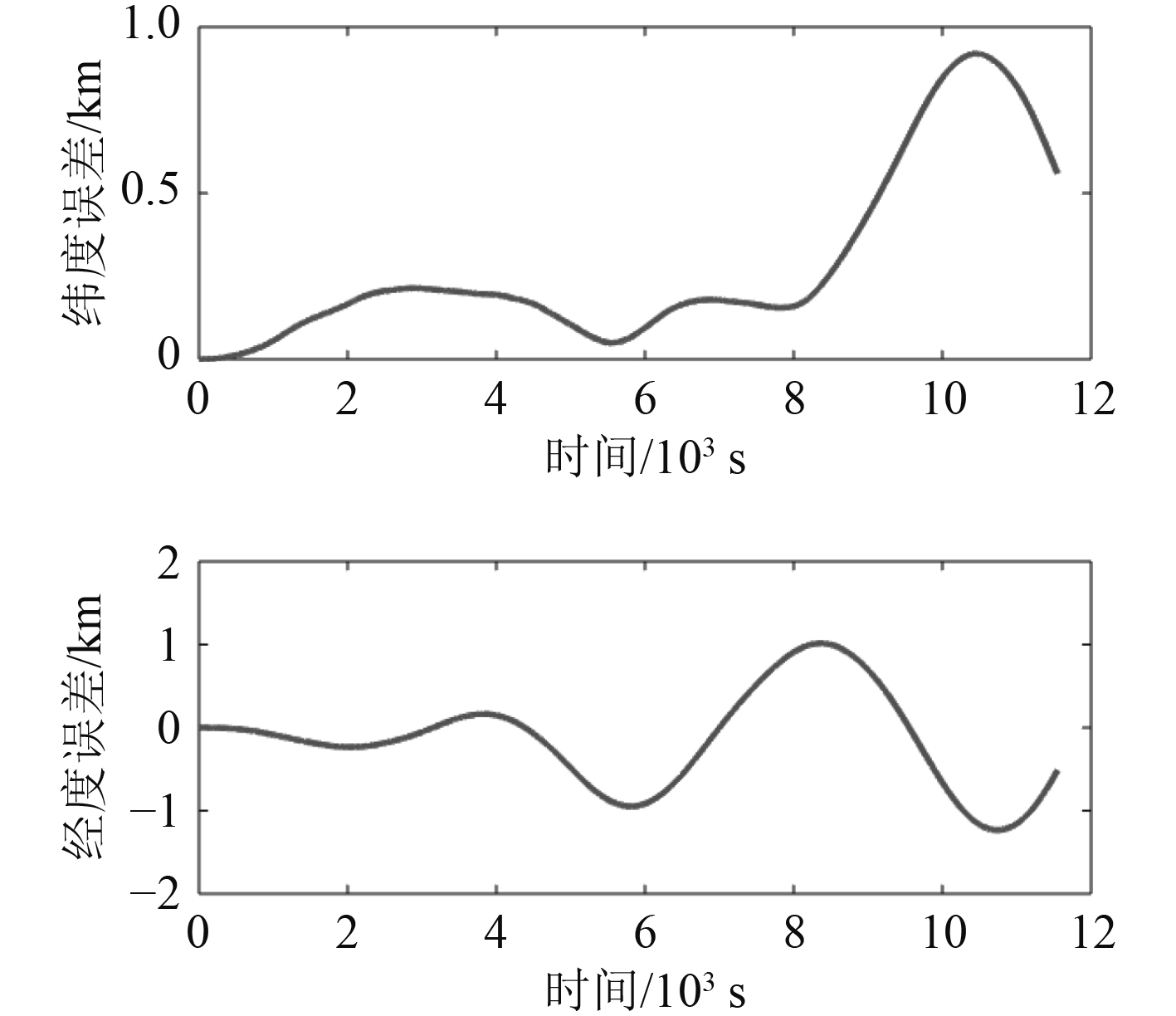
自主工作模式,组合工作模式与轨迹发生器的轨迹图像如图4所示。可以看到组合模式与轨迹发生器的轨迹基本重合,自主工作模式由于陀螺仪与加速度计的漂移与零偏使得在全程11 550 s的航行中出现了一定程度的发散,而组合工作模式通过引入GPS作为外部观测量,较好校正了平台式惯导的误差。为了便于更加准确的观察、分析与对比,图5和图6分别为自主、组合工作模式下的经纬度误差可以看到自主工作模式下的位置误差高达几百米甚至上千米,而组合导航的位置精度只有几米,仿真结果符合实际,证明了轨迹发生器设计的合理性。
|
图 4 三种模式生成轨迹示意图 Fig. 4 Three modes to generate trace diagram |
|
图 5 自主工作模式下的位置误差 Fig. 5 Position error in autonomous mode |

|
图 6 组合工作模式下的位置误差 Fig. 6 Position error in integrated navigation mode |
本文对船用指北平台式惯导模拟器中轨迹发生器进行了设计。基于舰船航行的实际,结合指北方位平台式惯导的特点,为模拟器设计一种解析式轨迹发生器软件,操作人员只需要设置起点与终点以及必要的运动参量,就可以符合要求的轨迹以及IMU参数,并通过仿真实验验证了算法设计的有效性。
| [1] |
牛其虎. 平台式惯导系统模拟器的设计及实现[D]. 哈尔滨: 哈尔滨工程大学, 2006.
|
| [2] |
张崇猛, 蔡智渊, 舒东亮, 等. 船舶惯性导航技术应用与展望[J]. 舰船科学技术, 2012, 34(6): 3-8. ZHANG Chong-meng, CAI Zhi-yuan, Shu Dong-liang, et al. Application and Prospect of ship inertial navigation technology[J]. Ship Science and Technology, 2012, 34(6): 3-8. DOI:10.3404/j.issn.1672-7649.2012.04.001 |
| [3] |
张宗麟. 惯性导航与组合导航[M]. 北京: 航空工业出版社, 2000.
|
| [4] |
梁德厚. 船舶INS/NSAP组合导航系统的设计及实现[J]. 舰船科学技术, 2017(10): 40-42. LIANG De-hou. Design and implementation of INS / NSAP integrated navigation system for ships[J]. Ship Science and Technology, 2017(10): 40-42. DOI:10.3404/j.issn.1672-7649.2017.10.007 |
| [5] |
赵现强. 平台式陆用惯性导航系统中控制回路的设计及实现[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
| [6] |
王慧婷, 陶靖. 捷联惯导系统软件模拟器研究[J]. 电子质量, 2018(7): 15-17. DOI:10.3969/j.issn.1003-0107.2018.07.005 |
| [7] |
乔海岩, 可伟, 姚廷伟. 舰船及舰载导弹运动轨迹模拟器设计[J]. 舰船科学技术, 2012, 34(12). QIAO Hai-yan, KE Wei, Yao Ting-wei. Design of motion track simulator for ship and shipborne missile[J]. Ship Science and Technology, 2012, 34(12). DOI:10.3404/j.issn.1672-7649.2012.12.031 |
| [8] |
卢建华, 吴晓男, 吴光彬. 某型飞机惯性导航系统模拟器软件设计[J]. 仪表技术, 2009(11): 7-9. LU Jian-hua, WU Xiao-nan, WU Guang-bin. Software design of an aircraft inertial navigation system simulator[J]. Instrument technology, 2009(11): 7-9. |
| [9] |
魏建仁. 平台式惯性导航系统模拟器的设计与实现[D]. 哈尔滨: 哈尔滨工程大学, 2009. WEI Jian-ren. Design and implementation of platform inertial navigation system simulator[D]. Harbin: Harbin Engineering University, 2009. |
| [10] |
严恭敏, 周馨怡. 基于实测轨迹的高精度捷联惯导模拟器[J]. 导航定位学报, 2015, 3(4): 27-31+37. YAN Gong-min, ZHOU Xin-yi. High precision sins simulator based on measured trajectory[J]. Journal of navigation and positioning, 2015, 3(4): 27-31+37. |
| [11] |
翟昆朋, 何文涛, 徐建华, 等. 捷联式惯性导航系统轨迹发生器设计与仿真[J]. 计算机仿真, 2013, 30(11): 58-61+181. DOI:10.3969/j.issn.1006-9348.2013.11.014 |
| [12] |
赵坤. 飞机轨迹发生器的设计与仿真[C]. 中国高科技产业化研究会智能信息处理产业化分会、中国高科技产业化研究会信号处理专家委员会: 中国高科技产业化研究会, 2014: 5.
|
| [13] |
李建文, 黄国荣, 张宗麟. 基于解析式轨迹的捷联惯导系统仿真研究[J]. 弹箭与制导学报, 2005(S4): 311-313. LI Jian-wen, BEN Guo-rong, ZHANG Zong-lin. Simulation of SINS based on analytic trajectory[J]. Journal of missile and guidance, 2005(S4): 311-313. |
 2021, Vol. 43
2021, Vol. 43
