2. 海军装备部装备项目管理中心,北京 100102
2. Naval Equipment Project Management Center, Beijing 100102, China
目标是雷达要检测的对象,也就是雷达所关心的物体。目标建模的方式有多种,根据现有雷达目标数据仿真领域,目标数据生成算法总体可以分为两类:数据级生成算法和信号级生成算法[1]。
信号级算法仿真逼真度较高,基本与实装一致。但是信号级算法需要的数据复杂度和计算量大,计算资源和成本高,相当于制造一个雷达样机,且该算法各参数和后期信号处理相关性强,后期可扩展性有限,且需要收集该型号装备真实参数数据并使用到模型当中。数据级生成算法从现象上模拟目标数据,所需计算资源和成本相对较低。尽管目标图像与实际有一定差距,但能达到训练所需的特定逼真度,同时,该算法不支持相应的数据处理。
本文采用全要素雷达目标建模算法,从雷达原理模型上实现目标数据生成。其原理是根据目标自有特性和雷达工作参数计算目标基础回波幅度,考虑天线水平方向波束、脉压波形对目标回波的动态影响,计算目标在脉冲间的相位变化,获取目标的IQ数据,将各数据进行叠加混合得出目标实际探测回波幅度。由于可以通过参数配置、基础数据替代等方式实现快速扩展,通过雷达参数配置化、数据化、可替换等特点,可以实现不同类型雷达目标的生成,这是信号级算法无法达到的优势。
1 目标特征要素对目标模型的影响目标自有特征是以目标本身状态为主要因素的特征[2-3],这些特征影响目标在雷达上的处理和显示效果,主要特征因素如表1所示。
|
|
表 1 目标自有特征及对目标仿真的影响 Tab.1 The target has its own characteristics and influence on the target simulation |
RCS决定目标反射截面积的统计特性,是监测周期间的平均值,相同条件下RCS大的目标反射回波强,显示幅度强,更容易被检测;反之,RCS小的目标反射回波弱,显示幅度弱,更难被检测。
RCS的大小受目标形状的反射方向性、目标体材质的反射率、雷达电磁波的波长影响,其中目标形状的反射方向性在目标运动改变方向、改变姿态过程,电磁波反射方向变化较大,导致在扫描周期内,同一目标的RCS值是不相同的。在模拟目标RCS过程中,采用估计平均值的方法来描述RCS值大小。
在目标模型仿真过程中,需要考虑雷达探测目标的RCS起伏[4]。为了使目标模拟仿真和实装实现一致,同时考虑工程的实现,就必须使用一个合理的概率模型来估计目标RCS起伏的影响。
目前通常使用的目标起伏模型是施威林(Swerling)模型,这种起伏模型有SwerlingI型、SwerlingⅡ型、SwerlingⅢ型和SwerlingⅣ型4种类型。4种起伏模型对应的概率分布与相关情况如表2所示。
|
|
表 2 起伏模型 Tab.2 Ups and downs model |
Swerling的4种模型考虑的是两类极端情况:扫描间独立和脉冲间独立。从实际情况分析,目标起伏特性在2种情况之间。目前已证明,其检测性能也介于两者之间。
由于雷达关注的主要是空中目标和海上目标,一般为由物理尺寸相同的许多独立起伏点散射体所构成的复杂目标,根据工程经验,一般采用SwerlingI模型。
2 雷达体制要素对目标模型的影响 2.1 有效辐射功率有效辐射功率(P)由雷达天线增益(发射Gt、接收Gr)、发射机的辐射峰值功率(Pt)、馈线系统的损耗和脉冲宽度共同决定[5]。其相互关系如下式:
| $ P=\frac{{P}_{t}{G}_{t}{G}_{r}\tau }{L} {\text{。}}$ | (1) |
雷达威力与
雷达接收机内部噪声会影响到雷达接收的回波信号[6]。为描述这种影响,出现了接收机噪声系数这一概念,接收机噪声系数F定义为:
| $ F=\frac{{N}_{o}}{{N}_{i}{G}_{a}}=\frac{{S}_{i}/{N}_{i}}{{S}_{i}{G}_{a}/{N}_{o}}=\frac{{\left(SNR\right)}_{i}}{{\left(SNR\right)}_{o}}\text{。}$ | (2) |
式中:
| $ {S}_{i}=k{T}_{0}BF{\left(SNR\right)}_{o} \text{。}$ | (3) |
若雷达的检测门限设置为最小输出信噪比
| $ {S}_{\min}=k{T}_{0}BF{\left(SNR\right)}_{o\min} ,$ | (4) |
雷达探测的最大距离可表示为:
| ${R_{\max }} = {\left[ {\frac{{{P_t}\sigma A_r^2}}{{4{\text{π}} {\lambda ^2}k{T_0}BFL{{(SNR)}_{o\min }}}}} \right]^{1/4}}{\text{。}}$ | (5) |
可见,雷达的最大作用距离与
天线方向图即天线在各方位的增益曲线,天线方向图决定了目标回波功率上的起伏特征,当天线增益越大时,天线波束越窄;反之当天线增益越小时,天线波束越宽。当天线波束较宽时,落在天线波束内的面杂波(海杂波)面积则越大,因此杂波回波功率就越强,目标检测所需要的改善因子则越高。
2.4 脉冲描述字脉冲描述字影响脉冲压缩效果,脉冲描述字主要包括:带宽、脉宽和波形。
对于线性调频,LFM信号复数表达式为:
| $ {S}_{LFM}\left(t\right)=u\left(t\right){e}^{j2{\text{π}} {f}_{0}t}=A\cdot rect\left(\frac{t}{\tau }\right){e}^{j2{\text{π}} \left({f}_{0}t+\frac{1}{2}\mu {t}^{2}\right)} \text{。}$ | (6) |
式中:τ为脉冲宽度;μ=B/τ为信号瞬时频率的变化斜率;B是信号带宽;
在脉冲宽度内,信号的角频率由
通过理论分析,匹配滤波器在雷达装备中,其传输特性可以表示为:
| $ H\left(w\right)=K{S}^{*}\left(w\right){e}^{-jw{t}_{0}} \text{。}$ | (7) |
其中:K为幅度归一化常数;
| $ h\left(t\right)=K{S}^{*}\left({t}_{0}-t\right) \text{。}$ | (8) |
频域数字脉冲压缩处理实现的原理是对回波数字信号x(n)和单位脉冲响应h(n)作变换运算,如图1所示。

|
图 1 频域数字脉冲压缩DFT原理框图 Fig. 1 Schematic diagram of frequency domain digital pulse compression |
分别设N,M为回波数字信号x(n)和匹配滤波器的单位脉冲响应h(n)的长度,根据DFT的循环卷积定理,x(n)和h(n)的N点圆周卷积为:
| $ DFT\left\{\left[x\left(n\right)\otimes h\left(n\right)\right]\right\}=DFT\left[x\left(n\right)\right]\times DFT\left[h\left(n\right)\right]\text{。} $ | (9) |
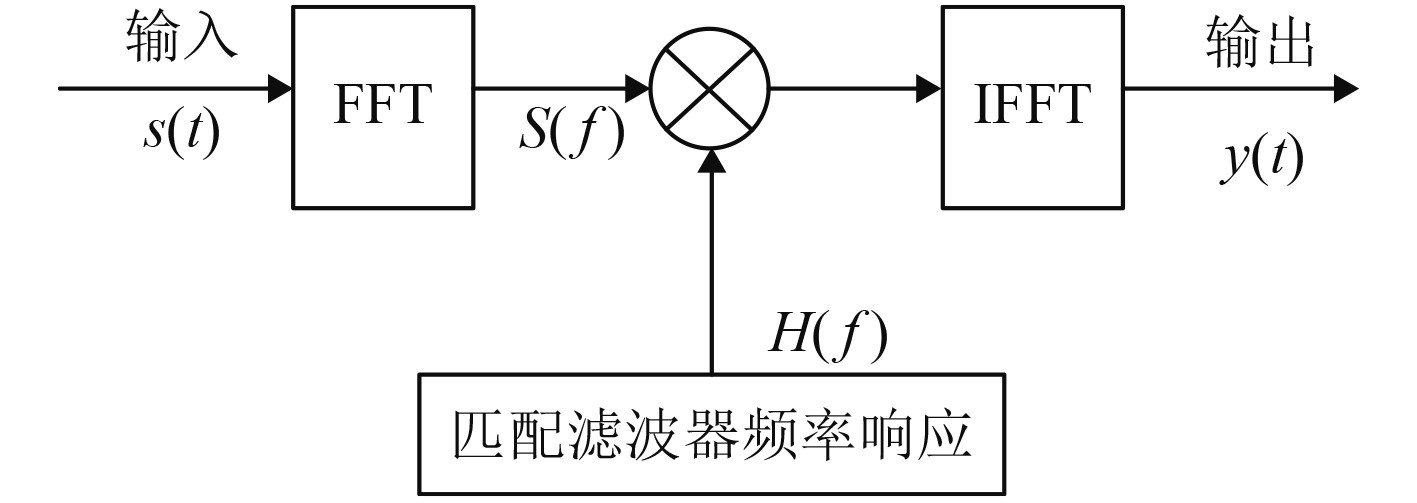
在工程中用应用广泛的还是频域进行脉冲压缩处理的方法,如图2和式(10)所示。
|
图 2 数字频域脉冲压缩原理图 Fig. 2 Schematic diagram of digital frequency domain pulse compression |
| $\left\{ {\begin{array}{l} {FFT\left[ {x(n) \otimes h(n)} \right] = FFT[x(n)] \times FFT[h(n)]} ,\\ {y(n) = IFFT\{ FFT[x(n)] \times FFT[h(n)]\} = IFFT}, \\ [X(f) \times H(f)] {\text{。}} \end{array}} \right.$ | (10) |
假设带宽为0.3 MHz,脉宽为1 ms,中心频率不定,重复周期1 μs,汉明窗加权系数,对应的脉压波形如图3所示。

|
图 3 带宽0.3MHz脉压波形图 Fig. 3 Bandwidth 0.3 MHz pulse pressure waveform |
改善因子是指杂波抑制滤波器输出端与输入端信杂比的比值:
| $ I=\frac{{S}_{o}/{C}_{o}}{{S}_{i}/{C}_{i}}=\frac{{S}_{o}}{{S}_{i}}\cdot \left(CA\right)=G\cdot \left(CA\right) \text{。}$ | (11) |
式中:
改善因子受众多因素限制,改善因子限制的计算公式为:
| $ I=\dfrac{1}{\dfrac{1}{{I}_{1}}+\dfrac{1}{{I}_{2}}+\dfrac{1}{{I}_{3}}+\dfrac{1}{{I}_{4}}+\dfrac{1}{{I}_{5}}} {\text{。}}$ | (12) |
式中:
电磁环境对目标特征的影响主要包括3个方面:面杂波、体杂波、压制干扰,其对目标模型的影响如表3所示。
|
|
表 3 雷达工作参数及性能指标对目标特征的影响 Tab.3 The influence of radar operating parameters and performance indexes on target characteristics |
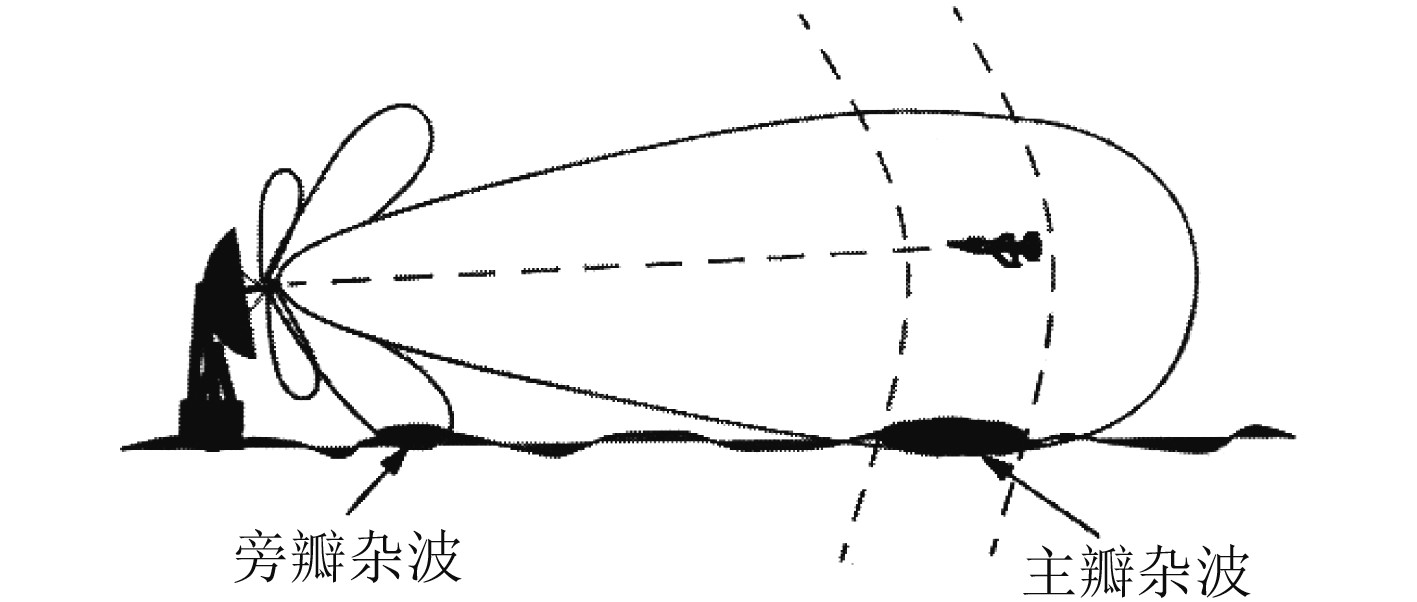
面杂波,又称区域杂波,即地面物体在雷达显示器呈现的回波,可以看作是干扰杂波。无论是机载雷达还是地面雷达,雷达发射的脉冲信号都存在大地能量,对雷达检测目标带来影响[7]。
地物回波包括从雷达主瓣进入的面杂波以及从雷达副瓣进入的面杂波,所以其RCS可表示为:
| $ {\sigma }_{c}={\sigma }_{MBc}+{\sigma }_{SLc} \text{。}$ | (13) |
其中:
|
图 4 地物杂波几何示意图 Fig. 4 Ground clutter geometry |
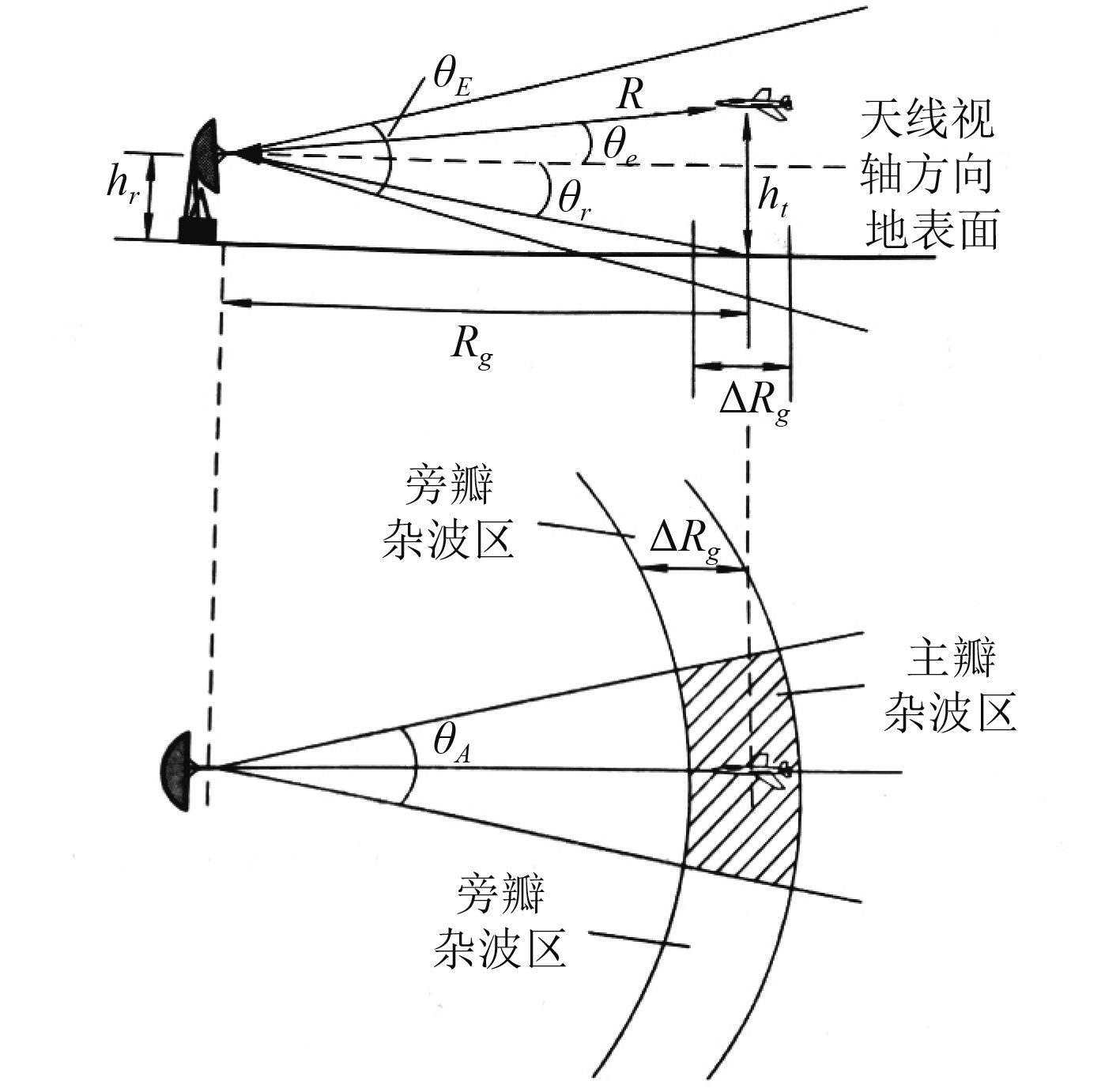
为计算面杂波的RCS,必须先算出主瓣和副瓣对应的RCS[8]。如图5所示,假设目标高度为
|
图 5 雷达杂波几何侧视图和下视图 Fig. 5 Radar clutter geometry(top view and bottom view) |
可推导出:
| $ {\theta }_{r}={\rm{arcsin}}\left(\frac{{h}_{r}}{R}\right) ,$ |
| $ {\theta }_{e}={\rm{arcsin}}\left(\frac{{h}_{t}-{h}_{r}}{R}\right) ,$ |
| $ ∆{\mathrm{R}}_{\mathrm{g}}=∆\mathrm{R}\mathrm{cos}{\mathrm{\theta }}_{\mathrm{r}} ,$ |
| $ ∆R=\mathrm{R}\mathrm{cos}{\theta }_{r} ,$ | (14) |
那么主瓣和旁瓣在杂波区的面积可表示为:
| $ {A}_{MBc}=\mathrm{R}\mathrm{\Delta }{R}_{g}{R}_{g}{\theta }_{A} ,$ |
| $ {A}_{SLc}=\mathrm{\Delta }{R}_{g}{R}_{g} {\text{π}} ,$ | (15) |
如果雷达天线的方向图函数为高斯型
| $ {G}\left(\theta \right)=\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{2.776{\theta }^{2}}{{\theta }_{E}^{2}}\right) ,$ | (16) |
那么主瓣杂波和旁瓣杂波的RCS如下式:
| $ {\sigma }_{MBc}={\sigma }^{0}{A}_{MBc}{G}^{2}\left({\theta }_{e}+{\theta }_{r}\right)={\sigma }^{0}\mathrm{\Delta }{R}_{g}{R}_{g}{\theta }_{a}{G}^{2}\left({\theta }_{e}+{\theta }_{r}\right) ,$ | (17) |
式中,
旁瓣杂波是除主瓣杂波外的其他方位的杂波,因主瓣仅占有较小的方位,与圆周相比可忽略,因此旁瓣杂波面积应为2π的关系式,而不像主瓣杂波仅覆盖极小方位。
| $ {\sigma }_{SLc}={\sigma }^{0}{A}_{SLc}{\left(S{L}_{rms}\right)}^{2}={\sigma }^{0}\mathrm{\Delta }{R}_{g}{R}_{g}{\text{π}} {\left(S{L}_{rms}\right)}^{2} ,$ | (18) |
式中,
综上,地物回波的RCS可认为是随距离变化的函数,如下式:
| $\sigma_{c}(R)=\frac{\sigma_{M B c}+\sigma_{S L c}}{1+\left(R / R_{h}\right)^{4}}=\frac{\sigma_{c}}{1+\left(R / R_{h}\right)^{4}}{\text{。}}$ | (19) |
式中,
气象杂波是一种体杂波,它的强度与很多因素有关,分别是天线波束照射体积、雷达距离分辨力、散射体的性质等 [9]。
| $ {S}_{气象}\left(f\right)={S}_{0}exp\left(-\frac{{\left(f-{f}_{d}\right)}^{2}}{2{\sigma }_{f}^{2}}\right) {\text{。}}$ | (20) |
式中:
压制式干扰是指外部噪声与杂波信号覆盖掉了雷达回波信号,从而使得雷达很难检测出真实目标。
压制式干扰对雷达的影响是增加有效输入温度[10],从接收机和自然环境决定的
| $ {T}_{j}=\frac{{P}_{j}{G}_{j}{A}_{r}{F}_{j}^{2}}{4{\text{π}} k{B}_{j}{R}^{2}{L}_{\alpha j}} ,$ | (21) |
或
| $ {T}_{j}=\frac{{P}_{j}{G}_{j}{G}_{r}{\lambda }^{2}{F}_{pj}^{2}{F}_{j}^{2}}{{\left(4{\text{π}} \right)}^{2}k{B}_{j}{R}^{2}{L}_{\alpha j}} {\text{。}}$ | (22) |
式中:
目标建模需要考虑目标自身特征、雷达体制要素和电磁环境的影响,最终需要得到的结果是雷达模拟器所需要的原始视频数据和检测视频数据。
4 目标视频生成模型 4.1 目标RCS确定一般雷达所探测的目标主要由多个反射点组成,因此适用于SwerlingI型起伏模型。该起伏模型符合自由度为2的
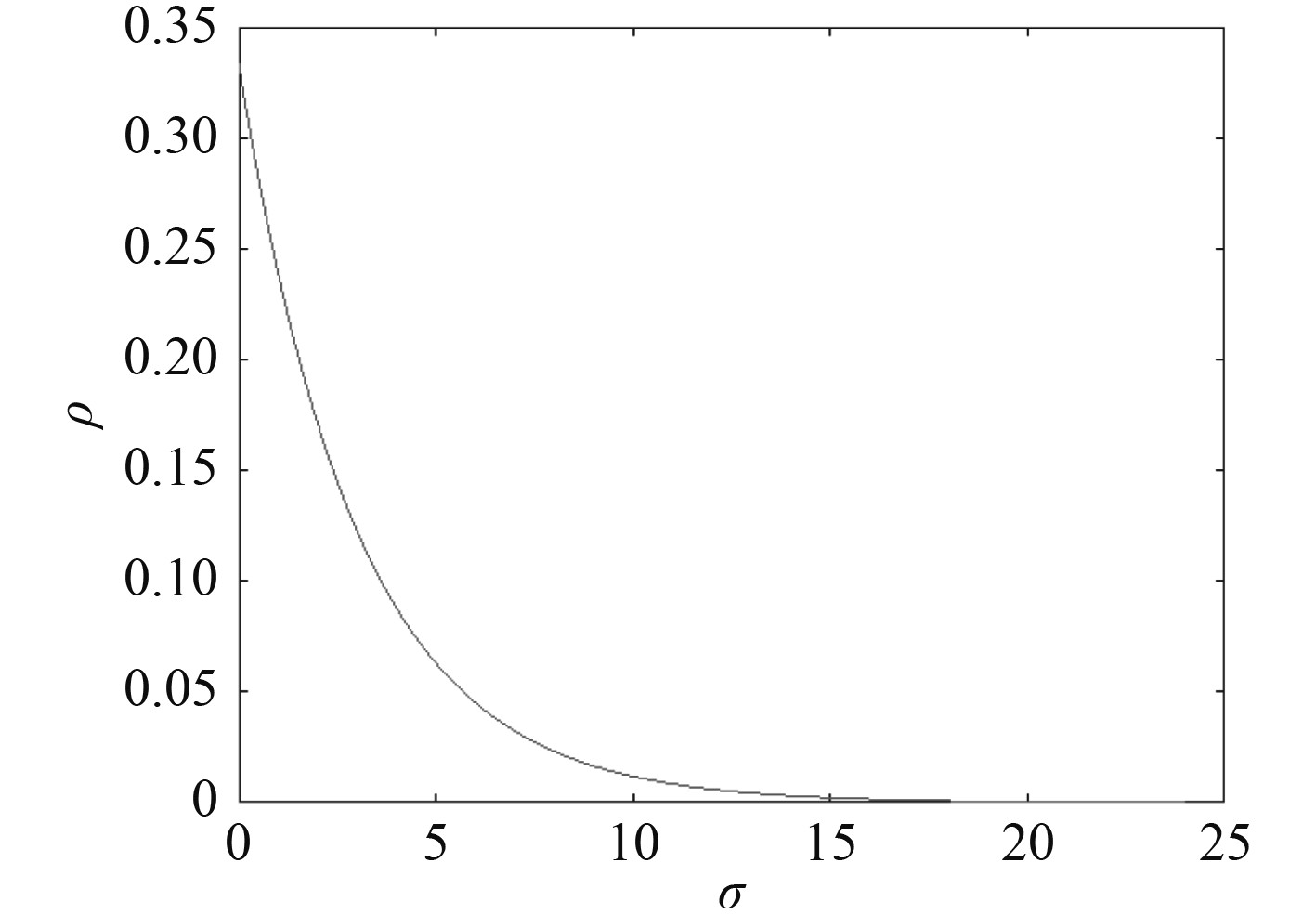
| $ p\left(\sigma \right)=\frac{1}{\stackrel{-}{\sigma }}exp\left(-\frac{\sigma }{\stackrel{-}{\sigma }}\right),\sigma \geqslant 0 {\text{。}}$ | (23) |
其概率曲线图如图6所示。
|
图 6
自由度为2的
|
根据目标描述字可以确定

|
图 7 SwerlingI型起伏模型RCS随机队列与概率密度函数 Fig. 7 SwerlingI random queue and probability density function of fluctuation model |
根据雷达探测原理有:
| $ {P}_{r}\propto \frac{{P}_{t}{G}_{t}\sigma {A}_{e}}{{\left(4{\text{π}} \right)}^{2}{R}^{4}} \text{。}$ | (24) |
式中:
当雷达工作模式未发生改变时,
| ${P_r} \propto \frac{\sigma }{{{R^4}}},$ | (25) |
即接收功率与目标的RCS成正比,与
雷达方程为:
| ${R_{\max }} = 239.3 \times {\left[ {\frac{{{P_t} \cdot \tau \cdot {G_t} \cdot {G_r} \cdot {\sigma _0}}}{{{f^2} \cdot {T_S} \cdot {D_0} \cdot {C_B} \cdot L}}} \right]^{1/4}}\text{。} $ | (26) |
其中:
| $ {D}_{0}=\frac{{P}_{{r}_{min}}}{{P}_{N}} \text{。}$ | (27) |
式中:
| $ {R_{max}} = 239.3 \times {\left[ {\frac{{{P_t} \cdot \tau \cdot {G_t} \cdot {G_r} \cdot {P_N} \cdot {\sigma _0}}}{{{f^2} \cdot {T_S} \cdot {C_B} \cdot L \cdot {P_{{r_{min}}}}}}} \right]^{1/4}} = k{\left[ {\frac{{{\sigma _0}}}{{{P_{{r_{min}}}}}}} \right]^{1/4}} ,$ |
即
| $\left\{ {\begin{array}{l} {k = {R_{max}}{{\left[ {\dfrac{{{P_{{r_{min}}}}}}{{{\sigma _0}}}} \right]}^{1/4}}},\\ {{P_{{r_{min}}}} = - 114 + NF + {\rm{lo}}{{\rm{g}}_{10}}{{B}} + {D_0}}\text{。} \end{array}} \right.$ | (28) |
式中:
计算目标回波功率公式如下:
| $ {P}_{r}=\frac{{k}^{4}}{{R}^{4}}\sigma {\text{。}}$ | (29) |
因此,当确定RCS(
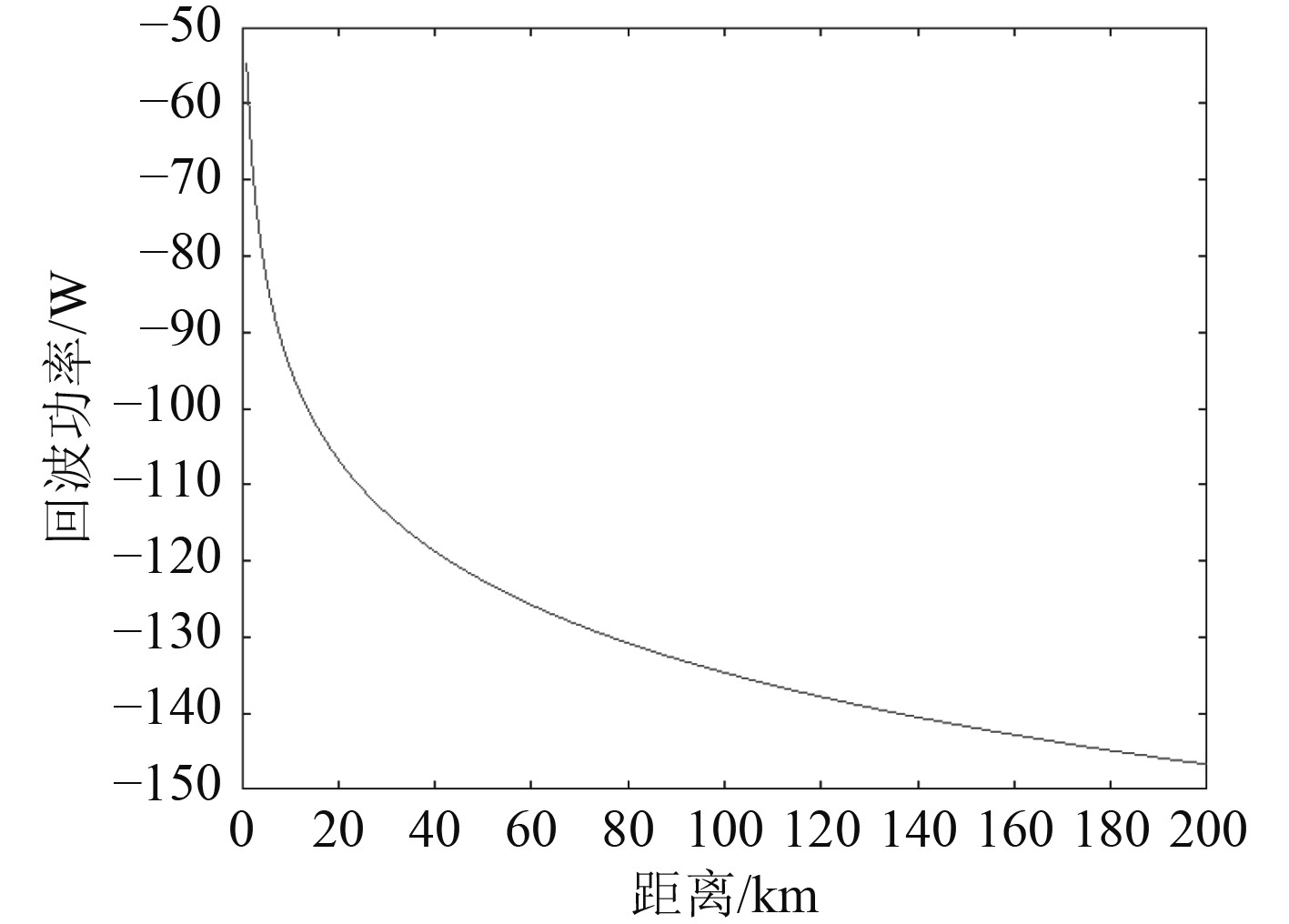
|
图 8 目标距离与回波功率变化曲线 Fig. 8 Change curve of target distance and echo ppower |
一般来说雷达探测方位和距离符合高斯分布。
| $ f\left(x\right)=\frac{1}{\sqrt{2\pi }\sigma }exp\left(-\frac{{\left(x-\mu \right)}^{2}}{2{\sigma }^{2}}\right) {\text{。}}$ | (30) |
式中:
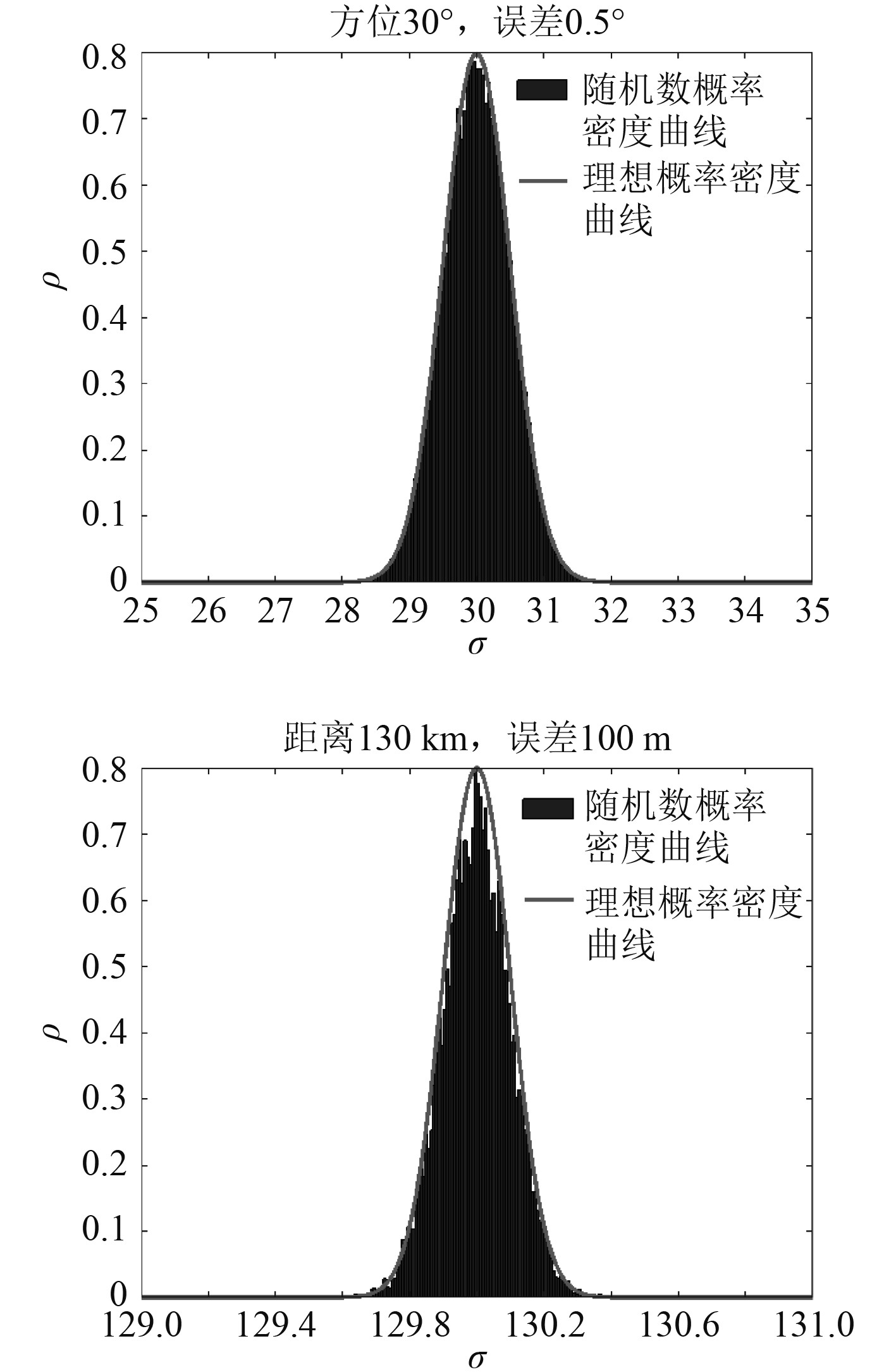
|
图 9 根据想定位置信息和测量精度调整目标位置 Fig. 9 Adjust the target position according to the desired position information and measurement accuracy |
目标在探测过程中受双程天线方向图调制。图10为接收(发射)天线方向图。
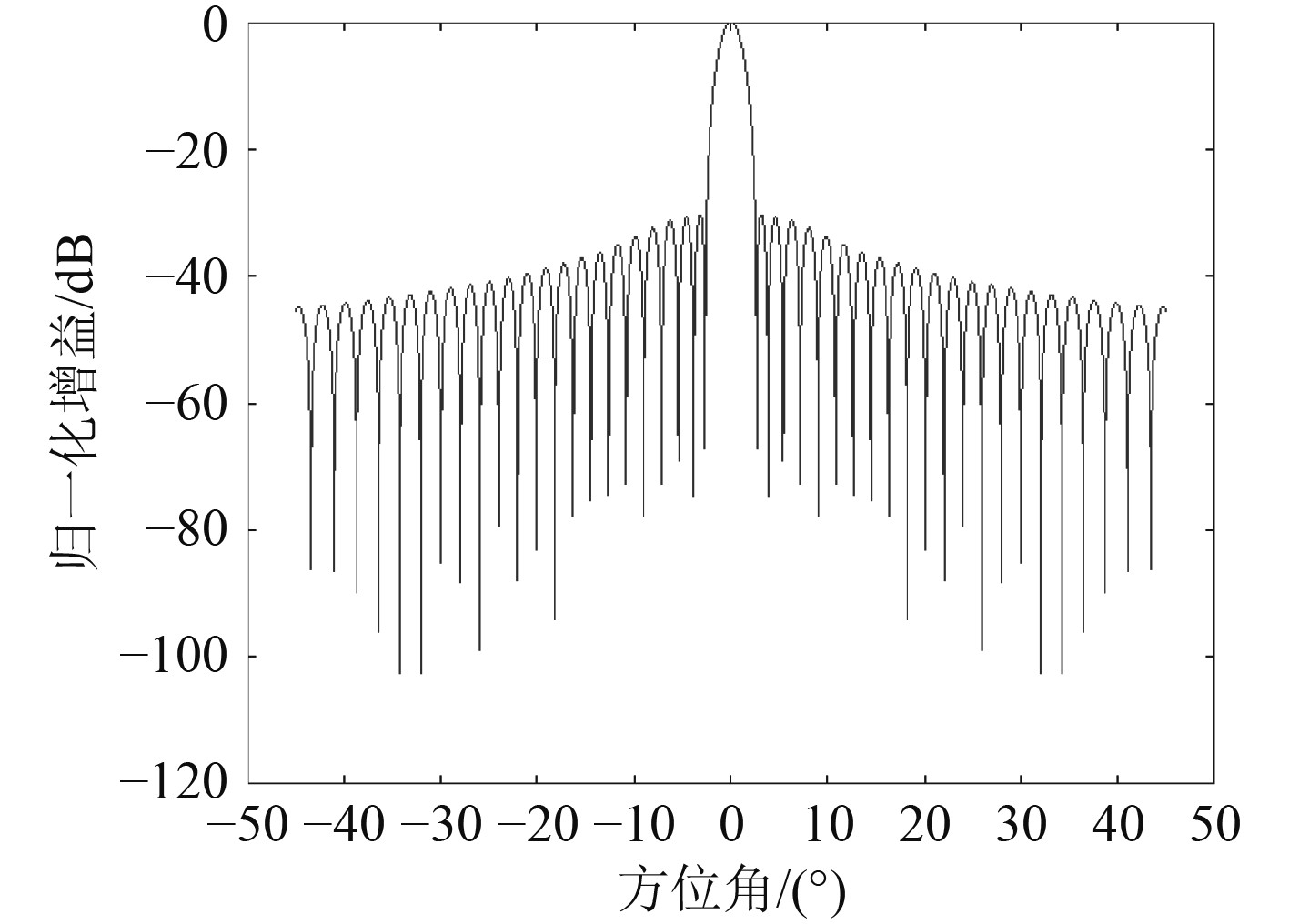
|
图 10 天线方向图 Fig. 10 Antenna pattern |
使用双程天线方向图调制目标功率及幅度效果如图11所示。
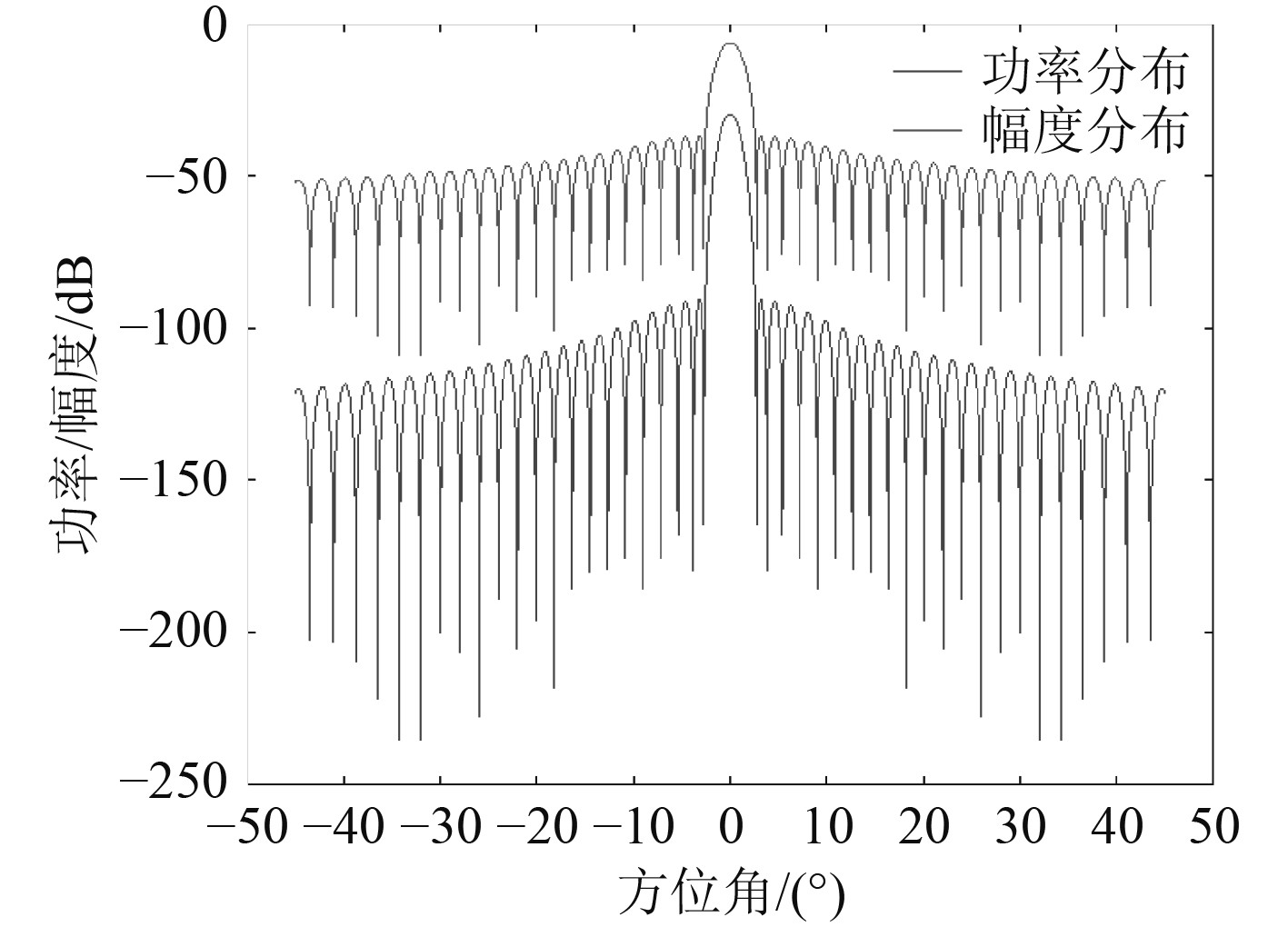
|
图 11 通过天线方向图调制目标功率和幅度效果 Fig. 11 Target power and amplitude effects are modulated by antenna pattern |
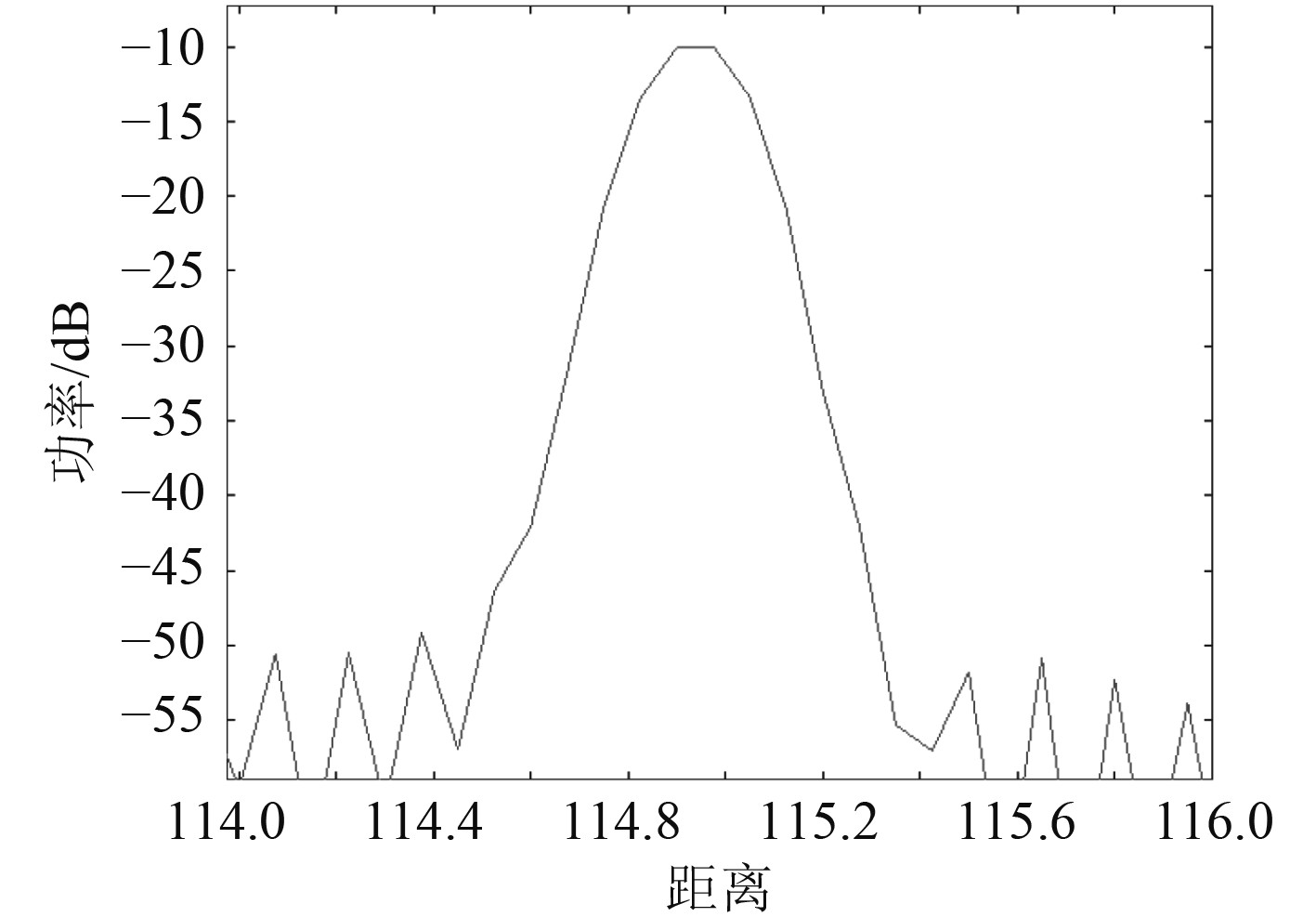
距离幅度分布与脉冲描述字相关,脉冲描述字包括:带宽、脉宽、波形和开窗方式[13]。雷达根据脉冲描述字进行脉冲压缩,在方位幅度分布的基础上,针对每个方位分布幅度值进行脉冲压缩,计算距离上的幅度分布,计算效果如图12所示。
|
图 12 目标距离上幅度分布计算效果 Fig. 12 Calculation effect of amplitude distribution on target distance |
通过上述5个步骤的计算,可以得出雷达目标的原始数据,该数据输入显控台,即为目标原始视频。
根据目标在某一时刻的原始视频,其三维开窗效果如图13所示。该显示效果是目标与噪声叠加的结果,符合雷达实际效果,因此目标原始视频产生的效果符合模型设计。

|
图 13 噪声中原始视频显示效果 Fig. 13 Original video display in noise |
本文通过对雷达目标数据生成算法对比分析,提出全要素雷达目标建模算法来实现目标数据生成。随后就影响目标生成的内、外部因素进行分析,包括RCS起伏等目标自身因素、雷达工作参数及性能指标的影响和电磁环境因素的影响,对目标因素、雷达自身因素及电磁环境因素进行详细的数学模型阐述,并介绍了目标原始视频数据生成的全过程。该方法可广泛应用于雷达模拟器、雷达环境生成器,对研究雷达目标检测、雷达抗干扰能力也有促进作用。
| [1] |
GEROGE W STIMSON. Introduction to airborne radar, Third Edition[M]. 北京: 电子工业出版社, 2005: 13−35.
|
| [2] |
ANTHONY P SZABO. Clutter simulation for airborne pulse_doppler radar[J]. Radar Conference, Proceedings of the International, 2003, 9: 608-613. |
| [3] |
LI Ming, LIN Yu-mei, RUAN Feng. A simple simulation method of ground clutter for airborne pulse doppler radar[J]. Radar Cie. International Conference, 2006, 10: 1-4. |
| [4] |
万长宁, 任波. 雷达威力计算数学模型的研究[J]. 现代雷达, 2011, 5(3): 69-72. |
| [5] |
邹鲲, 吴德伟, 李伟. 认知雷达起伏目标检测[J]. 系统工程与电子技术, 2017, 39(5): 207-211. |
| [6] |
焦培南, 张忠治. 雷达环境与电波传播特性[M]. 北京: 电子工业出版社, 2007: 35-48.
|
| [7] |
BILLINGSLEY J B. Statistical analysis of measured radar ground clutter data[J]. IEEE Transactions On Aerospace And Electronic Systems, 1999, .25(2): 579-593. |
| [8] |
DOO S. H., SMITH G., C. Baker RELIABLE. Target feature extraction and using potential target information[C]. Proc. IEEE Int. Radar Conf, US, 2015: 628−633.
|
| [9] |
周宇, 陈展野. 非均匀环境下利用雷达参数信息的STAP方法[J]. 电子科技大学学报, 2015, 45(6): 905-908. DOI:10.3969/j.issn.1001-0548.2015.06.019 |
| [10] |
杨鹏程, 吕晓德, 等. 基于频域分块RDS-LMS算法的机载外辐射源雷达杂波对消[J]. 电子与信息学报, 2017, 39(10): 20302-2305. |
| [11] |
Pei Jung CHUNG, ROBERTS. Recursive K-distribution parameter estimation[J]. IEEE Trans On Sp. 2005, 53(2): 397-402.
|
| [12] |
YANGSOO Kwon, NARAYANAN R M. Multi-target detection using total correlation for noise radar systems[J]. Aerospace And Electronic Systems, IEEE, 2013, 49(2): 1251-1262. DOI:10.1109/TAES.2013.6494411 |
| [13] |
陈伯孝. 现代雷达系统分析与设计[M]. 西安: 西安电子科技大学出版社, 2012: 24–46.
|
 2021, Vol. 43
2021, Vol. 43
