2. 天津航海仪器研究所九江分部,江西 九江 332007
2. Jiujiang Branch of Tianjin Nautical Instrument Research Institute, Jiujiang 332007, China
水下自主无人航行器(AUV)已广泛应用于海洋救助、打捞、海洋资源调查、石油开采等民用领域,并可承担扫雷、侦察、情报搜集及海洋探测等军事任务[1]。作为AUV的核心技术之一,运动控制技术得到国内外学者的广泛关注,相关人员开展了大量的理论研究和工程实践工作,推动了AUV控制技术的发展。1989年,Sur[2]采用滑模变结构控制方法,设计了NPSⅡAUV的深度控制算法;1994年,Hajosy[3]针对浅水环境中的UUV操纵控制,设计了六自由度滑模控制算法,并利用加权最小二乘法对其修正,获得了浅水环境下航向深度联合操纵的四自由度滑模控制算法,并利用21UUV对算法进行了验证。2005年,Hyun-Sik Kim等[4]针对水下飞行器(underwater flight vehicle,UFV)的深度控制,采用自适应模糊滑模控制原理,分别设计了UFV的深度和纵倾控制算法,并采用深度控制器和纵倾控制器相互切换的策略,实现了多操纵面控制的UFV深度控制。2017年,Raja Rout[5]考虑到AUV航迹偏差跟踪控制过程中需限制最大转首速度和操纵面的偏转角度,基于显式模型预测控制理论,设计了多约束条件下的AUV航迹跟踪模型预测控制算法,并在实验室验证了算法的有效性。高剑[6]采用级联系统稳定性理论和反馈线性化技术,设计了AUV的三维空间直线航迹跟踪控制算法,并证明了欠驱动UUV三维空间直线航迹跟踪的全局
AUV的深度控制可采用深度—纵倾控制策略[8],实现深度机动和深度保持,其关键是AUV的纵倾控制。
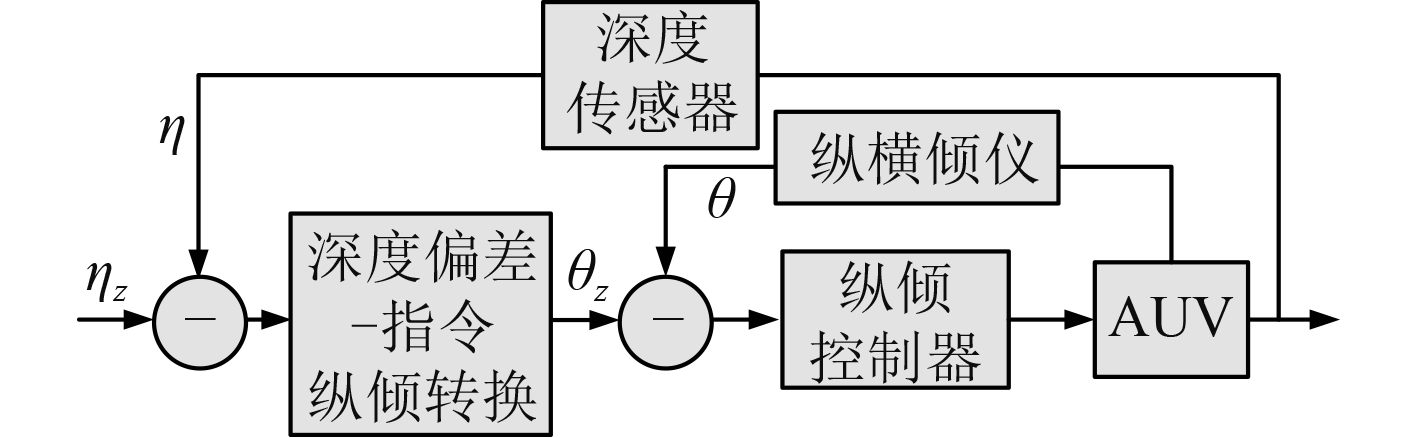
AUV的深度—纵倾内外环控制策略如图1所示。
|
图 1 深度—纵倾内外环控制策略框图 Fig. 1 Depth-Block diagram of inner and outer pitch control strategy |
深度偏差转换为指令纵倾的算法如下:
| $\left\{ \begin{aligned} {\theta _z} =& 0,\begin{array}{*{20}{c}} {}&{}&{\left| {\eta - {\eta _z}} \right| \leqslant a} \text{,} \end{array} \\ {\theta _z} =& 2{\rm{sign}}(\eta - {\eta _z}){\theta _z}_{\max }{\left(\dfrac{{\left| {\eta - {\eta _z}} \right| - a}}{{b - a}}\right)^2}\text{,}\\ & \begin{array}{*{20}{c}} {a < \left| {\eta - {\eta _z}} \right| \leqslant \dfrac{{(a + b)}}{2}} \text{,} \end{array} \\ {\theta _z} =& {\rm{sign}}(\eta - {\eta _z}){\theta _z}_{\max }\left(1 - 2{\left(\dfrac{{\left| {\eta - {\eta _z}} \right| - a}}{{b - a}}\right)^2}\right)\text{,}\\& \begin{array}{*{20}{c}} {\dfrac{{(a + b)}}{2} < \left| {\eta - {\eta _z}} \right| \leqslant b} \text{,} \end{array} \\ {\theta _z} =& {\rm{sign}}(\eta - {\eta _z}){\theta _z}_{\max }\begin{array}{*{20}{c}} {\left| {\eta - {\eta _z}} \right| > b} \text{。} \end{array} \\ \end{aligned} \right.$ | (1) |
以

|
图 2 深度偏差—指令纵倾转换曲线 Fig. 2 Depth deviation-commanded pitch conversion curve |
本文AUV的纵倾控制采用一种基于Laguerre函数逼近的模型预测控制方法[9],可用于AUV自主航行控制系统中。
AUV垂直面运动线性方程可用状态空间方程描述如下:
| $ \left[ {\begin{array}{*{20}{c}} {\dot w} \\ {\dot q} \\ {\dot \theta } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\rm{a}}_{11}}}&{{a_{12}}}&{{a_{13}}} \\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}} \\ 0&1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} w \\ q \\ \theta \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{b_1}} \\ {{b_2}} \\ 0 \end{array}} \right]{\delta _s}\text{,} $ | (2) |
| $ y = \left[ {\begin{array}{*{20}{c}} 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} w \\ q \\ \theta \end{array}} \right]\text{,} $ | (3) |
式(2)和式(3)简记为:
| $\begin{split} \dot x &= Ax + B\delta\text{,} \\ y &= Cx\text{,} \\ \end{split} $ | (4) |
利用后向差分法离散化式(4)后,可得:
| $ \begin{split} {x_m}(k + 1) &= {A_m}{x_m}(k) + {B_m}u(k) \text{,} \\ y(k) &= {C_m}{x_m}(k) \text{,} \\ \end{split} $ | (5) |
将式(5)两端差分运算后,可得:
| $\begin{split} {x_m}\left( {k + 1} \right) - {x_m}\left( k \right) &= {A_m}\left( {{x_m}\left( k \right) - {x_m}\left( {k - 1} \right)} \right) +\\ &\quad{B_m}\left( {u\left( k \right) - u\left( {k - 1} \right)} \right)\text{,} \\ y\left( {k + 1} \right) - y\left( k \right) &= {C_m}\left( {{x_m}\left( {k + 1} \right) - {x_m}\left( k \right)} \right) =\\ & Cm\Delta {x_m}\left( {k + 1} \right) \text{。} \\ \end{split} $ | (6) |
引入如下符号:
| $\begin{split} {\Delta {x_m}\left( {k + 1} \right) =}&{ {x_m}\left( {k + 1} \right) - {x_m}\left( k \right)},\\ {\Delta {x_m}\left( k \right) }= &{x_m}\left( k \right) - {x_m}\left( {k - 1} \right)\text{,} \\ {\Delta u\left( k \right)} =&{ u\left( k \right) - u\left( {k - 1} \right)}\text{,} \end{split}$ | (7) |
则可由式(7)得到如下增量式状态方程和状态输出方程:
| $\begin{split} & {\left[ {\begin{array}{*{20}{c}} {\Delta {x_m}\left( {k + 1} \right)} \\ {y\left( {k + 1} \right) } \end{array}} \right]} = \left[ {\begin{array}{*{20}{c}} {{A_m}}&0 \\ {{C_m}{A_m}}&1 \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {\Delta {x_m}\left( k \right)} \\ {y\left( k \right) } \end{array}} \right] + \\ &\quad\quad\quad\quad\quad\quad\quad\;\;\left[ {\begin{array}{*{20}{c}} {{B_m} } \\ {{C_m}{B_m}} \end{array}} \right] \Delta u\left( k \right) \text{,}\\ & {y\left( k \right) = \left[ {\begin{array}{*{20}{c}} 0&0&1 \end{array}} \right]} \left[ {\begin{array}{*{20}{c}} {\Delta {x_m}\left( k \right)} \\ {y\left( k \right) } \end{array}} \right] \text{,} \end{split}$ | (8) |
上式简记为:
| $\begin{split} {x\left( {k + 1} \right) }&{= Ax\left( k \right) + B\Delta u\left( k \right)}\text{,} \\ {y\left( k \right) }&{= Cx\left( k \right)} \text{,} \end{split}$ | (9) |
考虑纵倾为
| $x(k) = {[\Delta x(m),y - r({k_i})]^{\rm{T}}}\text{,}$ | (10) |
式(9)中的输出相应变换为纵倾偏差。后续的控制律代价函数中将采用式(10)所示的状态向量。
假设在
| $\Delta u\left( {k + m} \right) = L{\left( m \right)^{\rm T}}\eta \text{,}$ | (11) |
式中,
Laguerre函数向量具有下述正交特性:
| $\begin{gathered} \sum\limits_{m = 0}^{{N_p}} {{l_i}(m){l_j}(m) = 0} \begin{array}{*{20}{c}} {}&{i \ne j} \text{,} \end{array} \\ \sum\limits_{m = 0}^{{N_p}} {{l_i}(m){l_j}(m) = 1} \begin{array}{*{20}{c}} {}&{i = j} \text{,} \end{array} \\ \end{gathered} $ | (12) |
| $L(k + 1) = {A_l}L(k)\text{。}$ | (13) |
式中:
| $\begin{split} &{A_l} = \left[ {\begin{array}{*{20}{c}} \alpha &0&0\\ \beta &\alpha &0\\ { - \alpha \beta }&\beta &\alpha \\ {{\alpha ^2}\beta }&{ - \alpha \beta }&\beta \\ { - {\alpha ^3}\beta }&{{\alpha ^2}\beta }&{ - \alpha \beta } \\ \vdots & \vdots & \vdots \\ {( - {1^{N - 2}}){\alpha ^{N - 2}}\beta }&{( - {1^{N - 3}}){\alpha ^{N - 3}}\beta }&{( - {1^{N - 4}}){\alpha ^{N - 4}}\beta } \end{array}} \right.\\ &\qquad\left. {\begin{array}{*{20}{c}}0&0& \cdots &0\\ 0&0& \cdots &0\\ 0&0& \cdots &0\\ \alpha &0& \cdots &0\\ \beta &\alpha & \cdots &{}\\ \vdots & \vdots & \ddots &{} \\ {( - {1^{N - 5}}){\alpha ^{N - 5}}\beta }& \cdots & \cdots &\alpha \end{array}}\right],\;\\ &L(0) =\sqrt \beta \left[ {\begin{array}{*{20}{c}} 1 \\ { - \alpha } \\ {{\alpha ^2}} \\ { - {\alpha ^3}} \\ {{\alpha ^4}} \\ \vdots \\ {{{( - 1)}^{N - 1}}\alpha } \end{array}} \right] ,\;\beta = (1 - {\alpha ^2})\text{。} \end{split}$ |
假设在
| $\begin{split} {x\left( {k + m/k} \right) }=&{ {A^m}x\left( k \right) + \sum\limits_{j = 0}^{m - 1} {{A^{m - j - 1}}} BL{{\left( j \right)}^{\rm{T}}}\eta }=\\& { {A^m}x\left( k \right) + \phi {{\left( m \right)}^{\rm{T}}}\eta }\text{,} \\ \phi {\left( m \right)^{\rm{T}}} = &\sum\limits_{j = 0}^{m - 1} {{A^{m - j - 1}}} BL{\left( j \right)^{\rm{T}}}\text{。} \end{split}$ | (14) |
为设计纵倾预测控制律,设代价函数为:
| $J = \sum\limits_{m = 1}^{{N_p}} {x{{({k_i} + m|{k_i})}^{\rm{T}}}Q} x({k_i} + m|{k_i}) + \Delta {u^{\rm{T}}}R\Delta u\text{,}$ | (15) |
将式(14)所述预测状态代入上述代价函数,可得:
| $J = \sum\limits_{m = 1}^{{N_p}} {x{{({k_i} + m|{k_i})}^{\rm{T}}}Q} x({k_i} + m|{k_i}) + {\eta ^{\rm{T}}}R\eta\text{,} $ | (16) |
则利用Laguerre函数的正交特性,可得:
| $\begin{split} J =& {\eta ^{\rm{T}}}\left(\sum\limits_{m = 1}^{{N_p}} {\phi (m)} Q\phi {{(m)}^{\rm{T}}} + {R_L}\right)\eta + \\[-2pt] &2{\eta ^{\rm{T}}}\left(\sum\limits_{m = 1}^{{N_p}} {\phi (m)} Q{A^m}\right)x(k) + \sum\limits_{m = 1}^{{N_p}} {x{{(k)}^{\rm{T}}}} {{({A^{\rm{T}}})}^m}Q{A^m}x(k) =\\[-2pt] & {\eta ^{\rm{T}}}\Omega \eta {\kern 1pt} + {\kern 1pt} {\kern 1pt} 2{\eta ^{\rm{T}}}\Phi x(k) + \sum\limits_{m = 1}^{{N_p}} {x{{(k)}^{\rm{T}}}} {{({A^{\rm{T}}})}^m}Q{A^m}x(k) \text{。}\\[-20pt] \end{split}$ | (17) |
考虑到控制纵倾的水平舵在施加运动控制过程中存在角度和角速度物理限制,因而,上述代价函数的求解需考虑下述物理约束:
1)舵角限制
| ${u^{\min }} \leqslant u(k) \leqslant {u^{\max }}\text{。} $ |
舵角约束不等式为:
| ${u^{\min }} \leqslant \sum\limits_{i = 0}^{m - 1} {{L_1}{{(i)}^{\rm T}}} \eta + u({k_i} - 1) \leqslant {u^{\max }}\text{,}$ | (18) |
将
| $\begin{split} &\underbrace {\left[ \begin{gathered} L{(0)^{\rm{T}}} \\ \sum\limits_{i = 0}^1 {L{{(i)}^{\rm{T}}}} \\ \vdots \\ \sum\limits_{i = 0}^{m - 1} {L{{(i)}^{\rm{T}}}} \\ \end{gathered} \right]}_{{M_u}}\eta \leqslant \underbrace {\left[ \begin{gathered} {u^{\max }} - u({k_i} - 1) \\ {u^{\max }} - u({k_i} - 1) \\ \vdots \\ {u^{\max }} - u({k_i} - 1) \\ \end{gathered} \right]}_{{U^{\max }} - \bar u({k_i} - 1)},\\ &- \underbrace {\left[ \begin{gathered} L{(0)^{\rm{T}}} \\ \sum\limits_{i = 0}^1 {L{{(i)}^{\rm{T}}}} \\ \vdots \\ \sum\limits_{i = 0}^{m - 1} {L{{(i)}^{\rm{T}}}} \\ \end{gathered} \right]}_{{M_u}}\;\;\eta \leqslant \underbrace {\left[ \begin{gathered} {u^{\min }} + u({k_i} - 1) \\ {u^{\min }} + u({k_i} - 1) \\ \vdots \\ {u^{\min }} + u({k_i} - 1) \\ \end{gathered} \right]}_{ - {U^{\min }} + \bar u({k_i} - 1)}, \end{split}$ |
简记为:
| $\begin{gathered} {M_u}\eta \leqslant {U^{\max }} - \bar u({k_i} - 1)\text{,} \\ - {M_u}\eta \leqslant - {U^{\min }} + \bar u({k_i} - 1) \text{。} \\ \end{gathered} $ | (19) |
2)舵速限制
| $\Delta {U_{\min }} \leqslant \Delta U \leqslant \Delta {U_{\max }}\text{。} $ |
舵速约束不等式为:
| $\Delta {u^{\min }} \leqslant L{(m)^{\rm{T}}}\eta \leqslant \Delta {u^{\max }}\text{,}$ | (20) |
则将
| $\begin{split} \underbrace {\left[ \begin{gathered} L{(1)^{\rm{T}}} \\ L{(2)^{\rm{T}}} \\ \vdots \\ L{({n_c})^{\rm{T}}} \\ \end{gathered} \right]}_{{M_\Delta }}\eta \leqslant \underbrace {\left[ \begin{gathered} \Delta {u^{\max }} \\ \Delta {u^{\max }} \\ \vdots \\ \Delta {u^{\max }} \\ \end{gathered} \right]}_{\Delta {U^{\max }}}, \underbrace {\left[ \begin{gathered} - L{(1)^{\rm{T}}} \\ - L{(2)^{\rm{T}}} \\ \vdots \\ - L{({n_c})^{\rm{T}}} \\ \end{gathered} \right]}_{ - {M_\Delta }}\eta \leqslant \underbrace {\left[ \begin{gathered} - \Delta {u^{\min }} \\ - \Delta {u^{\min }} \\ \vdots \\ \Delta {u^{\min }} \\ \end{gathered} \right]}_{ - \Delta {U^{\min }}}, \end{split}$ |
简记为:
| $\begin{gathered} {M_\Delta }\eta \leqslant \Delta {U^{\max }} \text{,} \\ - {M_\Delta }\eta \leqslant - \Delta {U^{\min }} \text{,} \\ \end{gathered} $ | (21) |
将式(19)和上式联立后简记为:
| ${M_H}\eta \leqslant {\gamma _H}\text{。}$ | (22) |
3)纵倾角限制
| ${\theta _{\min }} \leqslant \theta \leqslant {\theta _{\max }}\text{。} $ |
在AUV的变深运动过程中,为了防止纵倾过大,一般还需对纵倾施加约束,变深过程中,在某些时间段内,可以适当突破该约束,故该约束为软约束。纵倾约束的推导过程如下:
由状态方程(9)和预测状态(14)可得:
| $\begin{array}{l} x\left( {k + m/k} \right) = {A^m}x\left( k \right) + \phi {\left( m \right)^{\rm{T}}}\eta \text{,}\\ y\left( {k + m/k} \right) = C{A^m}x\left( k \right) + C\phi {\left( m \right)^{\rm{T}}}\eta \text{,} \end{array} $ | (23) |
由此可得:
| $\begin{split} &{\theta _{\min }} \leqslant y({k_i} + m|{k_i}) \leqslant {\theta _{\max }} , \\ &{\theta _{\min }} \leqslant C{A^m}x({k_i}) + C\phi {\left( m \right)^{\rm{T}}}\eta \leqslant {\theta _{\max }} ,\\ & - C\phi {\left( m \right)^{\rm{T}}}\eta \leqslant - {\theta _{\min }} + C{A^m}x({k_i}) ,\\ &C\phi {\left( m \right)^{\rm{T}}}\eta \leqslant {\theta _{\max }} - C{A^m}x({k_i}) \text{。} \end{split} $ |
则有:
| $\begin{split} -& \left[ \begin{gathered} C\phi {\left( 1 \right)^{\rm{T}}} \\ C\phi {\left( 2 \right)^{\rm{T}}} \\ \vdots \\ C\phi {\left( {Np} \right)^{\rm{T}}} \\ \end{gathered} \right]\eta \leqslant - {\left[ \begin{gathered} 1 \\ 1 \\ \vdots \\ 1 \\ \end{gathered} \right]_{Np}}{\theta ^{\min }} + \left[ \begin{gathered} CA \\ C{A^2} \\ \vdots \\ C{A^{Np}} \\ \end{gathered} \right]x({k_i}) ,\\& \left[ \begin{gathered} C\phi {\left( 1 \right)^{\rm{T}}} \\ C\phi {\left( 2 \right)^{\rm{T}}} \\ \vdots \\ C\phi {\left( {Np} \right)^{\rm{T}}} \\ \end{gathered} \right]\eta \leqslant {\left[ \begin{gathered} 1 \\ 1 \\ \vdots \\ 1 \\ \end{gathered} \right]_{Np}}{\theta ^{\max }} - \left[ \begin{gathered} CA \\ C{A^2} \\ \vdots \\ C{A^{Np}} \\ \end{gathered} \right]x({k_i}) \text{。} \end{split}$ |
联立为矩阵不等式,简记为下式:
| ${M_S}\eta \leqslant {\gamma _S}\text{,}$ | (24) |
式(24)和式(22)联立,有
| $\underbrace {\left[ {\begin{array}{*{20}{c}} {{M_H}} \\ {{M_S}} \end{array}} \right]}_M\eta \leqslant \underbrace {\left[ {\begin{array}{*{20}{c}} {{\gamma _H}} \\ {{\gamma _S}} \end{array}} \right]}_\gamma \text{,}$ | (25) |
至此,纵倾MPC控制器的求解问题被转换为二次规划问题:
| $\left\{ \begin{aligned} &{J_1} = \dfrac{1}{2}{\mathit{\boldsymbol{\eta }}^{\rm{T}}}{\mathit{\boldsymbol{\Omega }}_\mathit{\boldsymbol{\Sigma }}}\mathit{\boldsymbol{\eta }} + {\mathit{\boldsymbol{\eta }}^{\rm{T}}}\mathit{\boldsymbol{\Phi x}}(k)\text{,}\\ &\mathit{\boldsymbol{M\eta }} \leqslant \mathit{\boldsymbol{\gamma }}\text{。} \end{aligned} \right.$ | (26) |
该二次规划问题采用活动集法求解,可利用Hildreth二次规划方法求解[8]。故纵倾MPC控制器可设计为:
| $\Delta u(k + 1) = \mathit{\boldsymbol{L}}{\left( 0 \right)^{\rm{T}}}\mathit{\boldsymbol{\eta }}\text{,}$ | (27) |
若AUV不具备垂向速度
| $\mathit{\boldsymbol{\hat x}}({k_i} + 1) = \mathit{\boldsymbol{A\hat x}}({k_i}) + \mathit{\boldsymbol{B\Delta u}}({k_i}) + {\mathit{\boldsymbol{K}}_{\mathit{\boldsymbol{ob}}}}\left(\mathit{\boldsymbol{y}}({k_i}) - \mathit{\boldsymbol{C\hat x}}\left({k_i}\right)\right)\text{。}$ | (28) |
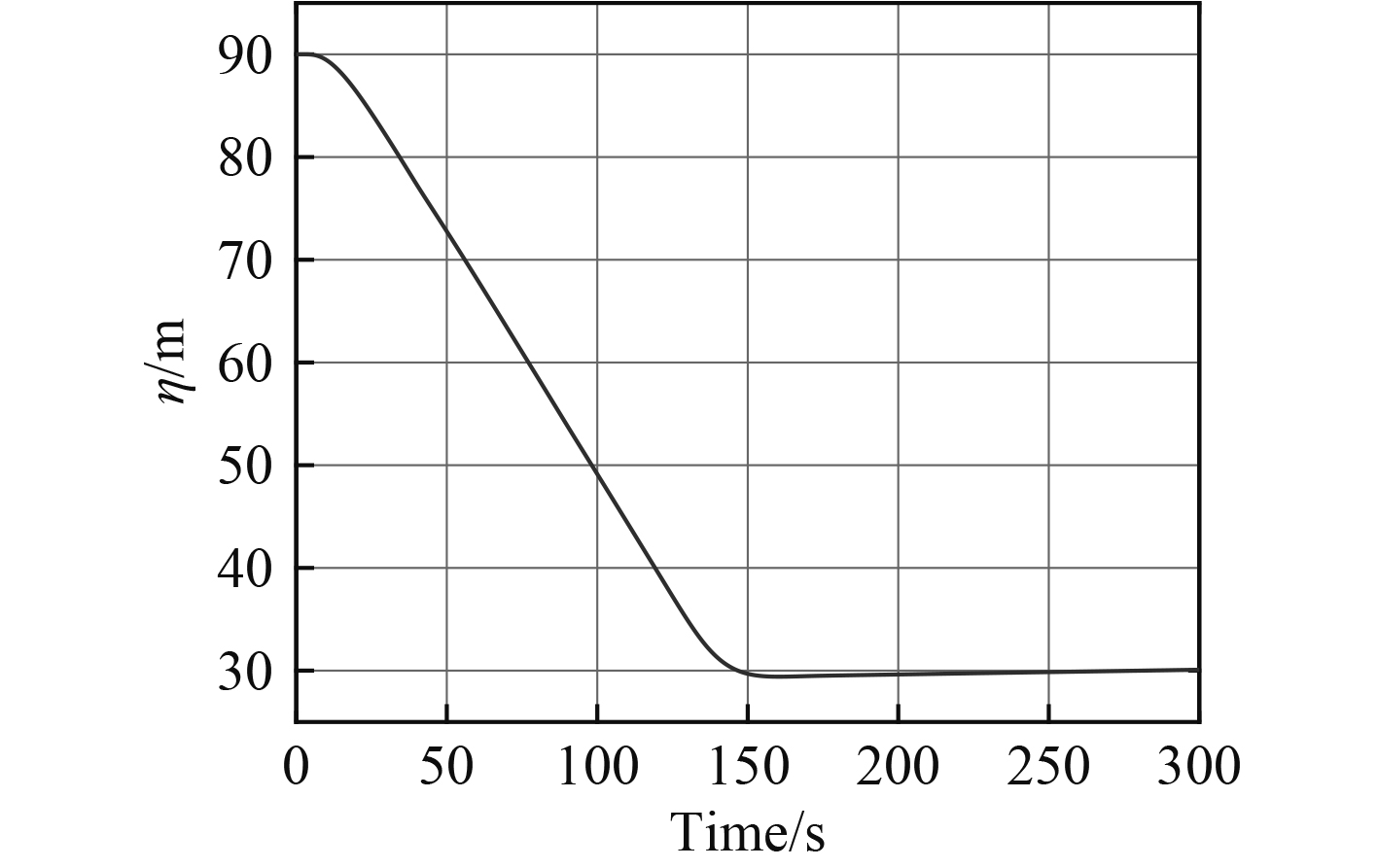
为了验证本文提出的深度—纵倾控制算法的有效性,利用文献[12]中的REMUS AUV的运动数学模型进行仿真验证。仿真结果如图 3~图8所示。其中图 3~图 5为3 kn航速下AUV由水下90 m上浮至30 m的仿真结果,图 6~图 8为5 kn航速AUV由水下40 m下潜至90 m的仿真结果。2组仿真试验中,均设置纵倾约束为
|
图 3 3kn航速深度变化曲线 Fig. 3 Speed depth curve of 3kn |
|
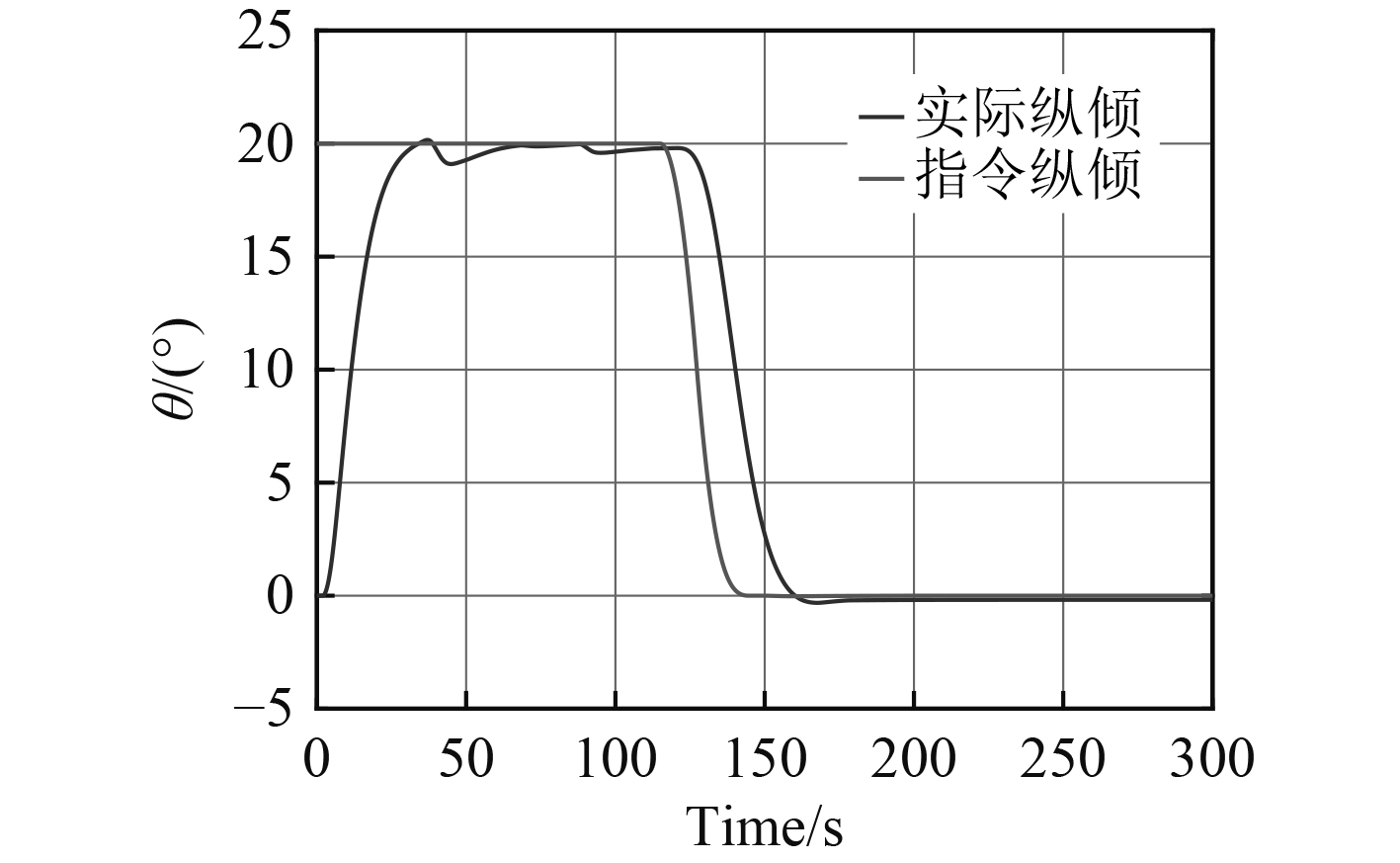
图 4 3kn航速纵倾变化曲线 Fig. 4 Speed pitch curve of 3kn |
|
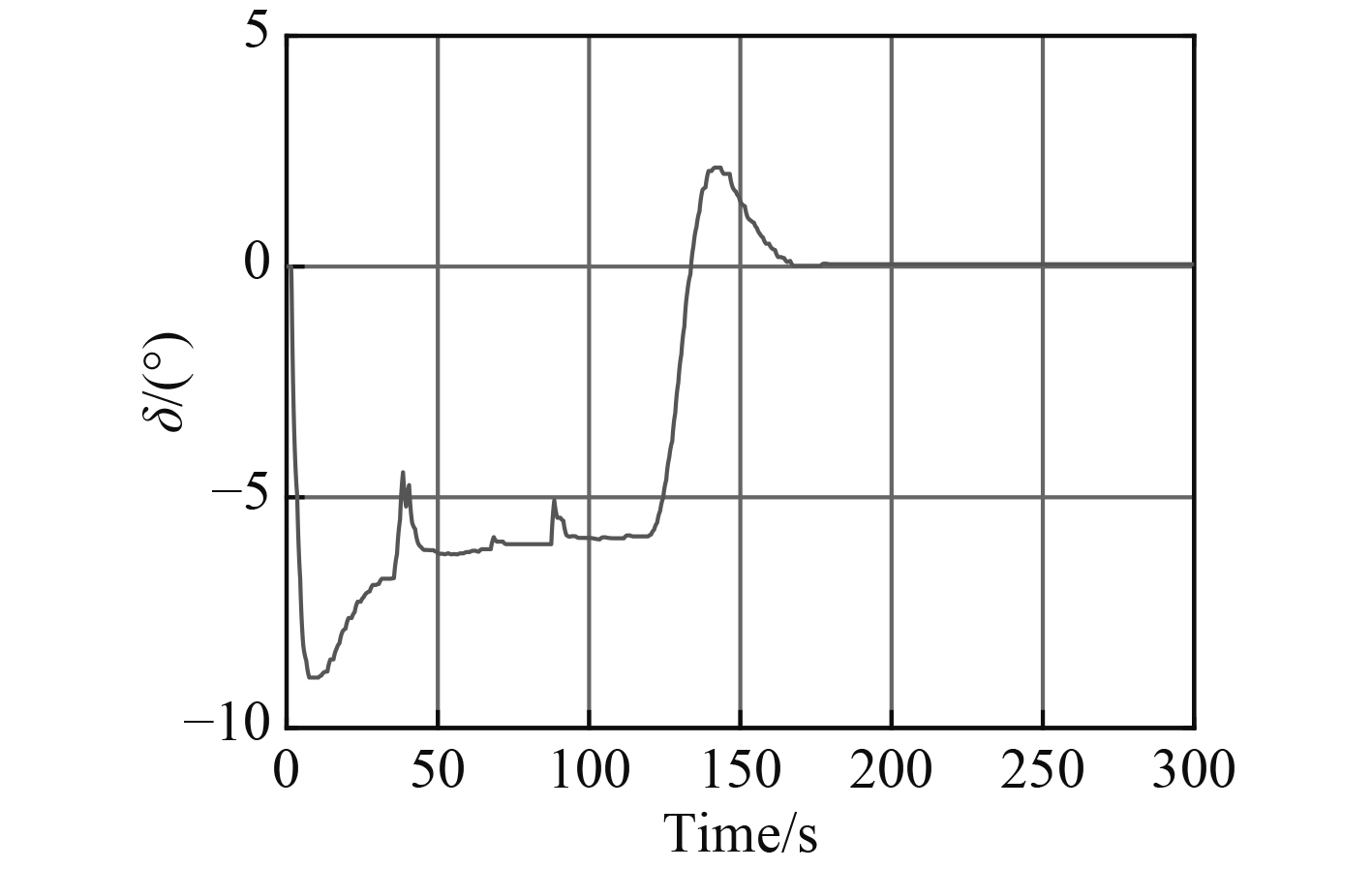
图 5 3kn航速尾水平舵变化曲线 Fig. 5 Speed stern hydroplane curve of 3kn |
|
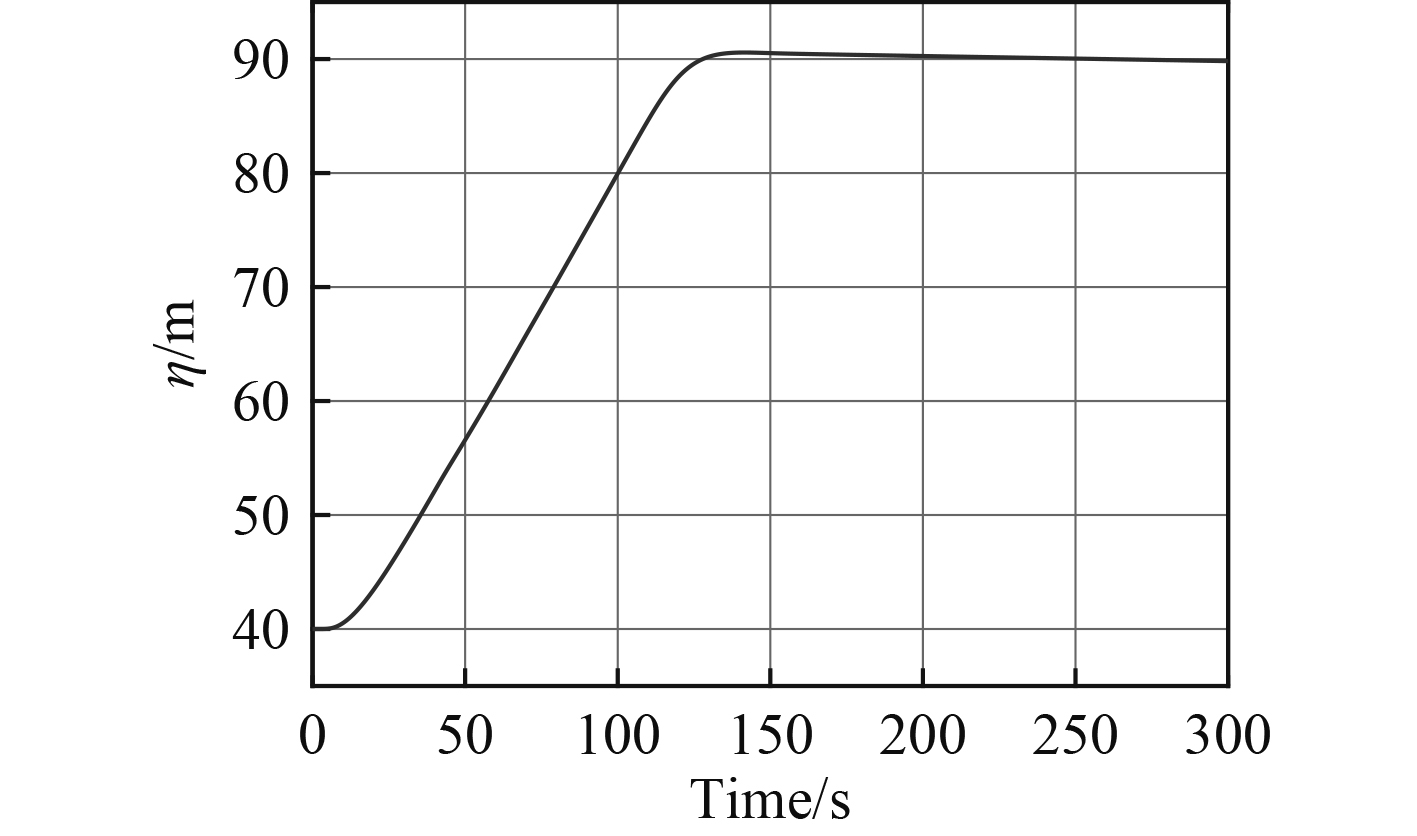
图 6 5kn航速深度变化曲线 Fig. 6 Speed depth curve of 5kn |

|
图 7 5kn航速纵倾变化曲线 Fig. 7 Speed pitch curve of 5kn |
|
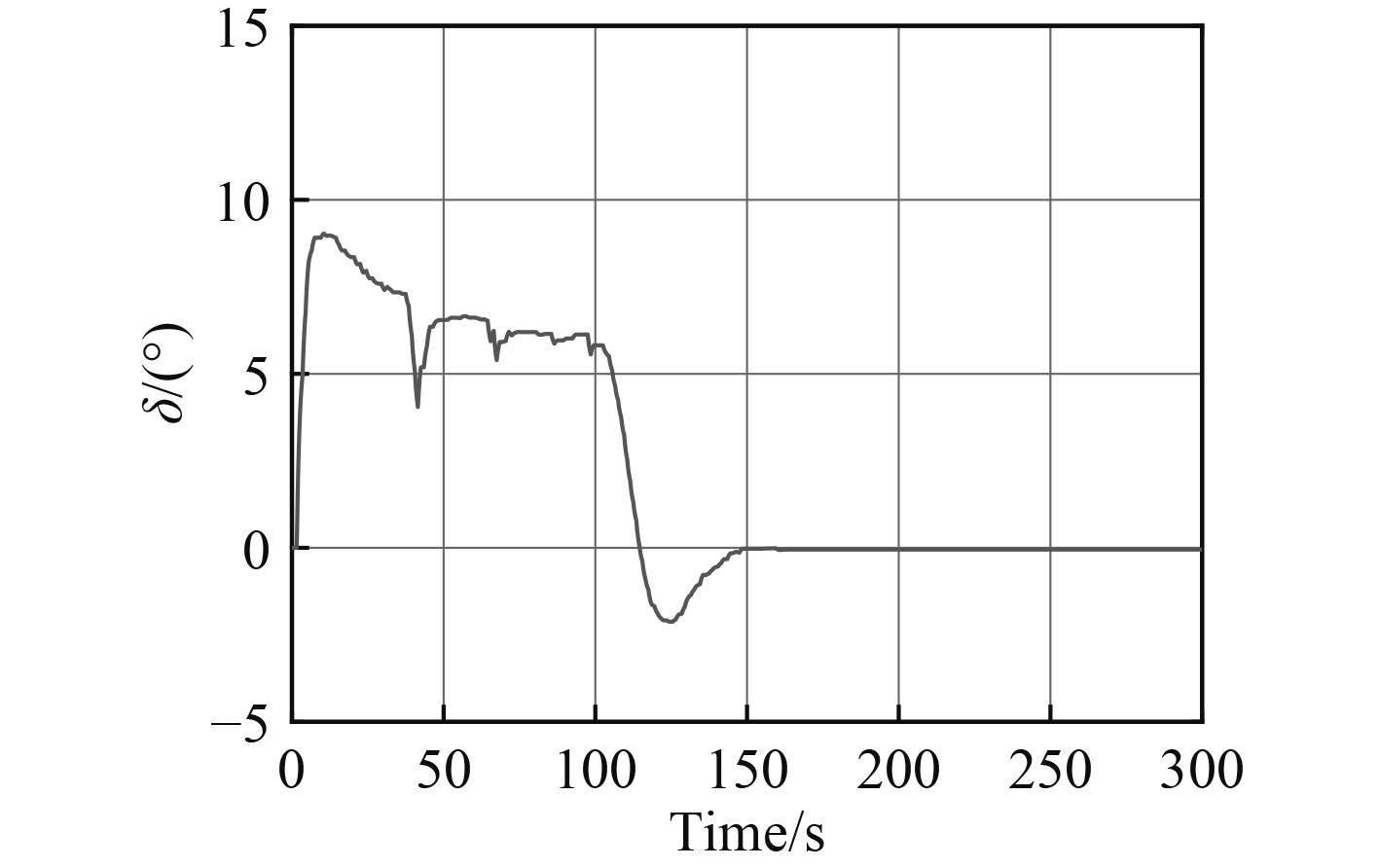
图 8 5kn航速尾水平舵变化曲线 Fig. 8 Speed stern hydroplane curve of 5kn |
由图 3和图 6可知,AUV在变深过程中运动平稳,无超调,无振荡,结合相应的纵倾变化曲线可知,在变深过程中,AUV深度偏差—指令纵倾变换合理,变深过程中,一旦纵倾约束被破坏,则纵倾约束条件被激活。如图 5和图 8所示,尾水平舵将立即收舵,调节纵倾回到约束内。2组仿真结果验证了AUV的多约束模型预测控制器具有良好的控制品质。
4 结 语本文针对AUV垂直面运动控制问题,提出一种变深过程中的深度偏差—指令纵倾转换方法,应用基于Lagurre函数的模型预测控制理论,设计纵倾、舵角和舵速约束条件下的AUV深度控制算法,实现了AUV的深度控制。仿真结果表明:1)本文设计的深度偏差—指令纵倾转化算法计算简洁,具有明晰的物理意义,且易于实现;2)本文设计的多约束条件模型预测控制算法具有良好的控制性能和控制品质,可应用于AUV的深度控制中;3)本文所应用的Hildreth二次规划方法可快速处理多种约束条件的二次规划问题,具有较大的工程实用价值。
| [1] |
伍尙慧, 路静. 国外无人潜航器的发展现状与张望, 电科防务研究, 2016.8. 25.
|
| [2] |
SUR, JOO-NO. Design and investigation of a dive plane sliding mode compensator for an autonomous underwater vehicle[D]. Naval Postgraduate School. USA 1989.
|
| [3] |
MICHAEL F. HAJOSY. Six degree of freedom vehicle controller design for the operation of an unmanned underwater vehicle in a shallow water environment[D]. Naval Postgraduate School. USA 1994.
|
| [4] |
HYUN-Sik KIM, YONG-Ku SHIN. Design of adaptive fuzzy sliding mode controller based on fuzzy basis function expansion for UFV depth control[J]. International journal of control, Automation and Systems, 2005, 3(2): 217-224. |
| [5] |
RAJA ROUT. Design and experimental realization of adaptive control schemes for an autonomous underwater vehicle[D]. National Institute of Technology Rourkela, India. 2017.
|
| [6] |
高剑著. 无人水下航行器自适应非线性控制技术[M]. 西安: 西北工业大学出版社, 2016: 143−149.
|
| [7] |
熊华胜, 边信黔, 施小成. 自治水下机器人深度的鲁棒H∞控制仿真[J]. 计算机仿真, 2007, 24(3).
|
| [8] |
CB/Z 259−96《潜艇空间机动控制规律》[R]. p5.
|
| [9] |
WANG Liuping. Model predictive control system design and implementation using Matlab®[M]. Verlag London Limited, 2009.
|
| [10] |
WANG Liuping, William R, CLUETT. From plant data to process control——Ideas for process identification and PID design[J]. Taylor & Francis, 2000: 10−11.
|
| [11] |
KATSUHIKO OGATA. Discrete-time controlsystems[M]. 北京: 机械工业出版社, 2004: 421−449.
|
| [12] |
PRESTERO T. Verification of a six-degree of freedom simulation model for the REMUS autonomous underwater vehicle[D]. Woods Hole Ocenographic Institu-tion, Departments of Ocean and Mechanical Engineering, MIT, MA, 2001
|
 2021, Vol. 43
2021, Vol. 43
