0 引　言

水面无人艇是一种无人驾驶、依靠遥控或自主方式在水面航行的智能化系统，具有监视侦察、扫雷、精确打击、反恐，中继通信等功能。世界各国对水面无人艇的设计都做了大量研究，尤其是在艇型和快速性、操纵性、耐波性等水动力性能方面。目前，由于能源短缺和船舶污染问题的日益凸显，多种能源的综合利用已成为绿色能源无人艇的重要发展方向。而双体无人艇更是以甲板面积大、稳性好、操纵性强和机动性高成为当前研究的热点。无人艇的艇型对其性能有显著影响，所以水面无人艇艇型的综合优化对无人艇的设计和发展具有重要意义。

国内已有学者对双体无人艇开展了研究。杨显原等^[1]基于最小阻力计入总布置对船型设计的限制对双体无人船船型方案进行优选，得到波浪中阻力性能较优的方案。吴铭浩^[2]在分析三体船水动力性能的基础上，建立了三体船阻力和耐波性能综合优化平台，并对三体船水动力性能进行了一系列船型优化研究。通过多学科优化方法,实现了三体船耐波性与阻力的综合优化。张胜^[3]改编完成一套兼顾到太阳能方案设计的双体船优化程序，得到对太阳能双体船综合性能影响较大的船型参数。马伟佳等^[4]结合线性兴波阻力理论,将给定约束条件下的艇型优化问题转换为数学优化问题,并采用非线性规划方法进行艇型优化，求解出最佳优型。魏子凡^[5]、刘曼^[6]等针对无人艇的各项性能和功能建立优化数学模型，设计出一系列综合优化平台，其中有针对单体翼滑艇、小水线面双体无人艇等不同艇型，能够计算出最佳的艇型参数，可弥补传统的母型改造法中确定船舶基本参数耗时、精度低等缺点。以上研究大都是针对单能源设计或者对单一性能考虑。

由于目前对于多种能源及性能综合优化的双体无人艇研究较少，所以为了探究双体无人艇的艇型最优设计，本文以一种绿色能源双体无人艇为研究对象，建立兼顾性能及太阳能和风帆的综合优化数学模型。基于该模型，采用遗传算法改编的综合优化设计软件对总目标函数最优情况下的遗传次数、种群规模、变异概率和交叉概率进行计算分析，并采用外部分层策略对混合算法的寻优效果及载波概率的影响进行了研究。

1 综合优化数学模型 1.1 设计变量

在满足基本设计要求的前提下，把对目标函数影响较大的参数选作设计变量。本文综合考虑性能和绿色能源共选取了24个设计变量，即螺旋桨直径 ${D_P}$ 和转速 $N$ 、盘面比 ${A_{eo}}$ 、螺距比 ${P_D}_P$ 、设计航速 $V$ 、重心垂向位置与型深比值 ${\delta _{ZD}}$ 、吃水与型深比值 $T/D$ 、片体间距 ${C_0}$ 、设计水线总宽 ${B_0}$ 、上层建筑的顶层与底层长度比值 ${\beta _{L1}}$ 、上层建筑的底层与船长的比值 ${\beta _{L2}}$ 、上层建筑宽度与船宽的比值 ${\beta _{Ba}}$ 、顶层上层建筑的高度 ${H_1}$ 、底层上层建筑的高度 ${H_2}$ 、迎风角 $\theta $ 、吃水T、方形系数 ${C_b}$ 、菱形系数 ${C_P}$ 、设计水线面系数 ${C_{wp}}$ 、浮心纵向位置 ${L_{cb}}$ 、排水量 ${D_m}$ 、湿面积 $S$ 、船长L、船宽B。其中最后8个设计变量都是根据响应面拟合的方法得出回归公式。

1.2 目标函数

本文对双体无人艇艇型优化采用多目标优化设计，一般而言，目标函数越多，设计的综合效果就越好^[7]。综合考虑了双体无人艇的快速性、操纵性、耐波性、抗倾覆性^[8]和太阳能及风帆系统，其中风帆系统以约束条件的形式表示，由于幂指数乘积的形式可以有效避开加权和形式总目标函数依赖的难以归一的问题，所以将这5个子目标函数以幂指数乘积的形式组合成总目标函数。总目标函数 $Q(x)$ 公式如下：

$Q(x) = {Q_1}{(x)^{\alpha 1}} \times {Q_2}{(x)^{\alpha 2}} \times {Q_3}{(x)^{\alpha 3}} \times {Q_4}{(x)^{\alpha 4}} \times {Q_5}{(x)^{\alpha 5}}{\text{。}}$

(1)

式中： ${\alpha _1} \text{，}{\alpha _2} \text{，}{\alpha _3} \text{，}{\alpha _4} \text{，}{\alpha _5}$ 分别为5个子目标函数的权重且都大于0， ${\alpha _1} \times \alpha {}_2 \times {\alpha _3} \times {\alpha _4} \times {\alpha _5} = 1$ 。

海军系数是用以估算船舶主机功率、航速或比较同型船舶快速性的系数，参照排水型船舶的海军系数公式，选取快速性衡准因子作为快速性的目标函数，公式如下：

${Q_1}\left( x \right) = \frac{{{V^3}{\Delta ^{2/3}}}}{{{P_S}}} = \frac{{{V^3}{\Delta ^{2/3}}{\eta _H}{\eta _O}{\eta _S}{\eta _R}}}{{{P_E}}}\text{。}$

(2)

船舶的操纵性能主要包括航向稳定性、回转性、改变及保持方向的性能等。本文只考虑航向稳定性来选取操纵性目标函数。稳定性衡准数 $C$ 是航向稳定性的判据，当 $C > 0$ 时，表示船舶在水平面运动具有直线稳定性。选用无因次化的稳定性衡准系数作为操纵性目标函数，公式如下：

${Q_2}\left( x \right) = C' = {Y_\nu }'{N_r}' - {N_v}'({Y_r}' - {m'})\text{。}$

(3)

式中： ${Y'_v}\text{，}{Y'_r}\text{，}{N'_v}\text{，}{N'_r}$ 为无因次速度流体动力导数， $m'$ 为无因次船体质量。

衡量耐波性的主要指标有：横摇、纵摇和垂荡运动的幅值。通常利用横摇无因次衰减系数 $\mu $ 预估横摇运动性能。 $\mu $ 越大，表明船舶横摇自由衰减越快，那么横摇性能就越好。本文的耐波性优化目标函数由无因次衰减系数 $\mu $ 表示，公式如下：

${Q_3}\left( x \right) = \mu = \frac{N}{{\sqrt {{{I'}_{xx}}\Delta GM} }}\text{。}$

(4)

抗倾覆性是在外力作用下偏离其初始平衡位置而倾斜，船舶具有抵抗过大外力造成船体失衡的能力。初稳性高的值过大会缩短船舶的横摇周期，但太小很容易导致倾覆。而自扶正性能主要依靠船舶横倾时的回复力实现。将初稳性高 $GM$ 和倾覆后稳性高的相反数 $\overline {G{M_1}} $ 构造为抗倾覆性目标函数，公式如下：

${Q_4}(x) = G{M^{{\eta _1}}}\times\overline {GM} _1^{{\eta _2}}\text{。}$

(5)

式中： ${\eta _1}{\text{，}}{\eta _2}$ 分别为正浮初稳性和自扶正性能的权重且都大于0，且 ${\eta _1} \times {\eta _2} = 1$ 。

假定无人艇是全天候工作，每天有效光照时长为4.5 h，单晶硅太阳能电池板的转化效率为18%，太阳辐射强度为1000 ${\rm W}/{{\rm m}^2}$ ，根据布置在双体无人艇上太阳能电池板的面积构造目标函数，公式如下：

${Q_5}\left( x \right) = S = \frac{{24\times{P_S}/4.5}}{{1000 \times 0.18}} = 0.03{P_S}\text{。}$

(6)

1.3 约束条件

1）等式约束

静水浮性约束即设计排水量与双体无人艇优化得到的排水量一致，公式如下：

$\Delta = 2\rho LBT{C_b}\text{；}$

(7)

转矩平衡约束即主机提供螺旋桨的转矩等于螺旋桨所承受的水动力转矩，公式如下：

$\frac{{{\eta _R}{\eta _s}{P_s}}}{{2\pi N}} = {K_Q}\rho {N^2}D_p^5\text{；}$

(8)

推力平衡约束即双体无人艇航行时承受的总阻力等于风帆产生的推力 $T{}_t$ 与双螺旋桨产生的有效推力之和，公式如下：

${R_t} = {T_t} + 2{N_p}{K_T}\rho {N^2}{D_p}^4(1 - t)\text{。}$

(9)

2）不等式约束

设计螺旋桨需满足空泡要求，公式如下：

$(1.3 + 0.3Z){T_e}/(({P_0} - {P_V})D_P^2) + K - {A_{eo}} \leqslant 0\text{；}$

(10)

为了符合船舶的稳性规范，正浮初稳性高需大于0.3 m，公式如下：

$GM > 0.3\text{；}$

(11)

上层建筑的总高度应大于翻转后的吃水，公式如下：

${T_1} < {H_1} + {H_2}\text{；}$

(12)

翻转后的初稳性高应要大于0，公式如下：

$G{M_1} > 0\text{；}$

(13)

太阳能电池板与无人艇甲板的总面积之间的关系如下：

$S < 1.2L{B_O}\text{；}$

(14)

考虑风帆对于稳性的影响，横倾角度小于12°，公式如下：

${\theta _1} < {12^\circ }\text{。}$

(15)

2 遗传算法的优化计算与分析

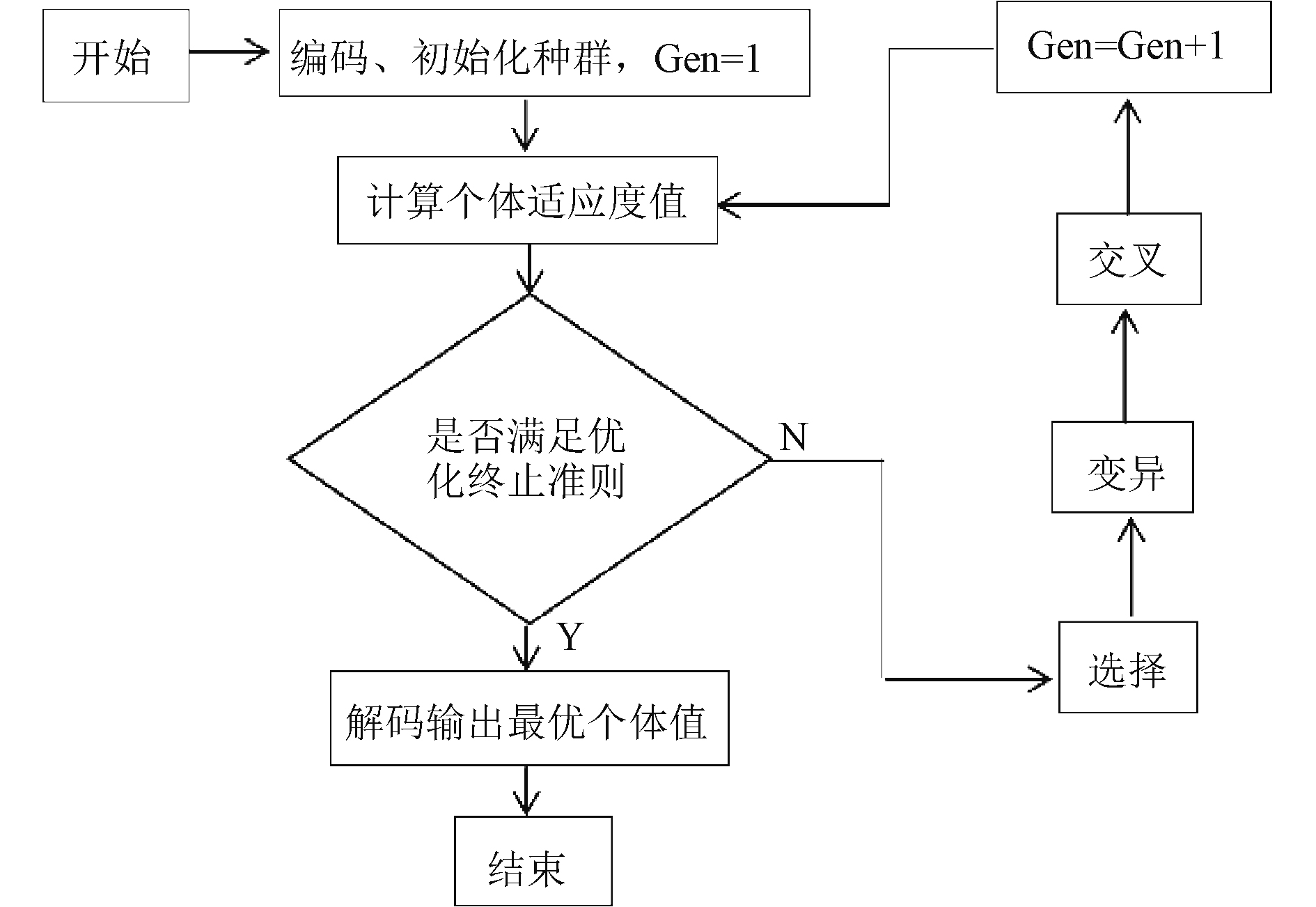
遗传算法（GA）采取二进制编码，在初始种群产生后，按照适者生存和优胜劣汰的原理，逐代演化出越来越好的近似解。在每一代中，根据问题域中个体适应度值的大小选择优秀的个体，并借助遗传算子进行组合交叉和变异产生出代表新的解集的种群。这个过程使种群像自然进化一样，后代比前代更加适应于环境，末代种群的最优个体经过解码，可以作为问题近似最优解^[9]。遗传算法的运算过程如图1所示。

基于所建立的综合优化数学模型和遗传算法以C#语言在Microsoft Visual Studio环境下改编了综合考虑性能和绿色能源的双体无人艇综合优化设计软件。首先在满足要求的前提下，进行权重设置。对约束条件及设计变量上下限的范围进行设置，得到遗传算法的优化计算结果。

不同遗传次数、种群规模、交叉概率和变异概率情况下对总目标函数值有重要影响。计算参数设置如下：选择交叉变异策略；内层载波概率：0.0001～0.01；种群规模：200～600；遗传次数：3000～8000；交叉概率：0.4～0.9、变异概率：0.001～0.01。设定单一情况变量，且每种情况需要进行多次计算，当浮性约束、推力约束及转矩约束的条件都满足99%时说明计算结果可用，最后选取总目标函数值最大时作为最优结果。

一般情况下，迭代一定次数以后，基本上不会再有更好的解出现。根据计算经验和计算时间设定遗传次数的讨论范围在3000～8000之间，表1为不同遗传次数的优化计算结果。可以发现，随着遗传次数的增大，总目标函数值起初是波动变化的，随后逐渐增大，当遗传次数达到7000和8000时，总目标函数值开始趋于稳定，但考虑到遗传次数越大时，优化计算时间会过长，因此后文讨论情况都设定遗传次数为7000。

遗传次数确定后，接下来讨论种群规模的影响。种群规模指每一代优化计算中个体的总数，种群规模越大越可能找到全局解，一般而言种群规模越大优化结果越好，但运行时间也相对较长。表2为种群规模在200～600之间的优化计算结果。可以看到，总目标函数值随着种群规模的增大总体呈增大的趋势，当种群规模为500和600时，总目标函数值是相等的，说明在种群规模为500时，已达到最优的结果，因此本文后续的讨论均采用种群规模为500。

除了遗传次数和种群规模外，交叉和变异概率对总目标函数值也有很大的影响。其中各代中交叉产生的子代数与种群中个体总数的比例称为交叉概率，交叉概率太大就会失去意义,而太小时则收敛速度太慢。本文讨论交叉概率在0.4～0.9之间对总目标函数值的影响，表3为不同交叉概率的计算结果。从表中发现当交叉概率为0.9时，总目标函数值最大，说明较高的交叉概率能达到更大的解空间，从而更容易达到最优解，因此后续的讨论情况下交叉概率取较高值0.9。

变异是在个体上自发地产生随机的变化，可以提供初始种群中不含有的基因，或者找到选择过程中丢失的基因，为种群提供新的内容^[10]。变异概率控制着新基因导入种群的比例，是允许少数个体存在变异情况，以避免限入局部最优解，其值不宜过大，一般在0.1以下。表4为不同变异概率的计算结果。从表中可以发现，变异概率为0.04时总目标函数值最大，即此时的优化效果最佳。

综上所述，以上优化计算结果均满足约束条件，且在本文的优化数学模型下，总目标函数最优时参数设定如下：遗传次数7000、种群规模500，交叉概率和变异概率分别选择0.9和0.04。

3 混合算法的比较分析

为了保证种群朝着最优个体进化，又能保存上一代个体的原始特征。在遗传算法的基础上可以采用外部分层策略进行继续寻优。外部分层策略的思想是下一代种群中最差的部分个体根据上一代最好的几个个体的特性在其邻域内随机产生的。首先选择记录几个最好的值，当一次优化完成后，根据软件记录的较好值，依据设定的载波概率（最优个体的邻域大小与整个寻优区间的比值），更新此时设计变量的上下限后，进行第2次优化计算。而第2次的优化计算可以选择相同或者不同的优化算法，本文除了遗传算法GA外还采用了粒子群算法PSO和混沌算法CA进行混合算法的计算分析。

参数设置如下：粒子群算法种群规模500，变权重0.9～0.4，最大粒子飞行速度与区间概率0.1，迭代次数7000代。混沌算法迭代次数100000，外层载波概率0.005。外部分层策略的计算结果如表5所示。可见约束条件均满足99%，说明计算结果可靠。通过对比可以得出，混合算法的寻优效果均高于单一遗传算法，且在采用遗传+粒子群算法时优化效果最佳，总目标函数值达到0.453。

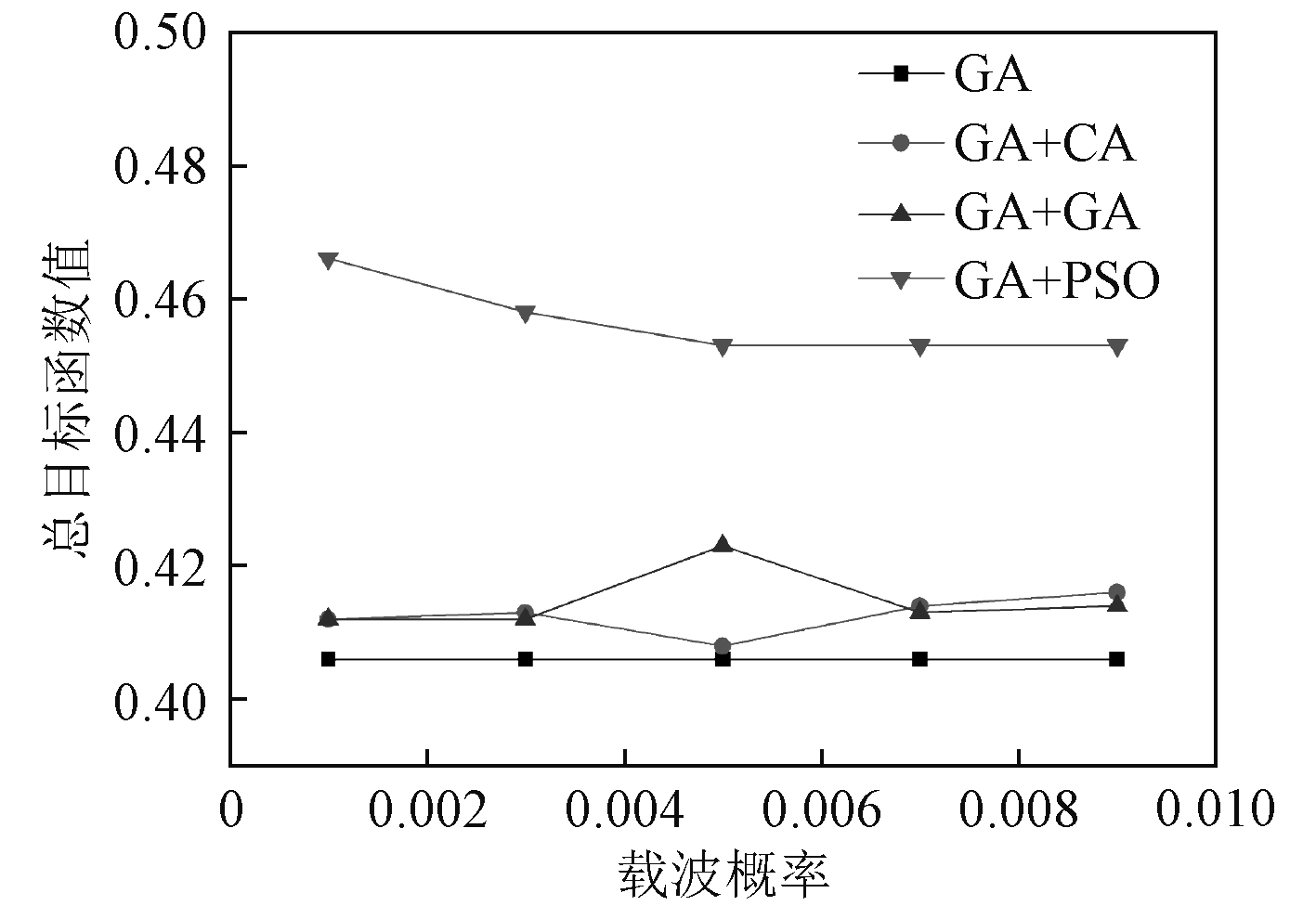
下面讨论不同载波概率时，单一算法和混合算法的寻优效果。图2为不同载波概率下各算法的总目标函数值。可以发现，在不同载波概率下混合算法的寻优效果亦均高于单一遗传算法，而遗传算法+粒子群算法的寻优效果又明显高于其他混合算法。另外可以看到，遗传算法+粒子群算法的总目标函数值随着载波概率的增加逐渐减小，并在0.005时趋于稳定值。

4 结　语

本文以一种绿色能源双体无人艇为研究对象，建立了兼顾性能及太阳能和风帆的综合优化数学模型。基于该模型，采用遗传算法改编的综合优化设计软件对总目标函数最优情况下的遗传次数、种群规模、变异概率和交叉概率进行计算分析，并采用外部分层策略对混合算法的寻优效果及载波概率的影响进行研究，结果如下：

1）总目标函数值基本随着遗传次数、种群规模的增加而变大，并最终趋于稳定值。由于遗传次数和种群规模过大时，会导致优化计算时间过长且不一定能得到更好的结果，所以有必要寻求最优值。对于本文的优化数学模型而言，当遗传次数为7000、种群规模为500时，总目标函数值已达到最大值，说明此时的优化效果已经最佳。

2）不同的变异概率和交叉概率对于总目标函数值存在不同影响。本文中当交叉概率为0.9时，总目标函数值最大，此时能达到更大的解空间，而变异概率为0.04时，优化结果最优，说明应在种群中适量导入新的基因。

3）相比于单一遗传算法，混合算法的优化效果更好，且在不同载波概率情况下，遗传算法+粒子群算法的优化效果均为最佳，外部分层策略可以有效提高寻优效果。