0 引　言

立管是进行海洋油气勘探开发的关键设备，连接工作平台与海底作业区。一般分为钻井立管和生产立管。钻井立管输送钻井用的液体，而生产立管把海底的油气输送到海面平台上。立管在均匀来流作用下受到的流体力可以分为升力F_L和阻力F_D。在阻力F_D的作用下，立管首先会产生一个流向（In-Line:IL）的变形，并以此位置为平衡位置进行流向振动。阻力F_D可进一步分解为平均阻力和周期阻力，即 ${F_d} = \mathop {{F_d}}\limits^ - + {F_d}(t)$ 。周期阻力引起立管流向振动，影响立管的疲劳性能。平均阻力主导立管的结构强度。

以往的研究表明，柔性立管的阻力特性与刚性圆柱阻力特性显著不同。柔性立管发生涡激振动（VIV）时，VIV对立管的阻力有放大效应。在亚临界雷诺数区间，柔性立管阻力系数CD通常大于1.2。而且由于目前对于涡激振动的机理并未有深入的理解，因此针对柔性立管的阻力特性，数值计算无法获得准确的预报。模型试验是研究柔性立管阻力特性的主要手段。Vandiver^[1]及Chaplin^[2]分别提出了基于模型试验的柔性立管平均阻力计算经验公式。宋磊建^[3] 针对立管表面应变时历，分析获得平均阻力及表征立管涡激振动响应的相关参数，并在此基础上拟合出平均阻力计算公式。

目前的模型试验相关的文献中缺乏明确的关于柔性立管试验特性试验数据处理技术的研究。而良好的数据处理技术是分析柔性立管阻力特性的关键部分。

为此，本文提出3种数据处理方法，通过分析立管表面初始应变，获得均匀来流作用下柔性立管的阻力分布。

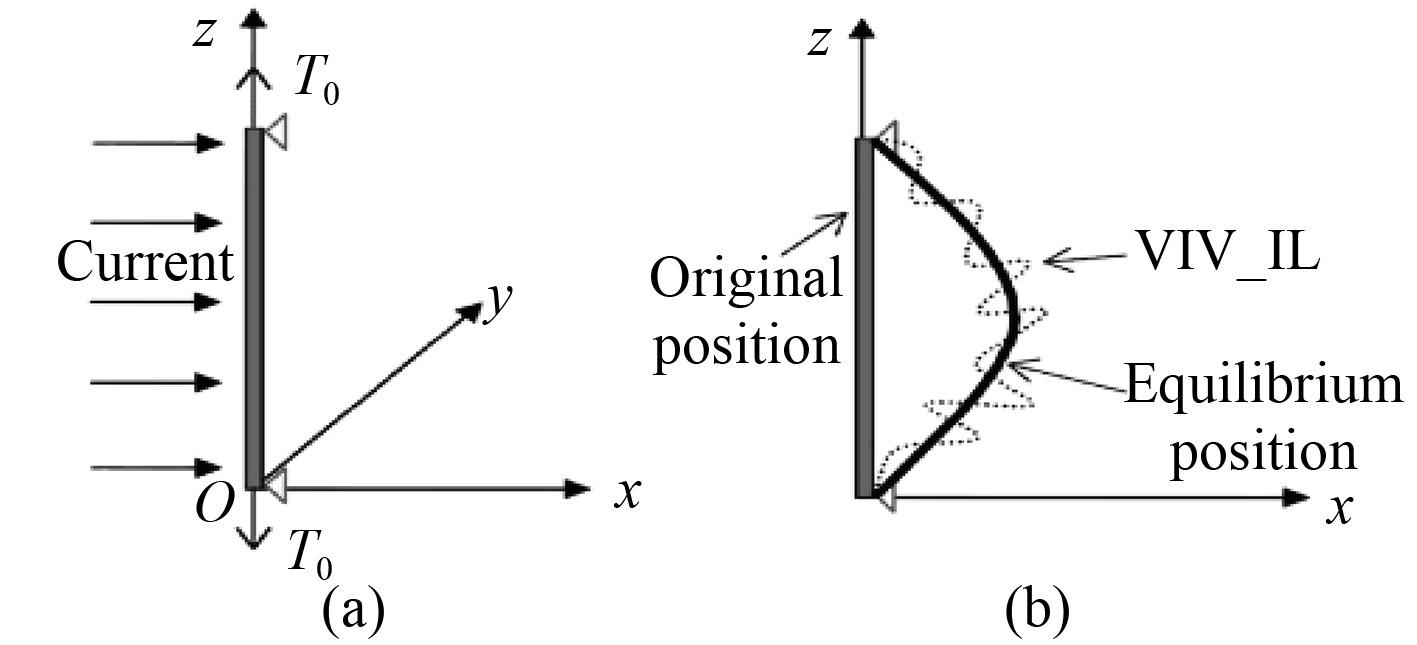
1 柔性立管初始弯曲及微分方程 1.1 立管初始弯曲与轴向张力

均匀来流中，柔性立管在平均阻力的作用下会产生一个流向的变形，并以此位置为平衡位置作IL向及CF向的振动，表现出复杂的流固耦合特性。均匀来流作用下柔性立管的初始变形如图1所示。

试验中，立管模型水平放置在水面下并通过两端弹簧装置固定。固定装置可施加轴向力并记录。整个试验装置由拖车拖动，模拟均匀来流。本文中立管模型的基本结构参数见表1。

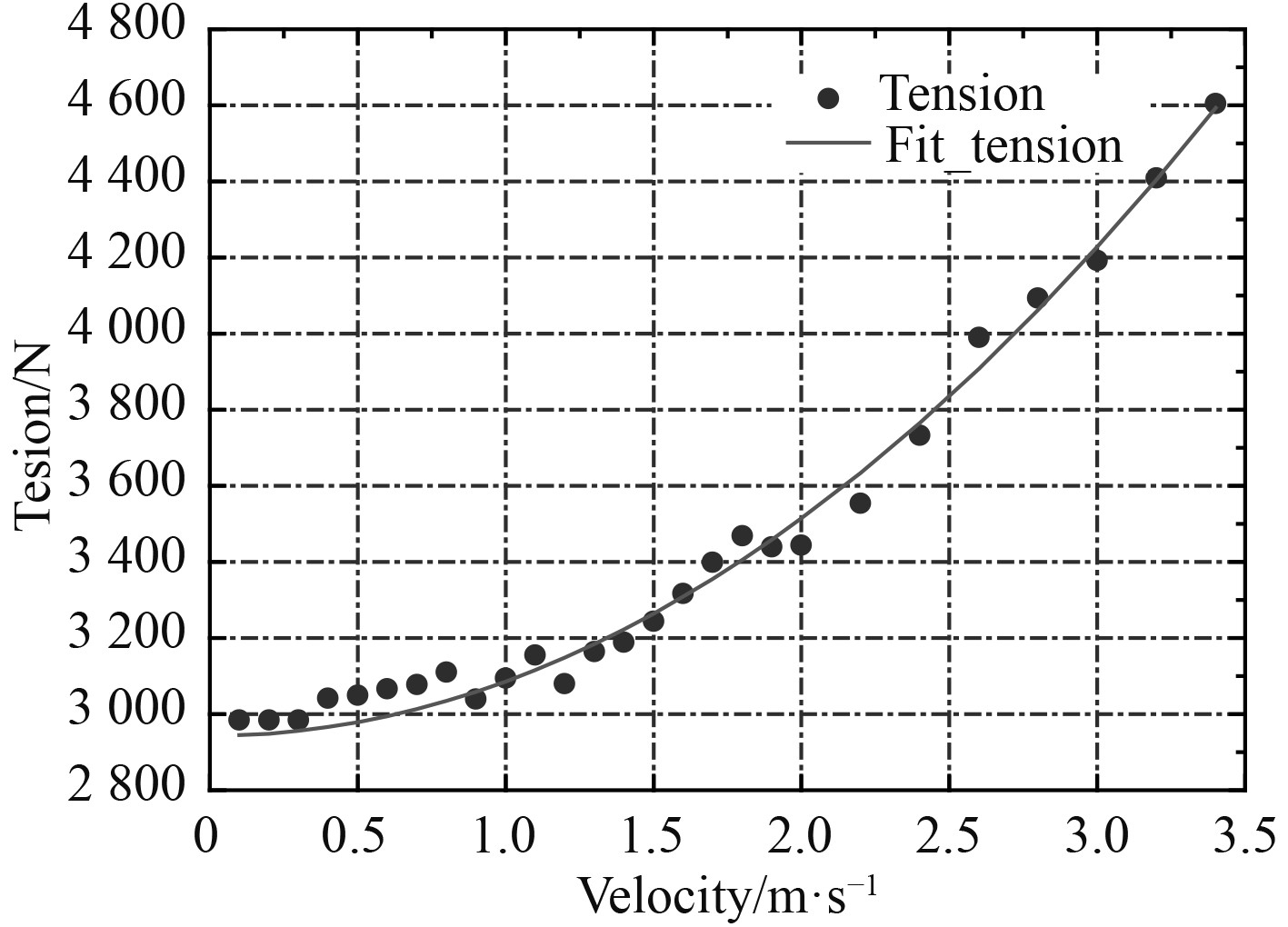
试验表明，立管两端轴向力随流速的增大而增大，不同流速下立管两端的轴向力如图2所示。可知，个别数据点（如 $v = 0.9\;{\rm{m/s}}$ ）表现出流速增大反而轴向力减小的情况。由于试验中最大雷诺数在10⁵左右，并未进入阻力危机区^[4]，因此上述情况可以认为是试验误差，同时也必须对立管两端的轴向力进行标定。参考Morision公式中计算阻力的部分，假设轴向力的增量正比于流速的平方，即 $\Delta {T_v} = {T_v} -{T_0} = $ k{v^2}$ ，对轴向力的实测数据进行拟合，标定后的立管轴向力用于计算立管初始阻力。

1.2 立管的复杂弯曲及初始应变

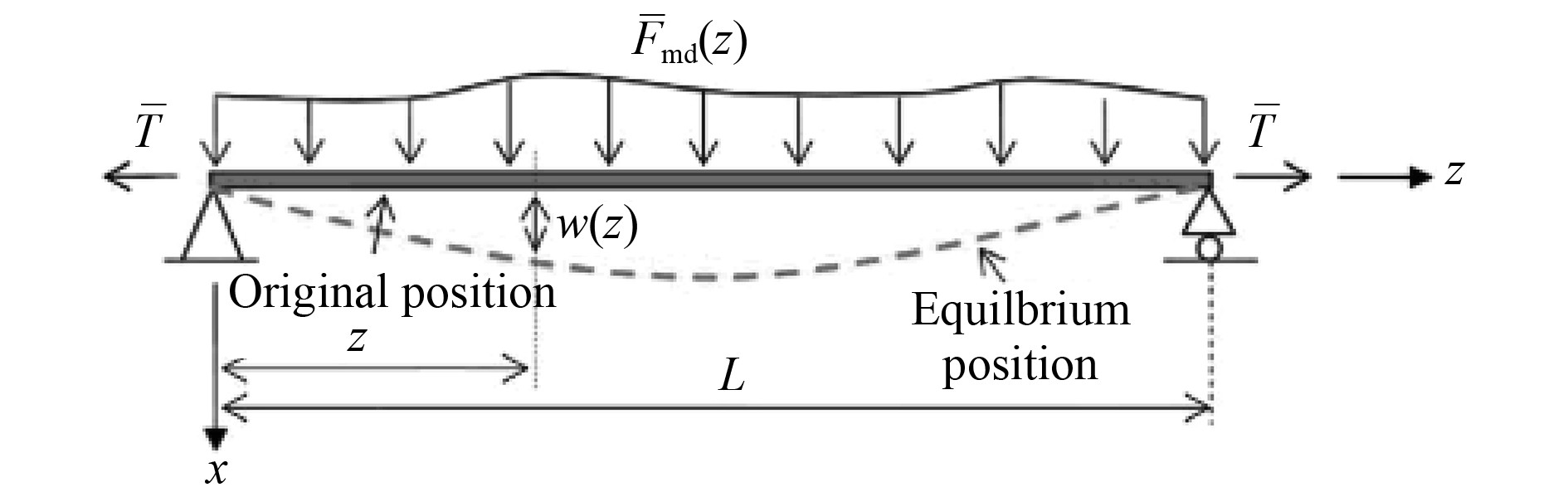
海洋立管可以简化为梁模型。假设立管水平，以立管一端作为坐标原点，沿立管轴向为z向，垂直向下为x向建立笛卡尔坐标系，如图2所示。

在平均拖曳力的作用下，立管变形的方程如下：

$EI\frac{{{\partial ^4}w(z)}}{{\partial {z^4}}} - \overline T \frac{{{\partial ^2}w(z)}}{{\partial {z^2}}} = {F_d}(z),$

(1)

其中： $w(x)$ 为立管初始变形挠度； $EI$ 为立管抗弯刚度； $\overline T $ 为立管模型平均张力； ${F_d}(z)$ 为沿立管轴向分布的平均拖曳力。根据梁弯曲理论，立管初始弯曲变形挠度与立管表面初始弯曲应变存在如下关系：

$\frac{{{\partial ^2}w(z)}}{{\partial {z^2}}} = \frac{{\varepsilon (z)}}{R}{\text{。}}$

(2)

其中：R为立管模型的半径； $\varepsilon (x)$ 为初始弯曲引起的立管表面应变，即初始应变。将式（2）代入式（1）后得到初始应变与初始阻力之间的关系：

$EI\frac{{{\partial ^2}\varepsilon (z)}}{{\partial {z^2}}} - \mathop T\limits^ - \varepsilon (z) = {F_d}(z)R,$

(3)

进一步地，根据Morision公式计算每一个截面出的阻力系数：

${C_d}(z) = \frac{{2{F_d}(z)}}{{\rho D{V^2}}},$

(4)

其中：D为立管的水动力直径，沿立管长度方向上取平均即可得到立管的平均阻力系数：

$\mathop {{C_d}}\limits^ - = \frac{{\int_0^L {{C_d}(z){\rm{d}}z} }}{L},$

(5)

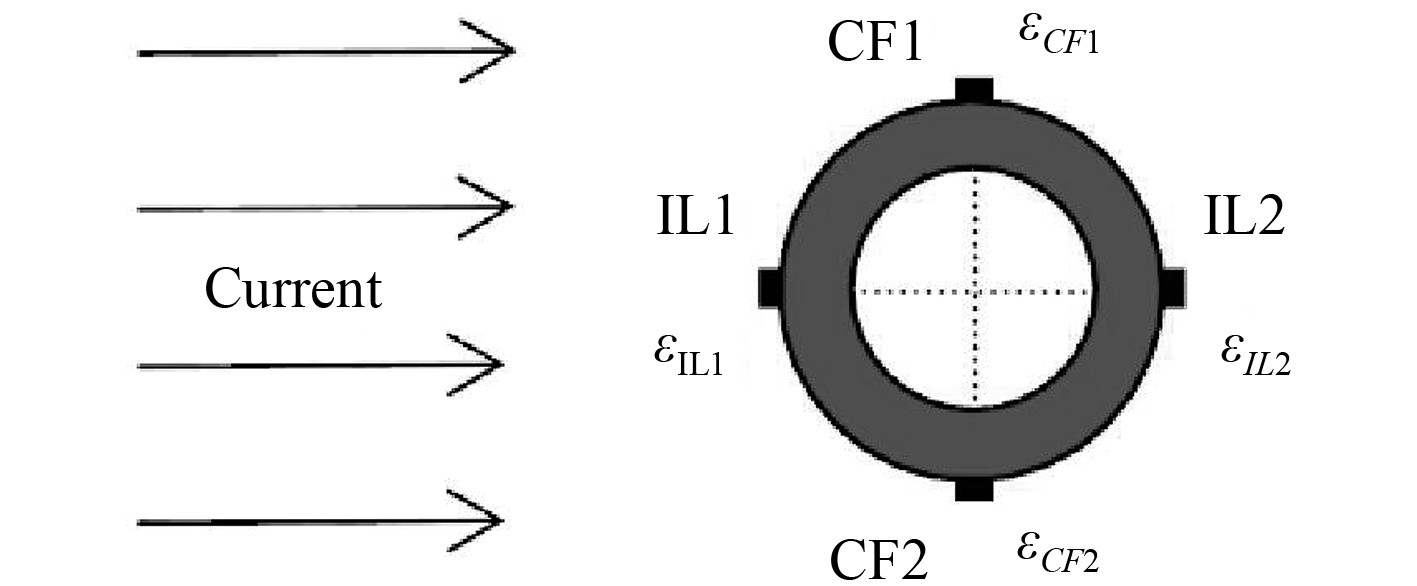
试验中，立管表面IL及CF方向分别布置一对传感器，如图4所示。

传感器记录的应变分为2个部分：轴向力引起的拉应变及流体阻力引起的弯曲应变，即

$\varepsilon (t) = {\varepsilon _T} + {\varepsilon _{{F_d}}}(t),$

(6)

而由式（3）可知，弯曲应变与流体阻力呈线性关系，即弯曲应变可表示为：

${\varepsilon _{{F_d}}}(t) = {\varepsilon _{\overline {{F_d}} }} + {\varepsilon _{{F_d}(t)}}(t),$

(7)

对于流向布置的一对传感器，弯曲应变符号相反，而拉应变相同，于是有：

$\begin{split} {\varepsilon _{IL1}}(t) = {\varepsilon _T} - ({\varepsilon _{\overline {{F_d}} }} + {\varepsilon _{{F_d}(t)}}(t)), \\ {\varepsilon _{IL2}}(t) = {\varepsilon _T} + ({\varepsilon _{\overline {{F_d}} }} + {\varepsilon _{{F_d}(t)}}(t)), \\ \end{split} $

(8)

消去对式（8）中的拉应变得到：

${\varepsilon _{\overline {{F_d}} }} + {\varepsilon _{{F_d}(t)}}(t) = \frac{{{\varepsilon _{IL2}}(t) - {\varepsilon _{IL1}}(t)}}{2},$

(9)

周期阻力 ${F_d}(t)$ 的时间平均为0，所以 ${\varepsilon _{{F_d}(t)}}(t)$ 的时间平均也为0，于是对式（9）取时间平均就可以得到平均阻力引起的弯曲应变，即

${\varepsilon _{\overline {{F_d}} }} = \overline {\frac{{{\varepsilon _{IL2}}(t) - {\varepsilon _{IL1}}(t)}}{2}} {\text{。}}$

(10)

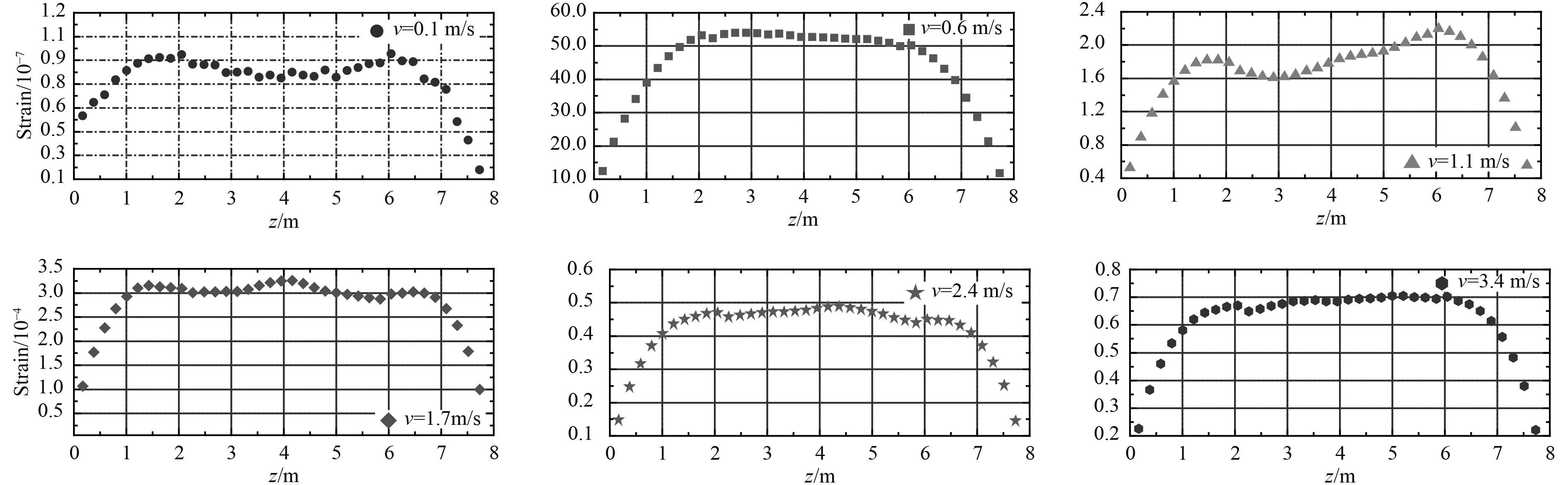
经过以上分析即可得到不同流速下立管表面的弯曲应变，如图5所示。可知：初始应变随流速的增大而增大；立管中间与两侧截面处的阻力特性不同，立管中间截面平均阻力可能更小。

2 柔性立管阻力试验数据分析原理

试验中的应变信号不可避免地包含噪声。如果噪声过大，应变信号将失去分析意义。良好的信号中，噪声必然不会太大。因此为简化分析，以下数据分析原理基于应变信号良好进行理论推导。同时通过在算例中设置包含噪声的应变信号以考察不同数据分析方法对于噪声的处理能力。

2.1 模态分析法原理（DPP_1）

由式（3）知，平均阻力的分析需要计算初始应变的2阶导数 $\dfrac{{{\partial ^2}\varepsilon (z)}}{{\partial {z^2}}}$ 。由图5可知，用差分方法估算应变的2阶导数，必然会产生较大的数值误差。因此，如果用光滑的函数拟合初始应变，对拟合后的函数求导将会避免上述误差的产生。由于立管两端铰接，两端弯矩为0。由 $EI\dfrac{\varepsilon }{R} = M$ ，所以拟合函数在边界必须满足 $\varepsilon (0) = \varepsilon (L) = 0$ 。傅里叶分析知道，任何信号都可以分解成一定量正弦信号的和，参考振动分析中的模态分析，可假设 $\varepsilon = \displaystyle\sum\limits_{i = 1}^n {{A_i}\sin \left( {i{{\text{π}}} \dfrac{z}{L}} \right)}$ 。对于第i阶模态 ${\varepsilon _i} = {A_i}\sin \left( {i{\text{π}} \frac{z}{L}} \right)$ ，代入式（3）后得到：

${F_d}{(z)_i} = - {A_i}\left( {EI{\left( {\frac{{i{\text{π}} }}{L}} \right)^2} + \mathop T\limits^ - } \right)\frac{1}{R}\sin \left( {i{\text{π}} \frac{z}{L}} \right){\text{。}}$

(11)

因此只需求出每阶模态权重 ${A_i}$ ，即可得到对应的平均阻力。显然分析的阶数越多，应变的拟合越准确，阻力的分析也相应越准确。与此同时由式（11）知，阻力的误差正比于阶数的平方。因此，分析阶数越高，误差也会相应越大。因此模态分析法中，分析阶数的太少或太多都会使结果不准确。

假设立管上布置有M个测点，对于第k个测点有 ${\varepsilon _k} = \displaystyle\sum\limits_{i = 1}^n {{A_i}\sin \left( {i{\text{π}} \dfrac{{{z_k}}}{L}} \right)}$ ，写成向量的形式为 ${\varepsilon _k} = [ {{A_1}} $ {{A_2}}\quad \cdots \quad {{A_n}}]{\left[ {\sin \left( {\dfrac{{\text{π}} }{L}{z_k}} \right)}\quad {\sin \left( {\dfrac{{2{\text{π}} }}{L}{z_k}} \right)}\quad \cdots \quad {\sin \left( {\dfrac{{n{\text{π}} }}{L}{z_k}} \right)}\right]^{\rm{T}}}$ 。对于所有测点，写成矩阵的形式为：

$\begin{split} \left[ {\varepsilon (z)} \right] &= \left[ {{A_1}}\quad{{A_2}} \quad \cdots\quad {{A_n}} \right]\times \\ &\quad{\left[ {\begin{array}{*{20}{c}} {\sin \left( {\dfrac{{\text{π}} }{L}{z_1}} \right)}&{\sin \left( {\dfrac{{2{\text{π}} }}{L}{z_1}} \right)}& \cdots &{\sin \left( {\dfrac{{n{\text{π}} }}{L}{z_1}} \right)} \\ {\sin \left( {\dfrac{{\text{π}} }{L}{z_2}} \right)}&{\sin \left( {\dfrac{{2{\text{π}}}}{L}{z_2}} \right)}& \cdots &{\sin \left( {\dfrac{{n{\text{π}}}}{L}{z_2}} \right)} \\ \vdots & \vdots & \ddots & \vdots \\ {\sin \left( {\dfrac{{\text{π}} }{L}{z_m}} \right)}&{\sin \left( {\dfrac{{2{\text{π}}}}{L}{z_m}} \right)}& \cdots &{\sin \left( {\dfrac{{n{\text{π}}}}{L}{z_m}} \right)} \end{array}} \right]^{\rm{T}}}_{n \times m} {\text{。}} \end{split}$

(12)

求解线性方程式（12）即可得到每一阶模态对应的模态权重，再由式（11）即可计算出立管每个截面处的对应的平均阻力。

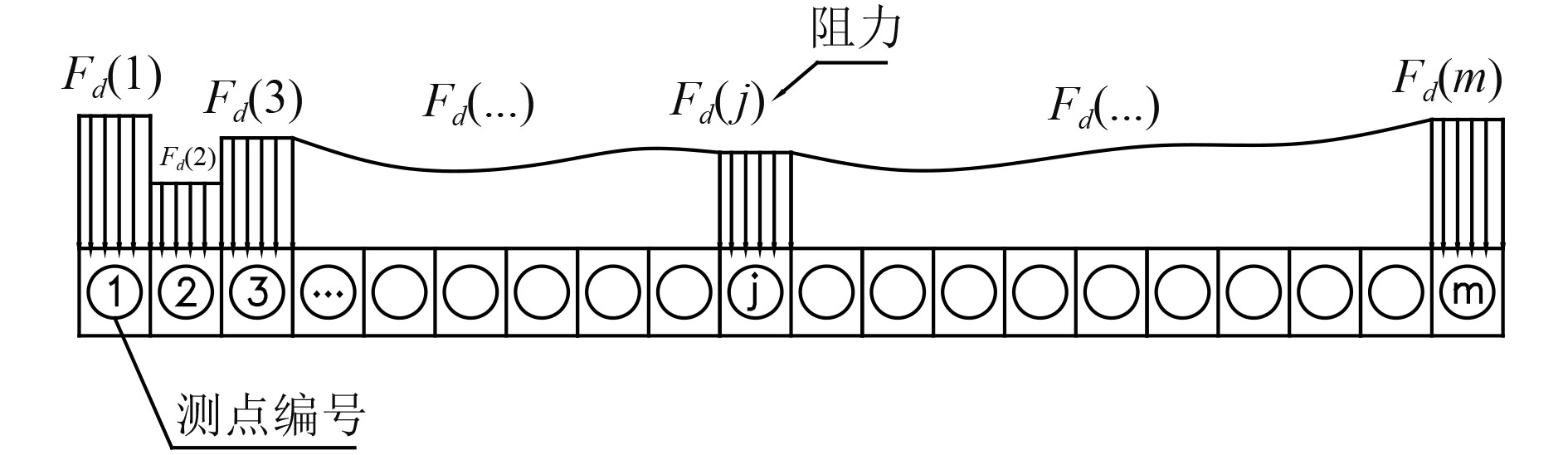
2.2 微段载荷分析法原理（DPP_2）

假设在立管轴向很小的范围内阻力是均匀分布的。将立管划分为m段，在第j段上流体阻力为 ${F_d}(j)$ ，如图6所示。这段阻力会在整根立管上产生弯曲应变， ${\varepsilon _{ij}}$ 表示第j段上的阻力在第i段上产生的弯曲应变。

现仅考虑立管在第j段上有微段载荷，假设第j段的起始坐标分别为 ${z_{sj}}$ ， ${z_{ej}}$ ，对应的应变假设为 $\varepsilon ({z_{sj}})$ ， $\varepsilon ({z_{ej}})$ 。在第j段之前应变满足方程：

$\begin{split} EI\frac{{{\partial ^2}\varepsilon (z)}}{{\partial {z^2}}} - \mathop T\limits^ - \varepsilon (z) = 0 , \\ \varepsilon {|_{z = 0}} = 0,\varepsilon {|_{z = {z_{js}}}} = \varepsilon ({z_{js}}) ,\\ \end{split} $

(13)

在j段上满足方程：

$\begin{split} EI\frac{{{\partial ^2}\varepsilon (z)}}{{\partial {z^2}}} - \mathop T\limits^ - \varepsilon (z) = {F_d}(j)R, \\ \varepsilon {|_{z = {z_{js}}}} = \varepsilon ({z_{js}}),\varepsilon {|_{z = ze}} = \varepsilon ({z_{je}}) , \\ \end{split} $

(14)

在j段以后满足方程：

$\begin{split} EI\frac{{{\partial ^2}\varepsilon (z)}}{{\partial {z^2}}} - \mathop T\limits^ - \varepsilon (z) = 0 ,\\ \varepsilon {|_{z = {z_{js}}}} = \varepsilon ({z_{js}}),\varepsilon {|_{z = L}} = 0 , \end{split} $

(15)

显然在j段的两端剪力为0，由弯曲梁理论知道 $EI\dfrac{\varepsilon }{R} = M$ ， $\dfrac{{\partial M}}{{\partial z}} = N$ ，于是在第j段的两端满足方程：

$\begin{split} \frac{{\partial \varepsilon }}{{\partial z}}{|_{z = {z_{js - }}}} = \frac{{\partial \varepsilon }}{{\partial z}}{|_{z = {z_{js + }}}} ,\\ \frac{{\partial \varepsilon }}{{\partial z}}{|_{z = {z_{je - }}}} = \frac{{\partial \varepsilon }}{{\partial z}}{|_{z = {z_{je + }}}} ,\\ \end{split} $

(16)

联立式（13）～式（16）即可求出微段载荷作用下立管的应变。显然 ${\varepsilon _{ij}}$ 与 ${F_d}(j)$ 呈线性关系，即

${\varepsilon _{ij}} = {R_{ij}}{F_d}(j),$

(17)

其中： ${R_{ij}}$ 与 ${F_d}(j)$ 的大小无关，表示第j段单位载荷引起的i段的应变。第i各测点的应变为每个微段上的阻力在第i段上产生的弯曲应变之和，即

$\begin{split} {\varepsilon _i} = \sum\limits_{j = 1}^m {{\varepsilon _{ij}}} = &\left[ {\begin{array}{*{20}{c}} {{F_d}(1)}&{{F_d}(2)}& \cdots &{{F_d}(m)} \end{array}} \right],\\[-8pt] &{\left[ {\begin{array}{*{20}{c}} {{R_{i1}}}&{{R_{i2}}}& \cdots &{{R_{im}}} \end{array}} \right]^{\rm{T}}} ,\end{split}$

(18)

于是在整根立管上有

$\begin{split}\left[ {\varepsilon (z)} \right] = & \left[ {\begin{array}{*{20}{c}} {{F_d}(1)}&{{F_d}(2)}& \cdots &{{F_d}(m)} \end{array}} \right]\times\\ &{\left[ {\begin{array}{*{20}{c}} {{R_{11}}}&{{R_{12}}}& \cdots &{{R_{1m}}} \\ {{R_{21}}}&{{R_{22}}}& \cdots &{{R_{2m}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{R_{m1}}}&{{R_{m2}}}& \cdots &{{R_{mm}}} \end{array}} \right]^{\rm{T}}}_{m \times m}{\text{。}}\end{split}$

(19)

求解式（19）即可得到每一个微段上作用的流体阻力。本方法避免了求解2阶导数的过程，可避免模态分析法放大误差的问题，也不存在阶数选择问题，不会引入人为误差。

2.3 逼近分析法原理（DPP_3）

文献[5]指出，漩涡在圆柱体表面脱落时的相关长度很小。因此可以认为漩涡的脱落是成片的，立管的阻力大致上是均匀分布的。因此首先假设阻力在立管上是完全均匀分布的，对应的初始阻力记为 ${F_{d1}}$ ，可以将 ${F_{d1}}$ 在坐标 ${z_i}$ 引起的弯曲应变表示为 $\varepsilon ({z_i}) = {F_{d1}}{R_{id1}}$ ，于是对于整根立管有：

$\begin{aligned}&\left[ {\varepsilon ({z_1}),\varepsilon ({z_2}), \cdots\varepsilon ({z_m})} \right] =\\ &{F_{d1}}\left[ {\begin{array}{*{20}{c}} {{R_{1d1}}}&{{R_{2d1}}}& \cdots &{{R_{md1}}} \end{array}} \right],\end{aligned}$

(20)

解式（20）可以得到第一次均布阻力 ${F_{d1}}$ 。

称 $\Delta 1\_\varepsilon =\left[ {\varepsilon ({z_1}),\varepsilon ({z_2}),\cdots\varepsilon ({z_m})} \right]-{F_{d1}} \left[ {{R_{1d1}}}\;{{R_{2d1}}}\cdots {{R_{md1}}} \right]$ 为一次差。显然如果阻力均匀分布，那么一次差 $\Delta 1\_\varepsilon $ 接近为0，反之则 $\Delta 1\_\varepsilon $ 不为0。若 $\Delta 1\_\varepsilon $ 不为0，可以假设立管在前1/2与后1/2上的阻力分别是均布的，对应的阻力分别为 ${F_{d21}}$ ， ${F_{d22}}$ ，其在坐标 ${z_i}$ 处的弯曲应变为：

${\varepsilon _i} = {R_{id21}}{F_{d21}} + {R_{id22}}{F_{d22}},$

(21)

对于整根立管有：

$\left[ {\Delta 1\_\varepsilon (z)} \right] = \left[ {{F_{d21}}}\quad {{F_{d22}}} \right]\left[ {\begin{array}{*{20}{c}} {{R_{1d21}}}&{{R_{2d21}}}& \cdots &{{R_{md21}}} \\ {{R_{1d22}}}&{{R_{2d22}}}& \cdots &{{R_{md22}}} \end{array}} \right]\text{。}$

(22)

解式（22）可以得到第二次均布阻力 ${F_{d21}}$ ， ${F_{d22}}$ 。类似地，可以求出二次差 $\Delta 2\_\varepsilon $ ，如果二次差不为0，可以将前后1/2分别继续均分，求出 ${F_{d41}}$ ， ${F_{d42}}$ ， ${F_{d43}}$ ， ${F_{d44}}$ ，即每1/4长度上的阻力。假设最终计算n次差 $\Delta n\_\varepsilon $ 相比于原始应变数据已经很小，那么就可以认为立管上阻力的计算已经足够准确。此时立管被均分为 ${2^{n - 1}}$ 段，第i段上的阻力

${F_{di}} = {F_{d{2^{n - 1}}i}} + {F_{d{2^{n - 2}}rup(i/2)}} + {F_{d{2^{n - 3}}rup(i/4)}} + \cdots + {F_{d1}},$

(23)

其中rup表示向上取整。

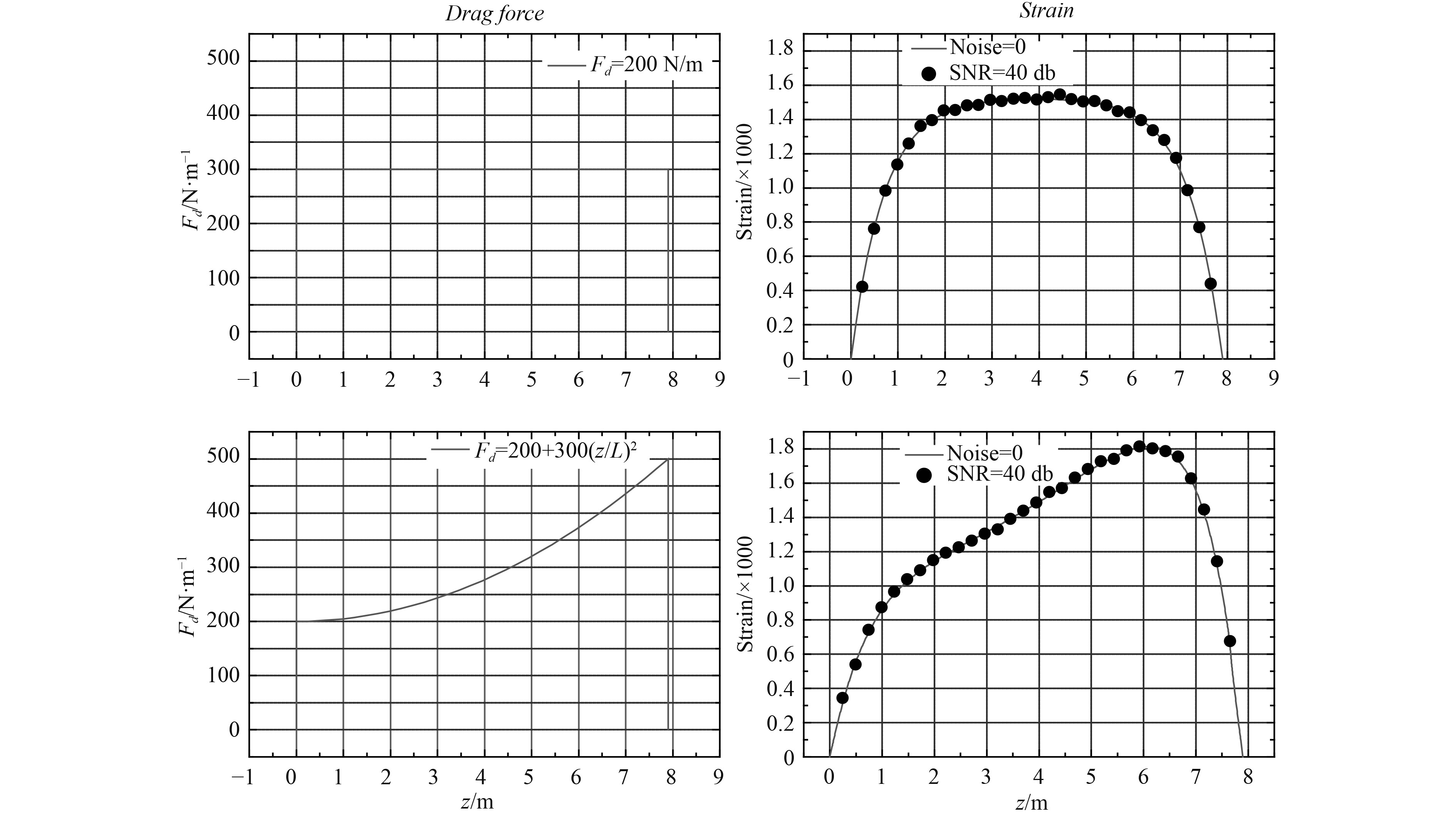
2.4 算例与分析

考虑立管在海洋中遭遇的2种典型来流情况：均匀来流和阶梯流，假设立管上分别作用均布载荷及阶梯分布载荷，通过求解式（3）计算立管表面弯曲应变，使用上述3种数据处理方法，分析应变数据，计算流体阻力的大小及分布。进一步地，对生成的弯曲应变增加白噪声信号，比较3种数据处理方法对包含噪声信号的处理能力。立管参数及轴向力按表1选取，流体阻力分别为 ${F_{d1}} = 300 \;{\rm{N/m}}$ ， ${F_{d2}} = 200 + 300 \times $ {\left( {\dfrac{z}{L}} \right)^2}(N/m)$ ，随机信号的信噪比设SNR为40 dB，计算出的弯曲应变如图7所示。

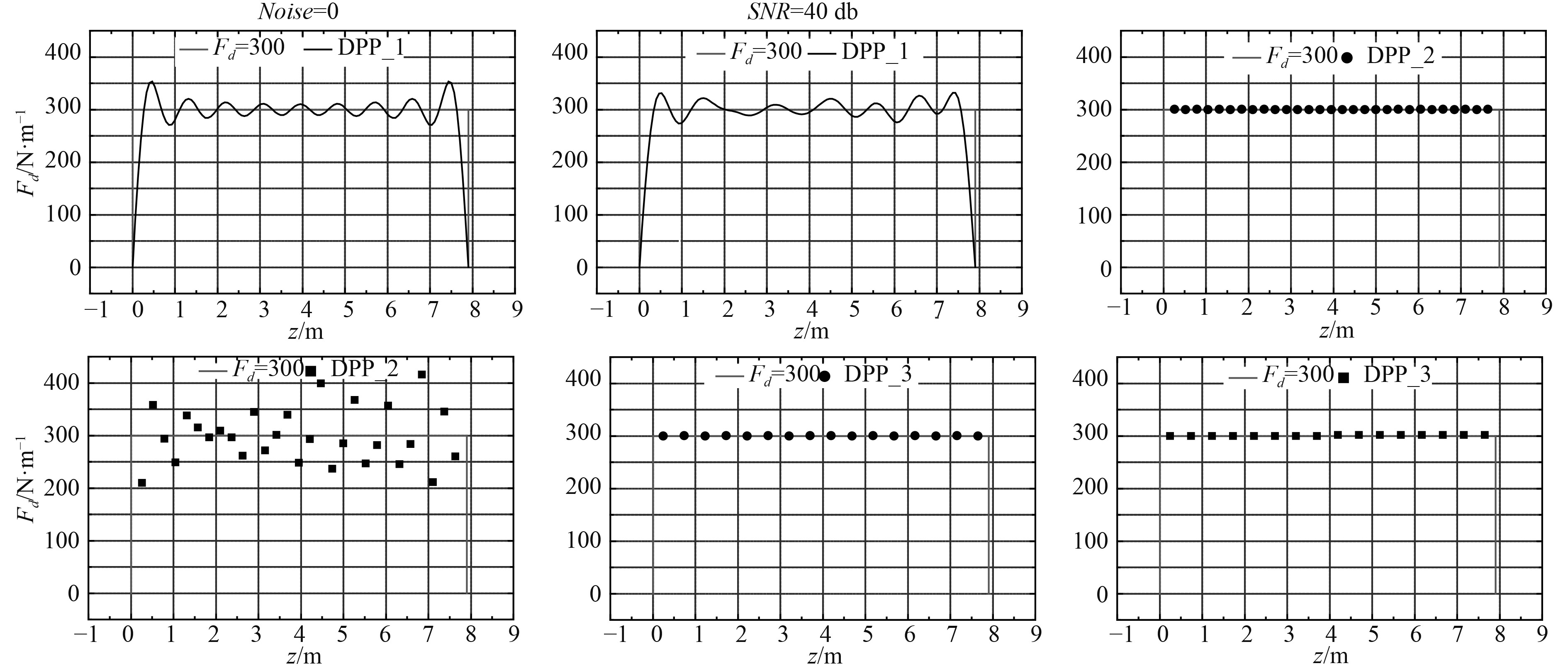
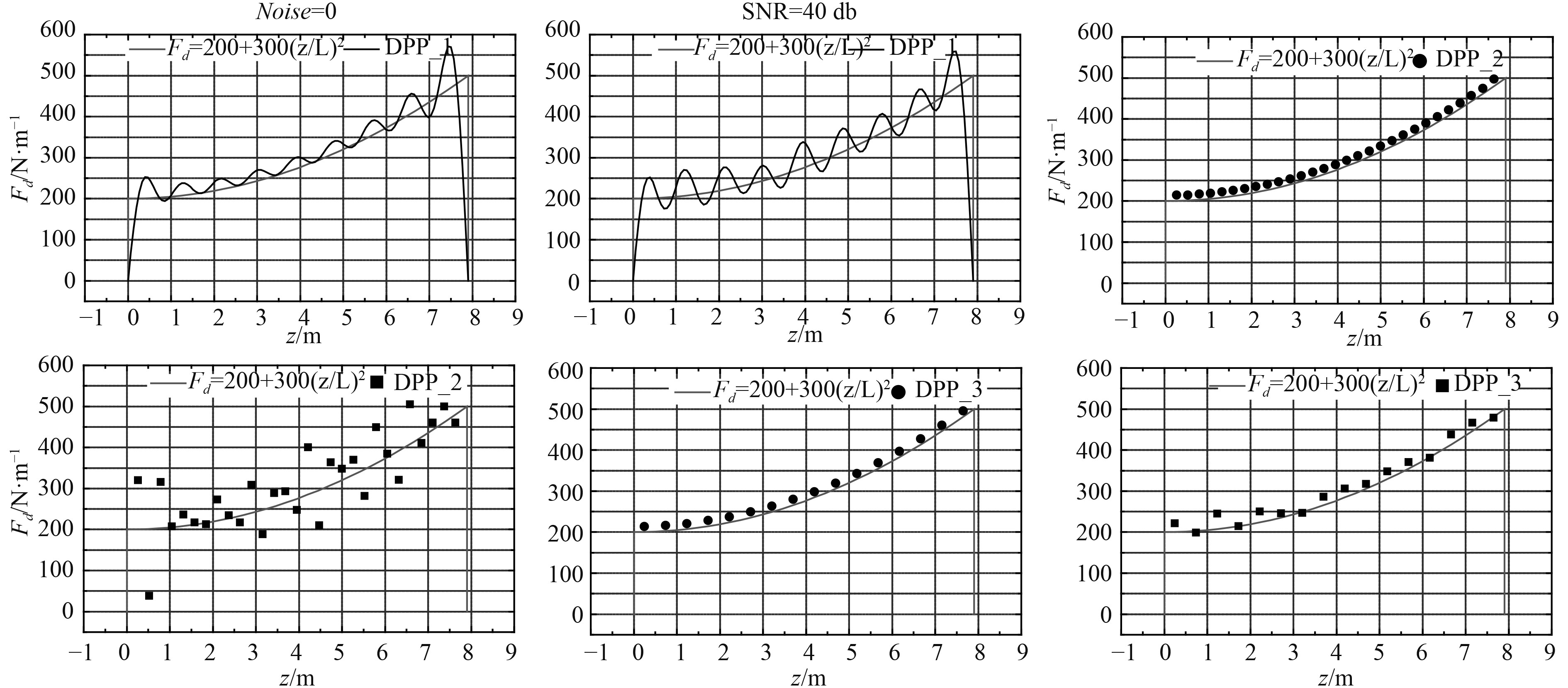
分别使用模态分析法（DPP_1），微段载荷分析法（DPP_2），逼近分析法（DPP_3）对生成的弯曲应变进行处理。均布载荷分析结果见如图8所示，阶梯载荷分析结果如图9所示。

可以看出，对于无噪声信号DPP_2及DPP_3的分析结果接近实际值，DPP_1的分析结果震荡变化，分布趋势接近实际值。由于DPP_1的结果是有限个正弦函数叠加的结果，所以在函数图像上自然会表现出“波峰”和“波谷”，这种起伏并不代表实际流体阻力的变化。同时由于正弦函数在边界的值始终接近于零，所以立管两端DPP_1的计算结果会始终接近于0，同时也导致立管两端附近的计算结果迅速增大，也就是说立管两端的计算结果误差较中间为大。

DPP_1对于噪声信号的分析结果和无噪声信号的分析结果基本一致，这说明一定范围内的噪声不会对模态分析法的结果产生较大的影响。也就是说若应变信号本身不包含较大的误差，模态分析法将会得到较为接近真实的结果。

DPP_2对于信号中的噪声十分敏感。若信号中包含噪声，DPP_2的计算结果将会和真实值有较大的偏离。反之，若DPP_2的分析结果和DPP_1的分析结果接近，就可以说明信号中的噪声并不十分大，两者的分析结果和真实值之间不会有较大的偏离。

DPP_3对于噪声信号的分析结果接近真实值，这说明通过监控n次差 $\Delta n\_\varepsilon $ ，控制计算次数，可以在很大程度上过滤掉噪声的影响，使分析结果接近真实值。

总之，如果DPP_2的分析结果和DPP_1及DPP_3的分析结果接近，这就说明应变信号良好，即噪声不大，使用任何一种方法都可得到可信的结果。如果DPP_2的分析结果和DPP_1及DPP_3的分析结果有较大的偏离，这就说明噪声较大。

3 试验数据处理结果分析 3.1 初始阻力的轴向分布及端面效应

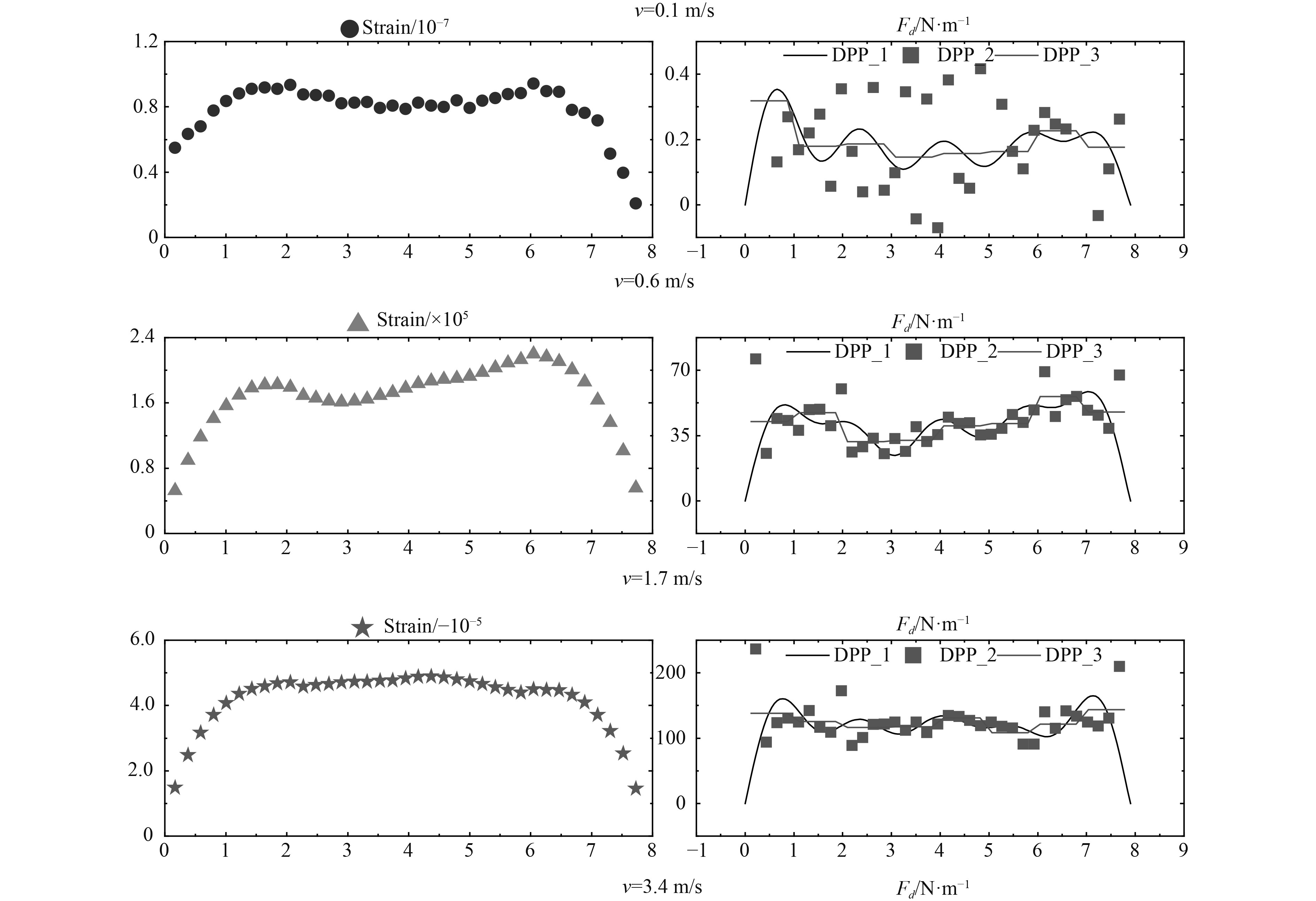
使用上述3种方法对初始应变进行分析，可以得到初始阻力沿立管轴向分布。图10为不同流速下立管的初始应变及平均阻力。

由分析结果可知：

1）DPP_1与DPP_3分析结果基本一致。除来流速度 $v = 0.1\;{\rm{m/s}}$ 外，DDP_2的分析结果和其他2种方法的分析结果趋势一致。平均阻力系数的计算表明，PP_1与DPP_3的相对误差在5%左右，DPP_2与DPP_3的相对误差在2%左右。这说明使用以上数据分析方法，可以获得比较准确的流体阻力。

2）流速越大，流体阻力越大。流体阻力沿着立管大致均匀分布，流体阻力沿立管中点大致对称，两端的流体阻力比中间区域大。圆柱绕流的数值计算表明，有限长圆柱两端的阻力比中间区域阻力大^[4]，称为端面效应。柔性立管的两端同样存在端面效应，即两端阻力较中间大。

4 结　语

本文针对试验中获取的立管轴向力及立管表面弯曲应变，提出3种计算平均阻力的数据处理方法，并进行算例验证与分析。最终使用3种方法分析试验数据，得到立管表面各截面处的阻力系数。本文的主要的结论如下：

1）微段载荷分析法对噪声敏感，其分析结果与其他两种结果的比较可用来判断应变信号是否良好。模态分析方法和逼近分析法有较好的抗噪声能力。模态分析法结果不能准确预报立管各截面出的阻力系数，平均阻力的计算结果较准确。逼近分析法由于避免了求导的过程，且根据立管表面漩涡脱落特性进行假设分析，因此其结果可大体上显示出立管表面阻力的分布特性。

2）由于立管两端的流场特性与中部不同，导致立管端面的流体的阻力比中间的部分大。逼近分析法的结果显示了立管表面流体阻力分布的端面效应。