2. 中国船舶及海洋工程设计研究院,上海 200011;
3. 上海海事大学,上海 201306
2. Marine Design and Research Institute of China, Shanghai 200011, China;
3. Shanghai Maritime University, Shanghai 201306, China
随着现代船舶的大型化与复杂化,船用动力系统的三大部分主机、螺旋桨与齿轮箱也日渐复杂。随着用于多机并车与分车甚至具有特殊用途齿轮箱的出现,与其相匹配的齿轮箱底架结构也趋向复杂。由于齿轮箱工作环境恶劣,工作时受到来自外部的激励而产生振动;齿轮在啮合过程中会产生冲击,冲击通过轴和轴承传递到齿轮箱体上而引起箱体振动;齿轮箱具有若干不同工况,工作频率范围宽,更有可能与结构共振频率重合而引起共振,箱体振动极易导致齿轮的不对中,甚至引起箱体与轴系的疲劳损伤破坏,降低齿轮箱的使用寿命[3]。因此,对齿轮箱底架的动力学性能分析至关重要。
本文选取某大型复杂齿轮箱的配套底架结构作为研究对象进行模态分析,分别进行现场模态试验与有限元模态分析,从而摸清该大型复杂齿轮箱底架的基础动力学特性。现今较为常用的研究思路是以在一定频率范围内的模态试验分析结果校核有限元模态分析结果,并对有限元模型进行适当的调整来逼近试验结果,以此提升有限元模型的准确性,再利用完善后的有限元模型的计算结果得到研究对象更多频率范围内的模态参数。然而随着研究对象的复杂化、大型化,常规的试验模态分析与有限元模态分析都遇到了不可避免的阻碍,因而本文主要介绍一种在一般分析条件下的近似模态分析方法。
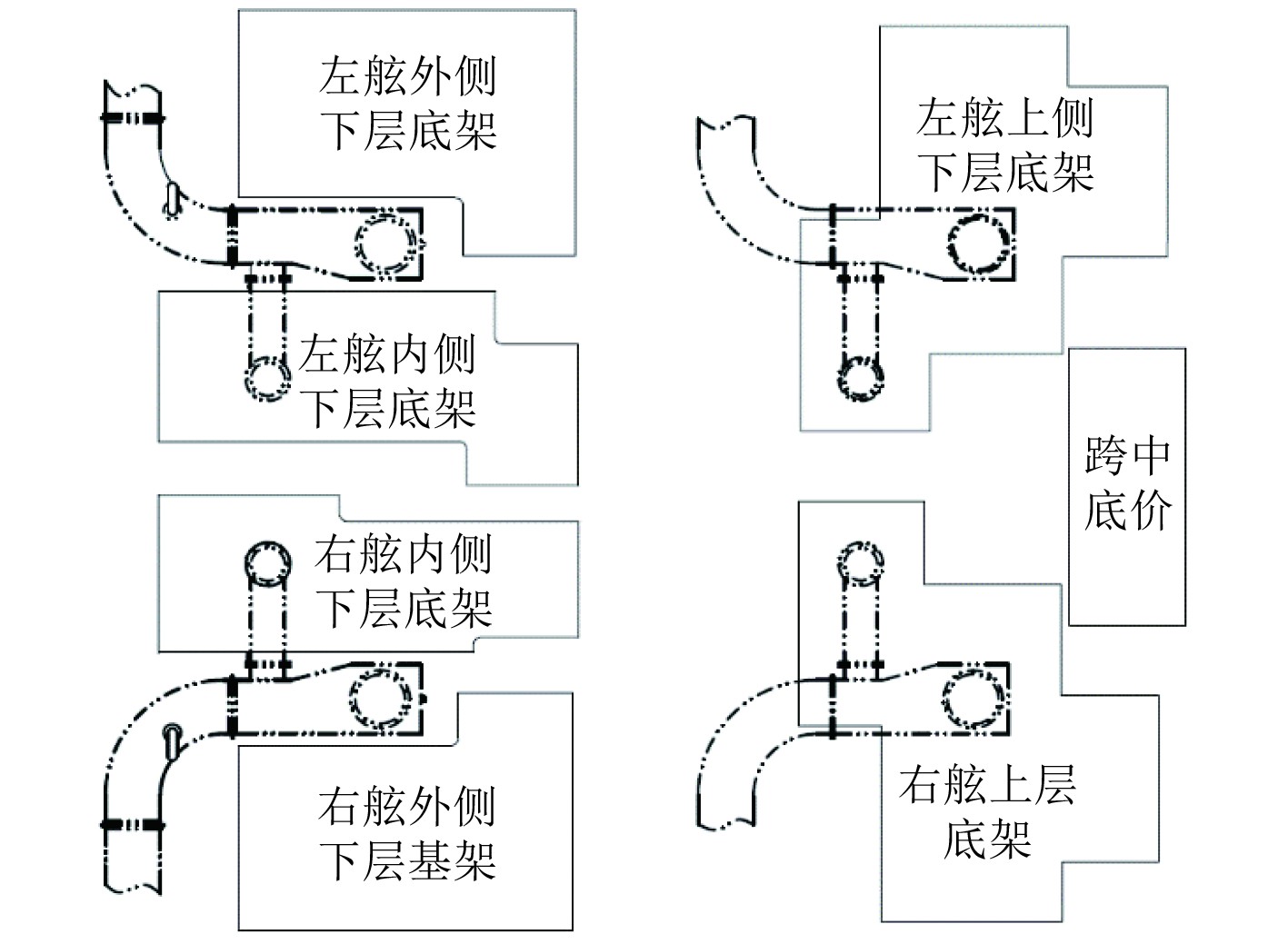
本文研究对象的基座结构分为7个部分,通过螺栓连接组合而成,左右两舷结构各设有上下2层结构,并在左右底层支架上设有一跨接结构用以承载跨接齿轮箱,其结构布置图如图1所示。
|
图 1 复杂齿轮箱底架结构布置图 Fig. 1 Structural layout of a complicated gearbox basement |
由于齿轮箱结构庞大,因而采用单输入多输出的力锤冲击试验。与激振器试验相比,力锤试验的激振设备简单,不需要支撑装置,对被测结构不产生附加质量,激振点的选择可以更加灵活,更适合于大型结构的现场测试[1]。这也是目前模态试验中最为常用的一种试验方式。然而该试验对象结构复杂,若要进行整体试验,传感器数量远远不够;若是测点分布过于分散,则非常容易造成模态丢失。因而只能对基座单体(左舷上层底架,跨接齿轮箱底架)采用LMSTEST.Lab 模态测试系统进行试验模态分析。
由于跨接齿轮箱底架结构相对简单,因而以跨接齿轮箱底架的试验结果如表1所示。
|
|
表 1 跨接齿轮箱底架模态试验结果 Tab.1 Outcome of operational modal analysis on bridging gearbox basement |
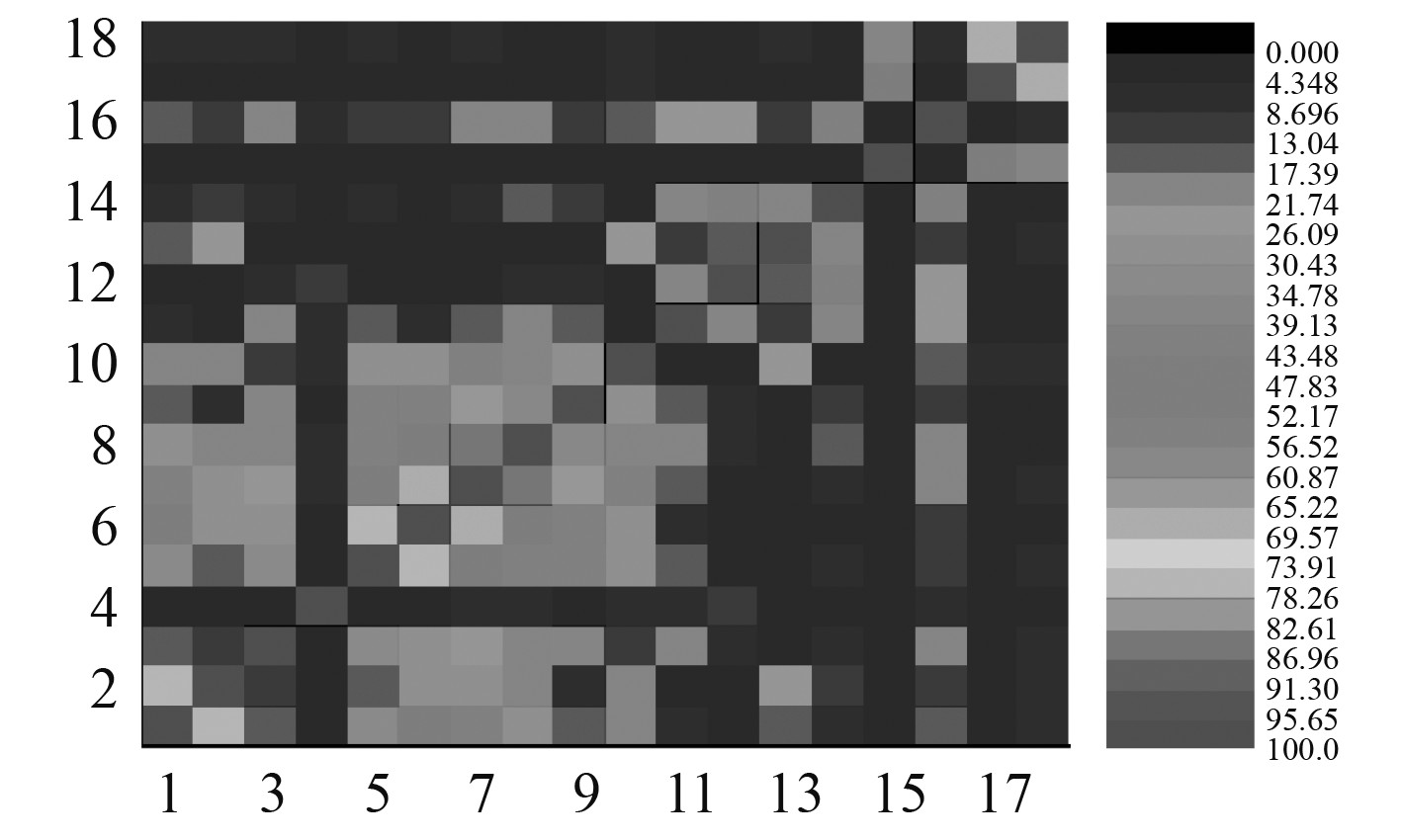
试验过程中,在较长的频带范围内,锤击能量会逐渐衰减,因此对模态分析的干扰较为强烈;而且该复杂结构质量与刚度分布特点不明,很难选择合适的锤头,因此需要反复试验以得到满意的结果。此外,结构质量与刚度过大,锤击激励能量相对较小,使得激发模态更为困难。可以观察到试验结果中存在部分MOV(模态复杂性)较小的模态,这说明个别模态有可能是噪声模态;另一种可能是由于个别测点安装在外伸的结构件位置,该位置相对于整体结构刚度较小,因而对频率敏感度较大,从而造成MOV值偏小。此外,通过图2所示的MAC值(模态置信准则),可见部分模态的MAC值也并不十分理想。由于试验条件并不完全达到理想状态,因而并不能直接判断为虚假模态,还需对部分正交性不理想的试验模态再进行考量。
|
图 2 跨接齿轮箱底架模态试验各阶模态振型MAC值 Fig. 2 MAC values of different modal vibration shapes in operational modal analysis on bridging gearbox basement |
由此可见,由于现场试验模态分析方法自身的激励源和测点布置的原因,以及对试验环境的要求等限制条件,仅要得到复杂大型结构单体的准确试验结果就非常困难,对于规模庞大的整体结构则更是难上加难。因而通过试验模态分析,仅能得到一个单体结构在一定频率范围内较为准确的模态参数,并且还需其他手段对MOV和MAC值较不理想的模态进一步讨论分析再做参考。
1.2 有限元模态分析对复杂齿轮箱底架的有限元模态分析采用MSC.patran/nastran建立有限元模型。由于该底架结构为典型的板架组合结构,因而采用二维板单元,单元大小取50mm×50mm,材料为普通碳钢,弹性模量取206 000MPa,泊松比为0.3,密度为7.85×10−9 t/mm3。建模过程中对螺栓垫板连接处、倒角圆弧处等进行适当的简化。有限元模型如图3所示。

|
图 3 复杂齿轮箱底架有限元模型(结构示意图) Fig. 3 Finite element model of a complicated gearbox basement (structural diagram) |
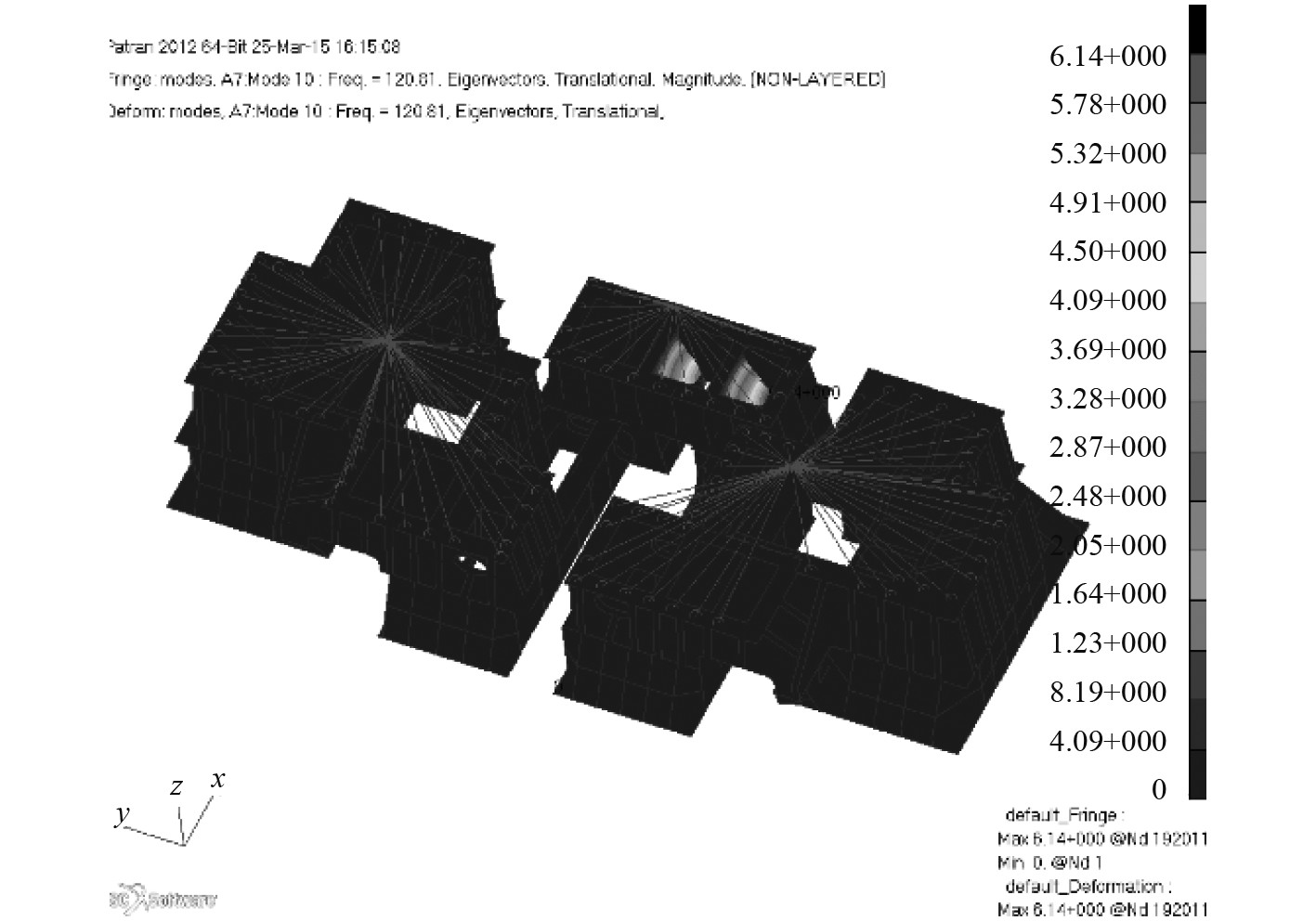
建模之后即可得到完整的结构刚度与质量分布,使结构底面按实际工况位置固支并用MPC单元与质量点单元模拟其上部齿轮箱设备质量,以此在软件中进行直接模态分析。然而该结构是由大量无加强筋的板材交错焊接装配而成,这就使得每块板材远离其他构件的区域的刚度远小于整体刚度,从而使计算结果全部都是局部模态。图4和图5即为直接模态分析得到的典型云图。

|
图 4 典型直接模态分析结果云图(Ⅰ) Fig. 4 Typical result nephogram of direct modal analysis (Ⅰ) |
|
图 5 典型直接模态分析结果云图(Ⅱ) Fig. 5 Typical result nephogram of direct modal analysis(Ⅱ) |
一般情况下的复杂结构,其结构部件的耦合程度高,即各个部分的刚度与质量都会对周围其他构件的质量与刚度产生不同程度的影响,从而使得各个部件能够形成一个整体结构,因此能观察到明显的低阶整体模态。然而,该齿轮箱基架的结构为大规格板材的组合结构,在各个板格中,板材与板材连接处的刚度与质量远大于板材中部的刚度与质量,简而言之,即板材中部区域会独立于整个系统产生一个附属在总系统之下独立的子系统,由于其自解耦性,板材中部会在整体运动下产生自身额外的运动,因而板材自身的形变远大于整体结构的形变。所以在对该齿轮箱基架的计算结果中很难观察到整体模态的效果云图,其主要原因就是由于板材中部的相对位移远大于整体的形变。
此外,直接模态计算还会造成小频段中存在大量密集模态,模态振型繁杂。由于大量低刚度部分的结构存在而造成的大量自由度,会产生大量与该齿轮箱实际工况无关的振型,极大地浪费了计算机资源,使得直接模态计算根本不能得到理想的计算结果。
2 近似的有限元模态分析方法 2.1 扫频频响分析原理直接进行有限元模态分析时,由于各个自由度上的振型混杂在一起,使得得到的结果数据过于庞大而无法得到有效的利用。通过模仿试验模态分析中的扫频激励法,在有限元软件中采用特定方向下的单位力扫频激励的方式,得到整体结构系统在所关心的自由度上的频响结果,从而间接地获取固有频率与近似的振型。
物理坐标系中的频响函数能够表示为模态频响函数的线性组合,即在有限元分析中获取的频响结果会包含所有相关的模态参数。
频响函数矩阵
| ${h_{jk}}(\omega ) = \frac{{{X_j}(\omega )}}{{{f_k}(\omega )}},$ | (1) |
而此处施加的激振力
另一方面,模态转换是从特征值求解过程中得到的,是用物理坐标
| $\left[ {{U}} \right] = \left[ {\left\{ {{U_1}} \right\}\left\{ {{U_2}} \right\}\left\{ {{U_3}} \right\}\cdots } \right],$ | (2) |
| $\left\{ {{x}} \right\} = \left[ U \right]\left\{ p \right\} = \left\{ {{u_1}} \right\}{p_1} + \left\{ {{u_2}} \right\}{p_2} + \left\{ {{u_3}} \right\}{p_3} + \cdots,$ | (3) |
进一步整理得到模态空间方程组
| $\begin{aligned} &\left[ {\begin{array}{*{20}{c}} {\overline {{m_1}} }&{}&{} \\ {}&{\overline {{m_2}} }&{} \\ {}&{}& \ddots \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {\mathop {{p_1}}\limits^{..} } \\ {\mathop {{p_2}}\limits^{..} } \\ \vdots \end{array}} \right\} + \left[ {\begin{array}{*{20}{c}} {\overline {{c_1}} }&{}&{} \\ {}&{\overline {{c_2}} }&{} \\ {}&{}& \ddots \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {\mathop {{p_1}}\limits^. } \\ {\mathop {{p_2}}\limits^. } \\ \vdots \end{array}} \right\} + \\& \left[ {\begin{array}{*{20}{c}} {\overline {{k_1}} }&{}&{} \\ {}&{\overline {k{k_2}} }&{} \\ {}&{}& \ddots \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{p_1}} \\ {{p_2}} \\ \vdots \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{{\left\{ {{u_1}} \right\}}^{\rm{T}}}\left\{ F \right\}} \\ {{{\left\{ {{u_2}} \right\}}^{\rm{T}}}\left\{ F \right\}} \\ \vdots \end{array}} \right\}{\text{。}}\end{aligned}$ | (4) |
方程右侧是模态振型的转置乘以施加到结构上的物理力向量,因此该模态振型值即外力大小与各阶模态分配的结果。此外,由于各阶模态具有明显的方向性,即结构对应的响应主要是在一个方向上而其他方向的响应很小或者没有响应,因此可以通过限制激励力的方向与作用点来激发出所关注的模态[2]。用该方法得到的计算结果并不意味得到了结构的所有阶模态,但可以得到与关注的激励方向和作用点下相关的固有频率与近似的模态振型。
2.2 使用虚拟梁单元提取整体振型由于刚度分布极不均匀的大面积板材不利于在有限元的结果云图中观察到振型,因此在所有结构刚度较大的板材连接处建立2节点的梁单元,该梁单元的剖面大小近似为0,因而不会对实际结构的刚度与质量矩阵产生影响,所以在此称为虚拟梁单元。
虚拟梁的变形能够近似等效为梁两端节点间的相对变形,若提取出所有虚拟梁单元的变形云图,就能够直观地得到系统中各个结构关键点之间的相对位移变化,从而得到整体振型。而对于该齿轮箱底架结构,结构关键点即是多块板材公共边的端部。由于是多个方向板材的连接位置,因此在各方向上都具有较大的刚度,所以最能体现整体的变形。
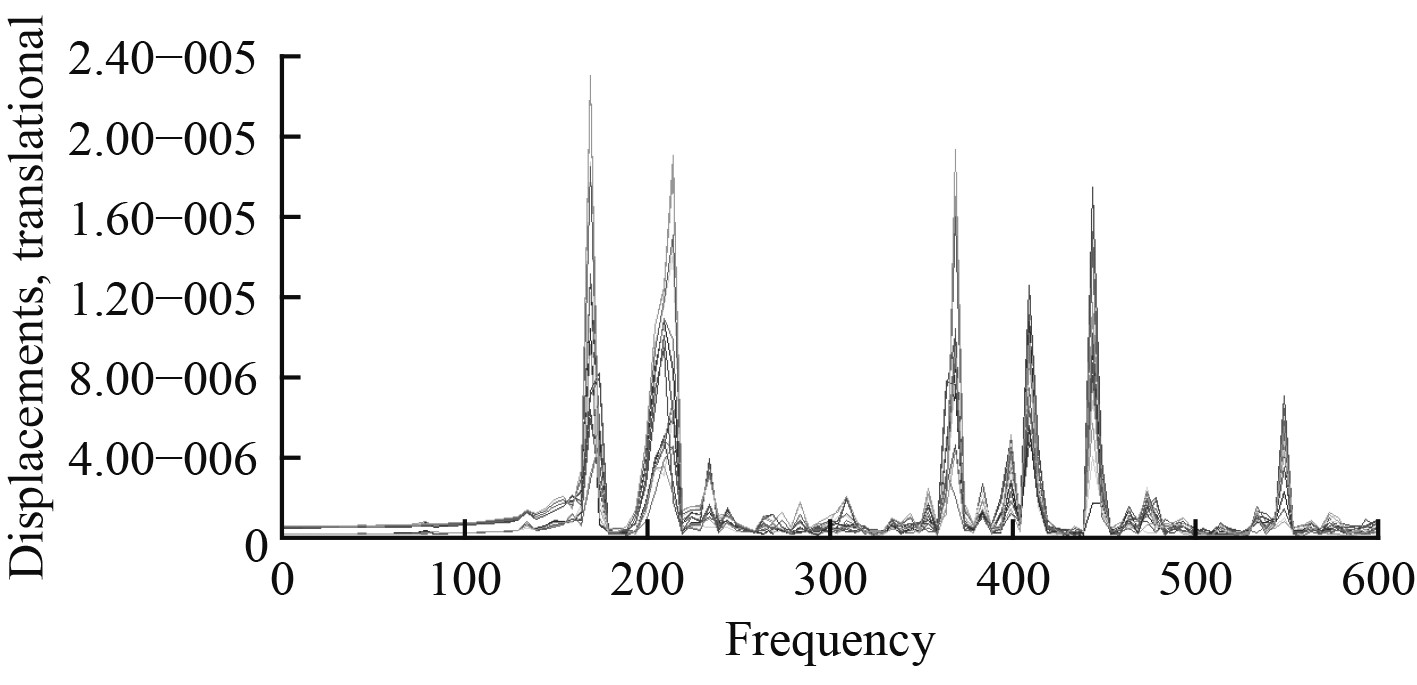
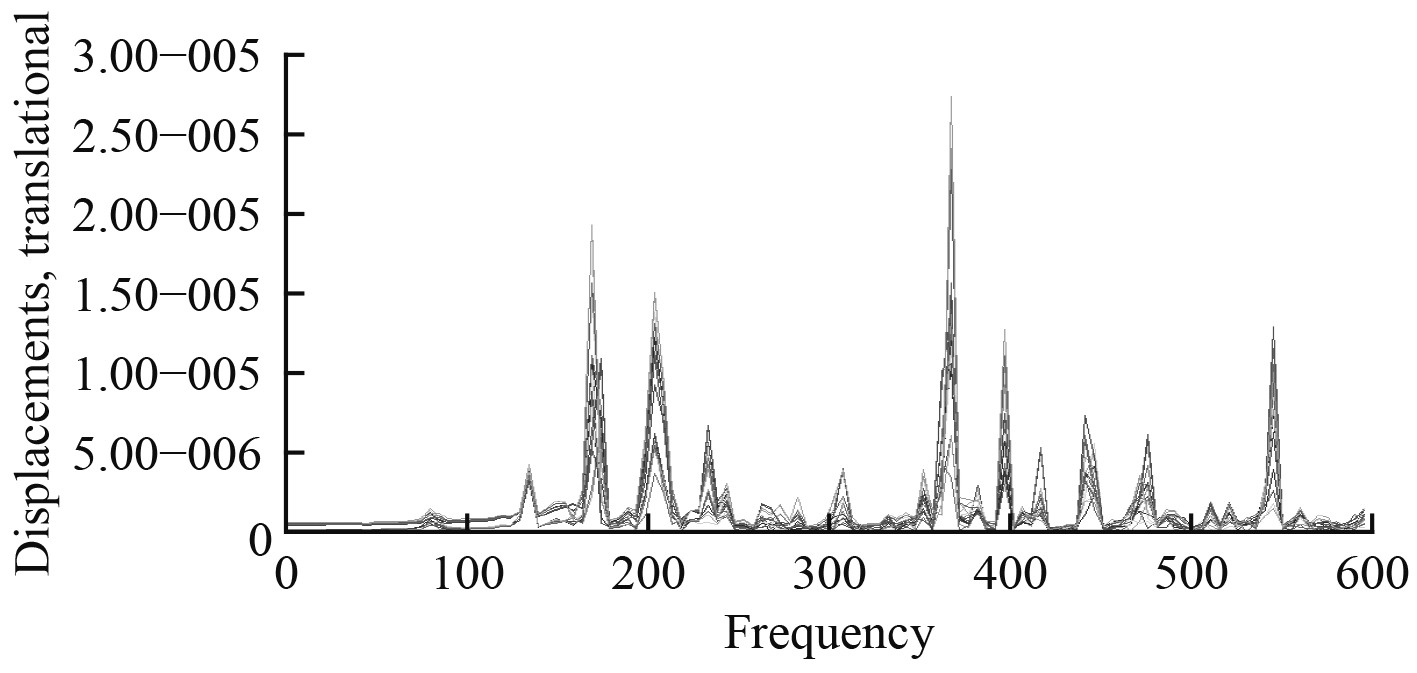
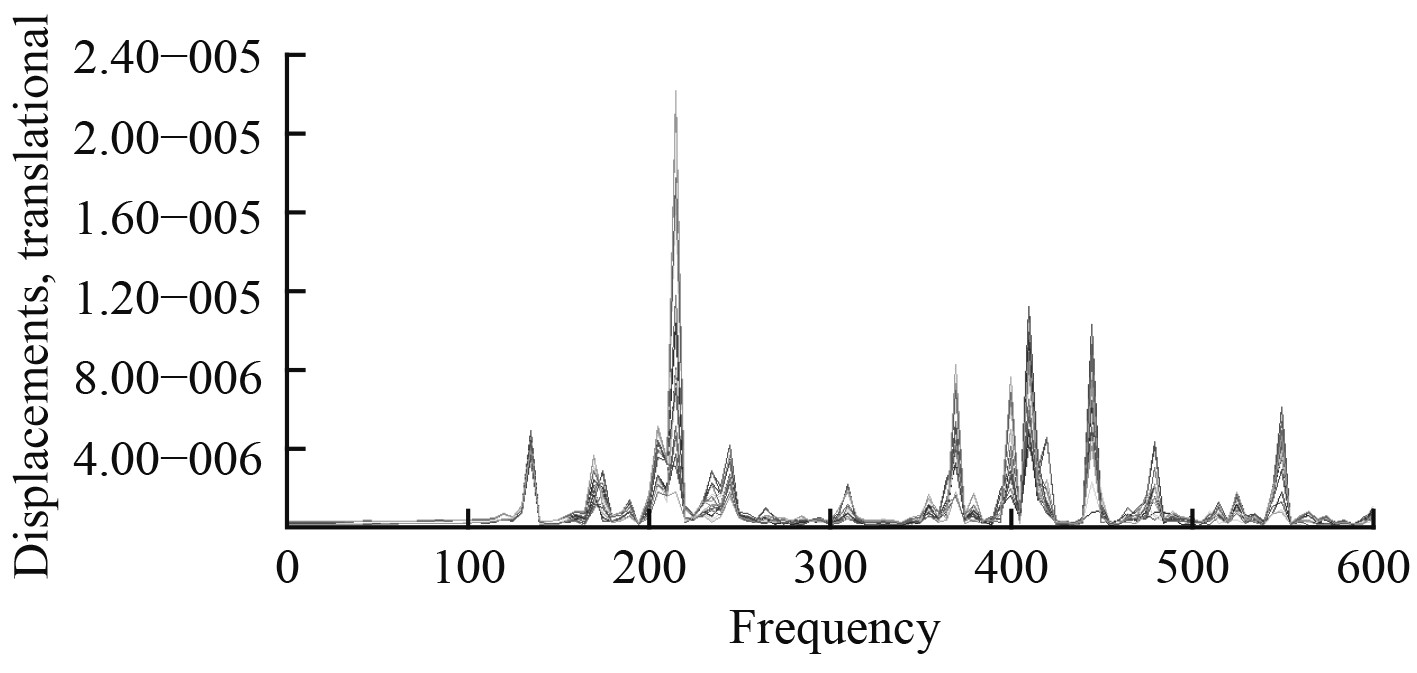
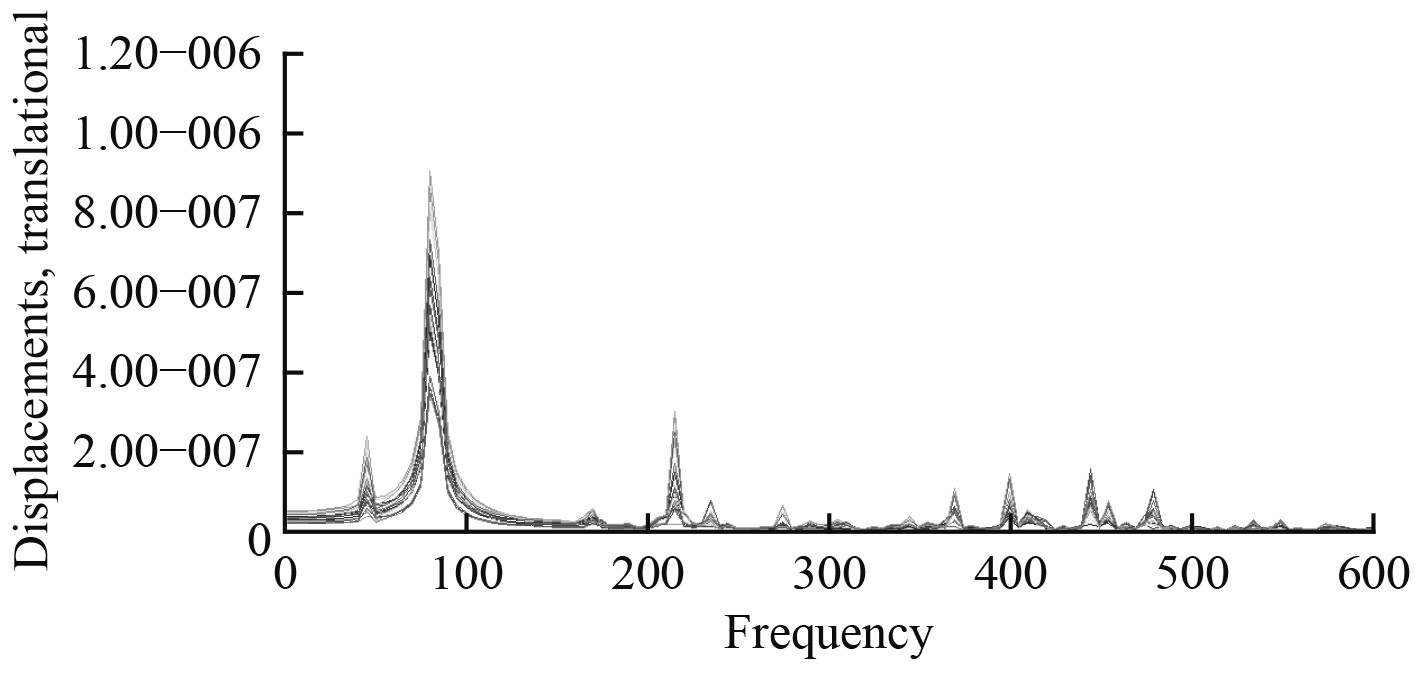
3 跨接齿轮箱底架有限元扫频分析结构的某一阶模态,可以理解为在某一特定方向与特定作用点激励下,在该结构的模态坐标中激发出的仅有的一种振型,该振型在模态空间中与其他所有模态正交。而频响分析是通过任意方向与作用点的激励力求出该结构在模态坐标系中所能激发出的所有振型的叠加结果。本文齿轮箱底架的激励作用点位置可以近似为在齿轮箱设备的重心,在模型中施加MPC单元来模拟齿轮箱设备。因此可以在有限元模型中的齿轮箱设备重心处施加三向单位激励,以5Hz为扫频步长来进行无阻尼频响分析,得到底架结构分别在3个方向上的频响曲线(见图6~图9)。通过拾取最大峰值点得到近似的固有频率,并通过虚拟梁的方式得到对应的近似模态振型。
|
图 6 在X方向激励下的频响曲线 Fig. 6 Frequency response curve under X-axis excitation |
|
图 9 在XYZ方向激励下的频响曲线 Fig. 9 Frequency response curve under XYZ-axis excitation |
使用上述方法对整体进行分析,并提取跨接齿轮箱底架计算结果与试验模态分析结果进行对比,以验证该方法的准确性。
由于是无阻尼频响计算,因此可以假定出现峰值的频率即为结构的固有频率。根据图6~图8曲线的峰值(其中剔除了响应相对较小的峰值),并结合试验结果汇总,如表2所示。
|
|
表 2 频响曲线峰值频率与模态试验固有频率汇总分析 Tab.2 Peak frequencies from frequency response curve compared with inherent frequencies from modal analysis |
|
图 7 在Y方向激励下的频响曲线 Fig. 7 Frequency response curve under Y-axis excitation |
|
图 8 在Z方向激励下的频响曲线 Fig. 8 Frequency response curve under Z-axis excitation |
表2中,前4行分别为在各个方向下(其中All为同时施加3个方向的激励力)频响曲线峰值所在的频率。Test行代表与计算值相接近的试验值。Error代表计算值与试验值的误差。
可以看到同时施加三向的激励力能够得到所有方向下的固有频率值。另一方面,由于模态试验的现场原因,有可能是因为激励能量不足而造成170~235 Hz的模态没有测出。但根据实验值与计算值能够相匹配的结果来看,两者误差较小,从固有频率来看,有限元计算模型的准确性满足要求。
3.2 响应振型分析根据频响曲线可以看到,随着激励方向的不同,其频响曲线也完全不同,其共振峰越大则说明该作用点与方向下的激励力越能够激发出该频率下的模态。因而从振型方面而言,频响曲线上共振峰越大的响应变形越近似为在该频率下的模态振型。
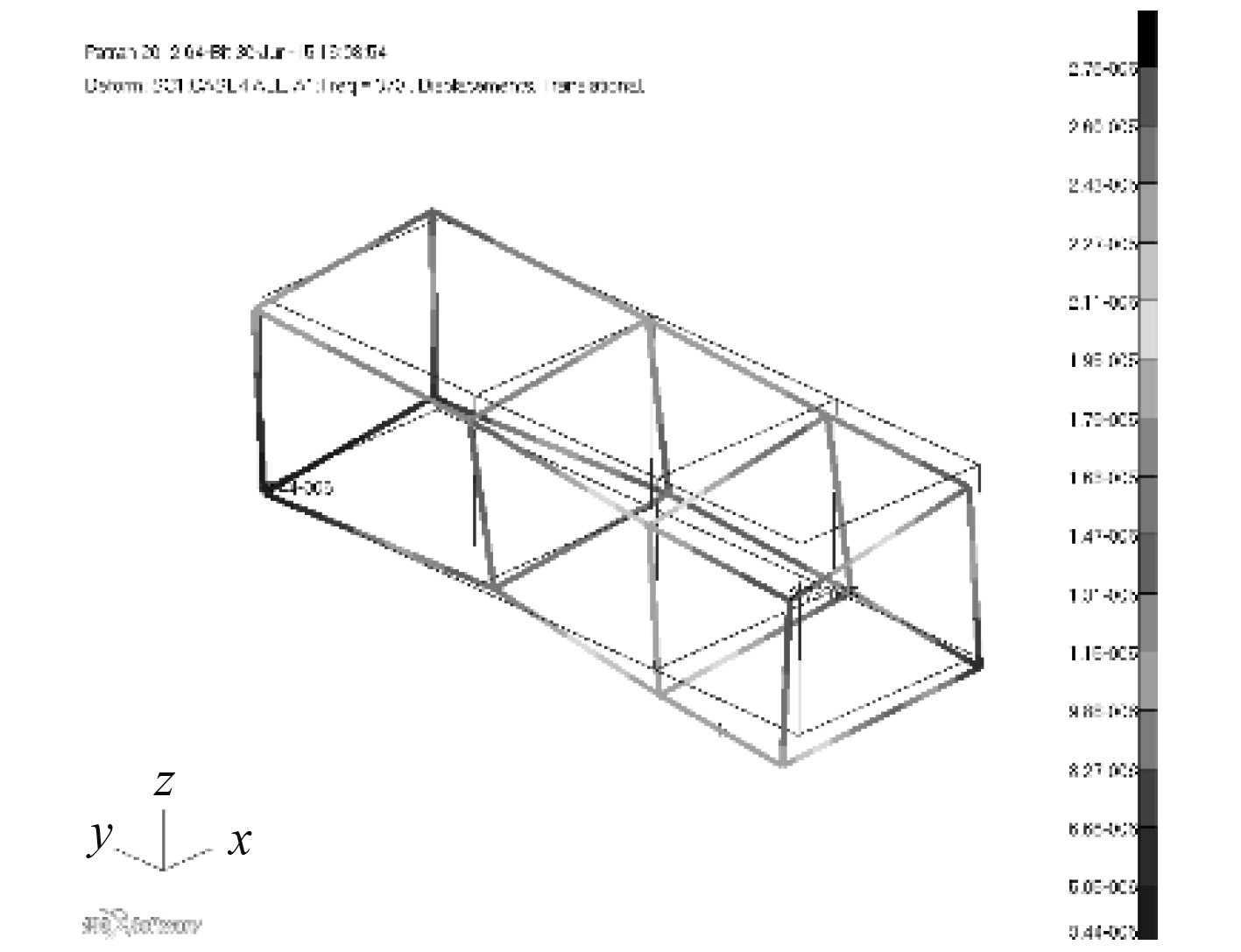
由图6~图8可以看到,在3个方向下,370 Hz都有较为明显的共振峰,并且由图9也可以看到,370 Hz下的共振峰峰值最大,这说明在370 Hz时,同时施加3个方向下的单位激励力能够较好地激发出该频率下的模态振型。提取该情况下的响应变形,并与试验模态所得的模态振型相比较,如图10所示。
|
图 10 三向激励下370 Hz有限元计算振型 Fig. 10 Modal shape at 370 Hz under XYZ-axis excitation in finite element modal analysis |
可以看到,振型基本运动趋势接近,然而变形并不完全吻合。主要是由于响应振型的激励位置与方向和该阶模态的模态力方向与位置并不完全相同,因此得到的响应振型只能作为模态振型的一种近似。不过作为研究结构在确定激励点位置与激励方向下的情况,使用该方法得到的响应振型更具有实际工程意义。
3.3 整体齿轮箱底架频响分析上述整体分析中,子结构的固有频率与振型分析基本与试验模态分析结果相符,由此可以推论有限元模型的准确性,同时验证了通过扫频频响分析与虚拟梁来得到近似的固有频率与固有频率下的响应振型。
由于齿轮箱底架的研究重点为齿轮箱设备与齿轮箱底架的接触面,因此为了便于观察,分别选取左右舷齿轮箱底架与跨接底架最上层的某一节点提取其频响曲线,如图11~图14所示。
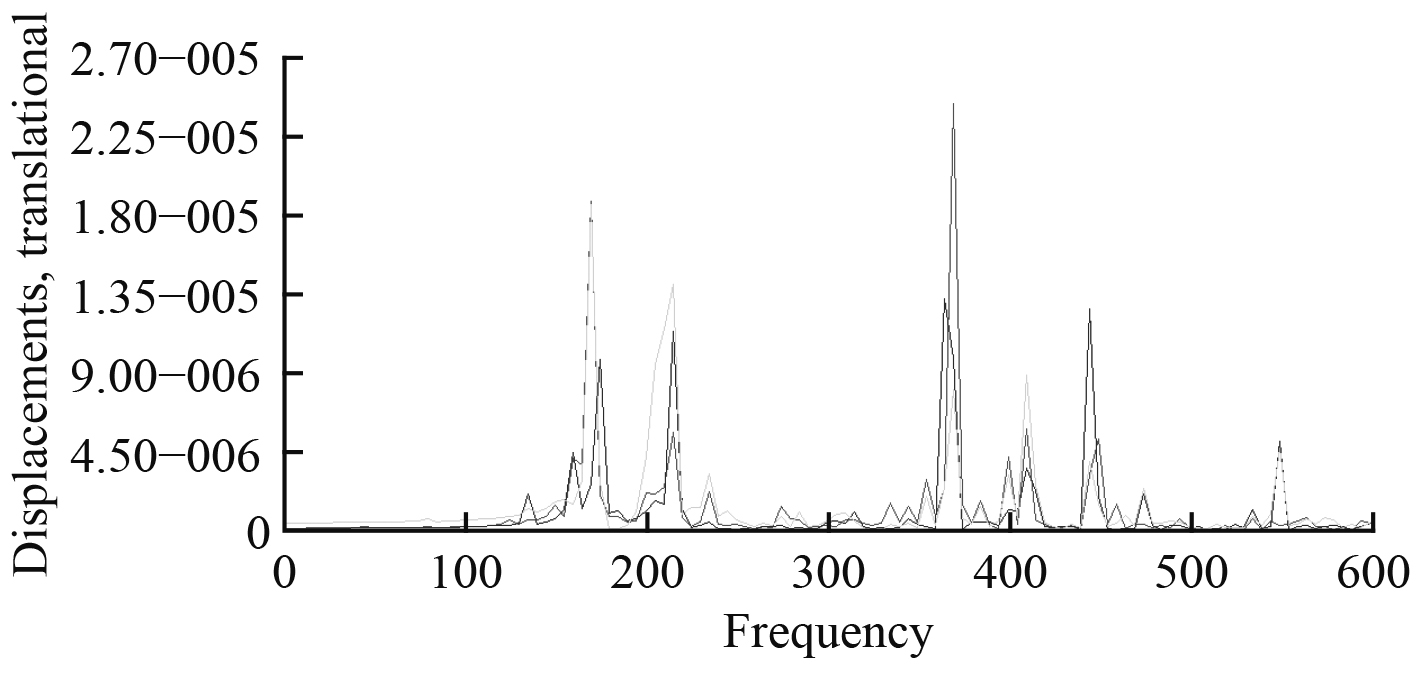
|
图 11 在X方向激励下齿轮箱底架上层频响曲线 Fig. 11 Frequency response curve of upper layer of gearbox basement under X-axis excitation |
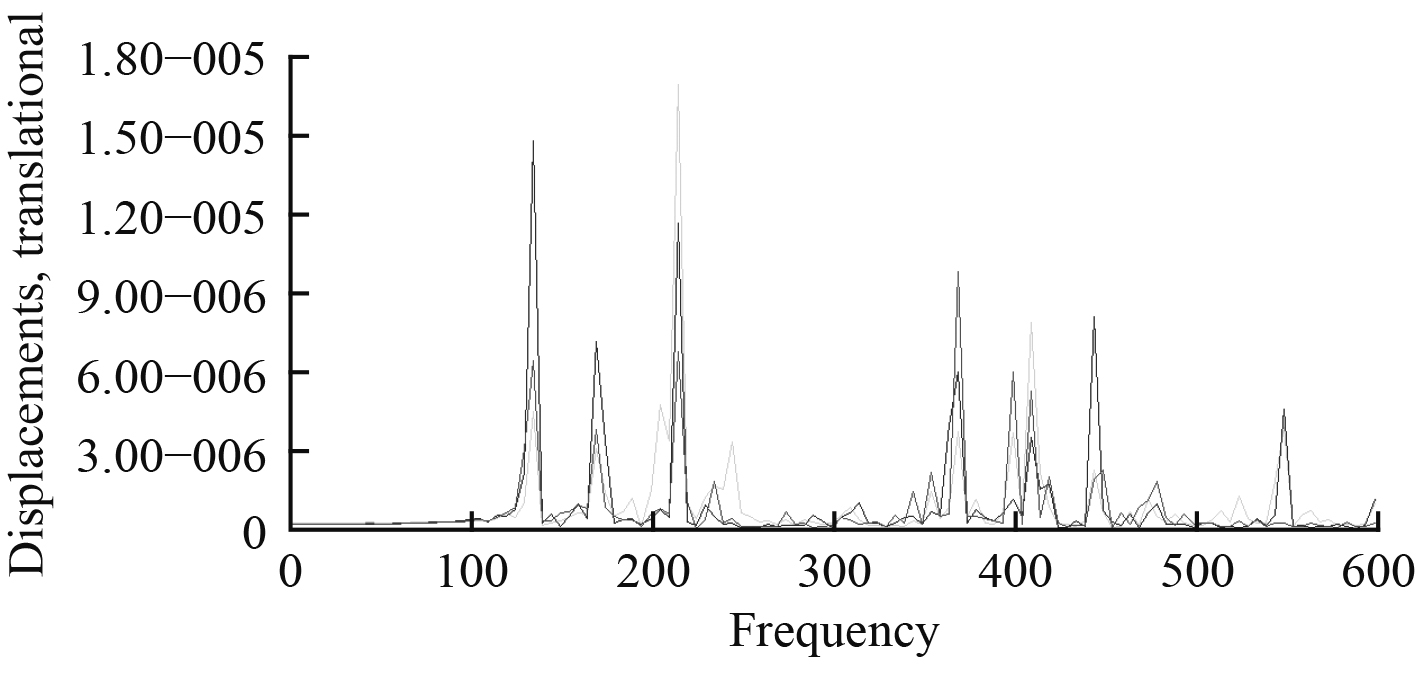
|
图 12 在Y方向激励下齿轮箱底架上层频响曲线 Fig. 12 Frequency response curve of upper layer of gearbox basement under Y-axis excitation |
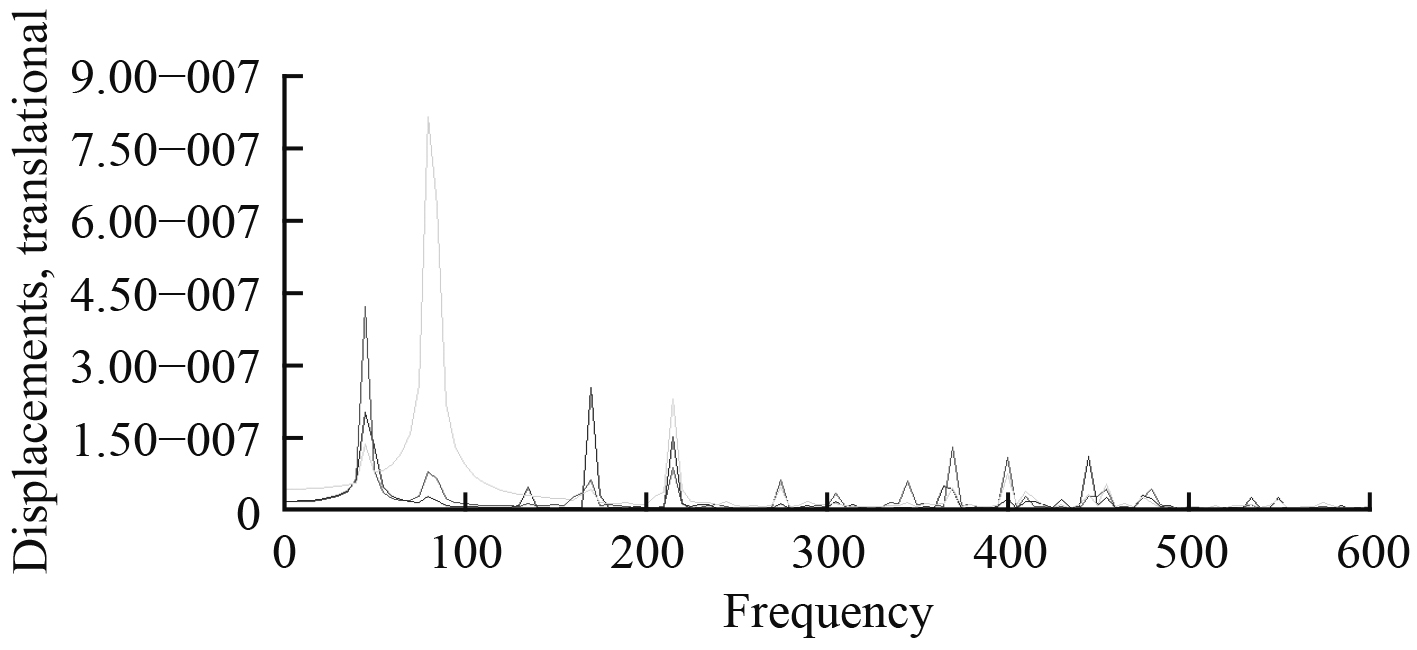
|
图 13 在Z方向下齿轮箱底架上层频响曲线 Fig. 13 Frequency response curve of upper layer of gearbox basement under Z-axis excitation |
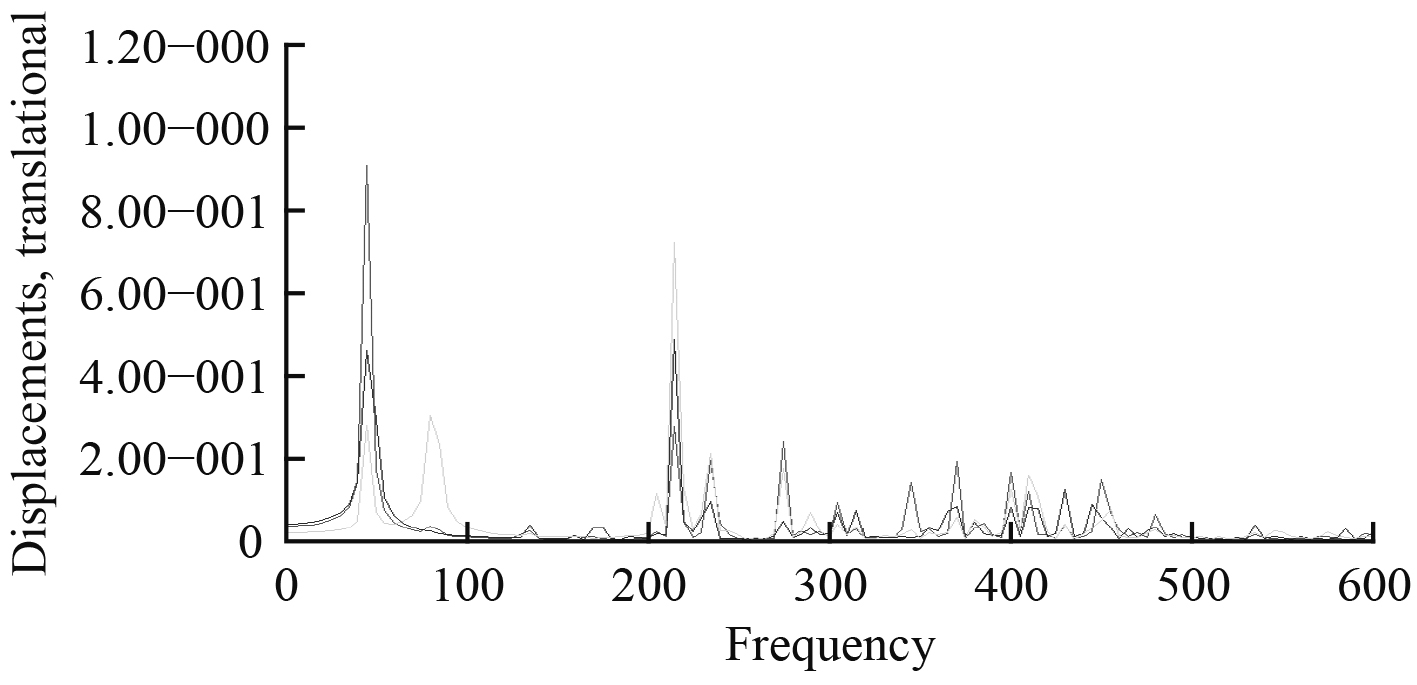
|
图 14 在合成力方向下齿轮箱底架上层频响曲线 Fig. 14 Frequency response curve of upper layer of gearbox basement under XYZ-axis excitation |
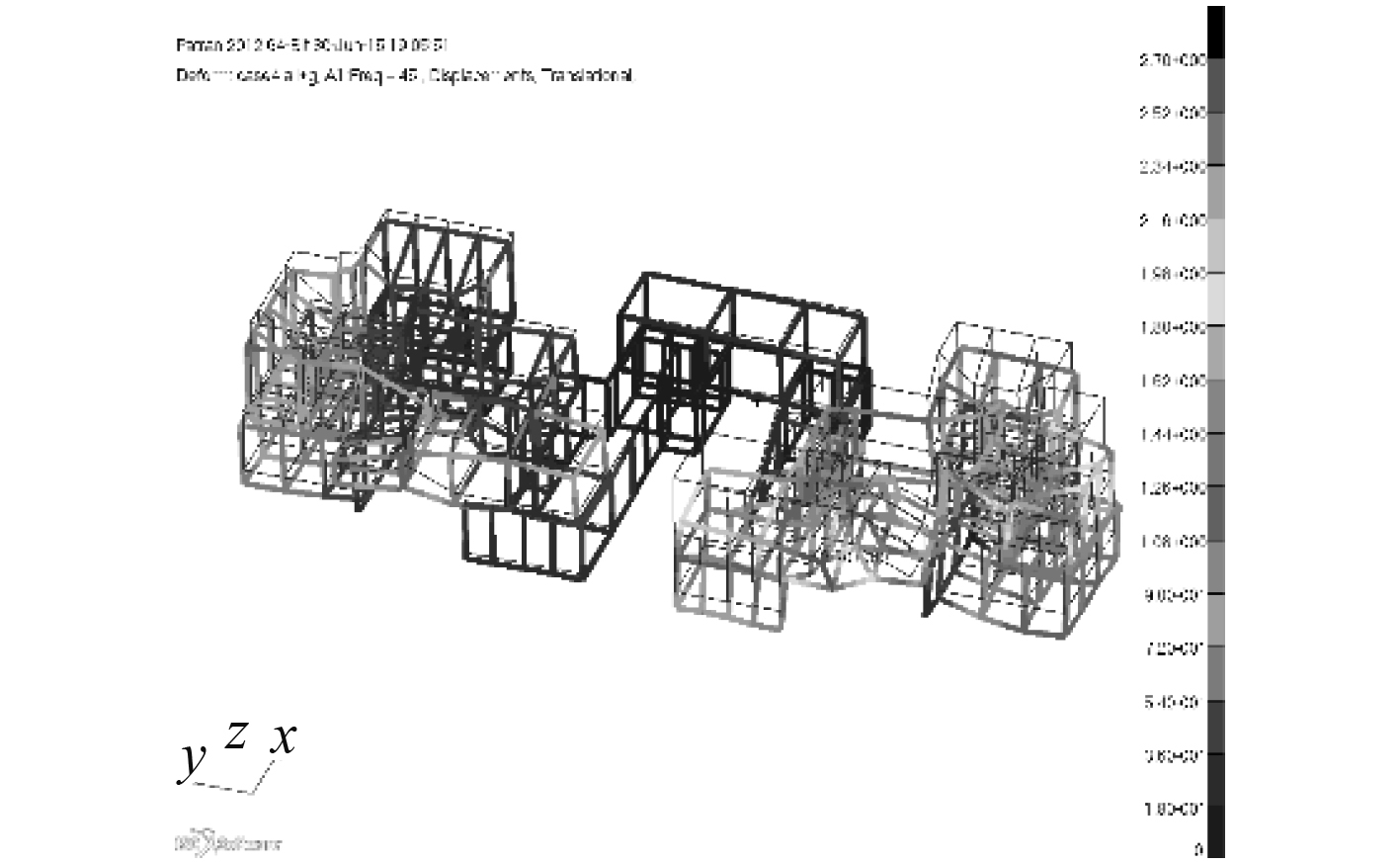
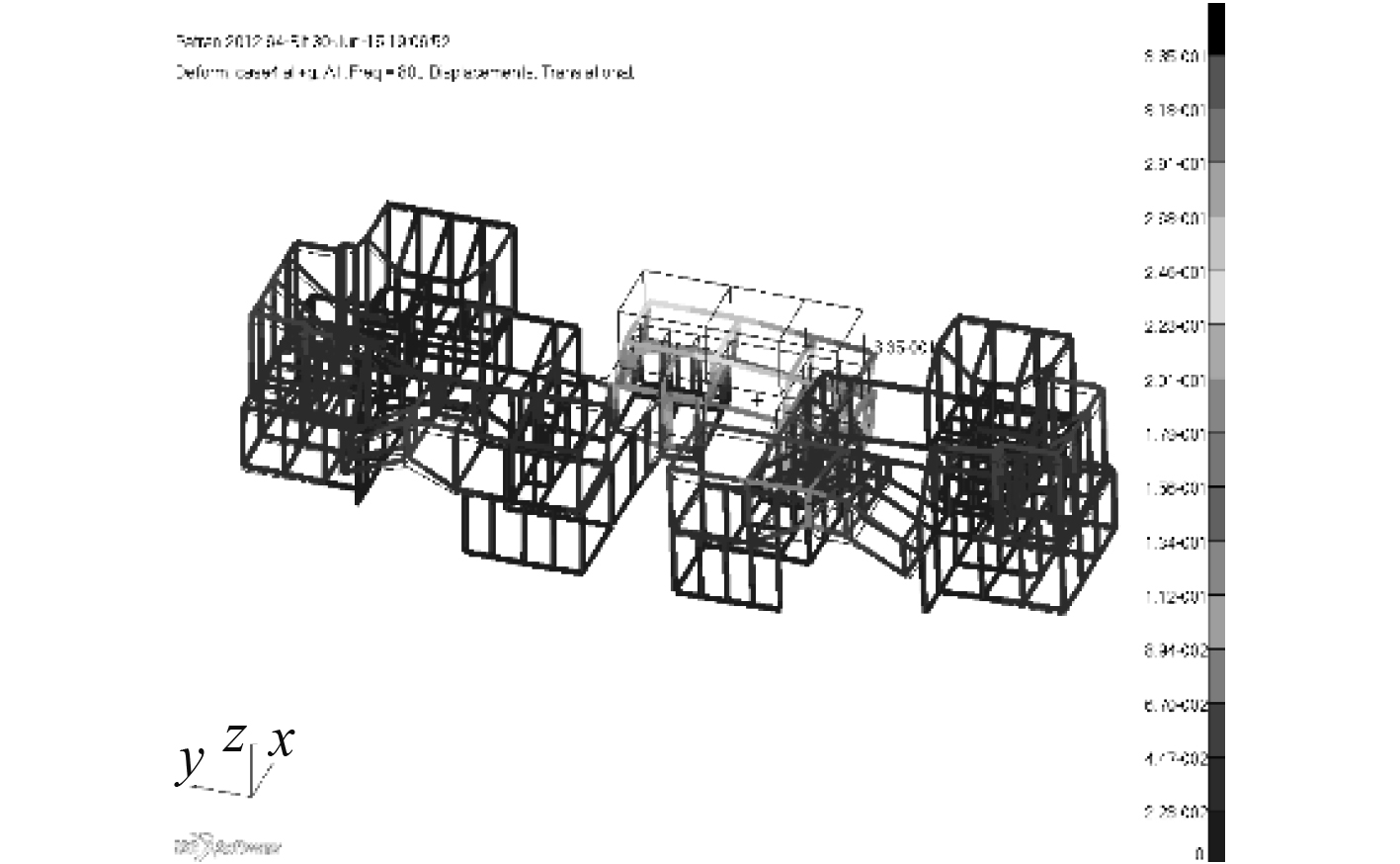
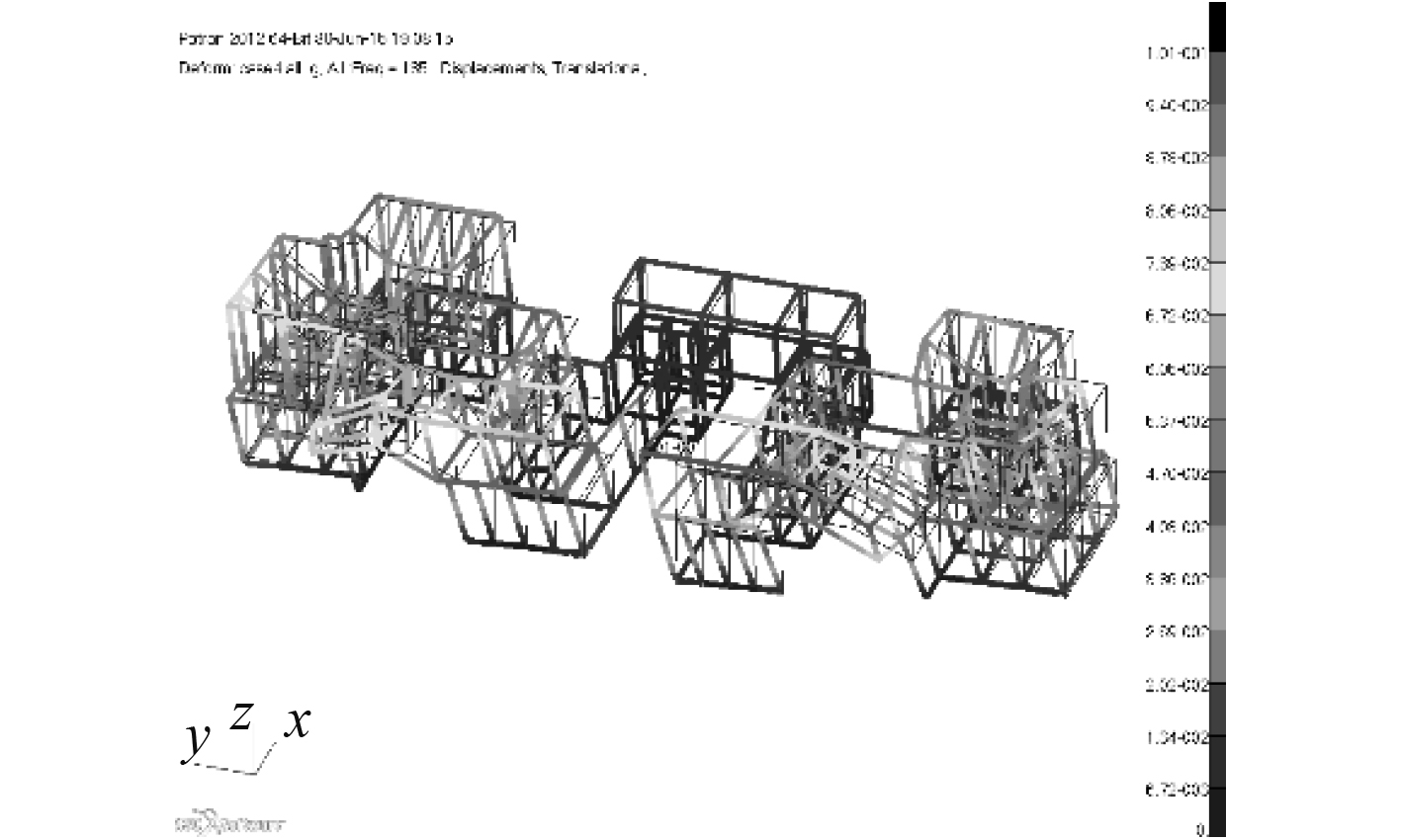
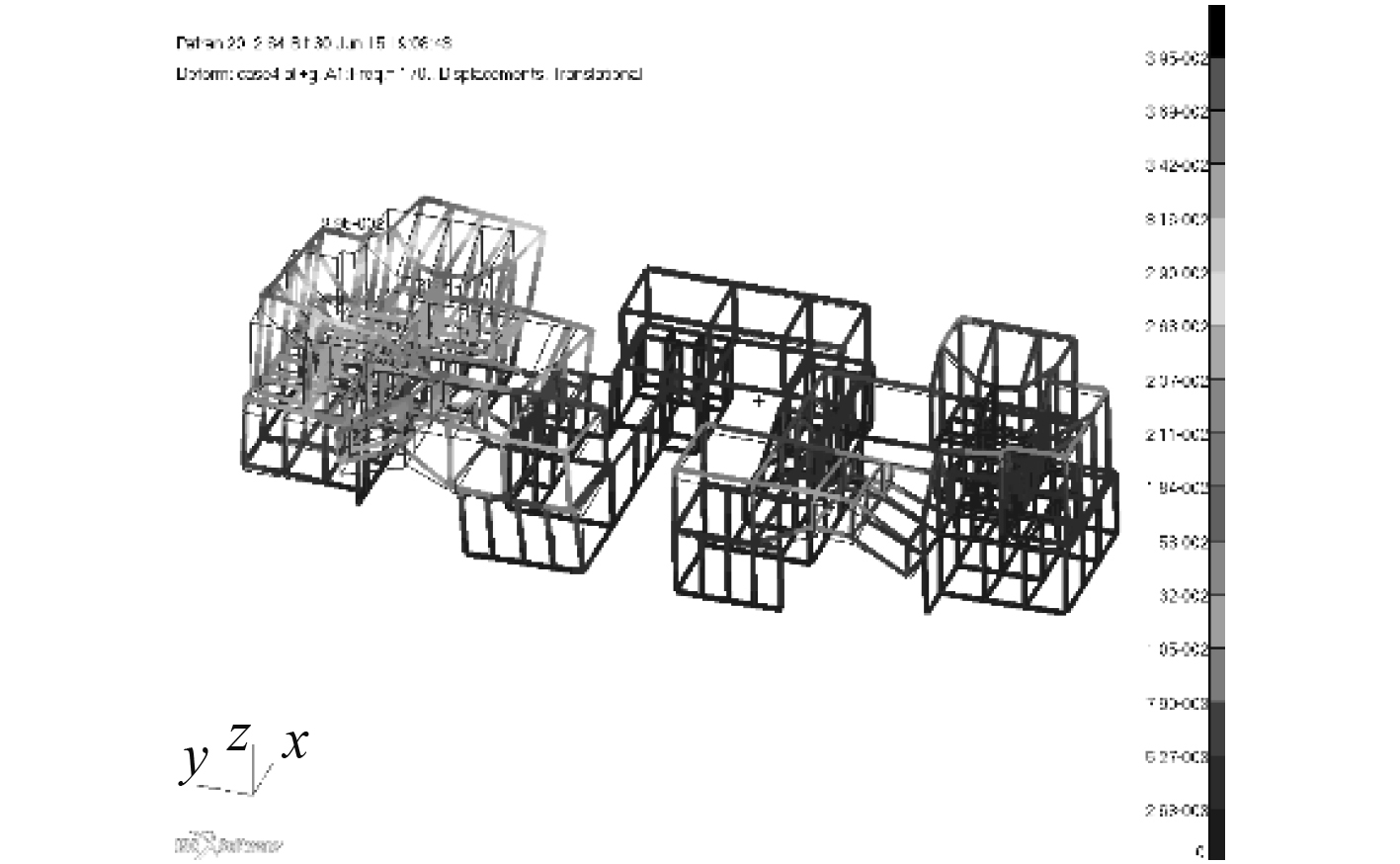
根据频响曲线,通过拾取峰值得到整体结构的固有频率,并得到相对应的响应振型。图15~图18为前4阶(45 Hz,80 Hz,135 Hz,170 Hz)的振型云图。
|
图 15 45 Hz整体结构响应云图 Fig. 15 Response nephogram of whole structure at 45 Hz |
|
图 16 80 Hz整体结构响应云图 Fig. 16 Response nephogram of whole structure at 80 Hz |
|
图 17 135 Hz整体结构响应云图 Fig. 17 Response nephogram of whole structure at 135 Hz |
|
图 18 170 Hz整体结构响应云图 Fig. 18 Response nephogram of whole structure at 170 Hz |
本文探讨了针对某大型复杂齿轮箱底架结构的一种模态特性分析方法。进行模态分析时面临着一些困难,如齿轮箱底架尺寸较大,其质量与刚度分布情况复杂;试验模态分析所需的试验条件要求高,对于力锤的选择与传感器数量都有较高的要求。此外,在有限元模态分析中会存在模态密集、模态向量繁杂、模态振型云图无法提取等问题。因此,本文提出以扫频分析为理论基础、以虚拟梁为间接工具的一种近似方法来求出该复杂大型结构的固有频率与振型。
该近似方法有以下几个特点:
1)扫频激励频响分析的计算结果不能得到结构的所有阶模态,但可以得到与关心的激励方向与作用点相关的固有频率与模态振型。
2)虚拟梁单元的剖面大小近似为0,因而不会对实际结构的刚度与质量矩阵产生影响,但能够充分显示出关心节点之间的相对变形。
3)根据一个在空间各个方向上有分量的激励力对结构进行的无阻尼频响分析所得到的频响曲线,可以得到所有响应峰值,以此得到结构的所有固有频率。
4)响应振型的激励位置与方向和对应阶数模态的模态力方向与作用点并不一致,因此得到的响应振型只能作为模态振型的一种近似。作为研究结构在确定激励点位置与激励方向下的情况,使用该方法得到的响应振型更具有实际工程意义。
5)根据该方法,最终可有效地得到复杂齿轮箱底架在任意频率范围内,在激励位置已知情况下的固有频率与近似的模态振型。
综上,对于大型的复杂结构,在无法直接用传统的有限元计算得到模态结果的情况下,可以通过已知的激励位置和方向,按上述方法进行扫频频响分析以近似等效模态分析。该方法计算复杂性不高,并且计算结果较直接,模态分析更能体现结构在工作状态下的模态情况,亦能对设备工作频率的选取以及结构刚度优化提供有益的帮助。
| [1] |
曹树谦, 张文德, 萧龙翔. 振动结构模态分析——理论, 试验与应用[M]. 天津: 天津大学出版社, 2014.
|
| [2] |
Rebert E. COLEMAN, Randall J. ALLEM. 试验结构动力学[M]. 北京: 清华大学出版社, 2012.
|
| [3] |
周立廷. 齿轮箱结构噪声预测与改进设计研究[D]. 大连: 大连理工大学, 2009.
|
| [4] |
周建星, 刘更, 吴立言. 含弹性支撑的船用减速器箱体动态特性[J]. 哈尔滨工业大学学报, 2012, 7(44): 97-101. |
| [5] |
林腾蛟, 蒋仁科, 李润方, 等. 船用齿轮箱动态响应及抗冲击性能数值仿真[J]. 振动与冲击, 2007, 12(26): 14-17. |
| [6] |
龙英, 滕召金, 赵福水. 有限元模态分析现状与发展趋势[J]. 湖南农机, 2009, 4(36): 27-28. |
| [7] |
曹妍妍, 赵登峰. 有限元模态分析理论及其应用[J]. 机械工程与自动化, 2007, 1(140): 73-74. |
| [8] |
李红华. 双螺杆挤出机传动箱体的有限元模态分析及结构优化设计[D]. 南京: 南京农业大学, 2012.
|
| [9] |
李耀明, 叶红玲, 张颜明, 等. 利用有限元软件进行虚拟正弦扫频试验与随机响应分析试验方法的研究[C]. 北京: 北京力学会学术年会, 2014.
|
| [10] |
田利思. MSC Nastran动力分析指南[M]. 北京: 中国水利水电出版社, 2012.
|
 2021, Vol. 43
2021, Vol. 43
