2. 中国特种飞行器研究所,湖北 荆门448035
2. AVIC Special Vehicle Research Institute, Jingmen 448035, China
随着节能减排力度的加强及油价持续上涨,减速航行已经成为降低船舶营运成本的重要措施。由于降速后船舶的流场特性不同于设计状态,为了提高船舶的水动力性能,需要对船体型线重新调整[1]。对于已运营的船舶,整船的优化涉及结构布置和关键区域的变动,不具有可行性。而球鼻艏凭借其结构布置简单、独立性好等优势成为重要的改装对象。
球鼻首改装的实质是对该部位的型线进行优化,相关学者对此进行了大量研究。贾瑞[2]利用切线搜索引擎来控制首部区域,结合遗传算法完成了某油船首部的优化;邓贤辉等[3]以ISIGHT集成平台为依托,运用母型船参数融合法和函数变换法完成了集装箱船首部的优化;MATULJA D[4]将贝塞尔曲面叠加在船体首部,以兴波阻力和波高为目标编写了优化算法程序,通过追踪控制点的方法实现某船球首的优化。
本文以某集装箱船为研究对象,以阻力系数为评价指标,对降速航行后的球鼻首展开优化。主要内容有:对球鼻首的外形进行参数化表达,采用拉丁超立方抽样产生不同形状的球鼻首;运用BP网络构建球鼻参数和阻力系数之间的近似关系模型;采用遗传算法对该网络模型进行极值寻优。结果表明,该方法有效降低了目标船型在减速航行后的阻力系数。
1 三维建模在适合进行球鼻首改装的船舶中,作为国际主要航线的集装箱船因具有投资少、回报快等优势是改装的主力军,本文以某集装箱船为研究对象,该船的主要参数由表1给出。
|
|
表 1 集装箱船基本参数 Tab.1 Basic parameters of container ship |
模型的创建在Catia创成式曲面设计模块中实现,其基本思路为:批量提取型线图中型值点的坐标,并对曲线的封闭性进行初步检查;利用Catia软件安装目录下的GSD Point Spline Loft From Excel.xls文件导入型值点,创建船体曲面采用分段生成的方式,对曲率变化大的首尾两端,通过添加水线等约束来保证模型质量。
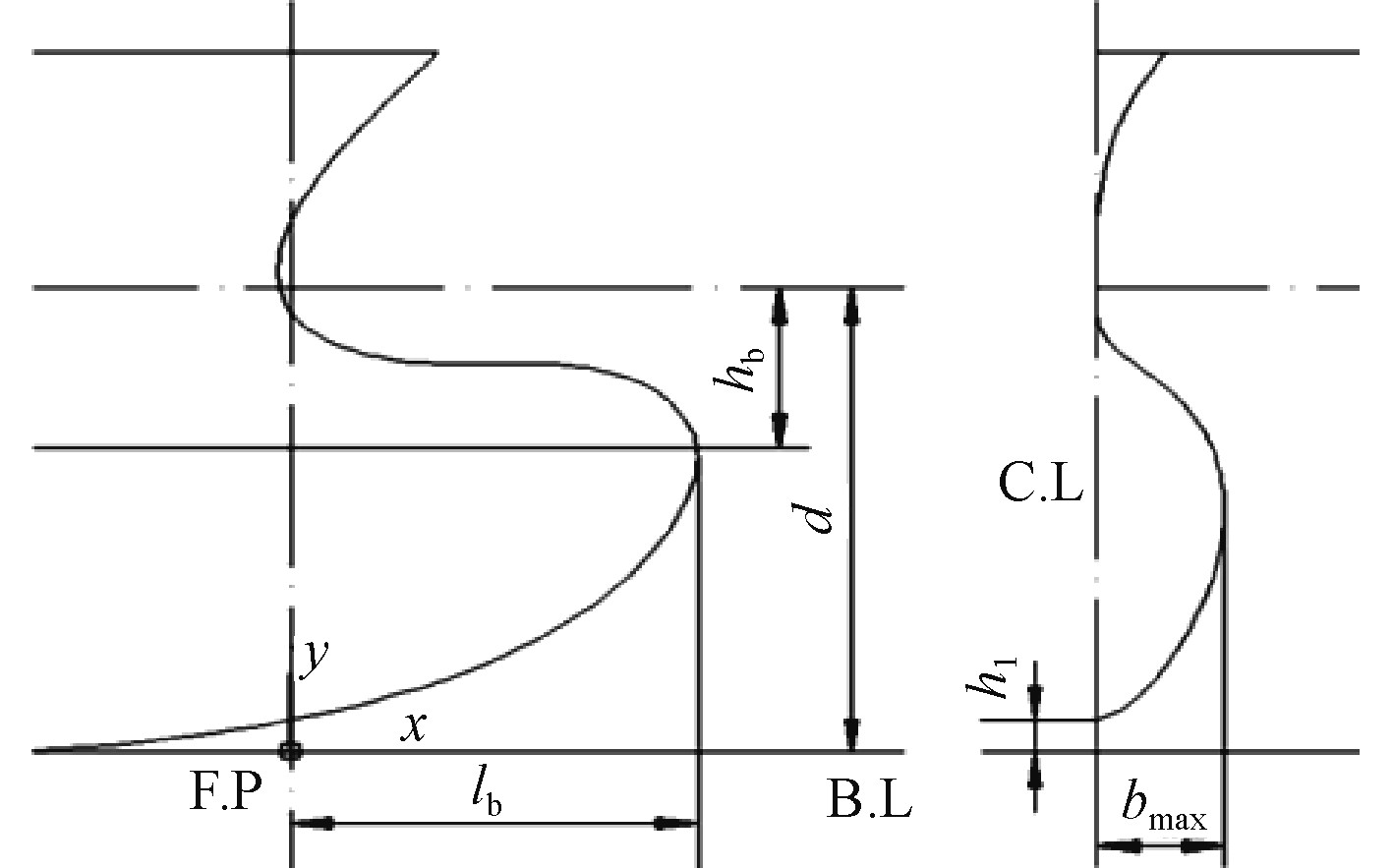
2 球鼻首参数化虽然球鼻外形复杂,参数化仍是其主要的研究方法,球鼻首的优化实质上是寻求和船体匹配的形状参数的过程。本文选取球鼻伸出长度lb、球鼻浸深hb、球鼻最大宽度bmax以及球鼻首中纵剖线在首垂线位置的最小高度值hi作为基本变量,各参数的具体含义如图1所示。
|
图 1 球鼻首特征参数 Fig. 1 Characteristic parameters of bulbous bow |
为了保持球鼻的基本外形,限制各参数的变化范围不超过原船相应变量的20%。采用拉丁超立方抽样方法产生不同形状的球鼻首,其基本思想为:根据变量的取值范围及样本点个数,将其等分为互不重叠的子区间,在每个区间内随机抽样,并将得到的数据进行不重复的随机组合获得最终样本点,表2给出了最终试验方案。
|
|
表 2 球鼻首形状方案 Tab.2 Shape forms of bulbous bow |
采用仿射变换法对船舶首部区域进行修改。为了提高计算效率,本文取计算模型的缩尺比λ=40,表3给出了不同船型在减速后的阻力值及换算结果,其中误差Error的计算公式为:
|
|
表 3 计算结果对比 Tab.3 Comparison of calculation results |
| $ Error = \dfrac{{{C_{ti}} - {C_{t0}}}}{{{C_{t0}}}} \times 100\% $ |
式中:Cti,Ct0分别为编号为i的船型和初始船型的阻力系数。
可以看出,球鼻形状对阻力有重要影响,合理的球首可取得一定的减阻效果,反之则会引起阻力的增加;各船型的摩擦阻力系数相近,但剩余阻力系数变化较大,说明球鼻首主要通过改变兴波阻力来影响总阻力的。因此,确定形状参数和阻力之间的变化关系是首部优化的关键。
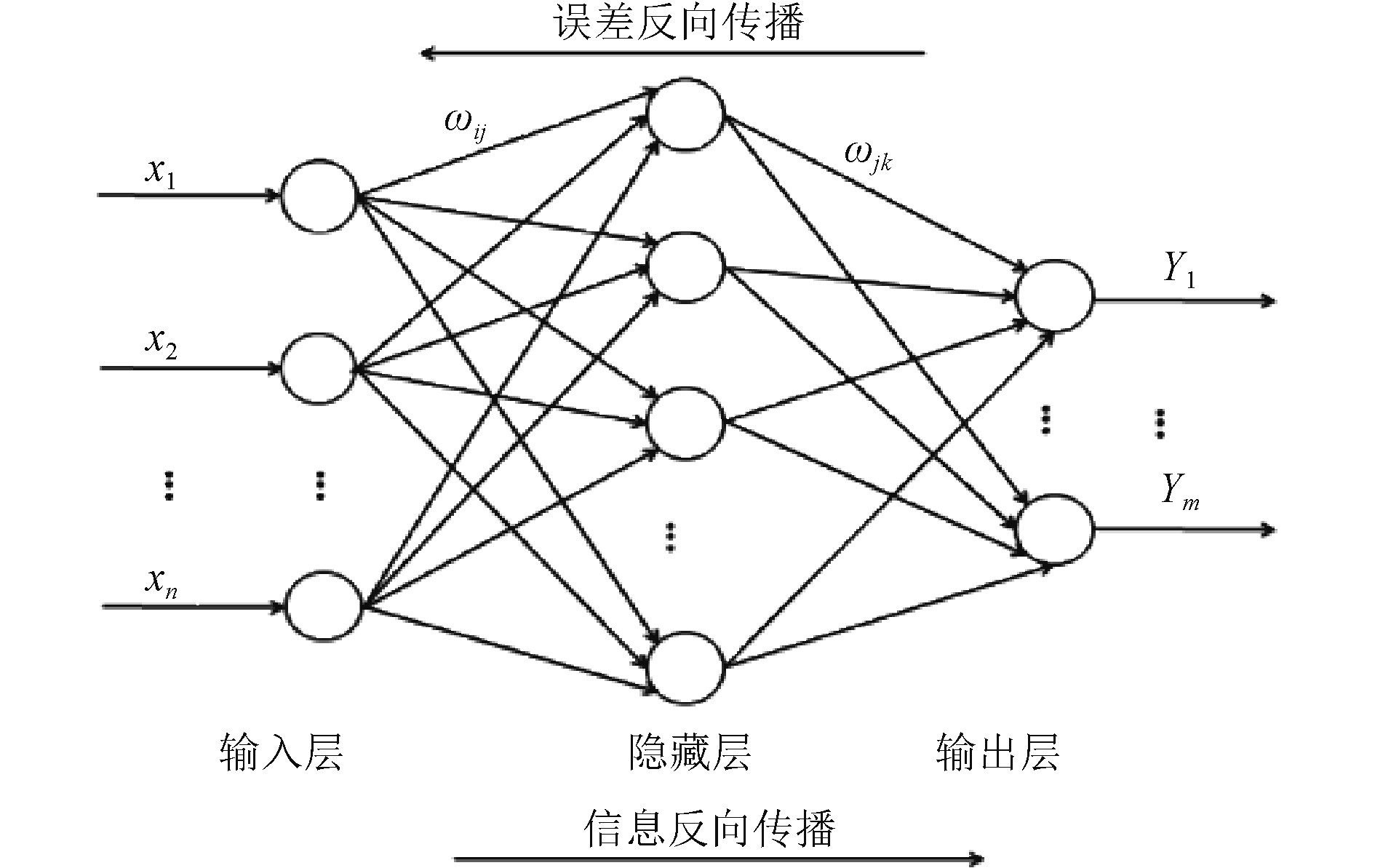
3 球鼻首优化分析 3.1 BP网络构建BP网络又称误差反向传播的神经网络,它具有较强的非线性映射能力和灵活的网络结构,仅凭数据本身就可以建立输入和输出之间的关系模型[5]。输入变量经过输入层、隐藏层向前传至输出层;网络对输出结果进行判断,当输出值和期望值有较大偏差时,误差反向传递,网络依据相关规则调整节点的权值系数和阈值,正向传递和反向传递交叉反复进行,直到获得较为满意的输出,训练到此结束。
|
图 2 BP网络拓补结构 Fig. 2 Topological structure of BP network |
为了避免训练出现“过拟合”,通常将输入数据分为训练集、验证集、测试集。训练集用于确定节点权值系数和阈值;验证集用于训练的监督,出现过拟合时,验证集便会终止网络训练;测试集用于检验训练后网络的预测精度。本文以球鼻参数为输入变量,阻力系数为输出变量,训练组随机选取10个样本点,验证组和测试组各取一个样本点,表4给出了训练后网络的输出和原始数据的对比情况。
|
|
表 4 网络输出结果对比 Tab.4 Comparison of network outputs |
可以看出,该网络的预测误差控制在2.1%以内,表明该网络具有可靠的预测精度,可作为球鼻参数和阻力系数之间的近似模型。
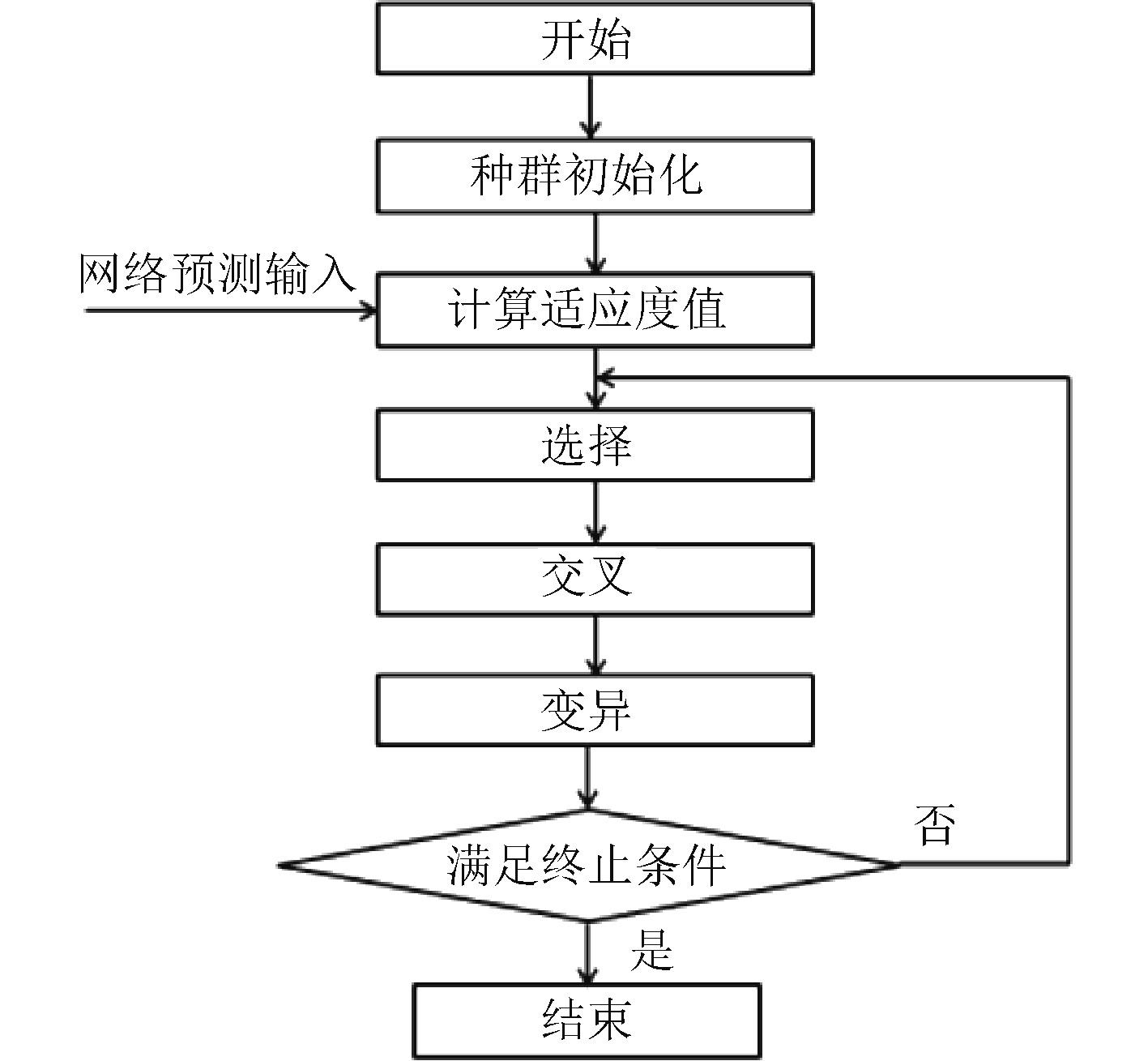
3.2 球鼻首形状参数极值寻优遗传算法通过模拟自然选择和遗传进化规律找到网络的最优解,它包括“选择”、“交叉”、“变异”基本流程,如图3所示。选择是指从群体中抽取部分个体作为父代,适应度越好的个体被选择的概率越大;交叉指从选好的群体中抽取个体,并以一定的概率对遗传编码进行交换组合以产生新个体;变异则通过改变染色体上的基因值,使种群有机会产生适应度更好的新个体。
|
图 3 球鼻首优化流程 Fig. 3 Optimization process of bulbous bow |
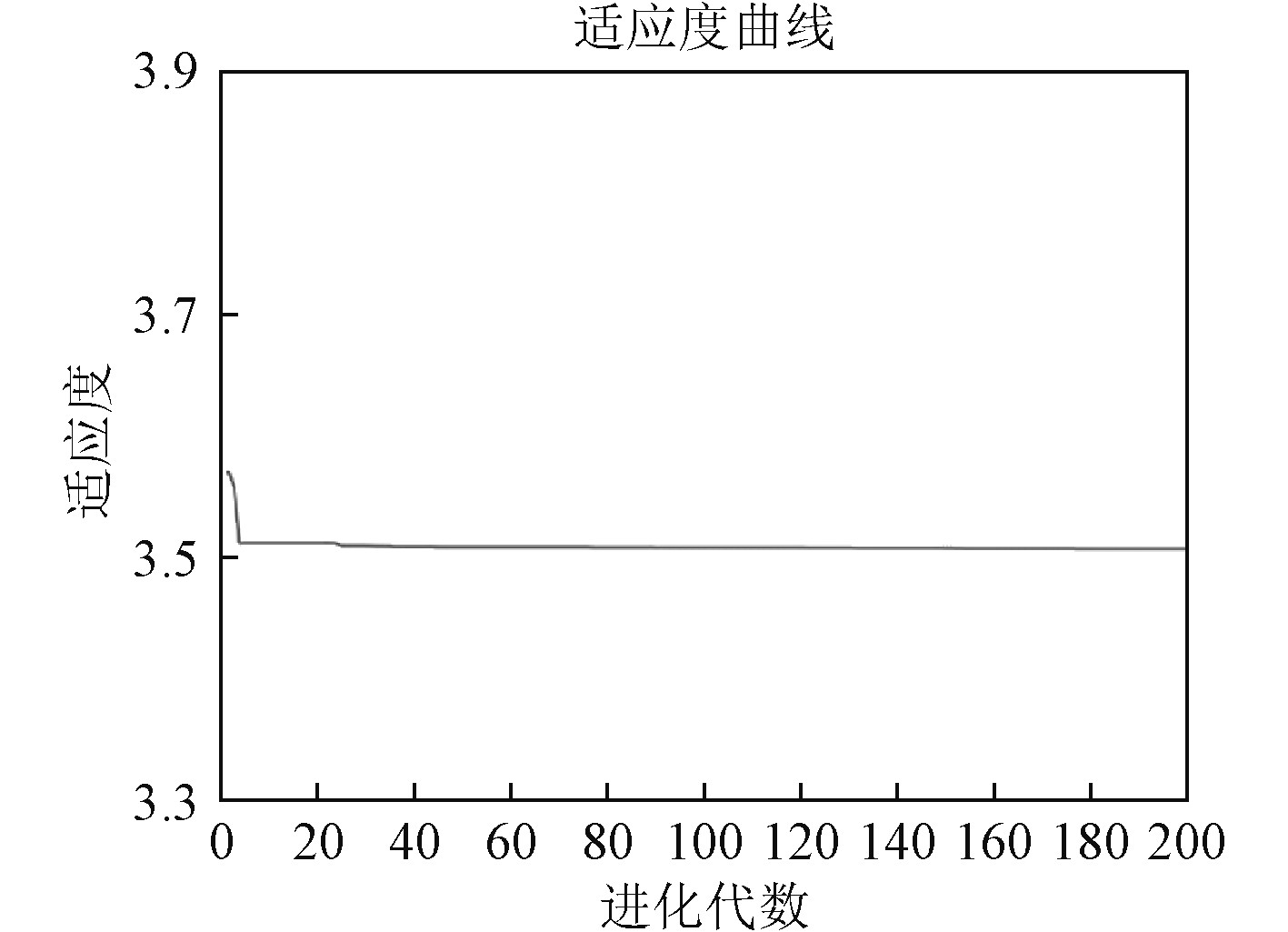
本文遗传算法各参数的设置为:种群数量100,最大迭代次数为200,交叉概率为0.4,变异率为0.2,寻优过程中最佳个体适应度收敛迭代曲线及具体参数信息如图4所示。
|
图 4 最优个体适应度收敛曲线 Fig. 4 Convergence curve of optimal individual fitness |
根据最优个体的参数值修改船型,设置优化船型和初始船型具有相同的网格节点分布规律、湍流模型及边界条件,图5和图6给出了优化船和原船型动压力云图和波高对比情况。

|
图 5 船体动压力对比云图 Fig. 5 Comparison of hull dynamic pressure |
|
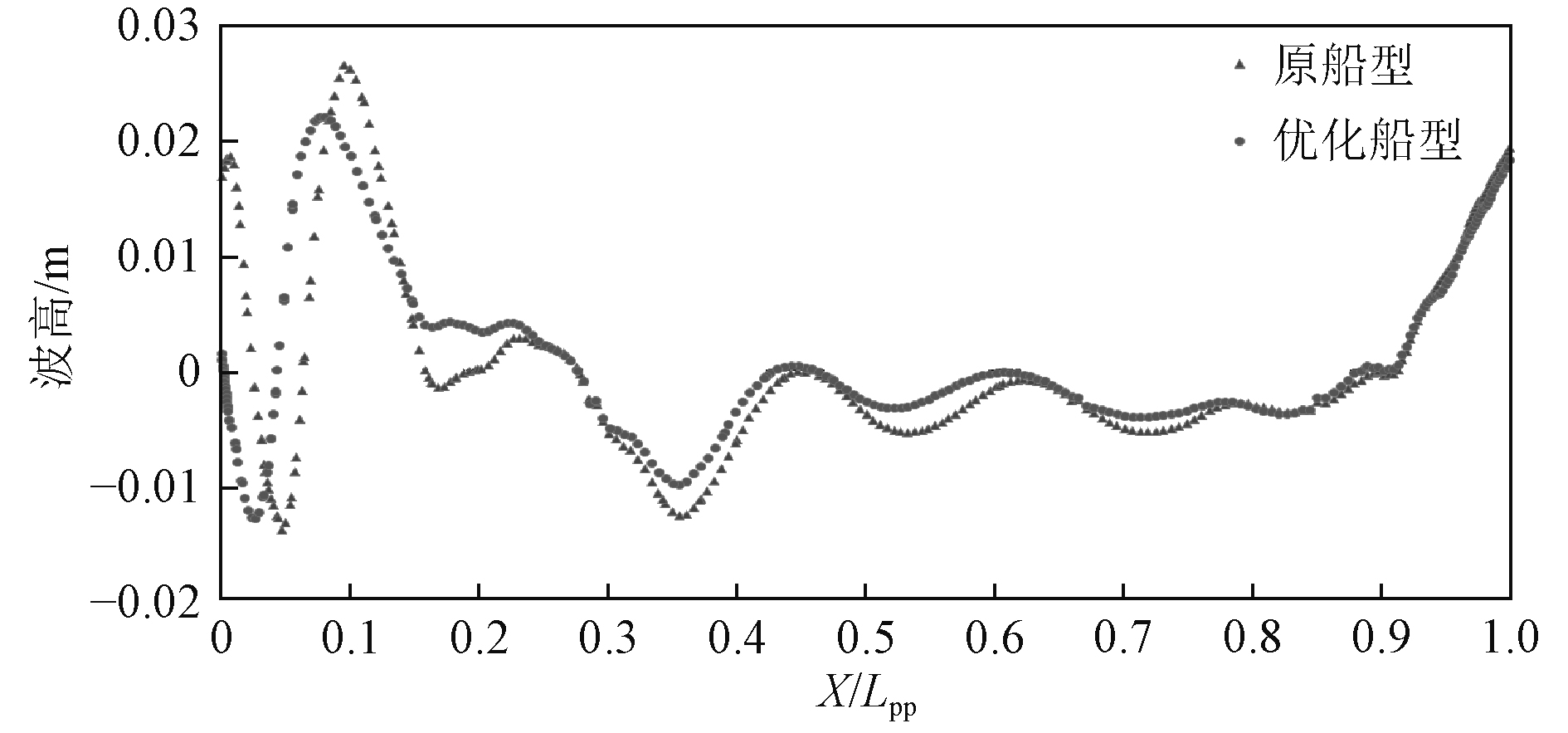
图 6 波形对比图 Fig. 6 Comparison of wave profile |
从图5可以看出,船首区域的压力最大,船体表面的压力沿船长方向先减小后增大,从船中到船尾又逐渐减小,这种纵向压力梯度变化是粘压阻力产生的根本原因,而优化船型首部的压力明显减小,说明新船首改善了粘压阻力。
在波高对比图中,横坐标表示船长的无因次距离,“0”代表船首,“1”代表船尾,纵坐标表示自由液面的升沉。可以看出,新船型首、中、尾区域的波幅明显降低,说明新球首和船体匹配较好,使得水流更加流畅,进而降低了兴波阻力。
根据计算结果,优化船型的阻力系数为3.528×10−3,与原船3.70×10−3相比降低了4.65%,而与网络预测的最佳适应度值3.504×10−3相比,预测误差为0.68%,在工程范围内是可以接受的,说明将该方法用于球鼻首的优化可行。
4 结 语本文围绕减速航行后球鼻首的优化展开,通过选取特征参数对球鼻形状进行构建,采用拉丁超立方试验设计方法确定了不同球鼻形状方案,球鼻首参数和阻力系数之间关系模型的构建则采用拟合能力较强的BP网络。为了找到最优的球鼻参数,以网络输出的阻力系数为适应度函数,采用遗传算法对其进行极值寻优。结果表明,该方法可以有效降低目标船型的阻力,对球鼻首的优化研究有一定的借鉴意义。
| [1] |
许欢, 刘伟, 徐梦洁. 船舶减速航行的现状、减排效果及产生的问题[J]. 交通企业管理, 2013, 28(9): 46-47. DOI:10.3963/j.issn.1006-8864.2013.9.020 |
| [2] |
贾瑞. 大型油船艏部线型优化[D]. 大连: 大连海事大学, 2014.
|
| [3] |
邓贤辉, 方昭昭, 赵丙乾. 基于计算流体动力学的最小阻力船型自动优化[J]. 中国舰船研究, 2015, 10(3): 19-25. DOI:10.3969/j.issn.1673-3185.2015.03.004 |
| [4] |
MATULJA D, DEJHALLA R. Genetic algorithm optimization of a ship's bulbous bow[A]. Annals of DAAAM for 2011 & Proceedings of the 22nd International DAAAM Symposium, Vienna, Austria, EU, 2011, 22(1): 15−17.
|
| [5] |
HECHT-NIELSEN R. Theory of the back-propagation neural network[J]. International Joint Conference on Neural Networks, 1989, 1(1): 593-605. |
 2021, Vol. 43
2021, Vol. 43
