2. 渤海造船厂集团有限公司,辽宁 葫芦岛 125005
2. Bohai Shipyard Group Co., Ltd., Huludao 125005, China
夹层板结构具有相对密度小、优良的抗冲击和中高频隔声性能,使得其越来越广泛地应用于舰船结构中[1]。由于夹层板结构在低频段隔声效果不是很理想,对于要求较高的场合来说,寻找一种轻质且在低频段拥有较好隔声效果的隔声材料仍是一个亟需解决的问题。近几年出现的薄膜型声学超材料为解决此类问题提供了新思路。
声学超材料结构最初实验模型是在环氧树脂中周期性嵌入表面涂有硅橡胶铅球的超材料结构[2],但其质量较大,很难满足轻质要求。香港科技大学的Yang等[3]制作出轻质的薄膜型声学超材料结构。一些研究者[4-5]针对薄膜型超材料结构中质量块的布放方式和布放位置进行了研究,并实现良好的低频隔声性能。同时,也有一些学者在传统隔声材料的基础上进行结构改进,制作出新型的薄膜型声学超材料。Ni等[6]在蜂窝板的一侧覆盖了一层张紧薄膜,经实验验证这种新型结构在低频时有较好的隔声效果。Lu等[7]将薄膜置于铝蜂窝板的蜂窝芯中间,得到改进的薄膜型声学超材料结构。
基于夹层板结构和薄膜型声学材料结构的特点,本文提出一种复合结构,在蜂窝夹层板中加入不同形状质量块的薄膜型声学超材料,利用comsol有限元软件进行仿真分析,并对边框形状、质量块大小以及薄膜预应力等对超材料结构隔声特性的影响进行探讨。
1 薄膜型超材料理论模型薄膜型声学超材料的单个胞元可以简化为四周固定的“薄膜-质量块”系统[8],图1为位于

|
图 1 薄膜型声学超材料的单个胞元结构示意图 Fig. 1 A unit cell of the MAM |
假设薄膜上任意一点产生的扰动不影响其他点的振动,忽略薄膜表面的声压叠加,薄膜被均匀拉伸且横向振动位移很小,忽略薄膜的弯曲刚度,质量块接触处的薄膜不受质量块刚度的影响。由经典的薄膜理论可知,均匀薄膜附加质块结构的运动微分方程可表述为:
| $\begin{split} {\rho _s}\frac{{{\partial ^2}w}}{{{\partial ^2}t}} + & {\rho _m}\hbar (x,y,{x_0},{y_0},{l_x},{l_y})\frac{{{\partial ^2}w}}{{{\partial ^2}t}} - \\ & T{\nabla ^2}w = {p_{inc}} + {p_{ref}} - {p_{tr}} \text{,}\end{split} $ | (1) |
式中:
薄膜接触面的声压由薄膜表面的振动速度决定,则
| $\frac{{\partial ({p_{inc}} + {p_{ref}})}}{{\partial z}} = \frac{{\partial {p_{tr}}}}{{\partial z}}{\rm{ = }} - i\omega \rho \frac{{\partial w}}{{\partial t}}\text{,}$ | (2) |
式中:
将式(2)代入式(1)整理得:
| ${\rho _s}\frac{{{\partial ^2}w}}{{\partial {t^2}}} + {\rho _m}\hbar \frac{{{\partial ^2}w}}{{\partial {t^2}}} - 2\rho c\frac{{\partial w}}{{\partial t}} - T{\nabla ^2}w = 2{p_{inc}}\text{,}$ | (3) |
基于模态叠加理论可得[9]:
| $w(x,y,t) = \sum\limits_{n = 1}^N {{W_n}} (x,y){q_n}(t),{q_n}(t) = {\tilde q_n}{e^{i\omega t}}\text{,}$ | (4) |
式中:
对整个薄膜进行积分,整理得:
| $ - {\omega ^2}\left\{ {\left[ {{M}} \right] + \left[ {{Q}} \right]} \right\}\left\{ {\ddot{\tilde{{q}}}} \right\} + i\omega \left[ {{C}} \right]\left\{ {\dot{\tilde{{q}}}} \right\} - \left[ K \right]\left\{ {\tilde {{q}}} \right\} = 2{P_i}\left\{ {{H}} \right\}\text{,} $ | (5) |
解方程(5)得:
| $\left\{ {\tilde {{q}}} \right\} = \frac{{2{P_{inc}}}}{{ - {\omega _2}\left\{ {\left[ {{M}} \right] + \left[ {{Q}} \right]} \right\} + i\omega \left[ {{C}} \right] - \left[ {{K}} \right]}}\left\{ {{H}} \right\}\text{,}$ | (6) |
对于小尺寸膜结构,可用膜结构表面振动平均速度幅值来求平均透射声压幅值:
| $\left\langle {{P_{tr}}} \right\rangle = \rho c\left\langle {\tilde v} \right\rangle = \frac{{i\omega \rho c}}{{{L_x}{L_y}}}{\left\{ {{H}} \right\}^{\rm T}}\left\{ {\tilde {{q}}} \right\}\text{,}$ | (7) |
则声压透射系数为:
| $\begin{split} {t_p} = &\frac{{\left| {\left\langle {{P_{tr}}} \right\rangle } \right|}}{{{P_{inc}}}} = \left| {\frac{{i2\rho c\omega }}{{{L_x}{L_y}}}{{\left\{ {{H}} \right\}}^{\rm T}}} \right. \times\\ & \left. {\frac{1}{{ - {\omega ^2}\left\{ {\left[ {{M}} \right] + \left[ {{Q}} \right]} \right\} + i\omega \left[ {{C}} \right] + \left[ {{K}} \right]}}\left\{ {{H}} \right\}} \right|\text{,} \end{split} $ | (8) |
薄膜型声学超材料隔声性能的传声损失STL为:
| $STL = 20\lg (1/{t_p})\text{。}$ | (9) |
传统的蜂窝夹层板结构符合质量定律,声学超材料结构利用带质量块的薄膜使结构在某些特定频率处呈现负的质量密度,从而获得优良的隔声效果。本文所设计的声学超材料夹层板结构包含由上下面板和蜂窝芯组成的蜂窝夹层板结构及夹在蜂窝芯中间带质量块张紧薄膜的声学超材料结构,其结构模型如图2所示。

|
图 2 薄膜型超材料夹层板结构示意图 Fig. 2 Schematic of MAM-honeycomb sandwich plate |
蜂窝夹层板材料采用轻质的碳纤维结构,面板厚度为1 mm,蜂窝芯高度10 mm。薄膜型超材料的薄膜采用0.3 mm厚的硅胶薄膜,质量块为不锈钢材质,其参数如表1所示。
|
|
表 1 薄膜型超材料参数 Tab.1 Parameters of MAM |
在薄膜型声学超材料结构中,质量块的布放方式和布放位置影响结构吸隔声特性,为此本文对圆环形、三角形、正方形、十字形和米字形质量块的薄膜型声学超材料隔声性能进行分析研究。设计的质量块以半径为2.5 mm,高度为2 mm的圆形质量块为基础,在各质量块质量相同的前提下设计结构尺寸。质量块结构如图3所示。采用基于comsol多物理场分析软件的有限元方法,对超材料结构吸隔声特性进行分析,计算过程中结构的边界条件为周期性边界条件。
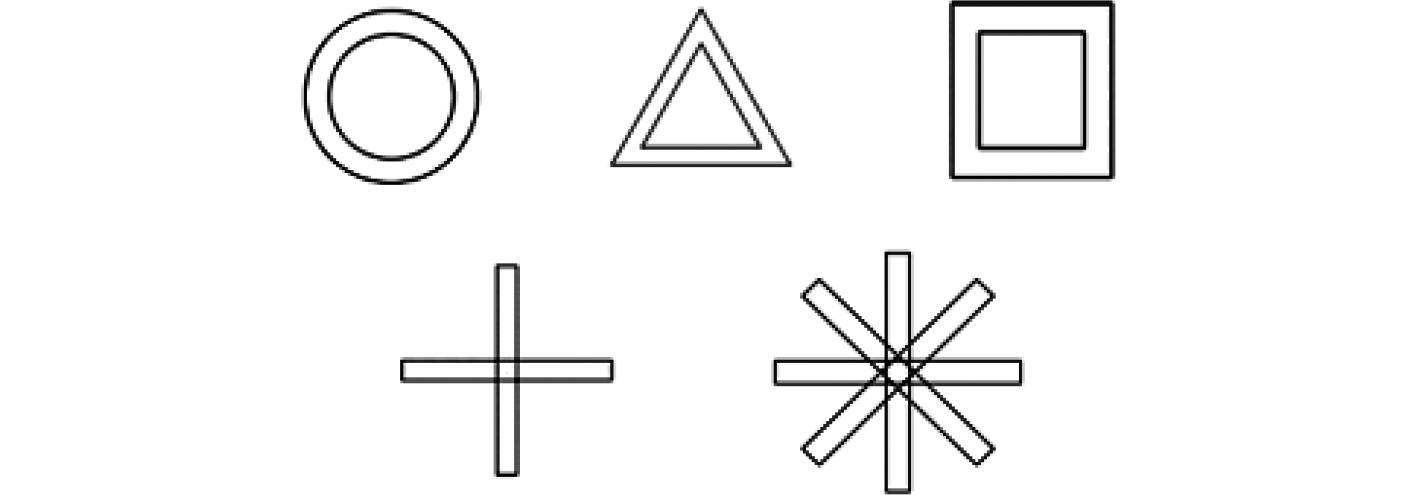
|
图 3 各种形状的分布质量块 Fig. 3 Distributed masses of various shapes |
图4为5种不同形状质量块声学超材料结构的隔声特性曲线。
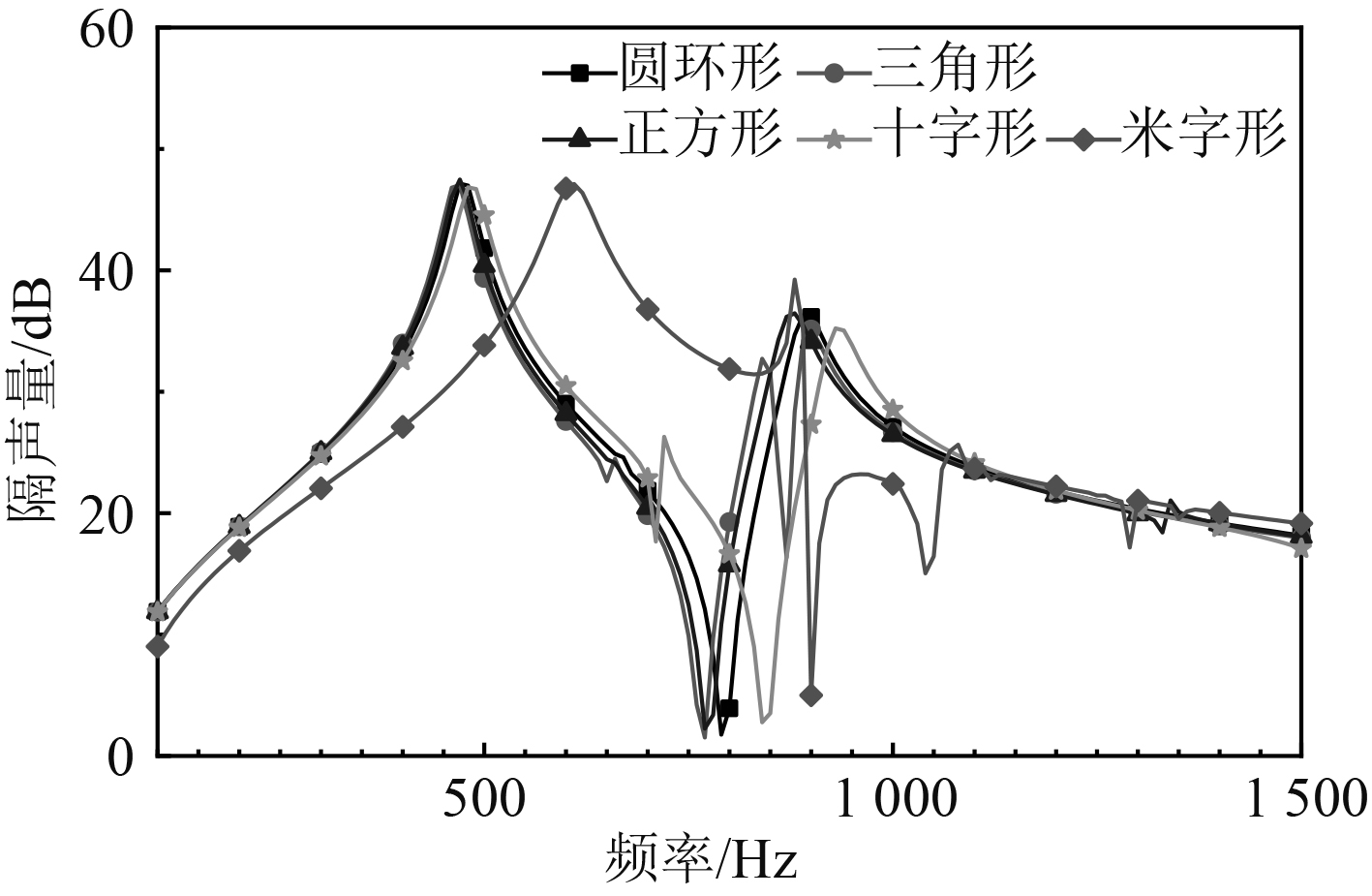
|
图 4 不同形状质量块的隔声特性曲线 Fig. 4 Sound transmission loss of masses with different shapes |
从图4可以看出,各种质量块的超材料结构最大隔声量差别不大,十字形分布质量块相较传统的圆形、三角形、四边形等形状来说,隔声峰的带宽略有增大。米字形超材料结构相比其他结构来说隔声峰往高频方向移动,但在1000 Hz以下的频带范围内拥有比其他形状更宽的隔声频带,因而综合来说,米字形相较于其他形状质量块的超材料结构拥有更好的隔声效果。
2.2 结构参数对隔声特性的影响夹层板及超材料结构参数的改变会影响超材料夹层板结构的隔声性能,因此本文针对低频具有较宽带隙特性的米字形超材料结构,开展夹层板的蜂窝结构、超材料质量块和薄膜等参数变化对超材料夹层板结构隔声性能的影响分析。
2.2.1 蜂窝结构形状对隔声特性的影响分别考虑蜂窝结构形状为圆形、四边形以及六边形3种形状结构对米字形声学超材料结构隔声性能的影响,计算结果如图5所示。
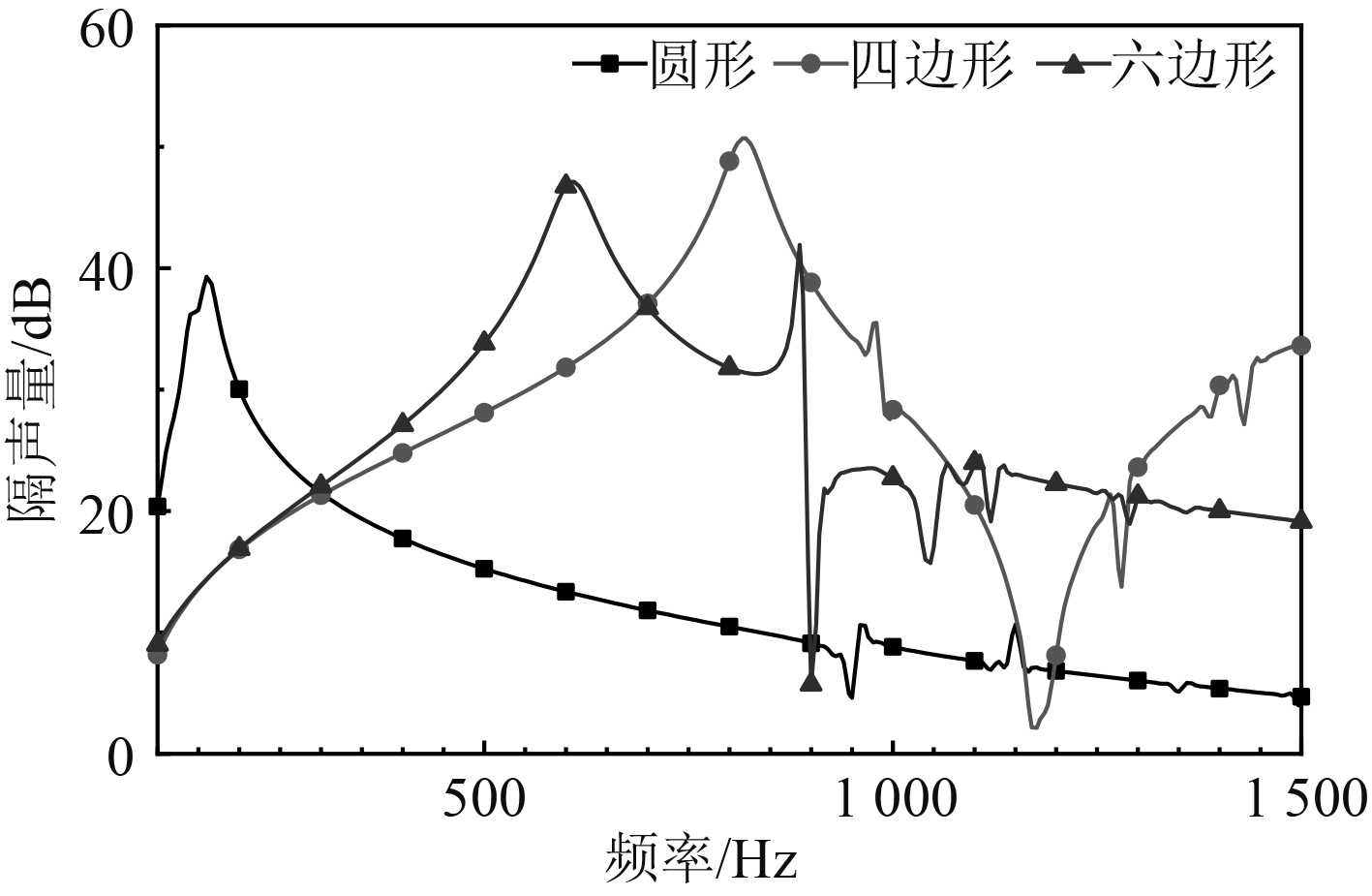
|
图 5 不同形状蜂窝结构的隔声特性曲线 Fig. 5 Sound transmission loss of honeycomb structures with different shapes |
从图5计算结果可以看出,四边形和六边形边框超材料结构的低频隔声效果明显优于圆形边框的超材料结构,六边形边框的超材料第一隔声峰所对应的频率更低,但四边形边框超材料在1000 Hz以下的隔声频带更宽。因而在实际的应用中可以综合考虑选择使用六边形或四边形边框结构。
2.2.2 质量块大小对隔声特性的影响保持质量块与薄膜接触面积不变,通过改变质量块高度改变质量块质量,考虑质量块高度分别为1 mm,1.5 mm,2 mm,2.5 mm和3 mm情况,结构隔声特性曲线如图6所示。

|
图 6 不同高度质量块的隔声特性曲线 Fig. 6 Sound transmission loss of masses with different heights |
可以看出,质量块质量越大,低频隔声效果越好。随质量块高度增加,其隔声峰往低频方向移动,同时最大隔声量随之增大,因此可通过调整质量块的大小来控制结构的隔声频带。但可以看出随着质量块的不断增大,其最大隔声量的增幅也减小,隔声频带变窄,因而在实际应用中要综合考虑进行设计。
2.2.3 薄膜预应力对隔声特性的影响分别考虑薄膜的预应力为100 N/m,200 N/m,300 N/m,400 N/m和500 N/m情况下,薄膜预应力对结构隔声特性的影响。图7为不同薄膜预应力情况下结构的隔声特性曲线。
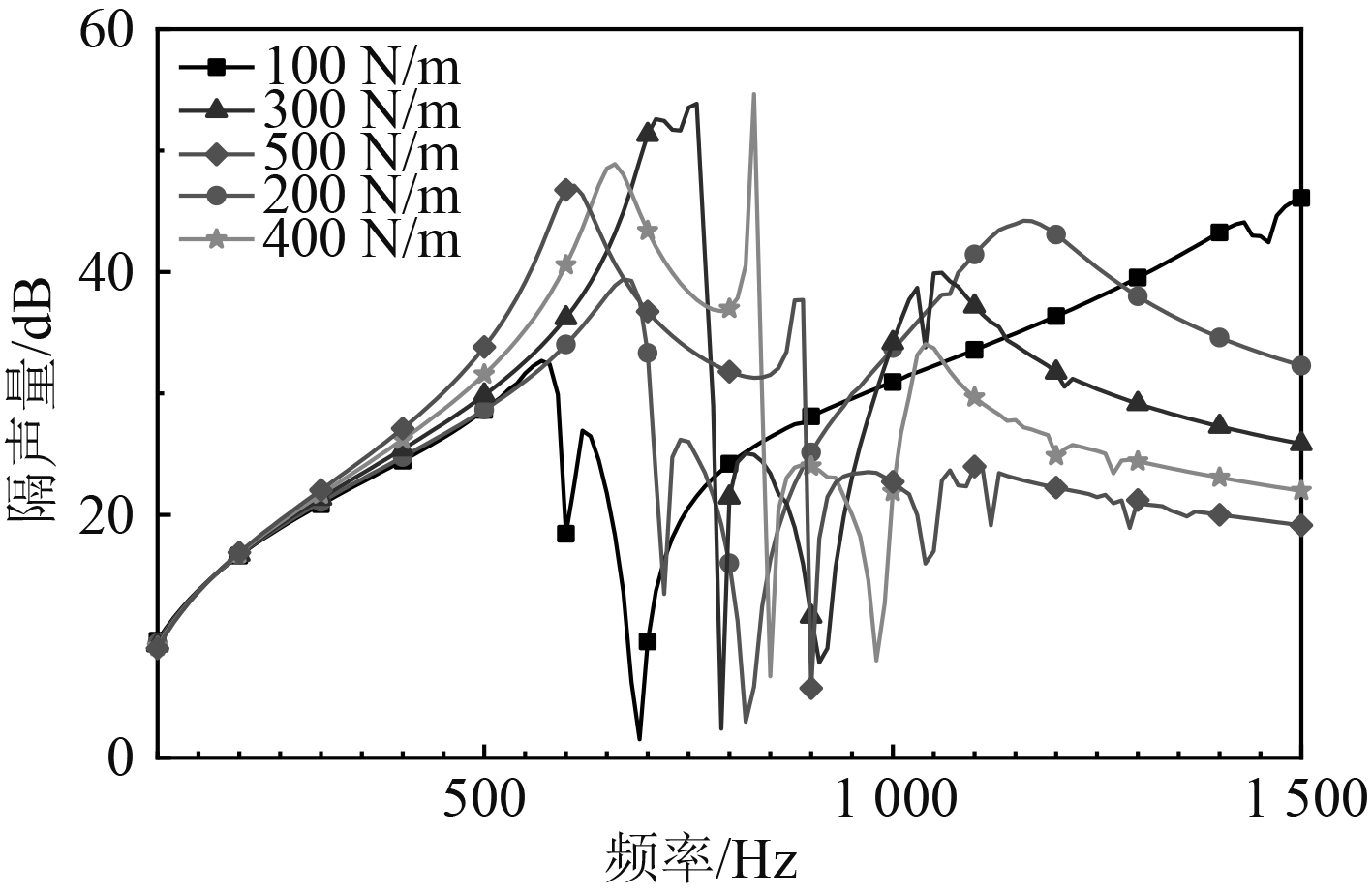
|
图 7 不同薄膜预应力的隔声特性曲线 Fig. 7 Sound transmission loss of different membrane tension |
从图7计算结果可以看出,薄膜预应力对结构的隔声特性有显著的影响。当预应力较小时,结构的低频隔声效果较差,高频隔声效果较好。薄膜预应力越大,低频的隔声效果越好,随着薄膜预应力的增大,2个隔声峰之间的距离变小,隔声峰的位置更加集中。因而可以通过改变薄膜预应力的大小来适应不同的低频隔声要求。
3 结 语本文基于夹层板和声学超材料结构提出一种新型薄膜-夹层板复合结构,针对不同形状质量块对薄膜型声学超材料隔声性能的影响进行分析研究,设计的米字形质量块相较于其他形状质量块的隔声效果更好。六边形或四边形相较于圆形边框蜂窝结构有更好的隔声性能。质量块大小以及薄膜预应力对隔声效果影响较大,在实际应用中,可以通过改变参数来设计不同的隔声频带。薄膜-夹层板复合超材料结构相比传统蜂窝隔声结构质量变化不大的情况下,取得了优良的隔声效果,因此超材料结构在舰船结构减振降噪设计中有广阔的应用前景。
| [1] |
刘建良, 梅志远, 唐宇航, 等. 几种典型复合材料板振动特性综合对比分析及设计规律研究[J]. 振动与冲击, 2019, 38(15): 65-72. LIU J L, MEI Z Y, TANG Y H, et al. Comprehensive comparative analysis for vibration characteristics of several typical composite panels and their design law[J]. Journal of Vibration and Shock, 2019, 38(15): 65-72. |
| [2] |
LIU Z, ZHANG X, MAO Y, et al. Locally resonant sonic materials[J]. Nature, 2000, 289: 1734-1736. |
| [3] |
YANG Z, DAI H M, CHAN N H, et al. Acoustic metamaterial panels for sound attenuation in the 50-1 000 Hz regime[J]. Applied Physics Letters, 2010, 96(4): 041906. DOI:10.1063/1.3299007 |
| [4] |
NAIFY C J, CHANG C M, MC Knight G, et al. Transmission loss of membrane-type acoustic metamaterials with coaxial ring masses[J]. Journal of Applied Physics, 2011, 110(12): 124903. DOI:10.1063/1.3665213 |
| [5] |
陈松乔. 多质量块声学超材料的隔声分析和减振研究[D]. 哈尔滨: 哈尔滨工业大学, 2017. CHEN S Q. Study on sound insulation and vibration reduction of multi-mass acoustic metamaterial[D]. Harbin: Harbin Institute of Technology, 2017. |
| [6] |
Ni SUI, Xiang YAN, Tai-Yun HUANG, et al. A lightweight yet sound-proof honeycomb acoustic metamaterial[J]. Applied Physics Letters, 2015, 106: 171905. DOI:10.1063/1.4919235 |
| [7] |
LU K, WU J H, GUAN D, et al. A lightweight low-frequency sound insulation membrane-type acoustic metamaterial[J]. AIP Advances, 2016, 6(2): 025116. DOI:10.1063/1.4942513 |
| [8] |
温激鸿, 等. 人工周期结构中弹性波的传播: 振动与声学特性[M]. 北京: 科学出版社, 2015.6.
|
| [9] |
KOPMAZ O, TELLI S. Free vibrations of a rectangular plate carrying a distributed mass[J]. Journal of Sound and Vibration, 2002, 251(1): 39-57. DOI:10.1006/jsvi.2001.3977 |
 2021, Vol. 43
2021, Vol. 43
