2. 上海交通大学 船舶海洋与建筑工程学院,上海 200240;
3. 高新船舶与深海开发装备协同创新中心,上海 200240;
4. 南通中远海运川崎船舶工程有限公司,江苏 南通 226000
2. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China;
3. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China;
4. Nantong COSCO KHI Ship Enginerring Co., Ltd., Nantong 226000, China
多用途船以其分舱灵活的特点,正逐步成为除集装箱船、油船和散货船三大主流船型以外的第4种主流船型。因此针对多用途船进行型线优化设计,以改善多用途船的阻力性能,对节能降耗和增加营运效益来说都具有重要意义。传统的型线设计模式主要依赖设计经验以及船舶型线数据库,耗时耗力,且方案非最优。而近些年提出的SBD(Simulation Based Design)技术,则是结合了最优化技术以及计算流体动力学,使得整个型线设计流程更加高效。
近十几年来,国内外船型优化尤其在以阻力最优为目标的船体型线优化方面得到了迅猛的发展,主要工作集中在对中高速船的船首或船的中前部型线进行优化,并获得了较好的减阻效果[1-3]。而对于低速肥大型船舶而言,相较于阻力性能,其尾部流场的品质也越来越受到设计研究者的重视[4-5]。
本文以某低速肥大型的多用途船为研究目标,以其阻力以及伴流场不均匀度为优化目标,通过RBF插值方法实现船体曲面变形,进而采用Shipflow软件计算船舶的总阻力和伴流场不均匀度,结合非劣分类遗传算法以及Kriging代理模型快速求解得到性能最优的型线,并通过STAR CCM+对优化结果进行验证,根据优化结果为该多用途船提出了首尾型线趋势性建议。
1 船体型线优化 1.1 优化目标以某多用途船作为研究对象,分别考虑船首和船尾形状改变对船舶水动力性能的影响。优化工况选取设计航速13.77 kn,吃水11 m。船首形状改变主要影响兴波阻力,因此以兴波阻力为优化目标;船尾型线优化时,则以总阻力和伴流场不均匀度为优化目标。该船的主尺度信息以及优化时的约束条件见表1。
|
|
表 1 多用途船参数及约束条件 Tab.1 Parameters and restrictions of multipurpose ship |
基于径向基函数[6](RBF)的曲面变形方法属于船体曲面局部变形方法,该方法主要通过局部控制点的位移实现船体曲面的变形,并保证变形后船体曲面的连续性与光滑性。
船体表面节点的位移可以通过插值函数
| $S({{x}}) = \sum\limits_{j = 1}^N {{\lambda _j}\phi \left(\left\| {{{x}} - {{{x}}_{{j}}}} \right\|\right)} + p({{x}})\text{。}$ | (1) |
式中:
| $\phi (\left\| {{x}} \right\|) = {(1 - \left\| {{x}} \right\|)^4}(4\left\| {{x}} \right\|{\rm{ + }}1)\text{。}$ | (2) |
式中:多项式
| $p({{x}}) = {c_1} + {c_2}x + {c_3}y + {c_4}z\text{。}$ | (3) |
基于上述方法,为了实现船首和船尾的变形,首先需要对可变控制点进行布置。布置的原则是可变控制点可以使得首尾形状UV度在一个较大的范围内变化,对于船首型线,可变控制点应该布置在船首的进流段,对于船尾型线,应该布置在船尾的去流段,所有可变控制点的变化方向均为Y方向。为了保证船中型线不受影响,还应在船中部分添加固定控制点。具体布置情况见图1,可变控制点的详细布置信息见表2。

|
图 1 可变控制点的位置 Fig. 1 Location of variable control points |
|
|
表 2 可变控制点的参数 Tab.2 Parameters of variable control points |
借助流体力学分析软件Shipflow进行水动力性能快速计算。该软件对不同的阻力成分,在计算和分析时会采用不同的理论模型:对于兴波阻力,计算时采用Rankine源非线性势流理论方法(船体表面压力积分和船尾能量法);对于摩擦阻力,采用边界层动量积分方法进行求解;对于低速肥大型船中占总阻力成分较小的粘压阻力,计算分析时采用
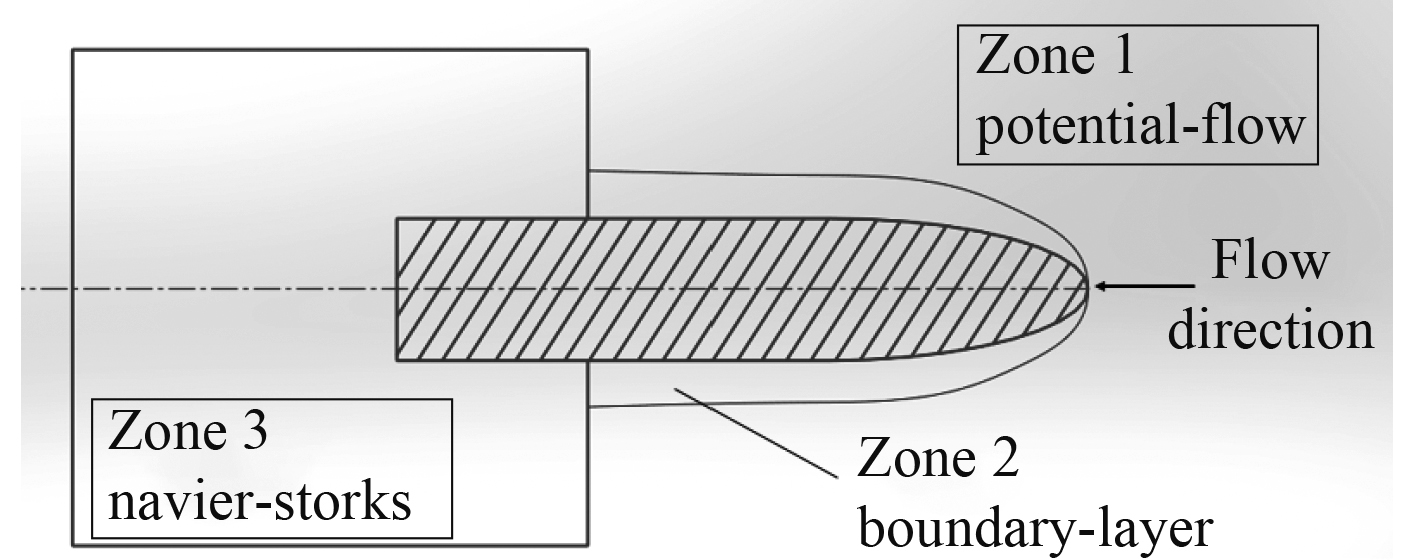
|
图 2 Shipflow计算区域划分 Fig. 2 Computational domain in Shipflow |
Shipflow通过对不同阻力成分进行分区计算,虽然可以大大缩短计算周期,但和完全基于RANS方程求解的CFD方法相比,计算精度却下降了。表3为该多用途船的阻力性能实验结果与Shipflow计算结果和完全基于RANS方法的流体力学计算软件STAR CCM+的计算结果对比。Shipflow对于总阻力的预报结果误差在5%左右,STAR CCM+的精度则更高,误差仅有0.51%。因此,对于船型优化来说,可以采用预报时间更短的Shipflow计算船舶水动力性能,采用预报精度更高的STAR CCM+来验证优化结果的可靠性。
|
|
表 3 多用途船阻力数值计算值与试验结果对比 Tab.3 Comparison between numerical simulation and test results of resistance of multipurpose ship |
对于多用途船的尾部伴流品质的评估,本文采用的是荷兰MARIN水池提出的伴流目标函数WOF(wake object function)[7]。WOF越小说明伴流越均匀,反之则均匀性越差。WOF的计算公式如下:
| $ WOF = \frac{{{{\sum\limits_{r = \frac{4}{7}R}^R {\sqrt {\dfrac{1}{{36}}\sum\limits_{\varphi = 0^\circ }^{350^\circ } {\left[ {{W_{axial}}(r,\varphi ) - \dfrac{1}{{36}}\sum\limits_{\varphi = 0^\circ }^{350^\circ } {{W_{axial}}(r,\varphi )} } \right]} } } }^2}}}{{\sum\limits_{r = \frac{4}{7}R}^R {\dfrac{1}{{36}}\sum\limits_{\varphi = 0^\circ }^{350^\circ } {{W_{axial}}(r,\varphi )} } }}\text{,} $ | (4) |
| $ {W_{axial}}(r,\varphi ) = 1 - \frac{{{V_{axial}}}}{V}\text{。} $ | (5) |
其中:R为螺旋桨半径;φ值为0°~350°,间隔10°;
采用带精英策略的非支配排序遗传算法NSGA-II[8]在设计空间搜索满足排水量约束条件的最优船型。考虑到时间成本与计算精度,船首优化时选取的初始种群个体数为30,迭代次数设置为30;船尾优化时选取的初始种群个体数为50,迭代次数设置为50。
2 Kriging近似模型通过引入代理模型,可以解决船型优化中传统CFD计算耗时的问题。首先通过拉丁超立方采样方法[9],生成100个样本集作为输入值;然后使用Shipflow对这些样本点所对应的船型进行水动力性能计算,计算结果作为输出值;最后利用这些输入输出值构造Kriging近似模型,并验证近似模型的可信度。
图3为尾部控制点变量1(Y1)和变量2(Y2)在取值范围内的分布,可以观察到变量是随机且均匀分布在取值范围内的。
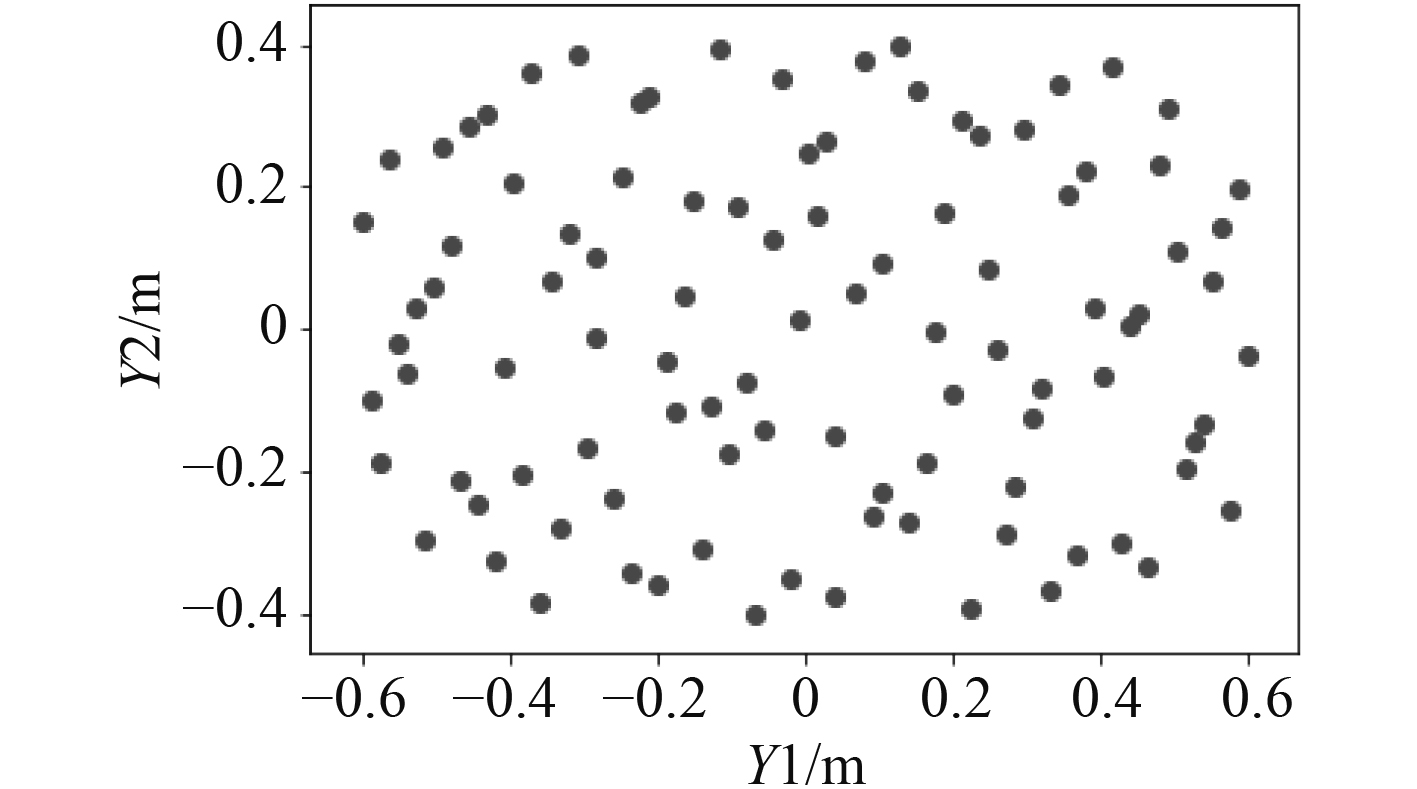
|
图 3 部分变量在二维空间投影 Fig. 3 Projection of part of variables |
Kriging[10]代理模型对于待测点的响应预测值表达如下:
| $ \hat y(x) = \hat \beta + {{{r}}^{\rm{T}}}{{{R}}^{ - 1}}({{Y}} - {{f}}\hat \beta )\text{。} $ | (6) |
其中:Y为由n个样本点所组成的n维列向量;f为常值列向量,其元素全部为1;R为n阶对称方阵,其元素为表示任意2个样本点
图4显示了船首优化时,Kriging模型响应预测值与实际CFD计算结果的对比,同时计算两者的均方根误差可以得到RMS=0.0176。可以看出,两者结果吻合良好。该代理模型可用于船型优化。
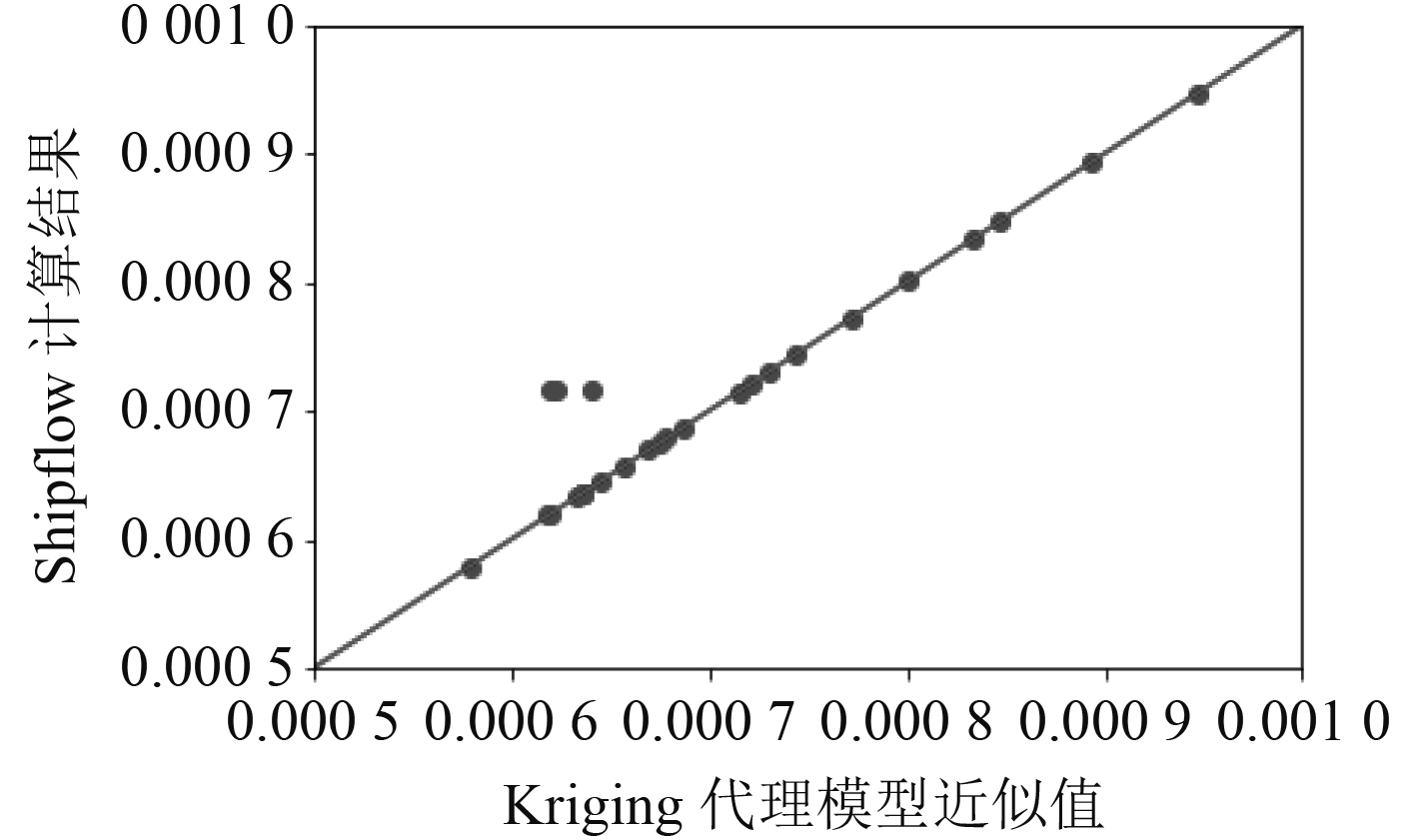
|
图 4 Kriging近似模型预测值与CFD计算值结果对比 Fig. 4 Comparison between Kriging approximation model predictive value and CFD results |
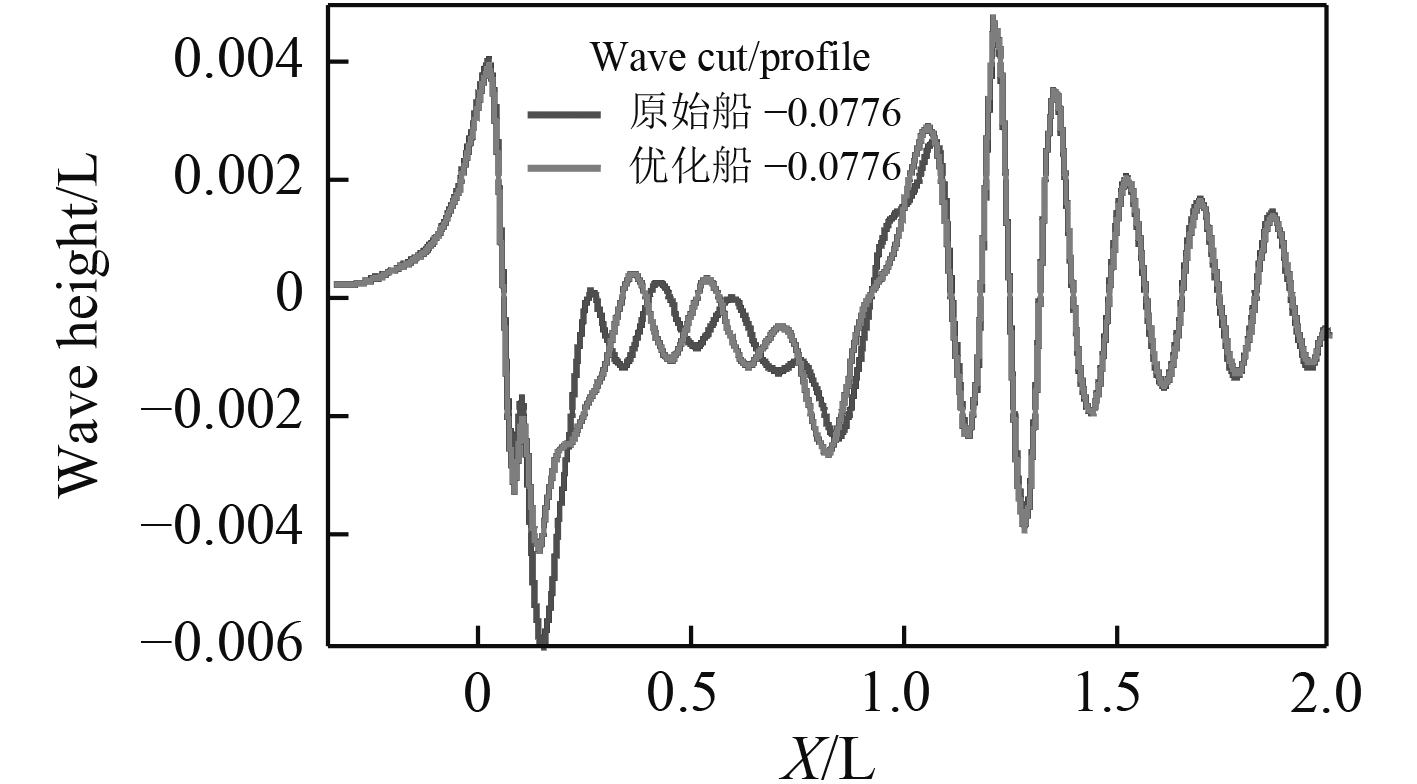
兴波阻力对船首形状变化敏感,因此将兴波阻力设为船首优化的目标函数。船首优化过程中兴波阻力优化迭代历程如图5所示。可以看出,船舶兴波阻力在迭代的过程中逐步地减小并逐步收敛至一稳定值。图6为多用途船船首优化前后船侧的波切图对比,可以观察到优化船在靠近船首的第一个波谷值的峰值有所下降,这是兴波阻力得到改善的原因。
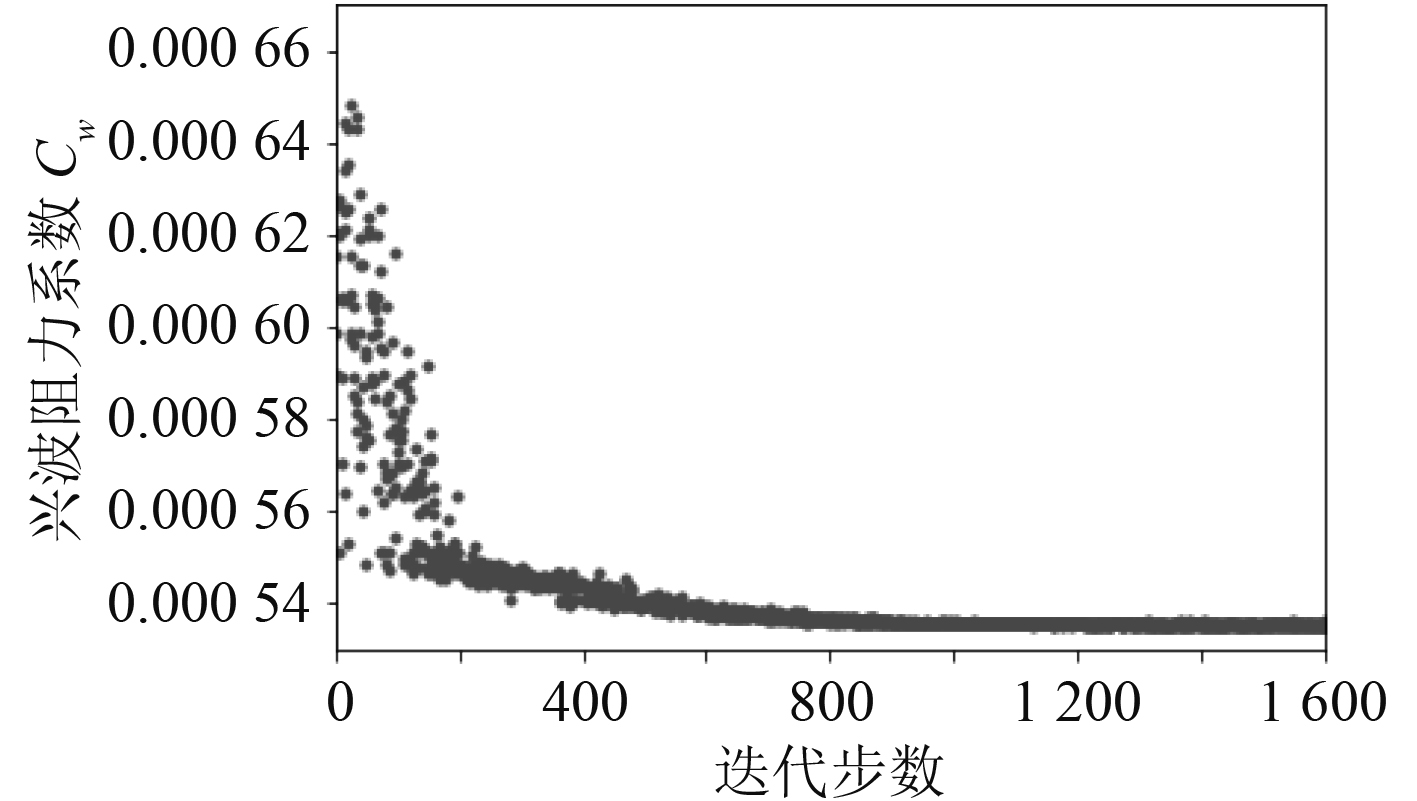
|
图 5 兴波阻力优化迭代历程 Fig. 5 Iteration process of wave resistance coefficient |
|
图 6 船首优化前后波切图对比 Fig. 6 Comparison of wave cut profile before and after bow optimization |
根据最终的Pareto解,得到4个可变控制点的变化值,从而得到了优化后的型线。通过对新的型线重新建模,并在高精度的CFD求解器STAR CCM+中进行验证,验证后的阻力成分对比见表4。结果显示,阻力优化趋势与Shipflow中的计算结果基本一致,其中剩余阻力减少2.47%,摩擦阻力减少0.37%,总阻力减少0.80%。
|
|
表 4 船首优化结果的STAR CCM+验证 Tab.4 STAR CCM + verification of bow optimization results |
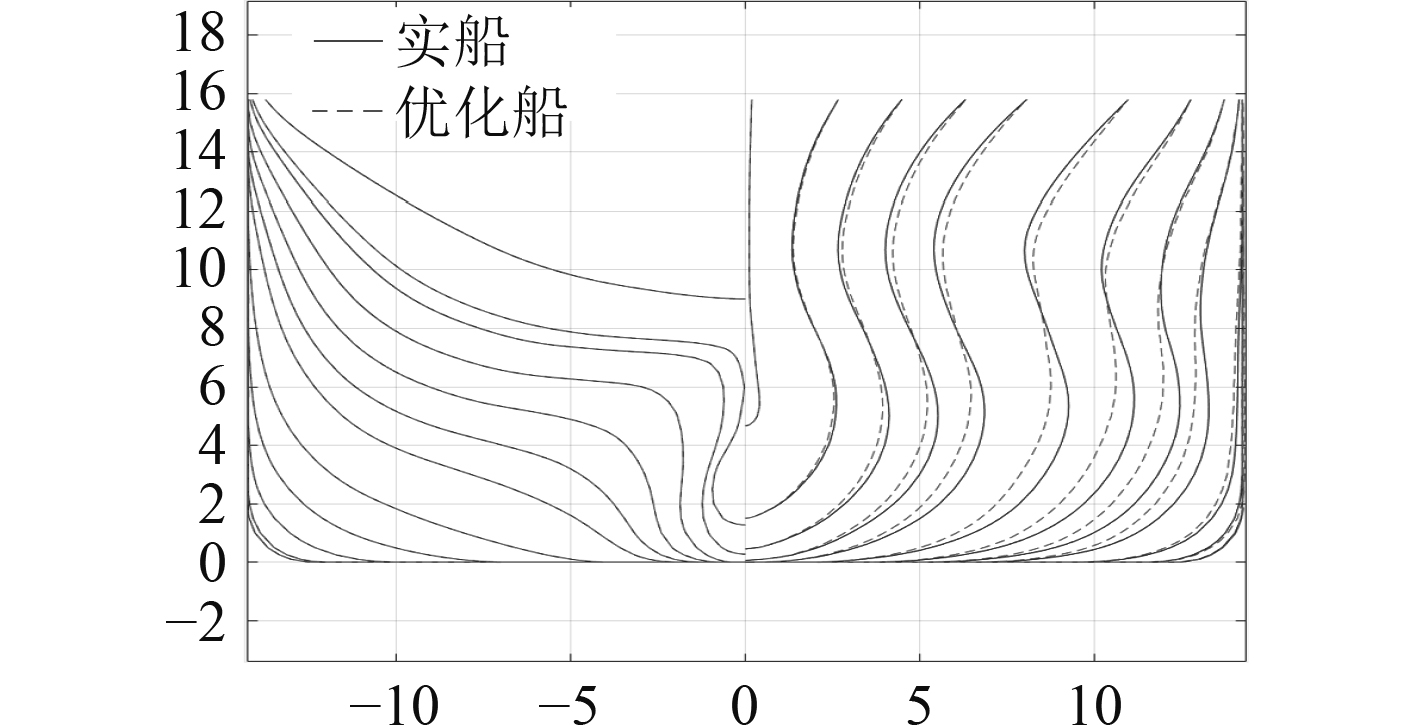
船舶型线的变化如图7所示。从型线变化的趋势来看,船首横剖线的形状由U型过渡为V型,V型船首较于U型船首湿面积小,因此可减小摩擦阻力。同时V型艏水下部分较瘦,易于使水流沿着纵剖线方向流动,从而减少舭部产生的旋涡,所以对剩余阻力性能也是有利的。
|
图 7 船首优化前后横剖线对比 Fig. 7 Cross-section lines before and after bow optimization |
因此对该多用途船来说,在保证排水量前提下,为了获得更好的阻力性能,首部横剖线形状应该更趋向于V型。
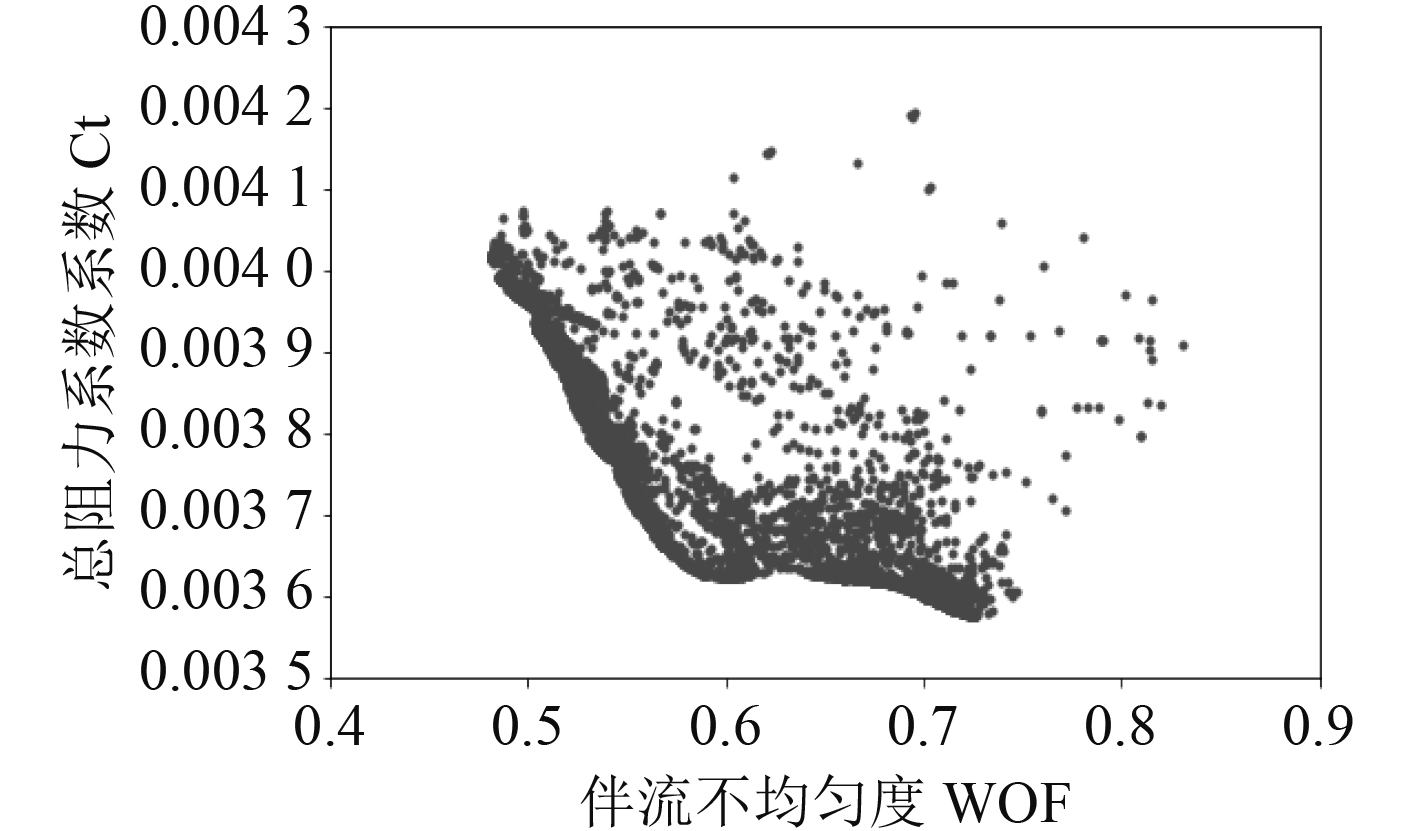
3.2 尾部型线优化结果船尾形状改变主要影响船舶粘性阻力以及尾部伴流场,因此船尾优化时以总阻力以及桨盘处伴流不均匀度作为优化目标。船尾优化过程中船舶总阻力与桨盘面伴流不均匀度迭代历程如图8所示。从优化结果上来看,船尾型线变化导致总阻力和艉部伴流场变化,且总体上呈现负相关的趋势,即船舶总阻力越小,伴流不均匀度越大。
|
图 8 船尾优化结果Pareto解集 Fig. 8 Pareto solution of Stern optimization result |
从图8 Pareto解集中挑选出2组具有代表性的解,对Kriging近似模型得到的优化结果进行验证,通过Shipflow计算结果见表5。可以观察到,当尾流场不均匀度大大减少了近29%时(opt1),船舶总阻力却增加了4.27%,这显然不是希望得到的优化船型。而方案opt2中的WOF值减小23.53%,同时总阻力也减小了2.79%。因此选择opt2中的优化船舶进行模型重建,并在STAR CCM+中进行验证。
|
|
表 5 优化方案及总阻力与伴流不均匀度变化 Tab.5 Optimization scheme and variation of total resistance and wake non-uniformity |
STAR CCM+验证后的阻力成分对比如表6所示。结果显示,船舶总阻力增加了0.89%,其中剩余阻力增加了5%左右,摩擦阻力减少了0.16%。这说明船舶阻力的改变主要是因为剩余阻力的变化引起的。
|
|
表 6 船尾优化结果的STAR CCM+验证 Tab.6 STAR CCM + verification of stern optimization results |
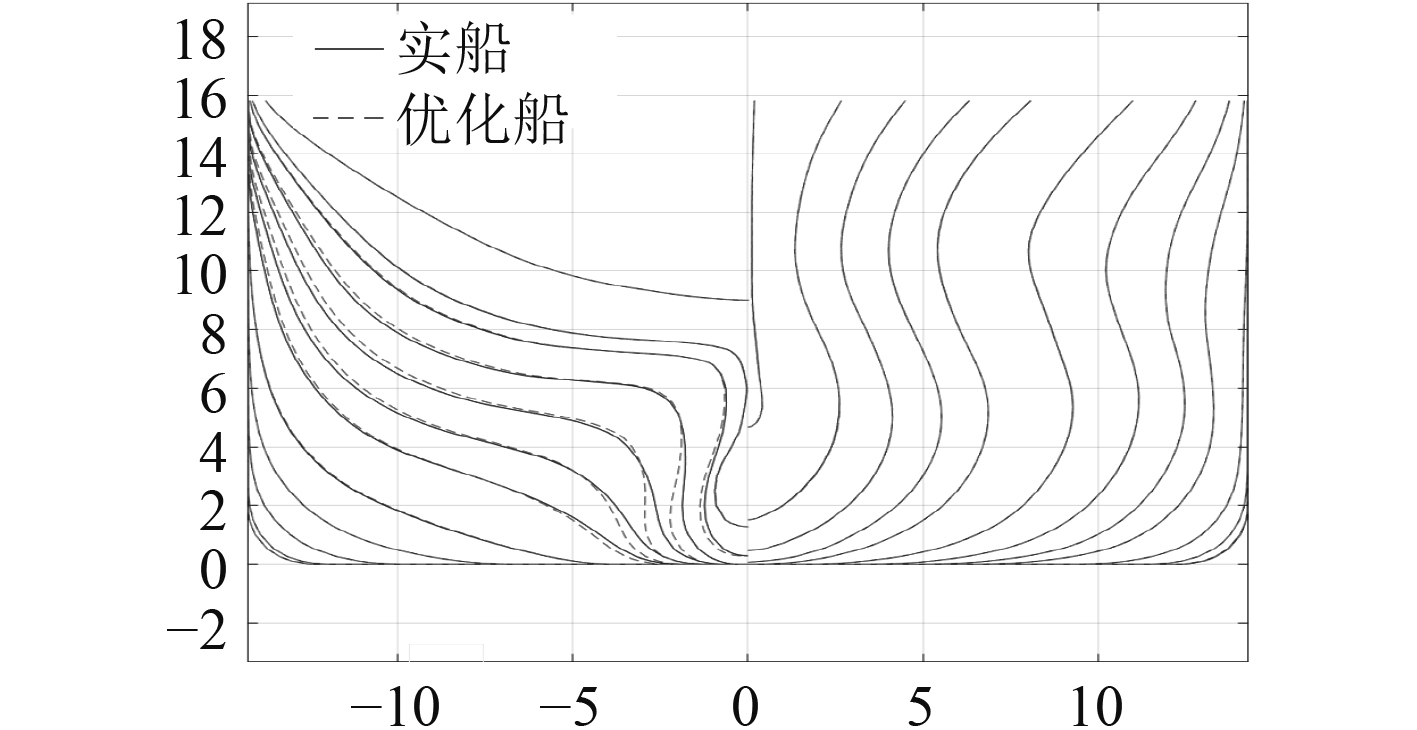
船舶型线的变化如图9所示。从优化结果来看,船尾型线在接近推进器时,形状逐渐由V型朝着U型变化。图10为尾部型线优化前后桨盘处速度云图。原始船V型尾的存在使得船底下部的流体顺着船体舭部流向螺旋桨盘面,由于边界层的影响,在螺旋桨盘面的中心垂直平面易形成高伴流区;优化船所对应的U型尾,在靠近尾轴处上方型线呈现“内凹”状,船尾舭部半径变小,因此水流在舭部更容易发生边界层分离,形成舭涡,从而削弱了桨盘面上部产生的伴流峰值,从而使得伴流场均匀性得到改善。但由于舭涡的存在会造成能量损失,因此优化船的粘压阻力较之前会有所增大。这正是优化船桨盘面处不均匀度得到改善,但总阻力有所增大的原因。
|
图 9 船尾优化前后横剖线对比 Fig. 9 Cross-section lines before and after stern optimization |
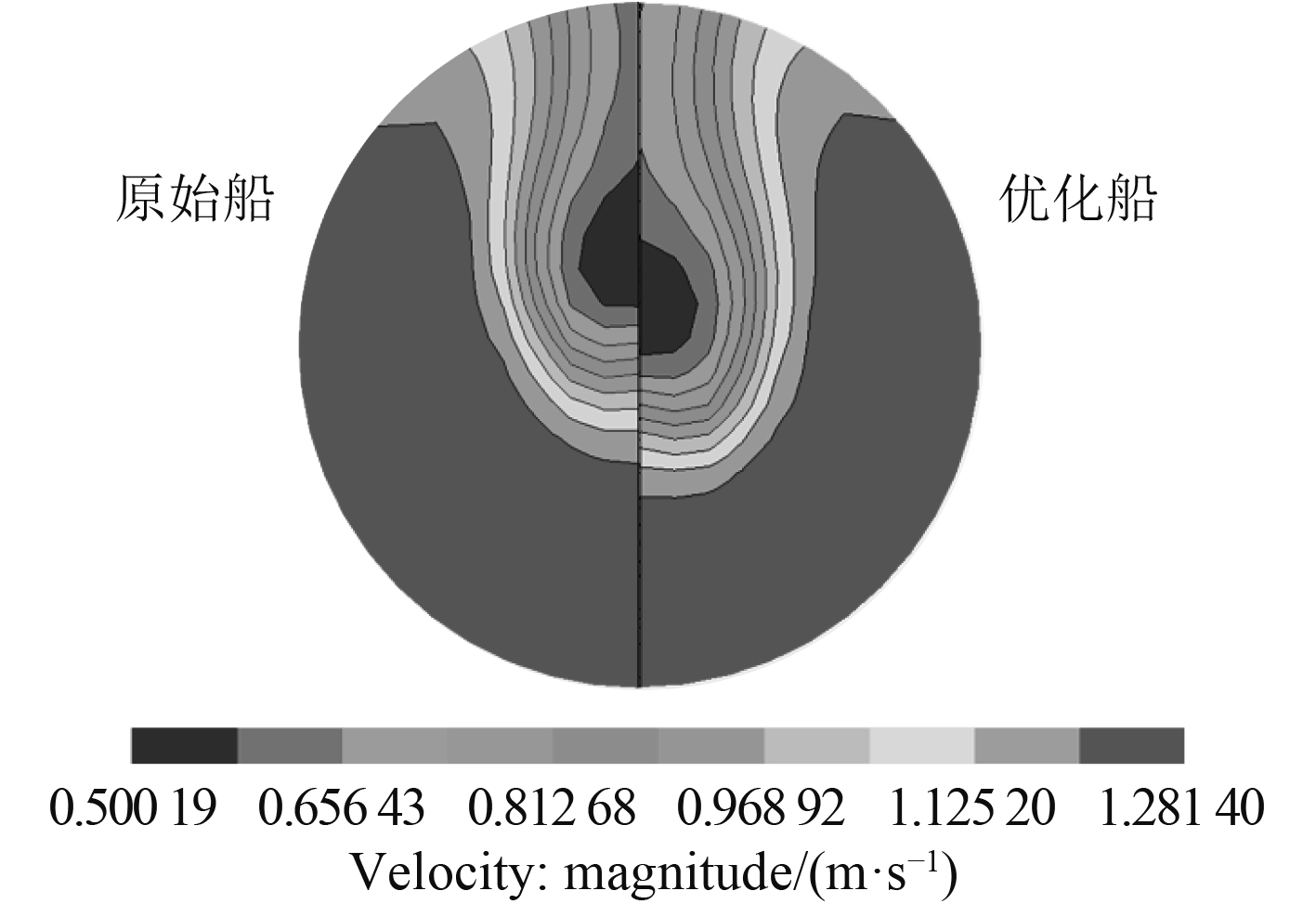
|
图 10 船尾优化前后桨盘面处速度分布对比 Fig. 10 Velocity distribution at propeller disk before and after stern optimization |
因此对该多用途船来说,为了获得更均匀伴流场,同时阻力不至于恶化太多,可以使船尾型线在接近推进器时,形状逐渐由V型朝着U型变化。
4 结 语本文将多用途船作为研究对象,采用径向基函数插值方法实现船体曲面变形,利用Kriging近似模型替代耗时的CFD计算以提高优化效率,分别对多用途船船首和船尾形状进行优化。优化结果表明:对于该多用途船船首形状,采用V型船首可以获得更好的阻力性能;对于船尾形状,由于尾部伴流场不均匀度与阻力性能呈现矛盾的关系,因此为了获得更均匀的伴流场同时阻力不至于恶化太多,可以使船尾横剖线在接近推进器时,形状逐渐由V型朝着U型变化。
| [1] |
YUSUKE T, DANIELE P, EMILIO F C, et al. Computational fluid dynamics-based multiobjective optimization of a surface combatant using a global optimization method[J]. Journal of Marine Science and Technology 13.2(2008): 95−116.
|
| [2] |
HYUNYUL KIM, CHI YANG. A new surface modification approach for CFD-based hull form Opthnization[C]//9th International Conferences Oil Hydrodynamics, October 11−15, 2010, Shanghai, China.
|
| [3] |
王刚成, 马宁, 顾解忡. 基于Kriging代理模型的船舶水动力性能多目标快速协同优化[J]. 上海交通大学学报(自然版), 2018, 52(6): 666-673. |
| [4] |
傅慧萍, 陈作钢. 以伴流均匀度为目标的艉部线型优化[J]. 上海交通大学学报, 2010, 44(10): 1429-1433. |
| [5] |
张萍. 船型参数化设计[D]. 无锡: 江南大学, 2009.
|
| [6] |
BUHMANN M D. Radial basis functions: Theory and implementations[M]. Cambridge University Press, 2004.
|
| [7] |
VAN D P A, HOEKSTRA M. Multi-objective optimization of a tanker afterbody using PARNASSOS[J]. 2009.
|
| [8] |
KALYANMOY D, AMRIT P, SAMEER A, et al.. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary. Computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017 |
| [9] |
刘晓路, 陈英武, 荆显荣, 等. 优化拉丁方试验设计方法及其应用[J]. 国防科技大学学报, 2011, 33(5): 73-77. DOI:10.3969/j.issn.1001-2486.2011.05.015 |
| [10] |
翟进乾. 克里金(kriging)插值方法在煤层分布检测中的应用研究[D]. 太原: 太原理工大学, 2008.
|
 2021, Vol. 43
2021, Vol. 43
