2. 上海海事大学 物流工程学院,上海 201306
2. College of Logistic Engineering, Shanghai Maritime University, Shanghai 201306, China
随着我国在海洋方面的深入探索,耐压圆柱壳作为各种水下设备的重要组成部分,其结构安全性研究显得尤为重要。圆柱形耐压壳主要受到外部静水压力作用,结构最典型的失效模式是屈曲,即当开始加载时,挠度随着荷载的增加而增大,当过了某一极值点,即便不增加荷载,挠度也会增大,最终导致结构破坏[1]。在生产壳板的过程中由于加工的方式,如焊接缺陷、焊接之后的残余应力、横剖面的不圆度以及除锈之类的加工导致壳面上具有小凹坑等,以上皆可统称为初始缺陷[2]。加肋骨的圆柱壳则可以在同等重量下提高自身的极限强度且降低初始缺陷的敏感度[3]。欧洲标准[4]指出,对于壳体在未知最差缺陷形状的情况下,建议采用模态缺陷分析壳体屈曲的特性。一致缺陷模态法是模态缺陷法中较为常用的,该方法认为结构缺陷分布的形式与最低阶模态吻合时,结构最容易发生屈曲[5]。随着有限元软件的快速发展,该方法得到了广泛应用。魏协宇等[6]通过对圆柱壳进行初始缺陷数值模拟与规范中的理论公式作对比,得出一致模态缺陷的结果相对于理论公式而言较为保守。万福腾[7]用弧长法、非线性稳定算法和显示动力3种数值模拟方法进行计算,再分别与3个薄壁圆柱壳实验得出的极限强度比对,发现弧长法与非线性稳定法对真实情况模拟的较为准确。受轴压的圆柱壳属于分枝型屈曲,即结构在特征值屈曲分析时可能有多组相等或者相近的屈曲特征值,导致高阶模态缺陷有可能比第一阶模态缺陷更为不利,要通过计算多阶的模态,找到结构的最低极限强度,该方法也被称为N阶特征缺陷模态法[8-10]。
本文对环向加肋圆柱壳有限元模型施加模态缺陷,采用Abaqus软件中的弧长法计算得到极限强度,并根据圆柱壳的线性模态形状,将其归为4类。将计算得到的极限强度与文献的实验数据进行比对,验证数值模拟的正确性。最后,分析了半径厚度比、缺陷幅值以及制造材料对含初始缺陷的环向加肋圆柱壳极限强度的影响。
1 模态缺陷方法 1.1 计算模型依据文献[11]中的试验模型,采用一端开口,一端封闭的圆柱壳,长度950 mm,圆柱壳的半径274.5 mm,圆柱壳厚度2.38 mm。采用外部加肋,加肋厚度为3.88 mm,底部厚度20 mm。环肋间距采用两端紧中间疏的排列方式,环肋在Z方向的坐标位置为50 mm,125 mm,225 mm,325 mm,425 mm,525 mm,625 mm,725 mm,825 mm,900 mm,950 mm。圆柱壳的弹性模量218800 MPa,泊松比0.3,屈服强度288.3 MPa;环向加肋材料弹性模量205300 MPa,泊松比0.3,屈服强度297.5 MPa。边界条件为底部完全固定;顶端自由。圆柱壳侧面与底部为均匀水压力覆盖,如图1所示。通过扫掠法生成网格,一共产生28087个节点,27900个S4R单元与186个S3R单元。

|
图 1 圆柱壳受力情况与约束条件 Fig. 1 Force condition and constraint conditions of cylindrical shell |
模态缺陷的添加分为3步实现:首先,采用线性特征值屈曲计算得到模型的前30阶模态。其次,通过潜水器规范[12]确定缺陷幅值,修改Inp文件使其作为模态的最大值嵌入到完好的模型中。最后,应用弧长法进行非线性屈曲计算,并将收敛的结果进行整理与分析。
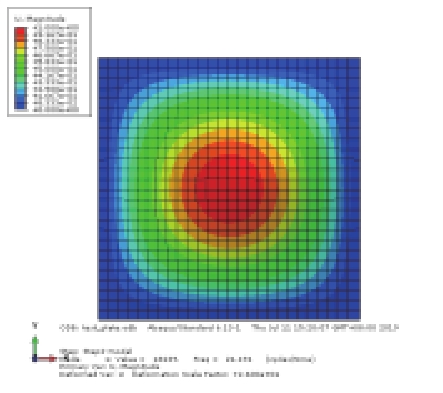
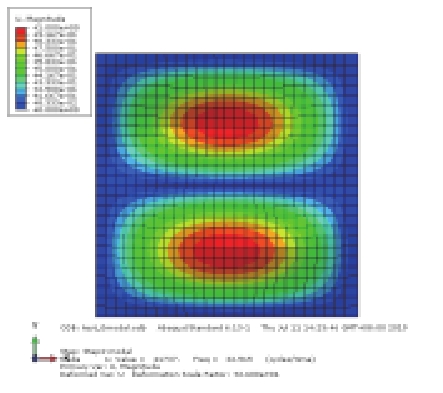
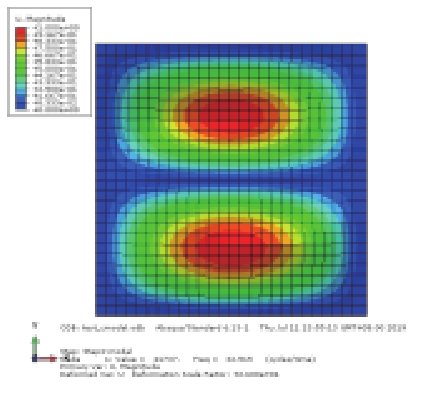
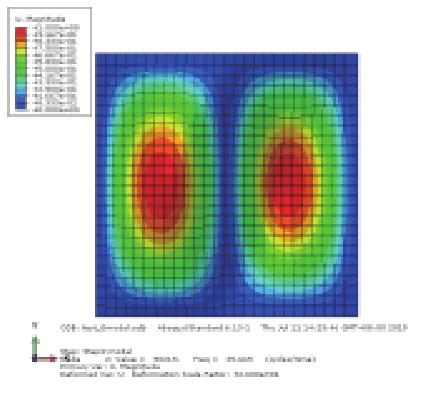
分析前30阶模态,发现圆柱壳模态形状的变化与峰值出现的次数有关,按照峰值出现次数不同将其分为4类,每一类所含阶数不连续且数量不同,如表1所示。通过比较,发现极限强度随着模态峰值出现次数的增加而增大,即发生第一类模态变化时,圆柱壳具有最小的极限强度。
|
|
表 1 前30阶模态分类与极限强度 Tab.1 Classification and ultimate strength of the first 30 modes |
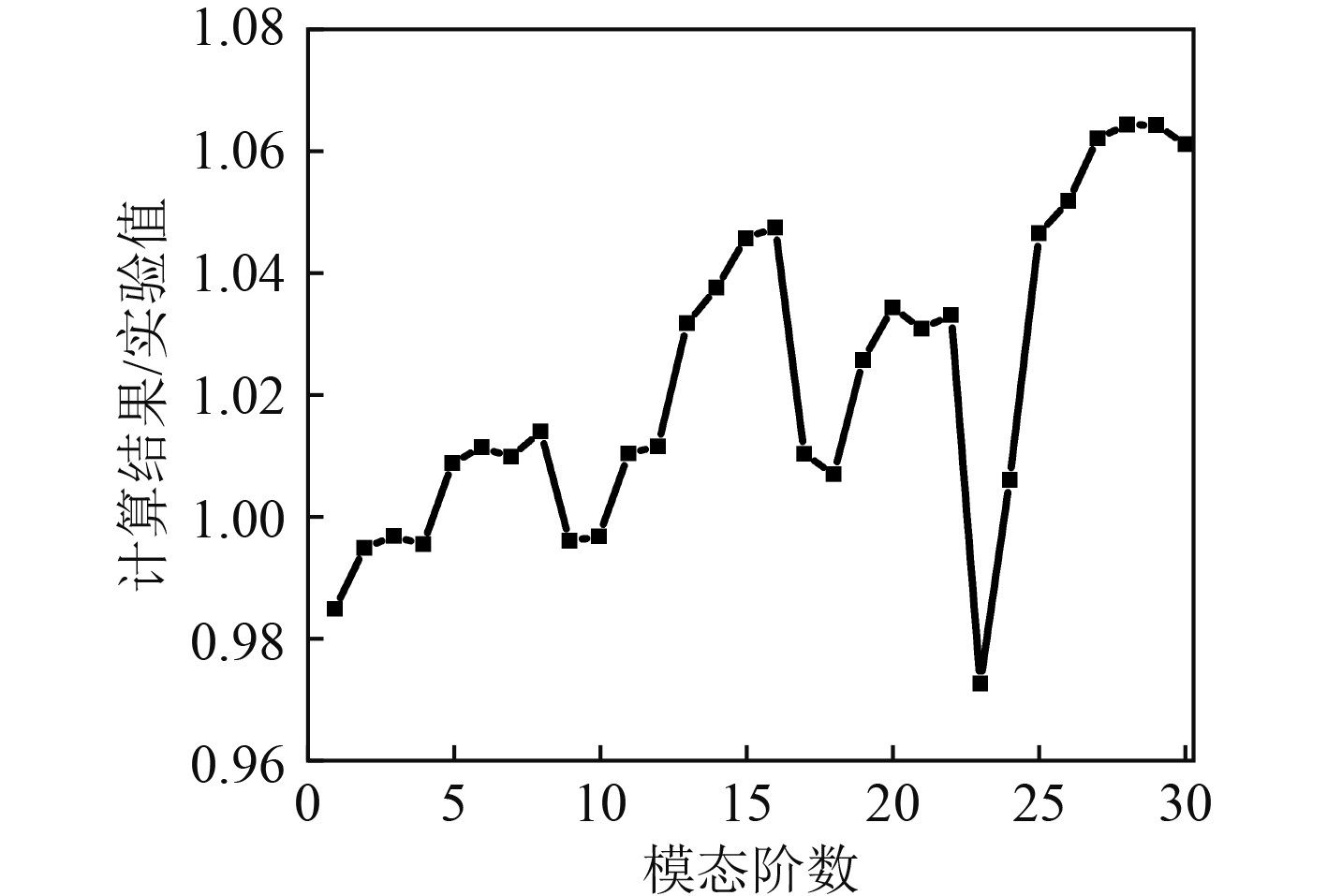
文献[11]做了环向加肋圆柱壳受均匀水压情况下的实验,通过电子测量仪器得出模型的最大不圆度为0.73。引用其实测数据,模型的极限强度Pexp=1.844 MPa。将实验数据对比前30阶模态缺陷圆柱壳的极限强度,如图2所示。第3阶模态缺陷与实验数据误差为0.4%;第23模态缺陷圆柱壳的极限强度最小,为1.79 MPa,与实验值误差为−2.7%;第27阶模态缺陷圆柱壳的极限强度最大,为1.963 MPa,与实验值误差为6.7%。从图2可以看出,计算得到的结果与实验数比值的整体趋势逐渐上升,极限强度计算值整体的趋势也是逐渐增大。
|
图 2 计算结果与实验值的比值 Fig. 2 Ratio of the result to the experimental value |
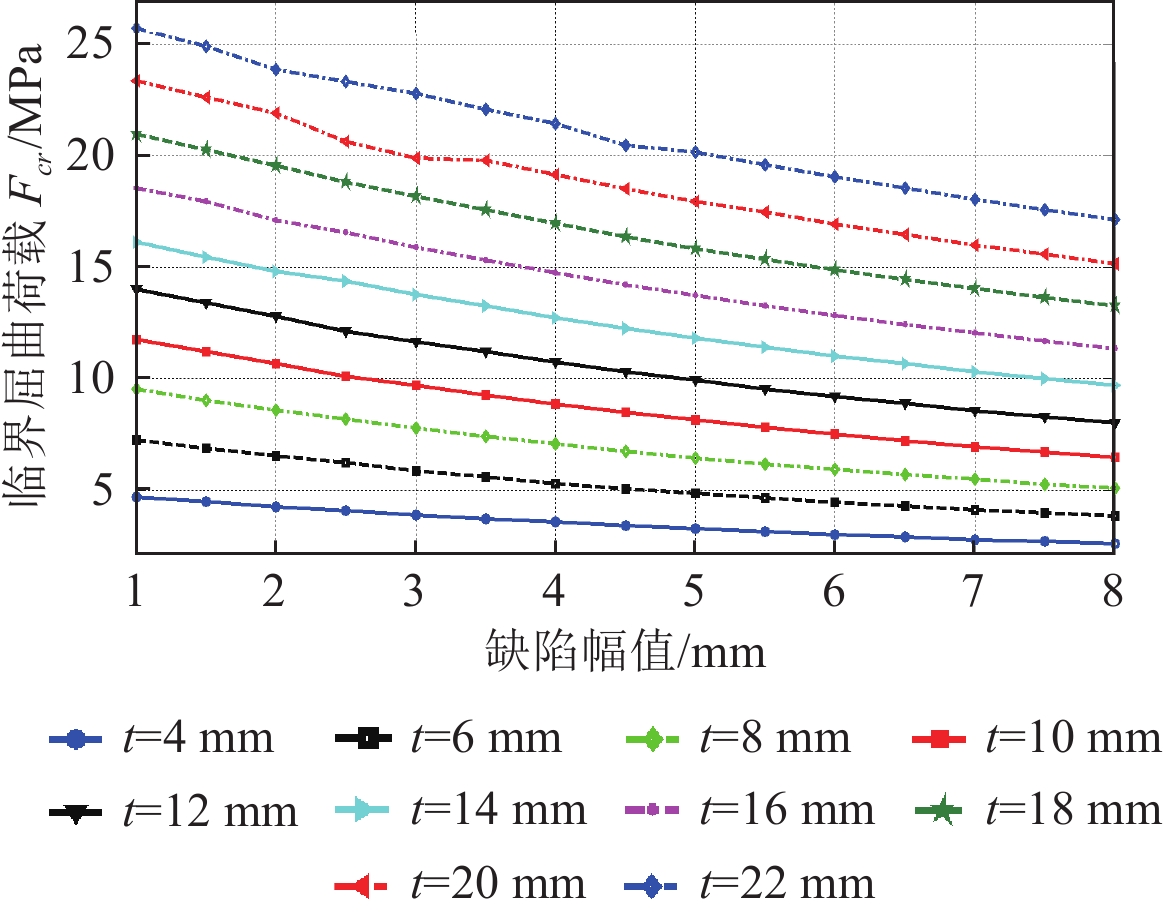
对同一厚度的圆柱壳,分别从1~8 mm等间隔0.5 mm设置了16种缺陷幅值,再分别取4~22 mm等间距为2 mm赋予了10种厚度,计算结果如图3所示。
|
图 3 缺陷幅值与临界屈曲荷载对应不同厚度的关系 Fig. 3 Relation between defect amplitude and critical buckling load corresponding to different thickness |
由图3可以看出:同一种厚度,随着缺陷幅值的增大,临界屈曲荷载逐渐减小;同一缺陷幅值,临界屈曲荷载随着厚度的增大而增大;厚度最大、缺陷幅值最小时得到的临界屈曲荷载为最大。厚度越大,临界屈曲荷载随着缺陷幅值的递减速率越快。例如图中t=25 mm的曲线,缺陷幅值从1 mm到8 mm,临界屈曲荷载下降了8.94 MPa;而t=5 mm时,缺陷幅值从1 mm到8 mm,临界屈曲荷载下降了2.28 MPa,降低了3.92倍。在制造工艺与成本允许的条件下,深潜器的厚度越大,对初始几何缺陷越不敏感。
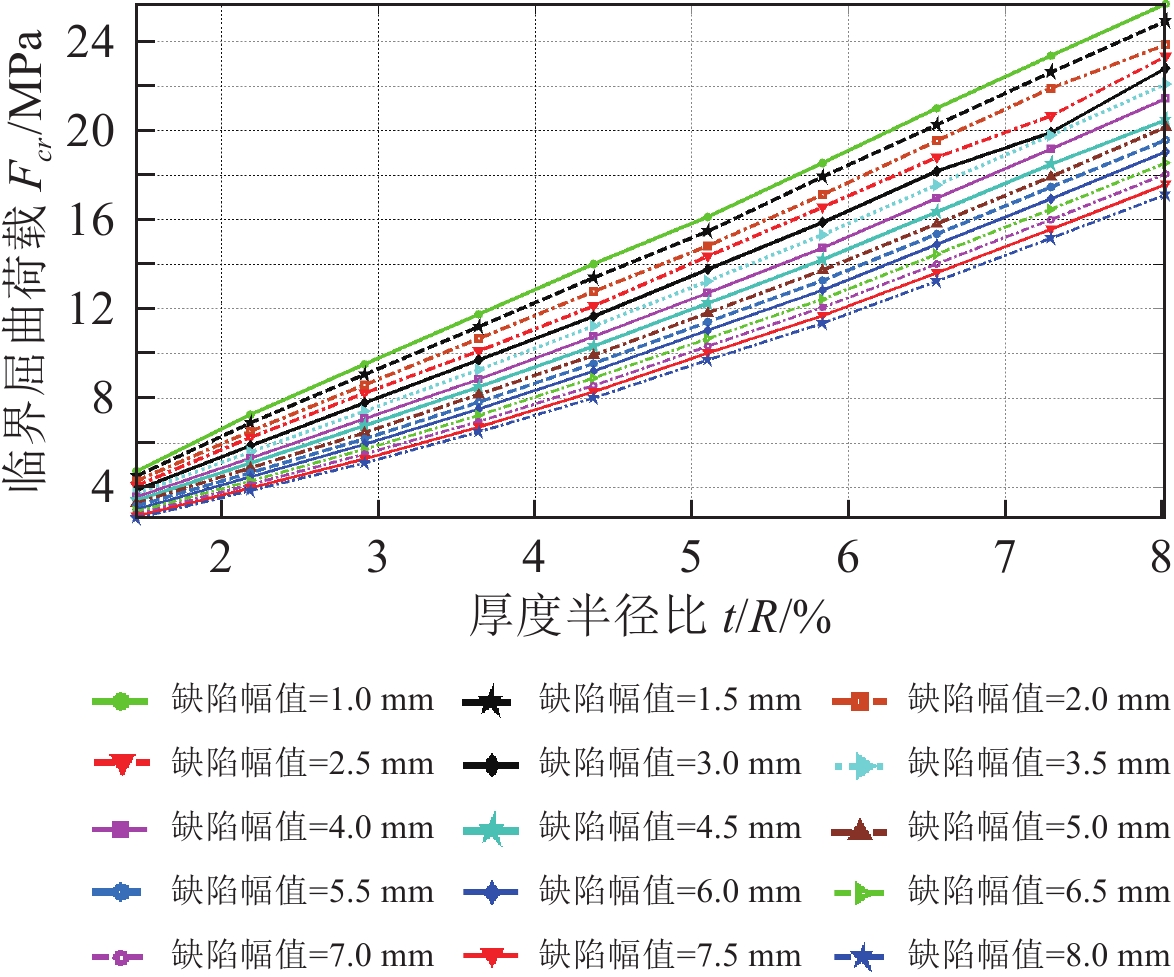
2.2 厚度半径比对临界屈曲荷载的影响圆柱壳的t/R值与临界屈曲荷载能较好地反映出不同尺寸的圆柱壳对缺陷的敏感性,对结构设计有一定的参考价值。分别对10种不同t/R的圆柱壳,施加1~8 mm共16种缺陷幅值,得到临界屈曲荷载与厚度半径比曲线,如图4所示。
|
图 4 厚度半径比与临界屈曲荷载之间的关系 Fig. 4 Relation between thickness radius ratio and critical buckling load |
对于同一缺陷幅值,随着t/R值的不断增大,除了缺陷幅值为3 mm且t/R在7~8 mm之间出现了波动,圆柱壳的临界屈曲荷载也呈线性增大。
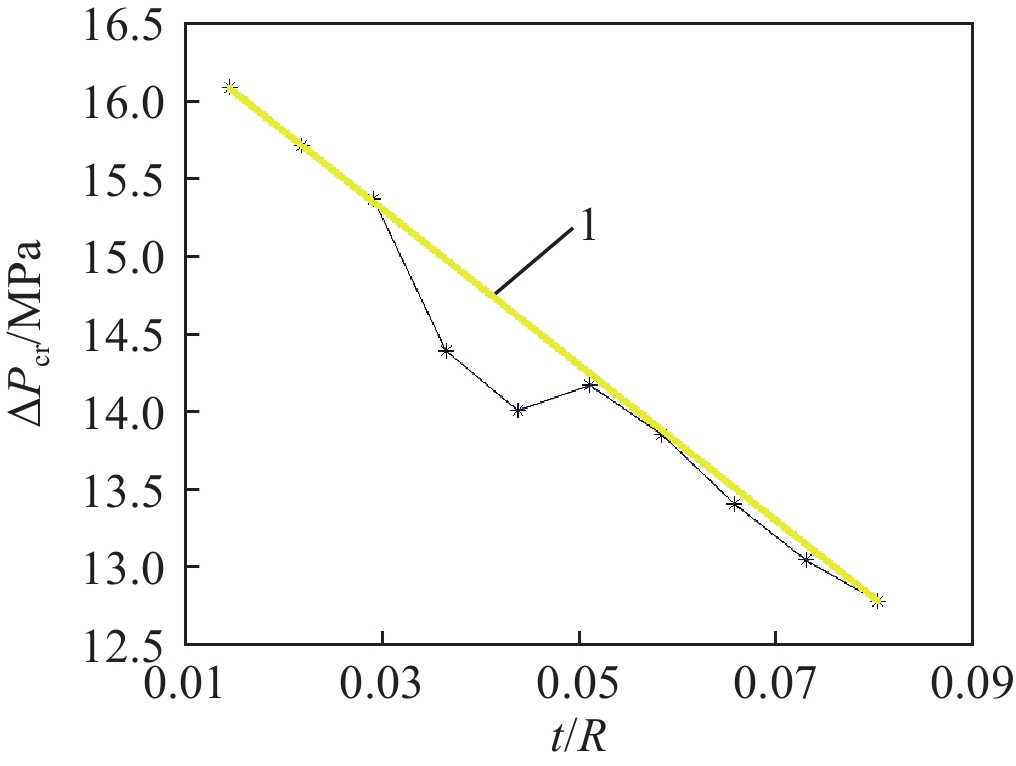
为了更好研究径厚比的影响,选取缺陷幅值δ=6 mm与δ=20 mm之间2条曲线的临界屈曲压力差值作为代表,图5为临界屈曲压力的差值ΔPcr动曲线。从图5发现:在0.01~0.043,0.051~0.08之间呈下降趋势,即同一缺陷幅值下,随着厚度的增大,临界屈曲压力的变化幅度减小;而在0.043~0.051之间,随着厚度的增加,临界屈曲压力的变化幅度增大,曲线呈上升趋势。将首尾连成一条线(线1),可以发现t/R在0.043~0.051之间的值均在线1的下方,即有着更低的极限强度差值,在该区域内对缺陷幅值的敏感性有所降低。
|
图 5 t/R值对应的临界屈曲压力差值ΔPcr Fig. 5 t/R value corresponding to the critical buckling pressure difference ΔPcr |
选取6种船舶与海洋工程材料[13-15]进行分析,运用2.1节的方法,对这6种不同材料的加肋圆柱壳极限强度分别进行计算,得到的结果如表2所示。
|
|
表 2 6种船舶海洋工程常用的材料属性及对应圆柱壳的极限强度 Tab.2 6 kinds of material properties commonly used in marine engineering and ultimate strength of corresponding cylindrical shell |
从表2可以看出,不同材料的最低极限荷载对应的模态阶数并不相同,但是由前述峰值出现次数的分类方法,这6种最低阶模态仍均归属于表1中的类别一,尽管每个不同材料的应力云图均不相同,但是所有破坏的趋势都是一样的,均呈现圆柱壳中间部分比其他地方更早达到屈服荷载,继而收缩导致圆柱壳最终被破坏。由于材料的不同所得到的极限强度并不相同,在6种材料中铝合金具有最小的屈服应力与弹性模量,计算出的极限强度值也最低。TC4材料是钛合金,具有很高的屈服应力,尽管其弹性模量不高,但是极限强度接近钢材。其余4种均为钢材,不考虑制造成本的因素可以发现,980钢是最为适合制造深潜器的材料。
3 结 语1)通过计算发现,第23阶模态缺陷的极限强度低于第1阶模态缺陷的极限强度。从模态形状上,这两者均属于表1中的类别一。计算时,可以针对该类别的模态进行计算,从而降低了数值模拟的计算量。
2)对含初始几何缺陷的耐压圆柱壳,缺陷幅值与径厚比的影响趋势均为线性,缺陷幅值越小,径厚比越大所得到的耐压圆柱壳的极限强度越大。本文取缺陷幅值δ=6 mm与δ=20 mm为例,观察ΔPcr曲线发现径厚比会在一个区域中相对应地降低缺陷幅值对极限强度的敏感性。
3)选取的6种材料属性对模态形状的影响不大,不同材料属性得到最低极限强度的模态均不相同,但均属于表1中类别一的模态形状。对于常用的金属材料,最不利的模态出现在类别一中。
| [1] |
万春华, 段世慧, 吴存利, 等. 初始几何缺陷对加筋结构后屈曲分析的影响[J]. 航空计算技, 2017, 47(1): 90-93. WAN CHUN-hua, DUAN Shi-hui, WU Cun-li, et al. Influence of initial geometrical imperfection on post-buckling analysis for stiffened structure[J]. Aeronautical Computer Technique, 2017, 47(1): 90-93. |
| [2] |
王林, 蒋理, 王仁华, 等. 初始缺陷对耐压圆柱壳塑性稳定性影响初探[J]. 江苏科技大学学报: 自然科版, 2007, 21(5): 1-3. WANG Lin, JIANG Li, WANG Ren-hua, et al. Original research on influence of initial deflection on plastic stability of ring-stiffened circular cylindrical shell[J]. Journal of Jiangsu University of Science and Technology: Natural Science Edition, 2007, 21(5): 1-3. |
| [3] |
乔丕忠, 王艳丽, 陆林军. 圆柱壳稳定性问题的研究进展[J]. 力学季刊, 2018, 39(2): 223-236. QIAO Pi-zhong, WANG Yan-li, LU Lin-jun. Advances in stability study of cylindrical shells[J]. Chinese Quarterly of Mechanics, 2018, 39(2): 223-236. |
| [4] |
European Committee for Standardization. Strength and stability of shell structures: EN 1993-1-6[S]. EN Special Publication, 2007.
|
| [5] |
沈世钊, 陈昕. 网壳结构稳定性[M]. 北京: 科学出版社, 1999.
|
| [6] |
魏协宇, 陈冰冰, 郑浣琪, 等. 压力容器设计标准中外压圆筒初始几何偏差规定的讨论[J]. 压力容器, 2015, 32(3): 20-28. WEI Xie-yu, CHEN Bing-bing, ZHENG Huan-qi, et al. Discussion of regulations of initial geometric deviations on cylindrical shells under external pressure in pressure vessel design standard[J]. Pressure Vessel Technology, 2015, 32(3): 20-28. DOI:10.3969/j.issn.1001-4837.2015.03.003 |
| [7] |
万福腾, 陈志平, 焦鹏, 等. 含初始几何缺陷薄壁圆柱壳屈曲载荷的数值模拟方法研究[J]. 压力容器, 2017, 34(3): 1-9. WAN Fu-teng, CHEN Zhi-ping, JIAO Peng, et al. Research on buckling load numerical method of cylindrical shells with initial imperfection[J]. Pressure Vessel Technology, 2017, 34(3): 1-9. DOI:10.3969/j.issn.1001-4837.2017.03.001 |
| [8] |
罗珊, 王纬波. 基于模态缺陷的受压球壳屈曲特性研究[J]. 计算力学学报, 2019, 36(04): 498-504. LUO Shan, WANG Wei-bo. Research on buckling behavior of the spherical pressure hull considering initial imperfections[J]. Chinese Journal of Computational Mechanics, 2019, 36(04): 498-504. |
| [9] |
张建, 周通, 王纬波, 等. 模态缺陷条件下复合材料柱形壳屈曲特性[J]. 复合材料学报, 2017, 34(3): 588-596. ZHANG Jian, ZHOU Tong, WANG Wei-bo, et al. Buckling property of a composite cylindrical shell considering mode imperfections[J]. Acta Materiae Compositae Sinica, 2017, 34(3): 588-596. |
| [10] |
罗昱. 改进的一致缺陷模态法在单层网壳稳定分析中的应用研究[D]. 天津: 天津大学, 2007. LUO Yu. The application of the improved uniform defect mode method to the stability analysis of single reticulated shell[D]. Tianjin: Tianjin university, 2007. |
| [11] |
CHO SR, MUTTAQIE T, DO QT, et al. Experimental investigations on the failure modes of ring-stiffened cylinders under external hydrostatic pressure[J]. International Journal of Naval Architecture and Ocean Engineering, 2017. |
| [12] |
潜水系统与潜水器入级规范[S]. 北京: 中国船级社, 2019. Classification specification for diving systems and submersibles[S]. Beijing: China Classification Society, 2019. |
| [13] |
雒高龙, 张淑茳, 任慧龙. 船用钢应力-应变关系的数学表达及其在计算加筋板屈曲应力中的应用[J]. 造船技术, 2006(3): 13-18. LUO Gao-long, ZHANG Shu-jiang, REN Hui-long. Mathematical expression of ship plate stress-strain relation and its use in calculating stiffened plate buckling[J]. Journal of Marine Technology, 2006(3): 13-18. DOI:10.3969/j.issn.1000-3878.2006.03.004 |
| [14] |
刘涛, 大深度潜水器结构分析与设计研究[D]. 无锡: 中国船舶科学研究中心, 2001. LIU Tao, Structural analysis and design of large depth submersible[D]. Wuxi: China ship science research center, 2001. |
| [15] |
姜旭胤, 刘涛, 张美荣, 等. 基于材料数据的耐压壳结构极限承载力弹塑性物理修正[J]. 船舶力学, 2013, 17(11): 1278-1291. JIANG Xu-yin, LIU Tao, ZHANG Mei-rong, et al. Plastic correction of pressure hull’s limit load considering material properties[J]. Journal of Ship Mechanics, 2013, 17(11): 1278-1291. DOI:10.3969/j.issn.1007-7294.2013.11.008 |
 2021, Vol. 43
2021, Vol. 43