2. 海军装备部北京局驻天津地区第一军事代表室,天津 300122
2. The First Military Representative Office of Haizhuang Beijing Bureau in Tianjin, Tianjing 300122, China
随着现代科技技术发展与进步,现代舰船上会配置各项导航设备,尤其是对于大型舰船、潜艇无一例外配备惯性导航系统。为安全考虑会配置多种惯性导航设备用以备份和数据比对,在同一类型惯导设备上也会考虑双机备份。那么惯导的阻尼势必会是研究的重点。在对惯性导航的阻尼研究中,一般是针对单个惯性导航系统的阻尼网络。本文针对舰船上配置2套或者多套精度误差指标相似的惯导系统情况下,选择了一种新的阻尼配置方案。由于惯导的误差指标相差不多,阻尼方案就可以有多种选择。本文着重在舰船配置双惯导状态下,分别选择2种不同的回路进行独立配置,让设计更加多样性[1],双惯导阻尼技术采用多种配置,对未来的技术发展也起到优化、多样和宽泛的作用。
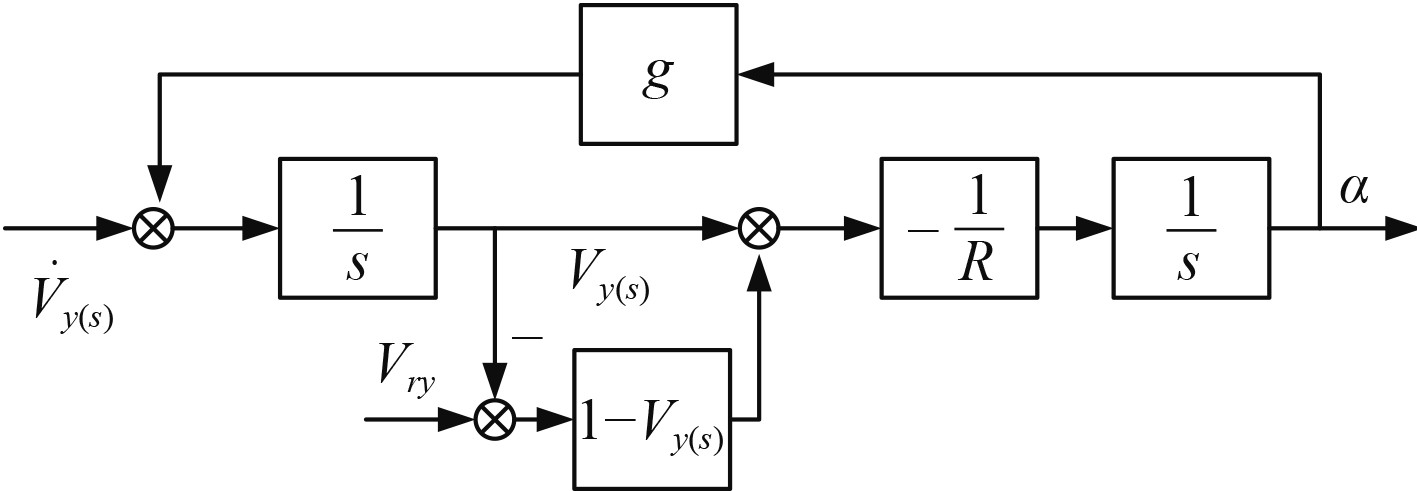
1 阻尼回路的选取在双惯导系统中,采用通道补偿的办法,利用外来速度进行阻尼。一般在惯导系统中,若使用外来速度进行补偿,那么加入进来的速度如果存在误差,会对惯导系统的精度有影响。如舰船上一般配有电磁计程仪、压差计程仪、多普勒测速仪等,其误差各有不同,而且有的是相对水流的速度,有的是相对大地的真实速度。这种惯导系统,也叫做外速度补偿阻尼惯性导航系统。单通道水平阻尼系统如图1所示,在阻尼网络中加入外速度
|
图 1 单通道北向水平外阻尼系统方块图 Fig. 1 Block diagram of single channel North horizontal external damping system |
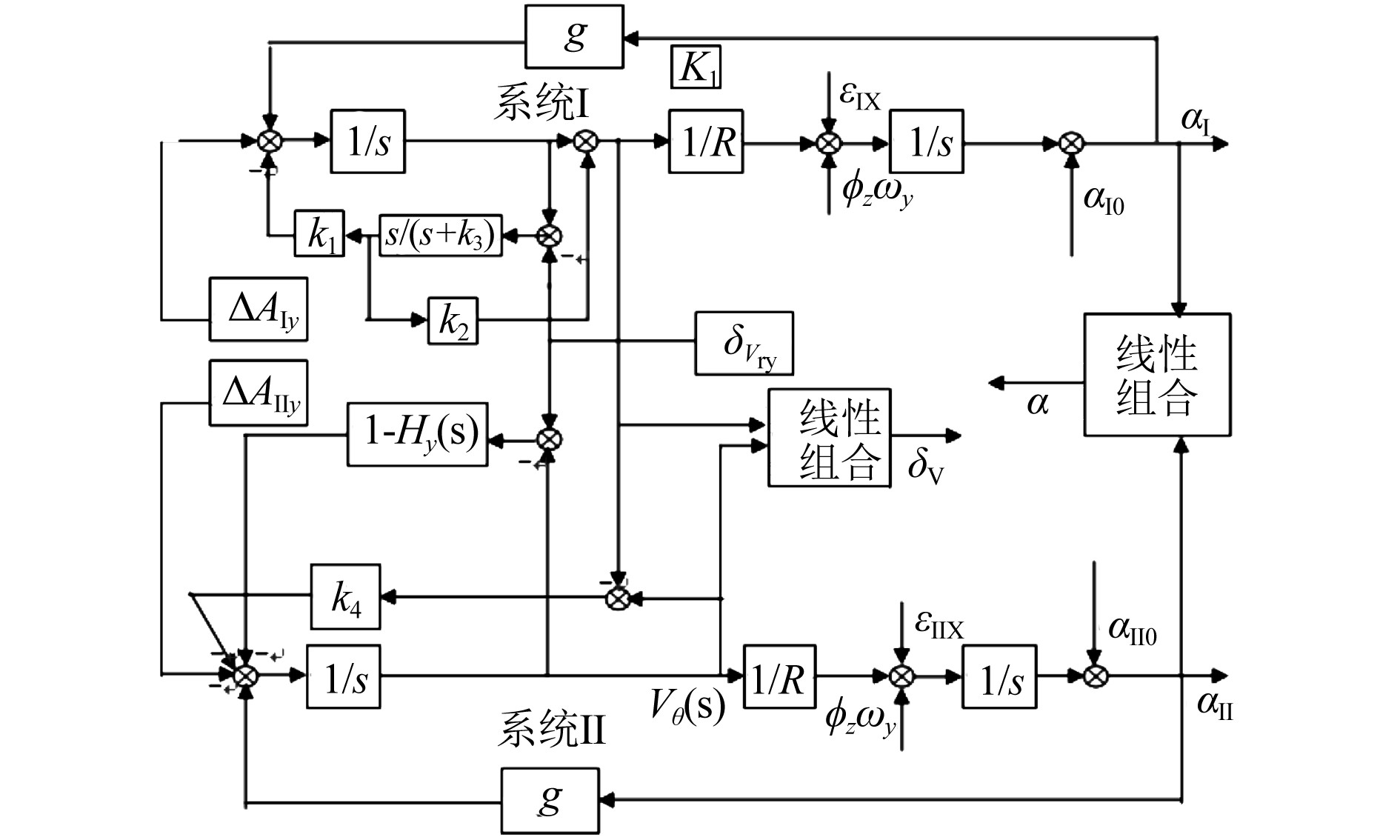
为了回避单一阻尼配置的缺陷,本文采用双惯导系统加入双水平阻尼网络实现,因为这样的阻尼配置在双惯导中有很大的灵活性,双惯导系统之间的速度、位置、加速度的差异和外来速度与惯导自身解算的速度之间的偏差形成了误差信号[3];在舒勒回路各节点上,这些误差信号可以被单独反馈上去,也可以先进行混合正、负后,再反馈上去,能够获得的组合更多一些。通过双惯导给出的数据中在进行相关的线性处理,即可以将系统指标更优化,如图2所示。
|
图 2 外来速度引入双系统数据处理图 Fig. 2 Data processing diagram of dual system with external speed introduction |
图中:
图2是两路阻尼作用于双惯导示例。
双惯导系统的系统Ⅰ的特征方程为:
| $\Delta {\rm{(s)}} = {{\rm{s}}^{\rm{3}}} + {s^2}({k_1} + {k_3}) + s(1 + {k_2})\frac{g}{R} + {k_3}\frac{g}{R}\text{。}$ | (1) |
令式(1)的根为:
| $ \begin{split}&{s}_{1}=-\sigma \text{,}\\ &{s}_{2、\rm{3}}=-\sigma \pm j{\omega }_{a}\text{,}\end{split}$ | (2) |
则得方程:
| $(s + \sigma )({s^2} + 2\sigma s + {\sigma ^2} + \omega _a^2) = 0\text{。}$ | (3) |
如果令
| $\begin{split} & \omega _c^2 = {\sigma ^2} + \omega _a^2 \text{,} \\ {\text{则}}\quad\quad\quad\quad\quad\;\;\;& \sigma = \xi {\omega _c} \text{。} \end{split} \quad\quad\quad\quad\quad\quad\;$ | (4) |
其中:
| ${\omega _a} = \sigma \sqrt {\frac{{1 - {\xi ^2}}}{{{\xi ^2}}}} \text{,}$ | (5) |
因此
| $ {s}_{2、\rm{3}}=-\sigma \pm j\sigma \sqrt{\frac{1-{\xi }^{2}}{{\xi }^{2}}}\text{,}$ | (6) |
可将式(3)整理如下:
| ${s^3} + 3\sigma {s^2} + \left(2 + \frac{1}{{{\xi ^2}}}\right){\sigma ^2}s + \frac{{{\sigma ^3}}}{{{\xi ^2}}} = 0\text{。}$ | (7) |
通过式(7)与式(1)可得到:
| $\begin{split} & {k_1} = 3\sigma \text{,}\\ & {k_2} = \left(2 + \frac{1}{{{\xi ^2}}}\right)\frac{{{\sigma ^2}}}{{\omega _s^2}} - 1 \text{,} \\ & {k_3} = \frac{{{\sigma ^3}}}{{{\xi ^2}\omega _s^2}} \text{。} \end{split} $ | (8) |
系统Ⅰ中能够求得
| $\begin{split} {\alpha _{\rm{1}}}(s) = &\frac{{{s^2}[s + {k_1} + {k_3}]}}{{\Delta (s)}}{\alpha _{{\rm I}0}}(s) - \frac{{s(1 + {k_2}) + {k_3}}}{{\Delta (s)}} \cdot \frac{{\Delta {A_{{\rm I}y}}(s)}}{R} + \\ & \frac{{s(s{k_2} - {k_1})}}{{\Delta (s)}} \cdot \frac{{\delta {V_{ry}}(s)}}{R} + \frac{{s(s + {k_1} + {k_3})}}{{\Delta (s)}}{\varepsilon _{{\rm I}x}}(s) \text{。}\\[-17pt] \end{split} $ | (9) |
将前个系统的速度与后系统速度差值代入后一系统。
假设从代入速度差差值是
| ${V_1}(s) = \{ [{\alpha _{\rm{1}}}(s) - {\alpha _{{\rm I}0}}]s + ({\phi _z}{\omega _y} - {\varepsilon _{{\rm I}x}})\} R\text{,}$ | (10) |
对于系统Ⅱ,
| $\begin{split}\left[ {\begin{array}{*{20}{c}} {{{{\rm{\dot V}}}_\theta }} \\ {{{\dot \alpha }_{\rm{2}}}} \end{array}} \right] = &\left[ {\begin{array}{*{20}{c}} {1 - {H_y}(s) - {k_4}}&g \\ {\dfrac{1}{R}}&0 \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {{{\rm{V}}_\theta }} \\ {{\alpha _2}} \end{array}} \right] + \\ &\left[ {\begin{array}{*{20}{c}} { - {V_1}(s){k_4} - \delta {V_{ry}}} \\ {{\varepsilon _x}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{{\rm{V}}_\theta }_0} \\ {{\alpha _2}} \end{array}} \right]\text{,}\end{split}$ | (11) |
式(11)可以整理为:
| $\begin{split} {\alpha _2}(s) =& \frac{{\delta V[1 \!-\! Hy(s)] \!-\! \Delta Ay \!+\! {\alpha _0}[Rs \!-\! RsHy(s) \!-\! Rs{k_4} \!-\! R{s^2}]}}{{ - RsHy(s) - R{s^2} - Rs{k_4} + Rs + g}}+\\ &\frac{{({\varepsilon _x} - {\phi _z}{\omega _y})[RHy(s) - R + R{k_4} + Rs] - {V_1}(s){k_4}}}{{ - RsHy(s) - R{s^2} - Rs{k_4} + Rs + g}} \text{。} \\[-18pt] \end{split} $ | (12) |
因为发现两系统的输出都有一定的误差存在,这里直接将其进行组合处理。处理后表达式可以改为:
| ${{{v}}_{\rm{c}}} = {{c}}{{{v}}_{\rm{1}}} + {{(1 - c)}}{{{v}}_{\rm{2}}}\text{,}$ | (13) |
设真实速度为v,系统Ⅰ的速度误差为
| $\begin{split} & {{{V}}_{\rm{1}}} = {{V}} + \delta {{{V}}_{\rm{1}}}\text{,} \\ & {{{V}}_{\rm{2}}} = {{V}} + \delta {{{V}}_{\rm{2}}}\text{,} \\ &{{{V}}_{\rm{T}}} = {{V}} + \delta {{{V}}_{\rm{T}}}\text{,} \end{split} $ | (14) |
把(14)代入式(13)得到:
| $\delta {{{V}}_{\rm{T}}} = {{C}}\delta {{{V}}_{\rm{1}}}{\rm{ + }}({{1 - C}})\delta {{{V}}_{\rm{2}}}\text{,}$ | (15) |
采取简单的取平均值方法,即取
| $\delta {{{V}}_{\rm{1}}} = = \delta {{{V}}_{\rm{2}}} = = \delta {{V}}\text{。}$ | (16) |
得到的结果是速度偏差完全相同,精度没有变化,这样的操作对实际应用来说是没有意义的。
为了使精度能够有所改善,选择线性处理,假设:
| $ \delta {{{V}}_{\rm{2}}} = {{k}}\delta {{{V}}_{\rm{1}}}\;\;(k \ne 1)\text{,} $ | (17) |
将式(17)代入式(13)即有:
| $ \delta {{{V}}_{\rm{T}}} = [{{C + }}({{1 - C}}){{k}}]\delta {{{V}}_{\rm{1}}}\text{。}$ | (18) |
如果这里选取
平台误差会在标校后变小,一般均小于等于0.66′[4]。
这里假设原始情况在系统Ⅰ。
惯性陀螺的随机漂移为:
| $ {\varepsilon _{xr}} = {\varepsilon _{yr}} = 0.002{(^ \circ }/h)\text{,}\;\;{\varepsilon _{zr}} = 0.004{(^ \circ }/h); $ |
陀螺常值漂移为:
| $ {\varepsilon _{x0}} = {\varepsilon _{y0}} = 0.003{(^ \circ }/h)\text{,}\;\;{\varepsilon _{z0}} = 0.006{(^ \circ }/h); $ |
加速度计零位误差为:
外速度随机误差为:
外速度常值误差为:
水平误差角初始值分别为:
方位误差角为:
经度、纬度初始值:
系统Ⅱ的水平误差角初始值分别为:
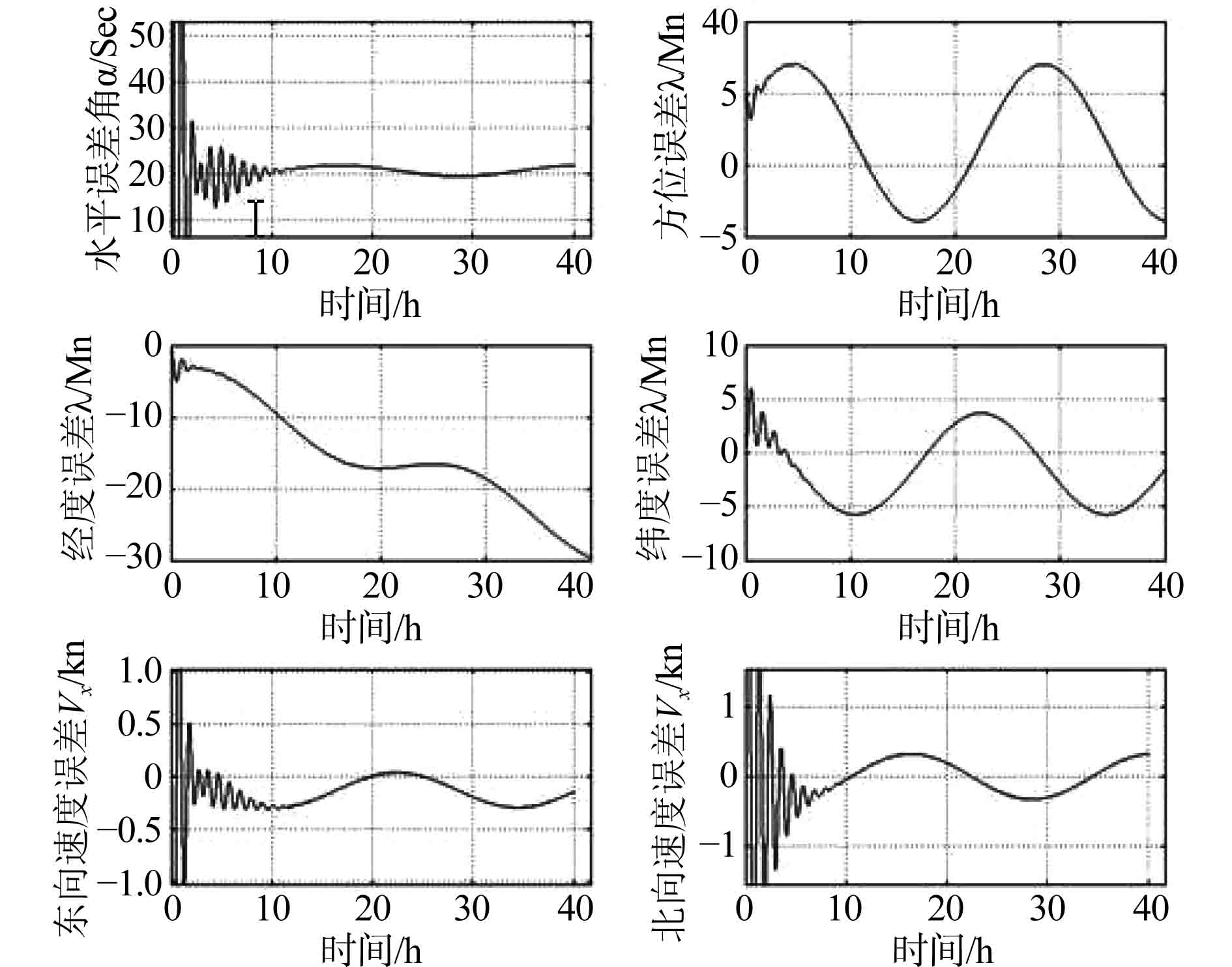
结果见图3和图4。单惯导加入外部速度时,单个惯导的阻尼网络及其参数与系统Ⅱ相同。系统Ⅰ选择了简单阻尼网络,它的等效传递函数形式[5]为:
|
图 3 外来速度代入的单系统偏差图 Fig. 3 Single system deviation caused by external speed |
|
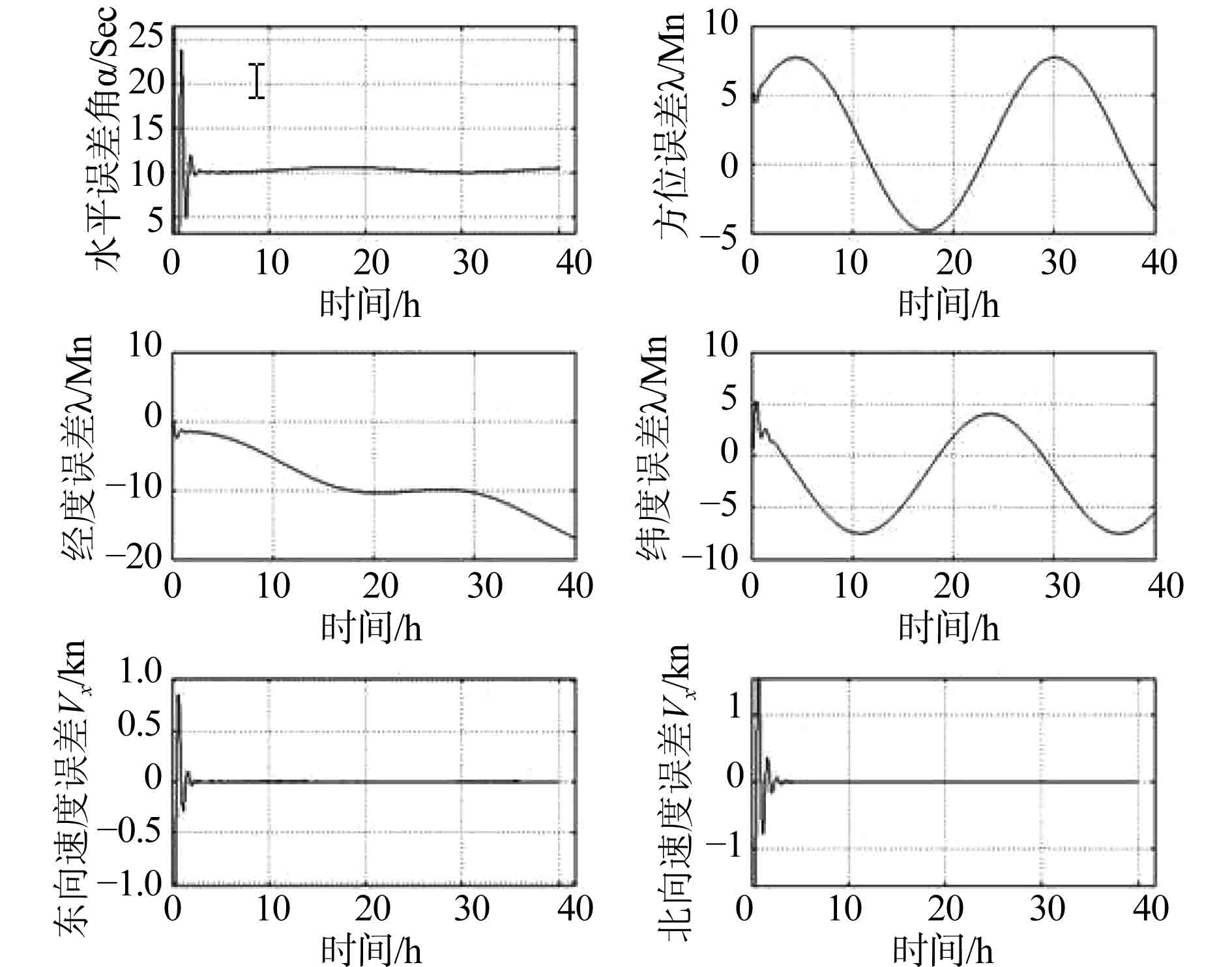
图 4 外来速度代入的双系统偏差图 Fig. 4 Dual system deviation caused by external speed |
| $ {H_{y1}}(s) = \dfrac{{{\omega _0}}}{{{\omega _1}}} \times \dfrac{{s + {\omega _3}}}{{s + {\omega _2}}}\text{,} $ |
而对于系统Ⅱ,采用渐进试验的方式,选择的等效传递函数形式:
| $ {H_{y2}}(s) = \dfrac{{(s + {\omega _4})(s + {\omega _7})}}{{(s + {\omega _5})(s + {\omega _6})}}\text{。} $ |
通过多次试验,才可以选择合适的网络形式以及阻尼参数,并且要确保其满足对应的阻尼网络原则。通过计算机模拟,择优确定网络形式和参数。
根据配置阻尼网络的区别,及各类误差源的代入,也会改变系统的响应特性;再由于2个系统的误差有差别,也进一步增加了2个系统响应的不同步。当内部扰动作用显著增加时,会产生更大的误差。所以,为了把内外部干扰的组合影响达到最小,这里就有必要改变组合系数。
模拟过程中,相关参数设置为:
针对舰船上配置双惯导系统或多套惯导情况,利用2套系统互相融合反馈的方案,并且对系统的输出进行必要的线性组合处理实现阻尼研究。通过仿真结果表明,该方案是可行的,可以缓解参考的速度精度对系统的影响,能够缩短系统的整体阻尼时间,并且对经度偏差的抑制作用非常明显。此方案对于今后舰船用双惯导或多惯导的系统输出数据的融合有积极意义,为将来舰船上配备多类型惯导,如静电惯导、激光惯导等进行多路数据融合研究提供参考。
| [1] |
Lawrence Newman. Navigation for sea based RPVS[C]//Proceedings of Bincentennial National Aerospace Symposium. 27-28 April, 1976, 48~52.
|
| [2] |
黄德鸣 程禄. 惯性导航系统[M]. 北京: 国防工业出版社. 1986.
|
| [3] |
Lawrence Newman. Dual ins velocity error reductin new damping techinques[C]//Proceedings of Bicentennial National Aerospace Symposium. 27-28 April, 1976, 153~158.
|
| [4] |
陈嘉鸿. 船载双惯导系统动态加速度计零位研究[J]. 装备指挥技术学院学报, 2004, 15(2): 59-62. |
| [5] |
孙增圻. 系统分析与控制[M]. 北京: 清华大学出版社. 1994.
|
 2021, Vol. 43
2021, Vol. 43

